SBAS590E March   2016  – June 2020 ADS131A02 , ADS131A04

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
    1.     Simplified Block Diagram
  4. 4 Revision History
  5. 5 Device Comparison Table
  6. 6 Pin Configuration and Functions
    1.     Pin Functions
  7. 7 Specifications
    1. 7.1  Absolute Maximum Ratings
    2. 7.2  ESD Ratings
    3. 7.3  Recommended Operating Conditions
    4. 7.4  Thermal Information
    5. 7.5  Electrical Characteristics
    6. 7.6  Timing Requirements: Asynchronous Interrupt Interface Mode
    7. 7.7  Switching Characteristics: Asynchronous Interrupt Interface Mode
    8. 7.8  Timing Requirements: Synchronous Master Interface Mode
    9. 7.9  Switching Characteristics: Synchronous Master Interface Mode
    10. 7.10 Timing Requirements: Synchronous Slave Interface Mode
    11. 7.11 Switching Characteristics: Synchronous Slave Interface Mode
    12. 7.12 Typical Characteristics
  8. 8 Parameter Measurement Information
    1. 8.1 Noise Measurements
  9. 9 Detailed Description
    1. 9.1 Overview
    2. 9.2 Functional Block Diagram
    3. 9.3 Feature Description
      1. 9.3.1 Clock
        1. 9.3.1.1 XTAL1/CLKIN and XTAL2
        2. 9.3.1.2 ICLK
        3. 9.3.1.3 MODCLK
        4. 9.3.1.4 Data Rate
      2. 9.3.2 Analog Input
      3. 9.3.3 Input Overrange and Underrange Detection
      4. 9.3.4 Reference
      5. 9.3.5 ΔΣ Modulator
      6. 9.3.6 Digital Decimation Filter
      7. 9.3.7 Watchdog Timer
    4. 9.4 Device Functional Modes
      1. 9.4.1 Low-Power and High-Resolution Mode
      2. 9.4.2 Power-Up
      3. 9.4.3 Standby and Wake-Up Mode
      4. 9.4.4 Conversion Mode
      5. 9.4.5 Reset (RESET)
    5. 9.5 Programming
      1. 9.5.1 Interface Protocol
        1. 9.5.1.1 Device Word Length
        2. 9.5.1.2 Fixed versus Dynamic-Frame Mode
        3. 9.5.1.3 Command Word
        4. 9.5.1.4 Status Word
        5. 9.5.1.5 Data Words
          1. 9.5.1.5.1 ADC Data Word 16-Bit Format
          2. 9.5.1.5.2 ADC Data Word 24-Bit Format
        6. 9.5.1.6 Hamming Code Error Correction
        7. 9.5.1.7 Cyclic Redundancy Check (CRC)
          1. 9.5.1.7.1 Computing the CRC
          2. 9.5.1.7.2 CRC With CRC_MODE = 1
          3. 9.5.1.7.3 CRC with CRC_MODE = 0
          4. 9.5.1.7.4 CRC Using the WREGS Command
      2. 9.5.2 SPI Interface
        1. 9.5.2.1 Asynchronous Interrupt Mode
          1. 9.5.2.1.1 Chip Select (CS)
          2. 9.5.2.1.2 Serial Clock (SCLK)
          3. 9.5.2.1.3 Data Input (DIN)
          4. 9.5.2.1.4 Data Output (DOUT)
          5. 9.5.2.1.5 Data Ready (DRDY)
          6. 9.5.2.1.6 Asynchronous Interrupt Mode Data Retrieval
        2. 9.5.2.2 Synchronous Master Mode
          1. 9.5.2.2.1 Serial Clock (SCLK)
          2. 9.5.2.2.2 Data Input (DIN)
          3. 9.5.2.2.3 Data Output (DOUT)
          4. 9.5.2.2.4 Data Ready (DRDY)
          5. 9.5.2.2.5 Chip Select (CS)
          6. 9.5.2.2.6 Synchronous Master Mode Data Retrieval
        3. 9.5.2.3 Synchronous Slave Mode
          1. 9.5.2.3.1 Chip Select (CS)
          2. 9.5.2.3.2 Serial Clock (SCLK)
          3. 9.5.2.3.3 Data Input (DIN)
          4. 9.5.2.3.4 Data Output (DOUT)
          5. 9.5.2.3.5 Data Ready (DRDY)
          6. 9.5.2.3.6 Synchronous Slave Mode Data Retrieval
        4. 9.5.2.4 ADC Frame Complete (DONE)
      3. 9.5.3 SPI Command Definitions
        1. 9.5.3.1  NULL: Null Command
        2. 9.5.3.2  RESET: Reset to POR Values
        3. 9.5.3.3  STANDBY: Enter Standby Mode
        4. 9.5.3.4  WAKEUP: Exit Standby Mode
        5. 9.5.3.5  LOCK: Lock ADC Registers
        6. 9.5.3.6  UNLOCK: Unlock ADC Registers
          1. 9.5.3.6.1 UNLOCK from POR or RESET
        7. 9.5.3.7  RREG: Read a Single Register
        8. 9.5.3.8  RREGS: Read Multiple Registers
        9. 9.5.3.9  WREG: Write Single Register
        10. 9.5.3.10 WREGS: Write Multiple Registers
    6. 9.6 Register Maps
      1. 9.6.1 User Register Description
        1. 9.6.1.1  ID_MSB: ID Control Register MSB (address = 00h) [reset = xxh]
          1. Table 16. ID_MSB Register Field Descriptions
        2. 9.6.1.2  ID_LSB: ID Control Register LSB (address = 01h) [reset = xxh]
          1. Table 17. ID_LSB Register Field Descriptions
        3. 9.6.1.3  STAT_1: Status 1 Register (address = 02h) [reset = 00h]
          1. Table 18. STAT_1 Register Field Descriptions
        4. 9.6.1.4  STAT_P: Positive Input Fault Detect Status Register (address = 03h) [reset = 00h]
          1. Table 19. STAT_P Register Field Descriptions
        5. 9.6.1.5  STAT_N: Negative Input Fault Detect Status Register (address = 04h) [reset = 00h]
          1. Table 20. STAT_N Register Field Descriptions
        6. 9.6.1.6  STAT_S: SPI Status Register (address = 05h) [reset = 00h]
          1. Table 21. STAT_S Register Field Descriptions
        7. 9.6.1.7  ERROR_CNT: Error Count Register (address = 06h) [reset = 00h]
          1. Table 22. ERROR_CNT Register Field Descriptions
        8. 9.6.1.8  STAT_M2: Hardware Mode Pin Status Register (address = 07h) [reset = xxh]
          1. Table 23. STAT_M2 Register Field Descriptions
        9. 9.6.1.9  Reserved Registers (address = 08h to 0Ah) [reset = 00h]
          1. Table 24. Reserved Registers Field Descriptions
        10. 9.6.1.10 A_SYS_CFG: Analog System Configuration Register (address = 0Bh) [reset = 60h]
          1. Table 25. A_SYS_CFG Register Field Descriptions
        11. 9.6.1.11 D_SYS_CFG: Digital System Configuration Register (address = 0Ch) [reset = 3Ch]
          1. Table 27. D_SYS_CFG Register Field Descriptions
        12. 9.6.1.12 CLK1: Clock Configuration 1 Register (address = 0Dh) [reset = 08h]
          1. Table 28. CLK1 Register Field Descriptions
        13. 9.6.1.13 CLK2: Clock Configuration 2 Register (address = 0Eh) [reset = 86h]
          1. Table 29. CLK2 Register Field Descriptions
        14. 9.6.1.14 ADC_ENA: ADC Channel Enable Register (address = 0Fh) [reset = 00h]
          1. Table 31. ADC_ENA Register Field Descriptions
        15. 9.6.1.15 Reserved Register (address = 10h) [reset = 00h]
          1. Table 32. Reserved Register Field Descriptions
      2. 9.6.2 ADCx: ADC Channel Digital Gain Configuration Registers (address = 11h to 14h) [reset = 00h]
        1. Table 33. ADCx Registers Field Descriptions
  10. 10Application and Implementation
    1. 10.1 Application Information
      1. 10.1.1 Unused Inputs and Outputs
      2. 10.1.2 Power Monitoring Specific Applications
      3. 10.1.3 Multiple Device Configuration
        1. 10.1.3.1 First Device Configured in Asynchronous Interrupt Mode
        2. 10.1.3.2 First Device Configured in Synchronous Master Mode
        3. 10.1.3.3 All Devices Configured in Synchronous Slave Mode
    2. 10.2 Typical Application
      1. 10.2.1 Design Requirements
      2. 10.2.2 Detailed Design Procedure
      3. 10.2.3 Application Curve
    3. 10.3 What To Do and What Not To Do
    4. 10.4 Initialization Set Up
  11. 11Power Supply Recommendations
    1. 11.1 Negative Charge Pump
    2. 11.2 Internal Digital LDO
    3. 11.3 Power-Supply Sequencing
    4. 11.4 Power-Supply Decoupling
  12. 12Layout
    1. 12.1 Layout Guidelines
    2. 12.2 Layout Example
  13. 13Device and Documentation Support
    1. 13.1 Documentation Support
      1. 13.1.1 Related Documentation
    2. 13.2 Related Links
    3. 13.3 Receiving Notification of Documentation Updates
    4. 13.4 Support Resources
    5. 13.5 Trademarks
    6. 13.6 Electrostatic Discharge Caution
    7. 13.7 Glossary
  14. 14Mechanical, Packaging, and Orderable Information

Package Options

Refer to the PDF data sheet for device specific package drawings

Mechanical Data (Package|Pins)
  • PBS|32
Thermal pad, mechanical data (Package|Pins)
Orderable Information

9.3.6 Digital Decimation Filter

The digital filter receives the modulator output and decimates the data stream to create the final conversion result. The digital filter on each channel consists of a third-order sinc filter. The oversampling ratio (OSR) determines the number of samples taken to create the output data word, and is set by the modulator rate divided by the data rate (fMOD / fDATA). The OSR of the sinc filters is adjusted by the OSR[3:0] bits in the CLK2 register. The OSR setting is a global setting that affects all channels and, therefore, all channels operate at the same data rate in the device. By adjusting the OSR, tradeoffs can be made between noise and data rate to optimize the signal chain: filter more for lower noise (thus creating lower data rates), filter less for higher data rates.

The sinc filter is a variable decimation rate, third-order, low-pass filter. Data are supplied to this section of the filter from the modulator at the rate of fMOD. Equation 6 shows the scaled sinc3 filter Z-domain transfer function. As shown in Table 6, the integer N is the set OSR and the integer K is a scaling factor for OSR values that are not an integer power of 2.

Equation 6. ADS131A02 ADS131A04 eq_Z_transfer_sbas590.gif

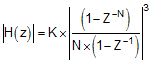
Equation 7 shows the sinc filter frequency domain transfer function. As shown in Table 6, the integer N is the set OSR and the integer K is a scaling factor for OSR values that are not an integer power of 2.

Equation 7. ADS131A02 ADS131A04 eq_Hf_transfer_sbas590.gif

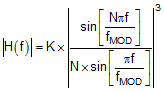
where

    Table 6. K Scaling Factor

    OSR (N) K SCALING VALUE
    800, 400, 200 0.9983778
    4096, 2048, 1024, 512, 256, 128, 64, 32 1.0
    768, 384, 192, 96, 48 1.00195313

    The sinc3 filter has notches (or zeroes) that occur at the output data rate and multiples thereof. At these frequencies, the filter has infinite attenuation. Figure 45 and Figure 46 illustrate the digital filter frequency response out to a normalized input frequency (fIN / fDATA) of 5 and 0.5, respectively. Figure 47, Figure 48, and Figure 49 illustrate the frequency response for OSR = 32, OSR = 512, and OSR = 4096 up to fMOD, respectively.

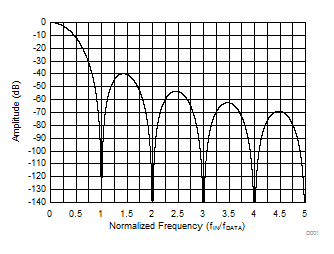    ADS131A02 ADS131A04 D001_sbas590.gifFigure 45. Sinc3 Filter Frequency Response
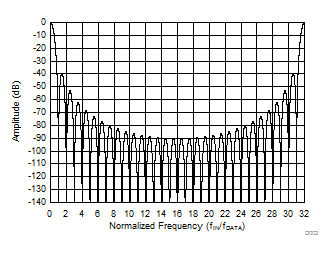    ADS131A02 ADS131A04 D003_sbas590.gifFigure 47. Sinc3 Filter Frequency Response (OSR 32)
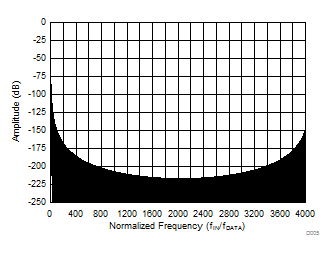    ADS131A02 ADS131A04 D005_sbas590.gifFigure 49. Sinc3 Filter Frequency Response (OSR 4096)
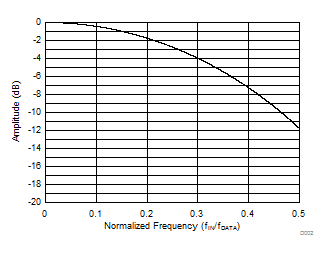    ADS131A02 ADS131A04 D002_sbas590.gifFigure 46. Sinc3 Filter Roll-Off
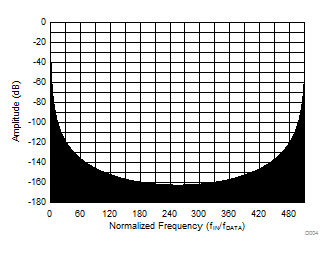    ADS131A02 ADS131A04 D004_sbas590.gifFigure 48. Sinc3 Filter Frequency Response (OSR 512)

    The K scaling factor for OSR values that are not an integer power of two adds a non-integer gain factor to the sinc3 frequency response across all frequencies. The host must account for the K scaling factor to obtain the ADC gain error given in the Electrical Characteristics table. Figure 50 overlays the digital filter frequency response for the three K scaling options in Table 6. Graph scaling is set to a narrow limit to show the small gain variation between OSR values.

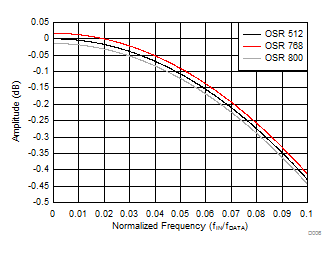    ADS131A02 ADS131A04 D006_sbas590.gifFigure 50. Non-Binary OSR Sinc3 Filter Frequency Response

    The ADS131A0x immediately begins ADC conversions when powered up and brought out of standby mode using the WAKEUP command. The DRDY falling edge indicates when each ADC conversion completes. The sinc3 digital filter requires three conversion cycles to settle (tSETTLE), assuming the analog input has settled to its final value. The output data are not gated when the digital filter settles, meaning that the first two ADC conversion results show unsettled data from the filter path before settled data are available for the third ADC conversion. The first two unsettled ADC conversions, though unsettled, can be used for diagnostic purposes to ensure the ADC is coming out of standby as expected.

    In addition to the sinc3 filter settling, the ADC requires an extra data period to report the conversion data. After the ADC accumulates the digital filter data, an additional data period is required for the ADC data to reach the DOUT buffer. Because of the digital filter settling and the DOUT buffer, the device requires four data periods to retrieve data from DOUT. Figure 51 shows the data ready behavior and time needed for the digital filter settling and data retrieval coming out of standby.

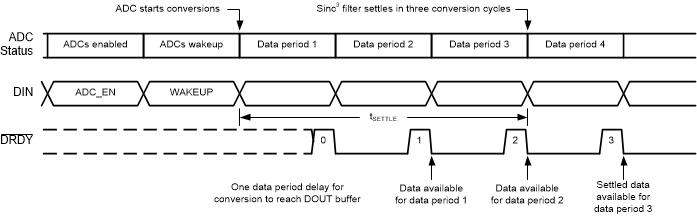    ADS131A02 ADS131A04 DigitalFilt_settle_sbas590.gifFigure 51. Sinc3 Filter Settling

    The digital filter uses a multiple stage linear-phase digital filter. Linear-phase filters exhibit constant delay time across all input frequencies (also known as constant group delay). This behavior results in zero-phase error when measuring multi-tone signals. For more information about group delay in delta-sigma ADCs, see the Accounting for delay from multiple sources in delta-sigma ADCs white paper.