DLPS178C may   2020  – july 2023 DLP4710LC

PRODUCTION DATA  

  1.   1
  2. 1 Features
  3. 2 Applications
  4. 3 Description
  5. 4 Revision History
  6. 5 Pin Configuration and Functions
  7. 6 Specifications
    1. 6.1  Absolute Maximum Ratings
    2. 6.2  Storage Conditions
    3. 6.3  ESD Ratings
    4. 6.4  Recommended Operating Conditions
    5. 6.5  Thermal Information
    6. 6.6  Electrical Characteristics
    7. 6.7  Timing Requirements
    8. 6.8  Switching Characteristics
    9. 6.9  System Mounting Interface Loads
    10. 6.10 Physical Characteristics of the Micromirror Array
    11. 6.11 Micromirror Array Optical Characteristics
    12. 6.12 Window Characteristics
    13. 6.13 Chipset Component Usage Specification
    14. 6.14 Software Requirements
  8. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1 Power Interface
      2. 7.3.2 Low-Speed Interface
      3. 7.3.3 High-Speed Interface
      4. 7.3.4 Timing
    4. 7.4 Device Functional Modes
    5. 7.5 Optical Interface and System Image Quality Considerations
      1. 7.5.1 Optical Interface and System Image Quality
        1. 7.5.1.1 Numerical Aperture and Stray Light Control
        2. 7.5.1.2 Pupil Match
        3. 7.5.1.3 Illumination Overfill
    6. 7.6 Micromirror Array Temperature Calculation
    7. 7.7 Micromirror Power Density Calculation
    8. 7.8 Micromirror Landed-On/Landed-Off Duty Cycle
      1. 7.8.1 Definition of Micromirror Landed-On and Landed-Off Duty Cycle
      2. 7.8.2 Landed Duty Cycle and Useful Life of the DMD
      3. 7.8.3 Landed Duty Cycle and Operational DMD Temperature
      4. 7.8.4 Estimating the Long-Term Average Landed Duty Cycle of a Product or Application
  9. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 Typical Application
      1.      46
      2. 8.2.1 Design Requirements
      3. 8.2.2 Detailed Design Procedure
      4. 8.2.3 Application Curve
  10. 9 Power Supply Recommendations
    1. 9.1 DMD Power Supply Power-Up Procedure
    2. 9.2 DMD Power Supply Power-Down Procedure
    3. 9.3 Power Supply Sequencing Requirements
  11. 10Layout
    1. 10.1 Layout Guidelines
    2. 10.2 Layout Example
  12. 11Device and Documentation Support
    1. 11.1 Device Support
      1. 11.1.1 Third-Party Products Disclaimer
      2. 11.1.2 Device Nomenclature
      3. 11.1.3 Device Markings
    2. 11.2 Related Links
    3. 11.3 Receiving Notification of Documentation Updates
    4. 11.4 Support Resources
    5. 11.5 Trademarks
    6. 11.6 Electrostatic Discharge Caution
    7. 11.7 Glossary
  13. 12Mechanical, Packaging, and Orderable Information

Package Options

Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information

7.8.4 Estimating the Long-Term Average Landed Duty Cycle of a Product or Application

During a given period of time, the landed duty cycle of a given pixel depends on the image content being displayed by that pixel.

In the simplest case for example, when the system displays pure-white on a given pixel for a given time period, that pixel operates very close to a 100/0 landed duty cycle during that time period. Likewise, when the system displays pure-black, the pixel operates very close to a 0/100 landed duty cycle.

Between the two extremes (ignoring for the moment color and any image processing that may be applied to an incoming image), the landed duty cycle tracks one-to-one with the gray scale value, as shown in Table 7-1.

Table 7-1 Grayscale Value and Landed Duty Cycle
Grayscale ValueNominal Landed Duty Cycle
0%0/100
10%10/90
20%20/80
30%30/70
40%40/60
50%50/50
60%60/40
70%70/30
80%80/20
90%90/10
100%100/0

To account for color rendition (and continuing to ignore image processing for this example) requires knowing both the color intensity (from 0% to 100%) for each constituent primary color (red, green, and/or blue) for the given pixel as well as the color cycle time for each primary color, where color cycle time describes the total percentage of the frame time that a given primary must be displayed in order to achieve the desired white point.

During a given period of time, the nominal landed duty cycle of a given pixel can be calculated as shown in Equation 1:

Equation 1. Landed Duty Cycle = (Red_Cycle_% × Red_Scale_Value) + (Green_Cycle_% × Green_Scale_Value) + (Blue_Cycle_% × Blue_Scale_Value)

where

  • Red_Cycle_% represents the percentage of the frame time that red displays to achieve the desired white point
  • Green_Cycle_% represents the percentage of the frame time that green displays to achieve the desired white point
  • Blue_Cycle_% represents the percentage of the frame time that blue displays to achieve the desired white point

For example, assume that the ratio of red, green and blue color cycle times are as listed in Table 7-2 (in order to achieve the desired white point) then the resulting nominal landed duty cycle for various combinations of red, green, blue color intensities are as shown in Table 7-3.

Table 7-2 Example Landed Duty Cycle for Full-Color Pixels
Red Cycle PercentageGreen Cycle PercentageBlue Cycle Percentage
50%20%30%
Table 7-3 Color Intensity Combinations
Red Scale ValueGreen Scale ValueBlue Scale ValueNominal Landed Duty Cycle
0%0%0%0/100
100%0%0%50/50
0%100%0%20/80
0%0%100%30/70
12%0%0%6/94
0%35%0%7/93
0%0%60%18/82
100%100%0%70/30
0%100%100%50/50
100%0%100%80/20
12%35%0%13/87
0%35%60%25/75
12%0%60%24/76
100%100%100%100/0

The last factor to consider when estimating the landed duty cycle is any applied image processing. In the DLPC34xx controller family, the two functions which influence the actual landed duty cycle are Gamma and IntelliBright™, and bitplane sequencing rules.

Gamma is a power function of the form Output_Level = A × Input_LevelGamma, where A is a scaling factor that is typically set to 1.

In the DLPC34xx controller family, gamma is applied to the incoming image data on a pixel-by-pixel basis. A typical gamma factor is 2.2, which transforms the incoming data as shown in Figure 7-2.

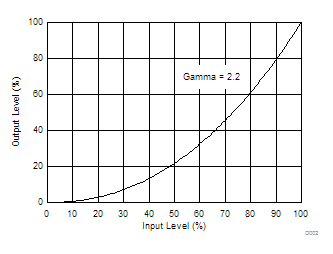GUID-90C45CB4-0F0C-4A5C-9F1A-9EBA420C11C0-low.gifFigure 7-2 Example of Gamma = 2.2

As shown in Figure 7-2, when the gray scale value of a given input pixel is 40% (before gamma is applied), then gray scale value is 13% after gamma is applied. Because gamma has a direct impact on the displayed gray scale level of a pixel, it also has a direct impact on the landed duty cycle of a pixel.

The IntelliBright algorithms content adaptive illumination control (CAIC) and local area brightness boost (LABB) also apply transform functions on the gray scale level of each pixel.

But while amount of gamma applied to every pixel (of every frame) is constant (the exponent, gamma, is constant), CAIC and LABB are both adaptive functions that can apply a different amounts of either boost or compression to every pixel of every frame.

Be sure to account for any image processing which occurs before the controller.