SBOS437K May 2008 – November 2023 INA210 , INA211 , INA212 , INA213 , INA214 , INA215
PRODUCTION DATA
- 1
- 1 Features
- 2 Applications
- 3 Description
- 4 Pin Configurations and Functions
- 5 Specifications
- 6 Detailed Description
- 7 Application and Implementation
- 8 Power Supply Recommendations
- 9 Layout
- 10Device and Documentation Support
- 11Revision History
- 12Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information
6.4.1 Input Filtering
An obvious and straightforward filtering location is at the device output. However, this location negates the advantage of the low output impedance of the internal buffer. The only other filtering option is at the device input pins. This location, though, does require consideration of the ±30% tolerance of the internal resistances. Figure 6-2 shows a filter placed at the inputs pins.
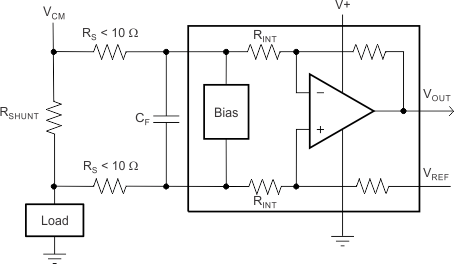 Figure 6-2 Filter at Input Pins
Figure 6-2 Filter at Input PinsThe addition of external series resistance, however, creates an additional error in the measurement so the value of these series resistors must be kept to 10 Ω (or less, if possible) to reduce impact to accuracy. The internal bias network shown in Figure 6-2 present at the input pins creates a mismatch in input bias currents when a differential voltage is applied between the input pins. If additional external series filter resistors are added to the circuit, the mismatch in bias currents results in a mismatch of voltage drops across the filter resistors. This mismatch creates a differential error voltage that subtracts from the voltage developed at the shunt resistor. This error results in a voltage at the device input pins that is different than the voltage developed across the shunt resistor. Without the additional series resistance, the mismatch in input bias currents has little effect on device operation. The amount of error these external filter resistors add to the measurement can be calculated using Equation 2 where the gain error factor is calculated using Equation 1.
The amount of variance in the differential voltage present at the device input relative to the voltage developed at the shunt resistor is based both on the external series resistance value as well as the internal input resistors, R3 and R4 (or RINT as shown in Figure 6-2). The reduction of the shunt voltage reaching the device input pins appears as a gain error when comparing the output voltage relative to the voltage across the shunt resistor. A factor can be calculated to determine the amount of gain error that is introduced by the addition of external series resistance. The equation used to calculate the expected deviation from the shunt voltage to what is measured at the device input pins is given in Equation 1:
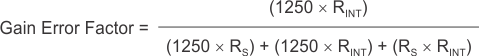
where:
- RINT is the internal input resistor (R3 and R4), and
- RS is the external series resistance.
With the adjustment factor from Equation 1, including the device internal input resistance, this factor varies with each gain version, as shown in Table 6-1. Each individual device gain error factor is shown in Table 6-2.
| PRODUCT | GAIN | RINT (kΩ) |
|---|---|---|
| INA210 | 200 | 5 |
| INA211 | 500 | 2 |
| INA212 | 1000 | 1 |
| INA213 | 50 | 20 |
| INA214 | 100 | 10 |
| INA215 | 75 | 13.3 |
| PRODUCT | SIMPLIFIED GAIN ERROR FACTOR |
|---|---|
| INA210 | 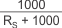 |
| INA211 | 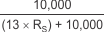 |
| INA212 | 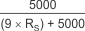 |
| INA213 | 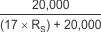 |
| INA214 | 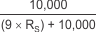 |
| INA215 | 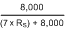 |
The gain error that can be expected from the addition of the external series resistors can then be calculated based on Equation 2:
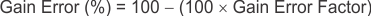
For example, using an INA212 and the corresponding gain error equation from Table 6-2, a series resistance of
10 Ω results in a gain error factor of 0.982. The corresponding gain error is then calculated using Equation 2, resulting in a gain error of approximately 1.77% solely because of the external 10-Ω series resistors. Using an INA213 with the same 10-Ω series resistor results in a gain error factor of 0.991 and a gain error of 0.84% again solely because of these external resistors.