SNOSDI7 December   2023 LDC5071-Q1

PRODUCTION DATA  

  1.   1
  2. 1 Features
  3. 2 Applications
  4. 3 Description
  5. 4 Pin Configuration and Functions
  6. 5 Specifications
    1. 5.1 Absolute Maximum Ratings
    2. 5.2 ESD Ratings
    3. 5.3 Recommended Operating Conditions
    4. 5.4 Thermal Information
    5. 5.5 Electrical Characteristics
    6. 5.6 Diagnostics
    7. 5.7 Switching Characteristics
    8. 5.8 Typical Characteristics
  7. 6 Detailed Description
    1. 6.1 Overview
    2. 6.2 Functional Block Diagram
    3. 6.3 Feature Description
      1. 6.3.1 Input Supply Voltage
      2. 6.3.2 Excitation Signal
      3. 6.3.3 Signal Processing Block
        1. 6.3.3.1 Demodulation
        2. 6.3.3.2 Fixed Gain Control
        3. 6.3.3.3 Automatic Gain Control
      4. 6.3.4 Output Stage
      5. 6.3.5 Diagnostics
        1. 6.3.5.1 Undervoltage Diagnostics
        2. 6.3.5.2 Initialization Diagnostics
        3. 6.3.5.3 Normal State Diagnostics
        4. 6.3.5.4 Fault State Diagnostics
    4. 6.4 Device Functional Modes
      1. 6.4.1 IDLE State
      2. 6.4.2 DIAGNOSTICS State
      3. 6.4.3 NORMAL State
      4. 6.4.4 FAULT State
      5. 6.4.5 DISABLED State
  8. 7 Application and Implementation
    1. 7.1 Application Information
    2. 7.2 Typical Applications
      1. 7.2.1 5-V Supply Mode
        1. 7.2.1.1 Design Requirements
        2. 7.2.1.2 Detailed Design Procedure
          1. 7.2.1.2.1 VREG and VCC
          2. 7.2.1.2.2 Output Capacitors
          3. 7.2.1.2.3 Automatic Gain Control (AGC) Mode
        3. 7.2.1.3 Application Curve
      2. 7.2.2 3.3-V Supply Mode
        1. 7.2.2.1 Design Requirements
        2. 7.2.2.2 Detailed Design Procedure
          1. 7.2.2.2.1 VREG and VCC
          2. 7.2.2.2.2 Output Capacitors
          3. 7.2.2.2.3 Fixed Gain Mode
      3. 7.2.3 Redundancy Mode
      4. 7.2.4 Single-Ended Mode
      5. 7.2.5 External Diagnostics Required for Loss of VCC or GND
    3. 7.3 Power Supply Recommendations
      1. 7.3.1 Mode 1: VCC = 5 V, VREG = 3.3 V
      2. 7.3.2 Mode 2: VCC = VREG = 3.3 V
    4. 7.4 Layout
      1. 7.4.1 Layout Guidelines
      2. 7.4.2 Layout Example
  9. 8 Device and Documentation Support
    1. 8.1 Receiving Notification of Documentation Updates
    2. 8.2 Support Resources
    3. 8.3 Trademarks
    4. 8.4 Electrostatic Discharge Caution
    5. 8.5 Glossary
  10. 9 Revision History
  11. 10Mechanical, Packaging, and Orderable Information

Package Options

Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information

6.3.3.1 Demodulation

The receive path for the sine path can be modeled by Equation 2 through Equation 5.

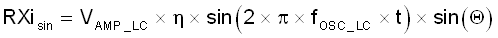
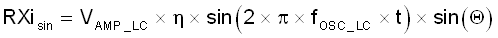
Equation 2. GUID-EC631486-D7A4-4A92-A2A6-44A65E78D4CE-low.gif

where

  • RXisin: Receiver path sine coil input
  • VAMP_LC: LC oscillator signal amplitude
  • η: Coupling factor between exciter and receive coil
  • fOSC_LC: LC oscillator excitation frequency
  • Θ: Instantaneous motor angle
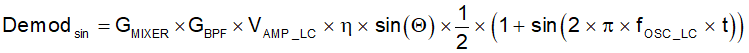
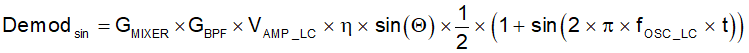
Equation 3. GUID-9F97BAF8-6DFB-49AE-9B07-F98FFC7AD088-low.gif

where

  • Demodsin: Demodulator sine path output
  • VAMP_LC: LC oscillator signal amplitude
  • η: Coupling factor between exciter and receive coil
  • fOSC_LC: LC oscillator excitation frequency
  • Θ: Instantaneous motor angle
  • GMIXER: Gain due to the mixer
  • GBPF: Gain due to the band-pass filter
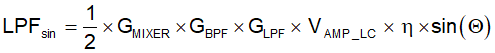
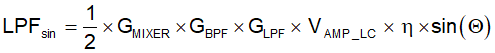
Equation 4. GUID-901767A7-8735-4F01-AE26-82220EF91231-low.gif

where

  • LPFsin: Low-pass filter sine path output
  • VAMP_LC: LC oscillator signal amplitude
  • η: Coupling factor between exciter and receive coil
  • Θ: Instantaneous motor angle
  • GMIXER: Gain due to the mixer
  • GBPF: Gain due to the band-pass filter
  • GLPF: Gain due to the low-pass filter
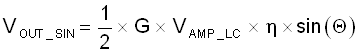
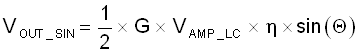
Equation 5. GUID-12825550-2781-4553-BB3B-A7862D50C60A-low.gif

where

  • Voutsin: Signal output at the end of sine path
  • VAMP_LC: LC oscillator signal amplitude
  • η: Coupling factor between exciter and receive coil
  • Θ: Instantaneous motor angle
  • G: Total combined gain of the signal path

The cosine path can be modeled in the same way as sine path.

The total gain of the system is a combination of the gain control, mixer gain, and fixed gain. Use Equation 6 to calculate the total gain:

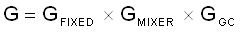
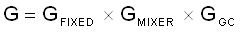
Equation 6. GUID-8DA5F544-AF07-4C75-A70B-99B058ADCB34-low.gif

where

  • GFIXED is the fixed gain in the signal path, including GLPF and GBPF
    • GFIXED = 43.2 for VCC = 5 V
    • GFIXED = 28.8 for VCC = 3.3 V
  • GMIXER is the gain due to the mixer. The typical value is 0.637.
  • GGC is the variable gain in the signal path. This is either selected by the AGC or the Fixed Gain Control depending on the voltage on the AGC_EN pin.