7.3.2.1 Concept of Power Measurements

Power measurement systems generally consists of two clearly distinguishable parts with different functions:

1. A power detector device, that generates a DC output signal (voltage) in response to the power level of the (RF) signal applied to its input.
2. An estimator that converts the measured detector output signal into a (digital) numeric value representing the power level of the signal at the detector input.

This conceptual configuration is shown in Figure 65.

Figure 65. Generic Concept of a Power Measurement System

The core of the estimator is usually implemented as a software algorithm, receiving a digitized version of the detector output voltage. Its transfer F_EST from detector output voltage to a numerical output must be equal to the inverse of the detector transfer F_DET from (RF) input power to DC output voltage. If the power measurement system is ideal, that is, if no errors are introduced into the measurement result by the detector or the estimator, the measured power P_EST(the output of the estimator) and the actual input power P_IN must be identical. In that case, the measurement error E, the difference between the two, should be identically zero:

Equation 1.

From Equation 1 it follows that one would design the F_EST transfer function to be the inverse of the F_DET transfer function.

In practice the power measurement error is not zero, due to the following effects:

• The detector transfer function is subject to various kinds of random errors that result in uncertainty in the detector output voltage; the detector transfer function is not exactly known.
• The detector transfer function might be too complicated to be implemented in a practical estimator.

The function of the estimator is then to estimate the input power P_IN, that is, to produce an output P_EST such that the power measurement error is, on average, minimized, based on the following information:

1. Measurement of the not-completely-accurate detector output voltage V_OUT
2. Knowledge about the detector transfer function F_DET, for example the shape of the transfer function, the types of errors present (part-to-part spread, temperature drift), and so forth.

Obviously the total measurement accuracy can be optimized by minimizing the uncertainty in the detector output signal (select an accurate power detector), and by incorporating as much accurate information about the detector transfer function into the estimator as possible.

The knowledge about the detector transfer function is condensed into a mathematical model for the detector transfer function, consisting of:

• A formula for the detector transfer function; and
• Values for the parameters in this formula.

The values for the parameters in the model can be obtained in various ways. They can be based on measurements of the detector transfer function in a precisely controlled environment (parameter extraction). If the parameter values are separately determined for each individual device, errors like part-to-part spread are eliminated from the measurement system.

Errors may occur when the operating conditions of the detector (for example, the temperature) become significantly different from the operating conditions during calibration (for example, room temperature). Examples of simple estimators for power measurements that result in a number of commonly used metrics for the power measurement error are discussed in LOG-Conformance Error, Temperature Drift Error, Temperature Compensation and Temperature Drift Error.

7.3.2.2 LOG-Conformance Error

Probably the simplest power measurement system that can be realized is obtained when the LOG-detector transfer function is modeled as a perfect linear-in-dB relationship between the input power and output voltage:

Equation 2.

where

• K_SLOPE represents the LOG-slope and P_INTERCEPT the LOG-intercept

The estimator based on Equation 2 implements the inverse of the model equation, that is:

Equation 3.

The resulting power measurement error, the LOG-conformance error, is thus equal to:

Equation 4.

The most important contributions to the LOG-conformance error are generally:

• The deviation of the actual detector transfer function from an ideal logarithm (the transfer function is nonlinear in dB).
• Drift of the detector transfer function over various environmental conditions, most importantly temperature; K_SLOPE and P_INTERCEPT are usually determined for room temperature only.
• Part-to-part spread of the (room temperature) transfer function.

The latter component is conveniently removed by means of calibration, that is, if the LOG slope and LOG-intercept are determined for each individual detector device (at room temperature). This can be achieved by measurement of the detector output voltage (at room temperature) for a series of different power levels in the LOG-linear range of the detector transfer function. The slope and intercept can then be determined by means of linear regression.

An example of this type of error and its relationship to the detector transfer function is shown in Figure 66.

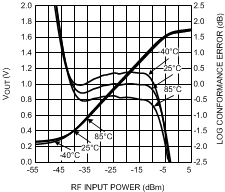Figure 66. LOG-Conformance Error and LOG-Detector Transfer Function

In the center of the dynamic range of the detector, the LOG-conformance error is small, especially at room temperature; in this region the transfer function closely follows the linear-in-dB relationship while K_SLOPE and P_INTERCEPT are determined based on room temperature measurements. At the temperature extremes the error in the center of the range is slightly larger due to the temperature drift of the detector transfer function. The error rapidly increases toward the top and bottom end of the detector's dynamic range; here the detector saturates and its transfer function starts to deviate significantly from the ideal LOG-linear model. The detector dynamic range is usually defined as the power range for which the LOG conformance error is smaller than a specified amount. Often an error of ±1 dB is used as a criterion.

7.3.2.3 Temperature Drift Error

A more accurate power measurement system can be obtained if the first error contribution, due to the deviation from the ideal LOG-linear model, is eliminated. This is achieved if the actual measured detector transfer function at room temperature is used as a model for the detector, instead of the ideal LOG-linear transfer function used in the previous section.

The formula used for such a detector is:

The transfer function of the corresponding estimator is thus the inverse of this:

Equation 6.

where

• V_OUT(T) represents the measured detector output voltage at the operating temperature T.

The resulting measurement error is only due to drift of the detector transfer function over temperature and can be expressed as in Equation 7:

Equation 7.

Unfortunately, the (numeric) inverse of the detector transfer function at different temperatures makes this expression rather impractical. However, because the drift error is usually small V_OUT(T) is only slightly different from V_OUT(T_O). This means that Equation 8 can be applied:

Equation 8.

This expression is easily simplified by taking the following considerations into account:

• The drift error at the calibration temperature E(T_O,T_O) equals zero (by definition).
• The estimator transfer F_DET(V_OUT,T_O) is not a function of temperature; the estimator output changes over temperature only due to the temperature dependence of V_OUT.
• The actual detector input power P_IN is not temperature dependent (in the context of this expression).
• The derivative of the estimator transfer function to V_OUT equals approximately 1/K_SLOPE in the LOG-linear region of the detector transfer function (the region of interest).

Taking into account the preceding considerations, the simplified expression would be:

Equation 9.

Equation 9 is very similar to Equation 4 determined previously. The only difference is that instead of the output of the ideal LOG-linear model, the actual detector output voltage at the calibration temperature is now subtracted from the detector output voltage at the operating temperature.

Figure 67 depicts an example of the drift error.

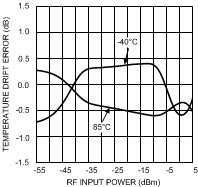Figure 67. Temperature Drift Error of the LMV221 at ƒ = 1855 MHz

In agreement with the definition, the temperature drift error is zero at the calibration temperature. Further, the main difference with the LOG-conformance error is observed at the top and bottom end of the detection range; instead of a rapid increase the drift error settles to a small value at high and low input power levels due to the fact that the detector saturation levels are relatively temperature independent.

In a practical application it may not be possible to use the exact inverse detector transfer function as the algorithm for the estimator. For example, it may require too much memory or too much factory calibration time. However, using the ideal LOG-linear model in combination with a few extra data points at the top and bottom end of the detection range — where the deviation is largest — can already significantly reduce the power measurement error.

7.3.2.3.1 Temperature Compensation

A further reduction of the power measurement error is possible if the operating temperature is measured in the application. For this purpose, the detector model used by the estimator should be extended to cover the temperature dependency of the detector.

Because the detector transfer function is generally a smooth function of temperature (the output voltage changes gradually over temperature), the temperature is in most cases adequately modeled by a first-order or second-order polynomial (see Equation 10).

Equation 10.

The required temperature dependence of the estimator, to compensate for the detector temperature dependence can be approximated similarly:

Equation 11.

The last approximation results from the fact that a first-order temperature compensation is usually sufficiently accurate. For second and higher-order compensation a similar approach can be followed.

Ideally, the temperature drift could be completely eliminated if the measurement system is calibrated at various temperatures and input power levels to determine the temperature sensitivity S₁. In a practical application, however, that is usually not possible due to the associated high costs. The alternative is to use the average temperature drift in the estimator, instead of the temperature sensitivity of each device individually. In this way it is possible to eliminate the systematic (reproducible) component of the temperature drift without the need for calibration at different temperatures during manufacturing. What remains is the random temperature drift, which differs from device to device. (see Figure 68). The graph at the left of Figure 68 schematically represents the behavior of the drift error versus temperature at a certain input power level for a large number of devices.

Figure 68. Elimination of the Systematic Component from the Temperature Drift

The mean drift error represents the reproducible (systematic) part of the error, while the mean ±3 sigma limits represent the combined systematic plus random error component. Obviously the drift error must be zero at calibration temperature T₀. If the systematic component of the drift error is included in the estimator, the total drift error becomes equal to only the random component, as shown in the graph at the right of Figure 68. A significant reduction of the temperature drift error can be achieved in this way only if:

• The systematic component is significantly larger than the random error component (otherwise the difference is negligible).
• The operating temperature is measured with sufficient accuracy.

It is essential for the effectiveness of the temperature compensation to assign the appropriate value to the temperature sensitivity S₁. Two different methods can be followed to determine this parameter:

1. Determination of a single value to be used over the entire operating temperature range.
2. Division of the operating temperature range in segments and use of separate values for each of the segments.

For the first method, the accuracy of the extracted temperature sensitivity increases when the number of measurement temperatures increases. Linear regression to temperature can then be used to determine the two parameters of the linear model for the temperature drift error: the first order temperature sensitivity S₁ and the best-fit (room temperature) value for the power estimate at T₀: F_DET[V_OUT(T),T₀]. Note that to achieve an overall (over all temperatures) minimum error, the room temperature drift error in the model can be non-zero at the calibration temperature (which is not in agreement with the strict definition).

The second method does not have this drawback but is more complex. In fact, segmentation of the temperature range is a form of higher-order temperature compensation using only a first-order model for the different segments: one for temperatures below 25°C, and one for temperatures above 25°C. The mean (or typical) temperature sensitivity is the value to be used for compensation of the systematic drift error component. Figure 69 and Figure 70 show the temperature drift error without and with temperature compensation using two segments. With compensation the systematic component is completely eliminated; the remaining random error component is centered around zero. Note that the random component is slightly larger at −40°C than at +85°C.

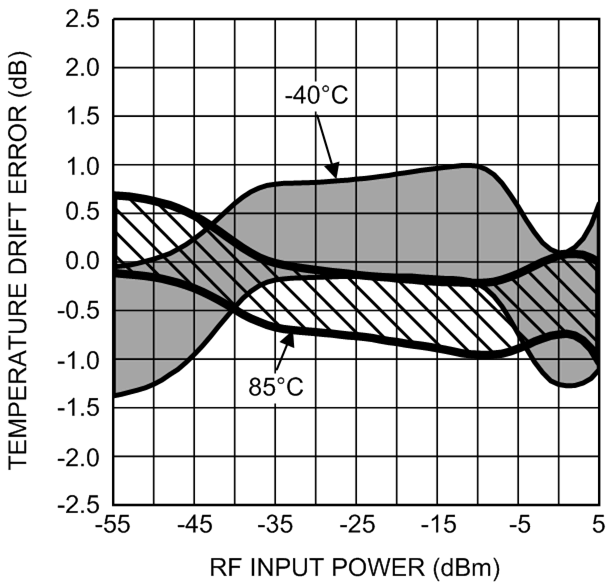Figure 69. Temperature Drift Error without Temperature Compensation

Figure 70. Temperature Drift Error With Temperature Compensation

In a practical power measurement system, temperature compensation is usually only applied to a small power range around the maximum power level for two reasons:

1. The various communication standards require the highest accuracy in this range to limit interference.
2. The temperature sensitivity itself is a function of the power level it becomes impractical to store a large number of different temperature sensitivity values for different power levels.

The 2.7-V DC and AC Electrical Characteristics specifies the temperature sensitivity for the aforementioned two segments at an input power level of −10 dBm (near the top-end of the detector dynamic range). The typical value represents the mean which is to be used for calibration.

7.3.2.3.2 Differential Power Errors

Many third-generation communication systems contain a power control loop through the base station and mobile unit that require frequent updates to the transmit-power level by a small amount (typically 1 dB). For such applications it is important that the actual change of the transmit power is sufficiently close to the requested power change.

The error metrics in this data sheet that describe the accuracy of the detector for a change in the input power are E_{1 dB} (for a 1-dB change in the input power) and E_{10 dB} (for a 10-dB step, or ten consecutive steps of 1 dB). Because it can be assumed that the temperature does not change during the power step the differential error equals the difference of the drift error at the two involved power levels:

Equation 12.

NOTE

The step error increases significantly when one (or both) power levels in the above expression are outside the detector dynamic range. For E_{10 dB} this occurs when P_IN is less than 10 dB below the maximum input power of the dynamic range, P_MAX.

7.4.1.1 Output Behavior in Shutdown

In order to save power, the LMV221 can be used in pulsed mode so that it is active to perform the power measurement only during a fraction of the time. During the remaining time the device is in low-power shutdown. Applications using this approach usually require that the output value is available at all times, including when the LMV221 is in shutdown. The settling time in active mode, however, must not become excessively large. This can be achieved by the combination of the LMV221 and a low pass output filter (see Figure 75).

In active mode, the filter capacitor C_S is charged to the output voltage of the LMV221, which in this mode has a low output impedance to enable fast settling. During shutdown mode, the capacitor should preserve this voltage. Discharge of C_S through any current path must therefore be avoided in shutdown. The output impedance of the LMV221 becomes high in shutdown, thus, the discharge current cannot flow from the capacitor top plate, through R_S and the device OUT pin to GND. This is detected by the internal shutdown mechanism of the output amplifier and by the switch depicted in Figure 79. Additionally, the ADC input impedance must be high to prevent a possible discharge path through the ADC.