Figure 6-4 shows that adding a second resistor (R_B) to the circuit and connecting the trigger input to the threshold input causes the timer to self-trigger and run as a multivibrator. The C_T capacitor charges through R_A and R_B and then only discharges through R_B. As a result, the values of R_A and R_B control the duty cycle. D_B is optional and typically used only when a duty cycle below 50% is required, as the diode bypasses R_B to allow faster charging of C_T.

This astable connection results in the C_T capacitor charging and discharging between the threshold-voltage level (≅ 0.67 × V_DD) and the trigger-voltage level (≅ 0.33 × V_DD). Driving the CONT pin externally shifts the threshold-voltage and trigger-voltage levels to V_CONT and 0.5 × V_CONT, respectively. As in the monostable circuit, charge and discharge times (and as a result, the frequency and duty cycle) are independent of the supply voltage.

Figure 6-4 Circuit for Astable Operation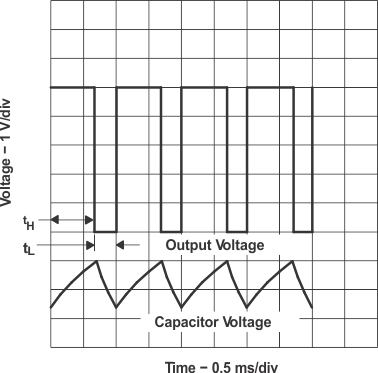

RA = 5kΩ

RB = 3kΩ

CT = 0.15µF

Figure 6-5 Typical Astable Waveforms

Figure 6-6 Trigger and Threshold Voltage Waveform

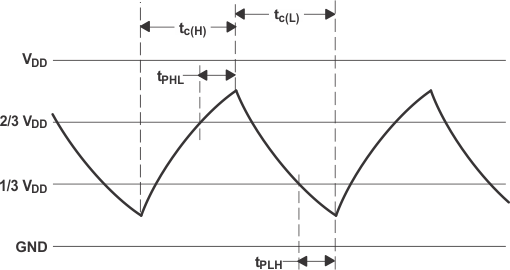
Figure 6-6 shows typical waveforms generated during astable operation. The output high-level duration (t_H) and low-level duration t_L can be calculated as follows:

Other useful relationships for period, frequency, and driver-referred and waveform-referred duty cycle are shown as follows:

These equations do not account for any propagation delay times from the TRIG and THRES inputs to DISCH output. These delay times add directly to the period and overcharge the capacitor, creating differences between calculated and actual values that increase with frequency. In addition, the discharge on-state resistance r_on during the discharge event contributes another source of timing error in the calculation when R_B is very low. The following equations provide better agreement with measured values. Equation 7 and Equation 8 represent the actual low and high times when used at higher frequencies (at 100kHz and beyond) because propagation delay and discharge on resistance is added to the formulas. The value of C_T includes both the nominal or deliberate timing capacitance, as well as parasitic capacitance on the PCB. Decoupling capacitance on CONT also affects the duty cycle, with an error contribution that depends on the capacitor leakage resistance. For additional discussion, see the Design low-duty-cycle timer circuits article.

These equations and those given earlier are similar in that a time constant is multiplied by the logarithm of a number or function. The limit values of the logarithmic terms must be between ln(2) at low frequencies, and ln(3) at extremely high frequencies. For a duty cycle close to 50%, an appropriate constant for the logarithmic terms can be substituted with good results. Output waveform duty cycles less than 50% require that t_c(H) / t_c(L) < 1 and possibly that R_A ≤ r_on. These conditions can be difficult to obtain. D_B can be used to reduce the effective R_B during the capacitor charging event, but has a nonlinear response. If using D_B, verify performance through simulation and bench evaluation before selecting final timing component values.

Figure 6-7 and Figure 6-8 show the nominal free-running frequency associated with various combinations of C_T and R_A + 2 × R_B for a 66% duty cycle (such that R_A = R_B). The values of r_on, t_{PD falling} and t_{PD rising} vary according to the device supply voltage and temperature. Tolerances of R_A, R_B, and C_T also contribute variation. The difference of simulation results calculated using the simplified and detailed equations becomes apparent by 100kHz, with approximately 2.15% error at V_DD = 15V and 2.6% error at V_DD = 5V. This error manifests as nonlinearity in the following curves. For applications where sub-1% error is required, use Equation 7 and Equation 8 for frequencies greater than 10kHz at V_DD = 5V, or greater than 30kHz at V_DD = 15V.

VDD = 5V

Figure 6-7 Simulated Astable Frequency

VDD = 15V

Figure 6-8 Simulated Astable Frequency