SLUS609J May   2004  – January 2018 TPS51116

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
    1.     Device Images
      1. 3.1 Typical Application
  4. 4 Revision History
  5. 5 Pin Configuration and Functions
    1.     Pin Functions
  6. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Dissipation Ratings
    5. 6.5 Thermal Information
    6. 6.6 Electrical Characteristics
    7. 6.7 Typical Characteristics
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1  VDDQ SMPS, Light Load Condition
      2. 7.3.2  Low-Side Driver
      3. 7.3.3  High-Side Driver
      4. 7.3.4  Current Sensing Scheme
      5. 7.3.5  PWM Frequency and Adaptive On-Time Control
      6. 7.3.6  VDDQ Output Voltage Selection
      7. 7.3.7  VTT Linear Regulator and VTTREF
      8. 7.3.8  Controling Outputs Using the S3 and S5 Pins
      9. 7.3.9  Soft-Start Function and Powergood Status
      10. 7.3.10 VDDQ and VTT Discharge Control
      11. 7.3.11 Current Protection for VDDQ
      12. 7.3.12 Current Protection for VTT
      13. 7.3.13 Overvoltage and Undervoltage Protection for VDDQ
      14. 7.3.14 Undervoltage Lockout (UVLO) Protection, V5IN (PWP), V5FILT (RGE)
      15. 7.3.15 Input Capacitor, V5IN (PWP), V5FILT (RGE)
      16. 7.3.16 Thermal Shutdown
    4. 7.4 Device Functional Modes
      1. 7.4.1 VDDQ SMPS, Dual PWM Operation Modes
      2. 7.4.2 Current Mode Operation
      3. 7.4.3 D-CAP™ Mode Operation
  8. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 DDR3 Application With Current Mode
      1. 8.2.1 Design Requirements
      2. 8.2.2 Detailed Design Procedure
        1. 8.2.2.1 Pin Connections
        2. 8.2.2.2 Choose the inductor
        3. 8.2.2.3 Choose rectifying (low-side) MOSFET
        4. 8.2.2.4 Choose output capacitance
        5. 8.2.2.5 Determine f0 and calculate RC
        6. 8.2.2.6 Calculate CC2
        7. 8.2.2.7 Calculate CC.
        8. 8.2.2.8 Determine the value of R1 and R2.
      3. 8.2.3 Application Curves
    3. 8.3 DDR3 Application With D−CAP™ Mode
      1. 8.3.1 Design Requirements
      2. 8.3.2 Detailed Design Procedure
        1. 8.3.2.1 Pin Connections
        2. 8.3.2.2 Choose the Components
      3. 8.3.3 Application Curves
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
    2. 10.2 Layout Example
  11. 11Device and Documentation Support
    1. 11.1 Receiving Notification of Documentation Updates
    2. 11.2 Community Resources
    3. 11.3 Trademarks
    4. 11.4 Electrostatic Discharge Caution
    5. 11.5 Glossary
  12. 12Mechanical, Packaging, and Orderable Information

Package Options

Refer to the PDF data sheet for device specific package drawings

Mechanical Data (Package|Pins)
  • RGE|24
  • PWP|20
Thermal pad, mechanical data (Package|Pins)
Orderable Information

7.4.2 Current Mode Operation

A buck converter using current mode operation can be partitioned into three portions, a voltage divider, an error amplifier and a switching modulator. By linearizing the switching modulator, we can derive the transfer function of the whole system. Because current mode scheme directly controls the inductor current, the modulator can be linearized as shown in Figure 36.

TPS51116 figa_lus609.gifFigure 36. Linearizing the Modulator

In this example, the inductor is located inside the local feedback loop and its inductance does not appear in the small signal model. As a result, a modulated current source including the power inductor can be modeled as a current source with its transconductance of 1/RS and the output capacitor represent the modulator portion. This simplified model is applicable in the frequency space up to approximately a half of the switching frequency. One note is, although the inductance has no influence to small signal model, it has influence to the large signal model as it limits slew rate of the current source. This means the buck converter’s load transient response, one of the large signal behaviors, can be improved by using smaller inductance without affecting the loop stability.

Equation 6 describes the total open loop transfer function of the entire system.

Equation 6. TPS51116 Q_hs_lus609.gif

Assuming RL>>ESR, RO>>RC and CC>>CC2, each transfer function of the three blocks is shown starting with Equation 7.

Equation 7. TPS51116 Q_h1s_lus609.gif
Equation 8. TPS51116 Q_h2s_lus609.gif
Equation 9. TPS51116 Q_h3s_lus609.gif

There are three poles and two zeros in H(s). Each pole and zero is given by the following five equations.

Equation 10. TPS51116 qwp1_lus609.gif
Equation 11. TPS51116 qwp2_lus609_.gif
Equation 12. TPS51116 qwp3_lus609.gif
Equation 13. TPS51116 qwz1_lus609_.gif
Equation 14. TPS51116 qwz2_lus609__.gif

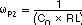
Usually, each frequency of those poles and zeros is lower than the 0 dB frequency, f0. However, the f0 should be kept under 1/3 of the switching frequency to avoid effect of switching circuit delay. Equation 15calculates the 0 dB frequency, f0.

Equation 15. TPS51116 Q_fo_lus609.gif