SLUSCJ3A April   2016  – June 2016 TPS53632G

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
  4. 4 Revision History
  5. 5 Pin Configuration and Functions
  6. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Thermal Information
    5. 6.5 Electrical Characteristics
  7. 7 Timing Requirements
  8. 8 Switching Characteristics
  9. 9 Typical Characteristics (Half-Bridge Operation)
  10. 10Detailed Description
    1. 10.1 Overview
    2. 10.2 Functional Block Diagram
    3. 10.3 Feature Description
      1. 10.3.1  Current Sensing
      2. 10.3.2  Load Transients
      3. 10.3.3  PWM and SKIP Signals
      4. 10.3.4  5-V, 3.3-V and 1.8-V Undervoltage Lockout (UVLO)
      5. 10.3.5  Output Undervoltage Protection (UVP)
      6. 10.3.6  Overcurrent Protection (OCP)
      7. 10.3.7  Overvoltage Protection
      8. 10.3.8  Analog Current Monitor, IMON and Corresponding Digital Output Current
      9. 10.3.9  Addressing
      10. 10.3.10 I2C Interface Operation
        1. 10.3.10.1 Key for Protocol Examples
        2. 10.3.10.2 Protocol Examples
      11. 10.3.11 Start-Up Sequence
      12. 10.3.12 Power Good Operation
      13. 10.3.13 Fault Behavior
    4. 10.4 Device Functional Modes
      1. 10.4.1 PWM Operation
    5. 10.5 Configuration and Programming
      1. 10.5.1 Operating Frequency
      2. 10.5.2 Overcurrent Protection (OCP) Level
      3. 10.5.3 IMON Gain
      4. 10.5.4 Slew Rate
      5. 10.5.5 Base Address
      6. 10.5.6 Ramp Selection
      7. 10.5.7 Active Phases
    6. 10.6 Register Maps
      1. 10.6.1 Voltage Select Register (VSR) (00h)
      2. 10.6.2 IMON Register (03h)
      3. 10.6.3 VMAX Register (04h)
      4. 10.6.4 Power State Register (06h)
      5. 10.6.5 SLEW Register (07h)
      6. 10.6.6 Lot Code Registers (10-13h)
      7. 10.6.7 Fault Register (14h)
  11. 11Applications and Implementation
    1. 11.1 Application Information
    2. 11.2 Typical Application
      1. 11.2.1 D-CAP+™ Half-Bridge Application
        1. 11.2.1.1 Design Requirements
        2. 11.2.1.2 Detailed Design Procedure
          1. 11.2.1.2.1 Step 1: Select Switching Frequency
          2. 11.2.1.2.2 Step 2: Set The Slew Rate
          3. 11.2.1.2.3 Step 3: Determine Inductor Value And Choose Inductor
          4. 11.2.1.2.4 Step 4: Determine Current Sensing Method
          5. 11.2.1.2.5 Step 5: DCR Current Sensing
          6. 11.2.1.2.6 Step 6: Select OCP Level
          7. 11.2.1.2.7 Step 7: Set the Load-Line Slope
          8. 11.2.1.2.8 Step 8: Current Monitor (IMON) Setting
        3. 11.2.1.3 Application Performance Plots
        4. 11.2.1.4 Loop Compensation for Zero Load-Line
  12. 12Power Supply Recommendations
  13. 13 Layout
    1. 13.1 Layout Guidelines
      1. 13.1.1 PCB Layout
      2. 13.1.2 Current Sensing Lines
      3. 13.1.3 Feedback Voltage Sensing Lines
      4. 13.1.4 PWM And SKIP Lines
        1. 13.1.4.1 Minimize High Current Loops
      5. 13.1.5 Power Chain Symmetry
      6. 13.1.6 Component Location
      7. 13.1.7 Grounding Recommendations
      8. 13.1.8 Decoupling Recommendations
      9. 13.1.9 Conductor Widths
    2. 13.2 Layout Example
  14. 14Device and Documentation Support
    1. 14.1 Trademarks
    2. 14.2 Electrostatic Discharge Caution
    3. 14.3 Glossary
  15. 15Mechanical, Packaging, and Orderable Information

Package Options

Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information

11 Applications and Implementation

11.1 Application Information

The TPS53632G device has a very simple design procedure. A Microsoft Excel®-based component value calculation tool is available. Please contact your local TI representative to get a copy of the spreadsheet.

11.2 Typical Application

11.2.1 D-CAP+™ Half-Bridge Application

TPS53632G app_complete_app_sluscj3.gif Figure 13. Half-Bridge Application with GaN Power Stage on Primary Side

11.2.1.1 Design Requirements

Design example specifications:

  • Input voltage range: 36 V to 72 V
  • VOUT = 1.0 V
  • ICC(max) = 50 A
  • Slew rate (minimum): 12 mV/µs
  • No Load Line

11.2.1.2 Detailed Design Procedure

11.2.1.2.1 Step 1: Select Switching Frequency

The switching frequency is selected by a resistor (RF) between the FREQ_P pin and GND. The frequency is approximate and expected to vary based on load and input voltage.

Table 2. TPS53632G Device Frequency Selection Table

SELECTION
RESISTOR (RF) VALUE (kΩ)		 OPERATING FREQUENCY
(fSW) (kHz)
20 300
24 400
30 500
39 600
56 700
75 800
100 900
150 1000

For this design, choose a switching frequency of 300 kHz. So, RF = 20 kΩ.

11.2.1.2.2 Step 2: Set The Slew Rate

A resistor to GND (RSLEWA) on SLEWA pin sets the slew rate. For a minimum 12 mV/µs slew rate, the resistor RSLEWA = 24 kΩ.

Table 3. Slew Rate Versus Selection Resistor

SELECTION RESISTOR
RSLEWA (kΩ)		 MINIMUM SLEW RATE
(mV/µs)
20 6
24 12
30 18
39 24
56 30
75 36
100 42
150 48

NOTE

The voltage on the SLEWA pin also sets the base address. For a base address of 00, the SLEWA pin should have only one resistor, RSLEW to GND. For other base addresses, a resistor can be connected between the SLEWA pin and the VREF pin (1.7 V). This resistor can be calculated to set the corresponding voltage for the required address listed in Table 4.

Table 4. Address Selection

SLEWA
VOLTAGE		 BASE
ADDRESS
VSLEWA ≤ 0.30 V 0
0.35 V ≤ VSLEWA ≤ 0.45 V 1
0.55 V ≤ VSLEWA ≤ 0.65 V 2
0.75 V ≤ VSLEWA ≤ 0.85 V 3
0.95 V ≤ VSLEWA ≤ 1.05 V 4
1.15 V ≤ VSLEWA ≤ 1.25 V 5
1.35 V ≤ VSLEWA ≤ 1.45 V 6
1.55 V ≤ VSLEWA ≤ 1.65 V 7

11.2.1.2.3 Step 3: Determine Inductor Value And Choose Inductor

Applications with smaller inductor values have better transient performance but also have higher voltage ripple and lower efficiency. Applications with higher inductor values have the opposite characteristics. It is common practice to limit the ripple current between 20% and 40% of the maximum current per phase. In this case, use 30%.

Equation 2. TPS53632G Q_Ipp_slusbw8.gif
Equation 3. TPS53632G q_de_l_slusbw8.gif

In this equation,

Equation 4. TPS53632G q_de_v_slusbw8.gif
Equation 5. TPS53632G q_de_dt_slusbw8.gif

So, calculating, L = 0.29 µH.

Choose an inductance value of 0.3 µH. The inductor must not saturate during peak loading conditions.

Equation 6. TPS53632G q_de_isat_slusbw8.gif

where

  • n is the number of phases

The factor of 1.2 allows for current sensing and current limiting tolerances.

The chosen inductor should have the following characteristics:

  • As flat as an inductance versus current curve as possible. Inductor DCR sensing is based on the idea L / DCR is approximately a constant through the current range of interest
  • Either high saturation or soft saturation
  • Low DCR for improved efficiency, but at least 0.6 mΩ for proper signal levels
  • DCR tolerance as low as possible for load-line accuracy

For this application, choose a 0.3-µH, 0.29-mΩ inductor.

11.2.1.2.4 Step 4: Determine Current Sensing Method

The TPS53632G device supports both resistor sensing and inductor DCR sensing. Inductor DCR sensing is chosen. For resistor sensing, substitute the resistor value for RCS(eff) in the subsequent equations.

11.2.1.2.5 Step 5: DCR Current Sensing

Design the thermal compensation network and selection of OCP. In most designs, NTC thermistors are used to compensate thermal variations in the resistance of the inductor winding. This winding is generally copper, and so has a resistance coefficient of 3900 PPM/°C. NTC thermistors, as an alternative, have very non-linear characteristics and need two or three resistors to linearize them over the range of interest. A typical DCR circuit is shown in Figure 14.

TPS53632G v12199_lusb32.gif Figure 14. Typical DCR Sensing Circuit

In this design example, the voltage across the CSENSE capacitor exactly equals the voltage across RDCR when:

Equation 7. TPS53632G q_de_l_over_rdcr_lusb32.gif
Equation 8. TPS53632G q_de_req_lusb32.gif

where

  • REQ is the series (or parallel) combination of RSEQU, RNTC, RSERIES and RPAR
Equation 9. TPS53632G q_de_rpn_lusb32.gif

Ensure that CSENSE is a capacitor type which is stable over temperature. Use X7R or better dielectric (C0G preferred).

Because calculating these values by hand is difficult, TI offers a spreadsheet using the Excel solver function available to calculate them for you. Contact a TI representative to get a copy of the spreadsheet.

In this design, the following values are input to the spreadsheet.

  • L = 0.3 µH
  • RDCR = 0.29 mΩ
  • Minimum Overcurrent Limit = 110 A
  • Thermistor R25 = 10 kΩ and “B” value = 3380 kΩ

The spreadsheet then calculates the OCP setting and the values of RSEQU, RSERIES, RPAR, and CSENSE. In this case, the OCP setting is the value of the resistor that is conencted between the OCP-I pin and GND. (100 kΩ ) The nearest standard component values are:

  • RSEQU = 1.47 kΩ
  • RSERIES = 1.65 kΩ
  • RPAR = 30.1 kΩ
  • CSENSE = 680 nF

Consider the effective divider ratio for the inductor DCR. Equation 10 shows the effective current sense resistance (RCS(eff) calculation.

Equation 10. TPS53632G q_de_rcseff_lusb32.gif

where

  • RP_N is the series and parallel combination of RNTC, RSERIES, and RPAR
Equation 11. TPS53632G q_de_rpn_lusb32.gif

where

  • RCS(eff) is 0.244 mΩ

11.2.1.2.6 Step 6: Select OCP Level

Set the OCP threshold level that corresponds to Equation 12.

Equation 12. TPS53632G q_de_ivalley1_lusb32.gif
Equation 13. TPS53632G q_de_ivalley2_lusb32.gif

Table 5. OCP Selection(1)

SELECTION RESISTOR
ROCP (kΩ)		 TYPICAL VCS(OCP)
(mV)
20 4
24 8
30 13
39 19
56 25
75 32
100 40
150 49
(1) If a corresponding match is not found, then select the next higher setting.

11.2.1.2.7 Step 7: Set the Load-Line Slope

The load-line slope is set by resistor, RDROOP (between the DROOP pin and the COMP pin) and resistor RCOMP (between the COMP pin and the VREF pin). The gain of the DROOP amplifier (ADROOP) is calculated in Equation 14.

Equation 14. TPS53632G Eq18_adroop_slusbw8.gif

Set the value of RDROOP to 10 kΩ, RCOMP as shown in Equation 15.

Equation 15. TPS53632G Eq19_rcomp_slusbw8.gif

Based on measurement, this value is adjusted to 9.75 kΩ.

NOTE

See Loop Compensation for Zero Load-Line for zero-load line.

11.2.1.2.8 Step 8: Current Monitor (IMON) Setting

Set the analog current monitor so that at ICC(max) the IMON pin voltage is 1.7 V. This corresponds to a digital IOUT value of ‘FF’ in I2C register 03H. The voltage on the IMON pin is shown in Equation 16.

Equation 16. TPS53632G vimon-pg1.png

So,

Equation 17. TPS53632G q_onepointseven_lusb32.gif

where

  • ICC(max)is 80 A
  • RCS(eff) is 0.244 mΩ
  • ROCP is 24 kΩ

Solving, RIMON = 169 kΩ. RIMON is connected from IMON pin to OCP-I pin.

11.2.1.3 Application Performance Plots

TPS53632G D002_sluscj3.gif
VOUT = 1 V
Figure 15. Output Voltage vs Output Current
TPS53632G D004_sluscj3.gif
VOUT = 1 V
Figure 17. Switching Frequency vs Output Current
TPS53632G D001_sluscj3.gif
VOUT = 1 V
Figure 16. Efficiency vs Output Current
TPS53632G D003_sluscj3.gif
VOUT = 1 V
Figure 18. IMON Voltage vs Output Current

11.2.1.4 Loop Compensation for Zero Load-Line

The TPS53632G device control architecture (current mode, constant on-time) has been analyzed by the Center for Power Electronics Systems (CPES) at Virginia Polytechnic and State University. The following equations are from the presentation: Equivalent Circuit Representation of Current-Mode Control from November 21, 2008.

A simplified control loop diagram is shown in Figure 19. One of the benefits of this technology is the lack of the sample and hold effect that limits the bandwidth of fixed frequency current mode controllers and causes sub-harmonic oscillations.

The open loop gain, GOL, is the gain of the error amplifier, multiplied by the control-to-output gain and is calculated in Equation 18.

Equation 18. TPS53632G q_gol_lusb32.gif

The control-to-output gain circuitry is shown in Figure 19.

TPS53632G output_control_lusbw8.gif Figure 19. Control To Output Gain Circuitry

The control-to-output gain is calculated in Equation 19.

Equation 19. TPS53632G q_vo_over_vc_lusb32.gif

where

  • TPS53632G q_kc_lusb32.gif
  • TPS53632G q_w1_lusb32.gif
  • TPS53632G q_q1_lusb32.gif
  • TPS53632G q_ton1_lusb32.gif
  • TPS53632G q_wa_lusb32.gif

For this converter, Ri = RCS(eff) × ACS

The theoretical control-to-output transfer function shows 0-dB bandwidth is approximately 20 kHz and the phase margin is greater than 90°. As a result, creating the desired loop response is a matter of adding an appropriate pole-zero or pole-zero-pole compensation for the high-gain system.

The loop compensation is designed to meet the following criteria:

  1. Phase margin ≥ 60°
    1. More stable and settles more quickly for repetitive transients
  2. Bandwidth: TPS53632G q_bw_lusb32.gif
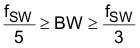
    1. High-enough BW for good transient response.
    2. If too high, the response for the voltage changes gets very “bumpy”, as each voltage step causes several pulses very quickly.
  3. The phase angle of the compensation at the switching frequency needs to be very near to 0 degrees (resistive)
    1. Otherwise, there is a phase shift between DROOP and ISUM
    2. Practically, this means the zero frequency should be < fSW / 2, and any high-frequency pole (for noise rejection) needs to be > 2 × fSW.

The voltage error amplifier is used in the design. The compensation technique used here is a type II compensator. Equation 20 describes the transfer function, which has a pole that occurs at the origin. The type II amplifier also has a 0 (fZ) that can be programmed by selecting R1 and C1 values. In addition, the type II compensation network has a pole (fP) that can be programmed by selecting R1 and C2.

Equation 20. TPS53632G q_gcomp_lusb32.gif
Equation 21. TPS53632G q_fz_lusb32.gif
Equation 22. TPS53632G q_fp_lusb32.gif

R1 sets the loop crossover to correct for the gain at control to output function. In this design, select R2 = 2 kΩ.

Equation 23. TPS53632G q_de_r1_slusbw8.gif

Capacitor C1 adds phase margin at crossover frequency and can be set between 10% and 20% of the switching frequency.

Equation 24. TPS53632G q_de_c1_slusbw8.gif

The last consideration for the voltage loop compensation design is C2. The purpose of C2 is to cancel the phase gain caused by the ESR of the output capacitor in the control-to-output function after the loop crossover. To ensure the gain continues to roll off after the voltage loop crossover, the C2 is selected to meet Equation 25.

Equation 25. TPS53632G q_de_c2_slusbw8.gif