SLVS996D September 2009 – September 2015 TPS54262-Q1
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Pin Configuration and Functions
- 6 Specifications
-
7 Detailed Description
- 7.1 Overview
- 7.2 Functional Block Diagram
- 7.3
Feature Description
- 7.3.1 Unregulated Input Voltage
- 7.3.2 Regulated Output Voltage
- 7.3.3 Regulation and Feedback Voltage
- 7.3.4 Enable and Shutdown
- 7.3.5 Soft Start
- 7.3.6 Oscillator Frequency
- 7.3.7 Slew Rate Control
- 7.3.8 Reset
- 7.3.9 Reset Delay
- 7.3.10 Reset Threshold and Undervoltage Threshold
- 7.3.11 Overvoltage Supervisor
- 7.3.12 Noise Filter on RST_TH and OV_TH Terminals
- 7.3.13 Boot Capacitor
- 7.3.14 Short Circuit Protection
- 7.3.15 Overcurrent Protection
- 7.3.16 Internal Undervoltage Lockout (UVLO)
- 7.3.17 Thermal Shutdown (TSD)
- 7.3.18 Loop Control Frequency Compensation - Type 3
- 7.4 Device Functional Modes
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Application
- 8.2.1 Design Requirements
- 8.2.2
Detailed Design Procedure
- 8.2.2.1
Component Selection
- 8.2.2.1.1 Input Capacitors (C1, C11)
- 8.2.2.1.2 Output Capacitor (C4, C12)
- 8.2.2.1.3 Soft-Start Capacitor (C6)
- 8.2.2.1.4 Bootstrap Capacitor (C3)
- 8.2.2.1.5 Power-On Reset Delay (PORdly) Capacitor (C2)
- 8.2.2.1.6 Output Inductor (L1)
- 8.2.2.1.7 Flyback Schottky Diode (D2)
- 8.2.2.1.8 Resistor to Set Slew Rate (R7)
- 8.2.2.1.9 Resistor to Select Switching Frequency (R8)
- 8.2.2.1.10 Resistors to Select Output Voltage (R4, R5)
- 8.2.2.1.11 Resistors to Set Undervoltage, Overvoltage, and Reset Thresholds (R1, R2, R3)
- 8.2.2.1.12 Low-Power Mode (LPM) Threshold
- 8.2.2.1.13 Enable Pin Pull-Up Resistor (R11) and Voltage Divider Resistor (R10)
- 8.2.2.1.14 Pull-Up Resistor (R12) at RST Pin
- 8.2.2.1.15 Type 3 Compensation Components (R5, R6, R9, C5, C7, C8)
- 8.2.2.1.16 Noise Filter on RST_TH and OV_TH Terminals (C9, C10)
- 8.2.2.2
Design Example 1
- 8.2.2.2.1 Calculate the Switching Frequency (fsw)
- 8.2.2.2.2 Calculate the Ripple Current (IRipple)
- 8.2.2.2.3 Calculate the Inductor Value (L1)
- 8.2.2.2.4 Calculate the Output Capacitor and ESR (C4)
- 8.2.2.2.5 Calculate the Feedback Resistors (R4, R5)
- 8.2.2.2.6 Calculate Type 3 Compensation Components
- 8.2.2.2.7 Calculate Soft-Start Capacitor (C6)
- 8.2.2.2.8 Calculate Bootstrap Capacitor (C3)
- 8.2.2.2.9 Calculate Power-On Reset Delay Capacitor (C2)
- 8.2.2.2.10 Calculate Input Capacitor (C1, C11)
- 8.2.2.2.11 Calculate Resistors to Control Slew Rate (R7)
- 8.2.2.2.12 Resistors to Select Undervoltage, Overvoltage and Reset Threshold Values (R1, R2, R3)
- 8.2.2.2.13 Diode D1 and D2 Selection
- 8.2.2.2.14 Noise Filter on RST_TH and OV_TH Terminals (C9 and C10)
- 8.2.2.2.15 Power Budget and Temperature Estimation
- 8.2.2.3
Design Example 2
- 8.2.2.3.1 Calculate the Switching Frequency (fsw)
- 8.2.2.3.2 Calculate the Ripple Current (IRipple)
- 8.2.2.3.3 Calculate the Inductor Value (L1)
- 8.2.2.3.4 Calculate the Output Capacitor and ESR (C4, C12)
- 8.2.2.3.5 Calculate the Feedback Resistors (R4, R5)
- 8.2.2.3.6 Calculate Type 3 Compensation Components
- 8.2.2.3.7 Calculate Soft-Start Capacitor (C6)
- 8.2.2.3.8 Calculate Bootstrap Capacitor (C3)
- 8.2.2.3.9 Calculate Power-On Reset Delay Capacitor (C2)
- 8.2.2.3.10 Calculate Input Capacitor (C1, C11)
- 8.2.2.3.11 Calculate Resistors to Control Slew Rate (R7)
- 8.2.2.3.12 Resistors to Select Undervoltage, Overvoltage and Reset Threshold Values (R1, R2, R3)
- 8.2.2.3.13 Diode D1 and D2 Selection
- 8.2.2.3.14 Noise Filter on RST_TH and OV_TH Terminals (C9 and C10)
- 8.2.2.3.15 Power Budget and Temperature Estimation
- 8.2.2.1
Component Selection
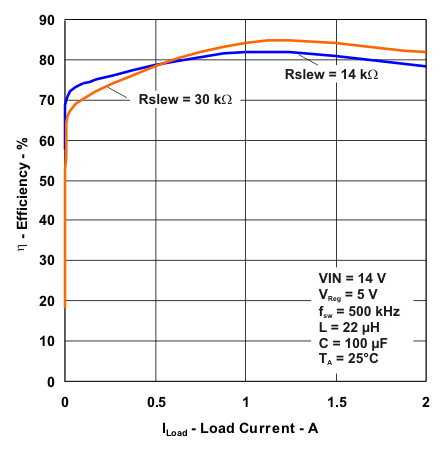
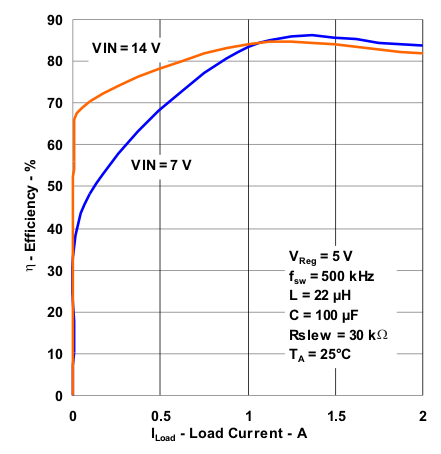
- 8.2.3 Application Curves
- 9 Power Supply Recommendations
- 10Layout
- 11Device and Documentation Support
- 12Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
- PWP|20
Thermal pad, mechanical data (Package|Pins)
- PWP|20
Orderable Information
8 Application and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
8.1 Application Information
The TPS54262-Q1 step-down DC-DC converter features an integrated NMOS switching FET and voltage supervisor circuit. It is designed to provide up to a 2-A output current from an input voltage source of 3.6 V to 48 V, and it can withstand transient voltages up to 60 V on its input pin. The device's input voltage line feed forward topology improves line transient regulation of the voltage mode buck regulator. The device also features low-power mode operation under light-load conditions, which reduces the supply current to 50 μA (typical). It can work for wide switching frequency range (200 kHz to 2.2 MHz), which allows regulator design to be optimized for efficiency or solution size.
8.2 Typical Application
This section explains considerations for the external components selection. Figure 26 shows the interconnection between external components and the device for a typical DC-DC step-down application.
The following examples demonstrate the design of a high frequency switching regulator using ceramic output capacitors. A few parameters must be known to start the design process. These parameters are typically determined at the system level.
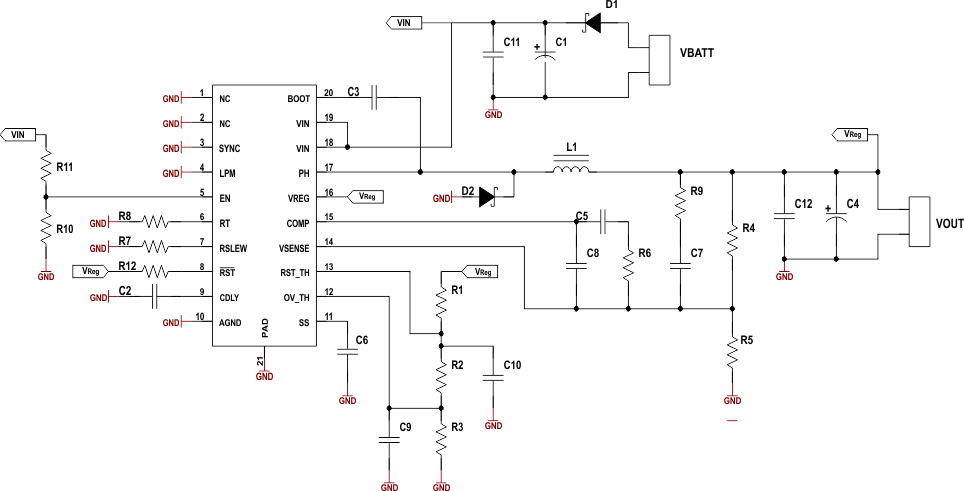 Figure 26. Typical Application Schematic
Figure 26. Typical Application Schematic
8.2.1 Design Requirements
The input voltage is supplied through VIN pins (pin 18 and 19), which must be externally protected against voltage levels greater than 60 V and reverse input polarity. An external diode is connected to protect these pins from reverse input polarity. The input current drawn from this pin is pulsed, with fast rise and fall times. Therefore, this input line requires a filter capacitor to minimize noise. Additionally, for EMI considerations, an input filter inductor may also be required.
For design considerations, VIN/VReg ratios must always be set such that the minimum required duty cycle pulse (tON-Min) is greater than 150 ns. The minimum off time (tOFF-Min) is 250 ns for all conditions. The Detailed Design Procedure section provides the necessary equations and guidelines for selecting external components for this regulator.
8.2.2 Detailed Design Procedure
8.2.2.1 Component Selection
8.2.2.1.1 Input Capacitors (C1, C11)
Input filter capacitor (C11) is used to filter out high frequency noise in the input line. Typical values of C11 are 0.1 µF to 0.01 µF. For higher frequency noise, low capacitor values are recommended.
To minimize the ripple voltage, input ceramic de-coupling capacitor (C1) of type X5R or X7R should be used. The DC voltage rating for the input decoupling capacitor must be greater than the maximum input voltage. This capacitor must have an input ripple current rating higher than the maximum input ripple current of the converter for the application; and is determined by Equation 25.
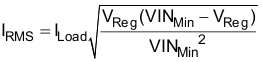
The input capacitors for power regulators are chosen to have a reasonable capacitance-to-volume ratio and fairly stable over temperature. The value of the input capacitance also determines the input ripple voltage of the regulator, shown by Equation 26.
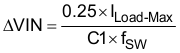
Input ceramic filter capacitors should be located in close proximity to the VIN terminal. Surface mount capacitors are recommended to minimize lead length and reduce noise coupling.
8.2.2.1.2 Output Capacitor (C4, C12)
The selection of the output capacitor will determine several parameters in the operation of the converter (for example, voltage drop on the output capacitor and the output ripple). The capacitor value also determines the modulator pole and the roll-off frequency due to the LC output filter double pole. This is expressed in Equation 12.
The minimum capacitance needed to maintain desired output voltage during high to low load transition and prevent over shoot is given by Equation 27.
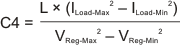
where
- L = output inductor
- ILoad-Max = maximum load current
- ILoad-Min = minimum load current
- VReg-Max = maximum tolerance of regulated output voltage
- VReg-Min = minimum tolerance of regulated output voltage
During a load step from no load to full load or changes in the input voltage, the output capacitor must hold up the output voltage above a certain level for a specified time and not issue a reset, until the main regulator control loop responds to the change. The minimum output capacitance required to allow sufficient drop on the output voltage without issuing a reset is determined by Equation 28.
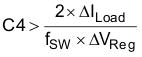
where
- ΔVReg = transient response during load stepping
The minimum capacitance needed for output voltage ripple specification is given by Equation 29.
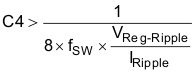
Additional capacitance deratings for temperature, aging, and DC bias must be factored in, and so a value of 100 µF with ESR calculated using Equation 30 of less than 100 mΩ should be used on the output stage.
Maximum ESR of the output capacitor is based on output ripple voltage specification in Equation 30. The output ripple voltage is a product of the output capacitor ESR and ripple current.
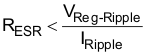
Output capacitor root mean square (RMS) ripple current is given by Equation 31. This is to prevent excess heating or failure due to high ripple currents. This parameter is sometimes specified by the manufacturers.
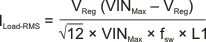
Filter capacitor (C12) of value 0.1 µF (typical) is used to filter out the noise in the output line.
8.2.2.1.3 Soft-Start Capacitor (C6)
The soft-start capacitor determines the minimum time to reach the desired output voltage during a power-up cycle. This is useful when a load requires a controlled voltage slew rate, and helps to limit the current draw from the input voltage supply line. TI recommends a 100-nF capacitor for start-up loads of 1 A (maximum).
8.2.2.1.4 Bootstrap Capacitor (C3)
A 0.1-µF ceramic capacitor must be connected between the PH and BOOT terminals for the converter to operate and regulate to the desired output voltage. TI recommends using a capacitor with X5R or better grade dielectric material, and the voltage rating on this capacitor of at least 25 V to allow for derating.
8.2.2.1.5 Power-On Reset Delay (PORdly) Capacitor (C2)
The value of this capacitor can be calculated using Equation 6.
8.2.2.1.6 Output Inductor (L1)
Use a low EMI inductor with a ferrite type shielded core. Other types of inductors may be used; however, they must have low EMI characteristics and should be placed away from the low-power traces and components in the circuit.
To calculate the minimum value of the inductor, the ripple current should be first calculated using Equation 32.
where
- ILoad = maximum output load current
- IRipple = allowable peak to peak inductor ripple current, typically 20% of maximum ILoad
- KIND = coefficient that represents the amount of inductor ripple current relative to the maximum output current.
The inductor ripple current is filtered by the output capacitor; therefore, KIND is typically in the range of 0.2 to 0.3, depending on the ESR and the ripple current rating of the output capacitor (C4).
The minimum value of output inductor can be calculated using Equation 33.
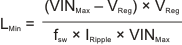
where
- VINMax = maximum input voltage
- VReg = regulated output voltage
- fsw = switching frequency
The RMS and peak currents flowing in the inductor are given by Equation 34 and Equation 35.
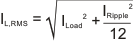
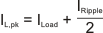
8.2.2.1.7 Flyback Schottky Diode (D2)
The TPS54262-Q1 requires an external Schottky diode connected between the PH and power ground termination. The absolute voltage at PH pin should not go beyond the values in Absolute Maximum Ratings. The Schottky diode conducts the output current during the off state of the internal power switch. This Schottky diode must have a reverse breakdown voltage higher than the maximum input voltage of the application. A Schottky diode is selected for its lower forward voltage. The Schottky diode is selected based on the appropriate power rating, which factors in the DC conduction losses and the AC losses due to the high switching frequencies; this is determined by Equation 36.
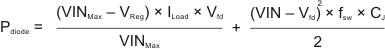
where
- Pdiode = power rating
- Vfd = forward conducting voltage of Schottky diode
- CJ = junction capacitance of the Schottky diode
Recommended part numbers are PDS 360 and SBR8U60P5.
8.2.2.1.8 Resistor to Set Slew Rate (R7)
The slew rate setting is asymmetrical; that is, for a selected value of R7, the rise time and fall time are different. R7 can be approximately determined from Figure 11 and Figure 12. The minimum recommended value is 10 kΩ.
8.2.2.1.9 Resistor to Select Switching Frequency (R8)
See Selecting the Switching Frequency, Figure 10 and Equation 4.
8.2.2.1.10 Resistors to Select Output Voltage (R4, R5)
To minimize the effect of leakage current on the VSENSE terminal, the current flowing through the feedback network should be greater than 5 mA to maintain output accuracy. Higher resistor values help improve the converter efficiency at low-output currents, but may introduce noise immunity problems. See Equation 1. TI recommends fixing R4 to a standard value (for example, 187 kΩ) and calculate R5.
8.2.2.1.11 Resistors to Set Undervoltage, Overvoltage, and Reset Thresholds (R1, R2, R3)
8.2.2.1.11.1 Overvoltage Resistor Selection
Using Equation 9, the value of R3 can be determined to set the overvoltage threshold at up to 106% to 110% of VReg. The sum of R1, R2, and R3 resistor network to ground should be approximately 100 kΩ .
8.2.2.1.11.2 Reset Threshold Resistor Selection
Using Equation 8 the value of R2 + R3 can be calculated, and knowing R3 from the OV_TH setting, R2 can be determined. Suggested value of reset threshold is 92% of VReg.
8.2.2.1.11.3 Undervoltage Threshold for Low-Power Mode and Load Transient Operation
This threshold is set above the reset threshold to ensure the regulator operates within the specified tolerances during output load transient of low load to high load and during discontinuous conduction mode. The typical voltage threshold can be determined using Equation 7. Suggested value of undervoltage threshold is 95% of VReg.
8.2.2.1.12 Low-Power Mode (LPM) Threshold
An approximation of the output load current at which the converter is operating in discontinuous mode can be obtained from Equation 23 with ± 30% hysteresis. The values used in Equation 3 for minimum and maximum input voltage will affect the duty cycle and the overall discontinuous mode load current. These are the nominal values, and other factors are not taken into consideration like external component variations with temperature and aging.
8.2.2.1.13 Enable Pin Pull-Up Resistor (R11) and Voltage Divider Resistor (R10)
An external pull-up resistor, R11= 30.1 kΩ, is recommended to enable the device for operation and R10 can be left open.
Based on the application needs, if the device needs to be turned on at certain input voltage using EN pin threshold, R10 can be used as a voltage divider resistor along with pull-up resistor (R11=30.1 kΩ) and R10 can be calculated accordingly.
8.2.2.1.14 Pull-Up Resistor (R12) at RST Pin
A standard pull-up resistor, R12 = 2 K Ω can be used at this pin
8.2.2.1.15 Type 3 Compensation Components (R5, R6, R9, C5, C7, C8)
First, make the ZEROs close to double pole frequency, using Equation 12, Equation 13, and Equation 11.
fz1 = (50% to 70%) fLC
fz2 = fLC
Second, make the POLEs above the crossover frequency, using Equation 18 and Equation 19.
fp1 = fESR
fp2 = ½fsw
8.2.2.1.15.1 Resistors
From Equation 1, knowing VReg and R4 (fix to a standard value), R5 can be calculated as shown in Equation 37:
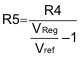
Using Equation 11 and Equation 15, R6 can be calculated as shown in Equation 38:
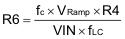
R9 can be calculated as shown in Equation 39:
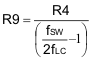
8.2.2.1.15.2 Capacitors
Using Equation 20, C5 can be calculated as shown in Equation 40:
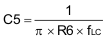
C7 can be calculated as shown in Equation 41:
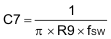
C8 can be calculated as shown in Equation 42:
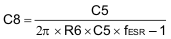
8.2.2.1.16 Noise Filter on RST_TH and OV_TH Terminals (C9, C10)
These capacitors may be required in some applications to filter the noise on RST_TH and OV_TH pins. Typical capacitor values for RST_TH and OV_TH pins are from 10 pF to 100 pF for total resistance on RST_TH/OV_TH divider of less than 200 kΩ. See Noise Filter on RST_TH and OV_TH Terminals.
8.2.2.2 Design Example 1
For this example, we will start with the following known and target parameters:
Table 8. Design Parameters – Example 1(1)
| PARAMETER TYPE | PARAMETER NAME | PARAMETER VALUE |
|---|---|---|
| Known | Input voltage, VIN | Minimum = 8 V, Maximum = 28 V, Typical = 14 V |
| Target | Output voltage, VReg | 5 V ± 2% |
| Maximum output current, ILoad-Max | 1.8 A | |
| Ripple/ transient occurring in input voltage, ΔVIN | 1% of VIN (minimum) | |
| Reset threshold, VReg_RST | 92% of VReg | |
| Overvoltage threshold, VReg_OV | 106% of VReg | |
| Undervoltage threshold, VReg_UV | 95% of VReg | |
| Transient response 0.25 A to 2-A load step, ΔVReg | 5% of VReg | |
| Power-on Reset delay, PORdly | 2.2 ms |
8.2.2.2.1 Calculate the Switching Frequency (fsw)
To reduce the size of output inductor and capacitor, higher switching frequency can be selected. It is important to understand that higher switching frequency results in higher switching losses, causing the device to heat up. This may result in degraded thermal performance. To prevent this, proper PCB layout guidelines must be followed (see Layout Guidelines).
Based upon the discussion in section Selecting the Switching Frequency, calculate the maximum and minimum duty cycle.
Knowing VReg and tolerance on VReg, the VReg-Max and VReg-Min are calculated to be:
VReg-Max = 102% of VReg = 5.1 V and VReg-Min = 98% of VReg = 4.9 V.
Using Equation 3, the minimum duty cycle is calculated to be, DMin = 17.5%
Knowing: tON-Min = 150 ns from the device specifications, and using Equation 4, maximum switching frequency is calculated to be, fsw-Max = 1166 kHz
Because the oscillator can also vary by ±10%, the switching frequency can be further reduced by 10% to add margin. Also, to improve efficiency and reduce power losses due to switching, the switching frequency can be further reduced by about 550 kHz. Therefore, fsw = 500 kHz.
From Figure 10, R8 can be approximately determined to be, R8 = 205 kΩ.
8.2.2.2.2 Calculate the Ripple Current (IRipple)
Using Equation 32, for KIND = 0.2 (typical), inductor ripple current is calculated to be: IRipple = 0.36 A.
The ripple current is chosen such that the converter enters discontinuous mode (DCM) at 20% of maximum load. The 20% is a typical value, it could go higher to a maximum of up to 40%.
8.2.2.2.3 Calculate the Inductor Value (L1)
Using Equation 33, the inductor value is calculated to be, LMin = 22.8 µH. A closest standard inductor value can be used.
8.2.2.2.4 Calculate the Output Capacitor and ESR (C4)
8.2.2.2.4.1 Calculate capacitance
To calculate the capacitance of the output capacitor, first determine the minimum load current. Typically, in standby mode the load current is 100 µA; however, this really depends on the application. With this value of minimum load current and using Equation 27, Equation 28, and Equation 29, C4 is calculated to be, C4 > 34 µF .
To allow wider operating conditions and improved performance in low-power mode, TI recommends using a 100-µF capacitor. A higher value of the output capacitor allows improved transient response during load stepping.
8.2.2.2.4.2 Calculate ESR
Using Equation 30, ESR is calculated to be, RESR < 555 mΩ.
Capacitors with lowest ESR values should be selected. To meet both the requirements, capacitance and low ESR, several low ESR capacitors may be connected in parallel. In this example, we will select a capacitor with ESR value as 30 mΩ.
Filter capacitor (C12) of value 0.1 µF can be added to filter out the noise in the output line.
8.2.2.2.5 Calculate the Feedback Resistors (R4, R5)
To keep the quiescent current low and avoid instability problems, TI recommends selecting R4 and R5 such that, R4 + R5 is approximately 250 kΩ.
Using Equation 1 and using a fixed standard value of R4 = 187 kΩ, R5 is calculated to be, R5 = 35.7 kΩ .
8.2.2.2.6 Calculate Type 3 Compensation Components
8.2.2.2.6.1 Resistances (R6, R9)
Using Equation 16, for VINTyp = 14 V, VRamp is calculated to be, VRamp = 1.4 V.
Using Equation 12, fLC is calculated to be, fLC = 3.33 kHz.
Using VRamp, fLC from above, assuming fc as 1/10th of fsw and Equation 38, R6 is calculated to be,
R6 = 280.65 kΩ.
Using Equation 39, R9 is calculated to be, R9 = 2.53 kΩ.
8.2.2.2.6.2 Capacitors (C5, C8, C7)
Using Equation 40, C5 is calculated to be, C5 = 340.45 pF.
Using Equation 13, fESR is calculated to be, fESR = 53.06 kHz.
Using Equation 42, C8 is calculated to be, C8 = 11.04 pF.
Using Equation 41, C7 is calculated to be, C7 = 250.07 pF.
8.2.2.2.7 Calculate Soft-Start Capacitor (C6)
The recommended value of soft-start capacitor is 100 nF (typical).
8.2.2.2.8 Calculate Bootstrap Capacitor (C3)
The recommended value of bootstrap capacitor is 0.1 µF (typical).
8.2.2.2.9 Calculate Power-On Reset Delay Capacitor (C2)
To achieve 2.2-ms delay, the reset delay capacitor can be calculated using Equation 6 to be C2 = 2.2 nF.
8.2.2.2.10 Calculate Input Capacitor (C1, C11)
Typical values for C11 are 0.1 µF and 0.01 µF.
Input capacitor (C1) should be rated more than the maximum input voltage (VINMax). The input capacitor should be big enough to maintain supply in case of transients in the input line. Using Equation 26, C1 is calculated to be, C1 = 1.2 µF. For improved transient response, TI recommends a higher value of C1 such as 220 µF.
8.2.2.2.11 Calculate Resistors to Control Slew Rate (R7)
The value of slew rate resistor (R7) can be approximately determined from Figure 11 and Figure 12 at different typical input voltages. The minimum recommended value is 10 kΩ. To achieve rise time, tr = 20 ns and fall time, tf = 35 ns, the slew rate resistor is approximately of value 30 kΩ.
8.2.2.2.12 Resistors to Select Undervoltage, Overvoltage and Reset Threshold Values (R1, R2, R3)
The sum of these three resistors should be approximately equal to 100 kΩ. In this example,
- VReg_OV = 106% of VReg = 5.3 V
- VReg_RST = 92% of VReg = 4.6 V
- VReg_UV = 95% of VReg = 4.75 V
Using Equation 9, R3 = 15 kΩ.
Using Equation 8, R2 = 2.29 kΩ.
Using Equation 7, R1 = 82.6 kΩ
8.2.2.2.13 Diode D1 and D2 Selection
Diode D1 is used to protect the IC from the reverse input polarity connection. The diode should be rated at maximum load current. Only Schottky diode should be connected at the PH pin. The recommended part numbers are PDS360 and SBR8U60P5.
8.2.2.2.14 Noise Filter on RST_TH and OV_TH Terminals (C9 and C10)
Typical capacitor values for RST_TH and OV_TH pins are from 10 pF to 100 pF for total resistance on RST_TH/ OV_TH divider of less than 200 kΩ.
8.2.2.2.15 Power Budget and Temperature Estimation
Using Equation 43, conduction losses for typical input voltage are calculated to be, PCON = 0.289 W.
Assuming slew resistance R7 = 30 kΩ, from Figure 11 and Figure 12, rise time, tr = 20 ns and fall time, tf = 35 ns. Using Equation 44, switching losses for typical input voltage are calculated to be, PSW = 0.693 W.
Using Equation 45, gate drive losses are calculated to be, PGate = 3 mW.
Using Equation 46, power supply losses are calculated to be, PIC = 1.8 mW.
Using Equation 47, the total power dissipated by the device is calculated to be, PTotal = 987 mW.
Using Equation 49, and knowing the thermal resistance of package = 35°C/W, the rise in junction temperature due to power dissipation is calculated to be, ∆T = 34.5°C.
Using Equation 50, for a given maximum junction temperature 150°C, the maximum ambient temperature at which the device can be operated is calculated to be, TA-Max = 115°C (approximately).
8.2.2.3 Design Example 2
For this example, start with the following known and target parameters:
Table 9. Design Parameters – Example 2(1)
| PARAMETER TYPE | PARAMETER NAME | PARAMETER VALUE |
|---|---|---|
| Known | Input voltage, VIN | minimum=8 V, maximum= 28 V, typical=14 V |
| Target | Output voltage, VReg | 3.3 V ± 2% |
| Maximum output current, ILoad-Max | 2 A | |
| Ripple/ transient occurring in input voltage, ΔVIN | 1% of VIN (minimum) | |
| Reset threshold, VReg_RST | 92% of VReg | |
| Overvoltage threshold, VReg_OV | 106% of VReg | |
| Undervoltage threshold, VReg_UV | 95% of VReg | |
| Transient response 0.25 A to 2 A load step, ΔVReg | 5% of VReg | |
| Power on Reset delay, PORdly | 2.2 ms |
8.2.2.3.1 Calculate the Switching Frequency (fsw)
To reduce the size of output inductor and capacitor, higher switching frequency can be selected. It is important to understand that higher switching frequency results in higher switching losses, causing the device to heat up. This may result in degraded thermal performance. To prevent this, proper PCB layout guidelines must be followed (see Layout Guidelines).
Based upon the discussion in section Selecting the Switching Frequency, calculate the maximum and minimum duty cycle.
Knowing VReg and tolerance on VReg, the VReg-Max and VReg-Min are calculated to be:
VReg-Max = 102% of VReg = 3.366 V and VReg-Min = 98% of VReg = 3.234 V.
Using Equation 3, the minimum duty cycle is calculated to be, DMin = 11.55%
Knowing tON-Min = 150 ns from the device specifications, and using Equation 4, maximum switching frequency is calculated to be, fsw-Max = 770 kHz.
Because the oscillator can also vary by ±10%, the switching frequency can be further reduced by 10% to add margin. Also, to improve efficiency and reduce power losses due to switching, the switching frequency can be further reduced by about 100 kHz. Therefore fsw = 593 kHz.
From Figure 10, R8 can be approximately determined to be, R8 = 170 kΩ.
8.2.2.3.2 Calculate the Ripple Current (IRipple)
Using , for KIND = 0.2 (typical), inductor ripple current is calculated to be: IRipple = 0.4 A.
The ripple current is chosen such that the converter enters discontinuous mode (DCM) at 20% of maximum load. The 20% is a typical value, although it could go higher to a maximum of up to 40%.
8.2.2.3.3 Calculate the Inductor Value (L1)
Using Equation 33, the inductor value is calculated to be, LMin = 12.3 µH. A closest standard inductor value can be used.
8.2.2.3.4 Calculate the Output Capacitor and ESR (C4, C12)
8.2.2.3.4.1 Calculate Capacitance
To calculate the capacitance of the output capacitor, minimum load current must be first determined. Typically, in standby mode the load current is 100 µA; however, this really depends on the application. With this value of minimum load current and using Equation 27, Equation 28, and Equation 29, C4 is calculated to be, C4 > 56 µF .
To allow wider operating conditions and improved performance in low-power mode, TI recommends using a 100-µF capacitor. An output capacitor with a higher value allows improved transient response during load stepping.
8.2.2.3.4.2 Calculate ESR
Using Equation 30, ESR is calculated to be, RESR < 330 mΩ.
Capacitors with lowest ESR values should be selected. To meet both the requirements, capacitance and low ESR, several low ESR capacitors may be connected in parallel. In this example, we will select a capacitor with ESR value as 30 mΩ.
Filter capacitor (C12) of value 0.1 µF can be added to filter out the noise in the output line.
8.2.2.3.5 Calculate the Feedback Resistors (R4, R5)
To keep the quiescent current low and avoid instability problems, TI recommends selecting R4 and R5 such that, R4 + R5 is approximately 250 kΩ.
Using Equation 1 and using a fixed standard value of R4 = 187 kΩ, R5 is calculated to be, R5 = 59.8 kΩ .
8.2.2.3.6 Calculate Type 3 Compensation Components
8.2.2.3.6.1 Resistances (R6, R9)
Using Equation 16, for VINTyp = 14 V, VRamp is calculated to be, VRamp = 1.4 V.
Using Equation 12, fLC is calculated to be, fLC = 4.54 kHz.
Using VRamp, fLC from above, assuming fc as 1/10th of fsw and Equation 38, R6 is calculated to be, R6 = 244 kΩ.
Using Equation 39, R9 is calculated to be, R9 = 2.9 kΩ.
8.2.2.3.6.2 Capacitors (C5, C8, C7)
Using Equation 40, C5 is calculated to be, C5 = 287.04 pF.
Using Equation 13, fESR is calculated to be, fESR = 53.06 kHz.
Using Equation 42, C8 is calculated to be, C8 = 12.84 pF.
Using Equation 41, C7 is calculated to be, C7 = 184.4 pF.
8.2.2.3.7 Calculate Soft-Start Capacitor (C6)
The recommended value of soft-start capacitor is 100 nF (typical).
8.2.2.3.8 Calculate Bootstrap Capacitor (C3)
The recommended value of bootstrap capacitor is 0.1 µF (typical).
8.2.2.3.9 Calculate Power-On Reset Delay Capacitor (C2)
To achieve 2.2-ms delay, the reset delay capacitor can be calculated using Equation 6 to be C2 = 2.2 nF.
8.2.2.3.10 Calculate Input Capacitor (C1, C11)
Typical values for C11 are 0.1 µF and 0.01 µF.
Input capacitor (C1) should be rated more than the maximum input voltage (VINMax). The input capacitor should be big enough to maintain supply in case of transients in the input line. Using Equation 26, C1 is calculated to be, C1 = 10.53 µF. For improved transient response, TI recommends a higher value of C1 such as 220 µF.
8.2.2.3.11 Calculate Resistors to Control Slew Rate (R7)
The value of slew rate resistor (R7) can be approximately determined from Figure 11 and Figure 12 at different typical input voltages. The minimum recommended value is 10 kΩ. To achieve rise time, tr = 20 ns and fall time, tf = 35 ns, the slew rate resistor is approximately of value 30 kΩ.
8.2.2.3.12 Resistors to Select Undervoltage, Overvoltage and Reset Threshold Values (R1, R2, R3)
The sum of these three resistors should be approximately equal to 100 kΩ. In this example,
VReg_OV = 106% of VReg = 3.498 V
VReg_RST = 92% of VReg = 3.036 V
VReg_UV = 95% of VReg = 3.135 V
Using Equation 9, R3 = 22.87 kΩ.
Using Equation 8, R2 = 3.48 kΩ.
Using Equation 7, R1 = 73.65 kΩ
8.2.2.3.13 Diode D1 and D2 Selection
Diode D1 is used to protect the IC from the reverse input polarity connection. The diode should be rated at maximum load current. Only Schottky diode should be connected at the PH pin. The recommended part numbers are PDS360 and SBR8U60P5.
8.2.2.3.14 Noise Filter on RST_TH and OV_TH Terminals (C9 and C10)
Typical capacitor values for RST_TH and OV_TH pins are from 10 pF to 100 pF for total resistance on RST_TH/ OV_TH divider of less than 200 kΩ.
8.2.2.3.15 Power Budget and Temperature Estimation
Using Equation 43, conduction losses for typical input voltage are calculated to be, PCON = 0.235 W.
Assuming slew resistance R7 = 30 kΩ, from Figure 17 and Figure 18, rise time, tr = 20 ns and fall time, tf = 35 ns. Using Equation 19, switching losses for typical input voltage are calculated to be, PSW = 0.913 W.
Using Equation 44, gate drive losses are calculated to be, PGate = 3.5 mW.
Using Equation 46, power supply losses are calculated to be, PIC = 1.8 mW.
Using Equation 47, the total power dissipated by the device is calculated to be, PTotal = 1.15 W.
Using Equation 49, and knowing the thermal resistance of package = 35°C/W, the rise in junction temperature due to power dissipation is calculated to be, ∆T = 40.4°C.
Using Equation 50, for a given maximum junction temperature 150°C, the maximum ambient temperature at which the device can be operated is calculated to be, TA-Max approximately 105°C.
8.2.3 Application Curves