8.2.2.10 Compensation

Several industry techniques are used to compensate dc-dc regulators. The method presented here yields high phase margins. For most conditions, the regulator has a phase margin between 60° and 90°. The method presented here ignores the effects of the slope compensation that is internal to the TPS57140-EP. Ignoring the slope compensation usually causes the actual crossover frequency to be lower than the crossover frequency used in the calculations.

Use SwitcherPro software for a more accurate design.

The uncompensated regulator has a dominant pole, typically located between 300 Hz and 3 kHz, due to the output capacitor and load resistance, and a pole due to the error amplifier. One zero exists due to the output capacitor and the ESR. The zero frequency is higher than either of the two poles.

If left uncompensated, the double pole created by the error amplifier and the modulator would lead to an unstable regulator. Stabilizing the regulator requires one pole to be canceled out. One design approach is to locate a compensating zero at the modulator pole. Then, select a crossover frequency that is higher than the modulator pole. Calculate the gain of the error amplifier to achieve the desired crossover frequency. The capacitor used to create the compensation zero, along with the output impedance of the error amplifier, forms a low-frequency pole to provide a minus-one slope through the crossover frequency. Then, adding a compensating pole cancels the zero due to the output-capacitor ESR. If the ESR zero resides at a frequency higher than the switching frequency, then it can be ignored.

To compensate the TPS57140-EP using this method, first calculate the modulator pole and zero using the following equations:

Equation 41.

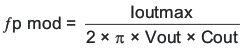
where

• Ioutmax is the maximum output current.
• Cout is the output capacitance.
• Vout is the nominal output voltage.

Equation 42.

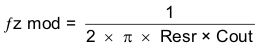
For the example design, the location of the modulator pole is at 1.5 kHz and the ESR zero is at 338 kHz.

Next, the designer must select a crossover frequency which determines the bandwidth of the control loop. The crossover-frequency location must be at a frequency at least 5× higher than the modulator pole. The crossover-frequency selection must also be such that the available gain of the error amplifier at the crossover frequency is high enough to allow for proper compensation.

Use Equation 47 to calculate the maximum crossover frequency when the ESR-zero location is at a frequency that is higher than the desired crossover frequency. This is usually the case for ceramic or low-ESR tantalum capacitors. Aluminum electrolytic and tantalum capacitors typically produce a modulator zero at a low frequency due to their high ESR.

The example application uses a low-ESR ceramic capacitor with 10 mΩ of ESR, making the zero at 338 kHz.

This value is much higher than typical crossover frequencies, so calculate the maximum crossover frequency using both Equation 43 and Equation 46.

Using Equation 46 gives a minimum crossover frequency of 7.6 kHz and Equation 43 gives a maximum crossover frequency of 45.3 kHz.

Arbitrarily select a crossover frequency of 45 kHz from this range.

Equation 43.

Equation 44.

Equation 45.

Equation 46.

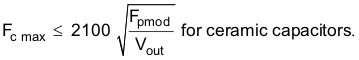
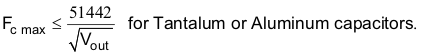
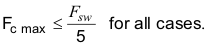
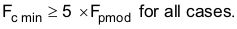
After selection of a crossover frequency, F_c, calculate the gain of the modulator at the crossover frequency using Equation 47.

Equation 47.

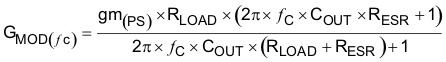
For the example problem, the gain of the modulator at the crossover frequency is 0.542. Next, calculate the compensation components. Use a resistor in series with a capacitor to create a compensating zero. A capacitor in parallel to these two components forms the compensating pole. However, calculating the values of these components varies, depending on whether the ESR-zero location is above or below the crossover frequency. For ceramic or low-ESR tantalum output capacitors, the zero location is usually above the crossover frequency. For aluminum electrolytic and tantalum capacitors, the modulator-zero location is usually lower in frequency than the crossover frequency. For cases where the modulator zero is higher than the crossover frequency (ceramic capacitors):

Equation 48.

Equation 49.

Equation 50.

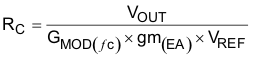
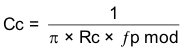
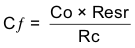
For cases where the modulator zero is less than the crossover frequency (aluminum or tantalum capacitors), the equations are:

Equation 51.

Equation 52.

Equation 53.

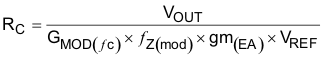
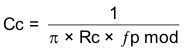
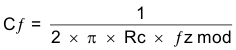
For the example problem, the ESR-zero location is at a higher frequency compared to the crossover frequency, so use Equation 50 through Equation 53 to calculate the compensation components. For the example problem, the calculated components are: Rc = 76.2 kΩ, Cc = 2710 pF, and Cf = 6.17 pF.

The calculated value of the Cf capacitor is not a standard value, so use a value of 2700 pF. Use 6.8 pF for Cc. The Rc resistor sets the gain of the error amplifier, which determines the crossover frequency. The calculated Rc resistor is not a standard value, so use 76.8 kΩ.