SLVSC10C October   2013  – April 2016 TPS65301-Q1

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
  4. 4 Revision History
  5. 5 Pin Configuration and Functions
  6. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Thermal Information
    5. 6.5 DC Characteristics
    6. 6.6 Typical Characteristics
      1. 6.6.1 5-V Linear Regulator (5 VO)
      2. 6.6.2 3.3-V Linear Regulator Controller (3.3 VO)
      3. 6.6.3 1.2-V Linear Regulator Controller (1.2 VO)
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1 Buck Converter
        1. 7.3.1.1  PWM Operation
        2. 7.3.1.2  Voltage-Mode Control Loop
        3. 7.3.1.3  Output Voltage 5.45 V (VREG)
        4. 7.3.1.4  Switching Frequency (RT/CLK)
        5. 7.3.1.5  Boost Capacitor (BOOT)
        6. 7.3.1.6  Soft Start (SS)
        7. 7.3.1.7  Power-On Delay (DELAY)
        8. 7.3.1.8  Reset (nRST)
        9. 7.3.1.9  Thermal Shutdown
        10. 7.3.1.10 Reset Function
      2. 7.3.2 Linear Regulators
        1. 7.3.2.1 Fixed Linear Regulator Output (5 V)
        2. 7.3.2.2 Fixed Linear Regulator Controller (3.3 V)
        3. 7.3.2.3 Fixed Linear Regulator Controller (1.2 V)
        4. 7.3.2.4 Protected Sensor Supply Output (5VS)
    4. 7.4 Device Functional Modes
      1. 7.4.1 Operational Mode
      2. 7.4.2 Buck Converter Modes of Operation
        1. 7.4.2.1 Modes of Operation
          1. 7.4.2.1.1 Continuous-Conduction Mode (CCM)
          2. 7.4.2.1.2 Discontinuous Mode (DCM)
        2. 7.4.2.2 Tracking Mode
  8. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 Typical Application
      1. 8.2.1 Design Requirements
      2. 8.2.2 Detailed Design Procedure
        1. 8.2.2.1 Duty Cycle
        2. 8.2.2.2 Output Inductor Selection (L)
        3. 8.2.2.3 Output Capacitor Selection (CO)
        4. 8.2.2.4 External Schottky Diode (D) Power Dissipation
        5. 8.2.2.5 Input Capacitor (CI)
        6. 8.2.2.6 Loop Compensation
          1. 8.2.2.6.1 Loop-Control Frequency Compensation
            1. 8.2.2.6.1.1 Type III Compensation
            2. 8.2.2.6.1.2 PWM Modulator Gain K
            3. 8.2.2.6.1.3 Resistor Values
            4. 8.2.2.6.1.4 Gain of Amplifier
            5. 8.2.2.6.1.5 Poles and Zero Frequencies
        7. 8.2.2.7 Power Dissipation
          1. 8.2.2.7.1 Switch-Mode Power-Supply Losses
          2. 8.2.2.7.2 Linear Regulator (5V) and Sensor Supply (5VS)
          3. 8.2.2.7.3 Total Power Dissipation
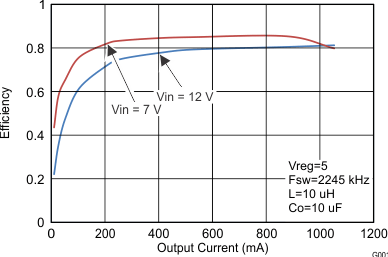
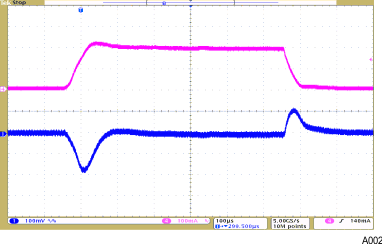
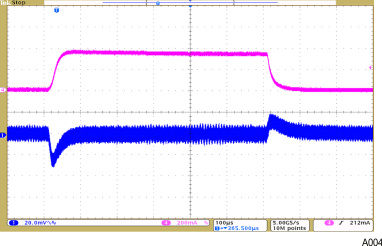
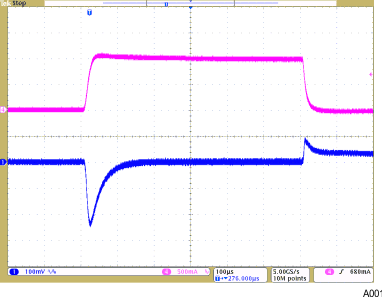
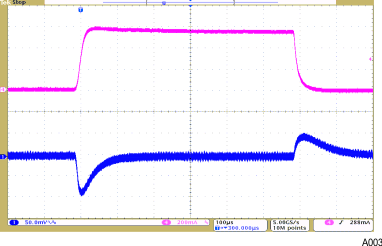
      3. 8.2.3 Application Curves
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
      1. 10.1.1 Inductor (L)
      2. 10.1.2 Input Filter Capacitors (CI)
      3. 10.1.3 Feedback
      4. 10.1.4 Traces and Ground Plane
    2. 10.2 Layout Example
  11. 11Device and Documentation Support
    1. 11.1 Documentation Support
      1. 11.1.1 Related Documentation
    2. 11.2 Community Resource
    3. 11.3 Trademarks
    4. 11.4 Electrostatic Discharge Caution
    5. 11.5 Glossary
  12. 12Mechanical, Packaging, and Orderable Information

Package Options

Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information

8 Application and Implementation

NOTE

Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.

8.1 Application Information

This section is a starting point and theoretical representation of the values to be used for the application, further optimization of the components derived may be required to improve the performance of the device.

8.2 Typical Application

TPS65301-Q1 AppSchem_SLVSC10.gif
L: B82462G4103MOOO (EPCOS) or XFL4020 472MEB (Coilcraft)
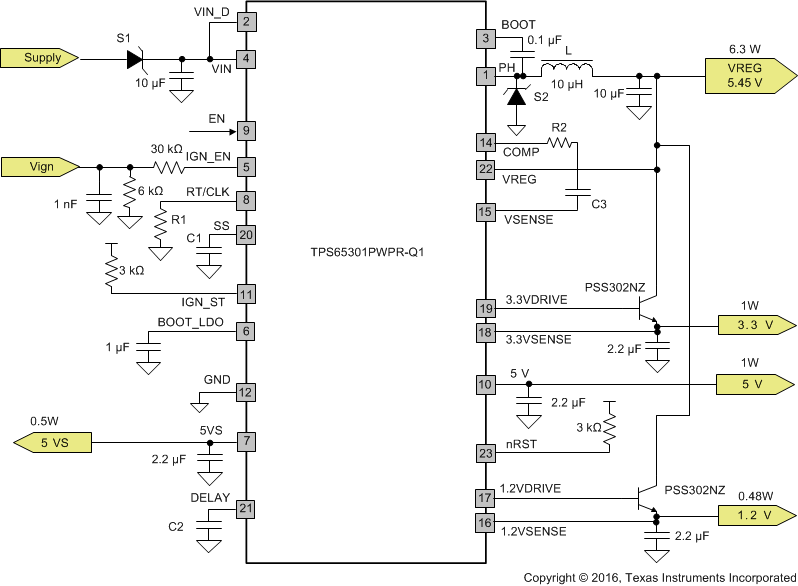
S1: MBRS310T3 (ON Semiconductors) or SS3H10 (Vishay)
S2: B240A, SS16 (Vishay)
External BJT: PBSS302NZ (NXP)
Figure 13. Application Schematic

8.2.1 Design Requirements

For this design example, use the parameters listed in Table 2.

Table 2. Switching Regulator Requirements

PARAMETER REQUIREMENT
Input voltage, VI 6.5 V to 27 V, typical 14 V
Output voltage, 5.45 V 5.45 VO ±2% at 6.3 W
Maximum output current I5.45V_max 1 A
Minimum output current I5.45V_min 0.01 A
Transient response 0.01 A to 0.8 A 5%
Reset threshold 90% of output voltage
5V 5 VO at 1 W
3.3V 3.3 VO at 1 W
1.2V 1.2 VO at 0.5 W
5VS 5 VO at 0.5 W
Switching frequency fSW 2.5 MHz
Overvoltage threshold 106% of output voltage
Undervoltage threshold 95% of output voltage

8.2.2 Detailed Design Procedure

The following design procedure provides typical application procedures as well as the details of a switching regulator design using the requirements listed in Table 2.

8.2.2.1 Duty Cycle

Use Equation 7 to calculate the duty cycle.

Equation 7. TPS65301-Q1 Eq16_SLVSBB6.gif

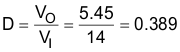
where

  • VO = Output voltage
  • VI = Input voltage

8.2.2.2 Output Inductor Selection (L)

The minimum inductor value is calculated using the coefficient KIND that represents the amount of inductor ripple current relative to the maximum output current. The inductor ripple current is filtered by the output capacitor, and so the typical range of this ripple current is in the range of KIND = 0.2 to 0.3, depending on the ESR and the ripple-current rating of the output capacitor.

For this design example, use Equation 8 to calculate the inductor ripple current.

Equation 8. TPS65301-Q1 Eq17_SLVSBB6.gif

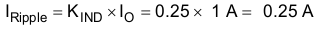
where

  • IO = Output current

The benefits of a low inductor value include the following:

  • Low inductor value gives high di/dt, which allows for fewer output capacitors for good load transient response.
  • Gives higher saturation current for the core due to fewer turns
  • Fewer turns yields low DCR and therefore less dc inductor losses in the windings.
  • High di/dt provides faster response to load steps.

The benefits of a high inductor value include the following:

  • Low ripple current leads to lower conduction losses in MOSFETs
  • Low ripple; means lower RMS ripple current for capacitors
  • Low ripple; yields low ac inductor losses in the core (flux) and windings (skin effect)
  • Low ripple; gives continuous inductor current flow over a wide load range

For this design example a value of 10 μH was selected because of variations in temperature and inductor tolerance. Use Equation 9 to find the value of LMin.

Equation 9. TPS65301-Q1 Eq18_SLVSBB6.gif

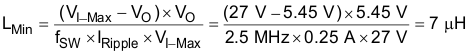
where

  • fSW = the regulator switching frequency
  • IRipple = Allowable ripple current in the inductor, typically ±20% of maximum output load IO

For this design, use Equation 10 to calculate the inductor peak current.

Equation 10. TPS65301-Q1 Eq39_SLVSBB6.gif

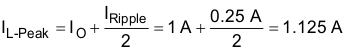
8.2.2.3 Output Capacitor Selection (CO)

The selection of the output capacitor determines several parameters in the operation of the converter, the modulator pole, the voltage droop on the output capacitor, and the output ripple.

During a load step from no load to full load or changes in the input voltage, the output capacitor must hold up the output voltage above a certain level for a specified time and not issue a reset until the main regulator control loop responds to the change. The capacitance value determines the modulator pole and the rolloff frequency due to the LC output-filter double pole—the output ripple voltage is a product of the output capacitor ESR and ripple current.

Use Equation 11 to calculate the minimum capacitance required to maintain desired output voltage during a high-to-low load transition and prevent overshoot.

Equation 11. TPS65301-Q1 Eq20_SLVSBB6.gif

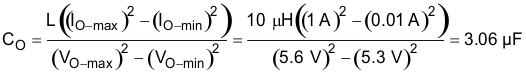
where

  • Io-max is the maximum output current
  • Io-min is the minimum output current
  • Vo-max is maximum tolerance of regulated output voltage
  • Vo-min is the minimum tolerance of regulated output voltage

Use Equation 12 to calculate the output capacitor root-mean-square (RMS) ripple current IO_RMS. This is to prevent excess heating or failure because of high ripple currents.

This parameter is sometimes specified by the manufacturer. Therefore, because of variations in temperature and manufacture, use a 10-μF capacitor with a voltage rating greater than the maximum 10-V output.

Equation 12. TPS65301-Q1 Eq21_SLVSBB6.gif
Equation 13.

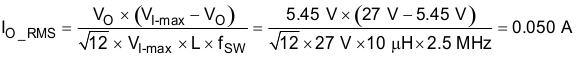
8.2.2.4 External Schottky Diode (D) Power Dissipation

The TPS65301-Q1 device requires an external ultrafast Schottky diode with fast reverse-recovery time connected between the PH and power ground pins. The diode conducts the output current during the off-state of the internal power switch. This diode must have a reverse breakdown higher than the maximum input voltage of the application. A Schottky diode is selected for its lower forward voltage. The Schottky diode is selected based on the appropriate power rating, which factors in the DC conduction losses and the AC losses because of the high switching frequencies. The power dissipation PD is calculated with Equation 14.

Equation 14. TPS65301-Q1 Eq22_SLVSBB6.gif

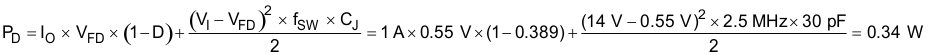
where

  • VFD = forward conducting voltage of Schottky diode
  • CJ = junction capacitance of the Schottky diode

8.2.2.5 Input Capacitor (CI)

The TPS65301-Q1 requires an input ceramic decoupling capacitor type X5R or X7R and bulk capacitance to minimize input ripple voltage. The dc voltage rating of this input capacitance must be greater than the maximum input voltage. The capacitor must have an input ripple-current rating higher than the maximum input ripple current of the converter for the application. The input capacitors for power regulators are chosen to have reasonable capacitance-to-volume ratio and to be fairly stable over temperature. The value of the input capacitance is based on the input voltage desired (∆VI).

Use Equation 15 to calculate the input capacitance.

Equation 15. TPS65301-Q1 Eq23_SLVSBB6.gif

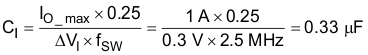
Use Equation 16 to calculate the input-capacitor root-mean-square (RMS) ripple current II_RMS.

Because of variations in temperature and manufacture, use a 10-μF capacitor with a voltage rating greater than the maximum 45-V transient.

Equation 16. TPS65301-Q1 Eq43_SLVSBB6.gif

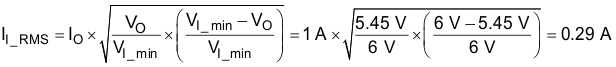
8.2.2.6 Loop Compensation

The double pole is due to the output-filter components inductor and capacitor. The calculations for the following equations use values taken from Figure 14.

8.2.2.6.1 Loop-Control Frequency Compensation

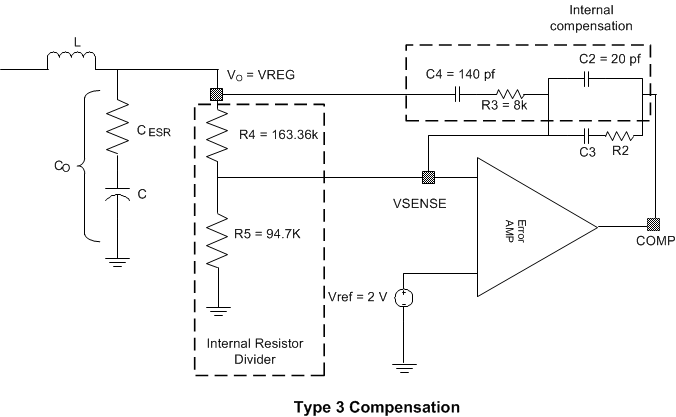TPS65301-Q1 FreqComp_SLVSC10.gif Figure 14. Loop-Control Frequency Compensation

8.2.2.6.1.1 Type III Compensation

fCO = fSW × 0.1 (the cutoff frequency when the gain is 1 is called the unity-gain frequency).

fCO is typically 1/5 to 1/10 of the switching frequency double-pole frequency response due to the LC output filter. The LC output filter gives a double pole, which has a –180° phase shift.

Make the two zeroes close to the double pole (LC), for example, fZ1 ≈ fZ2 ≈ ½π(LCOUT)½.

  1. Make the first zero below the filter double pole (approximately 50% to 75% of fLC)
  2. Make the second zero at the filter double pole (fLC)

    3. Make the two poles above the crossover frequency fCO.

  3. Make the first pole at the ESR frequency (fESR)
  4. Make the second pole at 0.5 the switching frequency

The following compensation components are integrated in the device with the following typical values. Guidelines for compensation components:

R3 = 8 kΩ, C4 = 140 pF, C2 = 20 pF

Use Equation 17 to calculate the double pole to calculate the output filter components LC.

Equation 17. TPS65301-Q1 Eq37_SLVSBB6.gif

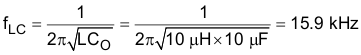
The ESR of the output capacitor C gives a zero that has a 90° phase shift. The ESR of the output capacitor should be in the range of 1 mΩ to 100 mΩ. Use Equation 18 to calculate the value of fESR.

Equation 18. TPS65301-Q1 Eq38_SLVSBB6.gif

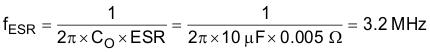
8.2.2.6.1.2 PWM Modulator Gain K

Equation 19. TPS65301-Q1 Eq31_SLVSBB6.gif

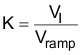
where

  • Vramp = VI / 10, VI = Input operating voltage

8.2.2.6.1.3 Resistor Values

In this design example, select a value of 94.7 kΩ for R5 and use Equation 20 to calculate the value of R4.

Equation 20. TPS65301-Q1 Eq24_SLVSBB6.gif

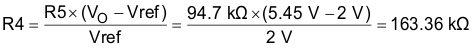
Use Equation 21 to calculate the value of R2 for this design example.

Equation 21. TPS65301-Q1 Eq25_SLVSBB6.gif

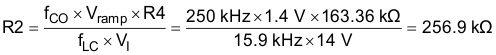
Calculate C3 based on placing a zero at 50% to 75% of the output-filter double-pole frequency (below set at 50%).

For this design example, use Equation 22 to calculate the value of C3 as 786 pF.

Equation 22. TPS65301-Q1 Eq26_SLVSBB6.gif

8.2.2.6.1.4 Gain of Amplifier

Equation 23. TPS65301-Q1 Eq35_SLVSBB6.gif

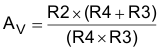
8.2.2.6.1.5 Poles and Zero Frequencies

The following equations were used in this design example:

Equation 24. TPS65301-Q1 Eq27_SLVSBB6.gif
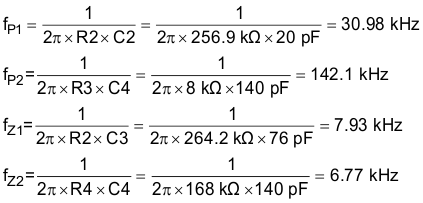
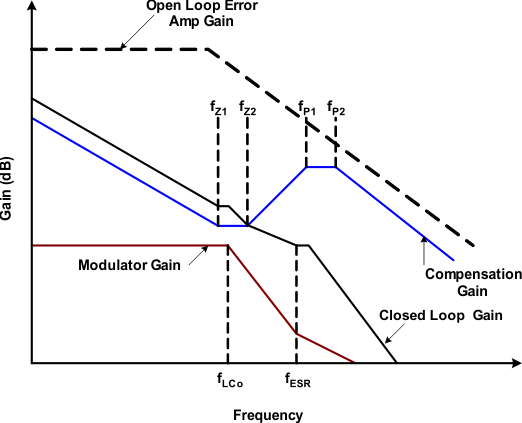TPS65301-Q1 TypGainVsFreq_SLVSBB6.gif Figure 15. Typical Gain vs Frequency

8.2.2.7 Power Dissipation

8.2.2.7.1 Switch-Mode Power-Supply Losses

The power dissipation losses are applicable for continuous-conduction mode operation (CCM).

  1. Conduction losses
    2. Equation 25. P5.45V_CON = IO2 × Rds(on) × (VO/VI)

    where

    • IO = Output current
    • VO = VREG = Output voltage
    • VI = Input voltage
    • fSW = Switching frequency
  2. Switching losses
    3. Equation 26. P5.45V_SW = ½ × VI × IO × (tr + tf) × fSW

    where

    • tr = FET switching rise time (tr max = 20 ns)
    • tf = FET switching fall time (tf max = 20 ns)
  3. Gate drive losses
    4. Equation 27. P5.45V_Gate = Vdrive × Qg × fsw

    where

    • Vdrive = FET gate-drive voltage (typically Vdrive = 6 V and Vdrive max = 8 V)
    • Qg = 1 × 10–9 (nC) (typical)
  4. Supply losses
    5. Equation 28. PIC = VI × Iq-normal

Therefore:

Equation 29. PTotal = PCON + PSW + PGate + P5V_Lin Reg + PIC

8.2.2.7.2 Linear Regulator (5V) and Sensor Supply (5VS)

Equation 30. P5V_Lin Reg = (VREG – 5 V) × IO_5V
Equation 31. P5VS_Lin Reg = (VREG – 5 V) × IO_5VS

Therefore, for this design, the following equations were used:

Equation 32. TPS65301-Q1 Eq28_SLVSBB6.gif

8.2.2.7.3 Total Power Dissipation

For given operating ambient temperature, TA:

Equation 33. TJ = TA + Rth × PTotal

where

  • TJ = Junction temperature in °C
  • TA = Ambient temperature in °C
  • Rth = Thermal resistance of package in (°C/W)
  • PTotal = Total power dissipation (watts)

For a given max junction temperature TJ-Max = 150°C

Equation 34. TA-Max = TJ-Max – Rth × PTotal

where

  • TA-Max = Maximum ambient temperature in °C
  • TJ-Max = Maximum junction temperature in °C

Other factors not included in the foregoing information which affect the overall efficiency and power losses are

  • Inductor AC and DC losses
  • Trace resistance and losses associated with the copper trace routing connection
  • Schottky diode
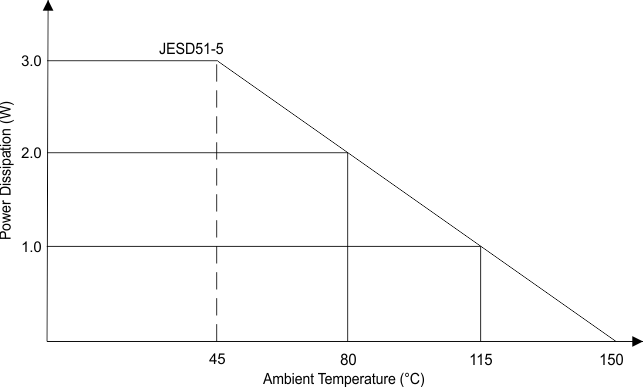TPS65301-Q1 PowerDiss_SLVSBB6.gif Figure 16. Power Dissipation Derating Profile, 24-Pin PWP Package With Thermal Pad

8.2.3 Application Curves

TPS65301-Q1 G001_SLVSBB6.gif
Figure 17. Efficiency vs Output Current on VREG
TPS65301-Q1 A002_SLVSBB6.gif
Figure 19. VREG Load Transient Response, 10 mA to 200 mA
TPS65301-Q1 A004_SLVSBB6.gif
Figure 21. VREG Load Transient Response, 10 mA to 350 mA
TPS65301-Q1 A001_SLVSBB6.gif
Figure 18. VREG Load Transient Response, 10 mA to 1 A
TPS65301-Q1 A003_SLVSBB6.gif
Figure 20. VREG Load Transient Response, 10 mA to 550 mA