JAJSFA5E September   2015  – April 2018 LMK03318

PRODUCTION DATA.  

  1. 1 特長
  2. 2 アプリケーション
  3. 3 概要
    1.     Device Images
      1.      LMK03318概略ブロック図
  4. 4 改訂履歴
  5. 5 概要（続き）
  6. 6 デバイス比較表
  7. 7 Pin Configuration and Functions
    1.     Pin Functions
  8. 8 Specifications
    1. 8.1  Absolute Maximum Ratings
    2. 8.2  ESD Ratings
    3. 8.3  Recommended Operating Conditions
    4. 8.4  Thermal Information
    5. 8.5  Thermal Information
    6. 8.6  Electrical Characteristics - Power Supply
    7. 8.7  Pullable Crystal Characteristics (SECREF_P, SECREF_N)
    8. 8.8  Non-Pullable Crystal Characteristics (SECREF_P, SECREF_N)
    9. 8.9  Clock Input Characteristics (PRIREF_P/PRIREF_N, SECREF_P/SECREF_N)
    10. 8.10 VCO Characteristics
    11. 8.11 PLL Characteristics
    12. 8.12 1.8-V LVCMOS Output Characteristics (OUT[7:0])
    13. 8.13 LVCMOS Output Characteristics (STATUS[1:0])
    14. 8.14 Open-Drain Output Characteristics (STATUS[1:0])
    15. 8.15 AC-LVPECL Output Characteristics
    16. 8.16 AC-LVDS Output Characteristics
    17. 8.17 AC-CML Output Characteristics
    18. 8.18 HCSL Output Characteristics
    19. 8.19 Power-On Reset Characteristics
    20. 8.20 2-Level Logic Input Characteristics (HW_SW_CTRL, PDN, GPIO[5:0])
    21. 8.21 3-Level Logic Input Characteristics (REFSEL, GPIO[3:1])
    22. 8.22 Analog Input Characteristics (GPIO[5])
    23. 8.23 I2C-Compatible Interface Characteristics (SDA, SCL)
    24. 8.24 Typical 156.25-MHz Closed-Loop Output Phase Noise Characteristics
    25. 8.25 Typical 161.1328125-MHz Closed-Loop Output Phase Noise Characteristics
    26. 8.26 Closed-Loop Output Jitter Characteristics
    27. 8.27 PCIe Clock Output Jitter
    28. 8.28 Typical Power Supply Noise Rejection Characteristics
    29. 8.29 Typical Power-Supply Noise Rejection Characteristics
    30. 8.30 Typical Closed-Loop Output Spur Characteristics
    31. 8.31 Typical Characteristics
  9. 9 Parameter Measurement Information
    1. 9.1 Test Configurations
  10. 10Detailed Description
    1. 10.1 Overview
    2. 10.2 Functional Block Diagram
    3. 10.3 Feature Description
      1. 10.3.1 Device Block-Level Description
      2. 10.3.2 Device Configuration Control
        1. 10.3.2.1 Hard-Pin Mode (HW_SW_CTRL = 1)
          1. 10.3.2.1.1 PLL Block
          2. 10.3.2.1.2 Output Buffer Auto Mute
          3. 10.3.2.1.3 Input Block
          4. 10.3.2.1.4 Channel Mux
          5. 10.3.2.1.5 Output Divider
          6. 10.3.2.1.6 Output Driver Format
          7. 10.3.2.1.7 Status MUX, Divider and Slew Rate
        2. 10.3.2.2 Soft-Pin Programming Mode (HW_SW_CTRL = 0)
          1. 10.3.2.2.1 Device Config Space
          2. 10.3.2.2.2 PLL Block
          3. 10.3.2.2.3 Output Buffer Auto Mute
          4. 10.3.2.2.4 Input Block
          5. 10.3.2.2.5 Channel Mux
          6. 10.3.2.2.6 Output Divider
          7. 10.3.2.2.7 Output Driver Format
          8. 10.3.2.2.8 Status MUX, Divider and Slew Rate
        3. 10.3.2.3 Register File Reference Convention
    4. 10.4 Device Functional Modes
      1. 10.4.1  Smart Input MUX
      2. 10.4.2  Universal Input Buffer (PRI_REF, SEC_REF)
      3. 10.4.3  Crystal Input Interface (SEC_REF)
      4. 10.4.4  Reference Doubler
      5. 10.4.5  Reference Divider (R)
      6. 10.4.6  Input Divider (M)
      7. 10.4.7  Feedback Divider (N)
      8. 10.4.8  Phase Frequency Detector (PFD)
      9. 10.4.9  Charge Pump
      10. 10.4.10 Loop Filter
      11. 10.4.11 VCO Calibration
      12. 10.4.12 Fractional Circuitry
        1. 10.4.12.1 Programmable Dithering Levels
        2. 10.4.12.2 Programmable Delta Sigma Modulator Order
      13. 10.4.13 Post Divider
      14. 10.4.14 High-Speed Output MUX
      15. 10.4.15 High-Speed Output Divider
      16. 10.4.16 High-Speed Clock Outputs
      17. 10.4.17 Output Synchronization
      18. 10.4.18 Status Outputs
        1. 10.4.18.1 Loss of Reference
        2. 10.4.18.2 Loss of Lock
    5. 10.5 Programming
      1. 10.5.1 I2C Serial Interface
      2. 10.5.2 Block Register Write
      3. 10.5.3 Block Register Read
      4. 10.5.4 Write SRAM
      5. 10.5.5 Write EEPROM
      6. 10.5.6 Read SRAM
      7. 10.5.7 Read EEPROM
      8. 10.5.8 Read ROM
      9. 10.5.9 Default Device Configurations in EEPROM and ROM
    6. 10.6 Register Maps
      1. 10.6.1   VNDRID_BY1 Register; R0
      2. 10.6.2   VNDRID_BY0 Register; R1
      3. 10.6.3   PRODID Register; R2
      4. 10.6.4   REVID Register; R3
      5. 10.6.5   PARTID Register; R4
      6. 10.6.6   PINMODE_SW Register; R8
      7. 10.6.7   PINMODE_HW Register; R9
      8. 10.6.8   SLAVEADR Register; R10
      9. 10.6.9   EEREV Register; R11
      10. 10.6.10  DEV_CTL Register; R12
      11. 10.6.11  INT_LIVE Register; R13
      12. 10.6.12  INT_MASK Register; R14
      13. 10.6.13  INT_FLAG_POL Register; R15
      14. 10.6.14  INT_FLAG Register; R16
      15. 10.6.15  INTCTL Register; R17
      16. 10.6.16  OSCCTL2 Register; R18
      17. 10.6.17  STATCTL Register; R19
      18. 10.6.18  MUTELVL1 Register; R20
      19. 10.6.19  MUTELVL2 Register; R21
      20. 10.6.20  OUT_MUTE Register; R22
      21. 10.6.21  STATUS_MUTE Register; R23
      22. 10.6.22  DYN_DLY Register; R24
      23. 10.6.23  REFDETCTL Register; R25
      24. 10.6.24  STAT0_INT Register; R27
      25. 10.6.25  STAT1 Register; R28
      26. 10.6.26  OSCCTL1 Register; R29
      27. 10.6.27  PWDN Register; R30
      28. 10.6.28  OUTCTL_0 Register; R31
      29. 10.6.29  OUTCTL_1 Register; R32
      30. 10.6.30  OUTDIV_0_1 Register; R33
      31. 10.6.31  OUTCTL_2 Register; R34
      32. 10.6.32  OUTCTL_3 Register; R35
      33. 10.6.33  OUTDIV_2_3 Register; R36
      34. 10.6.34  OUTCTL_4 Register; R37
      35. 10.6.35  OUTDIV_4 Register; R38
      36. 10.6.36  OUTCTL_5 Register; R39
      37. 10.6.37  OUTDIV_5 Register; R40
      38. 10.6.38  OUTCTL_6 Register; R41
      39. 10.6.39  OUTDIV_6 Register; R42
      40. 10.6.40  OUTCTL_7 Register; R43
      41. 10.6.41  OUTDIV_7 Register; R44
      42. 10.6.42  CMOSDIVCTRL Register; R45
      43. 10.6.43  CMOSDIV0 Register; R46
      44. 10.6.44  STATUS_SLEW Register; R49
      45. 10.6.45  IPCLKSEL Register; R50
      46. 10.6.46  IPCLKCTL Register; R51
      47. 10.6.47  PLL_RDIV Register; R52
      48. 10.6.48  PLL_MDIV Register; R53
      49. 10.6.49  PLL_CTRL0 Register; R56
      50. 10.6.50  PLL_CTRL1 Register; R57
      51. 10.6.51  PLL_NDIV_BY1 Register; R58
      52. 10.6.52  PLL_NDIV_BY0 Register; R59
      53. 10.6.53  PLL_FRACNUM_BY2 Register; R60
      54. 10.6.54  PLL_FRACNUM_BY1 Register; R61
      55. 10.6.55  PLL_FRACNUM_BY0 Register; R62
      56. 10.6.56  PLL_FRACDEN_BY2 Register; R63
      57. 10.6.57  PLL_FRACDEN_BY1 Register; R64
      58. 10.6.58  PLL_FRACDEN_BY0 Register; R65
      59. 10.6.59  PLL_MASHCTRL Register; R66
      60. 10.6.60  PLL_LF_R2 Register; R67
      61. 10.6.61  PLL_LF_C1 Register; R68
      62. 10.6.62  PLL_LF_R3 Register; R69
      63. 10.6.63  PLL_LF_C3 Register; R70
      64. 10.6.64  SEC_CTRL Register; R72
      65. 10.6.65  XO_MARGINING Register; R86
      66. 10.6.66  XO_OFFSET_GPIO5_STEP_1_BY1 Register; R88
      67. 10.6.67  XO_OFFSET_GPIO5_STEP_1_BY0 Register; R89
      68. 10.6.68  XO_OFFSET_GPIO5_STEP_2_BY1 Register; R90
      69. 10.6.69  XO_OFFSET_GPIO5_STEP_2_BY0 Register; R91
      70. 10.6.70  XO_OFFSET_GPIO5_STEP_3_BY1 Register; R92
      71. 10.6.71  XO_OFFSET_GPIO5_STEP_3_BY0 Register; R93
      72. 10.6.72  XO_OFFSET_GPIO5_STEP_4_BY1 Register; R94
      73. 10.6.73  XO_OFFSET_GPIO5_STEP_4_BY0 Register; R95
      74. 10.6.74  XO_OFFSET_GPIO5_STEP_5_BY1 Register; R96
      75. 10.6.75  XO_OFFSET_GPIO5_STEP_5_BY0 Register; R97
      76. 10.6.76  XO_OFFSET_GPIO5_STEP_6_BY1 Register; R98
      77. 10.6.77  XO_OFFSET_GPIO5_STEP_6_BY0 Register; R99
      78. 10.6.78  XO_OFFSET_GPIO5_STEP_7_BY1 Register; R100
      79. 10.6.79  XO_OFFSET_GPIO5_STEP_7_BY0 Register; R101
      80. 10.6.80  XO_OFFSET_GPIO5_STEP_8_BY1 Register; R102
      81. 10.6.81  XO_OFFSET_GPIO5_STEP_8_BY0 Register; R103
      82. 10.6.82  XO_OFFSET_SW_BY1 Register; R104
      83. 10.6.83  XO_OFFSET_SW_BY0 Register; R105
      84. 10.6.84  PLL_CTRL2 Register; R117
      85. 10.6.85  PLL_CTRL3 Register; R118
      86. 10.6.86  PLL_CALCTRL0 Register; R119
      87. 10.6.87  PLL_CALCTRL1 Register; R120
      88. 10.6.88  NVMCNT Register; R136
      89. 10.6.89  NVMCTL Register; R137
      90. 10.6.90  NVMLCRC Register; R138
      91. 10.6.91  MEMADR_BY1 Register; R139
      92. 10.6.92  MEMADR_BY0 Register; R140
      93. 10.6.93  NVMDAT Register; R141
      94. 10.6.94  RAMDAT Register; R142
      95. 10.6.95  ROMDAT Register; R143
      96. 10.6.96  NVMUNLK Register; R144
      97. 10.6.97  REGCOMMIT_PAGE Register; R145
      98. 10.6.98  XOCAPCTRL_BY1 Register; R199
      99. 10.6.99  XOCAPCTRL_BY0 Register; R200
      100. 10.6.100 EEPROM Map
  11. 11Application and Implementation
    1. 11.1 Application Information
    2. 11.2 Typical Applications
      1. 11.2.1 Application Block Diagram Examples
      2. 11.2.2 Jitter Considerations in Serdes Systems
      3. 11.2.3 Frequency Margining
        1. 11.2.3.1 Fine Frequency Margining
        2. 11.2.3.2 Coarse Frequency Margining
      4. 11.2.4 Design Requirements
        1. 11.2.4.1 Detailed Design Procedure
          1. 11.2.4.1.1 Device Selection
            1. 11.2.4.1.1.1 Calculation Using LCM
          2. 11.2.4.1.2 Device Configuration
          3. 11.2.4.1.3 PLL Loop Filter Design
            1. 11.2.4.1.3.1 PLL Loop Filter Design
          4. 11.2.4.1.4 Clock Output Assignment
        2. 11.2.4.2 Spur Mitigation Techniques
          1. 11.2.4.2.1 Phase Detector Spurs
          2. 11.2.4.2.2 Integer Boundary Fractional Spurs
          3. 11.2.4.2.3 Primary Fractional Spurs
          4. 11.2.4.2.4 Sub-Fractional Spurs
  12. 12Power Supply Recommendations
    1. 12.1 Device Power Up Sequence
    2. 12.2 Device Power Up Timing
    3. 12.3 Power Down
    4. 12.4 Power Rail Sequencing, Power Supply Ramp Rate, and Mixing Supply Domains
      1. 12.4.1 Mixing Supplies
      2. 12.4.2 Power-On Reset
      3. 12.4.3 Powering Up From Single-Supply Rail
      4. 12.4.4 Powering Up From Split-Supply Rails
      5. 12.4.5 Slow Power-Up Supply Ramp
      6. 12.4.6 Non-Monotonic Power-Up Supply Ramp
      7. 12.4.7 Slow Reference Input Clock Startup
    5. 12.5 Power Supply Bypassing
  13. 13Layout
    1. 13.1 Layout Guidelines
      1. 13.1.1 Ensure Thermal Reliability
      2. 13.1.2 Support for PCB Temperature up to 105°C
    2. 13.2 Layout Example
  14. 14デバイスおよびドキュメントのサポート
    1. 14.1 デバイス・サポート
      1. 14.1.1 デベロッパー・ネットワークの製品に関する免責事項
    2. 14.2 ドキュメントの更新通知を受け取る方法
    3. 14.3 コミュニティ・リソース
    4. 14.4 商標
    5. 14.5 静電気放電に関する注意事項
    6. 14.6 Glossary
  15. 15メカニカル、パッケージ、および注文情報

パッケージ・オプション

メカニカル・データ（パッケージ｜ピン）
サーマルパッド・メカニカル・データ
発注情報

10.4.12.2 Programmable Delta Sigma Modulator Order

The programmable fractional modulator order gives the opportunity to better optimize phase noise and spurs. Theoretically, higher order modulators push out phase noise to farther offsets, as described in Table 6.

Table 6. Delta Sigma Modulator Order Recommendations

ORDER APPLICATIONS
Integer Mode (Order = 0) If the fractional numerator is zero, it is best to run the PLL in integer mode to minimize phase noise and spurs.
First Order Modulator When the equivalent fractional denominator is 6 or less, the first order modulator theoretically has lower phase noise and spurs, so it always makes sense in these situations. When the fractional denoninator is between 6 and about 20, consider using the first order modulator because the spurs might be far enough outside the loop bandwidth that they will be filtered. The first order modulator also does not create any sub-fractional spurs or phase noise.
Second and Third Order Modulator The choice between 2nd and 3rd order modulator tends to be a little more application specific. If the fractional denominator is not divisible by 3, then the second and third order modulators will have spurs in the same offsets, so the third is generally better for spurs. However, if stronger levels of dithering is used, the third order modulator will create more close-in phase noise than the second order modulator.

Figure 59 and Figure 60 give an idea of the theoretical impact of the delta sigma modulator order on the shaping of the phase noise and spurs. In terms of phase noise, this is what one would theoretically expect if strong dithering was used for a well-randomized fraction. Dithering can be set to different levels or even disabled and the noise can be eliminated. In terms of spurs, they can change based on fraction, but they will theoretically pushed out to higher phase detector frequencies. However, one must be aware that these are just THEORETICAL graphs and for offsets that are less than 5% of the phase detector frequency, other factors can impact the noise and spurs. In Figure 59, the curves all cross at 1/6th of the phase detector frequency and that this transfer function peaks at half of the phase detector frequency, which is assumed to be well outside the loop bandwidth. Figure 60 shows the impact of the phase detector frequency on the modulator noise.

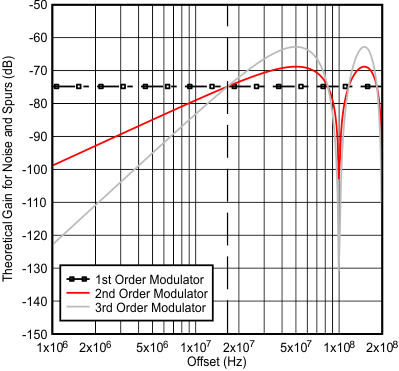LMK03318 theoretical_delta_sigma_noise_shaping_100mhz_snas668.gifFigure 59. Theoretical Delta Sigma Noise Shaping for a 100 MHz Phase Detector Frequency
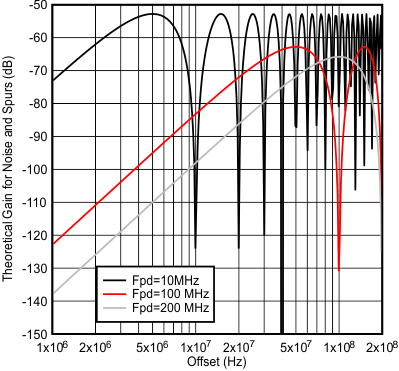LMK03318 theoretical_delta_sigma_noise_shaping_3rd_order_snas668.gifFigure 60. Theoretical Delta Sigma Noise Shaping for 3rd Order Modulator