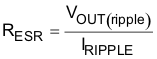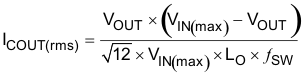8.2.2.3 Output Capacitor

The three primary considerations for selecting the value of the output capacitor are: the output capacitor determines the modulator pole, the output-voltage ripple, and how the regulator responds to a large change in load current. Select the output capacitance based on the most stringent of these three criteria.

The desired response to a large change in the load current is the first criterion. The output capacitor must supply the load with current when the regulator cannot. This situation would occur if there are desired hold-up times for the regulator where the output capacitor must hold the output voltage above a certain level for a specified amount of time after the input power is removed. The regulator also temporarily is not able to supply sufficient output current if there is a large, fast increase in the current needs of the load, such as transitioning from no load to a full load. The regulator usually needs two or more clock cycles for the control loop to see the change in load current and output voltage and adjust the duty cycle to react to the change. The output-capacitor size must be adequate to supply the extra current to the load until the control loop responds to the load change. The output capacitance must be large enough to supply the difference in current for two clock cycles while only allowing a tolerable amount of droop in the output voltage. Calculate the minimum output capacitance necessary to accomplish this using Equation 32.

For this example, the transient load response is specified as a 4% change in Vout for a load step from 0 A (no load) to 1.5 A (full load). For this example, ΔIout = 1.5 – 0 = 1.5 A and ΔVout = 0.04 × 3.3 V = 0.132 V. Using these numbers gives a minimum capacitance of 18.9 μF. This value does not take the ESR of the output capacitor into account in the output-voltage change. For ceramic capacitors, the ESR is usually small enough to ignore in this calculation. Aluminum electrolytic and tantalum capacitors have higher ESR that the designer must take into account.

The catch diode of the regulator cannot sink current, so any stored energy in the inductor produces an output voltage overshoot when the load current rapidly decreases, see Figure 53. The output capacitor must also be sized to absorb energy stored in the inductor when transitioning from a high load current to a lower load current. The excess energy that is stored in the output capacitor increases the voltage on the capacitor. The capacitor must be sized to maintain the desired output voltage during these transient periods. UseEquation 33 to calculate the minimum capacitance to keep the output voltage overshoot to a desired value. For this example, the worst-case load step is from 1.5 to 0 A. The output voltage increases during this load transition, and the stated maximum in our specification is 4% of the output voltage. This makes Vf = 1.04 × 3.3 = 3.432. Vi is the initial capacitor voltage, which is the nominal output voltage of 3.3 V. Using these numbers in Equation 33 yields a minimum capacitance of 25.3 μF.

Use Equation 34 to calculate the minimum output capacitance needed to meet the ripple specification for output voltage. Equation 34 yields 0.7 μF.

Use Equation 35 to calculate the maximum ESR an output capacitor can have to meet the ripple specification for the output voltage. Equation 35 indicates the ESR should be less than 147 mΩ.

The most stringent criterion for the output capacitor is 25.3 μF of capacitance to keep the output voltage in regulation during an unload transient.

Factor in additional capacitance deratings for aging, temperature, and dc bias, increasing this minimum value. For this example, select a 47-μF 6.3-V X7R ceramic capacitor with 5 mΩ of ESR.

Capacitors generally have limits to the amount of ripple current they can handle without failing or producing excess heat. Specify an output capacitor that can support the inductor ripple current. Some capacitor data sheets specify the root-mean-square (RMS) value of the maximum ripple current. Use Equation 36 to calculate the RMS ripple current that the output capacitor must support. For this application, Equation 36 yields 64.8 mA.

Equation 32.

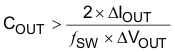
where

• ΔIout is the change in output current.
• ƒ_SW is the switching frequency of the regulator.
• ΔVout is the allowable change in the output voltage.

Equation 33.

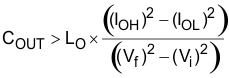
where

• L is the value of the inductor.
• I_OH is the output current under heavy load.
• I_OL is the output under light load.
• VF is the final peak output voltage.
• Vi is the initial capacitor voltage

Equation 34.

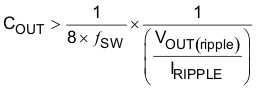
where

• ƒ_SW is the switching frequency.
• V_oripple is the maximum allowable output-voltage ripple.
• I_ripple is the ripple current of the inductor.

Equation 35.

Equation 36.