JAJSJ29E May 2020 – October 2024 TPS61378-Q1
PRODUCTION DATA
- 1
- 1 特長
- 2 アプリケーション
- 3 概要
- 4 Device Comparison Table
- 5 Pin Configuration and Functions
- 6 Specifications
-
7 Detailed Description
- 7.1 Overview
- 7.2 Functional Block Diagram
- 7.3
Feature Description
- 7.3.1 VCC Power Supply
- 7.3.2 Input Undervoltage Lockout (UVLO)
- 7.3.3 Enable and Soft Start
- 7.3.4 Shut Down
- 7.3.5 Switching Frequency Setting
- 7.3.6 Spread Spectrum Frequency Modulation
- 7.3.7 Adjustable Peak Current Limit
- 7.3.8 Bootstrap
- 7.3.9 Load Disconnect
- 7.3.10 MODE/SYNC Configuration
- 7.3.11 Overvoltage Protection (OVP)
- 7.3.12 Output Short Protection/Hiccup
- 7.3.13 Power-Good Indicator
- 7.3.14 Thermal Shutdown
- 7.4 Device Functional Modes
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Application
- 8.2.1 Design Requirements
- 8.2.2 Detailed Design Procedure
- 8.2.3 Application Curves
- 9 Power Supply Recommendations
- 10Layout
- 11Device and Documentation Support
- 12Revision History
- 13Mechanical, Packaging, and Orderable Information
パッケージ・オプション
メカニカル・データ(パッケージ|ピン)
- RTE|16
サーマルパッド・メカニカル・データ
- RTE|16
発注情報
8.2.2.4 Selecting the Inductor
A boost converter normally requires two main passive components for storing energy during power conversion: an inductor and an output capacitor. The inductor affects the steady state efficiency (including the ripple and efficiency), transient behavior, and loop stability, which makes the inductor the most critical component in application.
When selecting the inductor and the inductance, the other important parameters are:
- The maximum current rating (RMS and peak current should be considered)
- The series resistance
- Operating temperature
The TPS61378-Q1 has built-in slope compensation to avoid subharmonic oscillation associated with current mode control. If the inductor value is too low and makes the inductor peak-to-peak ripple higher than 2 A, the slope compensation may not be adequate, and the loop can be unstable. Therefore, it is recommended to make the peak-to-peak current ripple between 800 mA to 2 A when selecting the inductor.
The inductance can be calculated by Equation 6, Equation 7, and Equation 8:
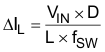
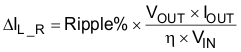
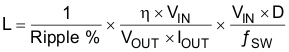
where
- ΔIL is the peak-peak inductor current ripple
- VIN is the input voltage
- D is the duty cycle
- L is the inductor
- ƒSW is the switching frequency
- Ripple % is the ripple ration versus the DC current
- VOUT is the output voltage
- IOUT is the output current
- η is the efficiency
The current flowing through the inductor is the inductor ripple current plus the average input current. During power up, load faults, or transient load conditions, the inductor current can increase above the peak inductor current calculated.
Inductor values can have ±20%, or even ±30%, tolerance with no current bias. When the inductor current approaches the saturation level, the inductance can decrease 20% to 35% from the value at 0-A bias current, depending on how the inductor vendor defines saturation. When selecting an inductor, make sure the rated current, especially the saturation current, is larger than its peak current during the operation.
The inductor peak current varies as a function of the load, switching frequency, and input and output voltages. The peak current can be calculated with Equation 9 and Equation 10.
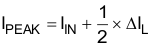
where
- IPEAK is the peak current of the inductor
- IIN is the input average current
- ΔIL is the ripple current of the inductor
The input DC current is determined by the output voltage. The output current can be calculated by:
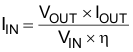
where
- IIN is the input current of the inductor
- VOUT is the output voltage
- VIN is the input voltage
- η is the efficiency
While the inductor ripple current depends on the inductance, the frequency, the input voltage, and duty cycle are calculated by Equation 6. Replace Equation 6 and Equation 10 into Equation 9 and get the inductor peak current:
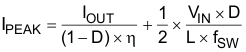
where
- IPEAK is the peak current of the inductor
- IOUT is the output current
- D is the duty cycle
- η is the efficiency
- VIN is the input voltage
- L is the inductor
- ƒSW is the switching frequency
The heat rating current (RMS) is can be calculated with Equation 12:
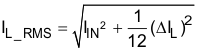
where
- IL_RMS is the RMS current of the inductor
- IIN is the input current of the inductor
- ΔIL is the ripple current of the inductor
It is important that the peak current does not exceed the inductor saturation current and the RMS current is not over the temperature-related rating current of the inductors.
For a given physical inductor size, increasing inductance usually results in an inductor with lower saturation current. The total losses of the coil consists of the DC resistance (DCR) loss and the following frequency-dependent loss:
- The losses in the core material (magnetic hysteresis loss, especially at high switching frequencies)
- Additional losses in the conductor from the skin effect (current displacement at high frequencies)
- Magnetic field losses of the neighboring windings (proximity effect)
For a certain inductor, the larger current ripple (smaller inductor) generates the higher DC and also the frequency-dependent loss. An inductor with lower DCR is basically recommended for higher efficiency. However, it is usually a tradeoff between the loss and foot print. Table 8-2 lists some recommended inductors.
| PART NUMBER | L (μH) | DCR TYP (mΩ) MAX | SATURATION CURRENT (A) | SIZE (L × W × H mm) | VENDOR(1) |
|---|---|---|---|---|---|
| XEL4030-471MEB | 0.47 | 4.1 | 15.5 | 4 x 4 x 3 | Coilcraft |
| XEL4030-102MEB | 1 | 8.9 | 9 | 4 x 4 x 3 | Coilcraft |
| DFE2HCAHR47MJ0L | 0.47 | 25 | 5.1 | 2.5 x 2 x 1.2 | Murata |
| DFE322520FD-1R0M | 1 | 22 | 7.5 | 3.2 x 2.5 x 2 | Murata |
| TFM322512ALMAR47MTAA | 0.47 | 16 | 7.6 | 3.2 x 2.5 x 1.2 | TDK |
| TFM322512ALMA1R0MTAA | 1 | 30 | 5.1 | 3.2 x 2.5 x 1.2 | TDK |