JAJU510H March 2018 – December 2022
- 概要
- リソース
- 特長
- アプリケーション
- 5
- 1System Description
- 2System Overview
-
3Hardware, Software, Testing Requirements, and Test Results
- 3.1 Required Hardware and Software
- 3.2 Testing and Results
- 4Design Files
- 5Trademarks
- 6About the Authors
- 7Revision History
2.3.6.1 Current Loop Design
For the inverter filter shown in Figure 2-45, using KCL and KVL Equation 49 can be written.
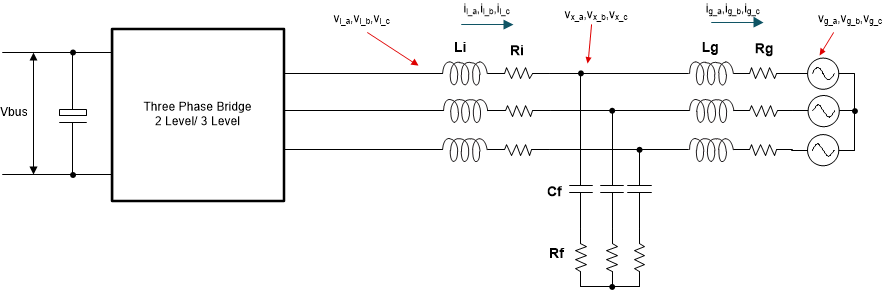 Figure 2-45 Inverter Model
Figure 2-45 Inverter Model
Upon re-arranging, Equation 49 can be written as Equation 36:
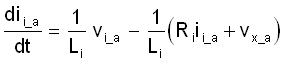
Similarly on another node, using KCL and KVL, Equation 37 can be written as Equation 37:

Assuming Rf is negligible Equation 38 can be written for the capacitor voltage:

Typically a synchronous reference frame control is designed, where a dq rotating reference frame at grid frequency speed, and oriented such that the d axis is aligned to the grid voltage vector is used. Using basic trigonometric identities, id and iq can be written as Equation 39 and Equation 40.

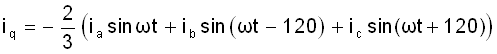
Taking the derivative, and using the partial derivative theorem, Equation 41 is written:
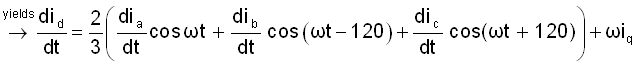

The following state equations can be written:


Hence, using these equations, and substituting in Equation 44:

Taking the Laplace function on the previous equations:

When written in control diagram format, this looks like the following. Feedforward elements are added to remove additional sources of disturbances and errors in the model, two feedforward elements are added,
- For the coupling term from the other axis in synchronous frame
- For the output grid voltage
The diagram is drawn as shown in Figure 2-46.
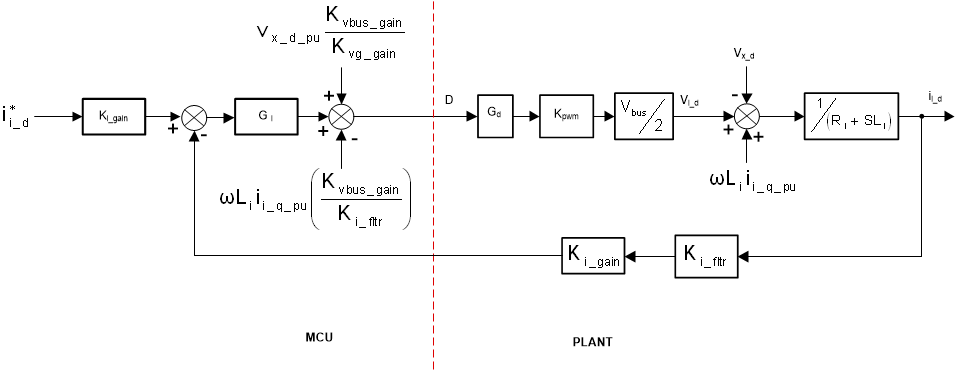
where:
- i*i_d is the current reference
- Ki_gain is the current sense scalar which is one over max current sense
- Ki_fltr is the filter that is connected on the current sense path. current sense scalar which is one over max current sense
- Kvbus_gain is the voltage sense scalar for the bus, which is one over max voltage sensed
- Kvg_gain is the voltage sense scalar for the grid voltage, which is one over max voltage sensed
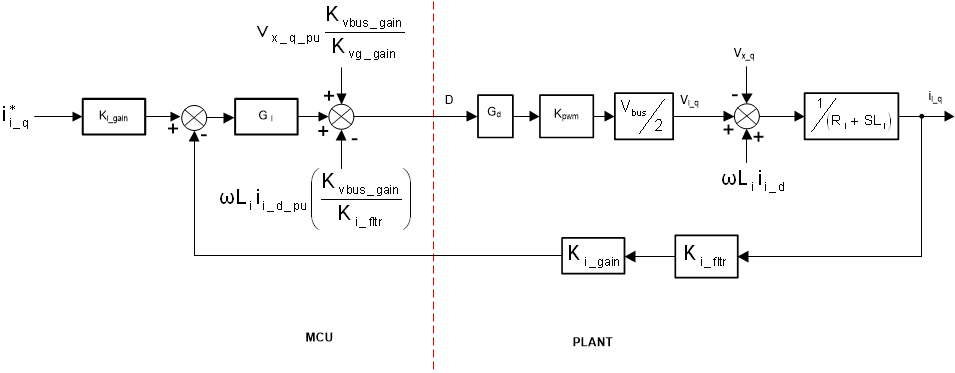 Figure 2-47 Iq Current Loop Model
Figure 2-47 Iq Current Loop ModelWith the feedforward elements, the small signal model can be written as Equation 46(Note: Separate scaling factors are applied to bus voltage and grid voltage due to the differences in the sensing range.):

In the case of an LCL filter, the following can be assumed as a simplified model as in Equation 47:

The current loop plant is compared with the SFRA measured data for the current loop as illustrated in Figure 2-48.
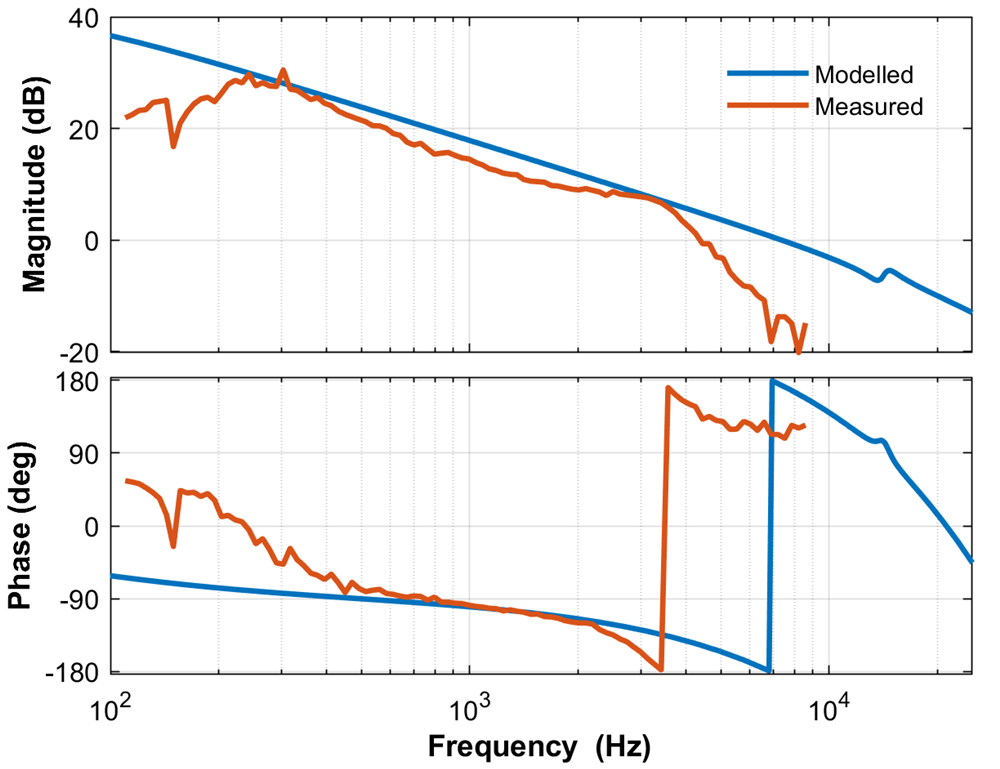 Figure 2-48 Current Loop Plant Frequency
Response Modelled vs Measured
Figure 2-48 Current Loop Plant Frequency
Response Modelled vs MeasuredEquation 48 represents the compensator designed for the closed-loop operation:

With which the open loop plot in Figure 2-49 is achieved, gives roughly > 1-kHz bandwidth in the Id and Iq loop.
 Figure 2-49 Current Loop, Open Loop
Response Modelled vs Measured
Figure 2-49 Current Loop, Open Loop
Response Modelled vs Measured