KOKT050 Technical article

KOKT050 February 2024 UCC28C50

1
2
1. 3
2. 관련 문서

John Betten

플라이백 컨버터는 연속 전도 모드(CCM) 또는 불연속 전도 모드(DCM)에서 작동할 수 있습니다. 그러나 많은 저전력 및 저전류 애플리케이션의 경우 DCM 플라이백 컨버터는 더 컴팩트하고 저렴한 옵션을 제공할 수 있습니다. 다음은 그러한 설계 과정을 단계별로 순서에 따라 설명한 것입니다.

DCM 작동은 다음 스위칭 사이클이 시작되기 전에 정류기 전류가 0으로 감소하는 컨버터가 특징입니다. 스위칭 전에 전류를 0으로 낮추면 전계 효과 트랜지스터(FET)의 소산이 줄어들고 정류기 손실이 감소하며, 변압기 크기 요구 사항도 줄어드는 경우가 많습니다.

이에 비해 CCM 작동은 스위칭 기간 종료 시 정류기 전류 전도를 유지합니다. 파워 팁 #76: 플라이백 컨버터 설계 고려 사항과 파워 팁 #77: CCM 플라이백 컨버터 설계하기에서 플라이백 설계 트레이드오프와 CCM 플라이백을 위한 전력계 방정식을 다룹니다. CCM 작동은 중간 전력~고전력 애플리케이션에 가장 적합하지만 DCM 플라이백을 사용할 수 있는 저전력 애플리케이션이 있는 경우 계속 읽어보십시오.

그림 1은(는) DCM 또는 CCM 모드에서 작동할 수 있는 간소화된 플라이백 회로도입니다. 또한 회로는 타이밍에 따라 모드 사이를 오갈 수 있습니다. DCM 모드에서 작동을 유지하려면(이것이 이 글의 평가 대상입니다) 주요 구성 요소 스위칭 파형은 그림 2에 나와 있는 특성을 가져야 합니다.

작동은 FET Q1이 듀티 사이클 기간 D에 대해 켜질 때 시작됩니다. T1차 권선의 전류는 항상 0에서 시작되며 1차 권선 인덕턴스, 입력 전압 및 온 시간 T1에 의해 설정된 피크에 도달합니다. 이 FET 온 타임 동안 다이오드 D1은 T1의 2차 권선 극성으로 인해 역방향 바이어스 상태가 됩니다. 따라서 t1과 t3 사이에는 출력 커패시터 COUT로 모든 출력 전류를 공급해야 합니다.

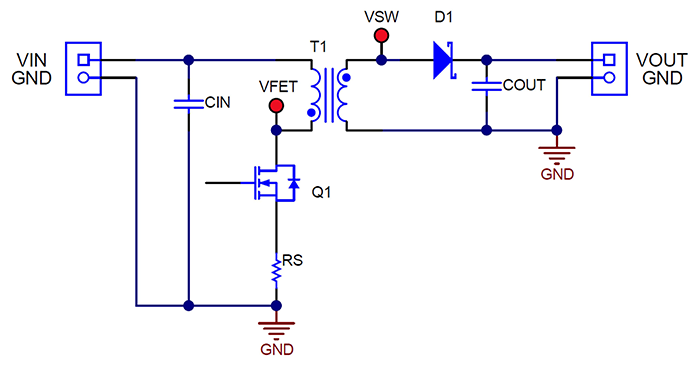그림 1 이 간소화된 플라이백 컨버터는 DCM 또는 CCM에서 작동할 수 있습니다.

기간 1-D 중 Q1이 꺼지면 T1의 2차 전압 극성이 역전되며, 그에 따라 D1이 부하로 전류를 전도하고 재충전할 수 있습니다. D1의 전류는 시간 t2에서 피크에서 0으로 선형적으로 감소합니다. T1의 저장 에너지가 소진되면 나머지 기간 t3 중에는 잔류 링잉만 발생합니다. 이 링잉은 주로 T1의 자화 인덕턴스와 Q1, D1 및 T1의 기생 커패시턴스로 인해 발생합니다. 이는 t3 중에 Q1의 드레인 전압으로 쉽게 확인할 수 있으며, T1은 전류 흐름이 중지되면 전압을 지원할 수 없기 때문에 VIN에 반사된 출력 전압을 더한 값은 다시 VIN으로 감소합니다. (참고: t3에 적절한 데드 타임이 없으면 CCM 작동이 발생할 수 있습니다.) CIN과 COUT의 전류는 Q1 및 D1의 전류와 동일하지만 DC 오프셋이 없습니다.

그림 2에서 음영 영역 A와 B는 t1과 t2 에서 변압기의 볼트-마이크로초 제품을 강조 표시한 것입니다. 이 제품은 포화를 방지하기 위해 균형을 유지해야 합니다. 영역 "A"는 (Vin/NPS) × t1을 나타내고, "B"는 (Vout+VD) × t2를 나타내며, 둘 다 2차측을 나타냅니다. Np/Ns는 변압기 1차 대비 2차 변환 비율입니다.

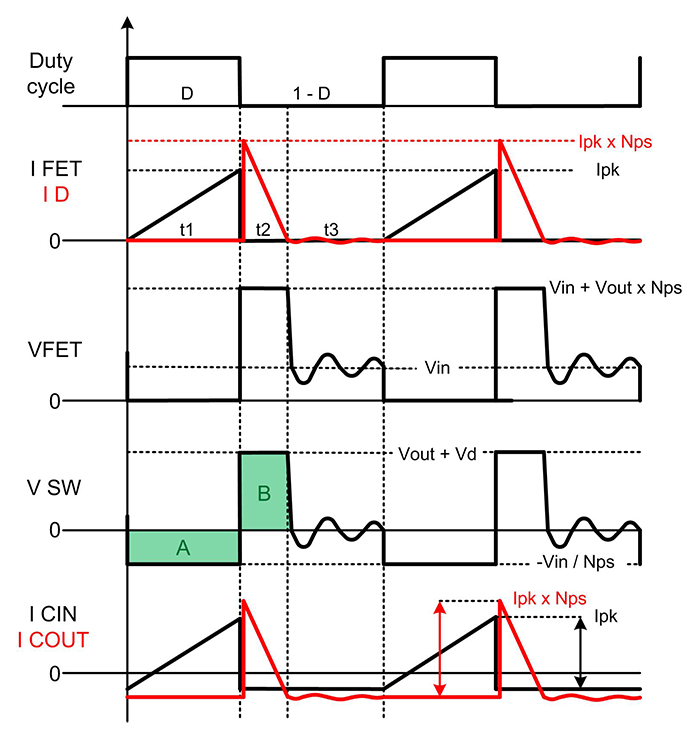그림 2 DCM 플라이백용 주요 전압 및 전류 스위칭 파형에는 설계자가 지정해야 하는 몇 가지 중요한 매개 변수가 포함되어 있습니다.

표 1은 CCM 대비 DCM 작동의 특성을 자세히 보여줍니다 한 가지 주요 DCM 속성은 변압기의 변환 비율에 관계없이 1차 인덕턴스가 낮아질 경우 듀티 사이클이 감소한다는 것입니다. 이 속성을 이용하면 설계에서 최대 듀티 사이클을 제한할 수 있습니다. 이는 특정 컨트롤러를 사용하거나 특정 켜짐 또는 꺼짐 시간 제한 내에 머무르려는 경우 중요할 수 있습니다. 인덕턴스가 낮을수록 평균 에너지 저장 장치(피크 FET 전류가 높기는 하지만)가 필요하며, 또한 CCM 설계에 필요한 것보다 더 작은 변압기를 허용하는 경우가 많습니다.

또 다른 DCM의 장점은 t2 의 끝에서 전류가 0이기 때문에 설계가 표준 정류기에서 D1 역방향 복구 손실을 제거한다는 점입니다. 역복구 손실은 Q1에서 소산 증가로 나타나는 경우가 많기 때문에 이것을 제거하면 스위칭 트랜지스터의 응력이 줄어듭니다. 이러한 이점은 더 높은 전압 정격 다이오드로 정류기에서 역방향 복구 시간이 증가하는 더 높은 출력 전압에서 그 중요성이 더 커집니다.

표 1 DCM 플라이백 설계에는 CCM 설계 대비 장점과 단점이 모두 있습니다.

DCM의 장점	DCM의 단점
1차 인덕턴스가 CCM에 비해 낮습니다	피크 1차 전류 더 높습니다
인덕턴스는 최대 듀티 사이클을 설정합니다	피크 정류기 전류가 더 높습니다
더 작은 변압기 가능	입력 커패시턴스 증가
정류기 역방향 복구 손실이 없습니다	출력 커패시턴스 증가
FET 턴온 손실이 없거나 최소 수준입니다	전자기 간섭이 증가할 수 있습니다
제어 루프에 오른쪽 반평면 0이 없습니다	CCM보다 듀티 사이클 작동 폭이 더 넓습니다
저출력 전력에 최적	대역폭 변화 증가

개발자는 기본 전기 사양과 함께 설계를 시작할 때 몇 가지 주요 매개 변수를 알아야 합니다. 스위칭 주파수(f_SW), 원하는 최대 작동 듀티 사이클(D_max) 및 예상 대상 효율성을 선택하는 것으로 시작합니다. 방정식 1에서는 그런 다음 시간 t1을 다음과 같이 계산합니다.

방정식 1.

t 1 = \frac{D m a x}{f s w}

다음, 방정식 2을(를) 사용하여 변압기의 피크 1차 전류 IPK를 추정합니다. 방정식 2에서는 FET의 온 전압(VDS_ON)과 전류 감지 저항 전압(VRS)의 경우 설계에 적합한 작은 전압 강하(예: 0.5V)를 가정합니다. 이 전압 강하는 나중에 업데이트할 수 있습니다.

방정식 2.

I p k = \frac{{P o u t}_{m a x} \times (\frac{2}{D_{m a x}})}{({V i n}_{m i n} - V d s_o n - V R S) \times (n)}

방정식 3은(는) 그림 2‌에서 동등한 영역 A 및 B를 기준으로 필요한 트랜스포머 변환 비율 Np/Ns를 계산합니다.

방정식 3.

\frac{N p}{N s} = \frac{({V i n}_{m i n} - V d s_o n - V R S) \times t 1}{(\frac{1}{f s w} \times (1 - x) - t 1) \times (V o u t + V d)}

여기서 x는 t3에 대해 원하는 최소 유휴 시간입니다(x = 0.2로 시작).

Np/Ns를 변경하려면 D_max를 조정하고 다시 반복하십시오.

그런 다음, 방정식 4 및 방정식 5을(를) 사용하여 Q1(VDS_max) 및 D1(VPIV_max)의 최대 "플랫 톱" 전압을 계산합니다.

방정식 4.

{V d s}_{m a x} = {V i n}_{m a x} + (V o u t + V d) \times \frac{N p}{N s}

방정식 5.

V P I V_m a x = V o u t + \frac{V i n_m a x}{\frac{N p}{N s}}

이러한 구성 요소에서는 일반적으로 변압기 누설 인덕턴스로 인해 링잉이 발생하므로 경험 법칙에 따르면 실제 값이 방정식 4 및 방정식 5 예측보다 10~30% 더 높을 것으로 예상됩니다 VDS_max가 예상보다 높은 경우 D_max를 줄이면 값이 낮아지지만 VPIV_max는 증가합니다. 어느 구성 요소 전압이 더 중요한지 확인하고 필요한 경우 다시 반복하십시오.

방정식 1을(를) 사용하여 t1_max를 계산합니다 . 이 값은 방정식 6에서 그 수치에 가까워야 합니다.

방정식 6.

t 1_m a x = \frac{(V o u t + V d) \times \frac{N p}{N s} \times (\frac{1}{f s w} \times (1 - x))}{{V i n}_{m i n} + (V o u t + V d) \times \frac{N p}{N s}}

방정식 7을(를) 이용하여 필요한 최대 1차 인덕턴스를 계산합니다.

방정식 7.

L p r i_m a x = \frac{{V i n_m i n}^{2} \times {t 1_m a x}^{2} \times n \times f s w}{2 \times V o u t \times I o u t_m a x}

방정식 7에서 표시하는 것보다 낮은 인덕턴스를 선택하는 경우 필요에 따라 반복하여 Np/Ns 및 Lpri_max 가 원하는 값과 일치할 때까지 x 를 늘리고 D_max를 줄입니다.

이제 방정식 7에서 D_max를 계산할 수 있습니다.

방정식 8.

D m a x = \sqrt{\frac{2 \times f s w \times V o u t \times I o u t_m a x \times L p r i}{{V i n_m i n}^{2} \times n}}

그리고 방정식 9와(과) 방정식 10을(를) 사용하여 최대 Ipk 및 최대 RMS(Root Mean-Square) 값을 각각 계산합니다.

방정식 9.

I p k m a x = \sqrt{\frac{2 \times V o u t \times I o u t_m a x}{L p r i \times f s w \times n}}

방정식 10.

I p k r m s = I p k m a x \sqrt{\frac{D m a x}{3}}

선택한 컨트롤러의 전류 감지 입력 최소 전류 한도 임계값인 VCS(방정식 11)를 기반으로 허용된 최대 전류 감지 저항 값을 계산합니다.

방정식 11.

R s m a x = \frac{V c s}{I p k m a x}

방정식 11의 Ipkmax 에 대해 계산된 값을 사용하여 방정식 2의 FET VDS 및 감지 저항 VRS에 대한 가정된 전압이 가까운지 확인하고, 상당히 다른 경우 다시 반복하십시오.

방정식 12와(과) 방정식 13을(를) 사용하여 방정식 10에서 Q1의 RS에서 소모되는 최대 전력과 전도 손실을 계산합니다.

방정식 12.

P R s n s = {I p k r m s}^{2} \times R S

방정식 13.

P F E T c o n d = {I p k r m s}^{2} \times R d s o n

FET 스위칭 손실은 일반적으로 Vinmax에서 가장 높으므로, 방정식 14을(를) 사용하여 Vin의 전체 범위에 걸쳐 Q1 스위칭 손실을 계산하는 것이 가장 좋습니다.

방정식 14.

P F E T s w = 0.25 \times (\frac{Q d r v}{I d r v}) \times f s w \times I p k \times V d s

여기서 Qdrv는 FET 총 게이트 전하이고, Idrv는 예상 피크 게이트 드라이브 전류입니다.

방정식 15와(과)* 방정식 16은(는) FET의 비선형 Coss 커패시턴스의 충전 및 방전으로 인한 총 전력 손실을 계산합니다. 방정식 15의 피적분 함수는 0V와 실제 작동 Vds 사이의 실제 FET의 Coss 데이터 시트 곡선과 가깝게 일치해야 합니다. Coss 손실은 일반적으로 고전압 애플리케이션에서, 또는 Coss 값이 더 큰, 초저 RDS(on) FET 사용 시 가장 큽니다.

방정식 15.

Q t o t = \int_{- V d s}^{0} [\frac{C o s s (0 V)}{{(1 - v)}^{0.5}}] d v

방정식 16.

P F E T c o s s = \frac{f s w \times Q t o t \times V d s}{2}

총 FET 손실은 방정식 13, 방정식 14 및 방정식 16의 결과를 합산하여 근사할 수 있습니다.

방정식 17은(는) 이 설계에서 다이오드 손실이 크게 간소화된다는 것을 보여줍니다. 2차 피크 전류에 대한 정격 다이오드를 선택해야 합니다. 이 전류는 일반적으로 IOUT보다 훨씬 더 큽니다.

방정식 17.

P D i o d e = \frac{I p k \times \frac{N p}{N s} \times t 2 \times f s w}{2} \times V d i o d e = I o u t \times V d i o d e

출력 커패시턴스는 일반적으로 방정식 18 방정식 19 중 더 큰 쪽으로 선택하는데, 이는 리플 전압과 등가 직렬 저항(방정식 18) 또는 부하 과도 응답(방정식 19)을 기준으로 커패시턴스를 계산합니다.

방정식 18.

C o u t 1 r i p p l e = \frac{I o u t_m a x \times (1 - D)}{(V o u t r i p - I p k \times \frac{N p}{N s} \times R e s r) \times f s w}

방정식 19.

C o u t 2 I t r a n = \frac{∆ I o u t}{2 π \times ∆ V o u t \times f B W}

여기서 ∆ IOUT 은 출력 부하 전류의 변화이며, ∆ VOUT은 허용 가능한 출력 전압 편파, fBW는 예상 컨버터 대역폭입니다.

방정식 20은(는) 출력 커패시터 RMS 전류를 다음과 같이 계산합니다.

방정식 20.

I C o u t r m s = \sqrt{\frac{I p k \times {(\frac{N p}{N s})}^{2} \times t 2 \times f s w}{3} - {I o u t_m a x}^{2}}

방정식 21 및 방정식 22은(는) 입력 커패시터의 매개 변수를 다음과 같이 추정합니다.

방정식 21.

C i n m i n = \frac{I p k \times D}{2 \times f s w \times V i n r i p}

방정식 22.

I C i n r m s = \sqrt{\frac{{I p k}^{2} \times D}{3} - {(\frac{P o u t_m a x}{V i n \times n})}^{2}}

방정식 23, 방정식 24 및 방정식 25은(는) 세 가지 주요 파형 시간 간격과 그 관계를 요약한 것입니다.

방정식 23.

t 1 = \sqrt{\frac{2 \times V o u t \times I o u t \times L p r i}{{V i n}^{2} \times f s w \times n}}

방정식 24.

t 2 = \frac{t 1 \times V i n}{(V o u t + V d) \times \frac{N p}{N s}}

방정식 25.

t 3 = \frac{1}{f s w} - t 1 - t 2

추가 2차 권선이 필요한 경우 방정식 26은(는) 추가 권선 Ns2를 쉽게 계산할 수 있습니다.

방정식 26.

\frac{N s 2}{N s 1} = \frac{V o u t 2 + V d 2}{V o u t 1 + V d 1}

여기서 VOUT1과 Ns1이 조정 출력 전압입니다.

트랜스포머 1차 RMS 전류는 방정식 10의 FET RMS 전류와 동일하며, 트랜스포머 2차 RMS 전류는 방정식 27에 나와 있습니다. 변압기 코어는 포화 없이 Ipk를 처리할 수 있어야 합니다. 코어 손실도 고려해야 하지만 이 문서의 범위를 벗어납니다.

방정식 27.

I s e c = I p k \times \frac{N p}{N s} \sqrt{\frac{t 2 \times f s w}{3}}

설명한 과정에서 볼 수 있듯이 DCM 플라이백의 설계는 반복적인 프로세스입니다. 스위칭 주파수, 인덕턴스 또는 회전 비율과 같은 초기 가정은 전력 손실과 같은 이후 계산에 따라 변경될 수 있습니다. 하지만 필요한 설계 매개 변수에도달하려면 그 만큼 부지런히 설계 단계를 진행해야 합니다. 최적화된 DCM 플라이백 설계는 작업을 기꺼이 수행할 경우 전원 컨버터 요구 사항에 저전력, 소형, 저비용 솔루션을 제공할 수 있습니다.

관련 문서