-
Under the Hood: Full-Scale and Dynamic Range Considerations of Current Sense Amplifiers
Under the Hood: Full-Scale and Dynamic Range Considerations of Current Sense Amplifiers
Trademarks
All trademarks are the property of their respective owners.
1 Dynamic Range (DR) and Full-Scale Range (FSR)
As applications continue to become more advanced in scope, designers find themselves needing to monitor greater ranges of current in their designs. From the scaling of high-power applications requiring the need for high current flow, to the advancement of semiconductor content allowing resolutions to be successfully measured down into the nanoamp range, designers are constantly looking for methods and topologies that allow them to achieve wider ranges of measurement.
There are several ways to define the range of an application, and these may be referred to either the input or the output of a certain device. In general, the ratio of largest-to-smallest input measurement range able to be measured by a device in an application is known as the dynamic range of the application, while the largest measurable quantity is called the full-scale range. Full-scale range is often used to describe the maximum value attainable in an analog-to-digital converter (ADC) design. For example, a current sense amplifier looking to achieve 5-A to 25-A measurement range would have a dynamic range of 5:1, and would have a full scale input range of 25 A. Full scale; however, could also refer to the highest possible output achievable by the amplifier, commonly referred to as the full-scale output range.
For current sense amplifier designs, the objective in the simplest sense, is to transduce a current signal range through a shunt resistor into a voltage range, and provide a chosen gain that will map that signal to the maximum output voltage range capable with the amplifier. For most current sense amplifiers, the output range able to be utilized spans from a few millivolts above ground to a few millivolts below the supply rail (although for optimal results, linear operating range of the amplifier should also be considered). This straightforward design plan begins to break down; however, as the DR of the application grows wider. From here, each design aspect can be discussed to understand the tradeoffs made and how the DR is affected.
When designing with a current sense amplifier, several degrees of freedom exist to form the design, with the typical equation relating the current measured in the shunt to the output of the amplifier given as Equation 6:
Observe from Equation 6 that there are essentially three options presented to the designer to help form their design: the magnitude of the supply voltage, the gain option chosen, and the sizing of the shunt resistor.
- Supply Voltage
In designs where wide DR is necessary, maximization of the supply voltage is recommended to provide the widest output range possible for the design, although downstream circuitry may also influence this choice. Supplying a VS lower than the recommended maximum directly reduces the dynamic range possible for a single device.
- Gain
Choosing an amplifier with larger gain is typically a tradeoff: this allows more signal integrity to be generated for a smaller signal against the offset voltage (larger gain choices also lead to increased resolution when digitizing the signal), thus reducing error in the lower region. However, this larger gain also results in more rapid maximization of the output of the amplifier, or in short, the size of the allowable dynamic range becomes smaller. Therefore, gain increase is typically more useful in precision range designs, where the dynamic range of measurement is reasonably small, or with amplifiers whose supply voltage range may also be extended to support the output on the higher end.
As an example, consider a system utilizing INA293 with a 5-V supply, where the desired range of the design is from 20 mA to 1 A. Disregarding common-mode rejection ratio (CMRR), if the designer were to implement a 200-mΩ shunt, the generated shunt voltage at the 20-mA condition is 4 mV, and, according to the Current Sense Amplifier Comparison and Error Tool, the error for the A1 variant at this point is 3.86%. Assuming better accuracy is needed, consider a step up to the A2 variant, which, for the same measurement case, now reduces the error to 2.12%. The tradeoff to this device migration, however, is that by stepping up to the higher gain, the design has diminished the maximum allowable range of which the amplifier can measure. In this case, while the error at the lower bound was reduced, this also invalidates the design, as 1 A is no longer an achievable measurement, with the A2 device reaching saturation at 485 mA for a 200-mΩ shunt, as demonstrated in Equation 2 and Equation 3.
Equation 2.Equation 3.Therefore, for wider ranges of measurement that are the subject of this paper, it is observed that smaller gains allow for maximization of dynamic range, so A1 variants are typically chosen for these types of designs. This example is summarized in Table 1-1.
Table 1-1 Gain Change Effects SummaryPart Number Gain (V/V) Error at 20 mV (%) Maximum Meas. Load (A) INA293A1 20 3.86 1.2125 INA293A2 50 2.12 .485 - Shunt Resistor
The shunt resistor is the final aspect that needs to be considered in the given system. The challenge of shunt resistor design is optimizing error at the low end versus shunt power loss at the high end. For a specific current point, Ohm's law is clear, to generate additional voltage signal against the offset voltage, the resistance of the shunt resistor must increase. This, however, comes at the expense of resistance losses in the form of heat, which in many cases may be become a challenge to manage successfully for a given design.
Take for example, an arbitrary, high-current application design using the INA240 to measure a maximum current of 100 amps. Taking the swing limitations of the INA240 into account, and assuming that the device is powered by a supply of 5 V, the maximum worst-case output the INA240 is capable of delivering is 4.8 V, and assuming the A1 variant (GAIN = 20 V/V) is used, the maximum possible shunt able to be designed in is:
Equation 4.This result shows that up to a 2.4-mΩ shunt may be chosen without risking device saturation (although some margin from the rail is typically advised), but this does not necessarily mean that this is the optimal shunt for the design. While on paper, this shunt choice maximizes signal integrity of the load under measurement, the power dissipated in the shunt at the maximum current level is 24 W.
Equation 5.Finally, as per the last example, the needed dynamic range may also be examined, as if a larger gain may be chosen while still capturing the necessary measurement range, the shunt may be reduced by this same factor.
For many applications, this has the potential to exceed the limits of manageable heat in the system, and the choice of the shunt needs to be revisited, rather than designing in this value. The alternative here is to select a shunt smaller in magnitude than the calculated maximum, as choosing a smaller shunt proportionally reduces the power consumed at the expense of signal integrity, that is, not utilizing the full scale output range achievable by the device. This also reduces the signal integrity of measurements at the lower end, leading to increased error where the offset of the amplifier has the potential to encroach on the accuracy of the measurement.
2 Error Over the Full Scale Range
At the lower end of the measurement range, the signal transduced by the shunt will suffer from greater influence of the offset voltage inherent to the amplifier. This results in an inverse proportionally increasing error as the measurement tends towards zero. Dependent on the shunt resistor chosen for the measurement maximum, it may even be found that the measurement at the lower bound is completely dominated by the offset voltage, and is effectively unusable due to the magnitude of the error. Current Sense Amplifier Error Curve Characteristics shows a generic error curve for a current sense amplifier, and the two dominating behaviors of the error curve as you move in each direction along the error curve.
As the measured signal diminishes, the proportion of the signal compared to the offset voltage of the device grows smaller, and offset error increasingly dominates the measurement, eventually rendering the measurement unacceptable in terms of error. As the signal grows and approaches the output limit of the amplifier, the voltage offset becomes a less important factor. However, constant error terms such as gain error and the tolerance error of the chosen shunt produce a y-axis asymptote that serves as a best case error measurement of the signal. For root sum square approximations that are often used to calculate total error, these static values become the dominant contribution at full scale, and result in a minimum limit achievable in terms of error.
3 Expansion of DR
A challenge that then arises from the limitations discussed in Section 1 is designing to a dynamic range that is often not easily achieved via the use of a single device.
The first potential option to be explored is that DR can be expanded via calibration. However, this is often not feasible due to scalability concerns. Typically then, for analog devices, what must be done in such a use case is the design of two (or more) separate amplifiers to effectively break up the DR into sections that are achievable by each of the individual stages in the design.
In this section, the design of one such topology for the INA190 is presented, for a use case of 10 µA to 100 mA, with a 24-V common-mode voltage, and a supply voltage of 5 V. The goal of the design is to achieve < 5% error at any given point on the measurement curve.
3.1 Unsuccessful Design With a Single Device
When designing amplifiers into the microamp range, one design aspect that must be considered is the input bias currents of the amplifier. As these currents will ultimately flow through the shunt to enter the IN– leg of the amplifier, the designer is restricted to amplifiers that exhibit input bias currents far less than the minimum desired measurement point. As such, the best choice from the TI portfolio for a design needing to measure microamps is the INA190, which has a worst-case bias current magnitude of 3 nA, which should minimize the impact of this error on the lower range. The sheer magnitude of this dynamic range (10000:1) presents an issue, however.
For the INA190, the maximum output achievable due to worst-case swing-to-rail limitation is 4.96 V, and thus for a 100-mA maximum measurement, the maximum possible calculated shunt is 1.984 Ω.
For the given conditions, Figure 3-1 gives the overall output error curve for the design utilizing this shunt, while Figure 3-2 examines the error curve only down to 0.1 mA, for better granularity.
 Figure 3-1 Total Output Error (%) Over
Measurement Range, RSHUNT = 1.984 Ω, 10 µA to 100 mA, Ideal Shunt
Tolerance
Figure 3-1 Total Output Error (%) Over
Measurement Range, RSHUNT = 1.984 Ω, 10 µA to 100 mA, Ideal Shunt
Tolerance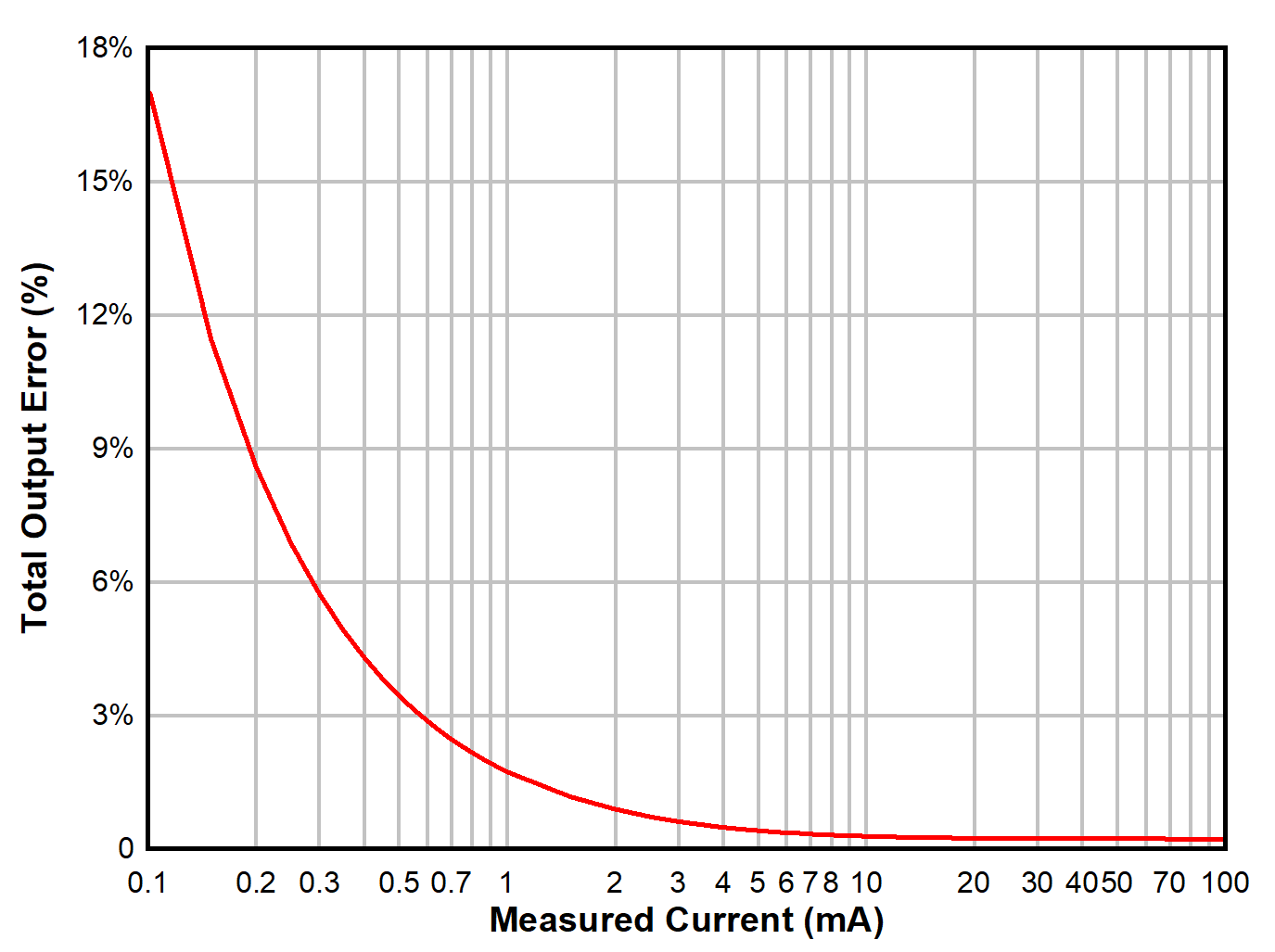 Figure 3-2 Total Output Error (%) Over
Measurement Range, RSHUNT = 1.984 Ω, 100 µA to 100 mA, Ideal Shunt
Tolerance
Figure 3-2 Total Output Error (%) Over
Measurement Range, RSHUNT = 1.984 Ω, 100 µA to 100 mA, Ideal Shunt
ToleranceFrom the latter curve, it is observed that the utilization of this device alone cannot satisfy the error specification of the design. The error becomes greater than 5% around 300 µA, above the needed design minimum of 10 μA. At this lower design end, for the current selections, effectively no signal integrity remains, resulting in > 150% error at 10 μA. This is made slightly worse once an actual E96 or E192 shunt value is chosen, along with its shunt tolerance error taken into consideration.
As a single device is incapable of achieving the needed error specification over the design range, the range may be broken down into separate pieces, where each individual stage is responsible for a portion of the range in which the desired specification is achievable. While many various topologies exist, the following topology utilizes two shunt resistors in series to break the range up into two separate measurement areas. A P-channel MOSFET acts as a virtual short across the larger of these resistors when biased, establishing the following shunt resistor conditions:
- When the PFET is OFF, the total shunt resistance is the combined total of RSHUNT, 1 and RSHUNT, 2.
- When the PFET is ON, it acts as a virtual short to RSHUNT, 1, and instead contributes approximately the RDS(ON) of the FET to the shunt measurement (the true contribution is RDS(ON) in parallel with RSHUNT, 1). The design may choose to treat the worst-case RDS(ON) of the FET as contributed error to RSHUNT, 2, or the designer may choose to include the nominal RDS(ON) of the FET to the proposed shunt resistance, thereby reducing the tolerance error to the observed difference between the nominal and worst-case RDS(ON) of the chosen FET.
To implement such a design on the high side requires a few additional components, to ensure that the PFET is able to be biased in the proper regions given that the voltage at the source of the FET is roughly that of the common mode of the design. This is achieved with a 2N3904 BJT transistor, a 5.1-V Zener diode, and several resistors. The pullup resistor in tandem with the BJT sets the gate voltage of the FET to VCM = 24 V when the BJT is unbiased, and the Zener diode forces the gate voltage to 5 V beneath VCM when the BJT is biased on, thus placing the PFET into forward operation. INA901 Schematic, 4 Decade Measurement shows the proposed design.
 Figure 3-3 INA901 Schematic, 4 Decade
Measurement
Figure 3-3 INA901 Schematic, 4 Decade
MeasurementUtilization of such a topology does not come without its share of challenges. First, resistor choices must be made that do not cause undue harm to the load due to burden voltage of the chosen shunt resistors. Also, distortion effects may manifest during turn on and turn off times of the switch network, making the measurement unreliable during these transitions. Finally, as the FET must be controlled and keep track of which state it is in, logic is required for the use of such a topology. This is discussed in Section 4.
The design procedure is provided in the following steps:
- Bound the Upper Region: Begin by designing a shunt to the full output range of the chosen amplifier, taking power considerations into account. As calculated earlier, the maximum possible shunt for the upper region as designed in the previous section was 1.984 Ω. As it was determined that this level of dynamic range for a single device for the specified accuracy is unacceptable, the goal is then to create a second design for the lower portion of the design, and then stitch these two together via the turn on voltage of the FET. Therefore, select a point on the output curve that will serve as the transition point between the two regions. Ensure that the point selected continues to meet the desired specification with some margin. As observed in Total Output Error (%) Over Measurement Range, RSHUNT = 1.984 Ω, 100 µA to 100 mA, Ideal Shunt Tolerance, at 1 mA, the expected total error before shunt selection is < 2%, so this point is chosen as the cutoff point. As 1.984 Ω is not a standard resistor value, the closest standard value, rounding down, of 1.96 Ω is chosen.
- Design the Lower Region:
Using the lower bound of the upper region chosen in step 1, set this as the full scale input of the device, and
recalculate a second total shunt value for this region. Equation 7.This calculation shows, for this region, up to a 198.4-Ω shunt may be used. Selecting a value lower than 198.4-Ω is typically recommended. This value allows headroom for sizing, as well as hysteresis for more stable transition through both regions, if necessary. For convenience, 100 Ω is chosen here as the value of the lower range. Examining this value for the lower region, Total Output Error (%) Over Measurement Range, RSHUNT = 100 Ω, 10 µA to 1 mA, Ideal Shunt Tolerances presents the expected total output error for this resistance.
 Figure 3-4 Total Output Error (%)
Over Measurement Range, RSHUNT = 100 Ω, 10 µA to 1 mA, Ideal
Shunt Tolerance
Figure 3-4 Total Output Error (%)
Over Measurement Range, RSHUNT = 100 Ω, 10 µA to 1 mA, Ideal
Shunt Tolerance - Choose the FET: Ideally, a
FET needs to be chosen with the smallest possible RDS(ON) available.
A challenge exists here in that typically, FETs with smaller RDS(ON)
values achieve this through larger substrates, so smaller values may be harder
to achieve for space-constrained applications. For this design, a CSD22206W
P-channel FET is chosen, with a maximum RDS(ON) of 5.7 mΩ (4.7 mΩ
typical) for
VGS = –4.5 V. - Confirm the Upper Shunt Value: For each of the design states, there is a combination of two elements that make up the shunt value of the design. When the FET is OFF, the elements are both RSHUNT, 1 and RSHUNT, 2 in series. As logic is used in such a design, the true nominal value may be programmed in logic, and the error is simply the worst-case tolerance values of the two resistors. As these resistors are in series and their values summed, provided the same tolerance value is chosen for both resistors, the worst-case tolerance error is simply the chosen tolerance value.
- Confirm the Lower Shunt
Value: When the FET is ON, the RDS(ON) becomes the dominant
contributing upper element, and the total shunt is this value in series with
RSHUNT, 2. Repeating the previous step for this region, it is
found that the nominal shunt value for the lower region is the sum of
RSHUNT, 2 and the typical RDS(ON) of the FET, or
1.9647 Ω. This is still less than the calculated maximum of 1.984 Ω, so is a
valid choice. While the tolerance of the RDS(ON) is large in
comparison to the resistance value of the FET, the overall contribution to the
total resistance value is small, and therefore does not cause excessive error,
as shown in Equation 8 and Equation 9. Equation 8.Equation 9.
- If Desired, Establish Hysteresis: If necessary, hysteretic set points may also be used to ensure stability of the FET transition point. The decision was made here to set hysteretic points at 1 mA and 1.5 mA to ensure smooth transition in the FET. This is discussed further in Control of the FET.
Output Voltage (V) Over Measurement Range, 10 µA to 100 mA shows the output range of the resulting design. Note that this curve shows the P-channel activation occurring at the 1.5 mA mark, in line with the previously-mentioned hysteretic forward point.
 Figure 3-5 Output Voltage (V) Over
Measurement Range, 10 µA to 100 mA
Figure 3-5 Output Voltage (V) Over
Measurement Range, 10 µA to 100 mAOne important aspect to pay attention to is the actual decades of current measurement specified. While examining the full range of a current sense amplifier, it often may seem foolish to a new designer that such a small amount of the actual sensing range is dedicated to one of the sections designed, but Output Voltage (V) Over Measurement Range, 10 µA to 100 mA, Log Scale shows the same data as in Figure 3-5, with the x-axis now logarithmically based:
 Figure 3-6 Output Voltage (V) Over
Measurement Range, 10 µA to 100 mA, Log Scale
Figure 3-6 Output Voltage (V) Over
Measurement Range, 10 µA to 100 mA, Log ScaleThe observation made viewing the range in log base is that each of these divisions occupies approximately the same proportional amount from a decades of measurement perspective, around 2 decades being handled per device. Various devices may be able to handle more or less by themselves, often dictated mainly by the worst-case offset voltage of the device.
The design was then simulated in TINA-TI to confirm the design expectations. INA190 Wide Measurement Schematic shows the simulation, along with measurement points.
 Figure 3-7 INA190 Wide Measurement
Schematic
Figure 3-7 INA190 Wide Measurement
SchematicFor the simulation, DC analysis was performed to examine expected outputs across the range. Table 3-1 lists the expected DC output for the circuit. Note that TINA-TI spice models contain typical parameters, so error at lower bounds is more in line with typical performance rather than worst case.
| Load Current | FET Status | Sense Voltage | INA Output Voltage, Actual | INA Output Voltage, Ideal(V) | Error (%) |
|---|---|---|---|---|---|
| 10 µA | OFF | 995.65 µV | 25.102 mV | 24.9 mV | 0.85 |
| 20 µA | OFF | 1.991 mV | 49.99 mV | 49.8 mV | 0.42 |
| 50 µA | OFF | 4.978 mV | 124.656 mV | 124 mV | 0.17 |
| 75 µA | OFF | 7.467 mV | 186.876 mV | 187 mV | 0.11 |
| 100 µA | OFF | 9.956 mV | 249.1 mV | 249 mV | 0.08 |
| 200 µA | OFF | 19.912 mV | 497.98mV | 498 mV | 0.04 |
| 500 µA | OFF | 49.779 mV | 1.245 V | 1.24 V | 0.01 |
| 750 µA | OFF | 74.669 mV | 1.867 V | 1.87 V | 0.01 |
| 1 mA | OFF | 99.558 mV | 2.489 V | 2.49 V | 0.01 |
| 2 mA | ON | 3.943 mV | 98.790 mV | 98.6 mV | 0.21 |
| 5 mA | ON | 9.837 mV | 246.118 mV | 246 mV | 0.08 |
| 7.5 mA | ON | 14.748 mV | 368.890 mV | 369 mV | 0.05 |
| 10 mA | ON | 19.66 mV | 491.663 mV | 491 mV | 0.04 |
| 20 mA | ON | 39.304 mV | 982.753 mV | 983 mV | 0.02 |
| 50 mA | ON | 98.238 mV | 2.456 V | 2.46 V | 0.01 |
| 75 mA | ON | 147.35 mV | 3.684 V | 3.68 V | 0.01 |
| 100 mA | ON | 196.461 mV | 4.911 V | 4.91 V | 0.01 |
For AC response, a time-based step response signal was utilized along with a time-based switch to mimic the transition of the GPIO pin controlling the gate. In implementation, this logic transition is performed via GPIO, using the digitized output as a feedback to keep track in logic, and would also exhibit some amount of delay. Note that as shown in Step Response (10-mVPP Input Step) of the INA190 Bidirectional, Low-Power, Zero-Drift, Wide Dynamic Range, Precision Current-Sense Amplifier With Enable data sheet, approximately 40 µs is needed for the INA190 output to settle to steady state. INA190 4-Decade Design Dynamic Response exhibits the values required for the INA190 output to settle to steady state.
 Figure 3-8 INA190 4-Decade Design Dynamic
Response
Figure 3-8 INA190 4-Decade Design Dynamic
ResponseAs expected, observe that there is some amount of distortion as the FET activates and changes the effective resistance between states.