SLOA011B January 2018 – July 2021 LF347 , LF353 , LM348 , MC1458 , TL022 , TL061 , TL062 , TL071 , TL072 , UA741
- 1Introduction
- 2Non-Inverting Amplifier
- 3Inverting Amplifier
- 4Simplified Op Amp Circuit Diagram
-
5Op Amp Specifications
- 5.1 Absolute Maximum Ratings and Recommended Operating Condition
- 5.2 Input Offset Voltage
- 5.3 Input Current
- 5.4 Input Common Mode Voltage Range
- 5.5 Differential Input Voltage Range
- 5.6 Maximum Output Voltage Swing
- 5.7 Large Signal Differential Voltage Amplification
- 5.8 Input Parasitic Elements
- 5.9 Output Impedance
- 5.10 Common-Mode Rejection Ratio
- 5.11 Supply Voltage Rejection Ratio
- 5.12 Supply Current
- 5.13 Slew Rate at Unity Gain
- 5.14 Equivalent Input Noise
- 5.15 Total Harmonic Distortion Plus Noise
- 5.16 Unity-Gain Bandwidth and Phase Margin
- 5.17 Settling Time
- 6References
- 7Glossary
- 8Revision History
1.1 Amplifier Basics
Before jumping into op amps, lets take a minute to review some amplifier fundamentals. An amplifier has an input port and an output port. In a linear amplifier, output signal = A × input signal, where A is the amplification factor or gain.
Depending on the nature of input and output signals, we can have four types of amplifier gain:
- Voltage (voltage out/voltage in)
- Current (current out/current in)
- Transresistance (voltage out/current in)
- Transconductance (current out/voltage in)
Since most op amps are voltage amplifiers, we will limit our discussion to voltage amplifiers.
Thevenin’s theorem can be used to derive a model of an amplifier, reducing it to the appropriate voltage sources and series resistances. The input port plays a passive role, producing no voltage of its own, and its Thevenin equivalent is a resistive element, Ri. The output port can be modeled by a dependent voltage source, AVi, with output resistance, Ro. To complete a simple amplifier circuit, we will include an input source and impedance, Vs and Rs, and output load, RL. Figure 1-1 shows the Thevenin equivalent of a simple amplifier circuit.
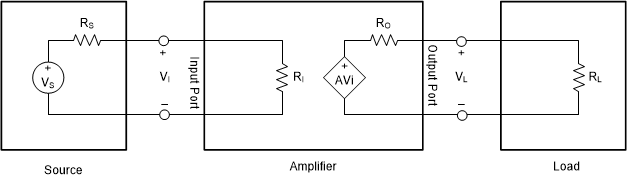 Figure 1-1 Thevenin Model of Amplifier with Source Load
Figure 1-1 Thevenin Model of Amplifier with Source LoadIt can be seen that we have voltage divider circuits at both the input port and the output port of the amplifier. This requires us to re-calculate whenever a different source and/or load is used and complicates circuit calculations.