SLUAA12 March   2020 TPS53681

 

  1.   Selection Considerations for Output Capacitors of Multiphase Voltage Regulators Part 1
    1.     Trademarks
    2. 1 Introduction
    3. 2 Current Transfer Function Gii_CL(s) of Load Current to Inductor Current
    4. 3 Output Capacitance Calculation Based on Load Transient
      1. 3.1 Steady-state Output Ripple
      2. 3.2 Load Step Transient Response
        1. 3.2.1 Case 1: Small-signal Transient with Unsaturated Loop
        2. 3.2.2 Case 2: Large-signal Transient with Saturated Loop
        3. 3.2.3 Criteria for Loop Saturation
    5. 4 Analytical Calculations and Experimental Verification
    6. 5 Conclusions
    7. 6 References

3.2.1 Case 1: Small-signal Transient with Unsaturated Loop

In Case 1, we assume that control loop never goes into saturation during transition period, the response of Isum will strictly follow the law of Gii_CL(s) linear system, and also the form of the input signal. Using fci=1.5fc as corner frequency, Gii_CL(s) can be estimated as a first-order system:

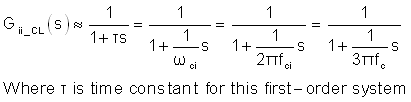
Equation 5. sluaa12-equation-5.gif

Figure 7 shows current waveforms of given input ramp-step signal Io and output response Isum, by taking unsaturated undershoot as example.

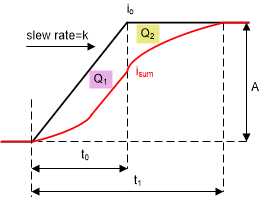sluaa12-current-waveforms-of-io-and-isum-in-case-1.gifFigure 7. Current Waveforms of Io and Isum in Case 1

Load step current can be expressed below:

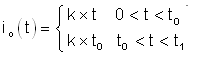
Equation 6. sluaa12-equation-6.gif

By using Laplace and inv-Laplace transformation, we can get equations of Isum:

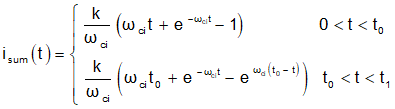
Equation 7. sluaa12-equation-7.gif

The total discharges of capacitors can be expressed by:

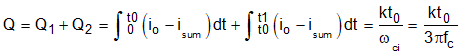
Equation 8. sluaa12-equation-8.gif

Thus, the undershoot(overshoot is the same) should be:

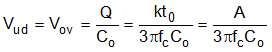
Equation 9. sluaa12-equation-9.gif

From formulas above, when the loop is unsaturated, for given output capacitance and loop bandwidth, undershoot(also overshoot) is decided by the bandwidth of loop gain, and the amplitude of load transient.

Experimental results of 150A load step can also prove that, the slew rate k of load step will hardly affect the undershoot value. Only if the slew rate k is very low, less than 0.01V difference can be found in this case. When k goes up to higher, almost no difference can be observed.

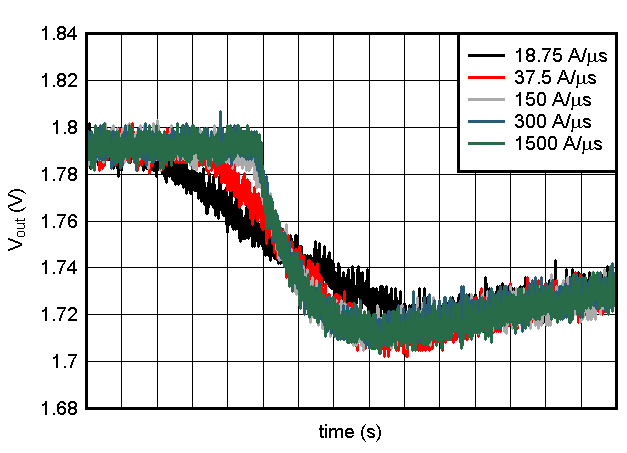D003_SLUAA12.gifFigure 8. 150A Load Transient with Different Slew Rate k in Case 1

Please note, loop bandwidth is related to output capacitance. When calculating, we are supposed to consider that they are coupled.