1 Ackermann Steering Curve Generation and Drawing Algorithm

The Ackermann steering model is commonly used throughout the automobile industry, to mathematically model the path that the tires of a car follow during a turn. As Figure 1-1 shows, the four tires follow a set of four concentric circles.

Figure 1-1 Ackermann Steering Curves

Given the wheelbase (L), tread (W), and inner tire steering angle (δ_i), the Ackermann steering model and the Pythagorean Theorem are used to determine the radius of the path of the front inner tire and the radii of the paths of the rear tires, as shown in Equation 1, Equation 2, and Equation 3. To generate the paths that the tires follow, in such a way that they can be mapped to a display, a conversion factor from inches to pixels must be applied before calculating the radii of the paths. The sample code in the Vision-SDK uses a conversion factor of 9 pixels to 1 inch.

Equation 1.

Equation 2.

Equation 3.

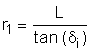
After finding the radii of the paths, the standard form equation of a circle can be used to generate the paths the tires follow. In the current implementation, for a given x value in the set xPathMin ≤ x ≤ xPathMax, the corresponding y value is calculated using Equation 4.

Equation 4.

Figure 1-2 and Figure 1-3 show the MATLAB outputs of a script which takes the inner tire steering angle (δ_i) and turning direction input, and then generates rearview curves using the previous equations. Figure 1-2 shows the rearview curve for a 0° steering angle, and Figure 1-3 shows the back up curve for a 45° steering angle left turning direction input.

Figure 1-2 Rearview Curve for 0° Steering Angle

Figure 1-3 45° Left Steering Angle

While the previous figures model the top-down view of the paths the tire follow, the rearview camera angle requires the rearview lines to appear to be converging to a finite vanishing point on the z-axis. The single-point projection transform manipulates the image such that points at infinity are mapped to a finite value in 3D space. In this case, the curves must be projected with respect to the y-axis, therefore Equation 5 was derived and used in the algorithm.

Equation 5.

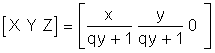
Before the transform can be properly applied, the center point of the rear axle is mapped to the origin. Specifically, the curves must be translated so that the path of the driver-side tires is in the second quadrant, and the path of the passenger-side tires is still the tread length away from the driver side tire. Figure 1-4 shows the MATLAB output of the previous transform applied to the curve generated in Figure 1-3.

Figure 1-4 Projected Rearview Lines From Figure 1-3

Lastly, the curves are translated so that they are in the rearview camera viewing window. Figure 1-5 shows the display output of the TDA3X RVP running the surround view + rearview use case, with the dynamic rearview lines being drawn using the draw2D API included in the Vision-SDK.

Figure 1-5 Display Output of Algorithm Running on TDA3x