SPRUIL1D May   2019  – December 2024 DRA829J , DRA829J-Q1 , DRA829V , DRA829V-Q1 , TDA4VM , TDA4VM-Q1

 

  1.   1
  2.   Read This First
    1.     About This Manual
    2.     Related Documentation From Texas Instruments
    3.     Support Resources
    4.     Glossary
    5.     Trademarks
    6.     Export Control Notice
  3. 1 Introduction
    1. 1.1 Device Overview
    2. 1.2 Device Block Diagram
    3. 1.3 Device Main Domain
      1. 1.3.1  Arm Cortex-A72 Subsystem
      2. 1.3.2  Arm Cortex-R5F Processor
      3. 1.3.3  C66x DSP Subsystem
      4. 1.3.4  C71x DSP Subsystem
      5. 1.3.5  Graphics Processing Unit
      6. 1.3.6  Multi-Standard HD Video Decoder
      7. 1.3.7  Multi-Standard HD Video Encoder
      8. 1.3.8  Vision Pre-processing Accelerator
      9. 1.3.9  Depth and Motion Perception Accelerator
      10. 1.3.10 Navigator Subsystem
      11. 1.3.11 Region-based Address Translation Module
      12. 1.3.12 Data Routing Unit
      13. 1.3.13 Display Subsystem
      14. 1.3.14 Camera Subsystem
      15. 1.3.15 Shared D-PHY Transmitter
      16. 1.3.16 Video Processing Front End
      17. 1.3.17 Multicore Shared Memory Controller
      18. 1.3.18 DDR Subsystem
      19. 1.3.19 Region-based Address Translation Module
      20. 1.3.20 General Purpose Input/Output Interface
      21. 1.3.21 Inter-Integrated Circuit Interface
      22. 1.3.22 Improved Inter-Integrated Circuit Interface
      23. 1.3.23 Multi-channel Serial Peripheral Interface
      24. 1.3.24 Universal Asynchronous Receiver/Transmitter
      25. 1.3.25 Gigabit Ethernet Switch
      26. 1.3.26 Peripheral Component Interconnect Express Subsystem
      27. 1.3.27 Universal Serial Bus (USB) Subsystem
      28. 1.3.28 SerDes
      29. 1.3.29 General Purpose Memory Controller with Error Location Module
      30. 1.3.30 Multimedia Card/Secure Digital Interface
      31. 1.3.31 Universal Flash Storage Interface
      32. 1.3.32 Enhanced Capture Module
      33. 1.3.33 Enhanced Pulse-Width Modulation Module
      34. 1.3.34 Enhanced Quadrature Encoder Pulse Module
      35. 1.3.35 Controller Area Network
      36. 1.3.36 Audio Tracking Logic
      37. 1.3.37 Multi-channel Audio Serial Port
      38. 1.3.38 Timers
      39. 1.3.39 Internal Diagnostics Modules
    4. 1.4 Device MCU Domain
      1. 1.4.1  MCU Arm Cortex-R5F Processor
      2. 1.4.2  MCU Region-based Address Translation Module
      3. 1.4.3  MCU Navigator Subsystem
      4. 1.4.4  MCU Analog-to-Digital Converter
      5. 1.4.5  MCU Inter-Integrated Circuit Interface
      6. 1.4.6  MCU Improved Inter-Integrated Circuit Interface
      7. 1.4.7  MCU Multi-channel Serial Peripheral Interface
      8. 1.4.8  MCU Universal Asynchronous Receiver/Transmitter
      9. 1.4.9  MCU Gigabit Ethernet Switch
      10. 1.4.10 MCU Octal Serial Peripheral Interface and HyperBus Memory Controller as a Flash Subsystem
      11. 1.4.11 MCU Controller Area Network
      12. 1.4.12 MCU Timers
      13. 1.4.13 MCU Internal Diagnostics Modules
    5. 1.5 Device WKUP Domain
      1. 1.5.1 WKUP Device Management and Security Controller
      2. 1.5.2 WKUP General Purpose Input/Output Interface
      3. 1.5.3 WKUP Inter-Integrated Circuit Interface
      4. 1.5.4 WKUP Universal Asynchronous Receiver/Transmitter
      5. 1.5.5 WKUP Internal Diagnostics Modules
    6. 1.6 Device Identification
  4. 2 Memory Map
    1. 2.1 MAIN Domain Memory Map
    2. 2.2 MCU Domain Memory Map
    3. 2.3 WKUP Domain Memory Map
    4. 2.4 Processors View Memory Map
    5. 2.5 Region-based Address Translation
  5. 3 System Interconnect
    1. 3.1 System Interconnect Overview
    2. 3.2 System Interconnect Integration
      1. 3.2.1 Interconnect Integration in WKUP Domain
      2. 3.2.2 Interconnect Integration in MCU Domain
      3. 3.2.3 Interconnect Integration in MAIN Domain
    3. 3.3 System Interconnect Functional Description
      1. 3.3.1 Master-Slave Connections
      2. 3.3.2 Quality of Service (QoS)
      3. 3.3.3 Route ID
      4. 3.3.4 Initiator-Side Security Controls and Firewalls
        1. 3.3.4.1 Initiator-Side Security Controls (ISC)
          1. 3.3.4.1.1 Special System Level Priv-ID
          2. 3.3.4.1.2 Priv ID and ISC Assignment
        2. 3.3.4.2 Firewalls (FW)
          1. 3.3.4.2.1 Peripheral Firewalls (FW)
          2. 3.3.4.2.2 Memory or Region-based Firewalls
            1. 3.3.4.2.2.1 Region Based Firewall Functional Description
          3. 3.3.4.2.3 Channelized Firewalls
            1. 3.3.4.2.3.1 Channelized Firewall Functional Description
            2. 3.3.4.2.3.2 Null Error Reporting
      5. 3.3.5 VBUSM_TIMEOUT_GASKET (MCU_TIMEOUT_64B2)
        1. 3.3.5.1 Overview and Feature List
          1. 3.3.5.1.1 Features Supported
          2. 3.3.5.1.2 Features Not Supported
        2. 3.3.5.2 Functional Description
          1. 3.3.5.2.1 Functional Operation
            1. 3.3.5.2.1.1  Overview
            2. 3.3.5.2.1.2  FIFOs
            3. 3.3.5.2.1.3  ID Allocator
            4. 3.3.5.2.1.4  Timer
            5. 3.3.5.2.1.5  Timeout Queue
            6. 3.3.5.2.1.6  Write Scoreboard
            7. 3.3.5.2.1.7  Read Scoreboard
            8. 3.3.5.2.1.8  Flush Mode
            9. 3.3.5.2.1.9  Flushing
            10. 3.3.5.2.1.10 Timeout Error Reporting
            11. 3.3.5.2.1.11 Command Timeout Error Reporting
            12. 3.3.5.2.1.12 Unexpected Response Reporting
            13. 3.3.5.2.1.13 Latency and Stalls
            14. 3.3.5.2.1.14 Bypass
            15. 3.3.5.2.1.15 Safety
        3. 3.3.5.3 Interrupt Conditions
          1. 3.3.5.3.1 Transaction Error Interrupt
            1. 3.3.5.3.1.1 Transaction Timeout
            2. 3.3.5.3.1.2 Unexpected Response
            3. 3.3.5.3.1.3 Command Timeout
        4. 3.3.5.4 Memory Map
          1. 3.3.5.4.1  Revision Register (Base Address + 0x00)
          2. 3.3.5.4.2  Configuration Register (Base Address + 0x04)
          3. 3.3.5.4.3  Info Register (Base Address + 0x08)
          4. 3.3.5.4.4  Enable Register (Base Address + 0x0C)
          5. 3.3.5.4.5  Flush Register (Base Address + 0x10)
          6. 3.3.5.4.6  Timeout Value Register (Base Address + 0x14)
          7. 3.3.5.4.7  Timer Register (Base Address + 0x18)
          8. 3.3.5.4.8  Error Interrupt Raw Status/Set Register (Base Address + 0x20)
          9. 3.3.5.4.9  Error Interrupt Enabled Status/Clear Register (Base Address + 0x24)
          10. 3.3.5.4.10 Error Interrupt Mask Set Register (Base Address + 0x28)
          11. 3.3.5.4.11 Error Interrupt Mask Clear Register (Base Address + 0x2C)
          12. 3.3.5.4.12 Timeout Error Info Register (Base Address + 0x30)
          13. 3.3.5.4.13 Unexpected Response Info Register (Base Address + 0x34)
          14. 3.3.5.4.14 Error Transaction Valid/Dir/RouteID Register (Base Address + 0x38)
          15. 3.3.5.4.15 Error Transaction Tag/CommandID Register (Base Address + 0x3C)
          16. 3.3.5.4.16 Error Transaction Bytecnt Register (Base Address + 0x40)
          17. 3.3.5.4.17 Error Transaction Upper Address Register (Base Address + 0x44)
          18. 3.3.5.4.18 Error Transaction Lower Address Register (Base Address + 0x48)
        5. 3.3.5.5 Integration Overview
          1. 3.3.5.5.1 Parameterization Requirements
        6. 3.3.5.6 I/O Description
          1. 3.3.5.6.1 Clockstop Idle
          2. 3.3.5.6.2 Flush
          3. 3.3.5.6.3 Module I/O
        7. 3.3.5.7 User’s Guide
          1. 3.3.5.7.1 Programmer’s Guide
            1. 3.3.5.7.1.1 Initialization
            2. 3.3.5.7.1.2 Software Flush
  6. 4 Initialization
    1. 4.1 Initialization Overview
      1. 4.1.1 ROM Code Overview
      2. 4.1.2 Bootloader Modes
      3. 4.1.3 Terminology
    2. 4.2 Boot Process
      1. 4.2.1 MCU ROM Code Architecture
        1. 4.2.1.1 Main Module
        2. 4.2.1.2 X509 Module
        3. 4.2.1.3 Buffer Manager Module
        4. 4.2.1.4 Log and Trace Module
        5. 4.2.1.5 System Module
        6. 4.2.1.6 Protocol Module
        7. 4.2.1.7 Driver Module
      2. 4.2.2 DMSC ROM Description
      3. 4.2.3 Boot Process Flow
      4. 4.2.4 MCU Only vs Normal Boot
    3. 4.3 Boot Mode Pins
      1. 4.3.1  MCU_BOOTMODE Pin Mapping
      2. 4.3.2  BOOTMODE Pin Mapping
        1. 4.3.2.1 Primary Boot Mode Selection
        2. 4.3.2.2 Backup Boot Mode Selection When MCU Only = 0
        3. 4.3.2.3 Primary Boot Mode Configuration
        4. 4.3.2.4 Backup Boot Mode Configuration
      3. 4.3.3  No-boot/Dev-boot Configuration
      4. 4.3.4  OSPI Boot Device Configuration
      5. 4.3.5  xSPI Boot Device Configuration
      6. 4.3.6  QSPI Boot Device Configuration
      7. 4.3.7  SPI Boot Device Configuration
      8. 4.3.8  I2C Boot Device Configuration
      9. 4.3.9  MMC/SD Card Boot Device Configuration
      10. 4.3.10 Ethernet Boot Device Configuration
      11. 4.3.11 USB Boot Device Configuration
      12. 4.3.12 PCIe Boot Device Configuration
      13. 4.3.13 UART Boot Device Configuration
      14. 4.3.14 GPMC NOR Boot Device Configuration
      15. 4.3.15 eMMC Boot Device Configuration
        1. 4.3.15.1 eMMC Flash
      16. 4.3.16 PLL Configuration
        1. 4.3.16.1 MCU_PLL0, MCU_PLL2, Main PLL0, and Main PLL3
        2. 4.3.16.2 MCU_PLL1
        3. 4.3.16.3 Main PLL1
        4. 4.3.16.4 Main PLL2
        5. 4.3.16.5 198
    4. 4.4 Boot Parameter Tables
      1. 4.4.1  Common Header
      2. 4.4.2  PLL Setup
      3. 4.4.3  PCIe Boot Parameter Table
      4. 4.4.4  I2C Boot Parameter Table
      5. 4.4.5  OSPI/QSPI/SPI/xSPI Boot Parameter Table
      6. 4.4.6  GPMC NOR Boot Parameter Table
      7. 4.4.7  Ethernet Boot Parameter Table
      8. 4.4.8  USB Boot Parameter Table
      9. 4.4.9  MMCSD Boot Parameter Table
      10. 4.4.10 UART Boot Parameter Table
    5. 4.5 Boot Image Format
      1. 4.5.1 Overall Structure
      2. 4.5.2 X.509 Certificate
      3. 4.5.3 Organizational Identifier (OID)
      4. 4.5.4 X.509 Extensions Specific to Boot
        1. 4.5.4.1 Boot Info (OID 1.3.6.1.4.1.294.1.1)
        2. 4.5.4.2 Image Integrity (OID 1.3.6.1.4.1.294.1.2)
      5. 4.5.5 Generating X.509 Certificates
        1. 4.5.5.1 Key Generation
          1. 4.5.5.1.1 Degenerate RSA Keys
        2. 4.5.5.2 Configuration Script
      6. 4.5.6 Image Data
    6. 4.6 Boot Modes
      1. 4.6.1  I2C Bootloader Operation
        1. 4.6.1.1 I2C Initialization Process
          1. 4.6.1.1.1 Block Size
          2. 4.6.1.1.2 226
        2. 4.6.1.2 I2C Loading Process
          1. 4.6.1.2.1 Loading a Boot Image From EEPROM
          2. 4.6.1.2.2 Loading Image In Slave Mode
      2. 4.6.2  SPI Bootloader Operation
        1. 4.6.2.1 SPI Initialization Process
        2. 4.6.2.2 SPI Loading Process
      3. 4.6.3  QSPI Bootloader Operation
        1. 4.6.3.1 QSPI Initialization Process
        2. 4.6.3.2 QSPI Loading Process
      4. 4.6.4  OSPI Bootloader Operation
        1. 4.6.4.1 OSPI Initialization Process
        2. 4.6.4.2 OSPI Loading Process
      5. 4.6.5  PCIe Bootloader Operation
        1. 4.6.5.1 PCIe Initialization Process
        2. 4.6.5.2 PCIe Loading Process
      6. 4.6.6  GPMC NOR Bootloader Operation
        1. 4.6.6.1 GPMC NOR Initialization Process
        2. 4.6.6.2 GPMC NOR Loading Process
      7. 4.6.7  Ethernet Bootloader Operation
        1. 4.6.7.1 Ethernet Initialization Process
        2. 4.6.7.2 Ethernet Loading Process
          1. 4.6.7.2.1 Ethernet Boot Data Formats
            1. 4.6.7.2.1.1 Limitations
            2. 4.6.7.2.1.2 BOOTP Request
              1. 4.6.7.2.1.2.1 MAC Header (DIX)
              2. 4.6.7.2.1.2.2 IPv4 Header
              3. 4.6.7.2.1.2.3 UDP Header
              4. 4.6.7.2.1.2.4 BOOTP Payload
              5. 4.6.7.2.1.2.5 TFTP
        3. 4.6.7.3 Ethernet Hand Over Process
      8. 4.6.8  USB Bootloader Operation
        1. 4.6.8.1 USB-Specific Attributes
          1. 4.6.8.1.1 DFU Device Mode
      9. 4.6.9  MMCSD Bootloader Operation
      10. 4.6.10 UART Bootloader Operation
        1. 4.6.10.1 Initialization Process
        2. 4.6.10.2 UART Loading Process
          1. 4.6.10.2.1 UART XMODEM
        3. 4.6.10.3 UART Hand-Over Process
    7. 4.7 Boot Memory Maps
      1. 4.7.1 Memory Layout/MPU
      2. 4.7.2 Global Memory Addresses Used by ROM Code
      3. 4.7.3 Memory Reserved by ROM Code
  7. 5 Device Configuration
    1. 5.1 Control Module (CTRL_MMR)
      1. 5.1.1 WKUP_CTRL_MMR0
        1. 5.1.1.1 WKUP_CTRL_MMR0 Overview
        2. 5.1.1.2 WKUP_CTRL_MMR0 Integration
        3. 5.1.1.3 WKUP_CTRL_MMR0 Functional Description
          1. 5.1.1.3.1 Description for WKUP_CTRL_MMR0 Register Types
            1. 5.1.1.3.1.1  Pad Configuration Registers
            2. 5.1.1.3.1.2  Kick Protection Registers
            3. 5.1.1.3.1.3  WKUP_CTRL_MMR0 Module Interrupts
            4. 5.1.1.3.1.4  Clock Selection Registers
            5. 5.1.1.3.1.5  Device Feature Registers
            6. 5.1.1.3.1.6  POK Module Registers
            7. 5.1.1.3.1.7  Power and Reset Related Registers
            8. 5.1.1.3.1.8  PRG Related Registers
            9. 5.1.1.3.1.9  Voltage Glitch Detect Control and Status Registers
            10. 5.1.1.3.1.10 I/O Debounce Control Registers
      2. 5.1.2 MCU_CTRL_MMR0
        1. 5.1.2.1 MCU_CTRL_MMR0 Overview
        2. 5.1.2.2 MCU_CTRL_MMR0 Integration
        3. 5.1.2.3 MCU_CTRL_MMR0 Functional Description
          1. 5.1.2.3.1 Description for MCU_CTRL_MMR0 Register Types
            1. 5.1.2.3.1.1 Kick Protection Registers
            2. 5.1.2.3.1.2 MCU_CTRL_MMR0 Module Interrupts
            3. 5.1.2.3.1.3 Inter-processor Communication Registers
            4. 5.1.2.3.1.4 Timer I/O Muxing Control Registers
            5. 5.1.2.3.1.5 Clock Muxing and Division Registers
            6. 5.1.2.3.1.6 MCU_CPSW0 MAC Address Registers
      3. 5.1.3 CTRL_MMR0
        1. 5.1.3.1 CTRL_MMR0 Overview
        2. 5.1.3.2 CTRL_MMR0 Integration
        3. 5.1.3.3 CTRL_MMR0 Functional Description
          1. 5.1.3.3.1 Description for CTRL_MMR0 Register Types
            1. 5.1.3.3.1.1  Pad Configuration Registers
            2. 5.1.3.3.1.2  Kick Protection Registers
            3. 5.1.3.3.1.3  CTRL_MMR0 Module Interrupts
            4. 5.1.3.3.1.4  Inter-processor Communication Registers
            5. 5.1.3.3.1.5  Timer I/O Muxing Control Registers
            6. 5.1.3.3.1.6  EHRPWM/EQEP Control and Status Registers
            7. 5.1.3.3.1.7  PRU_ICSSG Control Registers
            8. 5.1.3.3.1.8  Clock Muxing and Division Registers
            9. 5.1.3.3.1.9  Ethernet Port Operation Control Registers
            10. 5.1.3.3.1.10 PCIe Operation Control Registers
            11. 5.1.3.3.1.11 SERDES Lane Function Control Registers
            12. 5.1.3.3.1.12 DDRSS Dynamic Frequency Change Registers
    2. 5.2 Power
      1. 5.2.1 Power Management Overview
      2. 5.2.2 Power Management Subsystems
        1. 5.2.2.1 Power Management Unit
          1. 5.2.2.1.1 Power OK (POK) Modules
            1. 5.2.2.1.1.1 POK Programming Model
          2. 5.2.2.1.2 Power on Reset (POR) Module
            1. 5.2.2.1.2.1 POR Overview
            2. 5.2.2.1.2.2 POR Integration
            3. 5.2.2.1.2.3 POR Functional Description
            4. 5.2.2.1.2.4 POR Programming Model
          3. 5.2.2.1.3 PoR/Reset Generator (PRG) Modules
            1. 5.2.2.1.3.1 PRG Overview
            2. 5.2.2.1.3.2 PRG Integration
            3. 5.2.2.1.3.3 PRG Programming Model
          4. 5.2.2.1.4 Power Glitch Detect (PGD) Modules
          5. 5.2.2.1.5 Voltage and Thermal Manager (VTM)
            1. 5.2.2.1.5.1 VTM Overview
              1. 5.2.2.1.5.1.1 VTM Features
              2. 5.2.2.1.5.1.2 VTM Not Supported Features
            2. 5.2.2.1.5.2 VTM Integration
            3. 5.2.2.1.5.3 VTM Functional Description
              1. 5.2.2.1.5.3.1 VTM Temperature Status and Thermal Management
                1. 5.2.2.1.5.3.1.1 10-bit Temperature Values Versus Temperature
              2. 5.2.2.1.5.3.2 VTM Temperature Driven Alerts and Interrupts
              3. 5.2.2.1.5.3.3 VTM VID Voltage Domains
              4. 5.2.2.1.5.3.4 VTM Clocking
              5. 5.2.2.1.5.3.5 VTM Retention Interface
              6. 5.2.2.1.5.3.6 VTM ECC Aggregator
              7. 5.2.2.1.5.3.7 VTM Programming Model
                1. 5.2.2.1.5.3.7.1 VTM Maximum Temperature Outrange Alert
                2. 5.2.2.1.5.3.7.2 Temperature Monitor during Low Power Modes
                3. 5.2.2.1.5.3.7.3 Sensors Programming Sequences
              8. 5.2.2.1.5.3.8 AVS-Class0
          6. 5.2.2.1.6 Distributed Power Clock and Reset Controller (DPCR)
        2. 5.2.2.2 Power Control Modules
          1. 5.2.2.2.1 Power Sleep Controller and Local Power Sleep Controllers
            1. 5.2.2.2.1.1 PSC Terminology
            2. 5.2.2.2.1.2 PSC Features
            3. 5.2.2.2.1.3 PSC: Device Power-Management Layout
              1. 5.2.2.2.1.3.1 WKUP_PSC0 Device-Specific Information
              2. 5.2.2.2.1.3.2 PSC0 Device-Specific Information
              3. 5.2.2.2.1.3.3 LPSC Dependences Overview
            4. 5.2.2.2.1.4 PSC: Power Domain and Module States
              1. 5.2.2.2.1.4.1 Power Domain States
              2. 5.2.2.2.1.4.2 Module States
              3. 5.2.2.2.1.4.3 Local Reset
            5. 5.2.2.2.1.5 PSC: Executing State Transitions
              1. 5.2.2.2.1.5.1 Power Domain State Transitions
              2. 5.2.2.2.1.5.2 Module State Transitions
              3. 5.2.2.2.1.5.3 Concurrent Power Domain/Module State Transitions
              4. 5.2.2.2.1.5.4 Recommendations for Power Domain/Module Sequencing
            6. 5.2.2.2.1.6 PSC: Emulation Support in the PSC
            7. 5.2.2.2.1.7 PSC: A72SS, MSMC, MCU Cortex-R5F, C71SS0, and C66SS Subsystem Power-Up and Power-Down Sequences
              1. 5.2.2.2.1.7.1 ARMi_COREn Power State Transition
              2. 5.2.2.2.1.7.2 A72SS Power State Transition
              3. 5.2.2.2.1.7.3 GIC0 Sequencing to Support A72SS Power Management
              4. 5.2.2.2.1.7.4 Power management features supported by C7x Corepac
              5. 5.2.2.2.1.7.5 C7x CorePac Clkstop/Powerdown/Disconnect Sequencing
              6. 5.2.2.2.1.7.6 MSMC0 Clkstop/Powerdown/Disconnect Sequencing
              7. 5.2.2.2.1.7.7 MCU Cortex-R5F Power Modes
              8. 5.2.2.2.1.7.8 C66x_DSPSS Power Sequences
          2. 5.2.2.2.2 Integrated Power Management (DMSC)
            1. 5.2.2.2.2.1 DMSC Power Management Overview
              1. 5.2.2.2.2.1.1 DMSC Power Management Features
      3. 5.2.3 Device Power States
        1. 5.2.3.1 Overview of Device Low-Power Modes
        2. 5.2.3.2 Voltage Domains
        3. 5.2.3.3 Power Domains
        4. 5.2.3.4 Clock Sources States
        5. 5.2.3.5 Wake-up Sources
        6. 5.2.3.6 Device Power States and Transitions
          1. 5.2.3.6.1 LPM Entry Sequences
          2. 5.2.3.6.2 LPM Exit Sequences
          3. 5.2.3.6.3 IO Retention
      4. 5.2.4 Dynamic Power Management
        1. 5.2.4.1 AVS Support
        2. 5.2.4.2 Dynamic Frequency Scaling (DFS) Operations
      5. 5.2.5 Thermal Management
    3. 5.3 Reset
      1. 5.3.1 Reset Overview
      2. 5.3.2 Reset Sources
      3. 5.3.3 Reset Status
      4. 5.3.4 Reset Control
      5. 5.3.5 BOOTMODE Pins
      6. 5.3.6 Reset Sequences
        1. 5.3.6.1 MCU_PORz Overview
        2. 5.3.6.2 MCU_PORz Sequence
        3. 5.3.6.3 MCU_RESETz Sequence
        4. 5.3.6.4 PORz Sequence
        5. 5.3.6.5 RESET_REQz Sequence
      7. 5.3.7 PLL Behavior on Reset
    4. 5.4 Clocking
      1. 5.4.1 Overview
      2. 5.4.2 Clock Inputs
        1. 5.4.2.1 Overview
        2. 5.4.2.2 Mapping of Clock Inputs
      3. 5.4.3 Clock Outputs
        1. 5.4.3.1 Observation Clock Pins
          1. 5.4.3.1.1 MCU_OBSCLK0 Pin
          2. 5.4.3.1.2 415
          3. 5.4.3.1.3 OBSCLK0, OBSCLK1, and OBSCLK2 Pins
        2. 5.4.3.2 System Clock Pins
          1. 5.4.3.2.1 MCU_SYSCLKOUT0
          2. 5.4.3.2.2 SYSCLKOUT0
      4. 5.4.4 Device Oscillators
        1. 5.4.4.1 Device Oscillators Integration
          1. 5.4.4.1.1 Oscillators with External Crystal
          2. 5.4.4.1.2 Internal RC Oscillator
        2. 5.4.4.2 Oscillator Clock Loss Detection
      5. 5.4.5 PLLs
        1. 5.4.5.1  WKUP and MCU Domains PLL Overview
        2. 5.4.5.2  MAIN Domain PLLs Overview
        3. 5.4.5.3  PLL Reference Clocks
          1. 5.4.5.3.1 PLLs in MCU Domain
          2. 5.4.5.3.2 PLLs in MAIN Domain
        4. 5.4.5.4  Generic PLL Overview
          1. 5.4.5.4.1 PLLs Output Clocks Parameters
            1. 5.4.5.4.1.1 PLLs Input Clocks
            2. 5.4.5.4.1.2 PLL Output Clocks
              1. 5.4.5.4.1.2.1 PLLTS16FFCLAFRAC2 Type Output Clocks
              2. 5.4.5.4.1.2.2 PLLTS16FFCLAFRACF Type Output Clocks
              3. 5.4.5.4.1.2.3 PLLTS16FFCLVDESKEWC Type Output Clocks
              4. 5.4.5.4.1.2.4 PLL Lock
              5. 5.4.5.4.1.2.5 HSDIVIDER
              6. 5.4.5.4.1.2.6 ICG Module
              7. 5.4.5.4.1.2.7 PLL Power Down
              8. 5.4.5.4.1.2.8 PLL Calibration
          2. 5.4.5.4.2 PLL Spread Spectrum Modulation Module
            1. 5.4.5.4.2.1 Definition of SSMOD
            2. 5.4.5.4.2.2 SSMOD Configuration
        5. 5.4.5.5  PLLs Device-Specific Information
          1. 5.4.5.5.1 SSMOD Related Bitfields Table
          2. 5.4.5.5.2 Clock Synthesis Inputs to the PLLs
          3. 5.4.5.5.3 Clock Output Parameter
          4. 5.4.5.5.4 Calibration Related Bitfields
        6. 5.4.5.6  PLL and PLL Controller Connection
        7. 5.4.5.7  System Clocks Operating Frequency Ranges
        8. 5.4.5.8  Recommended Clock and Control Signal Transition Behavior
        9. 5.4.5.9  Interface Clock Specifications
        10. 5.4.5.10 PLL, PLLCTRL, and HSDIV Controllers Programming Guide
          1. 5.4.5.10.1 PLL Initialization
            1. 5.4.5.10.1.1 Kick Protection Mechanism
            2. 5.4.5.10.1.2 PLL Initialization to PLL Mode
            3. 5.4.5.10.1.3 PLL Programming Requirements
          2. 5.4.5.10.2 HSDIV PLL Programming
          3. 5.4.5.10.3 PLL Controllers Programming - Dividers PLLDIVn and GO Operation
            1. 5.4.5.10.3.1 GO Operation
            2. 5.4.5.10.3.2 Software Steps to Modify PLLDIV Ratios
          4. 5.4.5.10.4 Entire Sequence for Programming PLLCTRL, HSDIV, and PLL
  8. 6 Processors and Accelerators
    1. 6.1  Compute Cluster
      1. 6.1.1 Compute Cluster Overview
      2. 6.1.2 Compute Cluster Functional Description
        1. 6.1.2.1 Compute Cluster Memory Regions
        2. 6.1.2.2 Compute Cluster Firewalls
        3. 6.1.2.3 Compute Cluster ECC Aggregators
    2. 6.2  Dual-A72 MPU Subsystem
      1. 6.2.1 A72SS Overview
        1. 6.2.1.1 A72SS Introduction
        2. 6.2.1.2 A72SS Features
      2. 6.2.2 A72SS Integration
      3. 6.2.3 A72SS Functional Description
        1. 6.2.3.1  A72SS Block Diagram
        2. 6.2.3.2  A72SS A72 Cluster
        3. 6.2.3.3  A72SS Interfaces and Async Bridges
        4. 6.2.3.4  A72SS Interrupts
          1. 6.2.3.4.1 A72SS Interrupt Inputs
          2. 6.2.3.4.2 A72SS Interrupt Outputs
        5. 6.2.3.5  A72SS Power Management, Clocking and Reset
          1. 6.2.3.5.1 A72SS Power Management
          2. 6.2.3.5.2 A72SS Clocking
        6. 6.2.3.6  A72SS Debug Support
        7. 6.2.3.7  A72SS Timestamps
        8. 6.2.3.8  A72SS Watchdog
        9. 6.2.3.9  A72SS Internal Diagnostics
          1. 6.2.3.9.1 A72SS ECC Aggregators During Low Power States
          2. 6.2.3.9.2 A72SS CBASS Diagnostics
          3. 6.2.3.9.3 A72SS SRAM Diagnostics
          4. 6.2.3.9.4 A72SS SRAM ECC Aggregator Configurations
        10. 6.2.3.10 A72SS Cache Pre-Warming
        11. 6.2.3.11 A72SS Boot
        12. 6.2.3.12 A72SS IPC with Other CPUs
    3. 6.3  Dual-R5F MCU Subsystem
      1. 6.3.1 R5FSS Overview
        1. 6.3.1.1 R5FSS Features
        2. 6.3.1.2 R5FSS Not Supported Features
      2. 6.3.2 R5FSS Integration
        1. 6.3.2.1 R5FSS Integration in MCU Domain
        2. 6.3.2.2 R5FSS Integration in MAIN Domain
      3. 6.3.3 R5FSS Functional Description
        1. 6.3.3.1  R5FSS Block Diagram
        2. 6.3.3.2  R5FSS Cortex-R5F Core
          1. 6.3.3.2.1 L1 Caches
          2. 6.3.3.2.2 Tightly-Coupled Memories (TCMs)
          3. 6.3.3.2.3 R5FSS Special Signals
        3. 6.3.3.3  R5FSS Interfaces
          1. 6.3.3.3.1 Master Interfaces
          2. 6.3.3.3.2 Slave Interfaces
        4. 6.3.3.4  R5FSS Power, Clocking and Reset
          1. 6.3.3.4.1 R5FSS Power
          2. 6.3.3.4.2 R5FSS Clocking
            1. 6.3.3.4.2.1 Changing MCU_R5FSS0 CPU Clock Frequency
          3. 6.3.3.4.3 R5FSS Reset
        5. 6.3.3.5  R5FSS Lockstep Error Detection Logic
          1. 6.3.3.5.1 CPU Output Compare Block
            1. 6.3.3.5.1.1 Operating Modes
            2. 6.3.3.5.1.2 Compare Block Active Mode
            3. 6.3.3.5.1.3 Self Test Mode
            4. 6.3.3.5.1.4 Compare Match Test
            5. 6.3.3.5.1.5 Compare Mismatch Test
            6. 6.3.3.5.1.6 Error Forcing Mode
            7. 6.3.3.5.1.7 Self Test Error Forcing Mode
          2. 6.3.3.5.2 Inactivity Monitor Block
            1. 6.3.3.5.2.1 Operating Modes
            2. 6.3.3.5.2.2 Compare Block Active Mode
            3. 6.3.3.5.2.3 Self Test Mode
            4. 6.3.3.5.2.4 Compare Match Test
            5. 6.3.3.5.2.5 Compare Mismatch Test
            6. 6.3.3.5.2.6 Error Forcing Mode
            7. 6.3.3.5.2.7 Self Test Error Forcing Mode
          3. 6.3.3.5.3 Polarity Inversion Logic
        6. 6.3.3.6  R5FSS Vectored Interrupt Manager (VIM)
          1. 6.3.3.6.1 VIM Overview
          2. 6.3.3.6.2 VIM Interrupt Inputs
          3. 6.3.3.6.3 VIM Interrupt Outputs
          4. 6.3.3.6.4 VIM Interrupt Vector Table (VIM RAM)
          5. 6.3.3.6.5 VIM Interrupt Prioritization
          6. 6.3.3.6.6 VIM ECC Support
          7. 6.3.3.6.7 VIM Lockstep Mode
          8. 6.3.3.6.8 VIM IDLE State
          9. 6.3.3.6.9 VIM Interrupt Handling
            1. 6.3.3.6.9.1 Servicing IRQ Through Vector Interface
            2. 6.3.3.6.9.2 Servicing IRQ Through MMR Interface
            3. 6.3.3.6.9.3 Servicing IRQ Through MMR Interface (Alternative)
            4. 6.3.3.6.9.4 Servicing FIQ
            5. 6.3.3.6.9.5 Servicing FIQ (Alternative)
        7. 6.3.3.7  R5FSS Region Address Translation (RAT)
        8. 6.3.3.8  R5FSS ECC Support
        9. 6.3.3.9  R5FSS Memory View
        10. 6.3.3.10 R5FSS Interrupts
        11. 6.3.3.11 R5FSS Debug and Trace
        12. 6.3.3.12 R5FSS Boot Options
    4. 6.4  C66x DSP Subsystem
    5. 6.5  C71x DSP Subsystem
      1. 6.5.1 C71SS Overview
        1. 6.5.1.1 C71SS Features
      2. 6.5.2 C71SS Integration
      3. 6.5.3 C71SS Functional Description
        1. 6.5.3.1 C71x DSP CPU
        2. 6.5.3.2 C71x DSP Matrix Multiply Accelerator
        3. 6.5.3.3 C71x DSP Cache Memory System
          1. 6.5.3.3.1 C71x DSP L1 Program Memory
          2. 6.5.3.3.2 C71x DSP L1 Data Memory
          3. 6.5.3.3.3 C71x DSP L2 Memory
        4. 6.5.3.4 C71x DSP Streaming Engine
        5. 6.5.3.5 C71x DSP CorePac Memory Management Unit
        6. 6.5.3.6 C71x DSP ECC Support
        7. 6.5.3.7 C71x DSP Boot Configuration
        8. 6.5.3.8 C71x DSP Power-Up/Down Sequences
        9. 6.5.3.9 C71x DSP Interrupt Control
    6. 6.6  Graphics Accelerator (GPU)
      1. 6.6.1 GPU Overview
        1. 6.6.1.1 GPU Features Overview
        2. 6.6.1.2 GPU Not Supported Features
      2. 6.6.2 GPU Integration
        1. 6.6.2.1 GPU Integration in MAIN Domain
      3. 6.6.3 GPU Functional Description
        1. 6.6.3.1 GPU Block Diagram
        2. 6.6.3.2 GPU Clock Configuration
        3. 6.6.3.3 GPU Reset
        4. 6.6.3.4 GPU Power Management
        5. 6.6.3.5 GPU Interrupt Requests
    7. 6.7  Multi-Standard HD Video Decoder (DECODER)
      1. 6.7.1 DECODER Overview
        1. 6.7.1.1 DECODER Features
        2. 6.7.1.2 DECODER Not Supported Features
      2. 6.7.2 DECODER Integration
        1. 6.7.2.1 DECODER Integration in MAIN Domain
      3. 6.7.3 DECODER Functional Description
        1. 6.7.3.1 DECODER Clock Configuration
        2. 6.7.3.2 DECODER Reset
        3. 6.7.3.3 DECODER Interrupts
    8. 6.8  Multi-Standard HD Video Encoder (ENCODER)
      1. 6.8.1 ENCODER Overview
        1. 6.8.1.1 ENCODER Features
        2. 6.8.1.2 ENCODER Not Supported Features
      2. 6.8.2 ENCODER Integration
        1. 6.8.2.1 ENCODER Integration in MAIN Domain
      3. 6.8.3 ENCODER Functional Description
        1. 6.8.3.1 ENCODER Clock Configuration
        2. 6.8.3.2 ENCODER Reset
        3. 6.8.3.3 ENCODER Interrupts
    9. 6.9  Vision Pre-processing Accelerator (VPAC)
      1. 6.9.1 VPAC Overview
        1. 6.9.1.1 VPAC Features
      2. 6.9.2 VPAC Integration
      3. 6.9.3 VPAC Subsystem Level
        1. 6.9.3.1 VPAC Subsystem Clocks
        2. 6.9.3.2 VPAC Subsystem Resets
        3. 6.9.3.3 VPAC Subsystem Interrupts
        4. 6.9.3.4 VPAC Subsystem SL2 Memory Infrastructure
        5. 6.9.3.5 VPAC Subsystem DMA Infrastructure
        6. 6.9.3.6 VPAC Subsystem Data Formats Support
        7. 6.9.3.7 VPAC Subsystem Debug Features
        8. 6.9.3.8 VPAC Subsystem Security Features
      4. 6.9.4 VPAC Vision Imaging Subsystem (VISS)
        1. 6.9.4.1 VISS Top Level
          1. 6.9.4.1.1  VISS Features
          2. 6.9.4.1.2  VISS Block Diagram
          3. 6.9.4.1.3  VISS Data Flow within VPAC
            1. 6.9.4.1.3.1 VISS On-the-fly Processing
              1. 6.9.4.1.3.1.1 Non-WDR or Companded WDR Sensors
            2. 6.9.4.1.3.2 VISS Memory to Memory Image Processing
          4. 6.9.4.1.4  VISS Data Formats Support
          5. 6.9.4.1.5  VISS VPORT Interface
          6. 6.9.4.1.6  VISS Submodule Integration Specifics
            1. 6.9.4.1.6.1 LSE Integration
            2. 6.9.4.1.6.2 GLBCE Integration
              1. 6.9.4.1.6.2.1 GLBCE Startup
              2. 6.9.4.1.6.2.2 GLBCE Bypass
          7. 6.9.4.1.7  VISS Stall Handling
            1. 6.9.4.1.7.1 Stall Handling for Streaming Mode
          8. 6.9.4.1.8  VISS Interrupts
            1. 6.9.4.1.8.1 Interrupts Merging
            2. 6.9.4.1.8.2 Handling of Configuration Error Interrupts
          9. 6.9.4.1.9  VISS Error Correcting Code (ECC) Support
          10. 6.9.4.1.10 VISS Programmer's Guide
            1. 6.9.4.1.10.1 VISS Initialization Sequence
            2. 6.9.4.1.10.2 VISS Configuration Restrictions
            3. 6.9.4.1.10.3 VISS Real-time Operating Requirements
        2. 6.9.4.2 VISS Load Store Engine (LSE)
        3. 6.9.4.3 VISS RAW Frond-End (RAWFE)
          1. 6.9.4.3.1 RAWFE Overview
            1. 6.9.4.3.1.1 RAWFE Supported Features
          2. 6.9.4.3.2 RAWFE Functional Description
            1. 6.9.4.3.2.1 RAWFE Functional Operation
            2. 6.9.4.3.2.2 RAWFE ECC for RAMs
          3. 6.9.4.3.3 RAWFE Interrupts
            1. 6.9.4.3.3.1 RAWFE CPU Interrupts
            2. 6.9.4.3.3.2 RAWFE Debug Events
          4. 6.9.4.3.4 RAWFE Sub-Modules Details
            1. 6.9.4.3.4.1 RAWFE Decompanding Block
              1. 6.9.4.3.4.1.1 RAWFE Mask & Shift
              2. 6.9.4.3.4.1.2 RAWFE Piece Wise Linear Operation
              3. 6.9.4.3.4.1.3 RAWFE Offset/WB-1 Block
              4. 6.9.4.3.4.1.4 RAWFE LUT Based compression
            2. 6.9.4.3.4.2 RAWFE WDR Merge Block
              1. 6.9.4.3.4.2.1 RAWFE WDR Motion Adaptive Merge (MA1 / MA2)
              2. 6.9.4.3.4.2.2 RAWFE Companding LUT
            3. 6.9.4.3.4.3 RAWFE Defective Pixel Correction (DPC) Block
              1. 6.9.4.3.4.3.1 RAWFE LUT Based DPC
              2. 6.9.4.3.4.3.2 RAWFE On-The-Fly (OTF) DPC
            4. 6.9.4.3.4.4 RAWFE Lens Shading Correction (LSC) and Digital Gain (DG) Block
              1. 6.9.4.3.4.4.1 RAWFE LSC Features Supported
              2. 6.9.4.3.4.4.2 RAWFE LSC Image Framing with Respect to Gain Map Samples
            5. 6.9.4.3.4.5 RAWFE Gain & Offset Block
            6. 6.9.4.3.4.6 RAWFE H3A
              1. 6.9.4.3.4.6.1  RAWFE H3A Overview
              2. 6.9.4.3.4.6.2  RAWFE H3A Top-Level Block Diagram
              3. 6.9.4.3.4.6.3  RAWFE H3A Line Framing Logic
              4. 6.9.4.3.4.6.4  RAWFE H3A Optional Preprocessing
              5. 6.9.4.3.4.6.5  RAWFE H3A Autofocus Engine
                1. 6.9.4.3.4.6.5.1 RAWFE H3A Paxel Extraction
                2. 6.9.4.3.4.6.5.2 RAWFE H3A Horizontal FV Calculator
                3. 6.9.4.3.4.6.5.3 RAWFE H3A HFV Accumulator
                4. 6.9.4.3.4.6.5.4 RAWFE H3A VFV Calculator
                5. 6.9.4.3.4.6.5.5 RAWFE H3A VFV Accumulator
              6. 6.9.4.3.4.6.6  RAWFE H3A AE/AWB Engine
                1. 6.9.4.3.4.6.6.1 RAWFE H3A Subsampler
                2. 6.9.4.3.4.6.6.2 RAWFE H3A Additional Black Row of AE/AWB Windows
                3. 6.9.4.3.4.6.6.3 RAWFE H3A Saturation Check
                4. 6.9.4.3.4.6.6.4 RAWFE H3A AE/AWB Accumulators
              7. 6.9.4.3.4.6.7  RAWFE H3A DMA Interface
              8. 6.9.4.3.4.6.8  RAWFE H3A Events and Status Checking
              9. 6.9.4.3.4.6.9  RAWFE H3A Interface Mux
              10. 6.9.4.3.4.6.10 RAWFE H3A interface to LSE
              11. 6.9.4.3.4.6.11 RAWFE H3A Erratas
          5. 6.9.4.3.5 RAWFE Programmer’s Guide
            1. 6.9.4.3.5.1 RAWFE Core programming details
            2. 6.9.4.3.5.2 RAWFE Initialization Sequence
            3. 6.9.4.3.5.3 RAWFE Real-time Оperating Requirements
        4. 6.9.4.4 VISS Spatial Noise Filter (NSF4V)
          1. 6.9.4.4.1 NSF4V Introduction
            1. 6.9.4.4.1.1 NSF4V Features
            2. 6.9.4.4.1.2 NSF4V Not Supported Features
          2. 6.9.4.4.2 NSF4V Overview
            1. 6.9.4.4.2.1 Decomposition Kernel Representation
          3. 6.9.4.4.3 NSF4V Lens Shading Correction Compensation
          4. 6.9.4.4.4 NSF4V Noise Threshold Adaptation to Local Image Intensity
        5. 6.9.4.5 VISS Global/Local Brightness and Contrast Enhancement (GLBCE) Module
          1. 6.9.4.5.1 GLBCE Overview
          2. 6.9.4.5.2 GLBCE Interface
          3. 6.9.4.5.3 GLBCE Core
            1. 6.9.4.5.3.1 GLBCE Core Key Parameters
            2. 6.9.4.5.3.2 GLBCE Iridix Strength Calculation
            3. 6.9.4.5.3.3 GLBCE Iridix Configuration Registers
              1. 6.9.4.5.3.3.1  GLBCE Iridix Frame Width
              2. 6.9.4.5.3.3.2  GLBCE Iridix Frame Height
              3. 6.9.4.5.3.3.3  GLBCE Iridix Control 0
              4. 6.9.4.5.3.3.4  GLBCE Iridix Control 1
              5. 6.9.4.5.3.3.5  GLBCE Iridix Strength
              6. 6.9.4.5.3.3.6  GLBCE Iridix Variance
              7. 6.9.4.5.3.3.7  GLBCE Iridix Dither
              8. 6.9.4.5.3.3.8  GLBCE Iridix Amplification Limit
              9. 6.9.4.5.3.3.9  GLBCE Iridix Slope Min and Max
              10. 6.9.4.5.3.3.10 GLBCE Iridix Black Level
              11. 6.9.4.5.3.3.11 GLBCE Iridix White Level
              12. 6.9.4.5.3.3.12 GLBCE Iridix Asymmetry Function Look-up-table
              13. 6.9.4.5.3.3.13 GLBCE Iridix Forward and Reverse Perceptual Functions Look-up-tables
              14. 6.9.4.5.3.3.14 GLBCE Iridix WDR Look-up-table
          4. 6.9.4.5.4 GLBCE Embedded Memory
          5. 6.9.4.5.5 GLBCE General Processing
          6. 6.9.4.5.6 GLBCE Continuous Frame Processing
          7. 6.9.4.5.7 GLBCE Single Image Processing
        6. 6.9.4.6 VISS Flexible Color Processing (FCP) Module
          1. 6.9.4.6.1 FCP Overview
            1. 6.9.4.6.1.1 FCP Features Supported
          2. 6.9.4.6.2 FCP Functional Description
          3. 6.9.4.6.3 FCP Submodule Details
            1. 6.9.4.6.3.1 Flexible CFA / Demosaicing
              1. 6.9.4.6.3.1.1 Feature-set
              2. 6.9.4.6.3.1.2 Block Diagram of Flexible CFA
                1. 6.9.4.6.3.1.2.1 Gradient/Threshold Calculation
                2. 6.9.4.6.3.1.2.2 Software Controlled Direction Selection
            2. 6.9.4.6.3.2 Edge Enhancer Module Wrapper (WEE)
              1. 6.9.4.6.3.2.1 EE - Edge Enhancer Block
            3. 6.9.4.6.3.3 Flexible Color Conversion (CC)
              1. 6.9.4.6.3.3.1 Interface Mux
              2. 6.9.4.6.3.3.2 Color Conversion (CCM-1)
              3. 6.9.4.6.3.3.3 RGB to HSX Conversion
                1. 6.9.4.6.3.3.3.1 Weighted Average Block
                2. 6.9.4.6.3.3.3.2 Saturation Block
                3. 6.9.4.6.3.3.3.3 Division Block
                4. 6.9.4.6.3.3.3.4 LUT Based 12 to 8 Downsampling
              4. 6.9.4.6.3.3.4 Histogram
              5. 6.9.4.6.3.3.5 Contrast Stretch / Gamma
              6. 6.9.4.6.3.3.6 RGB-YUV Conversion
            4. 6.9.4.6.3.4 444-422/420 Chroma Down-sampler
          4. 6.9.4.6.4 FCP Interrupts
          5. 6.9.4.6.5 FCP Programmer’s Guide
            1. 6.9.4.6.5.1 HWA Core Programming Details
            2. 6.9.4.6.5.2 HWA HTS Programming Details
            3. 6.9.4.6.5.3 HWA Data Transfer Programming Details
            4. 6.9.4.6.5.4 Initialization Sequence
            5. 6.9.4.6.5.5 Real-time Operating Requirements
            6. 6.9.4.6.5.6 Power Up/Down Sequence
        7. 6.9.4.7 VISS Edge Enhancer (EE)
          1. 6.9.4.7.1 Edge Enhancer Introduction
            1. 6.9.4.7.1.1 Edge Enhancer Filter
            2. 6.9.4.7.1.2 Edge Sharpener Filter
            3. 6.9.4.7.1.3 Merge Block
          2. 6.9.4.7.2 Edge Enhancer Programming Model
      5. 6.9.5 VPAC Lens Distortion Correction (LDC) Module
        1. 6.9.5.1 LDC Overview
          1. 6.9.5.1.1 LDC Features
        2. 6.9.5.2 LDC Functional Description
          1. 6.9.5.2.1  LDC Block Diagram
          2. 6.9.5.2.2  LDC Clocks
          3. 6.9.5.2.3  LDC Interrupts
            1. 6.9.5.2.3.1 LDC Interrupt Events Description
              1. 6.9.5.2.3.1.1 PIX_IBLK_OUTOFBOUND
              2. 6.9.5.2.3.1.2 MESH_IBLK_OUTOFBOUND
              3. 6.9.5.2.3.1.3 IFR_OUTOFBOUND
              4. 6.9.5.2.3.1.4 INT_SZOVF
              5. 6.9.5.2.3.1.5 VPAC_LDC_FR_DONE_EVT
              6. 6.9.5.2.3.1.6 VPAC_LDC_SL2_WR_ERR
              7. 6.9.5.2.3.1.7 PIX_IBLK_MEMOVF
              8. 6.9.5.2.3.1.8 MESH_IBLK_MEMOVF
              9. 6.9.5.2.3.1.9 VPAC_LDC_VBUSM_RD_ERR
          4. 6.9.5.2.4  LDC Affine Transform
          5. 6.9.5.2.5  LDC Perspective Transformation
          6. 6.9.5.2.6  LDC Lens Distortion Back Mapping
            1. 6.9.5.2.6.1 LDC Mesh Table Storage Format
          7. 6.9.5.2.7  LDC Pixel Interpolation
          8. 6.9.5.2.8  LDC Buffer Management
            1. 6.9.5.2.8.1 LDC Buffer Management
          9. 6.9.5.2.9  LDC Multi Region with Variable Block size
            1. 6.9.5.2.9.1 LDC Region Skip Feature
            2. 6.9.5.2.9.2 LDC Support for sub-set of 3x3 regions
            3. 6.9.5.2.9.3 LDC Limitations of Multi Region Scheme
            4. 6.9.5.2.9.4 LDC Multi Region Block Constrains
          10. 6.9.5.2.10 LDC Multi-pass Frame processing
          11. 6.9.5.2.11 LDC Input/Output Data Formats
          12. 6.9.5.2.12 LDC YUV422 to YUV420 Conversion
          13. 6.9.5.2.13 LDC SL2 Interface (LSE)
            1. 6.9.5.2.13.1 LDC PSA (Parallel Signature Analysis)
          14. 6.9.5.2.14 LDC LUT Mapped Dual Output
          15. 6.9.5.2.15 LDC Band Width Controller
          16. 6.9.5.2.16 LDC Input Block Fetch Limit
          17. 6.9.5.2.17 LDC HTS Interface
          18. 6.9.5.2.18 LDC VBUSM Read Interface
        3. 6.9.5.3 LDC Programmers Guide
          1. 6.9.5.3.1 LDC Programming Geometric Distortion Mode
          2. 6.9.5.3.2 LDC Programming Rotational Video Stabilization (Affine Transformation)
          3. 6.9.5.3.3 LDC Programming Perspective Transformation
          4. 6.9.5.3.4 LDC Programming LSE
          5. 6.9.5.3.5 LDC Programming Restrictions and Special Cases
      6. 6.9.6 VPAC Multi-Scaler (MSC)
        1. 6.9.6.1 MSC Overview
          1. 6.9.6.1.1 MSC Features
          2. 6.9.6.1.2 MSC Not Supported Features
        2. 6.9.6.2 MSC Functional Description
          1. 6.9.6.2.1 MSC Functional Overview
            1. 6.9.6.2.1.1 MSC Submodule Details
              1. 6.9.6.2.1.1.1 MSC Load Store Engine (MSC_LSE)
                1. 6.9.6.2.1.1.1.1 MSC_LSE Overview
                  1. 9.6.2.1.1.1.1.1 MSC_LSE Features
                2. 6.9.6.2.1.1.1.2 MSC_LSE Internal Data Loopback Channel
                3. 6.9.6.2.1.1.1.3 MSC_LSE PSA Support
                4. 6.9.6.2.1.1.1.4 MSC_LSE Feature Detailed Description
              2. 6.9.6.2.1.1.2 MSC_CORE (HWA Core)
                1. 6.9.6.2.1.1.2.1 MSC_CORE Overview
                2. 6.9.6.2.1.1.2.2 Polyphase Filter of Vertical/Horizontal Resizers
                  1. 9.6.2.1.1.2.2.1 Filter Data Path Logic
                  2. 9.6.2.1.1.2.2.2 Filter Parameters
                  3. 9.6.2.1.1.2.2.3 Single-Phase Filter Parameters
                  4. 9.6.2.1.1.2.2.4 Interleaved Mode Handling
                  5. 9.6.2.1.1.2.2.5 Input Skip Line Support
                3. 6.9.6.2.1.1.2.3 Scaler Filter Thread Mapping
                4. 6.9.6.2.1.1.2.4 Filter Coefficients
                  1. 9.6.2.1.1.2.4.1 Filter Coefficient Parameter Configuration
                  2. 9.6.2.1.1.2.4.2 3/4/5-Tap Filter Configuration
                5. 6.9.6.2.1.1.2.5 Input/Output ROI Trimmers
          2. 6.9.6.2.2 Resizer Algorithm Details
            1. 6.9.6.2.2.1 Multiple Scales Generations
            2. 6.9.6.2.2.2 Polyphase Filter
              1. 6.9.6.2.2.2.1 Interpolation/Resampling
              2. 6.9.6.2.2.2.2 Phase Calculation and Re-sampler
              3. 6.9.6.2.2.2.3 Shared Coefficient Buffers
              4. 6.9.6.2.2.2.4 Border Pixel Padding
            3. 6.9.6.2.2.3 ROI Handling
          3. 6.9.6.2.3 MSC Data Formats Supported
        3. 6.9.6.3 MSC Interrupt Conditions
          1. 6.9.6.3.1 CPU Interrupts
          2. 6.9.6.3.2 Interrupt Event Description
            1. 6.9.6.3.2.1 VPAC_MSC_LSE_FR_DONE_EVT_0/1 Events
            2. 6.9.6.3.2.2 VPAC_MSC_LSE_SL2_RD_ERR Interrupt Event
            3. 6.9.6.3.2.3 VPAC_MSC_LSE_SL2_WR_ERR Interrupt Event
        4. 6.9.6.4 MSC Performance
        5. 6.9.6.5 MSC Clocking
        6. 6.9.6.6 MSC Reset
        7. 6.9.6.7 MSC Programmer’s Guide
          1. 6.9.6.7.1 Programming Model
            1. 6.9.6.7.1.1 MSC Programming Guidelines
            2. 6.9.6.7.1.2 MSC_Core Programming Details
            3. 6.9.6.7.1.3 MSC_LSE Programming Details
              1. 6.9.6.7.1.3.1 Input Thread Configuration:
              2. 6.9.6.7.1.3.2 Output Channel Configuration
            4. 6.9.6.7.1.4 MSC HTS Programming Details
            5. 6.9.6.7.1.5 MSC Data Transfer Programming Details
            6. 6.9.6.7.1.6 LSE Interrupt Programming
          2. 6.9.6.7.2 Initialization Sequence
          3. 6.9.6.7.3 Real-Time Operating Requirements
          4. 6.9.6.7.4 Power Up/Down Sequence
      7. 6.9.7 VPAC Noise Filter (NF)
        1. 6.9.7.1 NF Overview
          1. 6.9.7.1.1 NF Supported Features
        2. 6.9.7.2 NF Functional Description
          1. 6.9.7.2.1 Functional Operation
            1. 6.9.7.2.1.1 Overview
            2. 6.9.7.2.1.2 Algorithm Details
        3. 6.9.7.3 NF Interrupts
          1. 6.9.7.3.1 CPU Interrupts
          2. 6.9.7.3.2 Interrupt Event Description
            1. 6.9.7.3.2.1 NF_FRAME_DONE Event
            2. 6.9.7.3.2.2 NF_SL2_READ_ERROR Event
            3. 6.9.7.3.2.3 NF_SL2_WRITE_ERROR Event
        4. 6.9.7.4 NF Submodule Details
          1. 6.9.7.4.1 NF_CFG
          2. 6.9.7.4.2 NF_LSE
            1. 6.9.7.4.2.1 NF_LSE Overview
            2. 6.9.7.4.2.2 NF_LSE Feature Detailed Description
          3. 6.9.7.4.3 Synchronization With HTS
          4. 6.9.7.4.4 Noise Filter Core Block Diagram
            1. 6.9.7.4.4.1 Space Weight Details
            2. 6.9.7.4.4.2 Weight Calculation Logic
              1. 6.9.7.4.4.2.1 Combined LUT For Space And Range Weights
            3. 6.9.7.4.4.3 Reciprocal Calculation Logic
            4. 6.9.7.4.4.4 Border Handling
              1. 6.9.7.4.4.4.1 Border Handling (Simple)
          5. 6.9.7.4.5 Usage As Generic 2D Filter Engine
          6. 6.9.7.4.6 Adaptive Bilateral Weight Support
          7. 6.9.7.4.7 Chroma Handling (Interleaved Mode)
        5. 6.9.7.5 NF Programmer’s Guide
          1. 6.9.7.5.1 Programming Model
            1. 6.9.7.5.1.1 HWA Core Programming Details
            2. 6.9.7.5.1.2 NF SL2 Wrapper Interface Programming Details
            3. 6.9.7.5.1.3 HWA HTS Programming Details
            4. 6.9.7.5.1.4 HWA Data Transfer Programming Details
    10. 6.10 Depth and Motion Perception Accelerator (DMPAC)
      1. 6.10.1 DMPAC Overview
        1. 6.10.1.1 DMPAC Features
      2. 6.10.2 DMPAC Integration
      3. 6.10.3 DMPAC Functional Description
        1. 6.10.3.1  DMPAC Block Diagram
        2. 6.10.3.2  DMPAC Data Formats and Image Resolution
          1. 6.10.3.2.1 Resolution and Frame Rate
          2. 6.10.3.2.2 Input Data Formats
        3. 6.10.3.3  DMPAC Top Level Data Flow
        4. 6.10.3.4  DMPAC Stereo Functional Overview
          1. 6.10.3.4.1  Stereo Processing Dataflow
          2. 6.10.3.4.2  Disparity Range
          3. 6.10.3.4.3  Epipolar Rectification
          4. 6.10.3.4.4  Disparity Search Method
          5. 6.10.3.4.5  Cost Computation Method
          6. 6.10.3.4.6  Cost Plane Compression Method
          7. 6.10.3.4.7  Sub-Pixel Interpolation Method
          8. 6.10.3.4.8  Raw Disparity Output Cleaning Method
          9. 6.10.3.4.9  Confidence Score Computation Method
          10. 6.10.3.4.10 Disparity Map Post Filtering Method
          11. 6.10.3.4.11 Disparity Output Data Packing Format
        5. 6.10.3.5  DMPAC Optical Flow Functional Overview
          1. 6.10.3.5.1  Optical Flow Processing Dataflow
          2. 6.10.3.5.2  Flow Vector Range
          3. 6.10.3.5.3  Block Matching Process
          4. 6.10.3.5.4  Image Pyramid Generation Method
          5. 6.10.3.5.5  Cost Computation Method
          6. 6.10.3.5.6  Sub-Pixel Refinement Method
          7. 6.10.3.5.7  Confidence Score Computation Method
          8. 6.10.3.5.8  Flow Vector Post Filtering Method
          9. 6.10.3.5.9  Flow Vector Output Data Packing Format
          10. 6.10.3.5.10 Sparse Optical Flow Support
        6. 6.10.3.6  DMPAC Format Conversion (FOCO) Module Operation
          1. 6.10.3.6.1 FOCO Implementation Details
          2. 6.10.3.6.2 FOCO Core Details
        7. 6.10.3.7  DMPAC Clocks
        8. 6.10.3.8  DMPAC Resets
        9. 6.10.3.9  DMPAC Interrupts
        10. 6.10.3.10 DMPAC SL2 Memory Subsystem
        11. 6.10.3.11 DMPAC Common DMA
        12. 6.10.3.12 DMPAC Messaging and Control
          1. 6.10.3.12.1 DOF Node Scheduler
          2. 6.10.3.12.2 SDE Node Scheduler
        13. 6.10.3.13 DMPAC Hardware Security
          1. 6.10.3.13.1 Configuration Interconnect
          2. 6.10.3.13.2 SL2 Interconnect
        14. 6.10.3.14 DMPAC Debug
        15. 6.10.3.15 DMPAC Internal Diagnostic Features
        16. 6.10.3.16 DMPAC Memory Error Protection
      4. 6.10.4 DMPAC Programming Guide
        1. 6.10.4.1 DMPAC Optical Flow Initialization Sequence - 12-bit Packed Input Pixel Data
          1. 6.10.4.1.1 Optical Flow 12bb - DMPAC Top Level Configuration
          2. 6.10.4.1.2 Optical Flow 12bb - UTC Configuration
            1. 6.10.4.1.2.1 Reference Frame Growing Window Fetch
            2. 6.10.4.1.2.2 Current Frame Growing Window Fetch
            3. 6.10.4.1.2.3 Temporal Predictor Fetch
            4. 6.10.4.1.2.4 Pyramidal Predictor Fetch
            5. 6.10.4.1.2.5 Sparse Optical Flow Binary Map Fetch
            6. 6.10.4.1.2.6 Flow Vector Output
          3. 6.10.4.1.3 Optical Flow 12bb - HTS Configuration
        2. 6.10.4.2 DMPAC Stereo Disparity Initialization Sequence - 12-bit Packed Input Pixel Data
          1. 6.10.4.2.1 Stereo Disparity 12bpp - DMPAC Top Configuration
          2. 6.10.4.2.2 Stereo Disparity 12bpp - DMA Configuration
            1. 6.10.4.2.2.1 Reference Frame Growing Window Fetch
            2. 6.10.4.2.2.2 Base Frame Growing Window Fetch
            3. 6.10.4.2.2.3 Stereo Disparity Output
          3. 6.10.4.2.3 Stereo Disparity 12bpp - HTS Configuration
        3. 6.10.4.3 DMPAC End of Pipeline Processing
        4. 6.10.4.4 DMPAC Debug Restrictions
  9. 7 Interprocessor Communication
    1. 7.1 Mailbox
      1. 7.1.1 Mailbox Overview
        1. 7.1.1.1 Mailbox Features
        2. 7.1.1.2 Mailbox Parameters
        3. 7.1.1.3 Mailbox Not Supported Features
      2. 7.1.2 Mailbox Integration
        1. 7.1.2.1 System Mailbox Integration
      3. 7.1.3 Mailbox Functional Description
        1. 7.1.3.1 Mailbox Block Diagram
        2. 7.1.3.2 Mailbox Software Reset
        3. 7.1.3.3 Mailbox Power Management
        4. 7.1.3.4 Mailbox Interrupt Requests
        5. 7.1.3.5 Mailbox Assignment
          1. 7.1.3.5.1 Description
        6. 7.1.3.6 Sending and Receiving Messages
          1. 7.1.3.6.1 Description
        7. 7.1.3.7 Example of Communication
      4. 7.1.4 Mailbox Programming Guide
        1. 7.1.4.1 Mailbox Low-level Programming Models
          1. 7.1.4.1.1 Global Initialization
            1. 7.1.4.1.1.1 Surrounding Modules Global Initialization
            2. 7.1.4.1.1.2 Mailbox Global Initialization
              1. 7.1.4.1.1.2.1 Main Sequence - Mailbox Global Initialization
          2. 7.1.4.1.2 Mailbox Operational Modes Configuration
            1. 7.1.4.1.2.1 Mailbox Processing modes
              1. 7.1.4.1.2.1.1 Main Sequence - Sending a Message (Polling Method)
              2. 7.1.4.1.2.1.2 Main Sequence - Sending a Message (Interrupt Method)
              3. 7.1.4.1.2.1.3 Main Sequence - Receiving a Message (Polling Method)
              4. 7.1.4.1.2.1.4 Main Sequence - Receiving a Message (Interrupt Method)
          3. 7.1.4.1.3 Mailbox Events Servicing
            1. 7.1.4.1.3.1 Events Servicing in Sending Mode
            2. 7.1.4.1.3.2 Events Servicing in Receiving Mode
    2. 7.2 Spinlock
      1. 7.2.1 Spinlock Overview
        1. 7.2.1.1 Spinlock Not Supported Features
      2. 7.2.2 Spinlock Integration
      3. 7.2.3 Spinlock Functional Description
        1. 7.2.3.1 Spinlock Software Reset
        2. 7.2.3.2 Spinlock Power Management
        3. 7.2.3.3 About Spinlocks
        4. 7.2.3.4 Spinlock Functional Operation
      4. 7.2.4 Spinlock Programming Guide
        1. 7.2.4.1 Spinlock Low-level Programming Models
          1. 7.2.4.1.1 Surrounding Modules Global Initialization
          2. 7.2.4.1.2 Basic Spinlock Operations
            1. 7.2.4.1.2.1 Spinlocks Clearing After a System Bug Recovery
            2. 7.2.4.1.2.2 Take and Release Spinlock
  10. 8 Memory Controllers
    1. 8.1 Multicore Shared Memory Controller (MSMC)
      1. 8.1.1 MSMC Overview
        1. 8.1.1.1 MSMC Not Supported Features
      2. 8.1.2 MSMC Integration
        1. 8.1.2.1 MSMC Integration in MAIN Domain
        2. 8.1.2.2 1029
      3. 8.1.3 MSMC Functional Description
        1. 8.1.3.1  MSMC Block Diagram
        2. 8.1.3.2  MSMC On-Chip Memory Banking
        3. 8.1.3.3  MSMC Snoop Filter and Data Cache
          1. 8.1.3.3.1 Way Partitioning
          2. 8.1.3.3.2 Cache Size Configuration and Associativity
        4. 8.1.3.4  MSMC Access Protection Checks
        5. 8.1.3.5  MSMC Null Slave
        6. 8.1.3.6  MSMC Resource Arbitration
        7. 8.1.3.7  MSMC Error Detection and Correction
          1. 8.1.3.7.1 On-chip SRAM and Pipeline Data Protection
          2. 8.1.3.7.2 On-chip SRAM L3 Cache Tag and Snoop Filter Protection
          3. 8.1.3.7.3 On-chip SRAM Memory Mapped SRAM Snoop Filter Protection
          4. 8.1.3.7.4 Background Parity Refresh (Scrubbing)
        8. 8.1.3.8  MSMC Interrupts
          1. 8.1.3.8.1 Raw Interrupt Registers
          2. 8.1.3.8.2 Interrupt Enable Registers
          3. 8.1.3.8.3 Triggered and Enabled Interrupts
        9. 8.1.3.9  MSMC Memory Regions
        10. 8.1.3.10 MSMC Hardware Coherence
          1. 8.1.3.10.1 Snoop Filter Broadcast Mode
        11. 8.1.3.11 MSMC Quality-of-Service
        12. 8.1.3.12 MSMC Memory Regions Protection
        13. 8.1.3.13 MSMC Cache Tag View
    2. 8.2 DDR Subsystem (DDRSS)
      1. 8.2.1 DDRSS Overview
        1. 8.2.1.1 DDRSS Not Supported Features
      2. 8.2.2 DDRSS Environment
      3. 8.2.3 DDRSS Integration
        1. 8.2.3.1 DDRSS Integration in MAIN Domain
      4. 8.2.4 DDRSS Functional Description
        1. 8.2.4.1 DDRSS MSMC2DDR Bridge
          1. 8.2.4.1.1 VBUSM.C Threads
          2. 8.2.4.1.2 Class of Service (CoS)
          3. 8.2.4.1.3 AXI Write Data All-Strobes
          4. 8.2.4.1.4 Inline ECC for SDRAM Data
            1. 8.2.4.1.4.1 ECC Cache
            2. 8.2.4.1.4.2 ECC Statistics
          5. 8.2.4.1.5 Opcode Checking
          6. 8.2.4.1.6 Address Alias Prevention
          7. 8.2.4.1.7 Data Error Detection and Correction
          8. 8.2.4.1.8 AXI Bus Timeout
        2. 8.2.4.2 DDRSS Interrupts
        3. 8.2.4.3 DDRSS Memory Regions
        4. 8.2.4.4 DDRSS ECC Support
        5. 8.2.4.5 DDRSS Dynamic Frequency Change Interface
        6. 8.2.4.6 DDR Controller Functional Description
          1. 8.2.4.6.1  DDR PHY Interface (DFI)
          2. 8.2.4.6.2  Command Queue
            1. 8.2.4.6.2.1 Placement Logic
            2. 8.2.4.6.2.2 Command Selection Logic
          3. 8.2.4.6.3  Low Power Control
          4. 8.2.4.6.4  Transaction Processing
          5. 8.2.4.6.5  BIST Engine
          6. 8.2.4.6.6  ECC Engine
          7. 8.2.4.6.7  Address Mapping
          8. 8.2.4.6.8  Paging Policy
          9. 8.2.4.6.9  DDR Controller Initialization
          10. 8.2.4.6.10 Programming LPDDR4 Memories
            1. 8.2.4.6.10.1 Frequency Set Point (FSP)
              1. 8.2.4.6.10.1.1 FSP Mode Register Programming During Initialization
              2. 8.2.4.6.10.1.2 FSP Mode Register Programming During Normal Operation
              3. 8.2.4.6.10.1.3 FSP Mode Register Programming During Dynamic Frequency Scaling
            2. 8.2.4.6.10.2 Data Bus Inversion (DBI)
            3. 8.2.4.6.10.3 On-Die Termination
              1. 8.2.4.6.10.3.1 LPDDR4 DQ ODT
              2. 8.2.4.6.10.3.2 LPDDR4 CA ODT
            4. 8.2.4.6.10.4 Byte Lane Swapping
            5. 8.2.4.6.10.5 DQS Interval Oscillator
              1. 8.2.4.6.10.5.1 Oscillator State Machine
            6. 8.2.4.6.10.6 Per-Bank Refresh (PBR)
              1. 8.2.4.6.10.6.1 Normal Operation
              2. 8.2.4.6.10.6.2 Continuous Refresh Request Mode
        7. 8.2.4.7 DDR PHY Functional Description
          1. 8.2.4.7.1  Data Slice
          2. 8.2.4.7.2  Address Slice
            1. 8.2.4.7.2.1 Address Swapping
          3. 8.2.4.7.3  Address/Control Slice
          4. 8.2.4.7.4  Clock Slice
          5. 8.2.4.7.5  DDR PHY Initialization
          6. 8.2.4.7.6  DDR PHY Dynamic Frequency Scaling (DFS)
          7. 8.2.4.7.7  Chip Select and Frequency Based Register Settings
          8. 8.2.4.7.8  Low-Power Modes
          9. 8.2.4.7.9  Training Support
            1. 8.2.4.7.9.1 Write Leveling
            2. 8.2.4.7.9.2 Read Gate Training
            3. 8.2.4.7.9.3 Read Data Eye Training
            4. 8.2.4.7.9.4 Write DQ Training
            5. 8.2.4.7.9.5 CA Training
            6. 8.2.4.7.9.6 CS Training
          10. 8.2.4.7.10 Data Bus Inversion (DBI)
          11. 8.2.4.7.11 I/O Pad Calibration
          12. 8.2.4.7.12 DQS Error
        8. 8.2.4.8 PI Functional Description
          1. 8.2.4.8.1 PI Initialization
    3. 8.3 Virtualization Subsystem (VirtSS)
      1. 8.3.1 VirtSS Overview
        1. 8.3.1.1 VirtSS Features
        2. 8.3.1.2 Functional Description
          1. 8.3.1.2.1  Ports
          2. 8.3.1.2.2  CBASS
          3. 8.3.1.2.3  PAT
            1. 8.3.1.2.3.1 Bandwidth Splitting
          4. 8.3.1.2.4  PVU
            1. 8.3.1.2.4.1 Bandwidth Splitting
          5. 8.3.1.2.5  TBU
            1. 8.3.1.2.5.1 Bandwidth Splitting
            2. 8.3.1.2.5.2 Initialization Delay Requirement
          6. 8.3.1.2.6  TCU
          7. 8.3.1.2.7  DTI Interconnect
          8. 8.3.1.2.8  External DTI Ports
          9. 8.3.1.2.9  DMA Split
          10. 8.3.1.2.10 Port Routing Rules
        3. 8.3.1.3 VirtSS Configuration
          1. 8.3.1.3.1 PAT Parameters
          2. 8.3.1.3.2 PVU Parameters
          3. 8.3.1.3.3 TBU Parameters
          4. 8.3.1.3.4 TCU Parameters
          5. 8.3.1.3.5 ECC Aggregator Parameters
        4. 8.3.1.4 Theory of Operation
          1. 8.3.1.4.1 TBU Address Translation Module
          2. 8.3.1.4.2 DTI
          3. 8.3.1.4.3 TCU
          4. 8.3.1.4.4 1153
          5. 8.3.1.4.5 PAT Address Translation Module
            1. 8.3.1.4.5.1 Run-Time PAT Configuration
          6. 8.3.1.4.6 PVU Address Translation Module
      2. 8.3.2 Peripheral Virtualization Unit (PVU)
        1. 8.3.2.1 PVU Overview
          1. 8.3.2.1.1 PVU Features
          2. 8.3.2.1.2 PVU Parameters
          3. 8.3.2.1.3 PVU Not Supported Features
        2. 8.3.2.2 PVU Integration
        3. 8.3.2.3 PVU Functional Description
          1. 8.3.2.3.1  Functional Operation Overview
          2. 8.3.2.3.2  PVU Channels
          3. 8.3.2.3.3  TLB
          4. 8.3.2.3.4  TLB Entry
          5. 8.3.2.3.5  TLB Selection
          6. 8.3.2.3.6  DMA Classes
          7. 8.3.2.3.7  General virtIDs
          8. 8.3.2.3.8  TLB Lookup
          9. 8.3.2.3.9  TLB Miss
          10. 8.3.2.3.10 Multiple Matching Entries
          11. 8.3.2.3.11 TLB Disable
          12. 8.3.2.3.12 TLB Chaining
          13. 8.3.2.3.13 TLB Permissions
          14. 8.3.2.3.14 Translation
          15. 8.3.2.3.15 Memory Attributes
          16. 8.3.2.3.16 Faulted Transactions
          17. 8.3.2.3.17 Non-Virtual Transactions
          18. 8.3.2.3.18 Allowed virtIDs
          19. 8.3.2.3.19 Software Control
          20. 8.3.2.3.20 Fault Logging
          21. 8.3.2.3.21 Alignment Restrictions
      3. 8.3.3 Page Based Address Translation Unit (PAT)
        1. 8.3.3.1 PAT Overview
          1. 8.3.3.1.1 PAT Features
          2. 8.3.3.1.2 PAT Parameters
          3. 8.3.3.1.3 PAT Not Supported Features
        2. 8.3.3.2 PAT Integration
        3. 8.3.3.3 PAT Functional Description
          1. 8.3.3.3.1 Functional Operation Overview
          2. 8.3.3.3.2 Page Table
          3. 8.3.3.3.3 Alignment
          4. 8.3.3.3.4 Page Enables
          5. 8.3.3.3.5 Table Arbitration
          6. 8.3.3.3.6 Programming
          7. 8.3.3.3.7 Scratch RAM
          8. 8.3.3.3.8 Error Reporting
    4. 8.4 Region-based Address Translation (RAT) Module
      1. 8.4.1 RAT Functional Description
        1. 8.4.1.1 RAT Availability
        2. 8.4.1.2 RAT Operation
        3. 8.4.1.3 RAT Error Logging
  11. 9 Interrupts
    1. 9.1 Interrupt Architecture
    2. 9.2 Interrupt Controllers
      1. 9.2.1 Generic Interrupt Controller (GIC)
        1. 9.2.1.1 GIC Overview
          1. 9.2.1.1.1 GIC Features
          2. 9.2.1.1.2 GIC Not Supported Features
          3. 9.2.1.1.3 GIC Configuration Summary
        2. 9.2.1.2 GIC Integration
        3. 9.2.1.3 GIC Functional Description
          1. 9.2.1.3.1 GIC Block Diagram
          2. 9.2.1.3.2 Arm GIC-500
          3. 9.2.1.3.3 GIC Interrupt Types
          4. 9.2.1.3.4 GIC Interfaces
          5. 9.2.1.3.5 GIC Interrupt Outputs
          6. 9.2.1.3.6 GIC ECC Support
          7. 9.2.1.3.7 GIC Interrupt Edge Detection
          8. 9.2.1.3.8 GIC AXI2VBUSM and VBUSM2AXI Bridges
      2. 9.2.2 Cluster Level Event Controller (CLEC)
        1. 9.2.2.1 CLEC Overview
        2. 9.2.2.2 CLEC Integration
        3. 9.2.2.3 CLEC Functional Description
          1. 9.2.2.3.1 CLEC Interrupt Event Routing
          2. 9.2.2.3.2 CLEC Virtualization, Isolation and Access Control
          3. 9.2.2.3.3 CLEC Memory Protection
          4. 9.2.2.3.4 CLEC ECC Support
          5. 9.2.2.3.5 CLEC Intra-Core Communication
          6. 9.2.2.3.6 CLEC Event Maps
            1. 9.2.2.3.6.1 CLEC Output Event Routing
            2. 9.2.2.3.6.2 CLEC Input Event Map
            3. 9.2.2.3.6.3 CLEC ESM Event Routing
            4. 9.2.2.3.6.4 CLEC C7x DSP Input Event Map
      3. 9.2.3 Other Interrupt Controllers
    3. 9.3 Interrupt Routers
      1. 9.3.1 INTRTR Overview
      2. 9.3.2 INTRTR Integration
        1. 9.3.2.1 WKUP_GPIOMUX_INTRTR0 Integration
        2. 9.3.2.2 GPIOMUX_INTRTR0 Integration
        3. 9.3.2.3 MAIN2MCU_LVL_INTRTR0 Integration
        4. 9.3.2.4 MAIN2MCU_PLS_INTRTR0 Integration
        5. 9.3.2.5 C66SS0_INTRTR0 Integration
        6. 9.3.2.6 C66SS1_INTRTR0 Integration
        7. 9.3.2.7 R5FSS0_INTRTR0 Integration
        8. 9.3.2.8 R5FSS1_INTRTR0 Integration
    4. 9.4 Interrupt Sources
      1. 9.4.1 WKUP Domain Interrupt Maps
        1. 9.4.1.1 WKUP_DMSC0 Interrupt Map
        2. 9.4.1.2 WKUP_GPIOMUX_INTRTR0 Interrupt Map
        3. 9.4.1.3 WKUP_ESM0 Interrupt Map
      2. 9.4.2 MCU Domain Interrupt Maps
        1. 9.4.2.1 MCU_R5FSS0_CORE0 Interrupt Map
        2. 9.4.2.2 MCU_R5FSS0_CORE1 Interrupt Map
        3. 9.4.2.3 MCU_ESM0 Interrupt Map
      3. 9.4.3 MAIN Domain Interrupt Maps
        1. 9.4.3.1  COMPUTE_CLUSTER0 Interrupt Map
          1. 9.4.3.1.1 GIC500 PPI Interrupt Map
          2. 9.4.3.1.2 GIC500 SPI Interrupt Map
        2. 9.4.3.2  R5FSS0_CORE0 Interrupt Map
        3. 9.4.3.3  R5FSS0_CORE1 Interrupt Map
        4. 9.4.3.4  R5FSS1_CORE0 Interrupt Map
        5. 9.4.3.5  R5FSS1_CORE1 Interrupt Map
        6. 9.4.3.6  R5FSS0_INTRTR0 Interrupt Map
        7. 9.4.3.7  R5FSS1_INTRTR0 Interrupt Map
        8. 9.4.3.8  C66SS0 Interrupt Map
        9. 9.4.3.9  C66SS1 Interrupt Map
        10. 9.4.3.10 C66SS0_INTRTR0 Interrupt Map
        11. 9.4.3.11 C66SS1_INTRTR0 Interrupt Map
        12. 9.4.3.12 PRU-ICSSG0 Interrupt Map
        13. 9.4.3.13 PRU-ICSSG1 Interrupt Map
        14. 9.4.3.14 MAIN2MCU_LVL_INTRTR0 Interrupt Map
        15. 9.4.3.15 MAIN2MCU_PLS_INTRTR0 Interrupt Map
        16. 9.4.3.16 GPIOMUX_INTRTR0 Interrupt Map
        17. 9.4.3.17 ESM0 Interrupt Map
  12. 10Data Movement Architecture (DMA)
    1. 10.1 DMA Architecture
      1. 10.1.1 Overview
        1. 10.1.1.1  Navigator Subsystem
        2. 10.1.1.2  Ring Accelerator (RA)
        3. 10.1.1.3  Proxy
        4. 10.1.1.4  Secure Proxy
        5. 10.1.1.5  Interrupt Aggregator (INTA)
        6. 10.1.1.6  Interrupt Router (IR)
        7. 10.1.1.7  Unified DMA – Third Party Channel Controller (UDMA-C)
        8. 10.1.1.8  Unified Transfer Controller (UTC)
        9. 10.1.1.9  Data Routing Unit (DRU)
        10. 10.1.1.10 Unified DMA – Peripheral Root Complex (UDMA-P)
          1. 10.1.1.10.1 Channel Classes
        11. 10.1.1.11 Peripheral DMA (PDMA)
        12. 10.1.1.12 Embedded DMA
        13. 10.1.1.13 Definition of Terms
      2. 10.1.2 DMA Hardware/Software Interface
        1. 10.1.2.1 Data Buffers
        2. 10.1.2.2 Descriptors
          1. 10.1.2.2.1 Host Packet Descriptor
          2. 10.1.2.2.2 Host Buffer Descriptor
          3. 10.1.2.2.3 Monolithic Packet Descriptor
          4. 10.1.2.2.4 Transfer Request Descriptor
        3. 10.1.2.3 Transfer Request Record
          1. 10.1.2.3.1 Overview
          2. 10.1.2.3.2 Addressing Algorithm
            1. 10.1.2.3.2.1 Linear Addressing (Forward)
          3. 10.1.2.3.3 Transfer Request Formats
          4. 10.1.2.3.4 Flags Field Definition
            1. 10.1.2.3.4.1 Type: TR Type Field
            2. 10.1.2.3.4.2 STATIC: Static Field Definition
            3. 10.1.2.3.4.3 EVENT_SIZE: Event Generation Definition
            4. 10.1.2.3.4.4 TRIGGER INFO: TR Triggers
            5. 10.1.2.3.4.5 TRIGGERX_TYPE: Trigger Type
            6. 10.1.2.3.4.6 TRIGGERX: Trigger Selection
            7. 10.1.2.3.4.7 CMD ID: Command ID Field Definition
            8. 10.1.2.3.4.8 Configuration Specific Flags Definition
          5. 10.1.2.3.5 TR Address and Size Attributes
            1. 10.1.2.3.5.1  ICNT0
            2. 10.1.2.3.5.2  ICNT1
            3. 10.1.2.3.5.3  ADDR
            4. 10.1.2.3.5.4  DIM1
            5. 10.1.2.3.5.5  ICNT2
            6. 10.1.2.3.5.6  ICNT3
            7. 10.1.2.3.5.7  DIM2
            8. 10.1.2.3.5.8  DIM3
            9. 10.1.2.3.5.9  DDIM1
            10. 10.1.2.3.5.10 DADDR
            11. 10.1.2.3.5.11 DDIM2
            12. 10.1.2.3.5.12 DDIM3
            13. 10.1.2.3.5.13 DICNT0
            14. 10.1.2.3.5.14 DICNT1
            15. 10.1.2.3.5.15 DICNT2
            16. 10.1.2.3.5.16 DICNT3
          6. 10.1.2.3.6 FMTFLAGS
            1. 10.1.2.3.6.1 AMODE: Addressing Mode Definition
              1. 10.1.2.3.6.1.1 Linear Addressing
              2. 10.1.2.3.6.1.2 Circular Addressing
            2. 10.1.2.3.6.2 DIR: Addressing Mode Direction Definition
            3. 10.1.2.3.6.3 ELTYPE: Element Type Definition
            4. 10.1.2.3.6.4 DFMT: Data Formatting Algorithm Definition
            5. 10.1.2.3.6.5 SECTR: Secondary Transfer Request Definition
              1. 10.1.2.3.6.5.1 Secondary TR Formats
              2. 10.1.2.3.6.5.2 Secondary TR FLAGS
                1. 10.1.2.3.6.5.2.1 SEC_TR_TYPE: Secondary TR Type Field
                2. 10.1.2.3.6.5.2.2 Multiple Buffer Interleave
            6. 10.1.2.3.6.6 AMODE SPECIFIC: Addressing Mode Field
              1. 10.1.2.3.6.6.1 Circular Address Mode Specific Flags
                1. 10.1.2.3.6.6.1.1 CBK0 and CBK1: Circular Block Size Selection
                2. 10.1.2.3.6.6.1.2 Amx: Addressing Mode Selection
            7. 10.1.2.3.6.7 Cache Flags
        4. 10.1.2.4 Transfer Response Record
          1. 10.1.2.4.1 STATUS Field Definition
            1. 10.1.2.4.1.1 STATUS_TYPE Definition
              1. 10.1.2.4.1.1.1 Transfer Error
              2. 10.1.2.4.1.1.2 Aborted Error
              3. 10.1.2.4.1.1.3 Submission Error
              4. 10.1.2.4.1.1.4 Unsupported Feature
              5. 10.1.2.4.1.1.5 Transfer Exception
              6. 10.1.2.4.1.1.6 Teardown Flush
        5. 10.1.2.5 Queues
          1. 10.1.2.5.1 Queue Types
            1. 10.1.2.5.1.1 Transmit Queues (Pass By Reference)
            2. 10.1.2.5.1.2 Transmit Queues (Pass By Value)
            3. 10.1.2.5.1.3 Transmit Completion Queues (Pass By Reference)
            4. 10.1.2.5.1.4 Transmit Completion Queues (Pass By Value)
            5. 10.1.2.5.1.5 Receive Queues
            6. 10.1.2.5.1.6 Free Descriptor Queues
            7. 10.1.2.5.1.7 Free Descriptor/Buffer Queues
          2. 10.1.2.5.2 Ring Accelerator Queues Implementation
      3. 10.1.3 Operational Description
        1. 10.1.3.1  Resource Allocation
        2. 10.1.3.2  Ring Accelerator Operation
          1. 10.1.3.2.1 Queue Initialization
          2. 10.1.3.2.2 Queuing packets (Exposed Ring Mode)
          3. 10.1.3.2.3 De-queuing packets (Exposed Ring Mode)
          4. 10.1.3.2.4 Queuing packets (Queue Mode)
          5. 10.1.3.2.5 De-queuing packets (Queue Mode)
        3. 10.1.3.3  UDMA Internal Transmit Channel Setup (All Packet Types)
        4. 10.1.3.4  1378
        5. 10.1.3.5  UDMA Internal Transmit Channel Teardown (All Packet Types)
        6. 10.1.3.6  UDMA External Transmit Channel Setup
        7. 10.1.3.7  UDMA Transmit External Channel Teardown
        8. 10.1.3.8  UDMA-P Transmit Channel Pause
        9. 10.1.3.9  1383
        10. 10.1.3.10 UDMA-P Transmit Operation (Host Packet Type)
        11. 10.1.3.11 UDMA-P Transmit Operation (Monolithic Packet)
        12. 10.1.3.12 UDMA Transmit Operation (TR Packet)
        13. 10.1.3.13 UDMA Transmit Operation (Direct TR)
        14. 10.1.3.14 UDMA Transmit Error/Exception Handling
          1. 10.1.3.14.1 Null Icnt0 Error
          2. 10.1.3.14.2 Unsupported TR Type
          3. 10.1.3.14.3 Bus Errors
        15. 10.1.3.15 UDMA Receive Channel Setup (All Packet Types)
        16. 10.1.3.16 UDMA Receive Channel Teardown
        17. 10.1.3.17 UDMA-P Receive Channel Pause
        18. 10.1.3.18 UDMA-P Receive Free Descriptor/Buffer Queue Setup (Host Packets)
        19. 10.1.3.19 UDMA-P Receive FlowID Firewall Operation
        20. 10.1.3.20 UDMA-P Receive Operation (Host Packet)
        21. 10.1.3.21 UDMA-P Receive Operation (Monolithic Packet)
        22. 10.1.3.22 UDMA Receive Operation (TR Packet)
        23. 10.1.3.23 UDMA Receive Operation (Direct TR)
        24. 10.1.3.24 UDMA Receive Error/Exception Handling
          1. 10.1.3.24.1 Error Conditions
            1. 10.1.3.24.1.1 Bus Errors
            2. 10.1.3.24.1.2 Null Icnt0 Error
            3. 10.1.3.24.1.3 Unsupported TR Type
          2. 10.1.3.24.2 Exception Conditions Exception Conditions
            1. 10.1.3.24.2.1 Descriptor Starvation
            2. 10.1.3.24.2.2 Protocol Errors
            3. 10.1.3.24.2.3 Dropped Packets
            4. 10.1.3.24.2.4 Reception of EOL Delimiter
            5. 10.1.3.24.2.5 EOP Asserted Prematurely (Short Packet)
            6. 10.1.3.24.2.6 EOP Asserted Late (Long Packets)
        25. 10.1.3.25 UTC Operation
        26. 10.1.3.26 UTC Receive Error/Exception Handling
          1. 10.1.3.26.1 Error Handling
            1. 10.1.3.26.1.1 Null Icnt0 Error
            2. 10.1.3.26.1.2 Unsupported TR Type
          2. 10.1.3.26.2 Exception Conditions
            1. 10.1.3.26.2.1 Reception of EOL Delimiter
            2. 10.1.3.26.2.2 EOP Asserted Prematurely (Short Packet)
            3. 10.1.3.26.2.3 EOP Asserted Late (Long Packets)
    2. 10.2 Navigator Subsystem (NAVSS)
      1. 10.2.1  Main Navigator Subsystem (NAVSS)
        1. 10.2.1.1 NAVSS Overview
        2. 10.2.1.2 NAVSS Integration
          1. 10.2.1.2.1 NAVSS Interrupt Router Configuration
          2. 10.2.1.2.2 Global Event Map
          3. 10.2.1.2.3 PSI-L System Thread Map (All NAVSS)
          4. 10.2.1.2.4 NAVSS VBUSM Route ID Table
          5. 10.2.1.2.5 1430
        3. 10.2.1.3 NAVSS Functional Description
        4. 10.2.1.4 NAVSS Interrupt Configuration
          1. 10.2.1.4.1 NAVSS Event and Interrupt Flow
            1. 10.2.1.4.1.1 NAVSS Interrupts Description
            2. 10.2.1.4.1.2 Application Example
      2. 10.2.2  MCU Navigator Subsystem (MCU NAVSS)
        1. 10.2.2.1 MCU NAVSS Overview
        2. 10.2.2.2 MCU NAVSS Integration
          1. 10.2.2.2.1  MCU NAVSS Interrupt Router Configuration
          2. 10.2.2.2.2  MCU NAVSS UDMASS Interrupt Aggregator Configuration
          3. 10.2.2.2.3  MCU NAVSS UDMA Configuration
          4. 10.2.2.2.4  MCU NAVSS Ring Accelerator Configuration
          5. 10.2.2.2.5  MCU NAVSS Proxy Configuration
          6. 10.2.2.2.6  MCU NAVSS Secure Proxy Configuration
          7. 10.2.2.2.7  Global Event Map
          8. 10.2.2.2.8  PSI-L System Thread Map (All NAVSS)
          9. 10.2.2.2.9  MCU NAVSS VBUSM Route ID Table
          10. 10.2.2.2.10 1448
        3. 10.2.2.3 MCU NAVSS Functional Description
      3. 10.2.3  Unified DMA Controller (UDMA)
        1. 10.2.3.1 UDMA Overview
          1. 10.2.3.1.1 UDMA Features
          2. 10.2.3.1.2 UDMA Parameters
        2. 10.2.3.2 UDMA Integration
        3. 10.2.3.3 UDMA Functional Description
          1. 10.2.3.3.1 Block Diagram
          2. 10.2.3.3.2 General Functionality
            1. 10.2.3.3.2.1  Operational States
            2. 10.2.3.3.2.2  Tx Channel Allocation
            3. 10.2.3.3.2.3  Rx Channel Allocation
            4. 10.2.3.3.2.4  Tx Teardown
            5. 10.2.3.3.2.5  Rx Teardown
            6. 10.2.3.3.2.6  Tx Clock Stop
            7. 10.2.3.3.2.7  Rx Clock Stop
            8. 10.2.3.3.2.8  Rx Thread Enables
            9. 10.2.3.3.2.9  Events
              1. 10.2.3.3.2.9.1 Local Event Inputs
              2. 10.2.3.3.2.9.2 Inbound Tx PSI-L Events
              3. 10.2.3.3.2.9.3 Outbound Rx PSI-L Events
            10. 10.2.3.3.2.10 Emulation Control
          3. 10.2.3.3.3 Packet Oriented Transmit Operation
            1. 10.2.3.3.3.1 Packet Mode VBUSM Master Interface Command ID Selection
          4. 10.2.3.3.4 Packet Oriented Receive Operation
            1. 10.2.3.3.4.1 Rx Packet Drop
            2. 10.2.3.3.4.2 Rx Starvation and the Starvation Timer
          5. 10.2.3.3.5 Third Party Mode Operation
            1. 10.2.3.3.5.1 Events and Flow Control
              1. 10.2.3.3.5.1.1 Channel Triggering
              2. 10.2.3.3.5.1.2 Internal TR Completion Events
            2. 10.2.3.3.5.2 Transmit Operation
              1. 10.2.3.3.5.2.1 Transfer Request
              2. 10.2.3.3.5.2.2 Transfer Response
              3. 10.2.3.3.5.2.3 Data Transfer
              4. 10.2.3.3.5.2.4 Memory Interface Transactions
              5. 10.2.3.3.5.2.5 Error Handling
            3. 10.2.3.3.5.3 Receive Operation
              1. 10.2.3.3.5.3.1 Transfer Request
              2. 10.2.3.3.5.3.2 Transfer Response
              3. 10.2.3.3.5.3.3 Error Handling
            4. 10.2.3.3.5.4 Data Transfer
              1. 10.2.3.3.5.4.1 Memory Interface Transactions
              2. 10.2.3.3.5.4.2 Rx Packet Drop
      4. 10.2.4  Ring Accelerator (RINGACC)
        1. 10.2.4.1 RINGACC Overview
          1. 10.2.4.1.1 RINGACC Features
          2. 10.2.4.1.2 RINGACC Not Supported Features
          3. 10.2.4.1.3 RINGACC Parameters
        2. 10.2.4.2 RINGACC Integration
        3. 10.2.4.3 RINGACC Functional Description
          1. 10.2.4.3.1 Block Diagram
            1. 10.2.4.3.1.1  Configuration Registers
            2. 10.2.4.3.1.2  Source Command FIFO
            3. 10.2.4.3.1.3  Source Write Data FIFO
            4. 10.2.4.3.1.4  Source Read Data FIFO
            5. 10.2.4.3.1.5  Source Write Status FIFO
            6. 10.2.4.3.1.6  Main State Machine
            7. 10.2.4.3.1.7  Destination Command FIFO
            8. 10.2.4.3.1.8  Destination Write Data FIFO
            9. 10.2.4.3.1.9  Destination Read Data FIFO
            10. 10.2.4.3.1.10 Destination Write Status FIFO
          2. 10.2.4.3.2 RINGACC Functional Operation
            1. 10.2.4.3.2.1 Queue Modes
              1. 10.2.4.3.2.1.1 Ring Mode
              2. 10.2.4.3.2.1.2 Messaging Mode
              3. 10.2.4.3.2.1.3 Credentials Mode
              4. 10.2.4.3.2.1.4 Queue Manager Mode
              5. 10.2.4.3.2.1.5 Peek Support
              6. 10.2.4.3.2.1.6 Index Register Operation
            2. 10.2.4.3.2.2 VBUSM Slave Ring Operations
            3. 10.2.4.3.2.3 VBUSM Master Interface Command ID Selection
            4. 10.2.4.3.2.4 Ring Push Operation (VBUSM Write to Source Interface)
            5. 10.2.4.3.2.5 Ring Pop Operation (VBUSM Read from Source Interface)
            6. 10.2.4.3.2.6 Host Doorbell Access
            7. 10.2.4.3.2.7 Queue Push Operation (VBUSM Write to Source Interface)
            8. 10.2.4.3.2.8 Queue Pop Operation (VBUSM Read from Source Interface)
            9. 10.2.4.3.2.9 Mismatched Element Size Handling
          3. 10.2.4.3.3 Events
          4. 10.2.4.3.4 Bus Error Handling
          5. 10.2.4.3.5 Monitors
            1. 10.2.4.3.5.1 Threshold Monitor
            2. 10.2.4.3.5.2 Watermark Monitor
            3. 10.2.4.3.5.3 Starvation Monitor
            4. 10.2.4.3.5.4 Statistics Monitor
            5. 10.2.4.3.5.5 Overflow
            6. 10.2.4.3.5.6 Ring Update Port
            7. 10.2.4.3.5.7 Tracing
      5. 10.2.5  Proxy
        1. 10.2.5.1 Proxy Overview
          1. 10.2.5.1.1 Proxy Features
          2. 10.2.5.1.2 Proxy Parameters
          3. 10.2.5.1.3 Proxy Not Supported Features
        2. 10.2.5.2 Proxy Integration
        3. 10.2.5.3 Proxy Functional Description
          1. 10.2.5.3.1  Targets
            1. 10.2.5.3.1.1 Ring Accelerator
          2. 10.2.5.3.2  Proxy Sizes
          3. 10.2.5.3.3  Proxy Interleaving
          4. 10.2.5.3.4  Proxy Host States
          5. 10.2.5.3.5  Proxy Host Channel Selection
          6. 10.2.5.3.6  Proxy Host Access
            1. 10.2.5.3.6.1 Proxy Host Writes
            2. 10.2.5.3.6.2 Proxy Host Reads
          7. 10.2.5.3.7  Permission Inheritance
          8. 10.2.5.3.8  Buffer Size
          9. 10.2.5.3.9  Error Events
          10. 10.2.5.3.10 Debug Reads
      6. 10.2.6  Secure Proxy
        1. 10.2.6.1 Secure Proxy Overview
          1. 10.2.6.1.1 Secure Proxy Features
          2. 10.2.6.1.2 Secure Proxy Parameters
          3. 10.2.6.1.3 Secure Proxy Not Supported Features
        2. 10.2.6.2 Secure Proxy Integration
        3. 10.2.6.3 Secure Proxy Functional Description
          1. 10.2.6.3.1  Targets
            1. 10.2.6.3.1.1 Ring Accelerator
          2. 10.2.6.3.2  Buffers
            1. 10.2.6.3.2.1 Proxy Credits
            2. 10.2.6.3.2.2 Proxy Private Word
            3. 10.2.6.3.2.3 Completion Byte
          3. 10.2.6.3.3  Proxy Thread Sizes
          4. 10.2.6.3.4  Proxy Thread Interleaving
          5. 10.2.6.3.5  Proxy States
          6. 10.2.6.3.6  Proxy Host Access
            1. 10.2.6.3.6.1 Proxy Host Writes
            2. 10.2.6.3.6.2 Proxy Host Reads
            3. 10.2.6.3.6.3 Buffer Accesses
            4. 10.2.6.3.6.4 Target Access
            5. 10.2.6.3.6.5 Error State
          7. 10.2.6.3.7  Permission Inheritance
          8. 10.2.6.3.8  Resource Association
          9. 10.2.6.3.9  Direction
          10. 10.2.6.3.10 Threshold Events
          11. 10.2.6.3.11 Error Events
          12. 10.2.6.3.12 Bus Errors and Credits
          13. 10.2.6.3.13 Debug
      7. 10.2.7  Interrupt Aggregator (INTR_AGGR)
        1. 10.2.7.1 INTR_AGGR Overview
          1. 10.2.7.1.1 INTR_AGGR Features
          2. 10.2.7.1.2 INTR_AGGR Parameters
        2. 10.2.7.2 INTR_AGGR Integration
        3. 10.2.7.3 INTR_AGGR Functional Description
          1. 10.2.7.3.1 Submodule Descriptions
            1. 10.2.7.3.1.1 Status/Mask Registers
            2. 10.2.7.3.1.2 Interrupt Mapping Block
            3. 10.2.7.3.1.3 Global Event Input (GEVI) Counters
            4. 10.2.7.3.1.4 Local Event Input (LEVI) to Global Event Conversion
            5. 10.2.7.3.1.5 Global Event Multicast
          2. 10.2.7.3.2 General Functionality
            1. 10.2.7.3.2.1 Event to Interrupt Bit Steering
            2. 10.2.7.3.2.2 Interrupt Status
            3. 10.2.7.3.2.3 Interrupt Masked Status
            4. 10.2.7.3.2.4 Enabling/Disabling Individual Interrupt Source Bits
            5. 10.2.7.3.2.5 Interrupt Output Generation
            6. 10.2.7.3.2.6 Global Event Counting
            7. 10.2.7.3.2.7 Local Event to Global Event Conversion
            8. 10.2.7.3.2.8 Global Event Multicast
      8. 10.2.8  Packet Streaming Interface Link (PSI-L)
        1. 10.2.8.1 PSI-L Overview
        2. 10.2.8.2 PSI-L Functional Description
          1. 10.2.8.2.1 PSI-L Introduction
          2. 10.2.8.2.2 PSI-L Operation
            1. 10.2.8.2.2.1 Event Transport
            2. 10.2.8.2.2.2 Threads
            3. 10.2.8.2.2.3 Arbitration Protocol
            4. 10.2.8.2.2.4 Thread Configuration
              1. 10.2.8.2.2.4.1 Thread Pairing
                1. 10.2.8.2.2.4.1.1 Configuration Transaction Pairing
              2. 10.2.8.2.2.4.2 Configuration Registers Region
      9. 10.2.9  PSIL Subsystem (PSILSS)
        1. 10.2.9.1 PSILSS Overview
          1. 10.2.9.1.1 PSILSS Features
        2. 10.2.9.2 PSILSS Functional Description
          1. 10.2.9.2.1 PSILSS Basic Operation
          2. 10.2.9.2.2 PSILSS Event Routing
          3. 10.2.9.2.3 PSILSS Link Down Detection
          4. 10.2.9.2.4 PSILSS Configuration
      10. 10.2.10 NAVSS North Bridge (NB)
        1. 10.2.10.1 NB Overview
          1. 10.2.10.1.1 Features Supported
          2. 10.2.10.1.2 NB Parameters
            1. 10.2.10.1.2.1 Compliance to Standards
            2. 10.2.10.1.2.2 Features Not Supported
        2. 10.2.10.2 NB Functional Description
          1. 10.2.10.2.1  VBUSM Slave Interfaces
          2. 10.2.10.2.2  VBUSM Master Interface
          3. 10.2.10.2.3  VBUSM.C Interfaces
            1. 10.2.10.2.3.1 Multi-Threading
            2. 10.2.10.2.3.2 Write Command Crediting
            3. 10.2.10.2.3.3 Early Credit Response
            4. 10.2.10.2.3.4 Priority Escalation
          4. 10.2.10.2.4  Source M2M Bridges
          5. 10.2.10.2.5  Destination M2M Bridge
          6. 10.2.10.2.6  M2C Bridge
          7. 10.2.10.2.7  Memory Attribute Tables
          8. 10.2.10.2.8  Outstanding Read Data Limiter
          9. 10.2.10.2.9  Ordering
          10. 10.2.10.2.10 Quality of Service
          11. 10.2.10.2.11 IDLE Behavior
          12. 10.2.10.2.12 Clock Power Management
    3. 10.3 Peripheral DMA (PDMA)
      1. 10.3.1 PDMA Controller
        1. 10.3.1.1 PDMA Overview
          1. 10.3.1.1.1 PDMA Features
            1. 10.3.1.1.1.1  MCU_PDMA0 (MCU_PDMA_MISC_G0) Features
            2. 10.3.1.1.1.2  MCU_PDMA1 (MCU_PDMA_MISC_G1) Features
            3. 10.3.1.1.1.3  MCU_PDMA2 (MCU_PDMA_MISC_G2) Features
            4. 10.3.1.1.1.4  MCU_PDMA3 (MCU_PDMA_ADC) Features
            5. 10.3.1.1.1.5  PDMA0 (PDMA_AASRC) Features
            6. 10.3.1.1.1.6  PDMA2 (PDMA_DEBUG_CCMCU) Features
            7. 10.3.1.1.1.7  PDMA3 (PDMA_DEBUG_C66) Features
            8. 10.3.1.1.1.8  PDMA5 (PDMA_MCAN) Features
            9. 10.3.1.1.1.9  PDMA6 (PDMA_MCASP_G0) Features
            10. 10.3.1.1.1.10 PDMA7 (PDMA_MCASP_G1) Features
            11. 10.3.1.1.1.11 PDMA8 (PDMA_MISC_G0) Features
            12. 10.3.1.1.1.12 PDMA9 (PDMA_MISC_G1) Features
            13. 10.3.1.1.1.13 PDMA10 (PDMA_MISC_G2) Features
            14. 10.3.1.1.1.14 PDMA11 (PDMA_MISC_G3) Features
            15. 10.3.1.1.1.15 PDMA13 (PDMA_USART_G0) Features
            16. 10.3.1.1.1.16 PDMA14 (PDMA_USART_G1) Features
            17. 10.3.1.1.1.17 PDMA15 (PDMA_USART_G2) Features
        2. 10.3.1.2 PDMA Integration
          1. 10.3.1.2.1 PDMA Integration in MCU Domain
          2. 10.3.1.2.2 PDMA Integration in MAIN Domain
        3. 10.3.1.3 PDMA Functional Description
          1. 10.3.1.3.1 PDMA Functional Blocks
            1. 10.3.1.3.1.1 Scheduler
            2. 10.3.1.3.1.2 Tx Per-Channel Buffers (TCP FIFO)
            3. 10.3.1.3.1.3 Tx DMA Unit (Tx Engine)
            4. 10.3.1.3.1.4 Rx Per-Channel Buffers (RCP FIFO)
            5. 10.3.1.3.1.5 Rx DMA Unit (Rx Engine)
          2. 10.3.1.3.2 PDMA General Functionality
            1. 10.3.1.3.2.1 Operational States
            2. 10.3.1.3.2.2 Clock Stop
            3. 10.3.1.3.2.3 Emulation Control
          3. 10.3.1.3.3 PDMA Events and Flow Control
            1. 10.3.1.3.3.1 Channel Types
              1. 10.3.1.3.3.1.1 X-Y FIFO Mode
              2. 10.3.1.3.3.1.2 MCAN Mode
              3. 10.3.1.3.3.1.3 AASRC Mode
              4. 10.3.1.3.3.1.4 1690
            2. 10.3.1.3.3.2 Channel Triggering
            3. 10.3.1.3.3.3 Completion Events
          4. 10.3.1.3.4 PDMA Transmit Operation
            1. 10.3.1.3.4.1 Destination (Tx) Channel Allocation
            2. 10.3.1.3.4.2 Destination (Tx) Channel Out-of-Band Signals
            3. 10.3.1.3.4.3 Destination Channel Initialization
              1. 10.3.1.3.4.3.1 PSI-L Destination Thread Pairing
              2. 10.3.1.3.4.3.2 Static Transfer Request Setup
              3. 10.3.1.3.4.3.3 1699
              4. 10.3.1.3.4.3.4 PSI-L Destination Thread Enables
            4. 10.3.1.3.4.4 Data Transfer
              1. 10.3.1.3.4.4.1 X-Y FIFO Mode Channel
                1. 10.3.1.3.4.4.1.1 X-Y FIFO Burst Mode
              2. 10.3.1.3.4.4.2 MCAN Mode Channel
                1. 10.3.1.3.4.4.2.1 MCAN Burst Mode
              3. 10.3.1.3.4.4.3 AASRC Mode Channel
            5. 10.3.1.3.4.5 Tx Pause
            6. 10.3.1.3.4.6 Tx Teardown
            7. 10.3.1.3.4.7 Tx Channel Reset
            8. 10.3.1.3.4.8 Tx Debug/State Registers
          5. 10.3.1.3.5 PDMA Receive Operation
            1. 10.3.1.3.5.1 Source (Rx) Channel Allocation
            2. 10.3.1.3.5.2 Source Channel Initialization
              1. 10.3.1.3.5.2.1 PSI-L Source Thread Pairing
              2. 10.3.1.3.5.2.2 Static Transfer Request Setup
              3. 10.3.1.3.5.2.3 PSI-L Source Thread Enables
            3. 10.3.1.3.5.3 Data Transfer
              1. 10.3.1.3.5.3.1 X-Y FIFO Mode Channel
              2. 10.3.1.3.5.3.2 MCAN Mode Channel
                1. 10.3.1.3.5.3.2.1 MCAN Burst Mode
              3. 10.3.1.3.5.3.3 AASRC Mode Channel
            4. 10.3.1.3.5.4 Rx Pause
            5. 10.3.1.3.5.5 Rx Teardown
            6. 10.3.1.3.5.6 Rx Channel Reset
            7. 10.3.1.3.5.7 Rx Debug/State Register
          6. 10.3.1.3.6 PDMA ECC Support
      2. 10.3.2 PDMA Sources
        1. 10.3.2.1 MCU Domain PDMA Event Maps
          1. 10.3.2.1.1 MCU_PDMA_MISC_G0 Event Map
          2. 10.3.2.1.2 MCU_PDMA_MISC_G1 Event Map
          3. 10.3.2.1.3 MCU_PDMA_MISC_G2 Event Map
          4. 10.3.2.1.4 MCU_PDMA_ADC Event Map
        2. 10.3.2.2 MAIN Domain PDMA Event Maps
          1. 10.3.2.2.1  PDMA_AASRC Event Map
          2. 10.3.2.2.2  PDMA_DEBUG_CCMCU Event Map
          3. 10.3.2.2.3  PDMA_DEBUG_C66 Event Map
          4. 10.3.2.2.4  PDMA_MCAN Event Map
          5. 10.3.2.2.5  PDMA_MCASP_G0 Event Map
          6. 10.3.2.2.6  PDMA_MCASP_G1 Event Map
          7. 10.3.2.2.7  PDMA_MISC_G0 Event Map
          8. 10.3.2.2.8  PDMA_MISC_G1 Event Map
          9. 10.3.2.2.9  PDMA_MISC_G2 Event Map
          10. 10.3.2.2.10 PDMA_MISC_G3 Event Map
          11. 10.3.2.2.11 PDMA_USART_G0 Event Map
          12. 10.3.2.2.12 PDMA_USART_G1 Event Map
          13. 10.3.2.2.13 PDMA_USART_G2 Event Map
    4. 10.4 Data Routing Unit (DRU)
      1. 10.4.1 DRU Overview
      2. 10.4.2 DRU Integration
        1. 10.4.2.1 DRU Integration in MAIN Domain
      3. 10.4.3 DRU Functional Description
        1. 10.4.3.1 DRU Basic Functionality
          1. 10.4.3.1.1 Queues
          2. 10.4.3.1.2 Channel Configuration
            1. 10.4.3.1.2.1 Non-realtime Channel Configuration
            2. 10.4.3.1.2.2 Realtime Channel Configuration
          3. 10.4.3.1.3 TR Submission
            1. 10.4.3.1.3.1 Direct TR Submission
            2. 10.4.3.1.3.2 PSI-L TR Submission
          4. 10.4.3.1.4 TR Removal from Channel
          5. 10.4.3.1.5 Channel Tear Down
            1. 10.4.3.1.5.1 Tear Down Completion
        2. 10.4.3.2 DRU Output Events
        3. 10.4.3.3 DRU Address Fetch Algorithm, TR and CR Formats
          1. 10.4.3.3.1 Transpose
          2. 10.4.3.3.2 Circular Buffering
        4. 10.4.3.4 DRU Firewalls
        5. 10.4.3.5 DRU Errors
        6. 10.4.3.6 DRU Configurations
  13. 11Time Sync
    1. 11.1 Time Sync Module (CPTS)
      1. 11.1.1 CPTS Overview
        1. 11.1.1.1 CPTS Features
        2. 11.1.1.2 CPTS Not Supported Features
      2. 11.1.2 CPTS Integration
      3. 11.1.3 CPTS Functional Description
        1. 11.1.3.1  CPTS Architecture
        2. 11.1.3.2  CPTS Initialization
        3. 11.1.3.3  32-bit Time Stamp Value
        4. 11.1.3.4  64-bit Time Stamp Value
          1. 11.1.3.4.1 64-Bit Timestamp Nudge
          2. 11.1.3.4.2 64-bit Timestamp PPM
        5. 11.1.3.5  Event FIFO
        6. 11.1.3.6  Timestamp Compare Output
          1. 11.1.3.6.1 Non-Toggle Mode
          2. 11.1.3.6.2 Toggle Mode
        7. 11.1.3.7  Timestamp Sync Output
        8. 11.1.3.8  Timestamp GENF Output
          1. 11.1.3.8.1 GENFn Nudge
          2. 11.1.3.8.2 GENFn PPM
        9. 11.1.3.9  Time Sync Events
          1. 11.1.3.9.1 Time Stamp Push Event
          2. 11.1.3.9.2 Time Stamp Counter Rollover Event (32-bit mode only)
          3. 11.1.3.9.3 Time Stamp Counter Half-rollover Event (32-bit mode only)
          4. 11.1.3.9.4 Hardware Time Stamp Push Event
        10. 11.1.3.10 Timestamp Compare Event
        11. 11.1.3.11 CPTS Interrupt Handling
    2. 11.2 Timer Manager
      1. 11.2.1 Timer Manager Overview
        1. 11.2.1.1 Timer Manager Features
        2. 11.2.1.2 Timer Manager Not Supported Features
      2. 11.2.2 Timer Manager Integration
      3. 11.2.3 Timer Manager Functional Description
        1. 11.2.3.1 Timer Manager Function Overview
        2. 11.2.3.2 Timer Counter
          1. 11.2.3.2.1 Timer Counter Rollover
        3. 11.2.3.3 Timer Control Module (FSM)
        4. 11.2.3.4 Timer Reprogramming
          1. 11.2.3.4.1 Periodic Hardware Timers
        5. 11.2.3.5 Event FIFO
        6. 11.2.3.6 Output Event Lookup (OES RAM)
      4. 11.2.4 Timer Manager Programming Guide
        1. 11.2.4.1 Timer Manager Low-level Programming Models
          1. 11.2.4.1.1 Surrounding Modules Global Initialization
          2. 11.2.4.1.2 Initialization Sequence
          3. 11.2.4.1.3 Real-time Operating Requirements
            1. 11.2.4.1.3.1 Timer Touch
            2. 11.2.4.1.3.2 Timer Disable
            3. 11.2.4.1.3.3 Timer Enable
          4. 11.2.4.1.4 Power Up/Power Down Sequence
    3. 11.3 Time Sync and Compare Events
      1. 11.3.1 Time Sync Architecture
        1. 11.3.1.1 Time Sync Architecture Overview
      2. 11.3.2 Time Sync Routers
      3. 11.3.3 Time Sync Event Sources
        1. 11.3.3.1  CMPEVT_INTRTR0 Event Map
        2. 11.3.3.2  TIMESYNC_INTRTR0 Event Map
        3. 11.3.3.3  PRU_ICSSG0 Sync Event Map
        4. 11.3.3.4  PRU_ICSSG1 Sync Event Map
        5. 11.3.3.5  NAVSS0 Sync Event Map
        6. 11.3.3.6  PCIE0 Sync Event Map
        7. 11.3.3.7  PCIE1 Sync Event Map
        8. 11.3.3.8  PCIE2 Sync Event Map
        9. 11.3.3.9  PCIE3 Sync Event Map
        10. 11.3.3.10 MCU_CPSW0 Sync Event Map
        11. 11.3.3.11 CPSW0 Sync Event Map
        12. 11.3.3.12 I/O Sync Event Map
  14. 12Peripherals
    1. 12.1  General Connectivity Peripherals
      1. 12.1.1 Analog-to-Digital Converter (ADC)
        1. 12.1.1.1 ADC Overview
          1. 12.1.1.1.1 ADC Features
          2. 12.1.1.1.2 ADC Not Supported Features
        2. 12.1.1.2 ADC Environment
          1. 12.1.1.2.1 ADC Interface Signals
        3. 12.1.1.3 ADC Integration
          1. 12.1.1.3.1 ADC Integration in MCU Domain
        4. 12.1.1.4 ADC Functional Description
          1. 12.1.1.4.1 ADC FSM Sequencer Functional Description
            1. 12.1.1.4.1.1 Step Enable
            2. 12.1.1.4.1.2 Step Configuration
              1. 12.1.1.4.1.2.1 One-Shot (Single) or Continuous Mode
              2. 12.1.1.4.1.2.2 Software- or Hardware-Enabled Steps
              3. 12.1.1.4.1.2.3 Averaging of Samples
              4. 12.1.1.4.1.2.4 Analog Multiplexer Input Select
              5. 12.1.1.4.1.2.5 Differential Control
              6. 12.1.1.4.1.2.6 FIFO Select
              7. 12.1.1.4.1.2.7 Range Check Interrupt Enable
            3. 12.1.1.4.1.3 Open Delay and Sample Delay
              1. 12.1.1.4.1.3.1 Open Delay
              2. 12.1.1.4.1.3.2 Sample Delay
            4. 12.1.1.4.1.4 Interrupts
            5. 12.1.1.4.1.5 Power Management
            6. 12.1.1.4.1.6 DMA Requests
          2. 12.1.1.4.2 ADC AFE Functional Description
            1. 12.1.1.4.2.1 AFE Functional Block Diagram
            2. 12.1.1.4.2.2 ADC GPI Integration
          3. 12.1.1.4.3 ADC FIFOs and DMA
            1. 12.1.1.4.3.1 FIFOs
            2. 12.1.1.4.3.2 DMA
          4. 12.1.1.4.4 ADC Error Correcting Code (ECC)
            1. 12.1.1.4.4.1 Testing ECC Error Injection
          5. 12.1.1.4.5 ADC Functional Internal Diagnostic Debug Mode
        5. 12.1.1.5 ADC Programming Guide
          1. 12.1.1.5.1 ADC Low-Level Programming Models
            1. 12.1.1.5.1.1 Global Initialization
              1. 12.1.1.5.1.1.1 Surrounding Modules Global Initialization
              2. 12.1.1.5.1.1.2 General Programming Model
            2. 12.1.1.5.1.2 During Operation
      2. 12.1.2 General-Purpose Interface (GPIO)
        1. 12.1.2.1 GPIO Overview
          1. 12.1.2.1.1 GPIO Features
          2. 12.1.2.1.2 GPIO Not Supported Features
        2. 12.1.2.2 GPIO Environment
          1. 12.1.2.2.1 GPIO Interface Signals
        3. 12.1.2.3 GPIO Integration
          1. 12.1.2.3.1 GPIO Integration in WKUP Domain
          2. 12.1.2.3.2 GPIO Integration in MAIN Domain
        4. 12.1.2.4 GPIO Functional Description
          1. 12.1.2.4.1 GPIO Block Diagram
          2. 12.1.2.4.2 GPIO Function
          3. 12.1.2.4.3 GPIO Interrupt and Event Generation
            1. 12.1.2.4.3.1 Interrupt Enable (per Bank)
            2. 12.1.2.4.3.2 Trigger Configuration (per Bit)
            3. 12.1.2.4.3.3 Interrupt Status and Clear (per Bit)
          4. 12.1.2.4.4 GPIO Interrupt Connectivity
          5. 12.1.2.4.5 GPIO DeepSleep Mode
          6. 12.1.2.4.6 GPIO Emulation Halt Operation
        5. 12.1.2.5 GPIO Programming Guide
          1. 12.1.2.5.1 GPIO Low-Level Programming Models
            1. 12.1.2.5.1.1 Global Initialization
              1. 12.1.2.5.1.1.1 Surrounding Modules Global Initialization
              2. 12.1.2.5.1.1.2 GPIO Module Global Initialization
            2. 12.1.2.5.1.2 GPIO Operational Modes Configuration
              1. 12.1.2.5.1.2.1 GPIO Read Input Register
              2. 12.1.2.5.1.2.2 GPIO Set Bit Function
              3. 12.1.2.5.1.2.3 GPIO Clear Bit Function
      3. 12.1.3 Inter-Integrated Circuit (I2C) Interface
        1. 12.1.3.1 I2C Overview
          1. 12.1.3.1.1 I2C Features
          2. 12.1.3.1.2 I2C Not Supported Features
        2. 12.1.3.2 I2C Environment
          1. 12.1.3.2.1 I2C Typical Application
            1. 12.1.3.2.1.1 I2C Pins for Typical Connections in I2C Mode
            2. 12.1.3.2.1.2 I2C Interface Typical Connections
            3. 12.1.3.2.1.3 1916
          2. 12.1.3.2.2 I2C Typical Connection Protocol and Data Format
            1. 12.1.3.2.2.1  I2C Serial Data Format
            2. 12.1.3.2.2.2  I2C Data Validity
            3. 12.1.3.2.2.3  I2C Start and Stop Conditions
            4. 12.1.3.2.2.4  I2C Addressing
              1. 12.1.3.2.2.4.1 Data Transfer Formats in F/S Mode
              2. 12.1.3.2.2.4.2 Data Transfer Format in HS Mode
            5. 12.1.3.2.2.5  I2C Controller Transmitter
            6. 12.1.3.2.2.6  I2C Controller Receiver
            7. 12.1.3.2.2.7  I2C Target Transmitter
            8. 12.1.3.2.2.8  I2C Target Receiver
            9. 12.1.3.2.2.9  I2C Bus Arbitration
            10. 12.1.3.2.2.10 I2C Clock Generation and Synchronization
        3. 12.1.3.3 I2C Integration
          1. 12.1.3.3.1 I2C Integration in WKUP Domain
          2. 12.1.3.3.2 I2C Integration in MCU Domain
          3. 12.1.3.3.3 I2C Integration in MAIN Domain
        4. 12.1.3.4 I2C Functional Description
          1. 12.1.3.4.1 I2C Block Diagram
          2. 12.1.3.4.2 I2C Clocks
            1. 12.1.3.4.2.1 I2C Clocking
            2. 12.1.3.4.2.2 I2C Automatic Blocking of the I2C Clock Feature
          3. 12.1.3.4.3 I2C Software Reset
          4. 12.1.3.4.4 I2C Power Management
          5. 12.1.3.4.5 I2C Interrupt Requests
          6. 12.1.3.4.6 I2C Programmable Multitarget Channel Feature
          7. 12.1.3.4.7 I2C FIFO Management
            1. 12.1.3.4.7.1 I2C FIFO Interrupt Mode
            2. 12.1.3.4.7.2 I2C FIFO Polling Mode
            3. 12.1.3.4.7.3 I2C Draining Feature
          8. 12.1.3.4.8 I2C Noise Filter
          9. 12.1.3.4.9 I2C System Test Mode
        5. 12.1.3.5 I2C Programming Guide
          1. 12.1.3.5.1 I2C Low-Level Programming Models
            1. 12.1.3.5.1.1 I2C Programming Model
              1. 12.1.3.5.1.1.1 Main Program
                1. 12.1.3.5.1.1.1.1 Configure the Module Before Enabling the I2C Controller
                2. 12.1.3.5.1.1.1.2 Initialize the I2C Controller
                3. 12.1.3.5.1.1.1.3 Configure Target Address and the Data Control Register
                4. 12.1.3.5.1.1.1.4 Initiate a Transfer
                5. 12.1.3.5.1.1.1.5 Receive Data
                6. 12.1.3.5.1.1.1.6 Transmit Data
              2. 12.1.3.5.1.1.2 Interrupt Subroutine Sequence
              3. 12.1.3.5.1.1.3 Programming Flow-Diagrams
      4. 12.1.4 Improved Inter-Integrated Circuit (I3C) Interface
        1. 12.1.4.1 I3C Overview
          1. 12.1.4.1.1 I3C Features
          2. 12.1.4.1.2 I3C Not Supported Features
        2. 12.1.4.2 I3C Environment
          1. 12.1.4.2.1 I3C Typical Application
            1. 12.1.4.2.1.1 I3C Pins for Typical Connections
            2. 12.1.4.2.1.2 I3C Interface Typical Connections
            3. 12.1.4.2.1.3 1969
        3. 12.1.4.3 I3C Integration
          1. 12.1.4.3.1 I3C Integration in MCU Domain
          2. 12.1.4.3.2 I3C Integration in MAIN Domain
        4. 12.1.4.4 I3C Functional Description
          1. 12.1.4.4.1  I3C Block Diagram
          2. 12.1.4.4.2  I3C Clock Configuration
            1. 12.1.4.4.2.1 Setting Base Frequencies
            2. 12.1.4.4.2.2 Asymmetric Push-Pull SCL Timing
            3. 12.1.4.4.2.3 Open-Drain SCL Timing
            4. 12.1.4.4.2.4 Changing Programmed Frequencies
          3. 12.1.4.4.3  I3C Interrupt Requests
          4. 12.1.4.4.4  I3C Power Configuration
          5. 12.1.4.4.5  I3C Dynamic Address Management
          6. 12.1.4.4.6  I3C Retaining Registers Space
          7. 12.1.4.4.7  I3C Dynamic Address Assignment Procedure
          8. 12.1.4.4.8  I3C Sending CCC Messages
          9. 12.1.4.4.9  I3C In-Band Interrupt
            1. 12.1.4.4.9.1 Regular I3C Slave In-Band Interrupt
            2. 12.1.4.4.9.2 Current Master Takeover In-Band Interrupt
          10. 12.1.4.4.10 I3C Hot-Join Request
          11. 12.1.4.4.11 I3C Immediate Commands
          12. 12.1.4.4.12 I3C Host Commands
          13. 12.1.4.4.13 I3C Sending Private Data in SDR Messages
            1. 12.1.4.4.13.1 SDR Private Write Message
            2. 12.1.4.4.13.2 SDR Private Read Message
            3. 12.1.4.4.13.3 SDR Payload Length Adjustment
        5. 12.1.4.5 I3C Programming Guide
          1. 12.1.4.5.1 I3C Power-On Programming Model
          2. 12.1.4.5.2 I3C Static Devices Programming
          3. 12.1.4.5.3 I3C DAA Procedure Initiation
          4. 12.1.4.5.4 I3C SDR Write Message Programming Model
          5. 12.1.4.5.5 I3C SDR Read Message Programming Model
          6. 12.1.4.5.6 I3C DDR Write Message Programming Model
          7. 12.1.4.5.7 I3C DDR Read Message Programming Model
      5. 12.1.5 Multichannel Serial Peripheral Interface (MCSPI)
        1. 12.1.5.1 MCSPI Overview
          1. 12.1.5.1.1 SPI Features
          2. 12.1.5.1.2 MCSPI Not Supported Features
        2. 12.1.5.2 MCSPI Environment
          1. 12.1.5.2.1 Basic MCSPI Pins for Master Mode
          2. 12.1.5.2.2 Basic MCSPI Pins for Slave Mode
          3. 12.1.5.2.3 MCSPI Internal Connectivity
          4. 12.1.5.2.4 MCSPI Protocol and Data Format
            1. 12.1.5.2.4.1 Transfer Format
          5. 12.1.5.2.5 MCSPI in Controller Mode
          6. 12.1.5.2.6 MCSPI in Peripheral Mode
        3. 12.1.5.3 MCSPI Integration
          1. 12.1.5.3.1 MCSPI Integration in MCU Domain
          2. 12.1.5.3.2 MCSPI Integration in MAIN Domain
        4. 12.1.5.4 MCSPI Functional Description
          1. 12.1.5.4.1 SPI Block Diagram
          2. 12.1.5.4.2 MCSPI Reset
          3. 12.1.5.4.3 MCSPI Controller Mode
            1. 12.1.5.4.3.1 Controller Mode Features
            2. 12.1.5.4.3.2 Controller Transmit-and-Receive Mode (Full Duplex)
            3. 12.1.5.4.3.3 Controller Transmit-Only Mode (Half Duplex)
            4. 12.1.5.4.3.4 Controller Receive-Only Mode (Half Duplex)
            5. 12.1.5.4.3.5 Single-Channel Controller Mode
              1. 12.1.5.4.3.5.1 Programming Tips When Switching to Another Channel
              2. 12.1.5.4.3.5.2 Force SPIEN[i] Mode
              3. 12.1.5.4.3.5.3 Turbo Mode
            6. 12.1.5.4.3.6 Start-Bit Mode
            7. 12.1.5.4.3.7 Chip-Select Timing Control
            8. 12.1.5.4.3.8 Programmable MCSPI Clock (SPICLK)
              1. 12.1.5.4.3.8.1 Clock Ratio Granularity
          4. 12.1.5.4.4 MCSPI Peripheral Mode
            1. 12.1.5.4.4.1 Dedicated Resources
            2. 12.1.5.4.4.2 Peripheral Transmit-and-Receive Mode
            3. 12.1.5.4.4.3 Peripheral Transmit-Only Mode
            4. 12.1.5.4.4.4 Peripheral Receive-Only Mode
          5. 12.1.5.4.5 MCSPI 3-Pin or 4-Pin Mode
          6. 12.1.5.4.6 MCSPI FIFO Buffer Management
            1. 12.1.5.4.6.1 Buffer Almost Full
            2. 12.1.5.4.6.2 Buffer Almost Empty
            3. 12.1.5.4.6.3 End of Transfer Management
            4. 12.1.5.4.6.4 Multiple MCSPI Word Access
            5. 12.1.5.4.6.5 First MCSPI Word Delay
          7. 12.1.5.4.7 MCSPI Interrupts
            1. 12.1.5.4.7.1 Interrupt Events in Controller Mode
              1. 12.1.5.4.7.1.1 TXx_EMPTY
              2. 12.1.5.4.7.1.2 TXx_UNDERFLOW
              3. 12.1.5.4.7.1.3 RXx_ FULL
              4. 12.1.5.4.7.1.4 End Of Word Count
            2. 12.1.5.4.7.2 Interrupt Events in Peripheral Mode
              1. 12.1.5.4.7.2.1 TXx_EMPTY
              2. 12.1.5.4.7.2.2 TXx_UNDERFLOW
              3. 12.1.5.4.7.2.3 RXx_FULL
              4. 12.1.5.4.7.2.4 RX0_OVERFLOW
              5. 12.1.5.4.7.2.5 End Of Word Count
            3. 12.1.5.4.7.3 Interrupt-Driven Operation
            4. 12.1.5.4.7.4 Polling
          8. 12.1.5.4.8 MCSPI DMA Requests
          9. 12.1.5.4.9 MCSPI Power Saving Management
            1. 12.1.5.4.9.1 Normal Mode
            2. 12.1.5.4.9.2 Idle Mode
              1. 12.1.5.4.9.2.1 Force-Idle Mode
        5. 12.1.5.5 MCSPI Programming Guide
          1. 12.1.5.5.1 MCSPI Global Initialization
            1. 12.1.5.5.1.1 Surrounding Modules Global Initialization
            2. 12.1.5.5.1.2 MCSPI Global Initialization
              1. 12.1.5.5.1.2.1 Main Sequence – MCSPI Global Initialization
          2. 12.1.5.5.2 MCSPI Operational Mode Configuration
            1. 12.1.5.5.2.1 MCSPI Operational Modes
              1. 12.1.5.5.2.1.1 Common Transfer Sequence
              2. 12.1.5.5.2.1.2 End of Transfer Sequences
              3. 12.1.5.5.2.1.3 Transmit-and-Receive (Controller and Peripheral)
              4. 12.1.5.5.2.1.4 Transmit-Only (Controller and Peripheral)
                1. 12.1.5.5.2.1.4.1 Based on Interrupt Requests
                2. 12.1.5.5.2.1.4.2 Based on DMA Write Requests
              5. 12.1.5.5.2.1.5 Controller Normal Receive-Only
                1. 12.1.5.5.2.1.5.1 Based on Interrupt Requests
                2. 12.1.5.5.2.1.5.2 Based on DMA Read Requests
              6. 12.1.5.5.2.1.6 Controller Turbo Receive-Only
                1. 12.1.5.5.2.1.6.1 Based on Interrupt Requests
                2. 12.1.5.5.2.1.6.2 Based on DMA Read Requests
              7. 12.1.5.5.2.1.7 Peripheral Receive-Only
              8. 12.1.5.5.2.1.8 Transfer Procedures With FIFO
                1. 12.1.5.5.2.1.8.1 Common Transfer Sequence in FIFO Mode
                2. 12.1.5.5.2.1.8.2 End of Transfer Sequences in FIFO Mode
                3. 12.1.5.5.2.1.8.3 Transmit-and-Receive With Word Count
                4. 12.1.5.5.2.1.8.4 Transmit-and-Receive Without Word Count
                5. 12.1.5.5.2.1.8.5 Transmit-Only
                6. 12.1.5.5.2.1.8.6 Receive-Only With Word Count
                7. 12.1.5.5.2.1.8.7 Receive-Only Without Word Count
              9. 12.1.5.5.2.1.9 Common Transfer Procedures Without FIFO – Polling Method
                1. 12.1.5.5.2.1.9.1 Receive-Only Procedure – Polling Method
                2. 12.1.5.5.2.1.9.2 Receive-Only Procedure – Interrupt Method
                3. 12.1.5.5.2.1.9.3 Transmit-Only Procedure – Polling Method
                4. 12.1.5.5.2.1.9.4 Transmit-and-Receive Procedure – Polling Method
      6. 12.1.6 Universal Asynchronous Receiver/Transmitter (UART)
        1. 12.1.6.1 UART Overview
          1. 12.1.6.1.1 UART Features
          2. 12.1.6.1.2 IrDA Features
          3. 12.1.6.1.3 CIR Features
          4. 12.1.6.1.4 UART Not Supported Features
        2. 12.1.6.2 UART Environment
          1. 12.1.6.2.1 UART Functional Interfaces
            1. 12.1.6.2.1.1 System Using UART Communication With Hardware Handshake
            2. 12.1.6.2.1.2 UART Interface Description
            3. 12.1.6.2.1.3 UART Protocol and Data Format
            4. 12.1.6.2.1.4 UART 9-bit Mode Data Format
          2. 12.1.6.2.2 RS-485 Functional Interfaces
            1. 12.1.6.2.2.1 System Using RS-485 Communication
            2. 12.1.6.2.2.2 RS-485 Interface Description
          3. 12.1.6.2.3 IrDA Functional Interfaces
            1. 12.1.6.2.3.1 System Using IrDA Communication Protocol
            2. 12.1.6.2.3.2 IrDA Interface Description
            3. 12.1.6.2.3.3 IrDA Protocol and Data Format
              1. 12.1.6.2.3.3.1 SIR Mode
                1. 12.1.6.2.3.3.1.1 Frame Format
                2. 12.1.6.2.3.3.1.2 Asynchronous Transparency
                3. 12.1.6.2.3.3.1.3 Abort Sequence
                4. 12.1.6.2.3.3.1.4 Pulse Shaping
                5. 12.1.6.2.3.3.1.5 Encoder
                6. 12.1.6.2.3.3.1.6 Decoder
                7. 12.1.6.2.3.3.1.7 IR Address Checking
              2. 12.1.6.2.3.3.2 SIR Free-Format Mode
              3. 12.1.6.2.3.3.3 MIR Mode
                1. 12.1.6.2.3.3.3.1 MIR Encoder/Decoder
                2. 12.1.6.2.3.3.3.2 SIP Generation
              4. 12.1.6.2.3.3.4 FIR Mode
          4. 12.1.6.2.4 CIR Functional Interfaces
            1. 12.1.6.2.4.1 System Using CIR Communication Protocol With Remote Control
            2. 12.1.6.2.4.2 CIR Interface Description
            3. 12.1.6.2.4.3 CIR Protocol and Data Format
              1. 12.1.6.2.4.3.1 Carrier Modulation
              2. 12.1.6.2.4.3.2 Pulse Duty Cycle
              3. 12.1.6.2.4.3.3 Consumer IR Encoding/Decoding
        3. 12.1.6.3 UART Integration
          1. 12.1.6.3.1 UART Integration in WKUP Domain
          2. 12.1.6.3.2 UART Integration in MCU Domain
          3. 12.1.6.3.3 UART Integration in MAIN Domain
        4. 12.1.6.4 UART Functional Description
          1. 12.1.6.4.1 UART Block Diagram
          2. 12.1.6.4.2 UART Clock Configuration
          3. 12.1.6.4.3 UART Software Reset
            1. 12.1.6.4.3.1 Independent TX/RX
          4. 12.1.6.4.4 UART Power Management
            1. 12.1.6.4.4.1 UART Mode Power Management
              1. 12.1.6.4.4.1.1 Module Power Saving
              2. 12.1.6.4.4.1.2 System Power Saving
            2. 12.1.6.4.4.2 IrDA Mode Power Management
              1. 12.1.6.4.4.2.1 Module Power Saving
              2. 12.1.6.4.4.2.2 System Power Saving
            3. 12.1.6.4.4.3 CIR Mode Power Management
              1. 12.1.6.4.4.3.1 Module Power Saving
              2. 12.1.6.4.4.3.2 System Power Saving
            4. 12.1.6.4.4.4 Local Power Management
          5. 12.1.6.4.5 UART Interrupt Requests
            1. 12.1.6.4.5.1 UART Mode Interrupt Management
              1. 12.1.6.4.5.1.1 UART Interrupts
              2. 12.1.6.4.5.1.2 Wake-Up Interrupt
            2. 12.1.6.4.5.2 IrDA Mode Interrupt Management
              1. 12.1.6.4.5.2.1 IrDA Interrupts
              2. 12.1.6.4.5.2.2 Wake-Up Interrupts
            3. 12.1.6.4.5.3 CIR Mode Interrupt Management
              1. 12.1.6.4.5.3.1 CIR Interrupts
              2. 12.1.6.4.5.3.2 Wake-Up Interrupts
          6. 12.1.6.4.6 UART FIFO Management
            1. 12.1.6.4.6.1 FIFO Trigger
              1. 12.1.6.4.6.1.1 Transmit FIFO Trigger
              2. 12.1.6.4.6.1.2 Receive FIFO Trigger
            2. 12.1.6.4.6.2 FIFO Interrupt Mode
            3. 12.1.6.4.6.3 FIFO Polled Mode Operation
            4. 12.1.6.4.6.4 FIFO DMA Mode Operation
              1. 12.1.6.4.6.4.1 DMA sequence to disable TX DMA
              2. 12.1.6.4.6.4.2 DMA Transfers (DMA Mode 1, 2, or 3)
              3. 12.1.6.4.6.4.3 DMA Transmission
              4. 12.1.6.4.6.4.4 DMA Reception
          7. 12.1.6.4.7 UART Mode Selection
            1. 12.1.6.4.7.1 Register Access Modes
              1. 12.1.6.4.7.1.1 Operational Mode and Configuration Modes
              2. 12.1.6.4.7.1.2 Register Access Submode
              3. 12.1.6.4.7.1.3 Registers Available for the Register Access Modes
            2. 12.1.6.4.7.2 UART/RS-485/IrDA (SIR, MIR, FIR)/CIR Mode Selection
              1. 12.1.6.4.7.2.1 Registers Available for the UART Function
              2. 12.1.6.4.7.2.2 Registers Available for the IrDA Function
              3. 12.1.6.4.7.2.3 Registers Available for the CIR Function
          8. 12.1.6.4.8 UART Protocol Formatting
            1. 12.1.6.4.8.1 UART Mode
              1. 12.1.6.4.8.1.1 UART Clock Generation: Baud Rate Generation
              2. 12.1.6.4.8.1.2 Choosing the Appropriate Divisor Value
              3. 12.1.6.4.8.1.3 UART Data Formatting
                1. 12.1.6.4.8.1.3.1 Frame Formatting
                2. 12.1.6.4.8.1.3.2 Hardware Flow Control
                3. 12.1.6.4.8.1.3.3 Software Flow Control
                  1. 1.6.4.8.1.3.3.1 Receive (RX)
                  2. 1.6.4.8.1.3.3.2 Transmit (TX)
                4. 12.1.6.4.8.1.3.4 Autobauding Modes
                5. 12.1.6.4.8.1.3.5 Error Detection
                6. 12.1.6.4.8.1.3.6 Overrun During Receive
                7. 12.1.6.4.8.1.3.7 Time-Out and Break Conditions
                  1. 1.6.4.8.1.3.7.1 Time-Out Counter
                  2. 1.6.4.8.1.3.7.2 Break Condition
            2. 12.1.6.4.8.2 RS-485 Mode
              1. 12.1.6.4.8.2.1 RS-485 External Transceiver Direction Control
            3. 12.1.6.4.8.3 IrDA Mode
              1. 12.1.6.4.8.3.1 IrDA Clock Generation: Baud Generator
              2. 12.1.6.4.8.3.2 Choosing the Appropriate Divisor Value
              3. 12.1.6.4.8.3.3 IrDA Data Formatting
                1. 12.1.6.4.8.3.3.1  IR RX Polarity Control
                2. 12.1.6.4.8.3.3.2  IrDA Reception Control
                3. 12.1.6.4.8.3.3.3  IR Address Checking
                4. 12.1.6.4.8.3.3.4  Frame Closing
                5. 12.1.6.4.8.3.3.5  Store and Controlled Transmission
                6. 12.1.6.4.8.3.3.6  Error Detection
                7. 12.1.6.4.8.3.3.7  Underrun During Transmission
                8. 12.1.6.4.8.3.3.8  Overrun During Receive
                9. 12.1.6.4.8.3.3.9  Status FIFO
                10. 12.1.6.4.8.3.3.10 Multi-drop Parity Mode with Address Match
                11. 12.1.6.4.8.3.3.11 Time-guard
              4. 12.1.6.4.8.3.4 SIR Mode Data Formatting
                1. 12.1.6.4.8.3.4.1 Abort Sequence
                2. 12.1.6.4.8.3.4.2 Pulse Shaping
                3. 12.1.6.4.8.3.4.3 SIR Free Format Programming
              5. 12.1.6.4.8.3.5 MIR and FIR Mode Data Formatting
            4. 12.1.6.4.8.4 CIR Mode
              1. 12.1.6.4.8.4.1 CIR Mode Clock Generation
              2. 12.1.6.4.8.4.2 CIR Data Formatting
                1. 12.1.6.4.8.4.2.1 IR RX Polarity Control
                2. 12.1.6.4.8.4.2.2 CIR Transmission
                3. 12.1.6.4.8.4.2.3 CIR Reception
        5. 12.1.6.5 UART Programming Guide
          1. 12.1.6.5.1 UART Global Initialization
            1. 12.1.6.5.1.1 Surrounding Modules Global Initialization
            2. 12.1.6.5.1.2 UART Module Global Initialization
          2. 12.1.6.5.2 UART Mode selection
          3. 12.1.6.5.3 UART Submode selection
          4. 12.1.6.5.4 UART Load FIFO trigger and DMA mode settings
            1. 12.1.6.5.4.1 DMA mode Settings
            2. 12.1.6.5.4.2 FIFO Trigger Settings
          5. 12.1.6.5.5 UART Protocol, Baud rate and interrupt settings
            1. 12.1.6.5.5.1 Baud rate settings
            2. 12.1.6.5.5.2 Interrupt settings
            3. 12.1.6.5.5.3 Protocol settings
            4. 12.1.6.5.5.4 UART/RS-485/IrDA(SIR/MIR/FIR)/CIR
            5. 12.1.6.5.5.5 UART Multi-drop Parity Address Match Mode Configuration
          6. 12.1.6.5.6 UART Hardware and Software Flow Control Configuration
            1. 12.1.6.5.6.1 Hardware Flow Control Configuration
            2. 12.1.6.5.6.2 Software Flow Control Configuration
          7. 12.1.6.5.7 IrDA Programming Model
            1. 12.1.6.5.7.1 SIR mode
              1. 12.1.6.5.7.1.1 Receive
              2. 12.1.6.5.7.1.2 Transmit
            2. 12.1.6.5.7.2 MIR mode
              1. 12.1.6.5.7.2.1 Receive
              2. 12.1.6.5.7.2.2 Transmit
            3. 12.1.6.5.7.3 FIR mode
              1. 12.1.6.5.7.3.1 Receive
              2. 12.1.6.5.7.3.2 Transmit
    2. 12.2  High-speed Serial Interfaces
      1. 12.2.1 Gigabit Ethernet MAC (MCU_CPSW0)
        1. 12.2.1.1 MCU_CPSW0 Overview
          1. 12.2.1.1.1 MCU_CPSW0 Features
          2. 12.2.1.1.2 MCU_CPSW0 Not Supported Features
          3. 12.2.1.1.3 Terminology
        2. 12.2.1.2 MCU_CPSW0 Environment
          1. 12.2.1.2.1 MCU_CPSW0 RMII Interface
          2. 12.2.1.2.2 MCU_CPSW0 RGMII Interface
        3. 12.2.1.3 MCU_CPSW0 Integration
        4. 12.2.1.4 MCU_CPSW0 Functional Description
          1. 12.2.1.4.1 Functional Block Diagram
          2. 12.2.1.4.2 CPSW Ports
            1. 12.2.1.4.2.1 Interface Mode Selection
          3. 12.2.1.4.3 Clocking
            1. 12.2.1.4.3.1 Subsystem Clocking
            2. 12.2.1.4.3.2 Interface Clocking
              1. 12.2.1.4.3.2.1 RGMII Interface Clocking
              2. 12.2.1.4.3.2.2 RMII Interface Clocking
              3. 12.2.1.4.3.2.3 MDIO Clocking
          4. 12.2.1.4.4 Software IDLE
          5. 12.2.1.4.5 Interrupt Functionality
            1. 12.2.1.4.5.1 EVNT_PEND Interrupt
            2. 12.2.1.4.5.2 Statistics Interrupt (STAT_PEND0)
            3. 12.2.1.4.5.3 ECC DED Level Interrupt (ECC_DED_INT)
            4. 12.2.1.4.5.4 ECC SEC Level Interrupt (ECC_SEC_INT)
            5. 12.2.1.4.5.5 MDIO Interrupts
          6. 12.2.1.4.6 CPSW_2G
            1. 12.2.1.4.6.1  Address Lookup Engine (ALE)
              1. 12.2.1.4.6.1.1  Error Handling
              2. 12.2.1.4.6.1.2  Bypass Operations
              3. 12.2.1.4.6.1.3  OUI Deny or Accept
              4. 12.2.1.4.6.1.4  Statistics Counting
              5. 12.2.1.4.6.1.5  Automotive Security Features
              6. 12.2.1.4.6.1.6  CPSW Switching Solutions
                1. 12.2.1.4.6.1.6.1 Basics of 2-port Switch Type
              7. 12.2.1.4.6.1.7  VLAN Routing and OAM Operations
                1. 12.2.1.4.6.1.7.1 InterVLAN Routing
                2. 12.2.1.4.6.1.7.2 OAM Operations
              8. 12.2.1.4.6.1.8  Supervisory packets
              9. 12.2.1.4.6.1.9  Address Table Entry
                1. 12.2.1.4.6.1.9.1 Free Table Entry
                2. 12.2.1.4.6.1.9.2 Multicast Address Table Entry
                3. 12.2.1.4.6.1.9.3 VLAN/Multicast Address Table Entry
                4. 12.2.1.4.6.1.9.4 Unicast Address Table Entry
                5. 12.2.1.4.6.1.9.5 OUI Unicast Address Table Entry
                6. 12.2.1.4.6.1.9.6 VLAN/Unicast Address Table Entry
                7. 12.2.1.4.6.1.9.7 VLAN Table Entry
              10. 12.2.1.4.6.1.10 ALE Policing and Classification
                1. 12.2.1.4.6.1.10.1 ALE Classification
                  1. 2.1.4.6.1.10.1.1 Classifier to CPPI Transmit Flow ID Mapping
              11. 12.2.1.4.6.1.11 DSCP
              12. 12.2.1.4.6.1.12 Packet Forwarding Processes
                1. 12.2.1.4.6.1.12.1 Ingress Filtering Process
                2. 12.2.1.4.6.1.12.2 VLAN_Aware Lookup Process
                3. 12.2.1.4.6.1.12.3 Egress Process
                4. 12.2.1.4.6.1.12.4 Learning/Updating/Touching Processes
                  1. 2.1.4.6.1.12.4.1 Learning Process
                  2. 2.1.4.6.1.12.4.2 Updating Process
                  3. 2.1.4.6.1.12.4.3 Touching Process
              13. 12.2.1.4.6.1.13 VLAN Aware Mode
              14. 12.2.1.4.6.1.14 VLAN Unaware Mode
            2. 12.2.1.4.6.2  Packet Priority Handling
              1. 12.2.1.4.6.2.1 Priority Mapping and Transmit VLAN Priority
            3. 12.2.1.4.6.3  CPPI Port Ingress
            4. 12.2.1.4.6.4  Packet CRC Handling
              1. 12.2.1.4.6.4.1 Transmit VLAN Processing
                1. 12.2.1.4.6.4.1.1 Untagged Packets (No VLAN or Priority Tag Header)
                2. 12.2.1.4.6.4.1.2 Priority Tagged Packets (VLAN VID == 0 && EN_VID0_MODE ==0h)
                3. 12.2.1.4.6.4.1.3 VLAN Tagged Packets (VLAN VID != 0 || (EN_VID0_MODE ==1h && VLAN VID ==0))
              2. 12.2.1.4.6.4.2 Ethernet Port Ingress Packet CRC
              3. 12.2.1.4.6.4.3 Ethernet Port Egress Packet CRC
              4. 12.2.1.4.6.4.4 CPPI Port Ingress Packet CRC
              5. 12.2.1.4.6.4.5 CPPI Port Egress Packet CRC
            5. 12.2.1.4.6.5  FIFO Memory Control
            6. 12.2.1.4.6.6  FIFO Transmit Queue Control
              1. 12.2.1.4.6.6.1 CPPI Port Receive Rate Limiting
              2. 12.2.1.4.6.6.2 Ethernet Port Transmit Rate Limiting
            7. 12.2.1.4.6.7  Intersperced Express Traffic (IET – P802.3br/D2.0)
              1. 12.2.1.4.6.7.1 IET Configuration
            8. 12.2.1.4.6.8  Enhanced Scheduled Traffic (EST – P802.1Qbv/D2.2)
              1. 12.2.1.4.6.8.1 Enhanced Scheduled Traffic Overview
              2. 12.2.1.4.6.8.2 Enhanced Scheduled Traffic Fetch RAM
              3. 12.2.1.4.6.8.3 Enhanced Scheduled Traffic Time Interval
              4. 12.2.1.4.6.8.4 Enhanced Scheduled Traffic Fetch Values
              5. 12.2.1.4.6.8.5 Enhanced Scheduled Traffic Packet Fill
              6. 12.2.1.4.6.8.6 Enhanced Scheduled Traffic Time Stamp
              7. 12.2.1.4.6.8.7 Enhanced Scheduled Traffic Packets Per Priority
            9. 12.2.1.4.6.9  Audio Video Bridging
              1. 12.2.1.4.6.9.1 IEEE 802.1AS: Timing and Synchronization for Time-Sensitive Applications in Bridged Local Area Networks (Precision Time Protocol (PTP))
                1. 12.2.1.4.6.9.1.1 IEEE 1722: "Layer 2 Transport Protocol for Time-Sensitive Streams"
                  1. 2.1.4.6.9.1.1.1 Cross-timestamping and Presentation Timestamps
                2. 12.2.1.4.6.9.1.2 IEEE 1733: Extends RTCP for RTP Streaming over AVB-supported Networks
              2. 12.2.1.4.6.9.2 IEEE 802.1Qav: "Virtual Bridged Local Area Networks: Forwarding and Queuing for Time-Sensitive Streams"
                1. 12.2.1.4.6.9.2.1 Configuring the Device for 802.1Qav Operation
            10. 12.2.1.4.6.10 Ethernet MAC Sliver
              1. 12.2.1.4.6.10.1 2356
                1. 12.2.1.4.6.10.1.1 2357
                  1. 2.1.4.6.10.1.1.1 CRC Insertion
                  2. 2.1.4.6.10.1.1.2 MTXER
                  3. 2.1.4.6.10.1.1.3 Adaptive Performance Optimization (APO)
                  4. 2.1.4.6.10.1.1.4 Inter-Packet-Gap Enforcement
                  5. 2.1.4.6.10.1.1.5 Back Off
                  6. 2.1.4.6.10.1.1.6 Programmable Transmit Inter-Packet Gap
                  7. 2.1.4.6.10.1.1.7 Speed, Duplex and Pause Frame Support Negotiation
              2. 12.2.1.4.6.10.2 RMII Interface
                1. 12.2.1.4.6.10.2.1 Features
                2. 12.2.1.4.6.10.2.2 RMII Receive (RX)
                3. 12.2.1.4.6.10.2.3 RMII Transmit (TX)
              3. 12.2.1.4.6.10.3 RGMII Interface
                1. 12.2.1.4.6.10.3.1 Features
                2. 12.2.1.4.6.10.3.2 RGMII Receive (RX)
                3. 12.2.1.4.6.10.3.3 In-Band Mode of Operation
                4. 12.2.1.4.6.10.3.4 Forced Mode of Operation
                5. 12.2.1.4.6.10.3.5 RGMII Transmit (TX)
              4. 12.2.1.4.6.10.4 Frame Classification
              5. 12.2.1.4.6.10.5 Receive FIFO Architecture
            11. 12.2.1.4.6.11 Embedded Memories
            12. 12.2.1.4.6.12 Memory Error Detection and Correction
              1. 12.2.1.4.6.12.1 Packet Header ECC
              2. 12.2.1.4.6.12.2 Packet Protect CRC
              3. 12.2.1.4.6.12.3 Aggregator RAM Control
            13. 12.2.1.4.6.13 Ethernet Port Flow Control
              1. 12.2.1.4.6.13.1 Ethernet Receive Flow Control
                1. 12.2.1.4.6.13.1.1 Collision Based Receive Buffer Flow Control
                2. 12.2.1.4.6.13.1.2 IEEE 802.3X Based Receive Flow Control
              2. 12.2.1.4.6.13.2 Flow Control Trigger
              3. 12.2.1.4.6.13.3 Ethernet Transmit Flow Control
            14. 12.2.1.4.6.14 Energy Efficient Ethernet Support (802.3az)
            15. 12.2.1.4.6.15 Ethernet Switch Latency
            16. 12.2.1.4.6.16 MAC Emulation Control
            17. 12.2.1.4.6.17 MAC Command IDLE
            18. 12.2.1.4.6.18 CPSW Network Statistics
              1. 12.2.1.4.6.18.1  Rx-only Statistics Descriptions
                1. 12.2.1.4.6.18.1.1  Good Rx Frames (Offset = 3A000h - Port 0 or Offset = 3A200h - Port 1)
                2. 12.2.1.4.6.18.1.2  Broadcast Rx Frames (Offset = 3A004h - Port 0 or Offset = 3A204h - Port 1)
                3. 12.2.1.4.6.18.1.3  Multicast Rx Frames (Offset = 3A008h - Port 0 or Offset = 3A208h - Port 1)
                4. 12.2.1.4.6.18.1.4  Pause Rx Frames (Offset = 3A20Ch - Port 1)
                5. 12.2.1.4.6.18.1.5  Rx CRC Errors (Offset = 3A010h - Port 0 or Offset = 3A210h - Port 1)
                6. 12.2.1.4.6.18.1.6  Rx Align/Code Errors (Offset = 3A214h - Port 1)
                7. 12.2.1.4.6.18.1.7  Oversize Rx Frames (Offset = 3A018h - Port 0 or Offset = 3A218h - Port 1)
                8. 12.2.1.4.6.18.1.8  Rx Jabbers (Offset = 3A21Ch - Port 1)
                9. 12.2.1.4.6.18.1.9  Undersize (Short) Rx Frames (Offset = 3A020h- Port 0 or Offset = 3A220h - Port 1)
                10. 12.2.1.4.6.18.1.10 Rx Fragments (Offset = 3A024h - Port 0 or Offset = 3A224h - Port 1)
                11. 12.2.1.4.6.18.1.11 RX IPG Error (Offset = 3A25Ch - Port 1)
                12. 12.2.1.4.6.18.1.12 ALE Drop (Offset = 3A028h - Port 0 or Offset = 3A228h - Port 1)
                13. 12.2.1.4.6.18.1.13 ALE Overrun Drop (Offset = 3A02Ch - Port 0 or Offset = 3A22Ch - Port 1)
                14. 12.2.1.4.6.18.1.14 Rx Octets (Offset = 3A030h - Port 0 or Offset = 3A230h - Port 1)
                15. 12.2.1.4.6.18.1.15 Rx Bottom of FIFO Drop (Offset = 3A084h - Port 0 or Offset = 3A284h - Port 1)
                16. 12.2.1.4.6.18.1.16 Portmask Drop (Offset = 3A088h - Port 0 or Offset = 3A288h - Port 1)
                17. 12.2.1.4.6.18.1.17 Rx Top of FIFO Drop (Offset = 3A08Ch - Port 0 or Offset = 3A28Ch - Port 1)
                18. 12.2.1.4.6.18.1.18 ALE Rate Limit Drop (Offset = 3A090h - Port 0 or Offset = 3A290h - Port 1)
                19. 12.2.1.4.6.18.1.19 ALE VLAN Ingress Check Drop (Offset = 3A094h - Port 0 or Offset = 3A294h - Port 1)
                  1. 2.1.4.6.18.1.19.1  ALE DA=SA Drop (Offset = 3A098h - Port 0 or Offset = 3A298h - Port 1)
                  2. 2.1.4.6.18.1.19.2  Block Address Drop (Offset = 3A09Ch - Port 0 or Offset = 3A29Ch - Port 1)
                  3. 2.1.4.6.18.1.19.3  ALE Secure Drop (Offset = 3A0A0h - Port 0 or Offset = 3A2A0h - Port 1)
                  4. 2.1.4.6.18.1.19.4  ALE Authentication Drop (Offset = 3A0A4h - Port 0 or Offset = 3A2A4h - Port 1)
                  5. 2.1.4.6.18.1.19.5  ALE Unknown Unicast (Offset = 3A0A8h - Port 0 or Offset = 3A2A8h - Port 1)
                  6. 2.1.4.6.18.1.19.6  ALE Unknown Unicast Bytecount (Offset = 3A0ACh - Port 0 or Offset = 3A2ACh - Port 1)
                  7. 2.1.4.6.18.1.19.7  ALE Unknown Multicast (Offset = 3A0B0h - Port 0 or Offset = 3A2B0h - Port 1)
                  8. 2.1.4.6.18.1.19.8  ALE Unknown Multicast Bytecount (Offset = 3A0B4h - Port 0 or Offset = 3A2B4h - Port 1)
                  9. 2.1.4.6.18.1.19.9  ALE Unknown Broadcast (Offset = 3A0B8h - Port 0 or Offset = 3A2B8h - Port 1)
                  10. 2.1.4.6.18.1.19.10 ALE Unknown Broadcast Bytecount (Offset = 3A0BCh - Port 0 or Offset = 3A2BCh - Port 1)
                  11. 2.1.4.6.18.1.19.11 ALE Policer/Classifier Match (Offset = 3A0C0h - Port 0 or Offset = 3A2C0h - Port 1)
              2. 12.2.1.4.6.18.2  ALE Policer Match Red (Offset = 3A0C4h - Port 0 or Offset = 3A2C4h - Port 1)
              3. 12.2.1.4.6.18.3  ALE Policer Match Yellow (Offset = 3A0C8h - Port 0 or Offset = 3A2C8h - Port 1)
              4. 12.2.1.4.6.18.4  IET Receive Assembly Error (Offset = 3A140h - Port 0 or Offset = 3A340h - Port 1)
              5. 12.2.1.4.6.18.5  IET Receive Assembly OK (Offset = 3A144h - Port 0 or Offset = 3A344h - Port 1)
              6. 12.2.1.4.6.18.6  IET Receive SMD Error (Offset = 3A148h - Port 0 or Offset = 3A348h - Port 1)
              7. 12.2.1.4.6.18.7  IET Receive Merge Fragment Count (Offset = 3A14Ch - Port 0 or Offset = 3A34Ch - Port 1)
              8. 12.2.1.4.6.18.8  Tx-only Statistics Descriptions
                1. 12.2.1.4.6.18.8.1  Good Tx Frames (Offset = 3A034h - Port 0 or Offset = 3A234h - Port 1)
                2. 12.2.1.4.6.18.8.2  Broadcast Tx Frames (Offset = 3A038h - Port 0 or Offset = 3A238h - Port 1)
                3. 12.2.1.4.6.18.8.3  Multicast Tx Frames (Offset = 3A03Ch - Port 0 or Offset = 3A23Ch - Port 1)
                4. 12.2.1.4.6.18.8.4  Pause Tx Frames (Offset = 3A240h - Port 1)
                5. 12.2.1.4.6.18.8.5  Deferred Tx Frames (Offset = 3A244h - Port 1)
                6. 12.2.1.4.6.18.8.6  Collisions (Offset = 3A248h - Port 1)
                7. 12.2.1.4.6.18.8.7  Single Collision Tx Frames (Offset = 3A24Ch - Port 1)
                8. 12.2.1.4.6.18.8.8  Multiple Collision Tx Frames (Offset = 3A250h - Port 1)
                9. 12.2.1.4.6.18.8.9  Excessive Collisions (Offset = 3A254h - Port 1)
                10. 12.2.1.4.6.18.8.10 Late Collisions (Offset = 3A258h - Port 1)
                11. 12.2.1.4.6.18.8.11 Carrier Sense Errors (Offset = 3A260h - Port 1)
                12. 12.2.1.4.6.18.8.12 Tx Octets (Offset = 3A064h - Port 0 or Offset = 3A264h - Port 1 )
                13. 12.2.1.4.6.18.8.13 Transmit Priority 0-7 (Offset = 3A380h to 3A3A8h - Port 1)
                14. 12.2.1.4.6.18.8.14 Transmit Priority 0-7 Drop (Offset = 3A3C0h to 3A3E8 - Port 1)
                15. 12.2.1.4.6.18.8.15 Tx Memory Protect Errors (Offset = 3A17Ch - Port 0 or Offset = 3A37Ch - Port 1)
                16. 12.2.1.4.6.18.8.16 IET Transmit Merge Hold Count (Offset = 3A350h - Port 1)
                17. 12.2.1.4.6.18.8.17 IET Transmit Merge Fragment Count (Offset = 3A154h - Port 0 or Offset = 3A354h - Port 1)
              9. 12.2.1.4.6.18.9  Rx- and Tx (Shared) Statistics Descriptions
                1. 12.2.1.4.6.18.9.1 Rx + Tx 64 Octet Frames (Offset = 3A068h - Port 0 or Offset = 3A268h - Port 1)
                2. 12.2.1.4.6.18.9.2 Rx + Tx 65–127 Octet Frames (Offset = 3A06Ch - Port 0 or Offset = 3A26Ch - Port 1)
                3. 12.2.1.4.6.18.9.3 Rx + Tx 128–255 Octet Frames (Offset = 3A070h - Port 0 or Offset = 3A270h - Port 1)
                4. 12.2.1.4.6.18.9.4 Rx + Tx 256–511 Octet Frames (Offset = 3A074h - Port 0 or Offset = 3A274h - Port 1)
                5. 12.2.1.4.6.18.9.5 Rx + Tx 512–1023 Octet Frames (Offset = 3A078h - Port 0 or Offset = 3A278h - Port 1)
                6. 12.2.1.4.6.18.9.6 Rx + Tx 1024_Up Octet Frames (Offset = 3A07Ch - Port 0 or Offset = 3A27Ch - Port 1)
                7. 12.2.1.4.6.18.9.7 Net Octets (Offset = 3A080h - Port 0 or Offset = 3A280h - Port 1)
              10. 12.2.1.4.6.18.10 2456
          7. 12.2.1.4.7 Common Platform Time Sync (CPTS)
            1. 12.2.1.4.7.1  MCU_CPSW0 CPTS Integration
            2. 12.2.1.4.7.2  CPTS Architecture
            3. 12.2.1.4.7.3  CPTS Initialization
            4. 12.2.1.4.7.4  32-bit Time Stamp Value
            5. 12.2.1.4.7.5  64-bit Time Stamp Value
            6. 12.2.1.4.7.6  64-Bit Timestamp Nudge
            7. 12.2.1.4.7.7  64-bit Timestamp PPM
            8. 12.2.1.4.7.8  Event FIFO
            9. 12.2.1.4.7.9  Timestamp Compare Output
              1. 12.2.1.4.7.9.1 Non-Toggle Mode: 32-bit
              2. 12.2.1.4.7.9.2 Non-Toggle Mode: 64-bit
              3. 12.2.1.4.7.9.3 Toggle Mode: 32-bit
              4. 12.2.1.4.7.9.4 Toggle Mode: 64-bit
            10. 12.2.1.4.7.10 Timestamp Sync Output
            11. 12.2.1.4.7.11 Timestamp GENFn Output
              1. 12.2.1.4.7.11.1 GENFn Nudge
              2. 12.2.1.4.7.11.2 GENFn PPM
            12. 12.2.1.4.7.12 Timestamp ESTFn
            13. 12.2.1.4.7.13 Time Sync Events
              1. 12.2.1.4.7.13.1 Time Stamp Push Event
              2. 12.2.1.4.7.13.2 Time Stamp Counter Rollover Event (32-bit mode only)
              3. 12.2.1.4.7.13.3 Time Stamp Counter Half-rollover Event (32-bit mode only)
              4. 12.2.1.4.7.13.4 Hardware Time Stamp Push Event
              5. 12.2.1.4.7.13.5 Ethernet Port Events
                1. 12.2.1.4.7.13.5.1 Ethernet Port Receive Event
                2. 12.2.1.4.7.13.5.2 Ethernet Port Transmit Event
                3. 12.2.1.4.7.13.5.3 2484
            14. 12.2.1.4.7.14 Timestamp Compare Event
              1. 12.2.1.4.7.14.1 32-Bit Mode
              2. 12.2.1.4.7.14.2 64-Bit Mode
            15. 12.2.1.4.7.15 Host Transmit Event
            16. 12.2.1.4.7.16 CPTS Interrupt Handling
          8. 12.2.1.4.8 CPPI Streaming Packet Interface
            1. 12.2.1.4.8.1 Port 0 CPPI Transmit Packet Streaming Interface (CPSW_2G Egress)
            2. 12.2.1.4.8.2 Port 0 CPPI Receive Packet Streaming Interface (CPSW_2G Ingress)
            3. 12.2.1.4.8.3 CPPI Checksum Offload
              1. 12.2.1.4.8.3.1 CPPI Transmit Checksum Offload
                1. 12.2.1.4.8.3.1.1 IPV4 UDP
                2. 12.2.1.4.8.3.1.2 IPV4 TCP
                3. 12.2.1.4.8.3.1.3 IPV6 UDP
                4. 12.2.1.4.8.3.1.4 IPV6 TCP
            4. 12.2.1.4.8.4 CPPI Receive Checksum Offload
            5. 12.2.1.4.8.5 Egress Packet Operations
          9. 12.2.1.4.9 MII Management Interface (MDIO)
            1. 12.2.1.4.9.1 MDIO Frame Formats
            2. 12.2.1.4.9.2 MDIO Functional Description
        5. 12.2.1.5 MCU_CPSW0 Programming Guide
          1. 12.2.1.5.1 Initialization and Configuration of CPSW Subsystem
          2. 12.2.1.5.2 CPSW Reset
          3. 12.2.1.5.3 MDIO Software Interface
            1. 12.2.1.5.3.1 Initializing the MDIO Module
            2. 12.2.1.5.3.2 Writing Data To a PHY Register
            3. 12.2.1.5.3.3 Reading Data From a PHY Register
      2. 12.2.2 Gigabit Ethernet Switch (CPSW0)
        1. 12.2.2.1 CPSW0 Overview
          1. 12.2.2.1.1 CPSW0 Features
          2. 12.2.2.1.2 CPSW0 Not Supported Features
          3. 12.2.2.1.3 Terminology
        2. 12.2.2.2 CPSW0 Environment
          1. 12.2.2.2.1 CPSW0 RMII Interface
          2. 12.2.2.2.2 CPSW0 RGMII Interface
        3. 12.2.2.3 CPSW0 Integration
        4. 12.2.2.4 CPSW0 Functional Description
          1. 12.2.2.4.1 Functional Block Diagram
          2. 12.2.2.4.2 CPSW Ports
            1. 12.2.2.4.2.1 Interface Mode Selection
          3. 12.2.2.4.3 Clocking
            1. 12.2.2.4.3.1 Subsystem Clocking
            2. 12.2.2.4.3.2 Interface Clocking
              1. 12.2.2.4.3.2.1 RGMII Interface Clocking
              2. 12.2.2.4.3.2.2 RMII Interface Clocking
              3. 12.2.2.4.3.2.3 MDIO Clocking
          4. 12.2.2.4.4 Software IDLE
          5. 12.2.2.4.5 Interrupt Functionality
            1. 12.2.2.4.5.1 EVNT_PEND Interrupt
            2. 12.2.2.4.5.2 Statistics Interrupt (STAT_PEND0)
            3. 12.2.2.4.5.3 ECC DED Level Interrupt (ECC_DED_INT)
            4. 12.2.2.4.5.4 ECC SEC Level Interrupt (ECC_SEC_INT)
            5. 12.2.2.4.5.5 MDIO Interrupts
          6. 12.2.2.4.6 CPSW_9G
            1. 12.2.2.4.6.1  Address Lookup Engine (ALE)
              1. 12.2.2.4.6.1.1  Error Handling
              2. 12.2.2.4.6.1.2  Bypass Operations
              3. 12.2.2.4.6.1.3  OUI Deny or Accept
              4. 12.2.2.4.6.1.4  Statistics Counting
              5. 12.2.2.4.6.1.5  Automotive Security Features
              6. 12.2.2.4.6.1.6  CPSW Switching Solutions
                1. 12.2.2.4.6.1.6.1 Basics of 5-port Switch Type
              7. 12.2.2.4.6.1.7  VLAN Routing and OAM Operations
                1. 12.2.2.4.6.1.7.1 InterVLAN Routing
                2. 12.2.2.4.6.1.7.2 OAM Operations
              8. 12.2.2.4.6.1.8  Supervisory packets
              9. 12.2.2.4.6.1.9  Address Table Entry
                1. 12.2.2.4.6.1.9.1  Free Table Entry
                2. 12.2.2.4.6.1.9.2  Multicast Address Table Entry (Bit 40 == 0)
                3. 12.2.2.4.6.1.9.3  Multicast Address Table Entry (Bit 40 == 1)
                4. 12.2.2.4.6.1.9.4  VLAN Unicast Address Table Entry (Bit 40 == 0)
                5. 12.2.2.4.6.1.9.5  OUI Unicast Address Table Entry
                6. 12.2.2.4.6.1.9.6  VLAN/Unicast Address Table Entry (Bit 40 == 0)
                7. 12.2.2.4.6.1.9.7  VLAN/ Multicast Address Table Entry (Bit 40 == 1)
                8. 12.2.2.4.6.1.9.8  Inner VLAN Table Entry
                9. 12.2.2.4.6.1.9.9  Outer VLAN Table Entry
                10. 12.2.2.4.6.1.9.10 EtherType Table Entry
                11. 12.2.2.4.6.1.9.11 IPv4 Table Entry
                12. 12.2.2.4.6.1.9.12 IPv6 Table Entry High
                13. 12.2.2.4.6.1.9.13 IPv6 Table Entry Low
              10. 12.2.2.4.6.1.10 Multicast Address
                1. 12.2.2.4.6.1.10.1 Multicast Ranges
              11. 12.2.2.4.6.1.11 Supervisory Packets
              12. 12.2.2.4.6.1.12 Aging and Auto Aging
              13. 12.2.2.4.6.1.13 ALE Policing and Classification
                1. 12.2.2.4.6.1.13.1 ALE Policing
                2. 12.2.2.4.6.1.13.2 Classifier to Host Thread Mapping
                3. 12.2.2.4.6.1.13.3 ALE Classification
                  1. 2.2.4.6.1.13.3.1 Classifier to CPPI Transmit Flow ID Mapping
              14. 12.2.2.4.6.1.14 Mirroring
              15. 12.2.2.4.6.1.15 Trunking
              16. 12.2.2.4.6.1.16 DSCP
              17. 12.2.2.4.6.1.17 Packet Forwarding Processes
                1. 12.2.2.4.6.1.17.1 Ingress Filtering Process
                2. 12.2.2.4.6.1.17.2 VLAN_Aware Lookup Process
                3. 12.2.2.4.6.1.17.3 Egress Process
                4. 12.2.2.4.6.1.17.4 Learning/Updating/Touching Processes
                  1. 2.2.4.6.1.17.4.1 Learning Process
                  2. 2.2.4.6.1.17.4.2 Updating Process
                  3. 2.2.4.6.1.17.4.3 Touching Process
              18. 12.2.2.4.6.1.18 VLAN Aware Mode
              19. 12.2.2.4.6.1.19 VLAN Unaware Mode
            2. 12.2.2.4.6.2  Packet Priority Handling
              1. 12.2.2.4.6.2.1 Priority Mapping and Transmit VLAN Priority
            3. 12.2.2.4.6.3  CPPI Port Ingress
            4. 12.2.2.4.6.4  Packet CRC Handling
              1. 12.2.2.4.6.4.1 Transmit VLAN Processing
                1. 12.2.2.4.6.4.1.1 Untagged Packets (No VLAN or Priority Tag Header)
                2. 12.2.2.4.6.4.1.2 Priority Tagged Packets (VLAN VID == 0 && EN_VID0_MODE ==0h)
                3. 12.2.2.4.6.4.1.3 VLAN Tagged Packets (VLAN VID != 0 || (EN_VID0_MODE ==1h && VLAN VID ==0))
              2. 12.2.2.4.6.4.2 Ethernet Port Ingress Packet CRC
              3. 12.2.2.4.6.4.3 Ethernet Port Egress Packet CRC
              4. 12.2.2.4.6.4.4 CPPI Port Ingress Packet CRC
              5. 12.2.2.4.6.4.5 CPPI Port Egress Packet CRC
            5. 12.2.2.4.6.5  FIFO Memory Control
            6. 12.2.2.4.6.6  FIFO Transmit Queue Control
              1. 12.2.2.4.6.6.1 CPPI Port Receive Rate Limiting
              2. 12.2.2.4.6.6.2 Ethernet Port Transmit Rate Limiting
            7. 12.2.2.4.6.7  Intersperced Express Traffic (IET – P802.3br/D2.0)
              1. 12.2.2.4.6.7.1 IET Configuration
            8. 12.2.2.4.6.8  Enhanced Scheduled Traffic (EST – P802.1Qbv/D2.2)
              1. 12.2.2.4.6.8.1 Enhanced Scheduled Traffic Overview
              2. 12.2.2.4.6.8.2 Enhanced Scheduled Traffic Fetch RAM
              3. 12.2.2.4.6.8.3 Enhanced Scheduled Traffic Time Interval
              4. 12.2.2.4.6.8.4 Enhanced Scheduled Traffic Fetch Values
              5. 12.2.2.4.6.8.5 Enhanced Scheduled Traffic Packet Fill
              6. 12.2.2.4.6.8.6 Enhanced Scheduled Traffic Time Stamp
            9. 12.2.2.4.6.9  Audio Video Bridging
              1. 12.2.2.4.6.9.1 IEEE 802.1AS: Timing and Synchronization for Time-Sensitive Applications in Bridged Local Area Networks (Precision Time Protocol (PTP))
                1. 12.2.2.4.6.9.1.1 IEEE 1722: "Layer 2 Transport Protocol for Time-Sensitive Streams"
                  1. 2.2.4.6.9.1.1.1 Cross-timestamping and Presentation Timestamps
                2. 12.2.2.4.6.9.1.2 IEEE 1733: Extends RTCP for RTP Streaming over AVB-supported Networks
              2. 12.2.2.4.6.9.2 IEEE 802.1Qav: "Virtual Bridged Local Area Networks: Forwarding and Queuing for Time-Sensitive Streams"
                1. 12.2.2.4.6.9.2.1 Configuring the Device for 802.1Qav Operation
            10. 12.2.2.4.6.10 Ethernet MAC Sliver
              1. 12.2.2.4.6.10.1  CRC Insertion
              2. 12.2.2.4.6.10.2  MTXER
              3. 12.2.2.4.6.10.3  Adaptive Performance Optimization (APO)
              4. 12.2.2.4.6.10.4  Inter-Packet-Gap Enforcement
              5. 12.2.2.4.6.10.5  Back Off
              6. 12.2.2.4.6.10.6  Programmable Transmit Inter-Packet Gap
              7. 12.2.2.4.6.10.7  Speed, Duplex and Pause Frame Support Negotiation
              8. 12.2.2.4.6.10.8  RMII Interface
                1. 12.2.2.4.6.10.8.1 Features
                2. 12.2.2.4.6.10.8.2 RMII Receive (RX)
                3. 12.2.2.4.6.10.8.3 RMII Transmit (TX)
              9. 12.2.2.4.6.10.9  RGMII Interface
                1. 12.2.2.4.6.10.9.1 Features
                2. 12.2.2.4.6.10.9.2 RGMII Receive (RX)
                3. 12.2.2.4.6.10.9.3 In-Band Mode of Operation
                4. 12.2.2.4.6.10.9.4 Forced Mode of Operation
                5. 12.2.2.4.6.10.9.5 RGMII Transmit (TX)
              10. 12.2.2.4.6.10.10 Frame Classification
              11. 12.2.2.4.6.10.11 Receive FIFO Architecture
            11. 12.2.2.4.6.11 Embedded Memories
            12. 12.2.2.4.6.12 Memory Error Detection and Correction
              1. 12.2.2.4.6.12.1 Packet Header ECC
              2. 12.2.2.4.6.12.2 Packet Protect CRC
              3. 12.2.2.4.6.12.3 Aggregator RAM Control
            13. 12.2.2.4.6.13 Ethernet Port Flow Control
              1. 12.2.2.4.6.13.1 Ethernet Receive Flow Control
                1. 12.2.2.4.6.13.1.1 Collision Based Receive Buffer Flow Control
                2. 12.2.2.4.6.13.1.2 IEEE 802.3X Based Receive Flow Control
              2. 12.2.2.4.6.13.2 Qbb (10/100/1G/10G) Receive Priority Based Flow Control (PFC)
              3. 12.2.2.4.6.13.3 Ethernet Transmit Flow Control
            14. 12.2.2.4.6.14 PFC Trigger Rules
              1. 12.2.2.4.6.14.1 Destination Based Rule
              2. 12.2.2.4.6.14.2 Sum of Outflows Rule
              3. 12.2.2.4.6.14.3 Sum of Blocks Per Port Rule
              4. 12.2.2.4.6.14.4 Sum of Blocks Total Rule
              5. 12.2.2.4.6.14.5 Top of Receive FIFO Rule
            15. 12.2.2.4.6.15 Energy Efficient Ethernet Support (802.3az)
            16. 12.2.2.4.6.16 Ethernet Switch Latency
            17. 12.2.2.4.6.17 MAC Emulation Control
            18. 12.2.2.4.6.18 MAC Command IDLE
            19. 12.2.2.4.6.19 CPSW Network Statistics
              1. 12.2.2.4.6.19.1  Rx-only Statistics Descriptions
                1. 12.2.2.4.6.19.1.1  Good Rx Frames (Offset = 3A000h)
                2. 12.2.2.4.6.19.1.2  Broadcast Rx Frames (Offset = 3A004h)
                3. 12.2.2.4.6.19.1.3  Multicast Rx Frames (Offset = 3A008h)
                4. 12.2.2.4.6.19.1.4  Pause Rx Frames (Offset = 3A00Ch)
                5. 12.2.2.4.6.19.1.5  Rx CRC Errors (Offset = 3A010h)
                6. 12.2.2.4.6.19.1.6  Rx Align/Code Errors (Offset = 3A014h)
                7. 12.2.2.4.6.19.1.7  Oversize Rx Frames (Offset = 3A018h)
                8. 12.2.2.4.6.19.1.8  Rx Jabbers (Offset = 3A01Ch)
                9. 12.2.2.4.6.19.1.9  Undersize (Short) Rx Frames (Offset = 3A020h)
                10. 12.2.2.4.6.19.1.10 Rx Fragments (Offset = 3A024h)
                11. 12.2.2.4.6.19.1.11 RX IPG Error
                12. 12.2.2.4.6.19.1.12 ALE Drop (Offset = 3A028h)
                13. 12.2.2.4.6.19.1.13 ALE Overrun Drop (Offset = 3A02Ch)
                14. 12.2.2.4.6.19.1.14 Rx Octets (Offset = 3A030h)
                15. 12.2.2.4.6.19.1.15 Rx Bottom of FIFO Drop (Offset = 3A084h)
                16. 12.2.2.4.6.19.1.16 Portmask Drop (Offset = 3A088h)
                17. 12.2.2.4.6.19.1.17 Rx Top of FIFO Drop (Offset = 3A08Ch)
                18. 12.2.2.4.6.19.1.18 ALE Rate Limit Drop (Offset = 3A090h)
                19. 12.2.2.4.6.19.1.19 ALE VLAN Ingress Check Drop (Offset = 3A094h)
                  1. 2.2.4.6.19.1.19.1  ALE DA=SA Drop (Offset = 3A098h)
                  2. 2.2.4.6.19.1.19.2  Block Address Drop (Offset = 3A09Ch)
                  3. 2.2.4.6.19.1.19.3  ALE Secure Drop (Offset = 3A0A0h)
                  4. 2.2.4.6.19.1.19.4  ALE Authentication Drop (Offset = 3A0A4h)
                  5. 2.2.4.6.19.1.19.5  ALE Unknown Unicast (Offset = 3A0A8h)
                  6. 2.2.4.6.19.1.19.6  ALE Unknown Unicast Bytecount (Offset = 3A0ACh)
                  7. 2.2.4.6.19.1.19.7  ALE Unknown Multicast (Offset = 3A0B0h)
                  8. 2.2.4.6.19.1.19.8  ALE Unknown Multicast Bytecount (Offset = 3A0B4h)
                  9. 2.2.4.6.19.1.19.9  ALE Unknown Broadcast (Offset = 3A0B8h)
                  10. 2.2.4.6.19.1.19.10 ALE Unknown Broadcast Bytecount (Offset = 3A0BCh)
                  11. 2.2.4.6.19.1.19.11 ALE Policer/Classifier Match (Offset = 3A0C0h)
              2. 12.2.2.4.6.19.2  ALE Policer Match Red (Offset = 3A0C4h)
              3. 12.2.2.4.6.19.3  ALE Policer Match Yellow (Offset = 3A0C8h)
              4. 12.2.2.4.6.19.4  IET Receive Assembly Error (Offset = 3A140h)
              5. 12.2.2.4.6.19.5  IET Receive Assembly OK (Offset = 3A144h)
              6. 12.2.2.4.6.19.6  IET Receive SMD Error (Offset = 3A148h)
              7. 12.2.2.4.6.19.7  IET Receive Merge Fragment Count (Offset = 3A14Ch)
              8. 12.2.2.4.6.19.8  Tx-only Statistics Descriptions
                1. 12.2.2.4.6.19.8.1  Good Tx Frames (Offset = 3A034h)
                2. 12.2.2.4.6.19.8.2  Broadcast Tx Frames (Offset = 3A038h)
                3. 12.2.2.4.6.19.8.3  Multicast Tx Frames (Offset = 3A03Ch)
                4. 12.2.2.4.6.19.8.4  Pause Tx Frames (Offset = 3A040h)
                5. 12.2.2.4.6.19.8.5  Deferred Tx Frames (Offset = 3A044h)
                6. 12.2.2.4.6.19.8.6  Collisions (Offset = 3A048h)
                7. 12.2.2.4.6.19.8.7  Single Collision Tx Frames (Offset = 3A04Ch)
                8. 12.2.2.4.6.19.8.8  Multiple Collision Tx Frames (Offset = 3A050h)
                9. 12.2.2.4.6.19.8.9  Excessive Collisions (Offset = 3A054h)
                10. 12.2.2.4.6.19.8.10 Late Collisions (Offset = 3A058h)
                11. 12.2.2.4.6.19.8.11 Carrier Sense Errors (Offset = 3A060h)
                12. 12.2.2.4.6.19.8.12 Tx Octets (Offset = 3A064h)
                13. 12.2.2.4.6.19.8.13 Transmit Priority 0-7 (Offset = 3A180h to 3A1A8h)
                14. 12.2.2.4.6.19.8.14 Transmit Priority 0-7 Drop (Offset = 3A1C0h to 3A1E8h)
                15. 12.2.2.4.6.19.8.15 Tx Memory Protect Errors (Offset = 3A17Ch)
                16. 12.2.2.4.6.19.8.16 IET Transmit Merge Fragment Count (Offset = 3A14Ch)
                17. 12.2.2.4.6.19.8.17 IET Transmit Merge Hold Count (Offset = 3A150h)
              9. 12.2.2.4.6.19.9  Rx- and Tx (Shared) Statistics Descriptions
                1. 12.2.2.4.6.19.9.1 Rx + Tx 64 Octet Frames (Offset = 3A068h)
                2. 12.2.2.4.6.19.9.2 Rx + Tx 65–127 Octet Frames (Offset = 3A06Ch)
                3. 12.2.2.4.6.19.9.3 Rx + Tx 128–255 Octet Frames (Offset = 3A070h)
                4. 12.2.2.4.6.19.9.4 Rx + Tx 256–511 Octet Frames (Offset = 3A074h)
                5. 12.2.2.4.6.19.9.5 Rx + Tx 512–1023 Octet Frames (Offset = 3A078h)
                6. 12.2.2.4.6.19.9.6 Rx + Tx 1024_Up Octet Frames (Offset = 3A07Ch)
                7. 12.2.2.4.6.19.9.7 Net Octets (Offset = 3A080h)
              10. 12.2.2.4.6.19.10 2723
          7. 12.2.2.4.7 Common Platform Time Sync (CPTS)
            1. 12.2.2.4.7.1  CPSW0 CPTS Integration
            2. 12.2.2.4.7.2  CPTS Architecture
            3. 12.2.2.4.7.3  CPTS Initialization
            4. 12.2.2.4.7.4  32-bit Time Stamp Value
            5. 12.2.2.4.7.5  64-bit Time Stamp Value
            6. 12.2.2.4.7.6  64-Bit Timestamp Nudge
            7. 12.2.2.4.7.7  64-bit Timestamp PPM
            8. 12.2.2.4.7.8  Event FIFO
            9. 12.2.2.4.7.9  Timestamp Compare Output
              1. 12.2.2.4.7.9.1 Non-Toggle Mode: 32-bit
              2. 12.2.2.4.7.9.2 Non-Toggle Mode: 64-bit
              3. 12.2.2.4.7.9.3 Toggle Mode: 32-bit
              4. 12.2.2.4.7.9.4 Toggle Mode: 64-bit
            10. 12.2.2.4.7.10 Timestamp Sync Output
            11. 12.2.2.4.7.11 Timestamp GENFn Output
              1. 12.2.2.4.7.11.1 GENFn Nudge
              2. 12.2.2.4.7.11.2 GENFn PPM
            12. 12.2.2.4.7.12 Timestamp ESTFn
            13. 12.2.2.4.7.13 Time Sync Events
              1. 12.2.2.4.7.13.1 Time Stamp Push Event
              2. 12.2.2.4.7.13.2 Time Stamp Counter Rollover Event (32-bit mode only)
              3. 12.2.2.4.7.13.3 Time Stamp Counter Half-rollover Event (32-bit mode only)
              4. 12.2.2.4.7.13.4 Hardware Time Stamp Push Event
              5. 12.2.2.4.7.13.5 Ethernet Port Events
                1. 12.2.2.4.7.13.5.1 Ethernet Port Receive Event
                2. 12.2.2.4.7.13.5.2 Ethernet Port Transmit Event
                3. 12.2.2.4.7.13.5.3 2751
            14. 12.2.2.4.7.14 Timestamp Compare Event
              1. 12.2.2.4.7.14.1 32-Bit Mode
              2. 12.2.2.4.7.14.2 64-Bit Mode
            15. 12.2.2.4.7.15 Host Transmit Event
            16. 12.2.2.4.7.16 CPTS Interrupt Handling
          8. 12.2.2.4.8 CPPI Streaming Packet Interface
            1. 12.2.2.4.8.1 Port 0 CPPI Transmit Packet Streaming Interface (CPSW_9G Egress)
            2. 12.2.2.4.8.2 CPPI Receive Packet Streaming Interface (CPSW Ingress)
            3. 12.2.2.4.8.3 CPPI Checksum Offload
              1. 12.2.2.4.8.3.1 CPPI Transmit Checksum Offload
                1. 12.2.2.4.8.3.1.1 IPV4 UDP
                2. 12.2.2.4.8.3.1.2 IPV4 TCP
                3. 12.2.2.4.8.3.1.3 IPV6 UDP
                4. 12.2.2.4.8.3.1.4 IPV6 TCP
            4. 12.2.2.4.8.4 CPPI Receive Checksum Offload
            5. 12.2.2.4.8.5 Egress Packet Operations
          9. 12.2.2.4.9 MII Management Interface (MDIO)
            1. 12.2.2.4.9.1 MDIO Frame Formats
            2. 12.2.2.4.9.2 MDIO Functional Description
        5. 12.2.2.5 CPSW0 Programming Guide
          1. 12.2.2.5.1 Initialization and Configuration of CPSW Subsystem
          2. 12.2.2.5.2 Ethernet MAC Reset or XGMII/GMII Mode Change Configuration
          3. 12.2.2.5.3 MDIO Software Interface
            1. 12.2.2.5.3.1 Initializing the MDIO Module
            2. 12.2.2.5.3.2 Writing Data To a PHY Register
            3. 12.2.2.5.3.3 Reading Data From a PHY Register
      3. 12.2.3 Peripheral Component Interconnect Express (PCIe) Subsystem
        1. 12.2.3.1 PCIe Subsystem Overview
          1. 12.2.3.1.1 PCIe Subsystem Features
          2. 12.2.3.1.2 PCIe Subsystem Not Supported Features
        2. 12.2.3.2 PCIe Subsystem Environment
        3. 12.2.3.3 PCIe Subsystem Integration
        4. 12.2.3.4 PCIe Subsystem Functional Description
          1. 12.2.3.4.1  PCIe Subsystem Block Diagram
            1. 12.2.3.4.1.1 PCIe Core Module
            2. 12.2.3.4.1.2 PCIe PHY Interface
            3. 12.2.3.4.1.3 CBA Infrastructure
            4. 12.2.3.4.1.4 VBUSM to AXI Bridges
            5. 12.2.3.4.1.5 AXI to VBUSM Bridges
            6. 12.2.3.4.1.6 VBUSP to APB Bridge
            7. 12.2.3.4.1.7 Custom Logic
          2. 12.2.3.4.2  PCIe Subsystem Reset Schemes
            1. 12.2.3.4.2.1 PCIe Subsystem Conventional Reset
            2. 12.2.3.4.2.2 PCIe Subsystem Function Level Reset
            3. 12.2.3.4.2.3 Reset Isolation
              1. 12.2.3.4.2.3.1 Root Port Reset with Device Not Reset
              2. 12.2.3.4.2.3.2 Device Reset with Root Port Not Reset
              3. 12.2.3.4.2.3.3 End Point Device Reset with Root Port Not Reset
              4. 12.2.3.4.2.3.4 Device Reset with End Point Device Not Reset
            4. 12.2.3.4.2.4 PCIe Reset Limitations
            5. 12.2.3.4.2.5 PCIe Reset Requirements
          3. 12.2.3.4.3  PCIe Subsystem Power Management
            1. 12.2.3.4.3.1 CBA Power Management
          4. 12.2.3.4.4  PCIe Subsystem Interrupts
            1. 12.2.3.4.4.1 Interrupt Generation in EP Mode
              1. 12.2.3.4.4.1.1 Legacy Interrupt Generation in EP Mode
              2. 12.2.3.4.4.1.2 MSI and MSI-X Interrupt Generation
            2. 12.2.3.4.4.2 PCIe Interrupt Reception in EP Mode
              1. 12.2.3.4.4.2.1 PCIe Core Downstream Interrupts
              2. 12.2.3.4.4.2.2 PCIe Core Function Level Reset Interrupts
              3. 12.2.3.4.4.2.3 PCIe Core Power Management Event Interrupts
              4. 12.2.3.4.4.2.4 PCIe Core Hot Reset Request Interrupt
              5. 12.2.3.4.4.2.5 PTM Valid Interrupt
            3. 12.2.3.4.4.3 PCIe Interrupt Generation in RP Mode
            4. 12.2.3.4.4.4 PCIe Interrupt Reception in RP Mode
              1. 12.2.3.4.4.4.1 PCIe Legacy Interrupt Reception in RP Mode
              2. 12.2.3.4.4.4.2 MSI/MSI-X Interrupt Reception in RP Mode
              3. 12.2.3.4.4.4.3 Advanced Error Reporting Interrupt
            5. 12.2.3.4.4.5 PCIe Interrupt Reception in RP and EP Mode
              1. 12.2.3.4.4.5.1 PCIe Local Interrupt
              2. 12.2.3.4.4.5.2 PHY Interrupt
              3. 12.2.3.4.4.5.3 Link down Interrupt
              4. 12.2.3.4.4.5.4 Transaction Error Interrupts
              5. 12.2.3.4.4.5.5 Power Management Event Interrupt
              6. 12.2.3.4.4.5.6 Active Internal Diagnostics Interrupts
            6. 12.2.3.4.4.6 ECC Aggregator Interrupts
            7. 12.2.3.4.4.7 CPTS Interrupts
          5. 12.2.3.4.5  PCIe Subsystem DMA Support
            1. 12.2.3.4.5.1 PCIe DMA Support in Root Port Mode
            2. 12.2.3.4.5.2 PCIe DMA Support in End Point Mode
          6. 12.2.3.4.6  PCIe Transactions
            1. 12.2.3.4.6.1 PCIe Supported Transactions
            2. 12.2.3.4.6.2 PCIe Transaction Limitations
          7. 12.2.3.4.7  PCIe Subsystem Address Translation
            1. 12.2.3.4.7.1 PCIe Inbound Address Translation
              1. 12.2.3.4.7.1.1 Root Port Inbound PCIe to AXI Address Translation
              2. 12.2.3.4.7.1.2 End Point Inbound PCIe to AXI Address Translation
            2. 12.2.3.4.7.2 PCIe Outbound Address Translation
              1. 12.2.3.4.7.2.1 PCIe Outbound Address Translation Bypass
          8. 12.2.3.4.8  PCIe Subsystem Virtualization Support
            1. 12.2.3.4.8.1 EP SR-IOV support
            2. 12.2.3.4.8.2 RP ATS support
            3. 12.2.3.4.8.3 VirtID Mapping
          9. 12.2.3.4.9  PCIe Subsystem Quality-of-Service (QoS)
          10. 12.2.3.4.10 PCIe Subsystem Precision Time Measurement (PTM)
          11. 12.2.3.4.11 PCIe Subsystem Loopback
            1. 12.2.3.4.11.1 PCIe PIPE Loopback
              1. 12.2.3.4.11.1.1 PIPE Loopback Master Mode
              2. 12.2.3.4.11.1.2 PIPE Loopback Slave Mode
          12. 12.2.3.4.12 PCIe Subsystem Error Handling
            1. 12.2.3.4.12.1 PCIe AXI to/from VBUSM Bus Error Mapping
          13. 12.2.3.4.13 PCIe Subsystem Internal Diagnostics Features
            1. 12.2.3.4.13.1 PCIe Parity
            2. 12.2.3.4.13.2 ECC Aggregators
            3. 12.2.3.4.13.3 RAM ECC inversion
          14. 12.2.3.4.14 LTSSM State Encoding
      4. 12.2.4 Universal Serial Bus (USB) Subsystem
        1. 12.2.4.1 USB Overview
          1. 12.2.4.1.1 USB Features
          2. 12.2.4.1.2 USB Not Supported Features
          3. 12.2.4.1.3 USB Terminology
        2. 12.2.4.2 USB Environment
        3. 12.2.4.3 USB Integration
        4. 12.2.4.4 USB Functional Description
          1. 12.2.4.4.1 USB Type-C Connector Support
          2. 12.2.4.4.2 USB Controller Reset
          3. 12.2.4.4.3 Overcurrent Detection
          4. 12.2.4.4.4 Top-Level Initialization Sequence
      5. 12.2.5 2-L Serializer/Deserializer (SerDes)
        1. 12.2.5.1 2-L SerDes Overview
          1. 12.2.5.1.1 2-L SerDes Features
          2. 12.2.5.1.2 Industry Standards Compatibility
        2. 12.2.5.2 2-L SerDes Environment
          1. 12.2.5.2.1 2-L SerDes I/Os
        3. 12.2.5.3 2-L SerDes Integration
          1. 12.2.5.3.1 2-L WIZ Settings
            1. 12.2.5.3.1.1 Interface Selection
            2. 12.2.5.3.1.2 Internal Reference Clock Selection
        4. 12.2.5.4 2-L SerDes Functional Description
          1. 12.2.5.4.1 2-L SerDes Block Diagram
      6. 12.2.6 4-L Serializer/Deserializer (SerDes)
        1. 12.2.6.1 4-L SerDes Overview
          1. 12.2.6.1.1 4-L SerDes Features
          2. 12.2.6.1.2 Industry Standards Compatibility
        2. 12.2.6.2 4-L SerDes Environment
          1. 12.2.6.2.1 4-L SerDes I/Os
        3. 12.2.6.3 4-L SerDes Integration
          1. 12.2.6.3.1 4-L WIZ Settings
            1. 12.2.6.3.1.1 Interface Selection
            2. 12.2.6.3.1.2 Internal Reference Clock Selection
        4. 12.2.6.4 4-L SerDes Functional Description
          1. 12.2.6.4.1 4-L SerDes Block Diagram
    3. 12.3  Memory Interfaces
      1. 12.3.1 Flash Subsystem (FSS)
        1. 12.3.1.1 FSS Overview
          1. 12.3.1.1.1 FSS Features
          2. 12.3.1.1.2 FSS Not Supported Features
        2. 12.3.1.2 FSS Environment
          1. 12.3.1.2.1 FSS Typical Application
        3. 12.3.1.3 FSS Integration
          1. 12.3.1.3.1 FSS Integration in MCU Domain
        4. 12.3.1.4 FSS Functional Description
          1. 12.3.1.4.1 FSS Block Diagram
          2. 12.3.1.4.2 FSS ECC Support
            1. 12.3.1.4.2.1 FSS ECC Calculation
          3. 12.3.1.4.3 FSS Modes of Operation
          4. 12.3.1.4.4 FSS Read Operations
            1. 12.3.1.4.4.1 OSPI Read Pipeline Mode
          5. 12.3.1.4.5 FSS Memory Address Translation
          6. 12.3.1.4.6 FSS0 and FSS1 Regions
            1. 12.3.1.4.6.1 FSS0 and FSS1 Regions Boot Size Configuration
          7. 12.3.1.4.7 FSS Memory Regions
        5. 12.3.1.5 FSS Programming Guide
          1. 12.3.1.5.1 FSS Initialization Sequence
          2. 12.3.1.5.2 FSS Real-Time Operation
          3. 12.3.1.5.3 FSS Power Up/Down Sequence
      2. 12.3.2 Octal Serial Peripheral Interface (OSPI)
        1. 12.3.2.1 OSPI Overview
          1. 12.3.2.1.1 OSPI Features
          2. 12.3.2.1.2 OSPI Not Supported Features
        2. 12.3.2.2 OSPI Environment
        3. 12.3.2.3 OSPI Integration
          1. 12.3.2.3.1 OSPI Integration in MCU Domain
        4. 12.3.2.4 OSPI Functional Description
          1. 12.3.2.4.1  OSPI Block Diagram
            1. 12.3.2.4.1.1 Data Target Interface
            2. 12.3.2.4.1.2 Configuration Target Interface
            3. 12.3.2.4.1.3 OSPI Clock Domains
          2. 12.3.2.4.2  OSPI Modes
            1. 12.3.2.4.2.1 Read Data Capture
              1. 12.3.2.4.2.1.1 Mechanisms of Data Capturing
              2. 12.3.2.4.2.1.2 Data Capturing Mechanism Using Taps
              3. 12.3.2.4.2.1.3 Data Capturing Mechanism Using PHY Module
            2. 12.3.2.4.2.2 External Pull Down on DQS
          3. 12.3.2.4.3  OSPI Power Management
          4. 12.3.2.4.4  Auto HW Polling
          5. 12.3.2.4.5  Flash Reset
          6. 12.3.2.4.6  OSPI Memory Regions
          7. 12.3.2.4.7  OSPI Interrupt Requests
          8. 12.3.2.4.8  OSPI Data Interface
            1. 12.3.2.4.8.1 Data Interface Address Remapping
            2. 12.3.2.4.8.2 Write Protection
            3. 12.3.2.4.8.3 Access Forwarding
          9. 12.3.2.4.9  OSPI Direct Access Controller (DAC)
          10. 12.3.2.4.10 OSPI Indirect Access Controller (INDAC)
            1. 12.3.2.4.10.1 Indirect Read Controller
              1. 12.3.2.4.10.1.1 Indirect Read Transfer Process
            2. 12.3.2.4.10.2 Indirect Write Controller
              1. 12.3.2.4.10.2.1 Indirect Write Transfer Process
            3. 12.3.2.4.10.3 Indirect Access Queuing
            4. 12.3.2.4.10.4 Consecutive Writes and Reads Using Indirect Transfers
            5. 12.3.2.4.10.5 Accessing the SRAM
          11. 12.3.2.4.11 OSPI Software-Triggered Instruction Generator (STIG)
            1. 12.3.2.4.11.1 Servicing a STIG Request
            2. 12.3.2.4.11.2 2956
          12. 12.3.2.4.12 OSPI Arbitration Between Direct / Indirect Access Controller and STIG
          13. 12.3.2.4.13 OSPI Command Translation
          14. 12.3.2.4.14 Selecting the Flash Instruction Type
          15. 12.3.2.4.15 OSPI Data Integrity
          16. 12.3.2.4.16 OSPI PHY Module
            1. 12.3.2.4.16.1 PHY Pipeline Mode
            2. 12.3.2.4.16.2 Read Data Capturing by the PHY Module
        5. 12.3.2.5 OSPI Programming Guide
          1. 12.3.2.5.1 Configuring the OSPI Controller for Use After Reset
          2. 12.3.2.5.2 Configuring the OSPI Controller for Optimal Use
          3. 12.3.2.5.3 Using the Flash Command Control Register (STIG Operation)
          4. 12.3.2.5.4 Using SPI Legacy Mode
          5. 12.3.2.5.5 Entering XIP Mode from POR
          6. 12.3.2.5.6 Entering XIP Mode Otherwise
          7. 12.3.2.5.7 Exiting XIP Mode
      3. 12.3.3 HyperBus Interface
        1. 12.3.3.1 HyperBus Overview
          1. 12.3.3.1.1 HyperBus Features
          2. 12.3.3.1.2 HyperBus Not Supported Features
        2. 12.3.3.2 HyperBus Environment
        3. 12.3.3.3 HyperBus Integration
          1. 12.3.3.3.1 HyperBus Integration in MCU Domain
        4. 12.3.3.4 HyperBus Functional Description
          1. 12.3.3.4.1 HyperBus Interrupts
          2. 12.3.3.4.2 HyperBus ECC Support
            1. 12.3.3.4.2.1 ECC Aggregator
          3. 12.3.3.4.3 HyperBus Internal FIFOs
          4. 12.3.3.4.4 HyperBus Data Regions
          5. 12.3.3.4.5 HyperBus True Continuous Read (TCR) Mode
        5. 12.3.3.5 HyperBus Programming Guide
          1. 12.3.3.5.1 HyperBus Initialization Sequence
            1. 12.3.3.5.1.1 HyperFlash Access
            2. 12.3.3.5.1.2 HyperRAM Access
          2. 12.3.3.5.2 HyperBus Real-time Operating Requirements
          3. 12.3.3.5.3 HyperBus Power Up/Down Sequence
      4. 12.3.4 General-Purpose Memory Controller (GPMC)
        1. 12.3.4.1 GPMC Overview
          1. 12.3.4.1.1 GPMC Features
          2. 12.3.4.1.2 GPMC Not Supported Features
        2. 12.3.4.2 GPMC Environment
          1. 12.3.4.2.1 GPMC Modes
          2. 12.3.4.2.2 GPMC I/O Signals
        3. 12.3.4.3 GPMC Integration
          1. 12.3.4.3.1 GPMC Integration in MAIN Domain
        4. 12.3.4.4 GPMC Functional Description
          1. 12.3.4.4.1  GPMC Block Diagram
          2. 12.3.4.4.2  GPMC Clock Configuration
          3. 12.3.4.4.3  GPMC Power Management
          4. 12.3.4.4.4  GPMC Interrupt Requests
          5. 12.3.4.4.5  GPMC Interconnect Port Interface
          6. 12.3.4.4.6  GPMC Address and Data Bus
            1. 12.3.4.4.6.1 GPMC I/O Configuration Setting
          7. 12.3.4.4.7  GPMC Address Decoder and Chip-Select Configuration
            1. 12.3.4.4.7.1 Chip-Select Base Address and Region Size
            2. 12.3.4.4.7.2 Access Protocol
              1. 12.3.4.4.7.2.1 Supported Devices
              2. 12.3.4.4.7.2.2 Access Size Adaptation and Device Width
              3. 12.3.4.4.7.2.3 Address/Data-Multiplexing Interface
            3. 12.3.4.4.7.3 External Signals
              1. 12.3.4.4.7.3.1 WAIT Pin Monitoring Control
                1. 12.3.4.4.7.3.1.1 Wait Monitoring During Asynchronous Read Access
                2. 12.3.4.4.7.3.1.2 Wait Monitoring During Asynchronous Write Access
                3. 12.3.4.4.7.3.1.3 Wait Monitoring During Synchronous Read Access
                4. 12.3.4.4.7.3.1.4 Wait Monitoring During Synchronous Write Access
                5. 12.3.4.4.7.3.1.5 Wait With NAND Device
                6. 12.3.4.4.7.3.1.6 Idle Cycle Control Between Successive Accesses
                  1. 3.4.4.7.3.1.6.1 Bus Turnaround (BUSTURNAROUND)
                  2. 3.4.4.7.3.1.6.2 Idle Cycles Between Accesses to Same Chip-Select (CYCLE2CYCLESAMECSEN, CYCLE2CYCLEDELAY)
                  3. 3.4.4.7.3.1.6.3 Idle Cycles Between Accesses to Different Chip-Select (CYCLE2CYCLEDIFFCSEN, CYCLE2CYCLEDELAY)
                7. 12.3.4.4.7.3.1.7 Slow Device Support (TIMEPARAGRANULARITY Parameter)
              2. 12.3.4.4.7.3.2 DIR Pin
              3. 12.3.4.4.7.3.3 Reset
              4. 12.3.4.4.7.3.4 Write Protect Signal (nWP)
              5. 12.3.4.4.7.3.5 Byte Enable (nBE1/nBE0)
            4. 12.3.4.4.7.4 Error Handling
          8. 12.3.4.4.8  GPMC Timing Setting
            1. 12.3.4.4.8.1  Read Cycle Time and Write Cycle Time (RDCYCLETIME / WRCYCLETIME)
            2. 12.3.4.4.8.2  nCS: Chip-Select Signal Control Assertion/Deassertion Time (CSONTIME / CSRDOFFTIME / CSWROFFTIME / CSEXTRADELAY)
            3. 12.3.4.4.8.3  nADV/ALE: Address Valid/Address Latch Enable Signal Control Assertion/Deassertion Time (ADVONTIME / ADVRDOFFTIME / ADVWROFFTIME / ADVEXTRADELAY/ADVAADMUXONTIME/ADVAADMUXRDOFFTIME/ADVAADMUXWROFFTIME)
            4. 12.3.4.4.8.4  nOE/nRE: Output Enable/Read Enable Signal Control Assertion/Deassertion Time (OEONTIME / OEOFFTIME / OEEXTRADELAY / OEAADMUXONTIME / OEAADMUXOFFTIME)
            5. 12.3.4.4.8.5  nWE: Write Enable Signal Control Assertion/Deassertion Time (WEONTIME / WEOFFTIME / WEEXTRADELAY)
            6. 12.3.4.4.8.6  GPMC_CLKOUT
            7. 12.3.4.4.8.7  GPMC Output Clock and Control Signals Setup and Hold
            8. 12.3.4.4.8.8  Access Time (RDACCESSTIME / WRACCESSTIME)
              1. 12.3.4.4.8.8.1 Access Time on Read Access
              2. 12.3.4.4.8.8.2 Access Time on Write Access
            9. 12.3.4.4.8.9  Page Burst Access Time (PAGEBURSTACCESSTIME)
              1. 12.3.4.4.8.9.1 Page Burst Access Time on Read Access
              2. 12.3.4.4.8.9.2 Page Burst Access Time on Write Access
            10. 12.3.4.4.8.10 Bus Keeping Support
          9. 12.3.4.4.9  GPMC NOR Access Description
            1. 12.3.4.4.9.1 Asynchronous Access Description
              1. 12.3.4.4.9.1.1 Access on Address/Data Multiplexed Devices
                1. 12.3.4.4.9.1.1.1 Asynchronous Single-Read Operation on an Address/Data Multiplexed Device
                2. 12.3.4.4.9.1.1.2 Asynchronous Single-Write Operation on an Address/Data-Multiplexed Device
                3. 12.3.4.4.9.1.1.3 Asynchronous Multiple (Page) Write Operation on an Address/Data-Multiplexed Device
              2. 12.3.4.4.9.1.2 Access on Address/Address/Data-Multiplexed Devices
                1. 12.3.4.4.9.1.2.1 Asynchronous Single Read Operation on an AAD-Multiplexed Device
                2. 12.3.4.4.9.1.2.2 Asynchronous Single-Write Operation on an AAD-Multiplexed Device
                3. 12.3.4.4.9.1.2.3 Asynchronous Multiple (Page) Read Operation on an AAD-Multiplexed Device
            2. 12.3.4.4.9.2 Synchronous Access Description
              1. 12.3.4.4.9.2.1 Synchronous Single Read
              2. 12.3.4.4.9.2.2 Synchronous Multiple (Burst) Read (4-, 8-, 16-Word16 Burst With Wraparound Capability)
              3. 12.3.4.4.9.2.3 Synchronous Single Write
              4. 12.3.4.4.9.2.4 Synchronous Multiple (Burst) Write
            3. 12.3.4.4.9.3 Asynchronous and Synchronous Accesses in non-multiplexed Mode
              1. 12.3.4.4.9.3.1 Asynchronous Single-Read Operation on non-multiplexed Device
              2. 12.3.4.4.9.3.2 Asynchronous Single-Write Operation on non-multiplexed Device
              3. 12.3.4.4.9.3.3 Asynchronous Multiple (Page Mode) Read Operation on non-multiplexed Device
              4. 12.3.4.4.9.3.4 Synchronous Operations on a non-multiplexed Device
            4. 12.3.4.4.9.4 Page and Burst Support
            5. 12.3.4.4.9.5 System Burst vs External Device Burst Support
          10. 12.3.4.4.10 GPMC pSRAM Access Specificities
          11. 12.3.4.4.11 GPMC NAND Access Description
            1. 12.3.4.4.11.1 NAND Memory Device in Byte or 16-bit Word Stream Mode
              1. 12.3.4.4.11.1.1 Chip-Select Configuration for NAND Interfacing in Byte or Word Stream Mode
              2. 12.3.4.4.11.1.2 NAND Device Command and Address Phase Control
              3. 12.3.4.4.11.1.3 Command Latch Cycle
              4. 12.3.4.4.11.1.4 Address Latch Cycle
              5. 12.3.4.4.11.1.5 NAND Device Data Read and Write Phase Control in Stream Mode
              6. 12.3.4.4.11.1.6 NAND Device General Chip-Select Timing Control Requirement
              7. 12.3.4.4.11.1.7 Read and Write Access Size Adaptation
                1. 12.3.4.4.11.1.7.1 8-Bit-Wide NAND Device
                2. 12.3.4.4.11.1.7.2 16-Bit-Wide NAND Device
            2. 12.3.4.4.11.2 NAND Device-Ready Pin
              1. 12.3.4.4.11.2.1 Ready Pin Monitored by Software Polling
              2. 12.3.4.4.11.2.2 Ready Pin Monitored by Hardware Interrupt
            3. 12.3.4.4.11.3 ECC Calculator
              1. 12.3.4.4.11.3.1 Hamming Code
                1. 12.3.4.4.11.3.1.1 ECC Result Register and ECC Computation Accumulation Size
                2. 12.3.4.4.11.3.1.2 ECC Enabling
                3. 12.3.4.4.11.3.1.3 ECC Computation
                4. 12.3.4.4.11.3.1.4 ECC Comparison and Correction
                5. 12.3.4.4.11.3.1.5 ECC Calculation Based on 8-Bit Word
                6. 12.3.4.4.11.3.1.6 ECC Calculation Based on 16-Bit Word
              2. 12.3.4.4.11.3.2 BCH Code
                1. 12.3.4.4.11.3.2.1 Requirements
                2. 12.3.4.4.11.3.2.2 Memory Mapping of BCH Codeword
                  1. 3.4.4.11.3.2.2.1 Memory Mapping of Data Message
                  2. 3.4.4.11.3.2.2.2 Memory-Mapping of the ECC
                  3. 3.4.4.11.3.2.2.3 Wrapping Modes
                    1. 4.4.11.3.2.2.3.1  Manual Mode (0x0)
                    2. 4.4.11.3.2.2.3.2  Mode 0x1
                    3. 4.4.11.3.2.2.3.3  Mode 0xA (10)
                    4. 4.4.11.3.2.2.3.4  Mode 0x2
                    5. 4.4.11.3.2.2.3.5  Mode 0x3
                    6. 4.4.11.3.2.2.3.6  Mode 0x7
                    7. 4.4.11.3.2.2.3.7  Mode 0x8
                    8. 4.4.11.3.2.2.3.8  Mode 0x4
                    9. 4.4.11.3.2.2.3.9  Mode 0x9
                    10. 4.4.11.3.2.2.3.10 Mode 0x5
                    11. 4.4.11.3.2.2.3.11 Mode 0xB (11)
                    12. 4.4.11.3.2.2.3.12 Mode 0x6
                3. 12.3.4.4.11.3.2.3 Supported NAND Page Mappings and ECC Schemes
                  1. 3.4.4.11.3.2.3.1 Per-Sector Spare Mappings
                  2. 3.4.4.11.3.2.3.2 Pooled Spare Mapping
                  3. 3.4.4.11.3.2.3.3 Per-Sector Spare Mapping, with ECC Separated at the End of the Page
            4. 12.3.4.4.11.4 Prefetch and Write-Posting Engine
              1. 12.3.4.4.11.4.1 General Facts About the Engine Configuration
              2. 12.3.4.4.11.4.2 Prefetch Mode
              3. 12.3.4.4.11.4.3 FIFO Control in Prefetch Mode
              4. 12.3.4.4.11.4.4 Write-Posting Mode
              5. 12.3.4.4.11.4.5 FIFO Control in Write-Posting Mode
              6. 12.3.4.4.11.4.6 Optimizing NAND Access Using the Prefetch and Write-Posting Engine
              7. 12.3.4.4.11.4.7 Interleaved Accesses Between Prefetch and Write-Posting Engine and Other Chip-Selects
          12. 12.3.4.4.12 GPMC Use Cases and Tips
            1. 12.3.4.4.12.1 How to Set GPMC Timing Parameters for Typical Accesses
              1. 12.3.4.4.12.1.1 External Memory Attached to the GPMC Module
              2. 12.3.4.4.12.1.2 Typical GPMC Setup
                1. 12.3.4.4.12.1.2.1 GPMC Configuration for Synchronous Burst Read Access
                2. 12.3.4.4.12.1.2.2 GPMC Configuration for Asynchronous Read Access
                3. 12.3.4.4.12.1.2.3 GPMC Configuration for Asynchronous Single Write Access
            2. 12.3.4.4.12.2 How to Choose a Suitable Memory to Use With the GPMC
              1. 12.3.4.4.12.2.1 Supported Memories or Devices
                1. 12.3.4.4.12.2.1.1 Memory Pin Multiplexing
                2. 12.3.4.4.12.2.1.2 NAND Interface Protocol
                3. 12.3.4.4.12.2.1.3 NOR Interface Protocol
                4. 12.3.4.4.12.2.1.4 Other Technologies
        5. 12.3.4.5 GPMC Basic Programming Model
          1. 12.3.4.5.1 GPMC High-Level Programming Model Overview
          2. 12.3.4.5.2 GPMC Initialization
          3. 12.3.4.5.3 GPMC Configuration in NOR Mode
          4. 12.3.4.5.4 GPMC Configuration in NAND Mode
          5. 12.3.4.5.5 Set Memory Access
          6. 12.3.4.5.6 GPMC Timing Parameters
            1. 12.3.4.5.6.1 GPMC Timing Parameters Formulas
              1. 12.3.4.5.6.1.1 NAND Flash Interface Timing Parameters Formulas
              2. 12.3.4.5.6.1.2 Synchronous NOR Flash Timing Parameters Formulas
              3. 12.3.4.5.6.1.3 Asynchronous NOR Flash Timing Parameters Formulas
      5. 12.3.5 Error Location Module (ELM)
        1. 12.3.5.1 ELM Overview
          1. 12.3.5.1.1 ELM Features
          2. 12.3.5.1.2 ELM Not Supported Features
        2. 12.3.5.2 ELM Integration
          1. 12.3.5.2.1 ELM Integration in MAIN Domain
        3. 12.3.5.3 ELM Functional Description
          1. 12.3.5.3.1 ELM Software Reset
          2. 12.3.5.3.2 ELM Power Management
          3. 12.3.5.3.3 ELM Interrupt Requests
          4. 12.3.5.3.4 ELM Processing Initialization
          5. 12.3.5.3.5 ELM Processing Sequence
          6. 12.3.5.3.6 ELM Processing Completion
        4. 12.3.5.4 ELM Basic Programming Model
          1. 12.3.5.4.1 ELM Low-Level Programming Model
            1. 12.3.5.4.1.1 Processing Initialization
            2. 12.3.5.4.1.2 Read Results
            3. 12.3.5.4.1.3 3163
          2. 12.3.5.4.2 Use Case: ELM Used in Continuous Mode
          3. 12.3.5.4.3 Use Case: ELM Used in Page Mode
      6. 12.3.6 Multimedia Card Secure Digital (MMCSD) Interface
        1. 12.3.6.1 MMCSD Overview
          1. 12.3.6.1.1 MMCSD Features
          2. 12.3.6.1.2 MMCSD Not Supported Features
        2. 12.3.6.2 MMCSD Environment
          1. 12.3.6.2.1 Protocol and Data Format
            1. 12.3.6.2.1.1 Protocol
            2. 12.3.6.2.1.2 Data Format
              1. 12.3.6.2.1.2.1 Coding Scheme for Command Token
              2. 12.3.6.2.1.2.2 Coding Scheme for Response Token
              3. 12.3.6.2.1.2.3 Coding Scheme for Data Token
        3. 12.3.6.3 MMCSD Integration
          1. 12.3.6.3.1 MMCSD Integration in MAIN Domain
        4. 12.3.6.4 MMCSD Functional Description
          1. 12.3.6.4.1 Block Diagram
          2. 12.3.6.4.2 Memory Regions
          3. 12.3.6.4.3 Interrupt Requests
          4. 12.3.6.4.4 ECC Support
            1. 12.3.6.4.4.1 ECC Aggregator
          5. 12.3.6.4.5 Advanced DMA
          6. 12.3.6.4.6 eMMC PHY BIST
            1. 12.3.6.4.6.1 BIST Overview
            2. 12.3.6.4.6.2 BIST Modes
              1. 12.3.6.4.6.2.1 DS Mode
              2. 12.3.6.4.6.2.2 HS Mode with TXDLY using DLL
              3. 12.3.6.4.6.2.3 HS Mode with TXDLY using Delay Chain
              4. 12.3.6.4.6.2.4 DDR50 Mode with TXDLY using DLL
              5. 12.3.6.4.6.2.5 DDR50 Mode with TXDLY using Delay Chain
              6. 12.3.6.4.6.2.6 HS200 Mode with TX/RXDLY using DLL
              7. 12.3.6.4.6.2.7 HS200 Mode with TX/RXDLY using Delay Chain
              8. 12.3.6.4.6.2.8 HS400 Mode
            3. 12.3.6.4.6.3 BIST Functionality
            4. 12.3.6.4.6.4 Signal Interface
            5. 12.3.6.4.6.5 Programming Flow
              1. 12.3.6.4.6.5.1 DS Mode
                1. 12.3.6.4.6.5.1.1 Configuration
                2. 12.3.6.4.6.5.1.2 BIST Programming
              2. 12.3.6.4.6.5.2 HS Mode with DLY_CHAIN
                1. 12.3.6.4.6.5.2.1 Configuration
                2. 12.3.6.4.6.5.2.2 BIST Programming
              3. 12.3.6.4.6.5.3 HS Mode with DLL
                1. 12.3.6.4.6.5.3.1 Configuration
                2. 12.3.6.4.6.5.3.2 BIST Programming
              4. 12.3.6.4.6.5.4 DDR52 Mode with DLY_CHAIN
                1. 12.3.6.4.6.5.4.1 Configuration
                2. 12.3.6.4.6.5.4.2 BIST Programming
              5. 12.3.6.4.6.5.5 DDR52 Mode with DLL
                1. 12.3.6.4.6.5.5.1 Configuration
                2. 12.3.6.4.6.5.5.2 BIST Programming
              6. 12.3.6.4.6.5.6 HS200 Mode with DLY_CHAIN
                1. 12.3.6.4.6.5.6.1 Configuration
                2. 12.3.6.4.6.5.6.2 BIST Programming
              7. 12.3.6.4.6.5.7 HS200 Mode with DLL
                1. 12.3.6.4.6.5.7.1 Configuration
                2. 12.3.6.4.6.5.7.2 BIST Programming
              8. 12.3.6.4.6.5.8 HS400 Mode with DLL
                1. 12.3.6.4.6.5.8.1 Configuration
                2. 12.3.6.4.6.5.8.2 BIST Programming
            6. 12.3.6.4.6.6 HS200 BIST Result Check Procedure
        5. 12.3.6.5 MMCSD Programming Guide
          1. 12.3.6.5.1 Sequences
            1. 12.3.6.5.1.1  SD Card Detection
            2. 12.3.6.5.1.2  SD Clock Control
              1. 12.3.6.5.1.2.1 Internal Clock Setup Sequence
              2. 12.3.6.5.1.2.2 SD Clock Supply and Stop Sequence
              3. 12.3.6.5.1.2.3 SD Clock Frequency Change Sequence
            3. 12.3.6.5.1.3  SD Bus Power Control
            4. 12.3.6.5.1.4  Changing Bus Width
            5. 12.3.6.5.1.5  Timeout Setting on DAT Line
            6. 12.3.6.5.1.6  Card Initialization and Identification (for SD I/F)
              1. 12.3.6.5.1.6.1 Signal Voltage Switch Procedure (for UHS-I)
            7. 12.3.6.5.1.7  SD Transaction Generation
              1. 12.3.6.5.1.7.1 Transaction Control without Data Transfer Using DAT Line
                1. 12.3.6.5.1.7.1.1 The Sequence to Issue a SD Command
                2. 12.3.6.5.1.7.1.2 The Sequence to Finalize a Command
                3. 12.3.6.5.1.7.1.3 3241
              2. 12.3.6.5.1.7.2 Transaction Control with Data Transfer Using DAT Line
                1. 12.3.6.5.1.7.2.1 Not using DMA
                2. 12.3.6.5.1.7.2.2 Using SDMA
                3. 12.3.6.5.1.7.2.3 Using ADMA
            8. 12.3.6.5.1.8  Abort Transaction
              1. 12.3.6.5.1.8.1 Asynchronous Abort
              2. 12.3.6.5.1.8.2 Synchronous Abort
            9. 12.3.6.5.1.9  Changing Bus Speed Mode
            10. 12.3.6.5.1.10 Error Recovery
              1. 12.3.6.5.1.10.1 Error Interrupt Recovery
              2. 12.3.6.5.1.10.2 Auto CMD12 Error Recovery
            11. 12.3.6.5.1.11 Wakeup Control (Optional)
            12. 12.3.6.5.1.12 Suspend/Resume (Optional, Not Supported from Version 4.00)
              1. 12.3.6.5.1.12.1 Suspend Sequence
              2. 12.3.6.5.1.12.2 Resume Sequence
              3. 12.3.6.5.1.12.3 Stop At Block Gap/Continue Timing for Read Transaction
              4. 12.3.6.5.1.12.4 Stop At Block Gap/Continue Timing for Write Transaction
          2. 12.3.6.5.2 Driver Flow Sequence
            1. 12.3.6.5.2.1 Host Controller Setup and Card Detection
              1. 12.3.6.5.2.1.1 Host Controller Setup Sequence
              2. 12.3.6.5.2.1.2 Card Interface Detection Sequence
            2. 12.3.6.5.2.2 Boot Operation
              1. 12.3.6.5.2.2.1 Normal Boot Operation: (For Legacy eMMC 5.0)
              2. 12.3.6.5.2.2.2 Alternate Boot Operation (For Legacy eMMC 5.0):
              3. 12.3.6.5.2.2.3 Boot Code Chunk Read Operation (For Legacy eMMC 5.0):
            3. 12.3.6.5.2.3 Retuning procedure (For Legacy Interface)
              1. 12.3.6.5.2.3.1 Sampling Clock Tuning
              2. 12.3.6.5.2.3.2 Tuning Modes
              3. 12.3.6.5.2.3.3 Re-Tuning Mode 2
            4. 12.3.6.5.2.4 Command Queuing Driver Flow Sequence
              1. 12.3.6.5.2.4.1 Command Queuing Initialization Sequence
              2. 12.3.6.5.2.4.2 Task Issuance Sequence
              3. 12.3.6.5.2.4.3 Task Execution and Completion Sequence
              4. 12.3.6.5.2.4.4 Task Discard and Clear Sequence
              5. 12.3.6.5.2.4.5 Error Detect and Recovery when CQ is enabled
      7. 12.3.7 Universal Flash Storage (UFS) Interface
        1. 12.3.7.1 UFS Overview
          1. 12.3.7.1.1 UFS Features
        2. 12.3.7.2 UFS Environment
        3. 12.3.7.3 UFS Integration
          1. 12.3.7.3.1 UFS Integration in MAIN Domain
        4. 12.3.7.4 UFS Functional Description
          1. 12.3.7.4.1 UFS Block Diagrams
          2. 12.3.7.4.2 UFS ECC Support
        5. 12.3.7.5 UFS Programming Guide
          1. 12.3.7.5.1 UFS Start-Up Sequence
            1. 12.3.7.5.1.1 UniPro Initialization
              1. 12.3.7.5.1.1.1 UniPro Layer 2 Configuration
                1. 12.3.7.5.1.1.1.1 Layer 2 Threshold Value Calculation
                2. 12.3.7.5.1.1.1.2 DL_TC0TXFCThreshold
                3. 12.3.7.5.1.1.1.3 DL_AFC0CreditThreshold
                4. 12.3.7.5.1.1.1.4 DL_TC0OutAckThreshold
                5. 12.3.7.5.1.1.1.5 Layer 2 Timer Value Calculation
                6. 12.3.7.5.1.1.1.6 DL_FC0ProtectionTimeOutVal
                7. 12.3.7.5.1.1.1.7 DL_TC0ReplayTimeOutVal and DL_AFC0ReqTimeOut
              2. 12.3.7.5.1.1.2 UniPro CPort Connection Management
            2. 12.3.7.5.1.2 UFS Host Controller Initialization
            3. 12.3.7.5.1.3 HCE Bit
          2. 12.3.7.5.2 UFS Host Controller Programming
            1. 12.3.7.5.2.1 UFS Software Model
              1. 12.3.7.5.2.1.1 UFS Layers
              2. 12.3.7.5.2.1.2 UFS Protocol Elements
                1. 12.3.7.5.2.1.2.1 UPIU Types
                2. 12.3.7.5.2.1.2.2 UFS Protocol
              3. 12.3.7.5.2.1.3 UFS Host Data Structure
            2. 12.3.7.5.2.2 UFS Theory Of Operation
              1. 12.3.7.5.2.2.1 Building A UTP Transfer Request
              2. 12.3.7.5.2.2.2 Processing UTP Task Management Request Completion
              3. 12.3.7.5.2.2.3 Building UTP Task Management Request
              4. 12.3.7.5.2.2.4 Processing UTP Transfer Request Completion
              5. 12.3.7.5.2.2.5 UFS Host Processing
              6. 12.3.7.5.2.2.6 UFS Response Management Аnd Command Completion
          3. 12.3.7.5.3 UFS PHY Programming
          4. 12.3.7.5.4 UFS Hibernate Timings Considerations
    4. 12.4  Industrial and Control Interfaces
      1. 12.4.1 Enhanced Capture (ECAP) Module
        1. 12.4.1.1 ECAP Overview
          1. 12.4.1.1.1 ECAP Features
        2. 12.4.1.2 ECAP Environment
          1. 12.4.1.2.1 ECAP I/O Interface
        3. 12.4.1.3 ECAP Integration
          1. 12.4.1.3.1 Daisy-Chain Connectivity between ECAP Modules
        4. 12.4.1.4 ECAP Functional Description
          1. 12.4.1.4.1 Capture and APWM Operating Modes
            1. 12.4.1.4.1.1 ECAP Capture Mode Description
              1. 12.4.1.4.1.1.1 ECAP Event Prescaler
              2. 12.4.1.4.1.1.2 ECAP Edge Polarity Select and Qualifier
              3. 12.4.1.4.1.1.3 ECAP Continuous/One-Shot Control
              4. 12.4.1.4.1.1.4 ECAP 32-Bit Counter and Phase Control
              5. 12.4.1.4.1.1.5 CAP1-CAP4 Registers
              6. 12.4.1.4.1.1.6 ECAP Interrupt Control
              7. 12.4.1.4.1.1.7 ECAP Shadow Load and Lockout Control
            2. 12.4.1.4.1.2 ECAP APWM Mode Operation
          2. 12.4.1.4.2 Summary of ECAP Functional Registers
        5. 12.4.1.5 ECAP Use Cases
          1. 12.4.1.5.1 Absolute Time-Stamp Operation Rising Edge Trigger Example
            1. 12.4.1.5.1.1 Code Snippet for CAP Mode Absolute Time, Rising Edge Trigger
          2. 12.4.1.5.2 Absolute Time-Stamp Operation Rising and Falling Edge Trigger Example
            1. 12.4.1.5.2.1 Code Snippet for CAP Mode Absolute Time, Rising and Falling Edge Trigger
          3. 12.4.1.5.3 Time Difference (Delta) Operation Rising Edge Trigger Example
            1. 12.4.1.5.3.1 Code Snippet for CAP Mode Delta Time, Rising Edge Trigger
          4. 12.4.1.5.4 Time Difference (Delta) Operation Rising and Falling Edge Trigger Example
            1. 12.4.1.5.4.1 Code Snippet for CAP Mode Delta Time, Rising and Falling Edge Triggers
          5. 12.4.1.5.5 Application of the APWM Mode
            1. 12.4.1.5.5.1 Simple PWM Generation (Independent Channel/s) Example
              1. 12.4.1.5.5.1.1 Code Snippet for APWM Mode
            2. 12.4.1.5.5.2 Multichannel PWM Generation with Synchronization Example
              1. 12.4.1.5.5.2.1 Code Snippet for Multichannel PWM Generation with Synchronization
            3. 12.4.1.5.5.3 Multichannel PWM Generation with Phase Control Example
              1. 12.4.1.5.5.3.1 Code Snippet for Multichannel PWM Generation with Phase Control
      2. 12.4.2 Enhanced Pulse Width Modulation (EPWM) Module
        1. 12.4.2.1 EPWM Overview
          1. 12.4.2.1.1 EPWM Features
          2. 12.4.2.1.2 EPWM Not Supported Features
          3. 12.4.2.1.3 3356
        2. 12.4.2.2 EPWM Environment
          1. 12.4.2.2.1 EPWM I/O Interface
        3. 12.4.2.3 EPWM Integration
          1. 12.4.2.3.1 Device Specific EPWM Features
          2. 12.4.2.3.2 Daisy-Chain Connectivity between EPWM Modules
          3. 12.4.2.3.3 ADC start of conversion signals (PWM_SOCA and PWM_SOCB)
          4. 12.4.2.3.4 EPWM Modules Time Base Clock Gating
        4. 12.4.2.4 EPWM Functional Description
          1. 12.4.2.4.1  EPWM Submodule Features
            1. 12.4.2.4.1.1 Constant Definitions Used in the EPWM Code Examples
          2. 12.4.2.4.2  EPWM Time-Base (TB) Submodule
            1. 12.4.2.4.2.1 Overview
            2. 12.4.2.4.2.2 Controlling and Monitoring the EPWM Time-Base Submodule
            3. 12.4.2.4.2.3 Calculating PWM Period and Frequency
              1. 12.4.2.4.2.3.1 EPWM Time-Base Period Shadow Register
              2. 12.4.2.4.2.3.2 EPWM Time-Base Counter Synchronization
            4. 12.4.2.4.2.4 Phase Locking the Time-Base Clocks of Multiple EPWM Modules
            5. 12.4.2.4.2.5 EPWM Time-Base Counter Modes and Timing Waveforms
          3. 12.4.2.4.3  EPWM Counter-Compare (CC) Submodule
            1. 12.4.2.4.3.1 Overview
            2. 12.4.2.4.3.2 Controlling and Monitoring the EPWM Counter-Compare Submodule
            3. 12.4.2.4.3.3 Operational Highlights for the EPWM Counter-Compare Submodule
            4. 12.4.2.4.3.4 EPWM Counter-Compare Submodule Timing Waveforms
          4. 12.4.2.4.4  EPWM Action-Qualifier (AQ) Submodule
            1. 12.4.2.4.4.1 Overview
            2. 12.4.2.4.4.2 Controlling and Monitoring the EPWM Action-Qualifier Submodule
            3. 12.4.2.4.4.3 EPWM Action-Qualifier Event Priority
            4. 12.4.2.4.4.4 Waveforms for Common EPWM Configurations
          5. 12.4.2.4.5  EPWM Dead-Band Generator (DB) Submodule
            1. 12.4.2.4.5.1 Overview
            2. 12.4.2.4.5.2 Controlling and Monitoring the EPWM Dead-Band Submodule
            3. 12.4.2.4.5.3 Operational Highlights for the EPWM Dead-Band Generator Submodule
          6. 12.4.2.4.6  EPWM-Chopper (PC) Submodule
            1. 12.4.2.4.6.1 Overview
            2. 12.4.2.4.6.2 3391
            3. 12.4.2.4.6.3 Controlling the EPWM-Chopper Submodule
            4. 12.4.2.4.6.4 Operational Highlights for the EPWM-Chopper Submodule
            5. 12.4.2.4.6.5 EPWM-Chopper Waveforms
              1. 12.4.2.4.6.5.1 EPWM-Chopper One-Shot Pulse
              2. 12.4.2.4.6.5.2 EPWM-Chopper Duty Cycle Control
          7. 12.4.2.4.7  EPWM Trip-Zone (TZ) Submodule
            1. 12.4.2.4.7.1 Overview
            2. 12.4.2.4.7.2 Controlling and Monitoring the EPWM Trip-Zone Submodule
            3. 12.4.2.4.7.3 Operational Highlights for the EPWM Trip-Zone Submodule
            4. 12.4.2.4.7.4 Generating EPWM Trip-Event Interrupts
          8. 12.4.2.4.8  EPWM Event-Trigger (ET) Submodule
            1. 12.4.2.4.8.1 Overview
            2. 12.4.2.4.8.2 Controlling and Monitoring the EPWM Event-Trigger Submodule
            3. 12.4.2.4.8.3 Operational Overview of the EPWM Event-Trigger Submodule
            4. 12.4.2.4.8.4 3406
          9. 12.4.2.4.9  EPWM High Resolution (HRPWM) Submodule
            1. 12.4.2.4.9.1 Overview
            2. 12.4.2.4.9.2 Architecture of the High-Resolution PWM Submodule
            3. 12.4.2.4.9.3 Controlling and Monitoring the High-Resolution PWM Submodule
            4. 12.4.2.4.9.4 Configuring the High-Resolution PWM Submodule
            5. 12.4.2.4.9.5 Operational Highlights for the High-Resolution PWM Submodule
              1. 12.4.2.4.9.5.1 HRPWM Edge Positioning
              2. 12.4.2.4.9.5.2 HRPWM Scaling Considerations
              3. 12.4.2.4.9.5.3 HRPWM Duty Cycle Range Limitation
          10. 12.4.2.4.10 EPWM / HRPWM Functional Register Groups
          11. 12.4.2.4.11 Proper EPWM Interrupt Initialization Procedure
      3. 12.4.3 Enhanced Quadrature Encoder Pulse (EQEP) Module
        1. 12.4.3.1 EQEP Overview
          1. 12.4.3.1.1 EQEP Features
          2. 12.4.3.1.2 EQEP Not Supported Features
        2. 12.4.3.2 EQEP Environment
          1. 12.4.3.2.1 EQEP I/O Interface
        3. 12.4.3.3 EQEP Integration
          1. 12.4.3.3.1 Device Specific EQEP Features
        4. 12.4.3.4 EQEP Functional Description
          1. 12.4.3.4.1 EQEP Inputs
          2. 12.4.3.4.2 EQEP Quadrature Decoder Unit (QDU)
            1. 12.4.3.4.2.1 EQEP Position Counter Input Modes
              1. 12.4.3.4.2.1.1 Quadrature Count Mode
              2. 12.4.3.4.2.1.2 EQEP Direction-count Mode
              3. 12.4.3.4.2.1.3 EQEP Up-Count Mode
              4. 12.4.3.4.2.1.4 EQEP Down-Count Mode
            2. 12.4.3.4.2.2 EQEP Input Polarity Selection
            3. 12.4.3.4.2.3 EQEP Position-Compare Sync Output
          3. 12.4.3.4.3 EQEP Position Counter and Control Unit (PCCU)
            1. 12.4.3.4.3.1 EQEP Position Counter Operating Modes
              1. 12.4.3.4.3.1.1 EQEP Position Counter Reset on Index Event (EQEP_QDEC_QEP_CTL[29-28] PCRM] = 0b00)
              2. 12.4.3.4.3.1.2 EQEP Position Counter Reset on Maximum Position (EQEP_QDEC_QEP_CTL[29-28] PCRM=0b01)
              3. 12.4.3.4.3.1.3 Position Counter Reset on the First Index Event (EQEP_QDEC_QEP_CTL[29-28] PCRM = 0b10)
              4. 12.4.3.4.3.1.4 Position Counter Reset on Unit Time out Event (EQEP_QDEC_QEP_CTL[29-28] PCRM = 0b11)
            2. 12.4.3.4.3.2 EQEP Position Counter Latch
              1. 12.4.3.4.3.2.1 Index Event Latch
              2. 12.4.3.4.3.2.2 EQEP Strobe Event Latch
            3. 12.4.3.4.3.3 EQEP Position Counter Initialization
            4. 12.4.3.4.3.4 EQEP Position-Compare Unit
          4. 12.4.3.4.4 EQEP Edge Capture Unit
          5. 12.4.3.4.5 EQEP Watchdog
          6. 12.4.3.4.6 Unit Timer Base
          7. 12.4.3.4.7 EQEP Interrupt Structure
          8. 12.4.3.4.8 Summary of EQEP Functional Registers
      4. 12.4.4 Controller Area Network (MCAN)
        1. 12.4.4.1 MCAN Overview
          1. 12.4.4.1.1 MCAN Features
          2. 12.4.4.1.2 MCAN Not Supported Features
        2. 12.4.4.2 MCAN Environment
          1. 12.4.4.2.1 CAN Network Basics
        3. 12.4.4.3 MCAN Integration
          1. 12.4.4.3.1 MCAN Integration in MCU Domain
          2. 12.4.4.3.2 MCAN Integration in MAIN Domain
        4. 12.4.4.4 MCAN Functional Description
          1. 12.4.4.4.1  Module Clocking Requirements
          2. 12.4.4.4.2  Interrupt and DMA Requests
            1. 12.4.4.4.2.1 Interrupt Requests
            2. 12.4.4.4.2.2 DMA Requests
            3. 12.4.4.4.2.3 3466
          3. 12.4.4.4.3  Operating Modes
            1. 12.4.4.4.3.1 Software Initialization
            2. 12.4.4.4.3.2 Normal Operation
            3. 12.4.4.4.3.3 CAN FD Operation
            4. 12.4.4.4.3.4 Transmitter Delay Compensation
              1. 12.4.4.4.3.4.1 Description
              2. 12.4.4.4.3.4.2 Transmitter Delay Compensation Measurement
            5. 12.4.4.4.3.5 Restricted Operation Mode
            6. 12.4.4.4.3.6 Bus Monitoring Mode
            7. 12.4.4.4.3.7 Disabled Automatic Retransmission (DAR) Mode
              1. 12.4.4.4.3.7.1 Frame Transmission in DAR Mode
            8. 12.4.4.4.3.8 Power Down (Sleep Mode)
              1. 12.4.4.4.3.8.1 External Clock Stop Mode
              2. 12.4.4.4.3.8.2 Suspend Mode
              3. 12.4.4.4.3.8.3 Wakeup request
            9. 12.4.4.4.3.9 Test Modes
              1. 12.4.4.4.3.9.1 Internal Loopback Mode
          4. 12.4.4.4.4  Timestamp Generation
            1. 12.4.4.4.4.1 External Timestamp Counter
          5. 12.4.4.4.5  Timeout Counter
          6. 12.4.4.4.6  ECC Support
            1. 12.4.4.4.6.1 ECC Wrapper
            2. 12.4.4.4.6.2 ECC Aggregator
          7. 12.4.4.4.7  Rx Handling
            1. 12.4.4.4.7.1 Acceptance Filtering
              1. 12.4.4.4.7.1.1 Range Filter
              2. 12.4.4.4.7.1.2 Filter for specific IDs
              3. 12.4.4.4.7.1.3 Classic Bit Mask Filter
              4. 12.4.4.4.7.1.4 Standard Message ID Filtering
              5. 12.4.4.4.7.1.5 Extended Message ID Filtering
            2. 12.4.4.4.7.2 Rx FIFOs
              1. 12.4.4.4.7.2.1 Rx FIFO Blocking Mode
              2. 12.4.4.4.7.2.2 Rx FIFO Overwrite Mode
            3. 12.4.4.4.7.3 Dedicated Rx Buffers
              1. 12.4.4.4.7.3.1 Rx Buffer Handling
            4. 12.4.4.4.7.4 Debug on CAN Support
          8. 12.4.4.4.8  Tx Handling
            1. 12.4.4.4.8.1 Transmit Pause
            2. 12.4.4.4.8.2 Dedicated Tx Buffers
            3. 12.4.4.4.8.3 Tx FIFO
            4. 12.4.4.4.8.4 Tx Queue
            5. 12.4.4.4.8.5 Mixed Dedicated Tx Buffers/Tx FIFO
            6. 12.4.4.4.8.6 Mixed Dedicated Tx Buffers/Tx Queue
            7. 12.4.4.4.8.7 Transmit Cancellation
            8. 12.4.4.4.8.8 Tx Event Handling
          9. 12.4.4.4.9  FIFO Acknowledge Handling
          10. 12.4.4.4.10 Message RAM
            1. 12.4.4.4.10.1 Message RAM Configuration
            2. 12.4.4.4.10.2 Rx Buffer and FIFO Element
            3. 12.4.4.4.10.3 Tx Buffer Element
            4. 12.4.4.4.10.4 Tx Event FIFO Element
            5. 12.4.4.4.10.5 Standard Message ID Filter Element
            6. 12.4.4.4.10.6 Extended Message ID Filter Element
    5. 12.5  Audio Interfaces
      1. 12.5.1 Audio Tracking Logic (ATL)
        1. 12.5.1.1 ATL Overview
          1. 12.5.1.1.1 ATL Features Overview
          2. 12.5.1.1.2 ATL Not Supported Features
      2. 12.5.2 Multichannel Audio Serial Port (MCASP)
        1. 12.5.2.1 MCASP Overview
          1. 12.5.2.1.1 MCASP Features
          2. 12.5.2.1.2 MCASP Not Supported Features
        2. 12.5.2.2 MCASP Environment
          1. 12.5.2.2.1 MCASP Signals
          2. 12.5.2.2.2 MCASP Protocols and Data Formats
            1. 12.5.2.2.2.1 Protocols Supported
            2. 12.5.2.2.2.2 Definition of Terms
            3. 12.5.2.2.2.3 TDM Format
            4. 12.5.2.2.2.4 I2S Format
            5. 12.5.2.2.2.5 S/PDIF Coding Format
              1. 12.5.2.2.2.5.1 Biphase-Mark Code
              2. 12.5.2.2.2.5.2 S/PDIF Subframe Format
              3. 12.5.2.2.2.5.3 Frame Format
        3. 12.5.2.3 MCASP Integration
          1. 12.5.2.3.1 MCASP Integration in MAIN Domain
        4. 12.5.2.4 MCASP Functional Description
          1. 12.5.2.4.1  MCASP Block Diagram
          2. 12.5.2.4.2  MCASP Clock and Frame-Sync Configurations
            1. 12.5.2.4.2.1 MCASP Transmit Clock
            2. 12.5.2.4.2.2 MCASP Receive Clock
            3. 12.5.2.4.2.3 Frame-Sync Generator
            4. 12.5.2.4.2.4 Synchronous and Asynchronous Transmit and Receive Operations
          3. 12.5.2.4.3  MCASP Frame Sync Feedback for Cross Synchronization
          4. 12.5.2.4.4  MCASP Serializers
          5. 12.5.2.4.5  MCASP Format Units
            1. 12.5.2.4.5.1 Transmit Format Unit
              1. 12.5.2.4.5.1.1 TDM Mode Transmission Data Alignment Settings
              2. 12.5.2.4.5.1.2 DIT Mode Transmission Data Alignment Settings
            2. 12.5.2.4.5.2 Receive Format Unit
              1. 12.5.2.4.5.2.1 TDM Mode Reception Data Alignment Settings
          6. 12.5.2.4.6  MCASP State-Machines
          7. 12.5.2.4.7  MCASP TDM Sequencers
          8. 12.5.2.4.8  MCASP Software Reset
          9. 12.5.2.4.9  MCASP Power Management
          10. 12.5.2.4.10 MCASP Transfer Modes
            1. 12.5.2.4.10.1 Burst Transfer Mode
            2. 12.5.2.4.10.2 Time-Division Multiplexed (TDM) Transfer Mode
              1. 12.5.2.4.10.2.1 TDM Time Slots Generation and Processing
              2. 12.5.2.4.10.2.2 Special 384-Slot TDM Mode for Connection to External DIR
            3. 12.5.2.4.10.3 DIT Transfer Mode
              1. 12.5.2.4.10.3.1 Transmit DIT Encoding
              2. 12.5.2.4.10.3.2 Transmit DIT Clock and Frame-Sync Generation
              3. 12.5.2.4.10.3.3 DIT Channel Status and User Data Register Files
          11. 12.5.2.4.11 MCASP Data Transmission and Reception
            1. 12.5.2.4.11.1 Data Ready Status and Event/Interrupt Generation
              1. 12.5.2.4.11.1.1 Transmit Data Ready
              2. 12.5.2.4.11.1.2 Receive Data Ready
              3. 12.5.2.4.11.1.3 Transfers Through the Data Port (DATA)
              4. 12.5.2.4.11.1.4 Transfers Through the Configuration Bus (CFG)
              5. 12.5.2.4.11.1.5 Using a Device CPU for MCASP Servicing
              6. 12.5.2.4.11.1.6 Using the DMA for MCASP Servicing
          12. 12.5.2.4.12 MCASP Audio FIFO (AFIFO)
            1. 12.5.2.4.12.1 AFIFO Data Transmission
              1. 12.5.2.4.12.1.1 Transmit DMA Event Pacer
            2. 12.5.2.4.12.2 AFIFO Data Reception
              1. 12.5.2.4.12.2.1 Receive DMA Event Pacer
            3. 12.5.2.4.12.3 Arbitration Between Transmit and Receive DMA Requests
          13. 12.5.2.4.13 MCASP Events and Interrupt Requests
            1. 12.5.2.4.13.1 Transmit Data Ready Event and Interrupt
            2. 12.5.2.4.13.2 Receive Data Ready Event and Interrupt
            3. 12.5.2.4.13.3 Error Interrupt
            4. 12.5.2.4.13.4 Multiple Interrupts
          14. 12.5.2.4.14 MCASP DMA Requests
          15. 12.5.2.4.15 MCASP Loopback Modes
            1. 12.5.2.4.15.1 Loopback Mode Configurations
          16. 12.5.2.4.16 MCASP Error Reporting
            1. 12.5.2.4.16.1 Buffer Underrun Error -Transmitter
            2. 12.5.2.4.16.2 Buffer Overrun Error-Receiver
            3. 12.5.2.4.16.3 DATA Port Error - Transmitter
            4. 12.5.2.4.16.4 DATA Port Error - Receiver
            5. 12.5.2.4.16.5 Unexpected Frame Sync Error
            6. 12.5.2.4.16.6 Clock Failure Detection
              1. 12.5.2.4.16.6.1 Clock Failure Check Startup
              2. 12.5.2.4.16.6.2 Transmit Clock Failure Check and Recovery
              3. 12.5.2.4.16.6.3 Receive Clock Failure Check and Recovery
        5. 12.5.2.5 MCASP Programming Guide
          1. 12.5.2.5.1 MCASP Global Initialization
            1. 12.5.2.5.1.1 Surrounding Modules Global Initialization
            2. 12.5.2.5.1.2 MCASP Global Initialization
              1. 12.5.2.5.1.2.1 Main Sequence – MCASP Global Initialization for DIT-Transmission
                1. 12.5.2.5.1.2.1.1 Subsequence – Transmit Format Unit Configuration for DIT-Transmission
                2. 12.5.2.5.1.2.1.2 Subsequence – Transmit Frame Synchronization Generator Configuration for DIT-Transmission
                3. 12.5.2.5.1.2.1.3 Subsequence – Transmit Clock Generator Configuration for DIT-Transmission
                4. 12.5.2.5.1.2.1.4 Subsequence - MCASP Pins Functional Configuration
                5. 12.5.2.5.1.2.1.5 Subsequence – DIT-specific Subframe Fields Configuration
              2. 12.5.2.5.1.2.2 Main Sequence – MCASP Global Initialization for TDM-Reception
                1. 12.5.2.5.1.2.2.1 Subsequence – Receive Format Unit Configuration in TDM Mode
                2. 12.5.2.5.1.2.2.2 Subsequence – Receive Frame Synchronization Generator Configuration in TDM Mode
                3. 12.5.2.5.1.2.2.3 Subsequence – Receive Clock Generator Configuration
                4. 12.5.2.5.1.2.2.4 Subsequence—MCASP Receiver Pins Functional Configuration
              3. 12.5.2.5.1.2.3 Main Sequence – MCASP Global Initialization for TDM -Transmission
                1. 12.5.2.5.1.2.3.1 Subsequence – Transmit Format Unit Configuration in TDM Mode
                2. 12.5.2.5.1.2.3.2 Subsequence – Transmit Frame Synchronization Generator Configuration in TDM Mode
                3. 12.5.2.5.1.2.3.3 Subsequence – Transmit Clock Generator Configuration for TDM Cases
                4. 12.5.2.5.1.2.3.4 Subsequence—MCASP Transmit Pins Functional Configuration
          2. 12.5.2.5.2 MCASP Operational Modes Configuration
            1. 12.5.2.5.2.1 MCASP Transmission Modes
              1. 12.5.2.5.2.1.1 Main Sequence – MCASP DIT- /TDM- Polling Transmission Method
              2. 12.5.2.5.2.1.2 Main Sequence – MCASP DIT- /TDM - Interrupt Transmission Method
              3. 12.5.2.5.2.1.3 Main Sequence –MCASP DIT- /TDM - Mode DMA Transmission Method
            2. 12.5.2.5.2.2 MCASP Reception Modes
              1. 12.5.2.5.2.2.1 Main Sequence – MCASP Polling Reception Method
              2. 12.5.2.5.2.2.2 Main Sequence – MCASP TDM - Interrupt Reception Method
              3. 12.5.2.5.2.2.3 Main Sequence – MCASP TDM - Mode DMA Reception Method
            3. 12.5.2.5.2.3 MCASP Event Servicing
              1. 12.5.2.5.2.3.1 MCASP DIT-/TDM- Transmit Interrupt Events Servicing
              2. 12.5.2.5.2.3.2 MCASP TDM- Receive Interrupt Events Servicing
              3. 12.5.2.5.2.3.3 Subsequence – MCASP DIT-/TDM -Modes Transmit Error Handling
              4. 12.5.2.5.2.3.4 Subsequence – MCASP Receive Error Handling
    6. 12.6  Display Subsystem (DSS) and Peripherals
      1. 12.6.1 DSS Overview
        1. 12.6.1.1 DSS Features
        2. 12.6.1.2 DSS Not Supported Features
      2. 12.6.2 DSS Environment
        1. 12.6.2.1 DISPC Environment
          1. 12.6.2.1.1 RGB Data Output
          2. 12.6.2.1.2 YUV Data Output (BT.656/BT.1120)
          3. 12.6.2.1.3 Display Timing Diagrams
          4. 12.6.2.1.4 VSYNC/HSYNC/DE Signal Export to SoC Boundary
        2. 12.6.2.2 DSI Environment
        3. 12.6.2.3 EDP Environment
      3. 12.6.3 DSS Integration
        1. 12.6.3.1 DISPC Integration
        2. 12.6.3.2 DSI Integration
        3. 12.6.3.3 EDP Integration
      4. 12.6.4 Display Subsystem Controller (DISPC) with Frame Buffer Decompression Core (FBDC)
        1. 12.6.4.1  DISPC Overview
        2. 12.6.4.2  DISPC Clocks
        3. 12.6.4.3  DISPC Resets
        4. 12.6.4.4  DISPC Power Management
        5. 12.6.4.5  DISPC Interrupt Requests
        6. 12.6.4.6  DISPC DMA Controller
          1. 12.6.4.6.1  DISPC DMA Addressing and Bursts
          2. 12.6.4.6.2  DISPC Read DMA Buffers
          3. 12.6.4.6.3  DISPC Write DMA Buffer
          4. 12.6.4.6.4  DISPC Flip/Mirror Support
          5. 12.6.4.6.5  DISPC DMA Predecimation
          6. 12.6.4.6.6  DISPC DMA Buffer Sharing
          7. 12.6.4.6.7  DISPC DMA MFLAG Mechanism
          8. 12.6.4.6.8  DISPC DMA Priority Requests Control
          9. 12.6.4.6.9  DISPC DMA Arbitration
          10. 12.6.4.6.10 DISPC DMA Ultra-Low Power Mode
          11. 12.6.4.6.11 DISPC Compressed Data Format Support
            1. 12.6.4.6.11.1 FBDC Tile Request
            2. 12.6.4.6.11.2 FBDC Source Cropping
        7. 12.6.4.7  DISPC Pixel Data Formats
        8. 12.6.4.8  DISPC Video Pipeline
          1. 12.6.4.8.1 DISPC VID Replication Logic
          2. 12.6.4.8.2 DISPC VID VC-1 Range Mapping Unit
          3. 12.6.4.8.3 DISPC VID Color Look-Up Table (CLUT)
          4. 12.6.4.8.4 DISPC VID Chrominance Resampling
            1. 12.6.4.8.4.1 Chrominance Resampling for VID Pipeline
            2. 12.6.4.8.4.2 Chrominance Resampling for VIDL Pipeline
          5. 12.6.4.8.5 DISPC VID Scaler Unit
          6. 12.6.4.8.6 DISPC VID Color Space Conversion YUV to RGB
          7. 12.6.4.8.7 DISPC VID Brightness/Contrast/Saturation/Hue Control
          8. 12.6.4.8.8 DISPC VID Luma Key Support
          9. 12.6.4.8.9 DISPC VID Cropping Support
        9. 12.6.4.9  DISPC Write-Back Pipeline
          1. 12.6.4.9.1 DISPC WB Color Space Conversion RGB to YUV
          2. 12.6.4.9.2 DISPC WB Scaler Unit
        10. 12.6.4.10 DISPC Overlay Manager
          1. 12.6.4.10.1 DISPC Overlay Input Selector
          2. 12.6.4.10.2 DISPC Overlay Mechanism
            1. 12.6.4.10.2.1 Overlay Alpha Blender
            2. 12.6.4.10.2.2 Overlay Transparency Color Keys
          3. 12.6.4.10.3 Overlay 3D Support
          4. 12.6.4.10.4 Overlay Color Bar Insertion
        11. 12.6.4.11 DISPC Video Port Output
          1. 12.6.4.11.1  DISPC VP Gamma Correction Unit
          2. 12.6.4.11.2  DISPC VP Color Phase Rotation Unit
          3. 12.6.4.11.3  DISPC VP Color Space Conversion - RGB to YUV
          4. 12.6.4.11.4  DISPC VP BT.656 and BT.1120 Modes
            1. 12.6.4.11.4.1 DISPC BT Mode Blanking
            2. 12.6.4.11.4.2 DISPC BT Mode EAV and SAV
          5. 12.6.4.11.5  DISPC VP Spatial/Temporal Dithering
          6. 12.6.4.11.6  DISPC VP Multiple Cycle Output Format (TDM)
          7. 12.6.4.11.7  DISPC VP Stall Mode
          8. 12.6.4.11.8  DISPC VP Timing Generator and Display Panel Settings
          9. 12.6.4.11.9  DISPC VP Merge-Split-Sync (MSS) Module
            1. 12.6.4.11.9.1 MSS Clocking Scheme
            2. 12.6.4.11.9.2 MSS Merge with Scaling
          10. 12.6.4.11.10 DISPC Internal Diagnostic Features
            1. 12.6.4.11.10.1 Internal Diagnostic Check Regions
            2. 12.6.4.11.10.2 Internal Diagnostic Signature Generator Using MISR
            3. 12.6.4.11.10.3 Internal Diagnostic Checks
            4. 12.6.4.11.10.4 Internal Diagnostic Check Limitations
          11. 12.6.4.11.11 DISPC Security Management
            1. 12.6.4.11.11.1 Security Implementation
            2. 12.6.4.11.11.2 Secure Mode Configuration
          12. 12.6.4.11.12 DISPC Shadow Mechanism for Registers
          13. 12.6.4.11.13 DISPC Registers
            1. 12.6.4.11.13.1 DSS_COMMON Registers
            2. 12.6.4.11.13.2 DSS_VID Registers
            3. 12.6.4.11.13.3 DSS_OVR Registers
            4. 12.6.4.11.13.4 DSS_VP Registers
            5. 12.6.4.11.13.5 DSS_WB Registers
      5. 12.6.5 MIPI Display Serial Interface (DSI) Controller
        1. 12.6.5.1 DSI Block Diagram
        2. 12.6.5.2 DSI Clocking
        3. 12.6.5.3 DSI Reset
        4. 12.6.5.4 DSI Power Management
        5. 12.6.5.5 DSI Interrupts
        6. 12.6.5.6 DSI Internal Interfaces
          1. 12.6.5.6.1 Video Input Interfaces
            1. 12.6.5.6.1.1 Pixel Mapping
          2. 12.6.5.6.2 DPI (Pixel Stream Interface)
            1. 12.6.5.6.2.1 Signals
          3. 12.6.5.6.3 SDI (Serial Data Interface)
            1. 12.6.5.6.3.1 Secure Display Support
        7. 12.6.5.7 DSI Programming Guide
          1. 12.6.5.7.1  Application Guidelines
            1. 12.6.5.7.1.1 Overview of a Display Subsystem
            2. 12.6.5.7.1.2 D-PHY And DSI Configuration
            3. 12.6.5.7.1.3 DSI Controller Initialization
            4. 12.6.5.7.1.4 Panel Configuration Using Command Mode
            5. 12.6.5.7.1.5 VIDEO Interface Configuration
          2. 12.6.5.7.2  Application Considerations
            1. 12.6.5.7.2.1 D-PHY Timings Control
            2. 12.6.5.7.2.2 Control Block
            3. 12.6.5.7.2.3 Video Coherency
          3. 12.6.5.7.3  Start-up Procedure
          4. 12.6.5.7.4  Interrupt Management
            1. 12.6.5.7.4.1 Error and Status Registers
            2. 12.6.5.7.4.2 Interrupt Management for Direct Command Registers
          5. 12.6.5.7.5  Direct Command Usage
            1. 12.6.5.7.5.1 Trigger Mapping Information
            2. 12.6.5.7.5.2 Command Mode Settings
            3. 12.6.5.7.5.3 Bus Turnaround Sequence
            4. 12.6.5.7.5.4 Tearing Effect Control
            5. 12.6.5.7.5.5 Tearing Effect Control on Panels with Frame Buffer
            6. 12.6.5.7.5.6 Return Path Operation
            7. 12.6.5.7.5.7 EoT Packet Management
            8. 12.6.5.7.5.8 ECC Correction
            9. 12.6.5.7.5.9 LP Transmission and BTA
          6. 12.6.5.7.6  Low-power Management
          7. 12.6.5.7.7  Video Mode Settings
            1. 12.6.5.7.7.1 Video Stream Presentation
            2. 12.6.5.7.7.2 Video Stream Settings (VSG)
            3. 12.6.5.7.7.3 VCA Configuration
            4. 12.6.5.7.7.4 TVG Configuration
          8. 12.6.5.7.8  DPI To DSI Programming
            1. 12.6.5.7.8.1 DSI and DPHY Operation
            2. 12.6.5.7.8.2 Pixel Clock to TX_BYTE_CLK Variation
            3. 12.6.5.7.8.3 LP Operation
            4. 12.6.5.7.8.4 DPI Interface Burst Operation
          9. 12.6.5.7.9  Programming the DSITX Controller to Match the Incoming DPI Stream
            1. 12.6.5.7.9.1 Vertical Timing
            2. 12.6.5.7.9.2 Horizontal Timing for Non-Burst Mode with Sync Pulses
            3. 12.6.5.7.9.3 Event Mode Horizontal Timing
            4. 12.6.5.7.9.4 Burst Event Mode Horizontal Timing
            5. 12.6.5.7.9.5 Burst Mode Operation
            6. 12.6.5.7.9.6 Example Configurations
            7. 12.6.5.7.9.7 Stereoscopic Video Support
          10. 12.6.5.7.10 DSITX Video Stream Variable Refresh
      6. 12.6.6 Embedded DisplayPort (еDP) Transmitter
        1. 12.6.6.1 EDP Block Diagram
        2. 12.6.6.2 EDP Wrapper Functions
          1. 12.6.6.2.1 Video Stream Clock/Data Muxing
          2. 12.6.6.2.2 Secure Video Content Protection
          3. 12.6.6.2.3 DPI_DATA Input Pixel Format Supported
          4. 12.6.6.2.4 Audio Input Interface
            1. 12.6.6.2.4.1 Audio I2S Signals/Timing
            2. 12.6.6.2.4.2 Audio I2S Clock Frequency
        3. 12.6.6.3 EDP Transmitter Controller Subsystem (MHDPTX_TOP)
          1. 12.6.6.3.1 Display Stream Compression Encoder (DSC)
            1. 12.6.6.3.1.1 DSC Encoder Features
            2. 12.6.6.3.1.2 Usage Models for EDP
          2. 12.6.6.3.2 Display Port Transmitter Controller (MHDPTX Controller)
            1. 12.6.6.3.2.1 EDP Transmitter Controller Mode Configurations
        4. 12.6.6.4 EDP AUX_PHY Interface
        5. 12.6.6.5 EDP Clocks
          1. 12.6.6.5.1 Clock Diagram
            1. 12.6.6.5.1.1 DPI Interface Clock Sourcing
            2. 12.6.6.5.1.2 Memory Clock Gating
            3. 12.6.6.5.1.3 PHY Clock Connections
          2. 12.6.6.5.2 Clock Groups
        6. 12.6.6.6 EDP Resets
        7. 12.6.6.7 EDP Interrupt Requests
          1. 12.6.6.7.1 EDP_INTR Interrupt Description
          2. 12.6.6.7.2 EDP_INTR_ASF Interrupt Description
        8. 12.6.6.8 EDP Embedded Memories
          1. 12.6.6.8.1 MHDPTX Controller Memories
          2. 12.6.6.8.2 DSC Memories
          3. 12.6.6.8.3 ECC Aggregation
        9. 12.6.6.9 EDP Programmer's Guide
          1. 12.6.6.9.1 EDP Controller Programming
            1. 12.6.6.9.1.1  MHDPTX Register/Memory Regions
            2. 12.6.6.9.1.2  Boot Sequence
            3. 12.6.6.9.1.3  Setting Core Clock Frequency
            4. 12.6.6.9.1.4  Loading Firmware
            5. 12.6.6.9.1.5  FW Running indication
            6. 12.6.6.9.1.6  Software Events Handling
            7. 12.6.6.9.1.7  DisplayPort Source (TX) Sequence
            8. 12.6.6.9.1.8  HDCP
              1. 12.6.6.9.1.8.1 Embedded HDCP Crypto
              2. 12.6.6.9.1.8.2 Additional Security Features
                1. 12.6.6.9.1.8.2.1 KM-Key Encryption
                2. 12.6.6.9.1.8.2.2 Cyphertext Stealing
            9. 12.6.6.9.1.9  HD Display TX Controller
              1. 12.6.6.9.1.9.1 Info-Frame Handling
                1. 12.6.6.9.1.9.1.1 EDID Handling
                2. 12.6.6.9.1.9.1.2 Audio Control
                3. 12.6.6.9.1.9.1.3 Video Control
            10. 12.6.6.9.1.10 DPTX TX Controller
              1. 12.6.6.9.1.10.1 Protocol over Auxiliary
              2. 12.6.6.9.1.10.2 PHY (Physical layer) Handling
          2. 12.6.6.9.2 EDP PHY Wrapper Initialization
          3. 12.6.6.9.3 EDP PHY Programming
    7. 12.7  Camera Subsystem
      1. 12.7.1 Camera Streaming Interface Receiver (CSI_RX_IF)
        1. 12.7.1.1 CSI_RX_IF Overview
          1. 12.7.1.1.1 CSI_RX_IF Features
          2. 12.7.1.1.2 CSI_RX_IF Not Supported Features
        2. 12.7.1.2 CSI_RX_IF Environment
        3. 12.7.1.3 CSI_RX_IF Integration
          1. 12.7.1.3.1 CSI_RX_IF Integration in MAIN Domain
        4. 12.7.1.4 CSI_RX_IF Functional Description
          1. 12.7.1.4.1 CSI_RX_IF Block Diagram
          2. 12.7.1.4.2 CSI_RX_IF Hardware and Software Reset
          3. 12.7.1.4.3 CSI_RX_IF Clock Configuration
          4. 12.7.1.4.4 CSI_RX_IF Interrupt Events
          5. 12.7.1.4.5 CSI_RX_IF Data Memory Organization Details
          6. 12.7.1.4.6 CSI_RX_IF PSI_L (DMA) Interface
            1. 12.7.1.4.6.1 PSI_L DMA framing
            2. 12.7.1.4.6.2 PSI_L DMA error handling due to FIFO overflow
          7. 12.7.1.4.7 CSI_RX_IF ECC Protection Support
          8. 12.7.1.4.8 CSI_RX_IF Programming Guide
            1. 12.7.1.4.8.1  Overview
            2. 12.7.1.4.8.2  Controller Configuration
            3. 12.7.1.4.8.3  Power on Configuration
            4. 12.7.1.4.8.4  Stream Start and Stop
            5. 12.7.1.4.8.5  Error Control With Soft Resets
            6. 12.7.1.4.8.6  Stream Error Detected – No Error Bypass Mode
            7. 12.7.1.4.8.7  Stream Error Detected – Error Bypass Mode
            8. 12.7.1.4.8.8  Stream Error Detected – Soft Reset Recovery
            9. 12.7.1.4.8.9  Stream Monitor Configuration
            10. 12.7.1.4.8.10 Stream Monitor Frame Capture Control
            11. 12.7.1.4.8.11 Stream Monitor Timer interrupt
            12. 12.7.1.4.8.12 Stream Monitor Line/Byte Counters Interrupt
            13. 12.7.1.4.8.13 Example Controller Programming Sequence (Single Stream Operation)
            14. 12.7.1.4.8.14 CSI_RX_IF Programming Restrictions
            15. 12.7.1.4.8.15 CSI_RX_IF Real-time operating requirements
      2. 12.7.2 MIPI D-PHY Receiver (DPHY_RX)
        1. 12.7.2.1 DPHY_RX Overview
          1. 12.7.2.1.1 DPHY_RX Features
          2. 12.7.2.1.2 DPHY_RX Not Supported Features
        2. 12.7.2.2 DPHY_RX Environment
        3. 12.7.2.3 DPHY_RX Integration
          1. 12.7.2.3.1 DPHY_RX Integration in MAIN Domain
        4. 12.7.2.4 DPHY_RX Functional Description
          1. 12.7.2.4.1 DPHY_RX Programming Guide
            1. 12.7.2.4.1.1 Overview
            2. 12.7.2.4.1.2 Initial Configuration Programming
              1. 12.7.2.4.1.2.1 Start-up Sequence Timing Diagram
            3. 12.7.2.4.1.3 Common Configuration
            4. 12.7.2.4.1.4 Lane Configuration
            5. 12.7.2.4.1.5 Procedure: Clock Lane Low Power Analog Receiver Functions Test
              1. 12.7.2.4.1.5.1 Description of Procedure
              2. 12.7.2.4.1.5.2 Details of the Procedure
            6. 12.7.2.4.1.6 Procedure: Data Lane Low Power Analog Receiver Functions Test
              1. 12.7.2.4.1.6.1 Description of Procedure
              2. 12.7.2.4.1.6.2 Details of the Procedure
            7. 12.7.2.4.1.7 Procedure: Clock and Data Lane High Speed Receiver BIST Functions Test
              1. 12.7.2.4.1.7.1 Description of Procedure
              2. 12.7.2.4.1.7.2 Details of the Procedure
      3. 12.7.3 Camera Streaming Interface Transmitter (CSI_TX_IF)
        1. 12.7.3.1 CSI_TX_IF Overview
          1. 12.7.3.1.1 CSI_TX_IF Features
          2. 12.7.3.1.2 CSI_TX_IF Not Supported Features
        2. 12.7.3.2 CSI_TX_IF Environment
        3. 12.7.3.3 CSI_TX_IF Integration
          1. 12.7.3.3.1 CSI_TX_IF Integration in MAIN Domain
        4. 12.7.3.4 CSI_TX_IF Functional Description
          1. 12.7.3.4.1 CSI_TX_IF Block Diagram
          2. 12.7.3.4.2 CSI_TX_IF Hardware and Software Reset
          3. 12.7.3.4.3 CSI_TX_IF Clock Configuration
          4. 12.7.3.4.4 CSI_TX_IF Interrupt Events
          5. 12.7.3.4.5 CSI_TX_IF Data Memory Organization Details
          6. 12.7.3.4.6 CSI_TX_IF PSI_L (DMA) Interface
          7. 12.7.3.4.7 CSI_TX_IF ECC Protection Support
        5. 12.7.3.5 CSI_TX_IF Programming Guide
          1. 12.7.3.5.1  Programming (Configuration Mode)
          2. 12.7.3.5.2  System Initialization Programming
          3. 12.7.3.5.3  Lane Control Programming
          4. 12.7.3.5.4  Line Control
          5. 12.7.3.5.5  Line Control Arbitration
          6. 12.7.3.5.6  Lane Manager FSM
          7. 12.7.3.5.7  Data Lane Control FSM
          8. 12.7.3.5.8  Clock Lane Control
          9. 12.7.3.5.9  Clock Lane Control FSMs
          10. 12.7.3.5.10 CSI_TX_IF Configuration for PSI_L
          11. 12.7.3.5.11 CSI_TX_IF Configuration for Re-transmit
          12. 12.7.3.5.12 CSI_TX_IF Configuration for Color Bar
          13. 12.7.3.5.13 CSI_TX_IF Error Recovery
          14. 12.7.3.5.14 CSI_TX_IF Power Up/Down Sequence
    8. 12.8  Shared MIPI D-PHY Transmitter (DPHY_TX)
      1. 12.8.1 DPHY_TX Subsystem Overview
        1. 12.8.1.1 DPHY_TX Features
      2. 12.8.2 DPHY_TX Environment
      3. 12.8.3 DPHY_TX Integration
    9. 12.9  Video Processing Front End (VPFE)
      1. 12.9.1 VPFE Overview
        1. 12.9.1.1 VPFE Features
        2. 12.9.1.2 VPFE Not Supported Features
      2. 12.9.2 VPFE Environment
        1. 12.9.2.1 VPFE External System Interface
      3. 12.9.3 VPFE Integration
        1. 12.9.3.1 VPFE Integration in MAIN Domain
      4. 12.9.4 VPFE Functional Description
        1. 12.9.4.1 VPFE Block Diagram
          1. 12.9.4.1.1 CCD Controller (CCDC)
          2. 12.9.4.1.2 Shared Buffer Logic (SBL)
          3. 12.9.4.1.3 Region-based Address Translation
        2. 12.9.4.2 VPFE Power Management
        3. 12.9.4.3 VPFE Interrupts
        4. 12.9.4.4 VPFE Register Configuration
          1. 12.9.4.4.1 General Register Setup
          2. 12.9.4.4.2 Status
          3. 12.9.4.4.3 CCDC_VD Latched Registers
            1. 12.9.4.4.3.1 Inter-Frame Operations
        5. 12.9.4.5 VPFE Limitations
        6. 12.9.4.6 VPFE Interfaces
          1. 12.9.4.6.1 Interfaces Summary
          2. 12.9.4.6.2 Timing Generator and Frame Settings
          3. 12.9.4.6.3 ITU-R BT.656 Interface
          4. 12.9.4.6.4 Digital YCbCr Interface
        7. 12.9.4.7 VPFE Data / Image Processing
          1. 12.9.4.7.1 Raw Data Mode
            1. 12.9.4.7.1.1 Input Sampling and Formatting for Raw Data Mode
            2. 12.9.4.7.1.2 Optical Black Clamping for Raw Data Mode
            3. 12.9.4.7.1.3 Black Level Compensation
            4. 12.9.4.7.1.4 Output Formatter for Raw Data Mode
              1. 12.9.4.7.1.4.1 Low Pass Filter (LPF)
              2. 12.9.4.7.1.4.2 Culling
              3. 12.9.4.7.1.4.3 A-Law Transformation
              4. 12.9.4.7.1.4.4 Line Output Control
              5. 12.9.4.7.1.4.5 Output Format in External Memory for Raw Data Mode
          2. 12.9.4.7.2 YCbCr and BT.656 Modes
            1. 12.9.4.7.2.1 Input Sampling and Formatting for YCbCr and BT.656 Modes
            2. 12.9.4.7.2.2 Black Clamping for YCbCr and BT.656 Modes
            3. 12.9.4.7.2.3 Output Formatter for YCbCr and BT.656 Modes
              1. 12.9.4.7.2.3.1 Output Format in External Memory for YCbCr and BT.656 Modes
    10. 12.10 Timer Modules
      1. 12.10.1 Global Timebase Counter (GTC)
        1. 12.10.1.1 GTC Overview
          1. 12.10.1.1.1 GTC Features
          2. 12.10.1.1.2 GTC Not Supported Features
        2. 12.10.1.2 GTC Integration
        3. 12.10.1.3 GTC Functional Description
          1. 12.10.1.3.1 GTC Block Diagram
          2. 12.10.1.3.2 GTC Counter
          3. 12.10.1.3.3 GTC Gray Encoder
          4. 12.10.1.3.4 GTC Push Event Generation
          5. 12.10.1.3.5 GTC Register Partitioning
      2. 12.10.2 Windowed Watchdog Timer (WWDT)
        1. 12.10.2.1 RTI Overview
          1. 12.10.2.1.1 RTI Features
          2. 12.10.2.1.2 RTI Not Supported Features
        2. 12.10.2.2 RTI Integration
          1. 12.10.2.2.1 RTI Integration in MCU Domain
          2. 12.10.2.2.2 RTI Integration in MAIN Domain
        3. 12.10.2.3 RTI Functional Description
          1. 12.10.2.3.1 RTI Counter Operation
          2. 12.10.2.3.2 RTI Digital Watchdog
          3. 12.10.2.3.3 RTI Digital Windowed Watchdog
          4. 12.10.2.3.4 RTI Low Power Mode Operation
          5. 12.10.2.3.5 RTI Debug Mode Behavior
      3. 12.10.3 Timers
        1. 12.10.3.1 Timers Overview
          1. 12.10.3.1.1 Timers Features
          2. 12.10.3.1.2 Timers Not Supported Features
        2. 12.10.3.2 Timers Environment
          1. 12.10.3.2.1 Timer External System Interface
        3. 12.10.3.3 Timers Integration
          1. 12.10.3.3.1 Timers Integration in MCU Domain
          2. 12.10.3.3.2 Timers Integration in MAIN Domain
        4. 12.10.3.4 Timers Functional Description
          1. 12.10.3.4.1  Timer Block Diagram
          2. 12.10.3.4.2  Timer Power Management
            1. 12.10.3.4.2.1 Wake-Up Capability
          3. 12.10.3.4.3  Timer Software Reset
          4. 12.10.3.4.4  Timer Interrupts
          5. 12.10.3.4.5  Timer Mode Functionality
            1. 12.10.3.4.5.1 1-ms Tick Generation
          6. 12.10.3.4.6  Timer Capture Mode Functionality
          7. 12.10.3.4.7  Timer Compare Mode Functionality
          8. 12.10.3.4.8  Timer Prescaler Functionality
          9. 12.10.3.4.9  Timer Pulse-Width Modulation
          10. 12.10.3.4.10 Timer Counting Rate
          11. 12.10.3.4.11 Timer Under Emulation
          12. 12.10.3.4.12 Accessing Timer Registers
            1. 12.10.3.4.12.1 Writing to Timer Registers
              1. 12.10.3.4.12.1.1 Write Posting Synchronization Mode
              2. 12.10.3.4.12.1.2 Write Nonposting Synchronization Mode
            2. 12.10.3.4.12.2 Reading From Timer Counter Registers
              1. 12.10.3.4.12.2.1 Read Posted
              2. 12.10.3.4.12.2.2 Read Non-Posted
          13. 12.10.3.4.13 Timer Posted Mode Selection
        5. 12.10.3.5 Timers Low-Level Programming Models
          1. 12.10.3.5.1 Timer Global Initialization
            1. 12.10.3.5.1.1 Global Initialization of Surrounding Modules
            2. 12.10.3.5.1.2 Timer Module Global Initialization
              1. 12.10.3.5.1.2.1 Main Sequence – Timer Module Global Initialization
          2. 12.10.3.5.2 Timer Operational Mode Configuration
            1. 12.10.3.5.2.1 Timer Mode
              1. 12.10.3.5.2.1.1 Main Sequence – Timer Mode Configuration
            2. 12.10.3.5.2.2 Timer Compare Mode
              1. 12.10.3.5.2.2.1 Main Sequence – Timer Compare Mode Configuration
            3. 12.10.3.5.2.3 Timer Capture Mode
              1. 12.10.3.5.2.3.1 Main Sequence – Timer Capture Mode Configuration
              2. 12.10.3.5.2.3.2 Subsequence – Initialize Capture Mode
              3. 12.10.3.5.2.3.3 Subsequence – Detect Event
            4. 12.10.3.5.2.4 Timer PWM Mode
              1. 12.10.3.5.2.4.1 Main Sequence – Timer PWM Mode Configuration
    11. 12.11 Internal Diagnostics Modules
      1. 12.11.1 Dual Clock Comparator (DCC)
        1. 12.11.1.1 DCC Overview
          1. 12.11.1.1.1 DCC Features
          2. 12.11.1.1.2 DCC Not Supported Features
        2. 12.11.1.2 DCC Integration
          1. 12.11.1.2.1 DCC Integration in MCU Domain
          2. 12.11.1.2.2 DCC Integration in MAIN Domain
        3. 12.11.1.3 DCC Functional Description
          1. 12.11.1.3.1 DCC Counter Operation
          2. 12.11.1.3.2 DCC Low Power Mode Operation
          3. 12.11.1.3.3 DCC Suspend Mode Behavior
          4. 12.11.1.3.4 DCC Single-Shot Mode
          5. 12.11.1.3.5 DCC Continuous mode
            1. 12.11.1.3.5.1 DCC Continue on Error
            2. 12.11.1.3.5.2 DCC Error Count
          6. 12.11.1.3.6 DCC Control and count hand-off across clock domains
          7. 12.11.1.3.7 DCC Error Trajectory record
            1. 12.11.1.3.7.1 DCC FIFO capturing for Errors
            2. 12.11.1.3.7.2 DCC FIFO in continuous capture mode
            3. 12.11.1.3.7.3 DCC FIFO Details
            4. 12.11.1.3.7.4 DCC FIFO Debug mode behavior
          8. 12.11.1.3.8 DCC Count read registers
        4. 12.11.1.4 DCC Registers
      2. 12.11.2 Error Signaling Module (ESM)
        1. 12.11.2.1 ESM Overview
          1. 12.11.2.1.1 ESM Features
        2. 12.11.2.2 ESM Environment
        3. 12.11.2.3 ESM Integration
          1. 12.11.2.3.1 ESM Integration in WKUP Domain
          2. 12.11.2.3.2 ESM Integration in MCU Domain
          3. 12.11.2.3.3 ESM Integration in MAIN Domain
        4. 12.11.2.4 ESM Functional Description
          1. 12.11.2.4.1 ESM Interrupt Requests
            1. 12.11.2.4.1.1 ESM Configuration Error Interrupt
            2. 12.11.2.4.1.2 ESM Low Priority Error Interrupt
              1. 12.11.2.4.1.2.1 ESM Low Priority Error Level Event
              2. 12.11.2.4.1.2.2 ESM Low Priority Error Pulse Event
            3. 12.11.2.4.1.3 ESM High Priority Error Interrupt
              1. 12.11.2.4.1.3.1 ESM High Priority Error Level Event
              2. 12.11.2.4.1.3.2 ESM High Priority Error Pulse Event
          2. 12.11.2.4.2 ESM Error Event Inputs
          3. 12.11.2.4.3 ESM Error Pin Output
          4. 12.11.2.4.4 ESM Minimum Time Interval
          5. 12.11.2.4.5 ESM Protection for Registers
          6. 12.11.2.4.6 ESM Clock Stop
      3. 12.11.3 Memory Cyclic Redundancy Check (MCRC) Controller
        1. 12.11.3.1 MCRC Overview
          1. 12.11.3.1.1 MCRC Features
          2. 12.11.3.1.2 MCRC Not Supported Features
        2. 12.11.3.2 MCRC Integration
        3. 12.11.3.3 MCRC Functional Description
          1. 12.11.3.3.1  MCRC Block Diagram
          2. 12.11.3.3.2  MCRC General Operation
          3. 12.11.3.3.3  MCRC Modes of Operation
            1. 12.11.3.3.3.1 AUTO Mode
            2. 12.11.3.3.3.2 Semi-CPU Mode
            3. 12.11.3.3.3.3 Full-CPU Mode
          4. 12.11.3.3.4  PSA Signature Register
          5. 12.11.3.3.5  PSA Sector Signature Register
          6. 12.11.3.3.6  CRC Value Register
          7. 12.11.3.3.7  Raw Data Register
          8. 12.11.3.3.8  Example DMA Controller Setup
            1. 12.11.3.3.8.1 AUTO Mode Using Hardware Timer Trigger
            2. 12.11.3.3.8.2 AUTO Mode Using Software Trigger
            3. 12.11.3.3.8.3 Semi-CPU Mode Using Hardware Timer Trigger
          9. 12.11.3.3.9  Pattern Count Register
          10. 12.11.3.3.10 Sector Count Register/Current Sector Register
          11. 12.11.3.3.11 Interrupts
            1. 12.11.3.3.11.1 Compression Complete Interrupt
            2. 12.11.3.3.11.2 CRC Fail Interrupt
            3. 12.11.3.3.11.3 Overrun Interrupt
            4. 12.11.3.3.11.4 Underrun Interrupt
            5. 12.11.3.3.11.5 Timeout Interrupt
            6. 12.11.3.3.11.6 Interrupt Offset Register
            7. 12.11.3.3.11.7 Error Handling
          12. 12.11.3.3.12 Power Down Mode
          13. 12.11.3.3.13 Emulation
        4. 12.11.3.4 MCRC Programming Examples
          1. 12.11.3.4.1 Example: Auto Mode Using Time Based Event Triggering
            1. 12.11.3.4.1.1 DMA Setup
            2. 12.11.3.4.1.2 Timer Setup
            3. 12.11.3.4.1.3 CRC Setup
          2. 12.11.3.4.2 Example: Auto Mode Without Using Time Based Triggering
            1. 12.11.3.4.2.1 DMA Setup
            2. 12.11.3.4.2.2 CRC Setup
          3. 12.11.3.4.3 Example: Semi-CPU Mode
            1. 12.11.3.4.3.1 DMA Setup
            2. 12.11.3.4.3.2 Timer Setup
            3. 12.11.3.4.3.3 CRC Setup
          4. 12.11.3.4.4 Example: Full-CPU Mode
            1. 12.11.3.4.4.1 CRC Setup
      4. 12.11.4 ECC Aggregator
        1. 12.11.4.1 ECC Aggregator Overview
          1. 12.11.4.1.1 ECC Aggregator Features
        2. 12.11.4.2 ECC Aggregator Integration
        3. 12.11.4.3 ECC Aggregator Functional Description
          1. 12.11.4.3.1 ECC Aggregator Block Diagram
          2. 12.11.4.3.2 ECC Aggregator Register Groups
          3. 12.11.4.3.3 Read Access to the ECC Control and Status Registers
          4. 12.11.4.3.4 Serial Write Operation
          5. 12.11.4.3.5 Interrupts
          6. 12.11.4.3.6 Inject Only Mode
  15. 13On-Chip Debug
    1. 13.1 Introduction to SoC Debug Framework
  16.   Revision History
6.9.6.2.2.2.1 Interpolation/Resampling

Figure 6-129 illustrates the interpolation principle. The assumptions are that the input pixels are evenly spaced. The distance between each input pixel is assumed to be 1. The magnification ratio is given by 64/N and p/64 is the initial phase of the output data. The output pixels are evenly spaced as well. The distance between each output pixel is given by N/64 (in the example below, N > 64). The position of the n-th output pixel is given by (n x N + p) / 64.

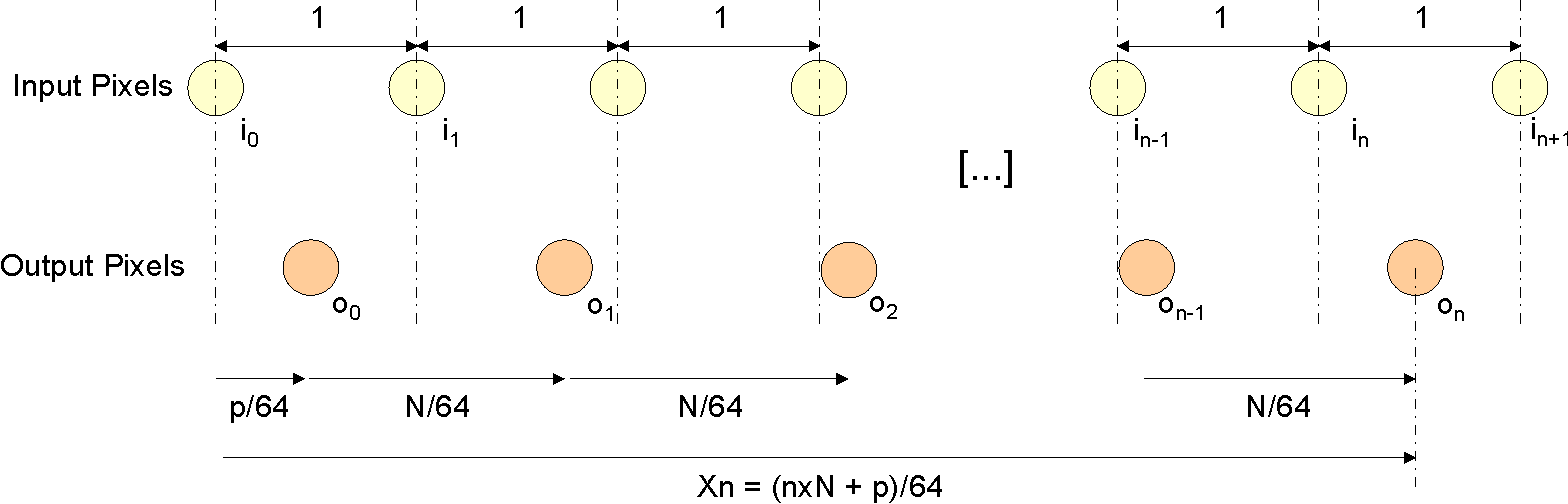Interpolation PrincipleFigure 6-129 Interpolation Principle

Figure 6-130 illustrates the interpolation principle at the n-th output pixel (on) at position xn. Interpolation method with m and d parameters, are described as:

m = floor((n x N + p) / 64)

d = ((n x N + p) / 64) - m

Figure 6-130 illustrates the concept when the filters are configured in 4-tap mode for non-integer rescaling (the first coefficient corresponding to Om-2 is set to zero).

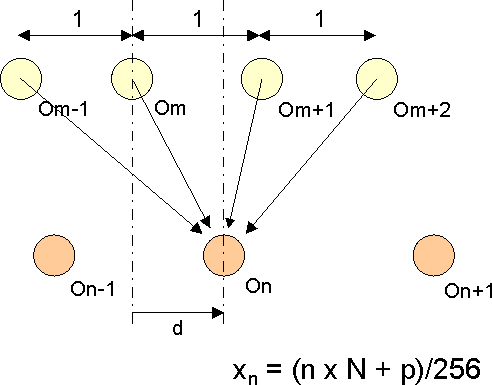Interpolation ProcessFigure 6-130 Interpolation Process

Figure 6-131 illustrates another explanation of the concept of a Polyphase filter using a simple 2-tap linear filter in a design which supports 5 phases.

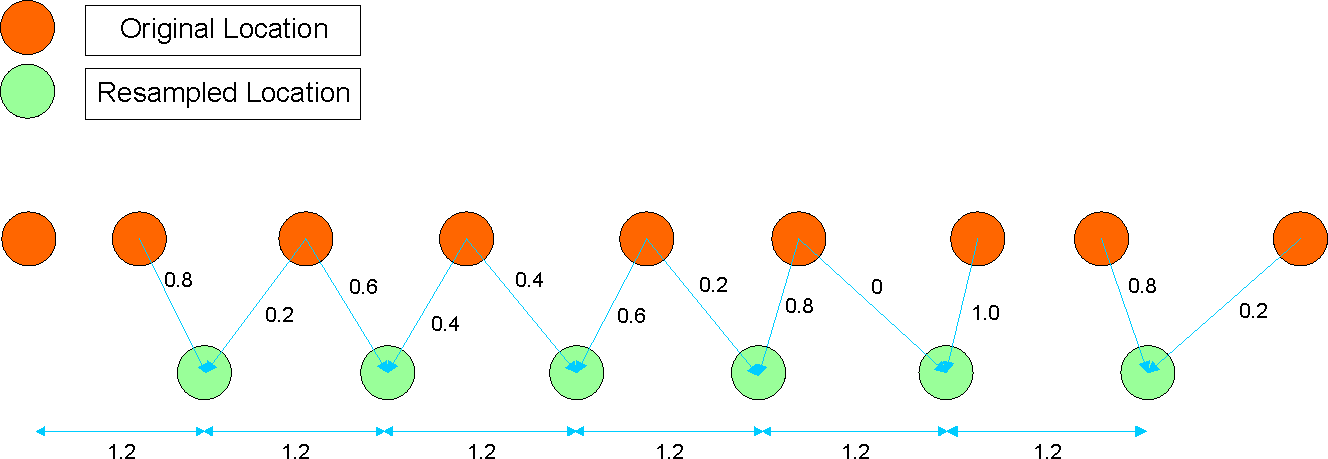Polyphase FilteringFigure 6-131 Polyphase Filtering

For each one of the 5 phases, the weights (or filter coefficients) are different and after the 5 phases the weights start repeating, see Figure 6-131.

Figure 6-132 depicts the architecture for the independent polyphase filter unit.

Polyphase Filter Unit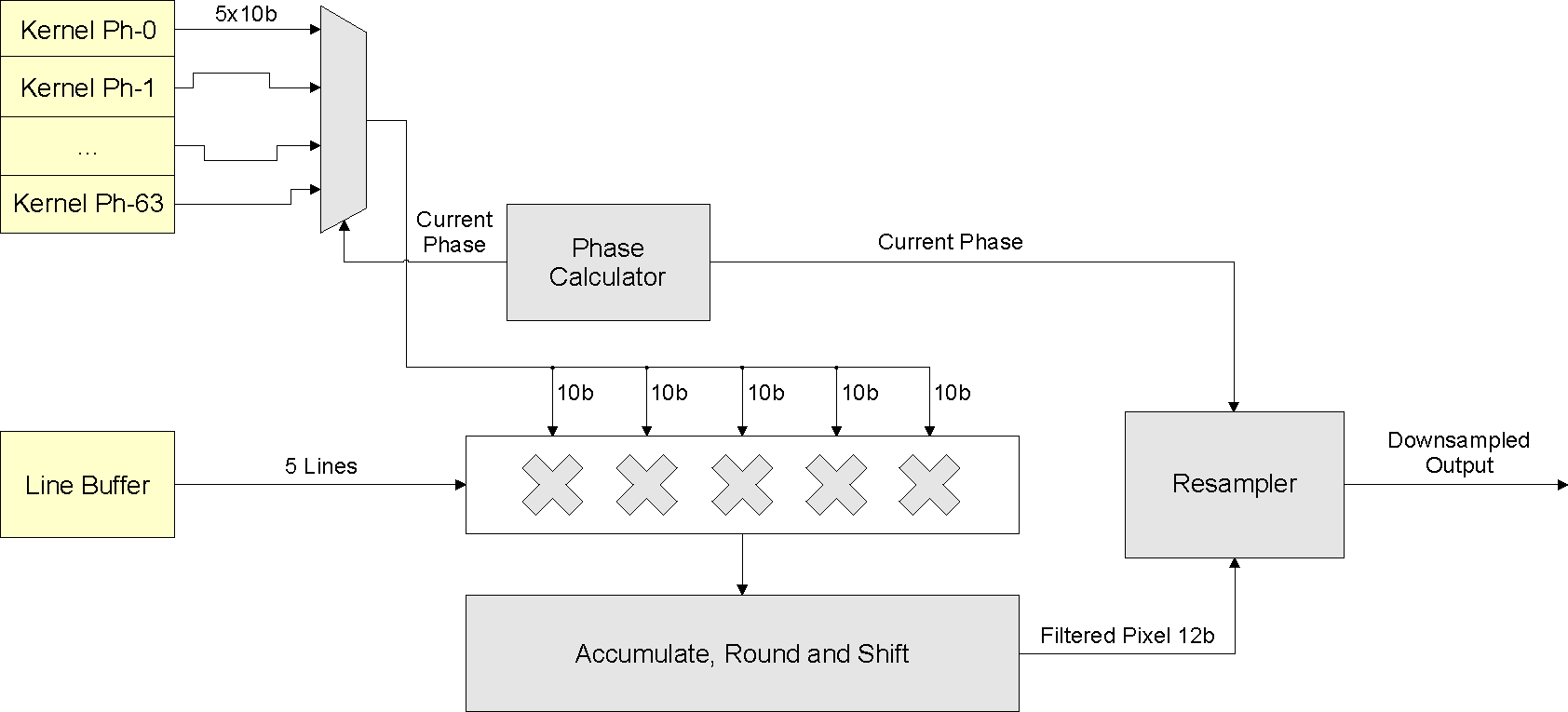Figure 6-132 Polyphase Filter Unit

Both the horizontal and vertical filter described earlier are an instance of the Polyphase filter unit, though only the vertical filter requires line memories (implemented in SL2 memory space). In all, there will be 20 instances of the Polyphase filter unit, 2 filters per channel and 10 total channels in the VPAC_MSC module.