SPRUIV7B May   2022  – September 2023 AM620-Q1 , AM623 , AM625 , AM625-Q1 , AM625SIP

 

  1.   1
  2.   Read This First
    1.     About This Manual
    2.     Glossary
    3.     Related Documentation From Texas Instruments
    4.     6
    5.     Support Resources
    6.     Trademarks
    7.     Export Control Notice
  3. 1 Introduction
    1. 1.1 Device Overview
    2. 1.2 Functional Block Diagram
    3. 1.3 Module Allocation and Instances within Device Domains
    4. 1.4 Device MAIN Domain
      1. 1.4.1  Arm Cortex-A53 Subsystem (A53SS)
      2. 1.4.2  Programmable Real-Time Unit Subsystem (PRUSS)
      3. 1.4.3  DDR 16-bit Subsystem (DDR16)
      4. 1.4.4  Region-based Address Translation Module (RAT)
      5. 1.4.5  Data Movement Subsystem (DMSS)
      6. 1.4.6  Mailbox (MAILBOX)
      7. 1.4.7  Spinlock (SPINLOCK)
      8. 1.4.8  General Purpose Input/Output Interface (GPIO)
      9. 1.4.9  Inter-Integrated Circuit Interface (I2C)
      10. 1.4.10 Serial Peripheral Interface (SPI)
      11. 1.4.11 Universal Asynchronous Receiver/Transmitter (UART)
      12. 1.4.12 3-port Gigabit Ethernet Switch (CPSW3G)
      13. 1.4.13 Universal Serial Bus (USB) Subsystem 2.0
      14. 1.4.14 General Purpose Memory Controller (GPMC)
      15. 1.4.15 Error Location Module (ELM)
      16. 1.4.16 Flash Subsystem (FSS) with Octal Serial Peripheral Interface (OSPI)
      17. 1.4.17 Multi-Media Card/Secure Digital Interface (MMCSD)
      18. 1.4.18 Enhanced Capture Module (ECAP)
      19. 1.4.19 Enhanced Pulse-Width Modulation Module (EPWM)
      20. 1.4.20 Enhanced Quadrature Encoder Pulse Module (EQEP)
      21. 1.4.21 Controller Area Network (MCAN)
      22. 1.4.22 Timers
      23. 1.4.23 Internal Diagnostics Modules
    5. 1.5 Device MCU Domain
      1. 1.5.1 MCU Arm Cortex M4F Subsystem (MCU_M4FSS)
      2. 1.5.2 MCU General Purpose Input/Output Interface (MCU_GPIO)
      3. 1.5.3 MCU Inter-Integrated Circuit Interface (MCU_I2C)
      4. 1.5.4 MCU Multi-channel Serial Peripheral Interface (MCU_SPI)
      5. 1.5.5 MCU Universal Asynchronous Receiver/Transmitter (MCU_UART)
      6. 1.5.6 MCU Timers
      7. 1.5.7 MCU Internal Diagnostics Modules
    6. 1.6 Device WKUP Domain
      1. 1.6.1 Arm Cortex-R5F Processor (R5FSS)
    7. 1.7 Device Identification
  4. 2 Memory Map
    1. 2.1 Memory Maps
      1. 2.1.1 Memory Map
    2. 2.2 SoC Address Aliasing
    3. 2.3 Processor Memory Map View
      1. 2.3.1 A53 Memory View
      2. 2.3.2 HSM M4F Memory View
      3. 2.3.3 MCU M4F Memory View
      4. 2.3.4 WKUP R5 Memory View
    4. 2.4 Memory Map Summary
    5. 2.5 MMU Optimization Note
  5. 3 System Interconnect
    1. 3.1 System Interconnect Overview
      1. 3.1.1  Domain Partition
      2. 3.1.2  IO Coherency Support
      3. 3.1.3  Timeout Gasket
        1. 3.1.3.1 Software Sequence to Enable Timeout Gasket
      4. 3.1.4  Route ID Allocation
      5. 3.1.5  Quality of Service (QoS)
      6. 3.1.6  Initiator-Side Security Controls and Firewalls
        1. 3.1.6.1 Initiator-Side Security Controls (ISC)
          1. 3.1.6.1.1 Priv-ID
          2. 3.1.6.1.2 Special System Level Priv-ID
        2. 3.1.6.2 Firewalls (FW)
          1. 3.1.6.2.1 Region-based Firewalls
            1. 3.1.6.2.1.1 Region Based Firewall Functional Description
            2. 3.1.6.2.1.2 Region Based Firewalls
          2. 3.1.6.2.2 Channelized Firewalls
            1. 3.1.6.2.2.1 Channelized Firewall Functional Description
      7. 3.1.7  Interconnect Error Reporting Feature
      8. 3.1.8  Connectivity Table
      9. 3.1.9  QoS Programming Guide
      10. 3.1.10 Performance Considerations
        1. 3.1.10.1 Initiator Timeout Gasket
        2. 3.1.10.2 Target Timeout Gasket
        3. 3.1.10.3 Latency Introduced by Auto Clock Gating Control
  6. 4 Module Integration
    1. 4.1  Memory Controllers
      1. 4.1.1 DDR16 Subsystem (DDR16SS)
        1. 4.1.1.1 DDR16SS Not Supported Features
    2. 4.2  Processors and Accelerators
      1. 4.2.1 Arm Cortex A53 Subsystem (A53SS)
        1. 4.2.1.1 A53SS Unsupported Features
        2. 4.2.1.2 Module Allocations
        3. 4.2.1.3 Resets, Interrupts, and Clocks
      2. 4.2.2 Arm Cortex R5F Subsystem (WKUP_R5FSS)
        1. 4.2.2.1 WKUP_R5FSS Unsupported Features
        2. 4.2.2.2 Module Allocations
        3. 4.2.2.3 Reference
      3. 4.2.3 Arm Cortex M4F Subsystem (MCU_M4FSS)
        1. 4.2.3.1 MCU_M4FSS Unsupported Features
        2. 4.2.3.2 Module Allocations
        3. 4.2.3.3 Resets, Interrupts, and Clocks
      4. 4.2.4 Programmable Real-Time Unit Subsystem (PRUSS)
        1. 4.2.4.1 PRUSS Unsupported Features
        2. 4.2.4.2 Module Allocations
        3. 4.2.4.3 Resets, Interrupts, and Clocks
    3. 4.3  Interprocessor Communication
      1. 4.3.1 Mailbox
        1. 4.3.1.1 Mailbox Unsupported Features
        2. 4.3.1.2 Reference
      2. 4.3.2 Spinlock
        1. 4.3.2.1 SPINLOCK Unsupported Features
        2. 4.3.2.2 Module Allocations
        3. 4.3.2.3 Resets, Interrupts, and Clocks
    4. 4.4  Device Configuration
      1. 4.4.1 Control Module (CTRL_MMR)
        1. 4.4.1.1 Module Allocations
        2. 4.4.1.2 Resets, Interrupts, and Clocks
      2. 4.4.2 Pad Configuration Module (PADCFG_CTRL)
        1. 4.4.2.1 Module Allocations
        2. 4.4.2.2 Resets, Interrupts, and Clocks
    5. 4.5  Data Movement Architecture
      1. 4.5.1 Data Movement Subsystem (DMSS)
        1. 4.5.1.1 DMSS Unsupported Features
        2. 4.5.1.2 Global Event Map
        3. 4.5.1.3 PSI-L System Thread Map
      2. 4.5.2 Peripheral DMA (PDMA)
        1. 4.5.2.1 PDMA Unsupported Features
    6. 4.6  Audio
      1. 4.6.1 Multichannel Audio Serial Port (MCASP)
        1. 4.6.1.1 MCASP Unsupported Features
        2. 4.6.1.2 Module Allocations
        3. 4.6.1.3 Resets, Interrupts, and Clocks
    7. 4.7  General Connectivity
      1. 4.7.1 General Purpose Input/Output (GPIO)
        1. 4.7.1.1 GPIO Unsupported Features
        2. 4.7.1.2 Module Allocation
        3. 4.7.1.3 Resets, Interrupts, and Clocks
        4. 4.7.1.4 GPIO0 Register/Pin Mapping
        5. 4.7.1.5 GPIO1 Register/Pin Mapping
        6. 4.7.1.6 MCU_GPIO0 Register/Pin Mapping
      2. 4.7.2 Inter-Integrated Circiuit (I2C)
        1. 4.7.2.1 I2C Unsupported Features
        2. 4.7.2.2 Module Allocations
        3. 4.7.2.3 Resets, Interrupts, and Clocks
      3. 4.7.3 Multichannel Serial Peripheral Interface (MCSPI)
        1. 4.7.3.1 SPI Unsupported Features
        2. 4.7.3.2 Module Allocations
        3. 4.7.3.3 Resets, Interrupts, and Clocks
      4. 4.7.4 Universal Asynchronous Receiver/Transmitter (UART)
        1. 4.7.4.1 UART Unsupported Features
        2. 4.7.4.2 Module Allocations
        3. 4.7.4.3 Resets, Interrupts, and Clocks
    8. 4.8  High-speed Serial Interfaces
      1. 4.8.1 Gigabit Ethernet Switch (CPSW)
        1. 4.8.1.1 CPSW Unsupported Features
        2. 4.8.1.2 Module Allocations
        3. 4.8.1.3 Resets, Interrupts, and Clocks
      2. 4.8.2 Universal Serial Bus Subsystem (USB)
        1. 4.8.2.1 USB2SS Unsupported Features
        2. 4.8.2.2 Module Allocations
        3. 4.8.2.3 Resets, Interrupts, and Clocks
    9. 4.9  Memory Interfaces
      1. 4.9.1 Flash Subsystem (FSS)
        1. 4.9.1.1 FSS Unsupported Features
        2. 4.9.1.2 Module Allocations
        3. 4.9.1.3 Resets, Interrupts, and Clocks
      2. 4.9.2 Octal Serial Peripheral Interface (OSPI)
        1. 4.9.2.1 OSPI Unsupported Features
        2. 4.9.2.2 Module Allocations
        3. 4.9.2.3 Resets, Interrupts, and Clocks
      3. 4.9.3 General-Purpose Memory Controller (GPMC)
        1. 4.9.3.1 GPMC Unsupported Features
        2. 4.9.3.2 Module Allocations
        3. 4.9.3.3 Resets, Interrupts, and Clocks
      4. 4.9.4 Error Location Module (ELM)
        1. 4.9.4.1 ELM Unsupported Features
        2. 4.9.4.2 Module Allocations
        3. 4.9.4.3 Resets, Interrupts, and Clocks
      5. 4.9.5 Multimedia Card Secure Digital (MMCSD)
        1. 4.9.5.1 MMCSD Unsupported Features
        2. 4.9.5.2 Module Allocations
        3. 4.9.5.3 Resets, Interrupts, and Clocks
    10. 4.10 Industrial and Control Interfaces
      1. 4.10.1 Modular Controller Area Network (MCAN)
        1. 4.10.1.1 MCAN Unsupported Features
        2. 4.10.1.2 Module Allocations
        3. 4.10.1.3 Resets, Interrupts, and Clocks
      2. 4.10.2 Enhanced Capture (ECAP)
        1. 4.10.2.1 ECAP Unsupported Features
        2. 4.10.2.2 Module Allocations
        3. 4.10.2.3 Resets, Interrupts, and Clocks
      3. 4.10.3 Enhanced Pulse Width Modulation (EPWM)
        1. 4.10.3.1 EPWM Unsupported Features
        2. 4.10.3.2 Module Allocations
        3. 4.10.3.3 Resets, Interrupts, and Clocks
      4. 4.10.4 Enhanced Quadrature Encoder Pulse (EQEP)
        1. 4.10.4.1 EQEP Unsupported Features
        2. 4.10.4.2 Module Allocations
        3. 4.10.4.3 Resets, Interrupts, and Clocks
    11. 4.11 Camera Subsystem
      1. 4.11.1 Camera Serial Interface Receiver (CSI_RX_IF)
        1. 4.11.1.1 CSI_RX_IF Unsupported Features
        2. 4.11.1.2 Module Allocations
        3. 4.11.1.3 Resets, Interrupts, and Clocks
      2. 4.11.2 MIPI D-PHY Receiver (DPHY_RX)
        1. 4.11.2.1 DPHY4RX Unsupported Features
        2. 4.11.2.2 Module Allocations
        3. 4.11.2.3 Resets, Interrupts, and Clocks
    12. 4.12 Timer Modules
      1. 4.12.1 Global Timebase Counter (GTC)
        1. 4.12.1.1 GTC Unsupported Features
        2. 4.12.1.2 Module Allocations
        3. 4.12.1.3 Resets, Interrupts, and Clocks
      2. 4.12.2 Real Time Interrupt (RTI)
        1. 4.12.2.1 RTI Unsupported Features
        2. 4.12.2.2 Module Allocations
        3. 4.12.2.3 Resets, Interrupts, and Clocks
      3. 4.12.3 Real-Time Clock (RTC)
        1. 4.12.3.1 RTC Unsupported Features
        2. 4.12.3.2 Module Allocations
        3. 4.12.3.3 Resets, Interrupts, and Clocks
      4. 4.12.4 Timer
        1. 4.12.4.1 Timer Unsupported Features
        2. 4.12.4.2 Module Allocations
        3. 4.12.4.3 Resets, Interrupts, and Clocks
    13. 4.13 Internal Diagnostic Modules
      1. 4.13.1 Dual Clock Comparator (DCC)
        1. 4.13.1.1 DCC Unsupported Features
        2. 4.13.1.2 Module Allocations
        3. 4.13.1.3 Resets, Interrupts, and Clocks
        4. 4.13.1.4 DCC Input Source Clock Mapping
      2. 4.13.2 Error Signaling Module (ESM)
        1. 4.13.2.1 ESM Unsupported Features
        2. 4.13.2.2 Module Allocations
        3. 4.13.2.3 Resets, Interrupts, and Clocks
      3. 4.13.3 Memory Cyclic Redundancy Check (MCRC64)
        1. 4.13.3.1 MCRC64 Unsupported Features
        2. 4.13.3.2 Module Allocations
        3. 4.13.3.3 Resets, Interrupts, and Clocks
      4. 4.13.4 ECC Aggregator (ECC_AGGR)
        1. 4.13.4.1 Module Allocations
        2. 4.13.4.2 Modules and Subsystems with ECC Aggregator
        3. 4.13.4.3 Resets, Interrupts, and Clocks
        4. 4.13.4.4 Interconnect ECC Aggregators
          1.        245
          2.        246
          3.        247
          4.        248
          5.        249
          6.        250
          7.        251
          8.        252
          9.        253
          10.        254
          11.        255
          12.        256
          13.        257
          14.        258
          15.        259
          16.        260
          17.        261
          18.        262
          19.        263
          20.        264
          21.        265
          22.        266
          23.        267
          24.        268
          25.        269
          26.        270
          27.        271
          28.        272
    14. 4.14 Graphics Processing Unit (GPU)
      1. 4.14.1 GPU Unsupported Features
      2. 4.14.2 Module Allocations
      3. 4.14.3 Resets, Interrupts, and Clocks
    15. 4.15 Display Subsystem (DSS)
      1. 4.15.1 DSS_UL Unsupported Features
      2. 4.15.2 Module Allocations
      3. 4.15.3 Resets, Interrupts, and Clocks
      4. 4.15.4 OLDI_TX Integration Features
    16. 4.16 Spinlock
      1. 4.16.1 SPINLOCK Unsupported Features
      2. 4.16.2 Module Allocations
      3. 4.16.3 Resets, Interrupts, and Clocks
  7. 5 Initialization
    1. 5.1 Initialization Overview
      1. 5.1.1 ROM Code Overview
      2. 5.1.2 Bootloader Modes
      3. 5.1.3 Terminology
    2. 5.2 Boot Process
      1. 5.2.1 Public ROM Code Architecture
        1. 5.2.1.1 Main Module
        2. 5.2.1.2 X509 Module
        3. 5.2.1.3 Buffer Manager Module
        4. 5.2.1.4 Log and Trace Module
        5. 5.2.1.5 System Module
        6. 5.2.1.6 Protocol Module
        7. 5.2.1.7 Driver Module
      2. 5.2.2 M4 ROM Description
      3. 5.2.3 Boot Process Flow
    3. 5.3 Boot Mode Pins
      1. 5.3.1 BOOTMODE Pin Mapping
        1. 5.3.1.1 Primary Boot Mode Selection and Configuration
        2. 5.3.1.2 Backup Boot Mode Selection and Configuration
    4. 5.4 Boot Modes
      1. 5.4.1  OSPI\xSPI\QSPI\SPI Boot
        1. 5.4.1.1 OSPI Boot
          1. 5.4.1.1.1 OSPI Bootloader Operation
            1. 5.4.1.1.1.1 OSPI Initialization Process
            2. 5.4.1.1.1.2 OSPI Loading Process
        2. 5.4.1.2 xSPI Boot
          1. 5.4.1.2.1 xSPI Bootloader Operation
        3. 5.4.1.3 QSPI Boot
          1. 5.4.1.3.1 QSPI Bootloader Operation
            1. 5.4.1.3.1.1 QSPI Initialization Process
            2. 5.4.1.3.1.2 QSPI Loading Process
        4. 5.4.1.4 SPI Boot
          1. 5.4.1.4.1 SPI Bootloader Operation
            1. 5.4.1.4.1.1 SPI Initialization Process
            2. 5.4.1.4.1.2 SPI Loading Process
      2. 5.4.2  I2C Boot
        1. 5.4.2.1 I2C Bootloader Operation
          1. 5.4.2.1.1 I2C Initialization Process
            1. 5.4.2.1.1.1 Block Size
            2. 5.4.2.1.1.2 Addressing
          2. 5.4.2.1.2 I2C Loading Process
            1. 5.4.2.1.2.1 Loading a Boot Image From EEPROM
      3. 5.4.3  SD Card Boot
        1. 5.4.3.1 SD Card Bootloader Operation
      4. 5.4.4  eMMC Boot
        1. 5.4.4.1 eMMC Bootloader Operation
      5. 5.4.5  Ethernet Boot
        1. 5.4.5.1 Ethernet Bootloader Operation
          1. 5.4.5.1.1 Ethernet Initialization Process
          2. 5.4.5.1.2 Ethernet Loading Process
            1. 5.4.5.1.2.1 Ethernet Boot Data Formats
              1. 5.4.5.1.2.1.1 Limitations
              2. 5.4.5.1.2.1.2 BOOTP Request
                1. 5.4.5.1.2.1.2.1 MAC Header (DIX)
                2. 5.4.5.1.2.1.2.2 IPv4 Header
                3. 5.4.5.1.2.1.2.3 UDP Header
                4. 5.4.5.1.2.1.2.4 BOOTP Payload
                5. 5.4.5.1.2.1.2.5 TFTP
          3. 5.4.5.1.3 Ethernet Hand Over Process
      6. 5.4.6  USB Boot
        1. 5.4.6.1 USB Bootloader Operation
          1. 5.4.6.1.1 USB-Specific Attributes
            1. 5.4.6.1.1.1 DFU Device Mode
      7. 5.4.7  UART Boot
        1. 5.4.7.1 UART Bootloader Operation
          1. 5.4.7.1.1 Initialization Process
          2. 5.4.7.1.2 UART Loading Process
            1. 5.4.7.1.2.1 UART XMODEM
          3. 5.4.7.1.3 UART Hand-Over Process
      8. 5.4.8  GPMC NOR Boot
        1. 5.4.8.1 GPMC NOR Bootloader Operation
      9. 5.4.9  GPMC NAND Boot
        1. 5.4.9.1 GPMC NAND Bootloader Operation
      10. 5.4.10 Serial NAND Boot
        1. 5.4.10.1 Serial NAND Bootloader Operation
        2. 5.4.10.2 Serial NAND Initialization Process
        3. 5.4.10.3 Serial NAND Loading Process
      11. 5.4.11 No boot/Development boot
    5. 5.5 PLL Configuration
    6. 5.6 Boot Parameter Tables
      1. 5.6.1  Common Header
      2. 5.6.2  PLL Setup
      3. 5.6.3  OSPI/QSPI/SPI Boot Parameter Table
      4. 5.6.4  UART Boot Parameter Table
      5. 5.6.5  I2C Boot Parameter Table
      6. 5.6.6  MMCSD/eMMC Boot Parameter Table
      7. 5.6.7  Ethernet Boot Parameter Table
      8. 5.6.8  xSPI Boot Parameter Table
      9. 5.6.9  USB DFU Boot Parameter Table
      10. 5.6.10 USB MSC Boot Parameter Table
      11. 5.6.11 GPMC NOR Boot Parameter Table
      12. 5.6.12 GPMC NAND Boot Parameter Table
    7. 5.7 Boot Image Format
      1. 5.7.1 Overall Structure
      2. 5.7.2 X.509 Certificate
      3. 5.7.3 Organizational Identifier (OID)
      4. 5.7.4 X.509 Extensions Specific to Boot
        1. 5.7.4.1 Boot Info (OID 1.3.6.1.4.1.294.1.1)
        2. 5.7.4.2 Image Integrity (OID 1.3.6.1.4.1.294.1.2)
      5. 5.7.5 Extended Boot Info Extension
        1. 5.7.5.1 Impact on HS Device
        2. 5.7.5.2 Extended Boot Info Details
        3. 5.7.5.3 Certificate / Component Types
        4. 5.7.5.4 Extended Boot Encryption Info
        5. 5.7.5.5 Component Ordering
        6. 5.7.5.6 Memory Load Sections Overlap with Executable Components
        7. 5.7.5.7 Device Type and Extended Boot Extension
      6. 5.7.6 Generating X.509 Certificates
        1. 5.7.6.1 Key Generation
          1. 5.7.6.1.1 Degenerate RSA Keys
        2. 5.7.6.2 Configuration Script
        3. 5.7.6.3 Image Data
    8. 5.8 Boot Memory Maps
      1. 5.8.1 Global Memory Addresses Used by ROM Code
  8. 6 Device Configuration
    1. 6.1 Memory Mapped Control Register Modules (CTRL_MMR)
      1. 6.1.1 General Purpose Control Register Modules
        1. 6.1.1.1 General Purpose Control Register Modules Overview
        2.       405
        3. 6.1.1.2 General Purpose Control Register Modules Functional Description
          1. 6.1.1.2.1 Description for General Purpose Control Register Module Register Types
            1. 6.1.1.2.1.1 Kick Protection Registers
            2. 6.1.1.2.1.2 I/O Debounce Control Registers
      2. 6.1.2 Pad Configuration Register Modules
        1. 6.1.2.1 Pad Configuration Register Modules Overview
        2.       412
      3. 6.1.3 Security Control Register Modules
        1. 6.1.3.1 Security Control Register Modules Overview
    2. 6.2 Power
      1. 6.2.1 Power Management Overview
      2. 6.2.2 Power Control Modules
        1. 6.2.2.1 Power Sleep Controller
          1. 6.2.2.1.1 PSC Architecture
          2. 6.2.2.1.2 PSC Configurations
            1. 6.2.2.1.2.1 Software Sequence to enable an IP through PSC
        2. 6.2.2.2 Device Manager
      3. 6.2.3 Power Management Techniques
        1. 6.2.3.1 Dynamic Frequency Scaling (DFS)
        2. 6.2.3.2 OPP Low
      4. 6.2.4 Power Modes
        1. 6.2.4.1  Active
        2. 6.2.4.2  Standby
        3. 6.2.4.3  MCU-Only
        4. 6.2.4.4  DeepSleep
        5. 6.2.4.5  Partial I/O
        6. 6.2.4.6  Power States and Transitions
        7. 6.2.4.7  Wakeup Sources/Events
        8. 6.2.4.8  USB Wakeup Scenarios
        9. 6.2.4.9  Main Oscillator Control During DeepSleep
        10. 6.2.4.10 Low Power Mode Sequencing with Device Manager
        11. 6.2.4.11 I/O Power Management and Daisy Chaining
      5. 6.2.5 Power Supply Modules
        1. 6.2.5.1 Power OK (POK) Modules
          1. 6.2.5.1.1 Configuration Registers
        2. 6.2.5.2 Power on Reset (POR) Module
          1. 6.2.5.2.1 POR Overview
          2. 6.2.5.2.2 POR Integration
        3. 6.2.5.3 PoR/Reset Generator (PRG) Modules
          1. 6.2.5.3.1 PRG Overview
        4. 6.2.5.4 Power Glitch Detect (PGD) Modules
        5. 6.2.5.5 Voltage and Thermal Manager (VTM)
          1. 6.2.5.5.1 VTM Overview
            1. 6.2.5.5.1.1 VTM Features
            2. 6.2.5.5.1.2 VTM Not Supported Features
          2. 6.2.5.5.2 VTM Functional Description
            1. 6.2.5.5.2.1 VTM Temperature Status and Thermal Management
              1. 6.2.5.5.2.1.1 10-bit Temperature Values Versus Temperature
    3. 6.3 Reset
      1. 6.3.1 Overview
        1. 6.3.1.1 MCU Domain Supported Resets
        2. 6.3.1.2 MAIN Domain Supported Resets
        3. 6.3.1.3 High-Level Reset Flow
        4. 6.3.1.4 Reset Terminology
        5. 6.3.1.5 Reset Architecture
          1. 6.3.1.5.1 Reset Architecture Block Diagram
          2. 6.3.1.5.2 SoC Reset Hardware Logic Diagram
          3. 6.3.1.5.3 MCU Domain Reset Hardware Logic Diagram
          4. 6.3.1.5.4 MAIN Domain Reset and PORz Hardware Logic Diagrams
      2. 6.3.2 Reset Sources
      3. 6.3.3 Reset Status
        1. 6.3.3.1 Reset Source Status Registers
        2. 6.3.3.2 MCU_RESETSTATz Status Pin
        3. 6.3.3.3 MCU_ERRORn Status Pin
        4. 6.3.3.4 RESETSTATz Status Pin
        5. 6.3.3.5 PORz_OUT Status Pin
      4. 6.3.4 Reset Controls
        1. 6.3.4.1 Reset Control Registers
        2. 6.3.4.2 Reset Isolation
      5. 6.3.5 Reset Details
        1. 6.3.5.1  POR Resets
          1. 6.3.5.1.1 SW_MAIN_PORz Reset
          2. 6.3.5.1.2 MCU_PORz Reset
        2. 6.3.5.2  Warm Resets
          1. 6.3.5.2.1 MAIN Domain Warm Reset Sequence Flow
          2. 6.3.5.2.2 MAIN_RESETz_REQ Reset
          3. 6.3.5.2.3 SW_MAIN_WARMRSTz Reset
          4. 6.3.5.2.4 MCU_RESETz Reset
          5. 6.3.5.2.5 SW_MCU_WARMRSTz Reset
        3. 6.3.5.3  SMS Resets
          1. 6.3.5.3.1 SMS_WARM_OUT_RST_n Reset (MAIN Domain)
          2. 6.3.5.3.2 SMS_COLD_OUT_RST_n Reset (MAIN Domain)
          3. 6.3.5.3.3 SMS_COLD_OUT_RST_n Reset (MCU Domain)
        4. 6.3.5.4  VTM Thermal Alert Reset
        5. 6.3.5.5  MAIN ESM_ERRORz Reset
        6. 6.3.5.6  MCU ESM_ERRORz Reset
        7. 6.3.5.7  DM_WDT_RST_n Reset
        8. 6.3.5.8  HHV
        9. 6.3.5.9  BOOTMODE Pin Latching
        10. 6.3.5.10 Power-on-Reset Sequence
        11. 6.3.5.11 Low Power Mode Reset Handling
    4. 6.4 Clocking
      1. 6.4.1 Overview
      2. 6.4.2 Clock Inputs
        1. 6.4.2.1 Overview
      3. 6.4.3 Clock Outputs
        1. 6.4.3.1 Observation Clock Pins
          1. 6.4.3.1.1 MCU_OBSCLK0 Pin
          2. 6.4.3.1.2 OBSCLK0 Pin
          3. 6.4.3.1.3 AUDIO_EXT_REFCLK
        2. 6.4.3.2 System Clock Pins
          1. 6.4.3.2.1 MCU_SYSCLKOUT0
          2. 6.4.3.2.2 SYSCLKOUT0
          3. 6.4.3.2.3 WKUP_CLKOUT0
      4. 6.4.4 Device Oscillators
        1. 6.4.4.1 Device Oscillators Integration
          1. 6.4.4.1.1 High-Frequency Oscillator with External Crystal
          2. 6.4.4.1.2 Low-Frequency Oscillator with External Crystal
          3. 6.4.4.1.3 Internal RC Oscillator
        2. 6.4.4.2 Oscillator Clock Loss Detection
      5. 6.4.5 PLLs
        1. 6.4.5.1 MCU Domain PLL Overview
        2. 6.4.5.2 MAIN Domain PLLs Overview
        3. 6.4.5.3 PLL Reference Clocks
          1. 6.4.5.3.1 PLLs in MCU Domain
          2. 6.4.5.3.2 PLLs in MAIN Domain
        4. 6.4.5.4 Generic PLL Overview
          1. 6.4.5.4.1 PLLs Output Clocks Parameters
            1. 6.4.5.4.1.1 PLLs Input Clocks
            2. 6.4.5.4.1.2 PLL Output Clocks
              1. 6.4.5.4.1.2.1 PLLTS16FFCLAFRACF2 Type Output Clocks
              2. 6.4.5.4.1.2.2 PLL Lock
              3. 6.4.5.4.1.2.3 HSDIVIDER
              4. 6.4.5.4.1.2.4 ICG Module
              5. 6.4.5.4.1.2.5 PLL Power Down
              6. 6.4.5.4.1.2.6 PLL Calibration
          2. 6.4.5.4.2 PLL Spread Spectrum Modulation Module
            1. 6.4.5.4.2.1 Definition of SSMOD
            2. 6.4.5.4.2.2 SSMOD Configuration
        5. 6.4.5.5 PLLs Device-Specific Information
          1. 6.4.5.5.1 SSMOD Related Bitfields Table
          2. 6.4.5.5.2 Clock Synthesis Inputs to the PLLs
          3. 6.4.5.5.3 Clock Output Parameter
          4. 6.4.5.5.4 Calibration Related Bitfields
        6. 6.4.5.6 PLL Controller (PLLCTRL)
        7. 6.4.5.7 PLL, PLLCTRL, and HSDIV Controllers Programming Guide
          1. 6.4.5.7.1 PLL Initialization
            1. 6.4.5.7.1.1 Kick Protection Mechanism
            2. 6.4.5.7.1.2 PLLCTRL Initialization
            3. 6.4.5.7.1.3 PLL Programming Requirements
          2. 6.4.5.7.2 HSDIV PLL Programming
          3. 6.4.5.7.3 PLL Controllers Programming - Dividers PLLDIVn and GO Operation
            1. 6.4.5.7.3.1 GO Operation
            2. 6.4.5.7.3.2 Software Steps to Modify PLLDIV Ratios
          4. 6.4.5.7.4 Entire Sequence for Programming PLLCTRL, HSDIV, and PLL
          5. 6.4.5.7.5 Dual Clock Comparator (DCC)
          6. 6.4.5.7.6 DeepSleep Clock Gating
            1. 6.4.5.7.6.1 Software responsibility of clock settings during deeplseep mode
  9. 7 Processors and Accelerators
    1. 7.1 Arm Cortex-A53 Subsystem (A53SS)
      1. 7.1.1 A53SS Overview
        1. 7.1.1.1 A53SS Introduction
        2. 7.1.1.2 A53SS Features
        3.       559
      2. 7.1.2 A53SS Functional Description
        1. 7.1.2.1  A53SS Block Diagram
        2. 7.1.2.2  Arm Cortex-A53 Cluster
        3. 7.1.2.3  A53SS Interfaces and Async Bridges
        4. 7.1.2.4  A53SS Interrupts
          1. 7.1.2.4.1 A53SS Interrupt Inputs
          2. 7.1.2.4.2 A53SS Interrupt Outputs
        5. 7.1.2.5  A53SS Power Management and Clocking
          1. 7.1.2.5.1 A53SS Power Management
          2. 7.1.2.5.2 A53SS Clocking
        6. 7.1.2.6  A53SS Debug
        7. 7.1.2.7  A53SS Global and Debug Timestamps
        8. 7.1.2.8  A53SS Watchdog
        9. 7.1.2.9  A53SS Functional Safety - ECC Error Injection Support
          1. 7.1.2.9.1 A53 ECC Aggregators During Low Power States
          2. 7.1.2.9.2 Auto-initialization of Memories
          3. 7.1.2.9.3 A53 SRAM Safety
          4. 7.1.2.9.4 A53 SRAM ECC Aggregator Configurations
        10. 7.1.2.10 A53SS Boot
        11. 7.1.2.11 A53SS Interprocessor Communication
    2. 7.2 Device Manager Cortex R5F Subsystem (WKUP_R5FSS)
      1. 7.2.1 WKUP_R5FSS Overview
        1. 7.2.1.1 WKUP_R5FSS Features
        2.       583
      2. 7.2.2 WKUP_R5FSS Functional Description
        1. 7.2.2.1  WKUP_R5FSS Block Diagram
        2. 7.2.2.2  WKUP_R5FSS Cortex-R5F Core
          1. 7.2.2.2.1 L1 Caches
          2. 7.2.2.2.2 Tightly-Coupled Memories (TCMs)
          3. 7.2.2.2.3 WKUP_R5FSS Special Signals
        3. 7.2.2.3  WKUP_R5FSS Interfaces
          1. 7.2.2.3.1 Initiator Interfaces
          2. 7.2.2.3.2 Target Interfaces
        4. 7.2.2.4  WKUP_R5FSS Power, Clocking and Reset
          1. 7.2.2.4.1 WKUP_R5FSS Power
          2. 7.2.2.4.2 WKUP_R5FSS Clocking
          3. 7.2.2.4.3 WKUP_R5FSS Reset
        5. 7.2.2.5  WKUP_R5FSS Vectored Interrupt Manager (VIM)
          1. 7.2.2.5.1 VIM Overview
          2. 7.2.2.5.2 VIM Interrupt Inputs
          3. 7.2.2.5.3 VIM Interrupt Outputs
          4. 7.2.2.5.4 VIM Interrupt Vector Table (VIM RAM)
          5. 7.2.2.5.5 VIM Interrupt Prioritization
          6. 7.2.2.5.6 VIM ECC Support
          7. 7.2.2.5.7 VIM IDLE State
          8. 7.2.2.5.8 VIM Interrupt Handling
            1. 7.2.2.5.8.1 Servicing IRQ Through Vector Interface
            2. 7.2.2.5.8.2 Servicing IRQ Through MMR Interface
            3. 7.2.2.5.8.3 Servicing IRQ Through MMR Interface (Alternative)
            4. 7.2.2.5.8.4 Servicing FIQ
            5. 7.2.2.5.8.5 Servicing FIQ (Alternative)
        6. 7.2.2.6  WKUP_R5FSS Region Address Translation (RAT)
          1. 7.2.2.6.1 WKUP R5FSS Usage
          2. 7.2.2.6.2 RAT Function
          3. 7.2.2.6.3 How to use RAT Block in R5
          4. 7.2.2.6.4 Example of Using RAT to Access Full 36b SoC Memory Map
        7. 7.2.2.7  WKUP_R5FSS ECC Support
        8. 7.2.2.8  WKUP_R5FSS Memory View
        9. 7.2.2.9  WKUP_R5FSS Interrupts
        10. 7.2.2.10 WKUP_R5FSS Debug and Trace
        11. 7.2.2.11 WKUP_R5FSS Boot Options
        12. 7.2.2.12 WKUP_R5FSS Core Memory ECC Events
      3. 7.2.3 Vectored Interrupt Manager (VIM)
        1. 7.2.3.1 VIM Overview
          1. 7.2.3.1.1 VIM Features
          2. 7.2.3.1.2 Unsupported Features
          3.        626
        2. 7.2.3.2 VIM Functional Description
          1. 7.2.3.2.1 Block Diagram
          2. 7.2.3.2.2 Interrupt Inputs
          3. 7.2.3.2.3 Interrupt Outputs
          4. 7.2.3.2.4 Priority Interrupt / Nested Interrupts
          5. 7.2.3.2.5 VIC Port
          6. 7.2.3.2.6 Latency
          7. 7.2.3.2.7 Safety
          8. 7.2.3.2.8 IDLE
        3. 7.2.3.3 Interrupt Conditions
          1. 7.2.3.3.1 CPU Interrupts
          2. 7.2.3.3.2 Interrupt Description
            1. 7.2.3.3.2.1 coreN_IRQn
            2. 7.2.3.3.2.2 coreN_FIQn
          3. 7.2.3.3.3 Interrupt Condition Control
            1. 7.2.3.3.3.1 coreN_IRQn
            2. 7.2.3.3.3.2 coreN_FIQn
          4. 7.2.3.3.4 Interrupt Handling
            1. 7.2.3.3.4.1 IRQ through the Vector Interface
            2. 7.2.3.3.4.2 IRQ through MMR Interface
            3. 7.2.3.3.4.3 IRQ through MMR Interface (Alternative)
            4. 7.2.3.3.4.4 FIQ
            5. 7.2.3.3.4.5 FIQ (Alternative)
        4. 7.2.3.4 Memory Map
        5. 7.2.3.5 Module I/O
          1. 7.2.3.5.1 Clocks, Reset, Emulation
          2. 7.2.3.5.2 VBUSP Target Interface
          3. 7.2.3.5.3 Interrupt Inputs
          4. 7.2.3.5.4 Interrupt Outputs
          5. 7.2.3.5.5 VIC Interfaces
          6. 7.2.3.5.6 Compare Outputs
          7. 7.2.3.5.7 ECC Control and Status Bus
          8. 7.2.3.5.8 DFT
          9. 7.2.3.5.9 RAM GPIO
        6. 7.2.3.6 Programmer's Guide
          1. 7.2.3.6.1 Initialization Sequence
          2. 7.2.3.6.2 DED Behavior
          3. 7.2.3.6.3 Power Up/Down Sequence
    3. 7.3 Cortex-M4F Subsystem (MCU_M4FSS)
      1. 7.3.1 MCU_M4FSS Overview
        1. 7.3.1.1 MCU_M4FSS Features
        2.       668
      2. 7.3.2 MCU_M4FSS Functional Description
        1. 7.3.2.1  MCU_M4FSS Block Diagram
        2. 7.3.2.2  MCU_M4FSS Processor
        3. 7.3.2.3  MCU_M4FSS Internal RAMs
        4. 7.3.2.4  MCU_M4FSS Interfaces
          1. 7.3.2.4.1 Controller Interfaces
          2. 7.3.2.4.2 Peripheral Interfaces
        5. 7.3.2.5  MCU_M4FSS Power, Clocking and Reset
        6. 7.3.2.6  MCU_M4FSS Memory View
        7. 7.3.2.7  MCU_M4FSS RAT
          1. 7.3.2.7.1 RAT Usage
          2. 7.3.2.7.2 RAT Function
          3. 7.3.2.7.3 How to use RAT Block in R5
          4. 7.3.2.7.4 Example of Using RAT to Access Full 36b SoC Memory Map
        8. 7.3.2.8  MCU_M4FSS ECC Support
        9. 7.3.2.9  MCU_M4FSS Interrupts
        10. 7.3.2.10 MCU_M4FSS Debug and Trace
        11. 7.3.2.11 MCU_M4FSS Time Sync
        12. 7.3.2.12 MCU_M4FSS SysTick
        13. 7.3.2.13 MCU_M4FSS Initialization
    4. 7.4 Programmable Real-Time Unit Subsystem (PRUSS)
      1. 7.4.1 PRUSS Overview
        1. 7.4.1.1 PRUSS Key Features
        2.       692
      2. 7.4.2 PRUSS Environment
        1. 7.4.2.1 PRUSS Internal Pinmux
          1.        PRUSS I/O Signals
        2. 7.4.2.2 PRUSS Fast GPIO pins
      3. 7.4.3 PRUSS Top Level Resources Functional Description
        1. 7.4.3.1 PRUSS Reset Management
        2. 7.4.3.2 PRUSS Power and Clock Management
          1. 7.4.3.2.1 PRUSS CORE Clock Generation
          2. 7.4.3.2.2 PRUSS Idle State
          3. 7.4.3.2.3 PRUSS Protect
          4. 7.4.3.2.4 Module Clock Configurations at PRUSS Top Level
        3. 7.4.3.3 Other PRUSS Module Functional Registers at Subsystem Level
        4. 7.4.3.4 PRUSS Memory Maps
          1. 7.4.3.4.1 PRUSS Local Memory Map
            1. 7.4.3.4.1.1 PRUSS Local Instruction Memory Map
            2. 7.4.3.4.1.2 PRUSS Local Data Memory Map
          2. 7.4.3.4.2 PRUSS Global Memory Map
      4. 7.4.4 PRUSS PRU Cores
        1. 7.4.4.1 PRU Cores Overview
        2. 7.4.4.2 PRU Cores Functional Description
          1. 7.4.4.2.1 PRU Constant Table
          2. 7.4.4.2.2 PRU Module Interface
            1. 7.4.4.2.2.1 Real-Time Status Interface Mapping (R31): Interrupt Events Input
            2. 7.4.4.2.2.2 Event Interface Mapping (R31): PRU System Events
            3. 7.4.4.2.2.3 General-Purpose Inputs (R31): Enhanced PRU GP Module
              1. 7.4.4.2.2.3.1 PRU EGPIs Direct Input
              2. 7.4.4.2.2.3.2 PRU EGPIs 16-Bit Parallel Capture
              3. 7.4.4.2.2.3.3 PRU EGPIs 28-Bit Shift In
                1. 7.4.4.2.2.3.3.1 PRU EGPI Programming Model
              4. 7.4.4.2.2.3.4 General-Purpose Outputs (R30): Enhanced PRU GP Module
                1. 7.4.4.2.2.3.4.1 PRU EGPOs Direct Output
                2. 7.4.4.2.2.3.4.2 PRU EGPO Shift Out
                  1. 4.4.2.2.3.4.2.1 PRU EGPO Programming Model
              5. 7.4.4.2.2.3.5 Sigma Delta (SD) Decimation Filtering
                1. 7.4.4.2.2.3.5.1 Sigma Delta Block Diagram and Signals
                2. 7.4.4.2.2.3.5.2 PRU R30 / R31 Interface
                3. 7.4.4.2.2.3.5.3 Sigma Delta Description
                4. 7.4.4.2.2.3.5.4 Sigma Delta Basic Programming Example
              6. 7.4.4.2.2.3.6 Three Channel Peripheral Interface
                1. 7.4.4.2.2.3.6.1 Peripheral Interface Block Diagram and Signal Configuration
                2. 7.4.4.2.2.3.6.2 PRU R30 and R31 Interface
                3. 7.4.4.2.2.3.6.3 Clock Generation
                  1. 4.4.2.2.3.6.3.1 Configuration
                  2. 4.4.2.2.3.6.3.2 Clock Output Start Conditions
                    1. 4.2.2.3.6.3.2.1 TX Mode (RX_EN = 0)
                    2. 4.2.2.3.6.3.2.2 RX Mode (RX_EN = 1)
                  3. 4.4.2.2.3.6.3.3 Stop Conditions
                4. 7.4.4.2.2.3.6.4 Three Peripheral Mode Basic Programming Model
                  1. 4.4.2.2.3.6.4.1 Clock Generation
                  2. 4.4.2.2.3.6.4.2 TX - Single Shot
                  3. 4.4.2.2.3.6.4.3 TX - Continuous FIFO Loading
                  4. 4.4.2.2.3.6.4.4 RX - Auto Arm or Non-Auto Arm
        3. 7.4.4.3 PRUSS RAM Index Allocation
      5. 7.4.5 PRUSS Broadside Accelerators
        1. 7.4.5.1 PRUSS Broadside Accelerators Overview
        2. 7.4.5.2 PRUSS Data Processing Accelerators Functional
          1. 7.4.5.2.1 PRU Multiplier with Accumulation (MPY/MAC)
            1. 7.4.5.2.1.1 PRU MAC Operations
              1. 7.4.5.2.1.1.1 PRU versus MAC Interface
              2. 7.4.5.2.1.1.2 Multiply only mode(default state), MAC_MODE = 0
                1. 7.4.5.2.1.1.2.1 Programming PRU MAC in "Multiply-ONLY" mode
              3. 7.4.5.2.1.1.3 Multiply and Accumulate Mode, MAC_MODE = 1
                1. 7.4.5.2.1.1.3.1 Programming PRU MAC in Multiply and Accumulate Mode
          2. 7.4.5.2.2 PRU CRC16/32 Module
            1. 7.4.5.2.2.1 PRU and CRC16/32 Interface
            2. 7.4.5.2.2.2 CRC Programming Model
            3. 7.4.5.2.2.3 PRU and CRC16/32 Interface (R9:R2)
          3. 7.4.5.2.3 PRUSS Scratch Pad Memory
            1. 7.4.5.2.3.1 PRU0/1 Scratch Pad Overview
            2. 7.4.5.2.3.2 PRU0 /1 Scratch Pad Operations
              1. 7.4.5.2.3.2.1 Optional XIN/XOUT Shift
              2. 7.4.5.2.3.2.2 Scratch Pad Operations Examples
        3. 7.4.5.3 PRUSS Data Movement Accelerators Functional
          1. 7.4.5.3.1 PRUSS XFR2VBUS Hardware Accelerator
            1. 7.4.5.3.1.1 Blocking Conditions
            2. 7.4.5.3.1.2 Read Operation with Auto Disabled
            3. 7.4.5.3.1.3 Read Operation with Auto Enabled
            4. 7.4.5.3.1.4 Write Operation with Auto Disabled
            5. 7.4.5.3.1.5 PRU to XFR2VBUS Interface
            6. 7.4.5.3.1.6 XFR2VBUS Programming Model
      6. 7.4.6 PRUSS Local INTC
        1. 7.4.6.1 PRUSS Interrupt Controller Functional Description
          1. 7.4.6.1.1 PRUSS Interrupt Controller Events
          2. 7.4.6.1.2 PRUSS Interrupt Controller System Events Flow
            1. 7.4.6.1.2.1 PRUSS Interrupt Processing
              1. 7.4.6.1.2.1.1 PRUSS Interrupt Enabling
            2. 7.4.6.1.2.2 PRUSS Interrupt Status Checking
            3. 7.4.6.1.2.3 PRUSS Interrupt Channel Mapping
              1. 7.4.6.1.2.3.1 PRUSS Host Interrupt Mapping
              2. 7.4.6.1.2.3.2 PRUSS Interrupt Prioritization
            4. 7.4.6.1.2.4 PRUSS Interrupt Nesting
            5. 7.4.6.1.2.5 PRUSS Interrupt Status Clearing
          3. 7.4.6.1.3 PRUSS Interrupt Disabling
        2. 7.4.6.2 PRUSS Interrupt Controller Basic Programming Model
        3. 7.4.6.3 PRUSS Interrupt Requests Mapping
      7. 7.4.7 PRUSS UART Module
        1. 7.4.7.1 PRUSS UART Overview
        2. 7.4.7.2 PRUSS UART Environment
          1. 7.4.7.2.1 PRUSS UART Pin Multiplexing
          2. 7.4.7.2.2 PRUSS UART Signal Descriptions
          3. 7.4.7.2.3 PRUSS UART Protocol Description and Data Format
            1. 7.4.7.2.3.1 PRUSS UART Transmission Protocol
            2. 7.4.7.2.3.2 PRUSS UART Reception Protocol
            3. 7.4.7.2.3.3 PRUSS UART Data Format
              1. 7.4.7.2.3.3.1 Frame Formatting
          4. 7.4.7.2.4 PRUSS UART Clock Generation and Control
        3. 7.4.7.3 PRUSS UART Functional Description
          1. 7.4.7.3.1 PRUSS UART Functional Block Diagram
          2. 7.4.7.3.2 PRUSS UART Reset Considerations
            1. 7.4.7.3.2.1 PRUSS UART Software Reset Considerations
            2. 7.4.7.3.2.2 PRUSS UART Hardware Reset Considerations
          3. 7.4.7.3.3 PRUSS UART Power Management
          4. 7.4.7.3.4 PRUSS UART Interrupt Support
            1. 7.4.7.3.4.1 PRUSS UART Interrupt Events and Requests
            2. 7.4.7.3.4.2 PRUSS UART Interrupt Multiplexing
          5. 7.4.7.3.5 808
          6. 7.4.7.3.6 PRUSS UART DMA Event Support
          7. 7.4.7.3.7 PRUSS UART Operations
            1. 7.4.7.3.7.1 PRUSS UART FIFO Modes
              1. 7.4.7.3.7.1.1 PRUSS UART FIFO Interrupt Mode
              2. 7.4.7.3.7.1.2 PRUSS UART FIFO Poll Mode
            2. 7.4.7.3.7.2 PRUSS UART Autoflow Control
              1. 7.4.7.3.7.2.1 PRUSS UART Signal UART0_RTS Behavior
              2. 7.4.7.3.7.2.2 PRUSS UART Signal UART0_CTS Behavior
            3. 7.4.7.3.7.3 PRUSS UART Loopback Control
          8. 7.4.7.3.8 PRUSS UART Emulation Considerations
          9. 7.4.7.3.9 PRUSS UART Exception Processing
            1. 7.4.7.3.9.1 PRUSS UART Divisor Latch Not Programmed
            2. 7.4.7.3.9.2 Changing Operating Mode During Busy Serial Communication of PRUSS UART
      8. 7.4.8 PRUSS ECAP Module
        1. 7.4.8.1 PRUSS eCAP Overview
          1. 7.4.8.1.1 Purpose of the PRUSS eCAP Peripheral
          2. 7.4.8.1.2 PRUSS eCAP Features
        2. 7.4.8.2 PRUSS ECAP Functional Description
          1. 7.4.8.2.1 PRUSS Capture and APWM Operating Mode
      9. 7.4.9 PRUSS IEP
        1. 7.4.9.1 PRUSS IEP Overview
        2. 7.4.9.2 PRUSS IEP Functional Description
          1. 7.4.9.2.1 PRUSS IEP Clock Generation
          2. 7.4.9.2.2 PRUSS IEP Timer
            1. 7.4.9.2.2.1 PRUSS IEP Timer Features
          3. 7.4.9.2.3 32-Bit Shadow Mode
          4. 7.4.9.2.4 PRUSS IEP Timer Basic Programming Sequence
          5. 7.4.9.2.5 Industrial Ethernet Mapping
          6. 7.4.9.2.6 PRUSS IEP Sync0/Sync1 Module
            1. 7.4.9.2.6.1 PRUSS IEP Sync0/Sync1 Features
            2. 7.4.9.2.6.2 PRUSS IEP Sync0/Sync1 Generation Modes
          7. 7.4.9.2.7 PRUSS IEP WatchDog
          8. 7.4.9.2.8 PRUSS IEP DIGIO
            1. 7.4.9.2.8.1 PRUSS IEP DIGIO Features
            2. 7.4.9.2.8.2 843
            3. 7.4.9.2.8.3 PRUSS IEP DIGIO Block Diagrams
            4. 7.4.9.2.8.4 PRUSS IEP Basic Programming Model
  10. 8 Interprocessor Communication (IPC)
    1. 8.1 Inter-processor Communication Scheme (IPC)
      1. 8.1.1 Mailbox
        1. 8.1.1.1 Mailbox Overview
          1. 8.1.1.1.1 Mailbox Features
          2.        851
        2. 8.1.1.2 Mailbox Functional Description
          1. 8.1.1.2.1 Mailbox Block Diagram
          2. 8.1.1.2.2 Mailbox Software Reset
          3. 8.1.1.2.3 Mailbox Power Management
          4. 8.1.1.2.4 Mailbox Interrupt Requests
          5. 8.1.1.2.5 Mailbox Assignment
            1. 8.1.1.2.5.1 Description
          6. 8.1.1.2.6 Sending and Receiving Messages
            1. 8.1.1.2.6.1 Description
          7. 8.1.1.2.7 Example of Communication
        3. 8.1.1.3 Mailbox Programming Guide
          1. 8.1.1.3.1 Mailbox Low-level Programming Models
            1. 8.1.1.3.1.1 Global Initialization
              1. 8.1.1.3.1.1.1 Surrounding Modules Global Initialization
              2. 8.1.1.3.1.1.2 Mailbox Global Initialization
                1. 8.1.1.3.1.1.2.1 Main Sequence - Mailbox Global Initialization
            2. 8.1.1.3.1.2 Mailbox Operational Modes Configuration
              1. 8.1.1.3.1.2.1 Mailbox Processing modes
                1. 8.1.1.3.1.2.1.1 Main Sequence - Sending a Message (Polling Method)
                2. 8.1.1.3.1.2.1.2 Main Sequence - Sending a Message (Interrupt Method)
                3. 8.1.1.3.1.2.1.3 Main Sequence - Receiving a Message (Polling Method)
                4. 8.1.1.3.1.2.1.4 Main Sequence - Receiving a Message (Interrupt Method)
            3. 8.1.1.3.1.3 Mailbox Events Servicing
              1. 8.1.1.3.1.3.1 Events Servicing in Sending Mode
              2. 8.1.1.3.1.3.2 Events Servicing in Receiving Mode
      2. 8.1.2 Spinlock
        1. 8.1.2.1 Spinlock Overview
          1.        879
        2. 8.1.2.2 Spinlock Functional Description
          1. 8.1.2.2.1 Spinlock Software Reset
          2. 8.1.2.2.2 Spinlock Power Management
          3. 8.1.2.2.3 About Spinlocks
          4. 8.1.2.2.4 Spinlock Functional Operation
        3. 8.1.2.3 Spinlock Programming Guide
          1. 8.1.2.3.1 Spinlock Low-level Programming Models
            1. 8.1.2.3.1.1 Surrounding Modules Global Initialization
            2. 8.1.2.3.1.2 Basic Spinlock Operations
              1. 8.1.2.3.1.2.1 Spinlocks Clearing After a System Bug Recovery
              2. 8.1.2.3.1.2.2 Take and Release Spinlock
      3. 8.1.3 Secure Proxy (SEC_PROXY)
  11. 9 Memory Controllers
    1. 9.1 DDR Subsystem (DDRSS)
      1. 9.1.1 DDRSS Overview
        1.       895
      2. 9.1.2 DDRSS Environment
      3. 9.1.3 DDRSS Functional Description
        1. 9.1.3.1 Class of Service (CoS)
        2. 9.1.3.2 AXI Write Data All-Strobes
        3. 9.1.3.3 Inline ECC for SDRAM Data
          1. 9.1.3.3.1 ECC Cache
          2. 9.1.3.3.2 ECC Cache Flush
          3. 9.1.3.3.3 ECC Statistics
        4. 9.1.3.4 Address Alias Prevention
        5. 9.1.3.5 AXI Bus Timeout
        6. 9.1.3.6 DDRSS Interrupts
        7. 9.1.3.7 DDRSS Memory Regions
        8. 9.1.3.8 DDRSS Dynamic Frequency Change Interface
        9. 9.1.3.9 DDR Controller Functional Description
          1. 9.1.3.9.1 DDR PHY Interface (DFI)
          2. 9.1.3.9.2 Command Queue
            1. 9.1.3.9.2.1 Placement Logic
            2. 9.1.3.9.2.2 Command Selection Logic
          3. 9.1.3.9.3 Transaction Processing
          4. 9.1.3.9.4 Paging Policy
          5. 9.1.3.9.5 DDR Controller Initialization
    2. 9.2 Region-based Address Translation (RAT) Module
      1. 9.2.1 RAT Functional Description
        1. 9.2.1.1 RAT Availability
        2. 9.2.1.2 RAT Operation
        3. 9.2.1.3 RAT Error Logging
  12. 10Interrupts
    1. 10.1 Interrupt Architecture
      1. 10.1.1  ESM Connectivity
        1. 10.1.1.1 Using MCU ESM to Monitor All Error Events in SoC
        2. 10.1.1.2 Using MAIN ESM to Monitor All Error Interrupts in SoC
        3. 10.1.1.3 ESM Configuration During Deep Sleep Mode
        4. 10.1.1.4 ESM0_INTERRUPT_MAP
        5. 10.1.1.5 WKUP_ESM0_INTERRUPT_MAP
      2. 10.1.2  Events
      3. 10.1.3  Interrupt Router (INTROUTER)
      4. 10.1.4  Time Synchronization Support
      5. 10.1.5  GPIO Interrupt Handling
      6. 10.1.6  Utilizing Miscellaneous Signals as Interrupt
        1. 10.1.6.1 Aggregated Interrupt from Timeout Gasket
        2. 10.1.6.2 Aggregated DCC Interrupt
        3. 10.1.6.3 Aggregated Access Error Interrupt from CBASS
        4. 10.1.6.4 Access Error to Control Register Block Interrupt Aggregation
          1. 10.1.6.4.1 EPWM Trip Signal Aggregation
      7. 10.1.7  Interrupt Connections for MCUSS NVIC
      8. 10.1.8  Interrupt Connections for GICSS
      9. 10.1.9  Interrupt Connections for R5FSS
      10. 10.1.10 Interrupt Connection for HSM
        1. 10.1.10.1 HSM0_INTERRUPT_MAP
      11. 10.1.11 Interrupt Connection for ICSSM
        1. 10.1.11.1 ICSSM0_INTERRUPT_MAP
      12. 10.1.12 Interrupt Connections Summary
  13. 11Data Movement Architecture
    1. 11.1 Data Movement Architecture Overview
      1. 11.1.1 Overview
        1. 11.1.1.1 Ring Accelerator (RINGACC)
        2. 11.1.1.2 Secure Proxy (SEC_PROXY)
        3. 11.1.1.3 Interrupt Aggregator (INTAGGR)
        4. 11.1.1.4 Packet DMA (PKTDMA)
          1. 11.1.1.4.1 PKTDMA Submodule Descriptions
            1. 11.1.1.4.1.1  Bus Interface Unit
            2. 11.1.1.4.1.2  Config CR
            3. 11.1.1.4.1.3  Configuration Registers
              1. 11.1.1.4.1.3.1 RX State Mapping
              2. 11.1.1.4.1.3.2 TX State Mapping
            4. 11.1.1.4.1.4  Tx Packet DMA Unit
            5. 11.1.1.4.1.5  Tx Packet Coherency Unit
            6. 11.1.1.4.1.6  Tx Per Channel Buffers
            7. 11.1.1.4.1.7  Rx Per Channel Buffers
            8. 11.1.1.4.1.8  Rx Packet DMA Unit
            9. 11.1.1.4.1.9  Rx Packet Coherency Unit
            10. 11.1.1.4.1.10 Event Handler
          2. 11.1.1.4.2 Channel Classes
        5. 11.1.1.5 Block Copy DMA (BCDMA)
          1. 11.1.1.5.1 BCDMA Submodule Descriptions
            1. 11.1.1.5.1.1  Bus Interface Unit
            2. 11.1.1.5.1.2  Config CR
            3. 11.1.1.5.1.3  Configuration Registers
              1. 11.1.1.5.1.3.1 BCDMA Mapping Table
            4. 11.1.1.5.1.4  Read Unit(s)
            5. 11.1.1.5.1.5  TR Coherency Unit
            6. 11.1.1.5.1.6  Per-Copy-Channel Buffers
            7. 11.1.1.5.1.7  Tx Per-Split-Channel Buffers
            8. 11.1.1.5.1.8  Rx Per-Split-Channel Buffers
            9. 11.1.1.5.1.9  Write Unit(s)
            10. 11.1.1.5.1.10 Event Coherency Unit
            11. 11.1.1.5.1.11 Event Handler
          2. 11.1.1.5.2 Channel Classes
      2. 11.1.2 Definition of Terms
      3. 11.1.3 DMSS Hardware/Software Interface
        1. 11.1.3.1 Data Buffers
        2. 11.1.3.2 Descriptors
          1. 11.1.3.2.1 Host Packet Descriptor
          2. 11.1.3.2.2 Host Buffer Descriptor
          3. 11.1.3.2.3 Transfer Request Descriptor
        3. 11.1.3.3 Transfer Request Record
          1. 11.1.3.3.1 Overview
          2. 11.1.3.3.2 Addressing Algorithm
            1. 11.1.3.3.2.1 Linear Addressing (Forward)
          3. 11.1.3.3.3 Transfer Request Formats
          4. 11.1.3.3.4 Flags Field Definition
            1. 11.1.3.3.4.1 Type: TR Type Field
            2. 11.1.3.3.4.2 EVENT_SIZE: Event Generation Definition
            3. 11.1.3.3.4.3 TRIGGER_INFO: TR Triggers
            4. 11.1.3.3.4.4 TRIGGERX_TYPE: Trigger Type
            5. 11.1.3.3.4.5 TRIGGERX: Trigger Selection
            6. 11.1.3.3.4.6 Configuration Specific Flags Definition
          5. 11.1.3.3.5 TR Address and Size Attributes
            1. 11.1.3.3.5.1  ICNT0
            2. 11.1.3.3.5.2  ICNT1
            3. 11.1.3.3.5.3  ADDR
            4. 11.1.3.3.5.4  DIM1
            5. 11.1.3.3.5.5  ICNT2
            6. 11.1.3.3.5.6  ICNT3
            7. 11.1.3.3.5.7  DIM2
            8. 11.1.3.3.5.8  DIM3
            9. 11.1.3.3.5.9  DDIM1
            10. 11.1.3.3.5.10 DADDR
            11. 11.1.3.3.5.11 DDIM2
            12. 11.1.3.3.5.12 DDIM3
            13. 11.1.3.3.5.13 DICNT0
            14. 11.1.3.3.5.14 DICNT1
            15. 11.1.3.3.5.15 DICNT2
            16. 11.1.3.3.5.16 DICNT3
        4. 11.1.3.4 Transfer Response Record
          1. 11.1.3.4.1 STATUS Field Definition
            1. 11.1.3.4.1.1 STATUS_TYPE Definitions
              1. 11.1.3.4.1.1.1 Transfer Error
              2. 11.1.3.4.1.1.2 Aborted Error
              3. 11.1.3.4.1.1.3 Submission Error
              4. 11.1.3.4.1.1.4 Unsupported Feature
              5. 11.1.3.4.1.1.5 Transfer Exception
              6. 11.1.3.4.1.1.6 Teardown Flush
        5. 11.1.3.5 Channels
        6. 11.1.3.6 Flows
        7. 11.1.3.7 Queues
          1. 11.1.3.7.1 Queue Types
            1. 11.1.3.7.1.1 Transmit Queues
            2. 11.1.3.7.1.2 Transmit Completion Queues
            3. 11.1.3.7.1.3 Free Descriptor / Buffer Queues
            4. 11.1.3.7.1.4 Receive Queues
            5. 11.1.3.7.1.5 Ring Based Queues Implementation
      4. 11.1.4 Operational Description
        1. 11.1.4.1  Resource Allocation
        2. 11.1.4.2  PKTDMA/BCDMA - Ring Operation
          1. 11.1.4.2.1 Queue Initialization
          2. 11.1.4.2.2 Queueing Entries
          3. 11.1.4.2.3 De-queueing Entries
        3. 11.1.4.3  PKTDMA/BCDMA - Output Event Generation
        4. 11.1.4.4  PKTDMA - Transmit Channel Setup
        5. 11.1.4.5  PKTDMA - Transmit Channel Pause
        6. 11.1.4.6  PKTDMA - Transmit Channel Teardown
        7. 11.1.4.7  PKTDMA - Transmit Operation
        8. 11.1.4.8  PKTDMA - Receive Free Descriptor / Buffer Queue Setup
        9. 11.1.4.9  PKTDMA - Receive Channel Setup
        10. 11.1.4.10 PKTDMA - Receive Channel Teardown
        11. 11.1.4.11 PKTDMA - Receive Channel Pause
        12. 11.1.4.12 PKTDMA - Receive Operation
        13. 11.1.4.13 BCDMA - Block Copy Channel Setup
        14. 11.1.4.14 BCDMA - Block Copy Channel Pause
        15. 11.1.4.15 BCDMA - Block Copy Channel Teardown
        16. 11.1.4.16 BCDMA - Block Copy Operation (TR Packet)
        17. 11.1.4.17 BCDMA - Block Copy Error/Exception Handling
          1. 11.1.4.17.1 Null Icnt0 Error
          2. 11.1.4.17.2 Unsupported TR Type
          3. 11.1.4.17.3 Bus Errors
        18. 11.1.4.18 BCDMA - Split Transmit Channel Setup
        19. 11.1.4.19 BCDMA - Split Transmit Operation Pause
        20. 11.1.4.20 BCDMA - Split Transmit Channel Teardown
        21. 11.1.4.21 BCDMA - Split Transmit Operation (TR Packet)
        22. 11.1.4.22 BCDMA - Split Transmit Error / Exception Handling
          1. 11.1.4.22.1 Null Icnt0 Error
          2. 11.1.4.22.2 Unsupported TR Type
          3. 11.1.4.22.3 Bus Errors
        23. 11.1.4.23 BCDMA - Split Receive Channel Setup
        24. 11.1.4.24 BCDMA - Split Receive Channel Pause
        25. 11.1.4.25 BCDMA - Split Receive Channel Teardown
        26. 11.1.4.26 BCDMA - Split Receive Operation (TR Packet)
        27. 11.1.4.27 BCDMA - Split Receive Error / Exception Handling
          1. 11.1.4.27.1 PKTDMA Exception Conditions
            1. 11.1.4.27.1.1 Descriptor Starvation
            2. 11.1.4.27.1.2 Protocol Errors
            3. 11.1.4.27.1.3 Dropped Packets
            4. 11.1.4.27.1.4 Long Packet
          2. 11.1.4.27.2 BCDMA Exception Conditions
            1. 11.1.4.27.2.1 Reception of EOL Delimiter
            2. 11.1.4.27.2.2 EOP Asserted Prematurely (Short Packet)
            3. 11.1.4.27.2.3 EOP Asserted Late (Long Packets)
            4. 11.1.4.27.2.4 Descriptor Starvation
    2. 11.2 Data Movement Subsystem (DMSS)
      1. 11.2.1 Data Movement Subsystem (DMSS)
        1. 11.2.1.1 DMSS Overview
        2.       1088
        3. 11.2.1.2 DMSS Functional Description
        4. 11.2.1.3 DMSS Interrupt Configuration
          1. 11.2.1.3.1 DMSS Event and Interrupt Flow
            1. 11.2.1.3.1.1 DMSS Interrupt Description
      2. 11.2.2 Ring Accelerator (RINGACC)
        1. 11.2.2.1 RINGACC Overview
          1. 11.2.2.1.1 RINGACC Features
          2.        1096
          3. 11.2.2.1.2 RINGACC Parameters
        2. 11.2.2.2 RINGACC Functional Description
          1. 11.2.2.2.1 Block Diagram
            1. 11.2.2.2.1.1  Configuration Registers
            2. 11.2.2.2.1.2  Source Command FIFO
            3. 11.2.2.2.1.3  Source Write Data FIFO
            4. 11.2.2.2.1.4  Source Read Data FIFO
            5. 11.2.2.2.1.5  Source Write Status FIFO
            6. 11.2.2.2.1.6  Main State Machine
            7. 11.2.2.2.1.7  Destination Command FIFO
            8. 11.2.2.2.1.8  Destination Write Data FIFO
            9. 11.2.2.2.1.9  Destination Read Data FIFO
            10. 11.2.2.2.1.10 Destination Write Status FIFO
          2. 11.2.2.2.2 RINGACC Functional Operation
            1. 11.2.2.2.2.1 Queue Modes
              1. 11.2.2.2.2.1.1 Ring Mode
              2. 11.2.2.2.2.1.2 Messaging Mode
              3. 11.2.2.2.2.1.3 Credentials Mode
              4. 11.2.2.2.2.1.4 Peek Support
              5. 11.2.2.2.2.1.5 Index Register Operation
            2. 11.2.2.2.2.2 VBUSM Target Ring Operations
            3. 11.2.2.2.2.3 VBUSM Initiator Interface Command ID Selection
            4. 11.2.2.2.2.4 Ring Push Operation (VBUSM Write to Source Interface)
            5. 11.2.2.2.2.5 Ring Pop Operation (VBUSM Read from Source Interface)
            6. 11.2.2.2.2.6 Host Doorbell Access
            7. 11.2.2.2.2.7 Queue Push Operation (VBUSM Write to Source Interface)
            8. 11.2.2.2.2.8 Queue Pop Operation (VBUSM Read from Source Interface)
            9. 11.2.2.2.2.9 Mismatched Element Size Handling
          3. 11.2.2.2.3 Events
          4. 11.2.2.2.4 Bus Error Handling
          5. 11.2.2.2.5 Monitors
            1. 11.2.2.2.5.1 Threshold Monitor
            2. 11.2.2.2.5.2 Watermark Monitor
            3. 11.2.2.2.5.3 Starvation Monitor
            4. 11.2.2.2.5.4 Statistics Monitor
            5. 11.2.2.2.5.5 Overflow
            6. 11.2.2.2.5.6 Ring Update Port
            7. 11.2.2.2.5.7 Tracing
      3. 11.2.3 Secure Proxy (SEC_PROXY)
        1. 11.2.3.1 Secure Proxy Overview
          1. 11.2.3.1.1 Secure Proxy Features
          2. 11.2.3.1.2 Secure Proxy Parameters
          3.        1139
        2. 11.2.3.2 Secure Proxy Functional Description
          1. 11.2.3.2.1  Targets
            1. 11.2.3.2.1.1 Ring Accelerator
          2. 11.2.3.2.2  Buffers
          3. 11.2.3.2.3  Proxy Credits
          4. 11.2.3.2.4  Proxy Private Word
          5. 11.2.3.2.5  Completion Byte
          6. 11.2.3.2.6  Proxy Thread Sizes
          7. 11.2.3.2.7  Proxy Thread Interleaving
          8. 11.2.3.2.8  Proxy States
          9. 11.2.3.2.9  Proxy Host Access
          10. 11.2.3.2.10 Proxy Host Writes
          11. 11.2.3.2.11 Proxy Host Reads
          12. 11.2.3.2.12 Buffer Accesses
          13. 11.2.3.2.13 Target Access
          14. 11.2.3.2.14 Error State
          15. 11.2.3.2.15 Permission Inheritance
          16. 11.2.3.2.16 Resource Association
          17. 11.2.3.2.17 Direction
          18. 11.2.3.2.18 Threshold Events
          19. 11.2.3.2.19 Error Events
          20. 11.2.3.2.20 Bus Error and Credits
          21. 11.2.3.2.21 Debug
      4. 11.2.4 Interrupt Aggregator (INTAGGR)
        1. 11.2.4.1 INTAGGR Overview
          1. 11.2.4.1.1 INTAGGR Features
          2.        1166
          3. 11.2.4.1.2 INTAGGR Parameters
        2. 11.2.4.2 INTAGGR Functional Description
          1. 11.2.4.2.1 Submodule Descriptions
            1. 11.2.4.2.1.1 Status/Mask Registers
            2. 11.2.4.2.1.2 Interrupt Mapping Block
            3. 11.2.4.2.1.3 Global Event Input (GEVI) Counters
            4. 11.2.4.2.1.4 Local Event Input (LEVI) to Global Event Conversion
            5. 11.2.4.2.1.5 Global Event Multicast
          2. 11.2.4.2.2 General Functionality
            1. 11.2.4.2.2.1 Event to Interrupt Bit Steering
            2. 11.2.4.2.2.2 Interrupt Status
            3. 11.2.4.2.2.3 Interrupt Masked Status
            4. 11.2.4.2.2.4 Enabling/Disabling Individual Interrupt Source Bits
            5. 11.2.4.2.2.5 Global Event Counting
            6. 11.2.4.2.2.6 Local Event to Global Event Conversion
            7. 11.2.4.2.2.7 Global Event Multicast
      5. 11.2.5 Packet Streaming Interface Link (PSI-L)
        1. 11.2.5.1 PSI-L Overview
        2. 11.2.5.2 PSI-L Functional Description
          1. 11.2.5.2.1 PSI-L Introduction
          2. 11.2.5.2.2 PSI-L Operation
          3. 11.2.5.2.3 Event Transport
          4. 11.2.5.2.4 Threads
          5. 11.2.5.2.5 Arbitration Protocol
          6. 11.2.5.2.6 Thread Configuration
            1. 11.2.5.2.6.1 Thread Pairing
              1. 11.2.5.2.6.1.1 Configuration Transaction Pairing
            2. 11.2.5.2.6.2 Configuration Registers Region
    3. 11.3 Peripheral DMA (PDMA)
      1. 11.3.1 PDMA Controller
        1. 11.3.1.1 PDMA Overview
          1. 11.3.1.1.1 PDMA Features
            1. 11.3.1.1.1.1 PDMA0 - SPI Features
            2. 11.3.1.1.1.2 PDMA1 - UART Features
            3. 11.3.1.1.1.3 PDMA2 - McASP Features
        2.       1202
        3. 11.3.1.2 Functional Description - SPI
          1. 11.3.1.2.1 Compliance to Standards
          2. 11.3.1.2.2 Functional Operation
            1. 11.3.1.2.2.1 Submodule Descriptions
              1. 11.3.1.2.2.1.1 Scheduler
              2. 11.3.1.2.2.1.2 Tx Per Channel Buffers
              3. 11.3.1.2.2.1.3 Tx DMA Unit
              4. 11.3.1.2.2.1.4 Rx Per Channel Buffers
              5. 11.3.1.2.2.1.5 Rx DMA Unit
            2. 11.3.1.2.2.2 General Functionality (Applicable to All Functions/Modes)
              1. 11.3.1.2.2.2.1 Operational States
              2. 11.3.1.2.2.2.2 Clock Stop
              3. 11.3.1.2.2.2.3 Emulation Control
              4. 11.3.1.2.2.2.4 Dynamic Clock Gating
            3. 11.3.1.2.2.3 Events and Flow Control
              1. 11.3.1.2.2.3.1 Channel Triggering
              2. 11.3.1.2.2.3.2 Completion Events
              3. 11.3.1.2.2.3.3 Channel Types
                1. 11.3.1.2.2.3.3.1 X-Y FIFO Mode
                2. 11.3.1.2.2.3.3.2 MCAN Mode
                3. 11.3.1.2.2.3.3.3 AASRC Mode
            4. 11.3.1.2.2.4 Transmit Operation
              1. 11.3.1.2.2.4.1 Destination (Tx) Channel Allocation
              2. 11.3.1.2.2.4.2 Destination (Tx) Channel Out of Band Signals
              3. 11.3.1.2.2.4.3 Destination Channel Initialization
                1. 11.3.1.2.2.4.3.1 PSI-L Destination Thread Pairing Registers
                  1. 3.1.2.2.4.3.1.1 Enable Register (PSIL Address 0x002)
                  2. 3.1.2.2.4.3.1.2 Local Capabilities Register (PSIL Address 0x040)
                2. 11.3.1.2.2.4.3.2 PSI-L Destination Thread Pairing
                3. 11.3.1.2.2.4.3.3 PSI-L Destination Thread Realtime Enable/Count Registers
                  1. 3.1.2.2.4.3.3.1 RT Enable Register (PSIL Address 0x408)
                  2. 3.1.2.2.4.3.3.2 Destination Thread Byte Count Register (PSIL Address 0x404)
                4. 11.3.1.2.2.4.3.4 Static Transfer Request Setup
                  1. 3.1.2.2.4.3.4.1 X-Y FIFO Mode Static TR
                  2. 3.1.2.2.4.3.4.2 MCAN Mode Static TR
                  3. 3.1.2.2.4.3.4.3 AASRC Mode Static TR
                  4. 3.1.2.2.4.3.4.4 AASRC TxFifoConfig (PSIL Address 0x405)
                  5. 3.1.2.2.4.3.4.5 AASRC TxOrderTable0 (PSIL Address 0x406)
                  6. 3.1.2.2.4.3.4.6 AASRC TxOrderTable1 (PSIL Address 0x407)
                5. 11.3.1.2.2.4.3.5 PSI-L Destination Thread Enables
              4. 11.3.1.2.2.4.4 Data Transfer
                1. 11.3.1.2.2.4.4.1 X-Y FIFO Mode Channel
                  1. 3.1.2.2.4.4.1.1 X-Y FIFO Burst Mode
                2. 11.3.1.2.2.4.4.2 MCAN Mode Channel
                  1. 3.1.2.2.4.4.2.1 MCAN Burst Mode
                3. 11.3.1.2.2.4.4.3 AASRC Channel
              5. 11.3.1.2.2.4.5 Transmit PSI-L Interface Transactions
              6. 11.3.1.2.2.4.6 Tx Pause
              7. 11.3.1.2.2.4.7 Tx Teardown
              8. 11.3.1.2.2.4.8 Tx Channel Reset
              9. 11.3.1.2.2.4.9 Tx Debug/State Register
            5. 11.3.1.2.2.5 Receive Operation
              1. 11.3.1.2.2.5.1 Source (Rx) Channel Allocation
              2. 11.3.1.2.2.5.2 Source Channel Initialization
                1. 11.3.1.2.2.5.2.1 PSI-L Source Thread Pairing Registers
                  1. 3.1.2.2.5.2.1.1 Peer Thread ID Register (PSIL Address 0x000)
                  2. 3.1.2.2.5.2.1.2 Peer Credit Register (PSIL Address 0x001)
                  3. 3.1.2.2.5.2.1.3 Enable Register (PSIL Address 0x002)
                2. 11.3.1.2.2.5.2.2 PSI-L Source Thread Realtime Enable/Count Registers
                  1. 3.1.2.2.5.2.2.1 RT Enable Register (PSIL Address 0x408)
                  2. 3.1.2.2.5.2.2.2 Source Thread Byte Count Register (PSIL Address 0x404)
                3. 11.3.1.2.2.5.2.3 PSI-L Source Thread Pairing
                4. 11.3.1.2.2.5.2.4 Static Transfer Request Setup
                  1. 3.1.2.2.5.2.4.1 X-Y FIFO Mode Static TR
                  2. 3.1.2.2.5.2.4.2 MCAN Mode Static TR
                  3. 3.1.2.2.5.2.4.3 AASRC Mode Static TR
                  4. 3.1.2.2.5.2.4.4 AASRC RxFifoConfig (PSIL Address 0x405)
                  5. 3.1.2.2.5.2.4.5 AASRC RxOrderTable0 (PSIL Address 0x406)
                  6. 3.1.2.2.5.2.4.6 AASRC RxOrderTable1 (PSIL Address 0x407)
                5. 11.3.1.2.2.5.2.5 PSI-L Source Thread Enables
              3. 11.3.1.2.2.5.3 Data Transfer
                1. 11.3.1.2.2.5.3.1 X-Y FIFO Mode Channel
                  1. 3.1.2.2.5.3.1.1 X-Y FIFO Burst Mode
                2. 11.3.1.2.2.5.3.2 MCAN Mode Channel
                  1. 3.1.2.2.5.3.2.1 MCAN Burst Mode
                3. 11.3.1.2.2.5.3.3 AASRC Channel
              4. 11.3.1.2.2.5.4 Receive PSI-L Interface Transactions
              5. 11.3.1.2.2.5.5 Rx Pause
              6. 11.3.1.2.2.5.6 Rx Teardown
              7. 11.3.1.2.2.5.7 Rx Channel Reset
              8. 11.3.1.2.2.5.8 Rx Debug/State Register
        4. 11.3.1.3 Functional Description - UART
          1. 11.3.1.3.1 Compliance to Standards
          2. 11.3.1.3.2 Functional Operation
            1. 11.3.1.3.2.1 Submodule Descriptions
              1. 11.3.1.3.2.1.1 Scheduler
              2. 11.3.1.3.2.1.2 Tx Per Channel Buffers
              3. 11.3.1.3.2.1.3 Tx DMA Unit
              4. 11.3.1.3.2.1.4 Rx Per Channel Buffers
              5. 11.3.1.3.2.1.5 Rx DMA Unit
            2. 11.3.1.3.2.2 General Functionality (Applicable to All Functions/Modes)
              1. 11.3.1.3.2.2.1 Operational States
              2. 11.3.1.3.2.2.2 Clock Stop
              3. 11.3.1.3.2.2.3 Emulation Control
              4. 11.3.1.3.2.2.4 Dynamic Clock Gating
            3. 11.3.1.3.2.3 Events and Flow Control
              1. 11.3.1.3.2.3.1 Channel Triggering
              2. 11.3.1.3.2.3.2 Completion Events
              3. 11.3.1.3.2.3.3 Channel Types
                1. 11.3.1.3.2.3.3.1 X-Y FIFO Mode
                2. 11.3.1.3.2.3.3.2 MCAN Mode
                3. 11.3.1.3.2.3.3.3 AASRC Mode
            4. 11.3.1.3.2.4 Transmit Operation
              1. 11.3.1.3.2.4.1 Destination (Tx) Channel Allocation
              2. 11.3.1.3.2.4.2 Destination (Tx) Channel Out of Band Signals
              3. 11.3.1.3.2.4.3 Destination Channel Initialization
                1. 11.3.1.3.2.4.3.1 PSI-L Destination Thread Pairing Registers
                  1. 3.1.3.2.4.3.1.1 Enable Register (PSIL Address 0x002)
                  2. 3.1.3.2.4.3.1.2 Local Capabilities Register (PSIL Address 0x040)
                2. 11.3.1.3.2.4.3.2 PSI-L Destination Thread Pairing
                3. 11.3.1.3.2.4.3.3 PSI-L Destination Thread Realtime Enable/Count Registers
                  1. 3.1.3.2.4.3.3.1 RT Enable Register (PSIL Address 0x408)
                  2. 3.1.3.2.4.3.3.2 Destination Thread Byte Count Register (PSIL Address 0x404)
                4. 11.3.1.3.2.4.3.4 Static Transfer Request Setup
                  1. 3.1.3.2.4.3.4.1 X-Y FIFO Mode Static TR
                  2. 3.1.3.2.4.3.4.2 MCAN Mode Static TR
                  3. 3.1.3.2.4.3.4.3 AASRC Mode Static TR
                  4. 3.1.3.2.4.3.4.4 AASRC TxFifoConfig (PSIL Address 0x405)
                  5. 3.1.3.2.4.3.4.5 AASRC TxOrderTable0 (PSIL Address 0x406)
                  6. 3.1.3.2.4.3.4.6 AASRC TxOrderTable1 (PSIL Address 0x407)
                5. 11.3.1.3.2.4.3.5 PSI-L Destination Thread Enables
              4. 11.3.1.3.2.4.4 Data Transfer
                1. 11.3.1.3.2.4.4.1 X-Y FIFO Mode Channel
                  1. 3.1.3.2.4.4.1.1 X-Y FIFO Burst Mode
                2. 11.3.1.3.2.4.4.2 MCAN Mode Channel
                  1. 3.1.3.2.4.4.2.1 MCAN Burst Mode
                3. 11.3.1.3.2.4.4.3 AASRC Channel
              5. 11.3.1.3.2.4.5 Transmit PSI-L Interface Transactions
              6. 11.3.1.3.2.4.6 Tx Pause
              7. 11.3.1.3.2.4.7 Tx Teardown
              8. 11.3.1.3.2.4.8 Tx Channel Reset
              9. 11.3.1.3.2.4.9 Tx Debug/State Register
            5. 11.3.1.3.2.5 Receive Operation
              1. 11.3.1.3.2.5.1 Source (Rx) Channel Allocation
              2. 11.3.1.3.2.5.2 Source Channel Initialization
                1. 11.3.1.3.2.5.2.1 PSI-L Source Thread Pairing Registers
                  1. 3.1.3.2.5.2.1.1 Peer Thread ID Register (PSIL Address 0x000)
                  2. 3.1.3.2.5.2.1.2 Peer Credit Register (PSIL Address 0x001)
                  3. 3.1.3.2.5.2.1.3 Enable Register (PSIL Address 0x002)
                2. 11.3.1.3.2.5.2.2 PSI-L Source Thread Realtime Enable/Count Registers
                  1. 3.1.3.2.5.2.2.1 RT Enable Register (PSIL Address 0x408)
                  2. 3.1.3.2.5.2.2.2 Source Thread Byte Count Register (PSIL Address 0x404)
                3. 11.3.1.3.2.5.2.3 PSI-L Source Thread Pairing
                4. 11.3.1.3.2.5.2.4 Static Transfer Request Setup
                  1. 3.1.3.2.5.2.4.1 X-Y FIFO Mode Static TR
                  2. 3.1.3.2.5.2.4.2 MCAN Mode Static TR
                  3. 3.1.3.2.5.2.4.3 AASRC Mode Static TR
                  4. 3.1.3.2.5.2.4.4 AASRC RxFifoConfig (PSIL Address 0x405)
                  5. 3.1.3.2.5.2.4.5 AASRC RxOrderTable0 (PSIL Address 0x406)
                  6. 3.1.3.2.5.2.4.6 AASRC RxOrderTable1 (PSIL Address 0x407)
                5. 11.3.1.3.2.5.2.5 PSI-L Source Thread Enables
              3. 11.3.1.3.2.5.3 Data Transfer
                1. 11.3.1.3.2.5.3.1 X-Y FIFO Mode Channel
                  1. 3.1.3.2.5.3.1.1 X-Y FIFO Burst Mode
                2. 11.3.1.3.2.5.3.2 MCAN Mode Channel
                  1. 3.1.3.2.5.3.2.1 MCAN Burst Mode
                3. 11.3.1.3.2.5.3.3 AASRC Channel
              4. 11.3.1.3.2.5.4 Receive PSI-L Interface Transactions
              5. 11.3.1.3.2.5.5 Rx Pause
              6. 11.3.1.3.2.5.6 Rx Teardown
              7. 11.3.1.3.2.5.7 Rx Channel Reset
              8. 11.3.1.3.2.5.8 Rx Debug/State Register
        5. 11.3.1.4 Functional Description - McASP
          1. 11.3.1.4.1 Compliance to Standards
          2. 11.3.1.4.2 Functional Operation
            1. 11.3.1.4.2.1 Submodule Descriptions
              1. 11.3.1.4.2.1.1 Scheduler
              2. 11.3.1.4.2.1.2 Tx Per Channel Buffers
              3. 11.3.1.4.2.1.3 Tx DMA Unit
              4. 11.3.1.4.2.1.4 Rx Per Channel Buffers
              5. 11.3.1.4.2.1.5 Rx DMA Unit
            2. 11.3.1.4.2.2 General Functionality (Applicable to All Functions/Modes)
              1. 11.3.1.4.2.2.1 Operational States
              2. 11.3.1.4.2.2.2 Clock Stop
              3. 11.3.1.4.2.2.3 Emulation Control
            3. 11.3.1.4.2.3 Events and Flow Control
              1. 11.3.1.4.2.3.1 Channel Triggering
              2. 11.3.1.4.2.3.2 Completion Events
              3. 11.3.1.4.2.3.3 Channel Types
                1. 11.3.1.4.2.3.3.1 X-Y FIFO Mode
                2. 11.3.1.4.2.3.3.2 MCAN Mode
                3. 11.3.1.4.2.3.3.3 AASRC Mode
            4. 11.3.1.4.2.4 Transmit Operation
              1. 11.3.1.4.2.4.1 Destination (Tx) Channel Allocation
              2. 11.3.1.4.2.4.2 Destination (Tx) Channel Out of Band Signals
              3. 11.3.1.4.2.4.3 Destination Channel Initialization
                1. 11.3.1.4.2.4.3.1 PSI-L Destination Thread Pairing Registers
                  1. 3.1.4.2.4.3.1.1 Enable Register (PSIL Address 0x002)
                  2. 3.1.4.2.4.3.1.2 Peer Credit Register (PSIL Address 0x040)
                2. 11.3.1.4.2.4.3.2 PSI-L Destination Thread Pairing
                3. 11.3.1.4.2.4.3.3 PSI-L Destination Thread Realtime Enable/Count Registers
                  1. 3.1.4.2.4.3.3.1 RT Enable Register (PSIL Address 0x408)
                  2. 3.1.4.2.4.3.3.2 Destination Thread Byte Count Register (PSIL Address 0x404)
                4. 11.3.1.4.2.4.3.4 Static Transfer Request Setup
                  1. 3.1.4.2.4.3.4.1 X-Y FIFO Mode Static TR
                  2. 3.1.4.2.4.3.4.2 MCAN Mode Static TR
                  3. 3.1.4.2.4.3.4.3 AASRC Mode Static TR
                  4. 3.1.4.2.4.3.4.4 AASRC TxFifoConfig (PSIL Address 0x405)
                  5. 3.1.4.2.4.3.4.5 AASRC TxOrderTable0 (PSIL Address 0x406)
                  6. 3.1.4.2.4.3.4.6 AASRC TxOrderTable1 (PSIL Address 0x407)
                5. 11.3.1.4.2.4.3.5 PSI-L Destination Thread Enables
              4. 11.3.1.4.2.4.4 Data Transfer
                1. 11.3.1.4.2.4.4.1 X-Y FIFO Mode Channel
                  1. 3.1.4.2.4.4.1.1 X-Y FIFO Burst Mode
                2. 11.3.1.4.2.4.4.2 MCAN Mode Channel
                3. 11.3.1.4.2.4.4.3 AASRC Channel
              5. 11.3.1.4.2.4.5 Transmit PSI-L Interface Transactions
              6. 11.3.1.4.2.4.6 Tx Pause
              7. 11.3.1.4.2.4.7 Tx Teardown
              8. 11.3.1.4.2.4.8 Tx Channel Reset
              9. 11.3.1.4.2.4.9 Tx Debug/State Register
            5. 11.3.1.4.2.5 Receive Operation
              1. 11.3.1.4.2.5.1 Source (Rx) Channel Allocation
              2. 11.3.1.4.2.5.2 Source Channel Initialization
                1. 11.3.1.4.2.5.2.1 PSI-L Source Thread Pairing Registers
                  1. 3.1.4.2.5.2.1.1 Peer Thread ID Register (PSIL Address 0x000)
                  2. 3.1.4.2.5.2.1.2 Peer Credit Register (PSIL Address 0x001)
                  3. 3.1.4.2.5.2.1.3 Enable Register (PSIL Address 0x002)
                2. 11.3.1.4.2.5.2.2 PSI-L Source Thread Realtime Enable/Count Registers
                  1. 3.1.4.2.5.2.2.1 RT Enable Register (PSIL Address 0x408)
                  2. 3.1.4.2.5.2.2.2 Source Thread Byte Count Register (PSIL Address 0x404)
                3. 11.3.1.4.2.5.2.3 PSI-L Source Thread Pairing
                4. 11.3.1.4.2.5.2.4 Static Transfer Request Setup
                  1. 3.1.4.2.5.2.4.1 X-Y FIFO Mode Static TR
                  2. 3.1.4.2.5.2.4.2 MCAN Mode Static TR
                  3. 3.1.4.2.5.2.4.3 AASRC Mode Static TR
                  4. 3.1.4.2.5.2.4.4 AASRC RxFifoConfig (PSIL Address 0x405)
                  5. 3.1.4.2.5.2.4.5 AASRC RxOrderTable0 (PSIL Address 0x406)
                  6. 3.1.4.2.5.2.4.6 AASRC RxOrderTable1 (PSIL Address 0x407)
                5. 11.3.1.4.2.5.2.5 PSI-L Source Thread Enables
              3. 11.3.1.4.2.5.3 Data Transfer
                1. 11.3.1.4.2.5.3.1 X-Y FIFO Mode Channel
                  1. 3.1.4.2.5.3.1.1 X-Y FIFO Burst Mode
                2. 11.3.1.4.2.5.3.2 MCAN Mode Channel
                3. 11.3.1.4.2.5.3.3 AASRC Channel
              4. 11.3.1.4.2.5.4 Receive PSI-L Interface Transactions
              5. 11.3.1.4.2.5.5 Rx Pause
              6. 11.3.1.4.2.5.6 Rx Teardown
              7. 11.3.1.4.2.5.7 Rx Channel Reset
              8. 11.3.1.4.2.5.8 Rx Debug/State Register
        6. 11.3.1.5 PDMA Registers
  14. 12Peripherals
    1. 12.1 Audio Peripherals
      1. 12.1.1 Multichannel Audio Serial Port (MCASP)
        1. 12.1.1.1 MCASP Overview
          1. 12.1.1.1.1 MCASP Features
          2.        1449
          3. 12.1.1.1.2 Unsupported Features
        2. 12.1.1.2 MCASP Environment
          1. 12.1.1.2.1 MCASP Signals
          2. 12.1.1.2.2 MCASP Protocols and Data Formats
            1. 12.1.1.2.2.1 Protocols Supported
            2. 12.1.1.2.2.2 Definition of Terms
            3. 12.1.1.2.2.3 TDM Format
            4. 12.1.1.2.2.4 I2S Format
            5. 12.1.1.2.2.5 S/PDIF Coding Format
              1. 12.1.1.2.2.5.1 Biphase-Mark Code
              2. 12.1.1.2.2.5.2 S/PDIF Subframe Format
              3. 12.1.1.2.2.5.3 Frame Format
        3. 12.1.1.3 Integration
        4. 12.1.1.4 MCASP Functional Description
          1. 12.1.1.4.1  MCASP Block Diagram
          2. 12.1.1.4.2  MCASP Clock and Frame-Sync Configurations
            1. 12.1.1.4.2.1 MCASP Transmit Clock
            2. 12.1.1.4.2.2 MCASP Receive Clock
            3. 12.1.1.4.2.3 Frame-Sync Generator
            4. 12.1.1.4.2.4 Synchronous and Asynchronous Transmit and Receive Operations
          3. 12.1.1.4.3  MCASP Serializers
          4. 12.1.1.4.4  MCASP Format Units
            1. 12.1.1.4.4.1 Transmit Format Unit
              1. 12.1.1.4.4.1.1 TDM Mode Transmission Data Alignment Settings
              2. 12.1.1.4.4.1.2 DIT Mode Transmission Data Alignment Settings
            2. 12.1.1.4.4.2 Receive Format Unit
              1. 12.1.1.4.4.2.1 TDM Mode Reception Data Alignment Settings
          5. 12.1.1.4.5  MCASP State-Machines
          6. 12.1.1.4.6  MCASP TDM Sequencers
          7. 12.1.1.4.7  MCASP Software Reset
          8. 12.1.1.4.8  MCASP Power Management
          9. 12.1.1.4.9  MCASP Transfer Modes
            1. 12.1.1.4.9.1 Burst Transfer Mode
            2. 12.1.1.4.9.2 Time-Division Multiplexed (TDM) Transfer Mode
              1. 12.1.1.4.9.2.1 TDM Time Slots Generation and Processing
              2. 12.1.1.4.9.2.2 Special 384-Slot TDM Mode for Connection to External DIR
            3. 12.1.1.4.9.3 DIT Transfer Mode
              1. 12.1.1.4.9.3.1 Transmit DIT Encoding
              2. 12.1.1.4.9.3.2 Transmit DIT Clock and Frame-Sync Generation
              3. 12.1.1.4.9.3.3 DIT Channel Status and User Data Register Files
          10. 12.1.1.4.10 MCASP Data Transmission and Reception
            1. 12.1.1.4.10.1 Data Ready Status and Event/Interrupt Generation
              1. 12.1.1.4.10.1.1 Transmit Data Ready
              2. 12.1.1.4.10.1.2 Receive Data Ready
              3. 12.1.1.4.10.1.3 Transfers Through the Data Port (DATA)
              4. 12.1.1.4.10.1.4 Transfers Through the Configuration Bus (CFG)
              5. 12.1.1.4.10.1.5 Using a Device CPU for MCASP Servicing
              6. 12.1.1.4.10.1.6 Using the DMA for MCASP Servicing
          11. 12.1.1.4.11 MCASP Audio FIFO (AFIFO)
            1. 12.1.1.4.11.1 AFIFO Data Transmission
              1. 12.1.1.4.11.1.1 Transmit DMA Event Pacer
            2. 12.1.1.4.11.2 AFIFO Data Reception
              1. 12.1.1.4.11.2.1 Receive DMA Event Pacer
            3. 12.1.1.4.11.3 Arbitration Between Transmit and Receive DMA Requests
          12. 12.1.1.4.12 MCASP Events and Interrupt Requests
            1. 12.1.1.4.12.1 Transmit Data Ready Event and Interrupt
            2. 12.1.1.4.12.2 Receive Data Ready Event and Interrupt
            3. 12.1.1.4.12.3 Error Interrupt
            4. 12.1.1.4.12.4 Multiple Interrupts
          13. 12.1.1.4.13 MCASP DMA Requests
          14. 12.1.1.4.14 MCASP Loopback Modes
            1. 12.1.1.4.14.1 Loopback Mode Configurations
          15. 12.1.1.4.15 MCASP Error Reporting
            1. 12.1.1.4.15.1 Buffer Underrun Error -Transmitter
            2. 12.1.1.4.15.2 Buffer Overrun Error-Receiver
            3. 12.1.1.4.15.3 DATA Port Error - Transmitter
            4. 12.1.1.4.15.4 DATA Port Error - Receiver
            5. 12.1.1.4.15.5 Unexpected Frame Sync Error
            6. 12.1.1.4.15.6 Clock Failure Detection
              1. 12.1.1.4.15.6.1 Clock Failure Check Startup
              2. 12.1.1.4.15.6.2 Transmit Clock Failure Check and Recovery
              3. 12.1.1.4.15.6.3 Receive Clock Failure Check and Recovery
        5. 12.1.1.5 MCASP Programming Guide
          1. 12.1.1.5.1 MCASP Global Initialization
            1. 12.1.1.5.1.1 Surrounding Modules Global Initialization
            2. 12.1.1.5.1.2 MCASP Global Initialization
              1. 12.1.1.5.1.2.1 Main Sequence – MCASP Global Initialization for DIT-Transmission
                1. 12.1.1.5.1.2.1.1 Subsequence – Transmit Format Unit Configuration for DIT-Transmission
                2. 12.1.1.5.1.2.1.2 Subsequence – Transmit Frame Synchronization Generator Configuration for DIT-Transmission
                3. 12.1.1.5.1.2.1.3 Subsequence – Transmit Clock Generator Configuration for DIT-Transmission
                4. 12.1.1.5.1.2.1.4 Subsequence - MCASP Pins Functional Configuration
                5. 12.1.1.5.1.2.1.5 Subsequence – DIT-specific Subframe Fields Configuration
              2. 12.1.1.5.1.2.2 Main Sequence – MCASP Global Initialization for TDM-Reception
                1. 12.1.1.5.1.2.2.1 Subsequence – Receive Format Unit Configuration in TDM Mode
                2. 12.1.1.5.1.2.2.2 Subsequence – Receive Frame Synchronization Generator Configuration in TDM Mode
                3. 12.1.1.5.1.2.2.3 Subsequence – Receive Clock Generator Configuration
                4. 12.1.1.5.1.2.2.4 Subsequence—MCASP Receiver Pins Functional Configuration
              3. 12.1.1.5.1.2.3 Main Sequence – MCASP Global Initialization for TDM -Transmission
                1. 12.1.1.5.1.2.3.1 Subsequence – Transmit Format Unit Configuration in TDM Mode
                2. 12.1.1.5.1.2.3.2 Subsequence – Transmit Frame Synchronization Generator Configuration in TDM Mode
                3. 12.1.1.5.1.2.3.3 Subsequence – Transmit Clock Generator Configuration for TDM Cases
                4. 12.1.1.5.1.2.3.4 Subsequence—MCASP Transmit Pins Functional Configuration
          2. 12.1.1.5.2 MCASP Operational Modes Configuration
            1. 12.1.1.5.2.1 MCASP Transmission Modes
              1. 12.1.1.5.2.1.1 Main Sequence – MCASP DIT- /TDM- Polling Transmission Method
              2. 12.1.1.5.2.1.2 Main Sequence – MCASP DIT- /TDM - Interrupt Transmission Method
              3. 12.1.1.5.2.1.3 Main Sequence –MCASP DIT- /TDM - Mode DMA Transmission Method
            2. 12.1.1.5.2.2 MCASP Reception Modes
              1. 12.1.1.5.2.2.1 Main Sequence – MCASP Polling Reception Method
              2. 12.1.1.5.2.2.2 Main Sequence – MCASP TDM - Interrupt Reception Method
              3. 12.1.1.5.2.2.3 Main Sequence – MCASP TDM - Mode DMA Reception Method
            3. 12.1.1.5.2.3 MCASP Event Servicing
              1. 12.1.1.5.2.3.1 MCASP DIT-/TDM- Transmit Interrupt Events Servicing
              2. 12.1.1.5.2.3.2 MCASP TDM- Receive Interrupt Events Servicing
              3. 12.1.1.5.2.3.3 Subsequence – MCASP DIT-/TDM -Modes Transmit Error Handling
              4. 12.1.1.5.2.3.4 Subsequence – MCASP Receive Error Handling
    2. 12.2 General Connectivity Peripherals
      1. 12.2.1 General-Purpose Interface (GPIO)
        1. 12.2.1.1 GPIO Overview
          1. 12.2.1.1.1 GPIO Features
          2. 12.2.1.1.2 Unsupported Features
          3.        1561
        2. 12.2.1.2 GPIO Environment
          1. 12.2.1.2.1 GPIO Interface Signals
        3. 12.2.1.3 Integration
        4. 12.2.1.4 GPIO Functional Description
          1. 12.2.1.4.1 GPIO Block Diagram
          2. 12.2.1.4.2 GPIO Function
          3. 12.2.1.4.3 Interrupt and Event Generation
            1. 12.2.1.4.3.1 Interrupt Enable (per Bank)
            2. 12.2.1.4.3.2 Trigger Configuration (per Bit)
            3. 12.2.1.4.3.3 Interrupt Status and Clear (per Bit)
          4. 12.2.1.4.4 GPIO Interrupt Connectivity
          5. 12.2.1.4.5 Emulation Halt Operation
        5. 12.2.1.5 GPIO Programming Guide
          1. 12.2.1.5.1 GPIO Low-Level Programming Models
            1. 12.2.1.5.1.1 Global Initialization
              1. 12.2.1.5.1.1.1 Surrounding Modules Global Initialization
              2. 12.2.1.5.1.1.2 GPIO Module Global Initialization
            2. 12.2.1.5.1.2 GPIO Operational Modes Configuration
              1. 12.2.1.5.1.2.1 GPIO Read Input Register
              2. 12.2.1.5.1.2.2 GPIO Set Bit Function
              3. 12.2.1.5.1.2.3 GPIO Clear Bit Function
      2. 12.2.2 Inter-Integrated Circuit (I2C) Interface
        1. 12.2.2.1 I2C Overview
          1. 12.2.2.1.1 I2C Features
          2. 12.2.2.1.2 Integration
          3. 12.2.2.1.3 Unsupported Features
          4.        1588
        2. 12.2.2.2 I2C Environment
          1. 12.2.2.2.1 I2C Typical Application
            1. 12.2.2.2.1.1 I2C Pins for Typical Connections in I2C Mode
            2. 12.2.2.2.1.2 I2C Interface Typical Connections
            3. 12.2.2.2.1.3 1593
          2. 12.2.2.2.2 I2C Typical Connection Protocol and Data Format
            1. 12.2.2.2.2.1  I2C Serial Data Format
            2. 12.2.2.2.2.2  I2C Data Validity
            3. 12.2.2.2.2.3  I2C Start and Stop Conditions
            4. 12.2.2.2.2.4  I2C Addressing
              1. 12.2.2.2.2.4.1 Data Transfer Formats in F/S Mode
              2. 12.2.2.2.2.4.2 Data Transfer Format in HS Mode
            5. 12.2.2.2.2.5  I2C Controller Transmitter
            6. 12.2.2.2.2.6  I2C Controller Receiver
            7. 12.2.2.2.2.7  I2C Target Transmitter
            8. 12.2.2.2.2.8  I2C Target Receiver
            9. 12.2.2.2.2.9  I2C Bus Arbitration
            10. 12.2.2.2.2.10 I2C Clock Generation and Synchronization
        3. 12.2.2.3 I2C Functional Description
          1. 12.2.2.3.1 I2C Block Diagram
          2. 12.2.2.3.2 I2C Clocks
            1. 12.2.2.3.2.1 I2C Clocking
            2. 12.2.2.3.2.2 I2C Automatic Blocking of the I2C Clock Feature
          3. 12.2.2.3.3 I2C Software Reset
          4. 12.2.2.3.4 I2C Power Management
          5. 12.2.2.3.5 I2C Interrupt Requests
          6. 12.2.2.3.6 I2C Programmable Multitarget Channel Feature
          7. 12.2.2.3.7 I2C FIFO Management
            1. 12.2.2.3.7.1 I2C FIFO Interrupt Mode
            2. 12.2.2.3.7.2 I2C FIFO Polling Mode
            3. 12.2.2.3.7.3 I2C Draining Feature
          8. 12.2.2.3.8 I2C Noise Filter
          9. 12.2.2.3.9 I2C System Test Mode
        4. 12.2.2.4 I2C Programming Guide
          1. 12.2.2.4.1 I2C Low-Level Programming Models
            1. 12.2.2.4.1.1 I2C Programming Model
              1. 12.2.2.4.1.1.1 Main Program
                1. 12.2.2.4.1.1.1.1 Configure the Module Before Enabling the I2C Controller
                2. 12.2.2.4.1.1.1.2 Initialize the I2C Controller
                3. 12.2.2.4.1.1.1.3 Configure Target Address and the Data Control Register
                4. 12.2.2.4.1.1.1.4 Initiate a Transfer
                5. 12.2.2.4.1.1.1.5 Receive Data
                6. 12.2.2.4.1.1.1.6 Transmit Data
              2. 12.2.2.4.1.1.2 Interrupt Subroutine Sequence
              3. 12.2.2.4.1.1.3 Programming Flow-Diagrams
      3. 12.2.3 Multichannel Serial Peripheral Interface (MCSPI)
        1. 12.2.3.1 MCSPI Overview
          1. 12.2.3.1.1 MCSPI Features
          2. 12.2.3.1.2 Unsupported Features
          3.        1638
        2. 12.2.3.2 MCSPI Environment
          1. 12.2.3.2.1 Basic MCSPI Pins for Controller Mode
          2. 12.2.3.2.2 Basic MCSPI Pins for Peripheral Mode
          3. 12.2.3.2.3 MCSPI Protocol and Data Format
            1. 12.2.3.2.3.1 Transfer Format
          4. 12.2.3.2.4 MCSPI in Controller Mode
          5. 12.2.3.2.5 MCSPI in Peripheral Mode
        3. 12.2.3.3 Integration
        4. 12.2.3.4 MCSPI Functional Description
          1. 12.2.3.4.1 MCSPI Block Diagram
          2. 12.2.3.4.2 MCSPI Reset
          3. 12.2.3.4.3 MCSPI Controller Mode
            1. 12.2.3.4.3.1 Controller Mode Features
            2. 12.2.3.4.3.2 Controller Transmit-and-Receive Mode (Full Duplex)
            3. 12.2.3.4.3.3 Controller Transmit-Only Mode (Half Duplex)
            4. 12.2.3.4.3.4 Controller Receive-Only Mode (Half Duplex)
            5. 12.2.3.4.3.5 Single-Channel Controller Mode
              1. 12.2.3.4.3.5.1 Programming Tips When Switching to Another Channel
              2. 12.2.3.4.3.5.2 Force SPIEN[i] Mode
              3. 12.2.3.4.3.5.3 Turbo Mode
            6. 12.2.3.4.3.6 Start-Bit Mode
            7. 12.2.3.4.3.7 Chip-Select Timing Control
            8. 12.2.3.4.3.8 Programmable MCSPI Clock (SPICLK)
              1. 12.2.3.4.3.8.1 Clock Ratio Granularity
          4. 12.2.3.4.4 MCSPI Peripheral Mode
            1. 12.2.3.4.4.1 Dedicated Resources
            2. 12.2.3.4.4.2 Peripheral Transmit-and-Receive Mode
            3. 12.2.3.4.4.3 Peripheral Transmit-Only Mode
            4. 12.2.3.4.4.4 Peripheral Receive-Only Mode
          5. 12.2.3.4.5 MCSPI 3-Pin or 4-Pin Mode
          6. 12.2.3.4.6 MCSPI FIFO Buffer Management
            1. 12.2.3.4.6.1 Buffer Almost Full
            2. 12.2.3.4.6.2 Buffer Almost Empty
            3. 12.2.3.4.6.3 End of Transfer Management
            4. 12.2.3.4.6.4 Multiple MCSPI Word Access
            5. 12.2.3.4.6.5 First MCSPI Word Delay
          7. 12.2.3.4.7 MCSPI Interrupts
            1. 12.2.3.4.7.1 Interrupt Events in Controller Mode
              1. 12.2.3.4.7.1.1 TXx_EMPTY
              2. 12.2.3.4.7.1.2 TXx_UNDERFLOW
              3. 12.2.3.4.7.1.3 RXx_ FULL
              4. 12.2.3.4.7.1.4 End Of Word Count
            2. 12.2.3.4.7.2 Interrupt Events in Peripheral Mode
              1. 12.2.3.4.7.2.1 TXx_EMPTY
              2. 12.2.3.4.7.2.2 TXx_UNDERFLOW
              3. 12.2.3.4.7.2.3 RXx_FULL
              4. 12.2.3.4.7.2.4 RX0_OVERFLOW
              5. 12.2.3.4.7.2.5 End Of Word Count
            3. 12.2.3.4.7.3 Interrupt-Driven Operation
            4. 12.2.3.4.7.4 Polling
          8. 12.2.3.4.8 MCSPI DMA Requests
          9. 12.2.3.4.9 MCSPI Power Saving Management
            1. 12.2.3.4.9.1 Normal Mode
            2. 12.2.3.4.9.2 Idle Mode
              1. 12.2.3.4.9.2.1 Force-Idle Mode
        5. 12.2.3.5 MCSPI Programming Guide
          1. 12.2.3.5.1 MCSPI Global Initialization
            1. 12.2.3.5.1.1 Surrounding Modules Global Initialization
            2. 12.2.3.5.1.2 MCSPI Global Initialization
              1. 12.2.3.5.1.2.1 Main Sequence – MCSPI Global Initialization
          2. 12.2.3.5.2 MCSPI Operational Mode Configuration
            1. 12.2.3.5.2.1 MCSPI Operational Modes
              1. 12.2.3.5.2.1.1 Common Transfer Sequence
              2. 12.2.3.5.2.1.2 End of Transfer Sequences
              3. 12.2.3.5.2.1.3 Transmit-and-Receive (Controller and Peripheral)
              4. 12.2.3.5.2.1.4 Transmit-Only (Controller and Peripheral)
                1. 12.2.3.5.2.1.4.1 Based on Interrupt Requests
                2. 12.2.3.5.2.1.4.2 Based on DMA Write Requests
              5. 12.2.3.5.2.1.5 Controller Normal Receive-Only
                1. 12.2.3.5.2.1.5.1 Based on Interrupt Requests
                2. 12.2.3.5.2.1.5.2 Based on DMA Read Requests
              6. 12.2.3.5.2.1.6 Controller Turbo Receive-Only
                1. 12.2.3.5.2.1.6.1 Based on Interrupt Requests
                2. 12.2.3.5.2.1.6.2 Based on DMA Read Requests
              7. 12.2.3.5.2.1.7 Peripheral Receive-Only
              8. 12.2.3.5.2.1.8 Transfer Procedures With FIFO
                1. 12.2.3.5.2.1.8.1 Common Transfer Sequence in FIFO Mode
                2. 12.2.3.5.2.1.8.2 End of Transfer Sequences in FIFO Mode
                3. 12.2.3.5.2.1.8.3 Transmit-and-Receive With Word Count
                4. 12.2.3.5.2.1.8.4 Transmit-and-Receive Without Word Count
                5. 12.2.3.5.2.1.8.5 Transmit-Only
                6. 12.2.3.5.2.1.8.6 Receive-Only With Word Count
                7. 12.2.3.5.2.1.8.7 Receive-Only Without Word Count
              9. 12.2.3.5.2.1.9 Common Transfer Procedures Without FIFO – Polling Method
                1. 12.2.3.5.2.1.9.1 Receive-Only Procedure – Polling Method
                2. 12.2.3.5.2.1.9.2 Receive-Only Procedure – Interrupt Method
                3. 12.2.3.5.2.1.9.3 Transmit-Only Procedure – Polling Method
                4. 12.2.3.5.2.1.9.4 Transmit-and-Receive Procedure – Polling Method
          3. 12.2.3.5.3 Common Transfer Procedures Without FIFO – Polling Method
            1. 12.2.3.5.3.1 Receive-Only Procedure – Polling Method
            2. 12.2.3.5.3.2 Receive-Only Procedure – Interrupt Method
            3. 12.2.3.5.3.3 Transmit-Only Procedure – Polling Method
            4. 12.2.3.5.3.4 Transmit-and-Receive Procedure – Polling Method
      4. 12.2.4 Universal Asynchronous Receiver/Transmitter (UART)
        1. 12.2.4.1 UART Overview
          1. 12.2.4.1.1 UART Features
          2. 12.2.4.1.2 Unsupported Features
          3.        1736
          4. 12.2.4.1.3 IrDA Features
          5. 12.2.4.1.4 CIR Features
        2. 12.2.4.2 UART Environment
          1. 12.2.4.2.1 UART Functional Interfaces
            1. 12.2.4.2.1.1 System Using UART Communication With Hardware Handshake
            2. 12.2.4.2.1.2 UART Interface Description
            3. 12.2.4.2.1.3 UART Protocol and Data Format
          2. 12.2.4.2.2 RS-485 Functional Interfaces
            1. 12.2.4.2.2.1 System Using RS-485 Communication
            2. 12.2.4.2.2.2 RS-485 Interface Description
          3. 12.2.4.2.3 IrDA Functional Interfaces
            1. 12.2.4.2.3.1 System Using IrDA Communication Protocol
            2. 12.2.4.2.3.2 IrDA Interface Description
            3. 12.2.4.2.3.3 IrDA Protocol and Data Format
              1. 12.2.4.2.3.3.1 SIR Mode
                1. 12.2.4.2.3.3.1.1 Frame Format
                2. 12.2.4.2.3.3.1.2 Asynchronous Transparency
                3. 12.2.4.2.3.3.1.3 Abort Sequence
                4. 12.2.4.2.3.3.1.4 Pulse Shaping
                5. 12.2.4.2.3.3.1.5 Encoder
                6. 12.2.4.2.3.3.1.6 Decoder
                7. 12.2.4.2.3.3.1.7 IR Address Checking
              2. 12.2.4.2.3.3.2 SIR Free-Format Mode
              3. 12.2.4.2.3.3.3 MIR Mode
                1. 12.2.4.2.3.3.3.1 MIR Encoder/Decoder
                2. 12.2.4.2.3.3.3.2 SIP Generation
              4. 12.2.4.2.3.3.4 FIR Mode
          4. 12.2.4.2.4 CIR Functional Interfaces
            1. 12.2.4.2.4.1 System Using CIR Communication Protocol With Remote Control
            2. 12.2.4.2.4.2 CIR Interface Description
            3. 12.2.4.2.4.3 CIR Protocol and Data Format
              1. 12.2.4.2.4.3.1 Carrier Modulation
              2. 12.2.4.2.4.3.2 Pulse Duty Cycle
              3. 12.2.4.2.4.3.3 Consumer IR Encoding/Decoding
        3. 12.2.4.3 Integration
        4. 12.2.4.4 UART Functional Description
          1. 12.2.4.4.1 UART Block Diagram
          2. 12.2.4.4.2 UART Clock Configuration
          3. 12.2.4.4.3 UART Software Reset
            1. 12.2.4.4.3.1 Independent TX/RX
          4. 12.2.4.4.4 UART Power Management
            1. 12.2.4.4.4.1 UART Mode Power Management
              1. 12.2.4.4.4.1.1 Module Power Saving
              2. 12.2.4.4.4.1.2 System Power Saving
            2. 12.2.4.4.4.2 IrDA Mode Power Management
              1. 12.2.4.4.4.2.1 Module Power Saving
              2. 12.2.4.4.4.2.2 System Power Saving
            3. 12.2.4.4.4.3 CIR Mode Power Management
              1. 12.2.4.4.4.3.1 Module Power Saving
              2. 12.2.4.4.4.3.2 System Power Saving
            4. 12.2.4.4.4.4 Local Power Management
          5. 12.2.4.4.5 UART Interrupt Requests
            1. 12.2.4.4.5.1 UART Mode Interrupt Management
              1. 12.2.4.4.5.1.1 UART Interrupts
              2. 12.2.4.4.5.1.2 Wake-Up Interrupt
            2. 12.2.4.4.5.2 IrDA Mode Interrupt Management
              1. 12.2.4.4.5.2.1 IrDA Interrupts
              2. 12.2.4.4.5.2.2 Wake-Up Interrupts
            3. 12.2.4.4.5.3 CIR Mode Interrupt Management
              1. 12.2.4.4.5.3.1 CIR Interrupts
              2. 12.2.4.4.5.3.2 Wake-Up Interrupts
          6. 12.2.4.4.6 UART FIFO Management
            1. 12.2.4.4.6.1 FIFO Trigger
              1. 12.2.4.4.6.1.1 Transmit FIFO Trigger
              2. 12.2.4.4.6.1.2 Receive FIFO Trigger
            2. 12.2.4.4.6.2 FIFO Interrupt Mode
            3. 12.2.4.4.6.3 FIFO Polled Mode Operation
            4. 12.2.4.4.6.4 FIFO DMA Mode Operation
              1. 12.2.4.4.6.4.1 DMA sequence to disable TX DMA
              2. 12.2.4.4.6.4.2 DMA Transfers (DMA Mode 1, 2, or 3)
              3. 12.2.4.4.6.4.3 DMA Transmission
              4. 12.2.4.4.6.4.4 DMA Reception
          7. 12.2.4.4.7 UART Mode Selection
            1. 12.2.4.4.7.1 Register Access Modes
              1. 12.2.4.4.7.1.1 Operational Mode and Configuration Modes
              2. 12.2.4.4.7.1.2 Register Access Submode
              3. 12.2.4.4.7.1.3 Registers Available for the Register Access Modes
            2. 12.2.4.4.7.2 UART/RS-485/IrDA (SIR, MIR, FIR)/CIR Mode Selection
              1. 12.2.4.4.7.2.1 Registers Available for the UART Function
              2. 12.2.4.4.7.2.2 Registers Available for the IrDA Function
              3. 12.2.4.4.7.2.3 Registers Available for the CIR Function
          8. 12.2.4.4.8 UART Protocol Formatting
            1. 12.2.4.4.8.1 UART Mode
              1. 12.2.4.4.8.1.1 UART Clock Generation: Baud Rate Generation
              2. 12.2.4.4.8.1.2 Choosing the Appropriate Divisor Value
              3. 12.2.4.4.8.1.3 UART Data Formatting
                1. 12.2.4.4.8.1.3.1 Frame Formatting
                2. 12.2.4.4.8.1.3.2 Hardware Flow Control
                3. 12.2.4.4.8.1.3.3 Software Flow Control
                  1. 2.4.4.8.1.3.3.1 Receive (RX)
                  2. 2.4.4.8.1.3.3.2 Transmit (TX)
                4. 12.2.4.4.8.1.3.4 Autobauding Modes
                5. 12.2.4.4.8.1.3.5 Error Detection
                6. 12.2.4.4.8.1.3.6 Overrun During Receive
                7. 12.2.4.4.8.1.3.7 Time-Out and Break Conditions
                  1. 2.4.4.8.1.3.7.1 Time-Out Counter
                  2. 2.4.4.8.1.3.7.2 Break Condition
            2. 12.2.4.4.8.2 RS-485 Mode
              1. 12.2.4.4.8.2.1 RS-485 External Transceiver Direction Control
            3. 12.2.4.4.8.3 IrDA Mode
              1. 12.2.4.4.8.3.1 IrDA Clock Generation: Baud Generator
              2. 12.2.4.4.8.3.2 Choosing the Appropriate Divisor Value
              3. 12.2.4.4.8.3.3 IrDA Data Formatting
                1. 12.2.4.4.8.3.3.1  IR RX Polarity Control
                2. 12.2.4.4.8.3.3.2  IrDA Reception Control
                3. 12.2.4.4.8.3.3.3  IR Address Checking
                4. 12.2.4.4.8.3.3.4  Frame Closing
                5. 12.2.4.4.8.3.3.5  Store and Controlled Transmission
                6. 12.2.4.4.8.3.3.6  Error Detection
                7. 12.2.4.4.8.3.3.7  Underrun During Transmission
                8. 12.2.4.4.8.3.3.8  Overrun During Receive
                9. 12.2.4.4.8.3.3.9  Status FIFO
                10. 12.2.4.4.8.3.3.10 Multi-drop Parity Mode with Address Match
                11. 12.2.4.4.8.3.3.11 Time-guard
              4. 12.2.4.4.8.3.4 SIR Mode Data Formatting
                1. 12.2.4.4.8.3.4.1 Abort Sequence
                2. 12.2.4.4.8.3.4.2 Pulse Shaping
                3. 12.2.4.4.8.3.4.3 SIR Free Format Programming
              5. 12.2.4.4.8.3.5 MIR and FIR Mode Data Formatting
            4. 12.2.4.4.8.4 CIR Mode
              1. 12.2.4.4.8.4.1 CIR Mode Clock Generation
              2. 12.2.4.4.8.4.2 CIR Data Formatting
                1. 12.2.4.4.8.4.2.1 IR RX Polarity Control
                2. 12.2.4.4.8.4.2.2 CIR Transmission
                3. 12.2.4.4.8.4.2.3 CIR Reception
        5. 12.2.4.5 UART Programming Guide
          1. 12.2.4.5.1 UART Global Initialization
            1. 12.2.4.5.1.1 Surrounding Modules Global Initialization
            2. 12.2.4.5.1.2 UART Module Global Initialization
          2. 12.2.4.5.2 UART Mode selection
          3. 12.2.4.5.3 UART Submode selection
          4. 12.2.4.5.4 UART Load FIFO trigger and DMA mode settings
            1. 12.2.4.5.4.1 DMA mode Settings
            2. 12.2.4.5.4.2 FIFO Trigger Settings
          5. 12.2.4.5.5 UART Protocol, Baud rate and interrupt settings
            1. 12.2.4.5.5.1 Baud rate settings
            2. 12.2.4.5.5.2 Interrupt settings
            3. 12.2.4.5.5.3 Protocol settings
            4. 12.2.4.5.5.4 UART/RS-485/IrDA(SIR/MIR/FIR)/CIR
            5. 12.2.4.5.5.5 UART Multi-drop Parity Address Match Mode Configuration
          6. 12.2.4.5.6 UART Hardware and Software Flow Control Configuration
            1. 12.2.4.5.6.1 Hardware Flow Control Configuration
            2. 12.2.4.5.6.2 Software Flow Control Configuration
          7. 12.2.4.5.7 IrDA Programming Model
            1. 12.2.4.5.7.1 SIR mode
              1. 12.2.4.5.7.1.1 Receive
              2. 12.2.4.5.7.1.2 Transmit
            2. 12.2.4.5.7.2 MIR mode
              1. 12.2.4.5.7.2.1 Receive
              2. 12.2.4.5.7.2.2 Transmit
            3. 12.2.4.5.7.3 FIR mode
              1. 12.2.4.5.7.3.1 Receive
              2. 12.2.4.5.7.3.2 Transmit
    3. 12.3 High-speed Serial Interfaces
      1. 12.3.1 Gigabit Ethernet Switch (CPSW3G)
        1. 12.3.1.1 CPSW0 Overview
          1. 12.3.1.1.1 CPSW0 Features
          2. 12.3.1.1.2 Unsupported Features
          3.        1895
          4. 12.3.1.1.3 CPSW Terminology
        2. 12.3.1.2 CPSW0 Environment
          1. 12.3.1.2.1 CPSW0 RMII Interface
          2. 12.3.1.2.2 CPSW0 RGMII Interface
        3. 12.3.1.3 Integration
        4. 12.3.1.4 CPSW0 Functional Description
          1. 12.3.1.4.1 Functional Block Diagram
          2. 12.3.1.4.2 CPSW Ports
            1. 12.3.1.4.2.1 Interface Mode Selection
          3. 12.3.1.4.3 Clocking
            1. 12.3.1.4.3.1 Subsystem Clocking
            2. 12.3.1.4.3.2 Interface Clocking
              1. 12.3.1.4.3.2.1 RGMII Interface Clocking
              2. 12.3.1.4.3.2.2 RMII Interface Clocking
              3. 12.3.1.4.3.2.3 MDIO Clocking
          4. 12.3.1.4.4 Software IDLE
          5. 12.3.1.4.5 Interrupt Functionality
            1. 12.3.1.4.5.1 EVNT_PEND Interrupt
            2. 12.3.1.4.5.2 Statistics Interrupt (STAT_PEND0)
            3. 12.3.1.4.5.3 ECC DED Level Interrupt (ECC_DED_INT)
            4. 12.3.1.4.5.4 ECC SEC Level Interrupt (ECC_SEC_INT)
            5. 12.3.1.4.5.5 MDIO Interrupts
          6. 12.3.1.4.6 CPSW_3G
            1. 12.3.1.4.6.1  Address Lookup Engine (ALE)
              1. 12.3.1.4.6.1.1  Error Handling
              2. 12.3.1.4.6.1.2  Bypass Operations
              3. 12.3.1.4.6.1.3  OUI Deny or Accept
              4. 12.3.1.4.6.1.4  Statistics Counting
              5. 12.3.1.4.6.1.5  Automotive Security Features
              6. 12.3.1.4.6.1.6  CPSW Switching Solutions
                1. 12.3.1.4.6.1.6.1 Basics of 3-port Switch Type
              7. 12.3.1.4.6.1.7  VLAN Routing and OAM Operations
                1. 12.3.1.4.6.1.7.1 InterVLAN Routing
                2. 12.3.1.4.6.1.7.2 OAM Operations
              8. 12.3.1.4.6.1.8  Supervisory packets
              9. 12.3.1.4.6.1.9  Address Table Entry
                1. 12.3.1.4.6.1.9.1  Multicast Address Table Entry
                2. 12.3.1.4.6.1.9.2  OUI Unicast Address Table Entry
                3. 12.3.1.4.6.1.9.3  Unicast Address Table Entry (Bit 40 == 0)
                4. 12.3.1.4.6.1.9.4  Multicast Address Table Entry (Bit 40==1)
                5. 12.3.1.4.6.1.9.5  VLAN/Unicast Address Table Entry (Bit 40 == 0)
                6. 12.3.1.4.6.1.9.6  VLAN/Multicast Address Table Entry (Bit 40==1)
                7. 12.3.1.4.6.1.9.7  Inner VLAN Table Entry
                8. 12.3.1.4.6.1.9.8  Outer VLAN Table Entry
                9. 12.3.1.4.6.1.9.9  EtherType Table Entry
                10. 12.3.1.4.6.1.9.10 IPv4 Table Entry
                11. 12.3.1.4.6.1.9.11 IPv6 Table Entry High
                12. 12.3.1.4.6.1.9.12 IPv6 Table Entry Low
              10. 12.3.1.4.6.1.10 Multicast Address
                1. 12.3.1.4.6.1.10.1 Multicast Ranges
              11. 12.3.1.4.6.1.11 Aging and Auto Aging
              12. 12.3.1.4.6.1.12 ALE Policing and Classification
                1. 12.3.1.4.6.1.12.1 ALE Policing
                2. 12.3.1.4.6.1.12.2 Classifier to Host Thread Mapping
                3. 12.3.1.4.6.1.12.3 ALE Classification
                  1. 3.1.4.6.1.12.3.1 Classifier to CPPI Transmit Flow ID Mapping
              13. 12.3.1.4.6.1.13 Mirroring
              14. 12.3.1.4.6.1.14 Trunking
              15. 12.3.1.4.6.1.15 DSCP
              16. 12.3.1.4.6.1.16 Packet Forwarding Processes
                1. 12.3.1.4.6.1.16.1 Ingress Filtering Process
                2. 12.3.1.4.6.1.16.2 VLAN_Aware Lookup Process
                3. 12.3.1.4.6.1.16.3 Egress Process
                4. 12.3.1.4.6.1.16.4 Learning/Updating/Touching Processes
                  1. 3.1.4.6.1.16.4.1 Learning Process
                  2. 3.1.4.6.1.16.4.2 Updating Process
                  3. 3.1.4.6.1.16.4.3 Touching Process
              17. 12.3.1.4.6.1.17 VLAN Aware Mode
              18. 12.3.1.4.6.1.18 VLAN Unaware Mode
            2. 12.3.1.4.6.2  Packet Priority Handling
              1. 12.3.1.4.6.2.1 Priority Mapping and Transmit VLAN Priority
            3. 12.3.1.4.6.3  CPPI Port Ingress
            4. 12.3.1.4.6.4  Packet CRC Handling
              1. 12.3.1.4.6.4.1 Transmit VLAN Processing
                1. 12.3.1.4.6.4.1.1 Untagged Packets (No VLAN or Priority Tag Header)
                2. 12.3.1.4.6.4.1.2 Priority Tagged Packets (VLAN VID == 0 && EN_VID0_MODE ==0h)
                3. 12.3.1.4.6.4.1.3 VLAN Tagged Packets (VLAN VID != 0 || (EN_VID0_MODE ==1h && VLAN VID ==0))
              2. 12.3.1.4.6.4.2 Ethernet Port Ingress Packet CRC
              3. 12.3.1.4.6.4.3 Ethernet Port Egress Packet CRC
              4. 12.3.1.4.6.4.4 CPPI Port Ingress Packet CRC
              5. 12.3.1.4.6.4.5 CPPI Port Egress Packet CRC
            5. 12.3.1.4.6.5  FIFO Memory Control
            6. 12.3.1.4.6.6  FIFO Transmit Queue Control
              1. 12.3.1.4.6.6.1 CPPI Port Receive Rate Limiting
              2. 12.3.1.4.6.6.2 Ethernet Port Transmit Rate Limiting
            7. 12.3.1.4.6.7  Intersperced Express Traffic (IET – P802.3br/D2.0)
              1. 12.3.1.4.6.7.1 IET Configuration
            8. 12.3.1.4.6.8  Enhanced Scheduled Traffic (EST – P802.1Qbv/D2.2)
              1. 12.3.1.4.6.8.1 Enhanced Scheduled Traffic Overview
              2. 12.3.1.4.6.8.2 Enhanced Scheduled Traffic Fetch RAM
              3. 12.3.1.4.6.8.3 Enhanced Scheduled Traffic Time Interval
              4. 12.3.1.4.6.8.4 Enhanced Scheduled Traffic Fetch Values
              5. 12.3.1.4.6.8.5 Enhanced Scheduled Traffic Packet Fill
              6. 12.3.1.4.6.8.6 Enhanced Scheduled Traffic Time Stamp
              7. 12.3.1.4.6.8.7 Enhanced Scheduled Traffic Packets Per Priority
            9. 12.3.1.4.6.9  Audio Video Bridging
              1. 12.3.1.4.6.9.1 IEEE 802.1AS: Timing and Synchronization for Time-Sensitive Applications in Bridged Local Area Networks (Precision Time Protocol (PTP))
                1. 12.3.1.4.6.9.1.1 IEEE 1722: "Layer 2 Transport Protocol for Time-Sensitive Streams"
                  1. 3.1.4.6.9.1.1.1 Cross-timestamping and Presentation Timestamps
                2. 12.3.1.4.6.9.1.2 IEEE 1733: Extends RTCP for RTP Streaming over AVB-supported Networks
              2. 12.3.1.4.6.9.2 IEEE 802.1Qav: "Virtual Bridged Local Area Networks: Forwarding and Queuing for Time-Sensitive Streams"
                1. 12.3.1.4.6.9.2.1 Configuring the Device for 802.1Qav Operation
            10. 12.3.1.4.6.10 Ethernet MAC Sliver
              1. 12.3.1.4.6.10.1 Ethernet MAC Sliver Overview
                1. 12.3.1.4.6.10.1.1 CRC Insertion
                2. 12.3.1.4.6.10.1.2 MTXER
                3. 12.3.1.4.6.10.1.3 Adaptive Performance Optimization (APO)
                4. 12.3.1.4.6.10.1.4 Inter-Packet-Gap Enforcement
                5. 12.3.1.4.6.10.1.5 Back Off
                6. 12.3.1.4.6.10.1.6 Programmable Transmit Inter-Packet Gap
                7. 12.3.1.4.6.10.1.7 Speed, Duplex and Pause Frame Support Negotiation
              2. 12.3.1.4.6.10.2 RMII Interface
                1. 12.3.1.4.6.10.2.1 Features
                2. 12.3.1.4.6.10.2.2 RMII Receive (RX)
                3. 12.3.1.4.6.10.2.3 RMII Transmit (TX)
              3. 12.3.1.4.6.10.3 RGMII Interface
                1. 12.3.1.4.6.10.3.1 Features
                2. 12.3.1.4.6.10.3.2 RGMII Receive (RX)
                3. 12.3.1.4.6.10.3.3 In-Band Mode of Operation
                4. 12.3.1.4.6.10.3.4 Forced Mode of Operation
                5. 12.3.1.4.6.10.3.5 RGMII Transmit (TX)
              4. 12.3.1.4.6.10.4 Frame Classification
              5. 12.3.1.4.6.10.5 Receive FIFO Architecture
            11. 12.3.1.4.6.11 Embedded Memories
            12. 12.3.1.4.6.12 Memory Error Detection and Correction
              1. 12.3.1.4.6.12.1 Packet Header ECC
              2. 12.3.1.4.6.12.2 Packet Protect CRC
              3. 12.3.1.4.6.12.3 Aggregator RAM Control
            13. 12.3.1.4.6.13 Ethernet Port Flow Control
              1. 12.3.1.4.6.13.1 Ethernet Receive Flow Control
                1. 12.3.1.4.6.13.1.1 Collision Based Receive Buffer Flow Control
                2. 12.3.1.4.6.13.1.2 IEEE 802.3X Based Receive Flow Control
              2. 12.3.1.4.6.13.2 Flow Control Trigger
              3. 12.3.1.4.6.13.3 Ethernet Transmit Flow Control
            14. 12.3.1.4.6.14 Energy Efficient Ethernet Support (802.3az)
            15. 12.3.1.4.6.15 Ethernet Switch Latency
            16. 12.3.1.4.6.16 MAC Emulation Control
            17. 12.3.1.4.6.17 MAC Command IDLE
            18. 12.3.1.4.6.18 CPSW Network Statistics
              1. 12.3.1.4.6.18.1  Rx-only Statistics Descriptions
                1. 12.3.1.4.6.18.1.1  Good Rx Frames (Offset = 3A000h)
                2. 12.3.1.4.6.18.1.2  Broadcast Rx Frames (Offset = 3A004h)
                3. 12.3.1.4.6.18.1.3  Multicast Rx Frames (Offset = 3A008h)
                4. 12.3.1.4.6.18.1.4  Pause Rx Frames (Offset = 3A00Ch)
                5. 12.3.1.4.6.18.1.5  Rx CRC Errors (Offset = 3A010h)
                6. 12.3.1.4.6.18.1.6  Rx Align/Code Errors (Offset = 3A014h)
                7. 12.3.1.4.6.18.1.7  Oversize Rx Frames (Offset = 3A018h)
                8. 12.3.1.4.6.18.1.8  Rx Jabbers (Offset = 3A01Ch)
                9. 12.3.1.4.6.18.1.9  Undersize (Short) Rx Frames (Offset = 3A020h)
                10. 12.3.1.4.6.18.1.10 Rx Fragments (Offset = 3A024h)
                11. 12.3.1.4.6.18.1.11 RX IPG Error (Offset = 3A05Ch)
                12. 12.3.1.4.6.18.1.12 ALE Drop (Offset = 3A028h)
                13. 12.3.1.4.6.18.1.13 ALE Overrun Drop (Offset = 3A02Ch)
                14. 12.3.1.4.6.18.1.14 Rx Octets (Offset = 3A030h)
                15. 12.3.1.4.6.18.1.15 Rx Bottom of FIFO Drop (Offset = 3A084h)
                16. 12.3.1.4.6.18.1.16 Portmask Drop (Offset = 3A088h)
                17. 12.3.1.4.6.18.1.17 Rx Top of FIFO Drop (Offset = 3A08Ch)
                18. 12.3.1.4.6.18.1.18 ALE Rate Limit Drop (Offset = 3A090h)
                19. 12.3.1.4.6.18.1.19 ALE VLAN Ingress Check Drop (Offset = 3A094h)
                  1. 3.1.4.6.18.1.19.1  ALE DA=SA Drop (Offset = 3A098h)
                  2. 3.1.4.6.18.1.19.2  Block Address Drop (Offset = 3A09Ch)
                  3. 3.1.4.6.18.1.19.3  ALE Secure Drop (Offset = 3A0A0h)
                  4. 3.1.4.6.18.1.19.4  ALE Authentication Drop (Offset = 3A0A4h)
                  5. 3.1.4.6.18.1.19.5  ALE Unknown Unicast (Offset = 3A0A8h)
                  6. 3.1.4.6.18.1.19.6  ALE Unknown Unicast Bytecount (Offset = 3A0ACh)
                  7. 3.1.4.6.18.1.19.7  ALE Unknown Multicast (Offset = 3A0B0h)
                  8. 3.1.4.6.18.1.19.8  ALE Unknown Multicast Bytecount (Offset = 3A0B4h)
                  9. 3.1.4.6.18.1.19.9  ALE Unknown Broadcast (Offset = 3A0B8h)
                  10. 3.1.4.6.18.1.19.10 ALE Unknown Broadcast Bytecount (Offset = 3A0BCh)
                  11. 3.1.4.6.18.1.19.11 ALE Policer/Classifier Match (Offset = 3A0C0h)
              2. 12.3.1.4.6.18.2  ALE Policer Match Red (Offset = 3A0C4h)
              3. 12.3.1.4.6.18.3  ALE Policer Match Yellow (Offset = 3A0C8h)
              4. 12.3.1.4.6.18.4  IET Receive Assembly Error (Offset = 3A140h)
              5. 12.3.1.4.6.18.5  IET Receive Assembly OK (Offset = 3A144h)
              6. 12.3.1.4.6.18.6  IET Receive SMD Error (Offset = 3A148h)
              7. 12.3.1.4.6.18.7  IET Receive Merge Fragment Count (Offset = 3A14Ch)
              8. 12.3.1.4.6.18.8  Rx Cut Thru with No Delay
              9. 12.3.1.4.6.18.9  Rx Cut Thru with Delay
              10. 12.3.1.4.6.18.10 Rx Cut Thru Store-and-Forward
              11. 12.3.1.4.6.18.11 Tx-only Statistics Descriptions
                1. 12.3.1.4.6.18.11.1  Good Tx Frames (Offset = 3A034h)
                2. 12.3.1.4.6.18.11.2  Broadcast Tx Frames (Offset = 3A038h)
                3. 12.3.1.4.6.18.11.3  Multicast Tx Frames (Offset = 3A03Ch)
                4. 12.3.1.4.6.18.11.4  Pause Tx Frames (Offset = 3A040h)
                5. 12.3.1.4.6.18.11.5  Deferred Tx Frames (Offset = 3A044h)
                6. 12.3.1.4.6.18.11.6  Collisions (Offset = 3A048h)
                7. 12.3.1.4.6.18.11.7  Single Collision Tx Frames (Offset = 3A04Ch)
                8. 12.3.1.4.6.18.11.8  Multiple Collision Tx Frames (Offset = 3A050h)
                9. 12.3.1.4.6.18.11.9  Excessive Collisions (Offset = 3A054h)
                10. 12.3.1.4.6.18.11.10 Late Collisions (Offset = 3A058h)
                11. 12.3.1.4.6.18.11.11 Carrier Sense Errors (Offset = 3A060h)
                12. 12.3.1.4.6.18.11.12 Tx Octets (Offset = 3A064h)
                13. 12.3.1.4.6.18.11.13 Transmit Priority 0-7 (Offset = 3A180h to 3A1A8h)
                14. 12.3.1.4.6.18.11.14 Transmit Priority 0-7 Drop (Offset = 3A1C0h to 3A1E8)
                15. 12.3.1.4.6.18.11.15 Tx Memory Protect Errors (Offset = 3A17Ch)
                16. 12.3.1.4.6.18.11.16 IET Transmit Merge Hold Count (Offset = 3A150h)
                17. 12.3.1.4.6.18.11.17 IET Transmit Merge Fragment Count (Offset = 3A14Ch)
                18. 12.3.1.4.6.18.11.18 Tx CRC Errors
                19. 12.3.1.4.6.18.11.19 Tx Cut Thru
                20. 12.3.1.4.6.18.11.20 Tx Cut Thru Store-and-Forward
              12. 12.3.1.4.6.18.12 Rx- and Tx (Shared) Statistics Descriptions
                1. 12.3.1.4.6.18.12.1 Rx + Tx 64 Octet Frames (Offset = 3A068h)
                2. 12.3.1.4.6.18.12.2 Rx + Tx 65–127 Octet Frames (Offset = 3A06Ch)
                3. 12.3.1.4.6.18.12.3 Rx + Tx 128–255 Octet Frames (Offset = 3A070h)
                4. 12.3.1.4.6.18.12.4 Rx + Tx 256–511 Octet Frames (Offset = 3A074h)
                5. 12.3.1.4.6.18.12.5 Rx + Tx 512–1023 Octet Frames (Offset = 3A078h)
                6. 12.3.1.4.6.18.12.6 Rx + Tx 1024_Up Octet Frames (Offset = 3A07Ch)
                7. 12.3.1.4.6.18.12.7 Net Octets (Offset = 3A080h)
              13. 12.3.1.4.6.18.13 2104
          7. 12.3.1.4.7 Common Platform Time Sync (CPTS)
            1. 12.3.1.4.7.1  CPSW0 CPTS Integration
            2. 12.3.1.4.7.2  CPTS Architecture
            3. 12.3.1.4.7.3  CPTS Initialization
            4. 12.3.1.4.7.4  32-bit Time Stamp Value
            5. 12.3.1.4.7.5  64-bit Time Stamp Value
            6. 12.3.1.4.7.6  64-Bit Timestamp Nudge
            7. 12.3.1.4.7.7  64-bit Timestamp PPM
            8. 12.3.1.4.7.8  Event FIFO
            9. 12.3.1.4.7.9  Timestamp Compare Output
              1. 12.3.1.4.7.9.1 Non-Toggle Mode: 32-bit
              2. 12.3.1.4.7.9.2 Non-Toggle Mode: 64-bit
              3. 12.3.1.4.7.9.3 Toggle Mode: 32-bit
              4. 12.3.1.4.7.9.4 Toggle Mode: 64-bit
            10. 12.3.1.4.7.10 Timestamp Sync Output
            11. 12.3.1.4.7.11 Timestamp GENFn Output
              1. 12.3.1.4.7.11.1 GENFn Nudge
              2. 12.3.1.4.7.11.2 GENFn PPM
            12. 12.3.1.4.7.12 Timestamp ESTFn
            13. 12.3.1.4.7.13 Time Sync Events
              1. 12.3.1.4.7.13.1 Time Stamp Push Event
              2. 12.3.1.4.7.13.2 Time Stamp Counter Rollover Event (32-bit mode only)
              3. 12.3.1.4.7.13.3 Time Stamp Counter Half-rollover Event (32-bit mode only)
              4. 12.3.1.4.7.13.4 Hardware Time Stamp Push Event
              5. 12.3.1.4.7.13.5 Ethernet Port Events
                1. 12.3.1.4.7.13.5.1 Ethernet Port Receive Event
                2. 12.3.1.4.7.13.5.2 Ethernet Port Transmit Event
                3. 12.3.1.4.7.13.5.3 2132
            14. 12.3.1.4.7.14 Timestamp Compare Event
              1. 12.3.1.4.7.14.1 32-Bit Mode
              2. 12.3.1.4.7.14.2 64-Bit Mode
            15. 12.3.1.4.7.15 Host Transmit Event
            16. 12.3.1.4.7.16 CPTS Interrupt Handling
          8. 12.3.1.4.8 CPPI Streaming Packet Interface
            1. 12.3.1.4.8.1 Port 0 CPPI Transmit Packet Streaming Interface (CPSW_3G Egress)
            2. 12.3.1.4.8.2 Port 0 CPPI Receive Packet Streaming Interface (CPSW_3G Ingress)
            3. 12.3.1.4.8.3 Cut-Thru
              1. 12.3.1.4.8.3.1 Host Port Cut-Thru Operations
              2. 12.3.1.4.8.3.2 Cut-Thru Error Packets
            4. 12.3.1.4.8.4 Port Speed
            5. 12.3.1.4.8.5 CPPI Checksum Offload
              1. 12.3.1.4.8.5.1 CPPI Transmit Checksum Offload
                1. 12.3.1.4.8.5.1.1 IPV4 UDP
                2. 12.3.1.4.8.5.1.2 IPV4 TCP
                3. 12.3.1.4.8.5.1.3 IPV6 UDP
                4. 12.3.1.4.8.5.1.4 IPV6 TCP
            6. 12.3.1.4.8.6 CPPI Receive Checksum Offload
            7. 12.3.1.4.8.7 Egress Packet Operations
          9. 12.3.1.4.9 MII Management Interface (MDIO)
            1. 12.3.1.4.9.1 MDIO Frame Formats
            2. 12.3.1.4.9.2 MDIO Functional Description
        5. 12.3.1.5 CPSW0 Programming Guide
          1. 12.3.1.5.1 Initialization and Configuration of CPSW Subsystem
          2. 12.3.1.5.2 CPSW Reset
          3. 12.3.1.5.3 MDIO Software Interface
            1. 12.3.1.5.3.1 Initializing the MDIO Module
            2. 12.3.1.5.3.2 Writing Data To a PHY Register
            3. 12.3.1.5.3.3 Reading Data From a PHY Register
      2. 12.3.2 Universal Serial Bus Subsystem (USBSS)
        1. 12.3.2.1 USB Overview
          1. 12.3.2.1.1 USB Features
          2. 12.3.2.1.2 Unsupported Features
        2. 12.3.2.2 USB Environment
          1. 12.3.2.2.1 USB Pin List
          2. 12.3.2.2.2 Typical Pin Connections of Device
        3. 12.3.2.3 Integration
        4. 12.3.2.4 Use Cases
          1. 12.3.2.4.1 USB Operational Mode Determination
          2. 12.3.2.4.2 VBUS Voltage Sourcing Control
          3. 12.3.2.4.3 VBUS Detection
          4. 12.3.2.4.4 Pull-up/Pull-down Resistors
    4. 12.4 Memory Interfaces
      1. 12.4.1 Flash Subsystem (FSS)
        1. 12.4.1.1 FSS Overview
          1. 12.4.1.1.1 FSS Features
          2. 12.4.1.1.2 Unsupported Features
          3.        2181
        2. 12.4.1.2 FSS Environment
          1. 12.4.1.2.1 FSS Typical Application
        3. 12.4.1.3 Integration
        4. 12.4.1.4 FSS Functional Description
          1. 12.4.1.4.1 FSS Block Diagram
          2. 12.4.1.4.2 FSS Regions
            1. 12.4.1.4.2.1 FSS Regions Boot Size Configuration
          3. 12.4.1.4.3 FSS Memory Regions
        5. 12.4.1.5 FSS Programming Guide
          1. 12.4.1.5.1 FSS Initialization Sequence
          2. 12.4.1.5.2 FSS Power Up/Down Sequence
      2. 12.4.2 Octal Serial Peripheral Interface (OSPI)
        1. 12.4.2.1 OSPI Overview
          1. 12.4.2.1.1 OSPI Features
          2. 12.4.2.1.2 Unsupported Features
          3.        2197
        2. 12.4.2.2 OSPI Environment
        3. 12.4.2.3 Integration
        4. 12.4.2.4 OSPI Functional Description
          1. 12.4.2.4.1  OSPI Block Diagram
            1. 12.4.2.4.1.1 Data Target Interface
            2. 12.4.2.4.1.2 Configuration Target Interface
            3. 12.4.2.4.1.3 OSPI Clock Domains
          2. 12.4.2.4.2  OSPI Modes
            1. 12.4.2.4.2.1 Read Data Capture
              1. 12.4.2.4.2.1.1 Mechanisms of Data Capturing
              2. 12.4.2.4.2.1.2 Data Capturing Mechanism Using Taps
              3. 12.4.2.4.2.1.3 Data Capturing Mechanism Using PHY Module
              4. 12.4.2.4.2.1.4 External Pull Down on DQS
          3. 12.4.2.4.3  OSPI Power Management
          4. 12.4.2.4.4  Auto HW Polling
          5. 12.4.2.4.5  Flash Reset
          6. 12.4.2.4.6  OSPI Memory Regions
          7. 12.4.2.4.7  OSPI Interrupt Requests
          8. 12.4.2.4.8  OSPI Data Interface
            1. 12.4.2.4.8.1 Data Interface Address Remapping
            2. 12.4.2.4.8.2 Write Protection
            3. 12.4.2.4.8.3 Access Forwarding
          9. 12.4.2.4.9  OSPI Direct Access Controller (DAC)
          10. 12.4.2.4.10 OSPI Indirect Access Controller (INDAC)
            1. 12.4.2.4.10.1 Indirect Read Controller
              1. 12.4.2.4.10.1.1 Indirect Read Transfer Process
            2. 12.4.2.4.10.2 Indirect Write Controller
              1. 12.4.2.4.10.2.1 Indirect Write Transfer Process
            3. 12.4.2.4.10.3 Indirect Access Queuing
            4. 12.4.2.4.10.4 Consecutive Writes and Reads Using Indirect Transfers
            5. 12.4.2.4.10.5 Accessing the SRAM
          11. 12.4.2.4.11 OSPI Software-Triggered Instruction Generator (STIG)
            1. 12.4.2.4.11.1 Servicing a STIG Request
          12. 12.4.2.4.12 OSPI Arbitration Between Direct / Indirect Access Controller and STIG
          13. 12.4.2.4.13 OSPI Command Translation
          14. 12.4.2.4.14 Selecting the Flash Instruction Type
          15. 12.4.2.4.15 OSPI Data Interface
          16. 12.4.2.4.16 OSPI PHY Module
            1. 12.4.2.4.16.1 PHY Pipeline Mode
            2. 12.4.2.4.16.2 Read Data Capturing by the PHY Module
        5. 12.4.2.5 OSPI Programming Guide
          1. 12.4.2.5.1 Configuring the OSPI Controller for Use After Reset
          2. 12.4.2.5.2 Configuring the OSPI Controller for Optimal Use
          3. 12.4.2.5.3 Using the Flash Command Control Register (STIG Operation)
          4. 12.4.2.5.4 Using SPI Legacy Mode
          5. 12.4.2.5.5 Entering XIP Mode from POR
          6. 12.4.2.5.6 Entering XIP Mode Otherwise
          7. 12.4.2.5.7 Exiting XIP Mode
      3. 12.4.3 General-Purpose Memory Controller (GPMC)
        1. 12.4.3.1 GPMC Overview
          1. 12.4.3.1.1 GPMC Features
          2. 12.4.3.1.2 Unsupported Features
          3.        2250
        2. 12.4.3.2 GPMC Environment
          1. 12.4.3.2.1 GPMC Modes
          2. 12.4.3.2.2 GPMC I/O Signals
        3. 12.4.3.3 Integration
        4. 12.4.3.4 GPMC Functional Description
          1. 12.4.3.4.1  GPMC Block Diagram
          2. 12.4.3.4.2  GPMC Clock Configuration
          3. 12.4.3.4.3  GPMC Power Management
          4. 12.4.3.4.4  GPMC Interrupt Requests
          5. 12.4.3.4.5  GPMC Interconnect Port Interface
          6. 12.4.3.4.6  GPMC Address and Data Bus
            1. 12.4.3.4.6.1 GPMC I/O Configuration Setting
          7. 12.4.3.4.7  GPMC Address Decoder and Chip-Select Configuration
            1. 12.4.3.4.7.1 Chip-Select Base Address and Region Size
            2. 12.4.3.4.7.2 Access Protocol
              1. 12.4.3.4.7.2.1 Supported Devices
              2. 12.4.3.4.7.2.2 Access Size Adaptation and Device Width
              3. 12.4.3.4.7.2.3 Address/Data-Multiplexing Interface
            3. 12.4.3.4.7.3 External Signals
              1. 12.4.3.4.7.3.1 WAIT Pin Monitoring Control
                1. 12.4.3.4.7.3.1.1 Wait Monitoring During Asynchronous Read Access
                2. 12.4.3.4.7.3.1.2 Wait Monitoring During Asynchronous Write Access
                3. 12.4.3.4.7.3.1.3 Wait Monitoring During Synchronous Read Access
                4. 12.4.3.4.7.3.1.4 Wait Monitoring During Synchronous Write Access
                5. 12.4.3.4.7.3.1.5 Wait With NAND Device
                6. 12.4.3.4.7.3.1.6 Idle Cycle Control Between Successive Accesses
                  1. 4.3.4.7.3.1.6.1 Bus Turnaround (BUSTURNAROUND)
                  2. 4.3.4.7.3.1.6.2 Idle Cycles Between Accesses to Same Chip-Select (CYCLE2CYCLESAMECSEN, CYCLE2CYCLEDELAY)
                  3. 4.3.4.7.3.1.6.3 Idle Cycles Between Accesses to Different Chip-Select (CYCLE2CYCLEDIFFCSEN, CYCLE2CYCLEDELAY)
                7. 12.4.3.4.7.3.1.7 Slow Device Support (TIMEPARAGRANULARITY Parameter)
              2. 12.4.3.4.7.3.2 DIR Pin
              3. 12.4.3.4.7.3.3 Reset
              4. 12.4.3.4.7.3.4 Write Protect Signal (nWP)
              5. 12.4.3.4.7.3.5 Byte Enable (nBE1/nBE0)
            4. 12.4.3.4.7.4 Error Handling
          8. 12.4.3.4.8  GPMC Timing Setting
            1. 12.4.3.4.8.1  Read Cycle Time and Write Cycle Time (RDCYCLETIME / WRCYCLETIME)
            2. 12.4.3.4.8.2  nCS: Chip-Select Signal Control Assertion/Deassertion Time (CSONTIME / CSRDOFFTIME / CSWROFFTIME / CSEXTRADELAY)
            3. 12.4.3.4.8.3  nADV/ALE: Address Valid/Address Latch Enable Signal Control Assertion/Deassertion Time (ADVONTIME / ADVRDOFFTIME / ADVWROFFTIME / ADVEXTRADELAY/ADVAADMUXONTIME/ADVAADMUXRDOFFTIME/ADVAADMUXWROFFTIME)
            4. 12.4.3.4.8.4  nOE/nRE: Output Enable/Read Enable Signal Control Assertion/Deassertion Time (OEONTIME / OEOFFTIME / OEEXTRADELAY / OEAADMUXONTIME / OEAADMUXOFFTIME)
            5. 12.4.3.4.8.5  nWE: Write Enable Signal Control Assertion/Deassertion Time (WEONTIME / WEOFFTIME / WEEXTRADELAY)
            6. 12.4.3.4.8.6  GPMC_CLKOUT
            7. 12.4.3.4.8.7  GPMC Output Clock and Control Signals Setup and Hold
            8. 12.4.3.4.8.8  Access Time (RDACCESSTIME / WRACCESSTIME)
              1. 12.4.3.4.8.8.1 Access Time on Read Access
              2. 12.4.3.4.8.8.2 Access Time on Write Access
            9. 12.4.3.4.8.9  Page Burst Access Time (PAGEBURSTACCESSTIME)
              1. 12.4.3.4.8.9.1 Page Burst Access Time on Read Access
              2. 12.4.3.4.8.9.2 Page Burst Access Time on Write Access
            10. 12.4.3.4.8.10 Bus Keeping Support
          9. 12.4.3.4.9  GPMC NOR Access Description
            1. 12.4.3.4.9.1 Asynchronous Access Description
              1. 12.4.3.4.9.1.1 Access on Address/Data Multiplexed Devices
                1. 12.4.3.4.9.1.1.1 Asynchronous Single-Read Operation on an Address/Data Multiplexed Device
                2. 12.4.3.4.9.1.1.2 Asynchronous Single-Write Operation on an Address/Data-Multiplexed Device
                3. 12.4.3.4.9.1.1.3 Asynchronous Multiple (Page) Write Operation on an Address/Data-Multiplexed Device
              2. 12.4.3.4.9.1.2 Access on Address/Address/Data-Multiplexed Devices
                1. 12.4.3.4.9.1.2.1 Asynchronous Single Read Operation on an AAD-Multiplexed Device
                2. 12.4.3.4.9.1.2.2 Asynchronous Single-Write Operation on an AAD-Multiplexed Device
                3. 12.4.3.4.9.1.2.3 Asynchronous Multiple (Page) Read Operation on an AAD-Multiplexed Device
            2. 12.4.3.4.9.2 Synchronous Access Description
              1. 12.4.3.4.9.2.1 Synchronous Single Read
              2. 12.4.3.4.9.2.2 Synchronous Multiple (Burst) Read (4-, 8-, 16-Word16 Burst With Wraparound Capability)
              3. 12.4.3.4.9.2.3 Synchronous Single Write
              4. 12.4.3.4.9.2.4 Synchronous Multiple (Burst) Write
            3. 12.4.3.4.9.3 Asynchronous and Synchronous Accesses in non-multiplexed Mode
              1. 12.4.3.4.9.3.1 Asynchronous Single-Read Operation on non-multiplexed Device
              2. 12.4.3.4.9.3.2 Asynchronous Single-Write Operation on non-multiplexed Device
              3. 12.4.3.4.9.3.3 Asynchronous Multiple (Page Mode) Read Operation on non-multiplexed Device
              4. 12.4.3.4.9.3.4 Synchronous Operations on a non-multiplexed Device
            4. 12.4.3.4.9.4 Page and Burst Support
            5. 12.4.3.4.9.5 System Burst vs External Device Burst Support
          10. 12.4.3.4.10 GPMC pSRAM Access Specificities
          11. 12.4.3.4.11 GPMC NAND Access Description
            1. 12.4.3.4.11.1 NAND Memory Device in Byte or 16-bit Word Stream Mode
              1. 12.4.3.4.11.1.1 Chip-Select Configuration for NAND Interfacing in Byte or Word Stream Mode
              2. 12.4.3.4.11.1.2 NAND Device Command and Address Phase Control
              3. 12.4.3.4.11.1.3 Command Latch Cycle
              4. 12.4.3.4.11.1.4 Address Latch Cycle
              5. 12.4.3.4.11.1.5 NAND Device Data Read and Write Phase Control in Stream Mode
              6. 12.4.3.4.11.1.6 NAND Device General Chip-Select Timing Control Requirement
              7. 12.4.3.4.11.1.7 Read and Write Access Size Adaptation
                1. 12.4.3.4.11.1.7.1 8-Bit-Wide NAND Device
                2. 12.4.3.4.11.1.7.2 16-Bit-Wide NAND Device
            2. 12.4.3.4.11.2 NAND Device-Ready Pin
              1. 12.4.3.4.11.2.1 Ready Pin Monitored by Software Polling
              2. 12.4.3.4.11.2.2 Ready Pin Monitored by Hardware Interrupt
            3. 12.4.3.4.11.3 ECC Calculator
              1. 12.4.3.4.11.3.1 Hamming Code
                1. 12.4.3.4.11.3.1.1 ECC Result Register and ECC Computation Accumulation Size
                2. 12.4.3.4.11.3.1.2 ECC Enabling
                3. 12.4.3.4.11.3.1.3 ECC Computation
                4. 12.4.3.4.11.3.1.4 ECC Comparison and Correction
                5. 12.4.3.4.11.3.1.5 ECC Calculation Based on 8-Bit Word
                6. 12.4.3.4.11.3.1.6 ECC Calculation Based on 16-Bit Word
              2. 12.4.3.4.11.3.2 BCH Code
                1. 12.4.3.4.11.3.2.1 Requirements
                2. 12.4.3.4.11.3.2.2 Memory Mapping of BCH Codeword
                  1. 4.3.4.11.3.2.2.1 Memory Mapping of Data Message
                  2. 4.3.4.11.3.2.2.2 Memory-Mapping of the ECC
                  3. 4.3.4.11.3.2.2.3 Wrapping Modes
                    1. 3.4.11.3.2.2.3.1  Manual Mode (0x0)
                    2. 3.4.11.3.2.2.3.2  Mode 0x1
                    3. 3.4.11.3.2.2.3.3  Mode 0xA (10)
                    4. 3.4.11.3.2.2.3.4  Mode 0x2
                    5. 3.4.11.3.2.2.3.5  Mode 0x3
                    6. 3.4.11.3.2.2.3.6  Mode 0x7
                    7. 3.4.11.3.2.2.3.7  Mode 0x8
                    8. 3.4.11.3.2.2.3.8  Mode 0x4
                    9. 3.4.11.3.2.2.3.9  Mode 0x9
                    10. 3.4.11.3.2.2.3.10 Mode 0x5
                    11. 3.4.11.3.2.2.3.11 Mode 0xB (11)
                    12. 3.4.11.3.2.2.3.12 Mode 0x6
                3. 12.4.3.4.11.3.2.3 Supported NAND Page Mappings and ECC Schemes
                  1. 4.3.4.11.3.2.3.1 Per-Sector Spare Mappings
                  2. 4.3.4.11.3.2.3.2 Pooled Spare Mapping
                  3. 4.3.4.11.3.2.3.3 Per-Sector Spare Mapping, with ECC Separated at the End of the Page
            4. 12.4.3.4.11.4 Prefetch and Write-Posting Engine
              1. 12.4.3.4.11.4.1 General Facts About the Engine Configuration
              2. 12.4.3.4.11.4.2 Prefetch Mode
              3. 12.4.3.4.11.4.3 FIFO Control in Prefetch Mode
              4. 12.4.3.4.11.4.4 Write-Posting Mode
              5. 12.4.3.4.11.4.5 FIFO Control in Write-Posting Mode
              6. 12.4.3.4.11.4.6 Optimizing NAND Access Using the Prefetch and Write-Posting Engine
              7. 12.4.3.4.11.4.7 Interleaved Accesses Between Prefetch and Write-Posting Engine and Other Chip-Selects
          12. 12.4.3.4.12 GPMC Use Cases and Tips
            1. 12.4.3.4.12.1 How to Set GPMC Timing Parameters for Typical Accesses
              1. 12.4.3.4.12.1.1 External Memory Attached to the GPMC Module
              2. 12.4.3.4.12.1.2 Typical GPMC Setup
                1. 12.4.3.4.12.1.2.1 GPMC Configuration for Synchronous Burst Read Access
                2. 12.4.3.4.12.1.2.2 GPMC Configuration for Asynchronous Read Access
                3. 12.4.3.4.12.1.2.3 GPMC Configuration for Asynchronous Single Write Access
            2. 12.4.3.4.12.2 How to Choose a Suitable Memory to Use With the GPMC
              1. 12.4.3.4.12.2.1 Supported Memories or Devices
                1. 12.4.3.4.12.2.1.1 Memory Pin Multiplexing
                2. 12.4.3.4.12.2.1.2 NAND Interface Protocol
                3. 12.4.3.4.12.2.1.3 NOR Interface Protocol
                4. 12.4.3.4.12.2.1.4 Other Technologies
        5. 12.4.3.5 GPMC Basic Programming Model
          1. 12.4.3.5.1 GPMC High-Level Programming Model Overview
          2. 12.4.3.5.2 GPMC Initialization
          3. 12.4.3.5.3 GPMC Configuration in NOR Mode
          4. 12.4.3.5.4 GPMC Configuration in NAND Mode
          5. 12.4.3.5.5 Set Memory Access
          6. 12.4.3.5.6 GPMC Timing Parameters
            1. 12.4.3.5.6.1 GPMC Timing Parameters Formulas
              1. 12.4.3.5.6.1.1 NAND Flash Interface Timing Parameters Formulas
              2. 12.4.3.5.6.1.2 Synchronous NOR Flash Timing Parameters Formulas
              3. 12.4.3.5.6.1.3 Asynchronous NOR Flash Timing Parameters Formulas
      4. 12.4.4 Error Location Module (ELM)
        1. 12.4.4.1 ELM Overview
          1. 12.4.4.1.1 ELM Features
          2. 12.4.4.1.2 Unsupported Features
          3.        2404
        2. 12.4.4.2 Integration
        3. 12.4.4.3 ELM Functional Description
          1. 12.4.4.3.1 ELM Software Reset
          2. 12.4.4.3.2 ELM Power Management
          3. 12.4.4.3.3 ELM Interrupt Requests
          4. 12.4.4.3.4 ELM Processing Initialization
          5. 12.4.4.3.5 ELM Processing Sequence
          6. 12.4.4.3.6 ELM Processing Completion
        4. 12.4.4.4 ELM Basic Programming Model
          1. 12.4.4.4.1 ELM Low-Level Programming Model
            1. 12.4.4.4.1.1 Processing Initialization
            2. 12.4.4.4.1.2 Read Results
            3. 12.4.4.4.1.3 2417
          2. 12.4.4.4.2 Use Case: ELM Used in Continuous Mode
          3. 12.4.4.4.3 Use Case: ELM Used in Page Mode
      5. 12.4.5 Multi-Media Card Secure Digital (MMCSD) Interface
        1. 12.4.5.1 MMCSD Overview
          1. 12.4.5.1.1 MMCSD Features
          2. 12.4.5.1.2 Unsupported Features
          3.        2424
        2. 12.4.5.2 MMCSD Environment
          1. 12.4.5.2.1 Protocol and Data Format
            1. 12.4.5.2.1.1 Protocol
            2. 12.4.5.2.1.2 Data Format
              1. 12.4.5.2.1.2.1 Coding Scheme for Command Token
              2. 12.4.5.2.1.2.2 Coding Scheme for Response Token
              3. 12.4.5.2.1.2.3 Coding Scheme for Data Token
        3. 12.4.5.3 Integration
        4. 12.4.5.4 MMCSD Functional Description
          1. 12.4.5.4.1 Block Diagram
          2. 12.4.5.4.2 Interrupt Requests
          3. 12.4.5.4.3 ECC Support
            1. 12.4.5.4.3.1 ECC Aggregator
          4. 12.4.5.4.4 Advanced DMA
        5. 12.4.5.5 MMCSD Programming Guide
          1. 12.4.5.5.1 Sequences
            1. 12.4.5.5.1.1  SD Card Detection
            2. 12.4.5.5.1.2  SD Clock Control
              1. 12.4.5.5.1.2.1 Internal Clock Setup Sequence
              2. 12.4.5.5.1.2.2 SD Clock Supply and Stop Sequence
              3. 12.4.5.5.1.2.3 SD Clock Frequency Change Sequence
            3. 12.4.5.5.1.3  SD Bus Power Control
            4. 12.4.5.5.1.4  Changing Bus Width
            5. 12.4.5.5.1.5  Timeout Setting on DAT Line
            6. 12.4.5.5.1.6  Card Initialization and Identification (for SD I/F)
              1. 12.4.5.5.1.6.1 Signal Voltage Switch Procedure (for UHS-I)
            7. 12.4.5.5.1.7  SD Transaction Generation
              1. 12.4.5.5.1.7.1 Transaction Control without Data Transfer Using DAT Line
                1. 12.4.5.5.1.7.1.1 The Sequence to Issue a SD Command
                2. 12.4.5.5.1.7.1.2 The Sequence to Finalize a Command
                3. 12.4.5.5.1.7.1.3 2455
              2. 12.4.5.5.1.7.2 Transaction Control with Data Transfer Using DAT Line
                1. 12.4.5.5.1.7.2.1 Not using DMA
                2. 12.4.5.5.1.7.2.2 Using SDMA
                3. 12.4.5.5.1.7.2.3 Using ADMA
            8. 12.4.5.5.1.8  Abort Transaction
              1. 12.4.5.5.1.8.1 Asynchronous Abort
              2. 12.4.5.5.1.8.2 Synchronous Abort
            9. 12.4.5.5.1.9  Changing Bus Speed Mode
            10. 12.4.5.5.1.10 Error Recovery
              1. 12.4.5.5.1.10.1 Error Interrupt Recovery
              2. 12.4.5.5.1.10.2 Auto CMD12 Error Recovery
            11. 12.4.5.5.1.11 Wakeup Control (Optional)
            12. 12.4.5.5.1.12 Suspend/Resume (Optional, Not Supported from Version 4.00)
              1. 12.4.5.5.1.12.1 Suspend Sequence
              2. 12.4.5.5.1.12.2 Resume Sequence
              3. 12.4.5.5.1.12.3 Stop At Block Gap/Continue Timing for Read Transaction
              4. 12.4.5.5.1.12.4 Stop At Block Gap/Continue Timing for Write Transaction
          2. 12.4.5.5.2 Driver Flow Sequence
            1. 12.4.5.5.2.1 Host Controller Setup and Card Detection
              1. 12.4.5.5.2.1.1 Host Controller Setup Sequence
              2. 12.4.5.5.2.1.2 Card Interface Detection Sequence
            2. 12.4.5.5.2.2 Boot Operation
              1. 12.4.5.5.2.2.1 Normal Boot Operation: (For Legacy eMMC 5.0)
              2. 12.4.5.5.2.2.2 Alternate Boot Operation (For Legacy eMMC 5.0):
              3. 12.4.5.5.2.2.3 Boot Code Chunk Read Operation (For Legacy eMMC 5.0):
            3. 12.4.5.5.2.3 Retuning procedure (For Legacy Interface)
              1. 12.4.5.5.2.3.1 Sampling Clock Tuning
              2. 12.4.5.5.2.3.2 Tuning Sequence
              3. 12.4.5.5.2.3.3 Re-Tuning Modes
            4. 12.4.5.5.2.4 Command Queuing Driver Flow Sequence
              1. 12.4.5.5.2.4.1 Command Queuing Initialization Sequence
              2. 12.4.5.5.2.4.2 Task Issuance Sequence
              3. 12.4.5.5.2.4.3 Task Execution and Completion Sequence
              4. 12.4.5.5.2.4.4 Task Discard and Clear Sequence
              5. 12.4.5.5.2.4.5 Error Detect and Recovery when CQ is enabled
    5. 12.5 Industrial and Control Interfaces
      1. 12.5.1 Modular Controller Area Network (MCAN)
        1. 12.5.1.1 MCAN Overview
          1. 12.5.1.1.1 MCAN Features
          2. 12.5.1.1.2 Unsupported Features
          3.        2496
        2. 12.5.1.2 MCAN Environment
          1. 12.5.1.2.1 CAN Network Basics
        3. 12.5.1.3 Integration
        4. 12.5.1.4 MCAN Functional Description
          1. 12.5.1.4.1  Module Clocking Requirements
          2. 12.5.1.4.2  Interrupt and DMA Requests
            1. 12.5.1.4.2.1 Interrupt Requests
            2. 12.5.1.4.2.2 DMA Requests
          3. 12.5.1.4.3  Operating Modes
            1. 12.5.1.4.3.1 Software Initialization
            2. 12.5.1.4.3.2 Normal Operation
            3. 12.5.1.4.3.3 CAN FD Operation
            4. 12.5.1.4.3.4 Transmitter Delay Compensation
              1. 12.5.1.4.3.4.1 Description
              2. 12.5.1.4.3.4.2 Transmitter Delay Compensation Measurement
            5. 12.5.1.4.3.5 Restricted Operation Mode
            6. 12.5.1.4.3.6 Bus Monitoring Mode
            7. 12.5.1.4.3.7 Disabled Automatic Retransmission (DAR) Mode
              1. 12.5.1.4.3.7.1 Frame Transmission in DAR Mode
            8. 12.5.1.4.3.8 Power Down (Sleep Mode)
              1. 12.5.1.4.3.8.1 External Clock Stop Mode
              2. 12.5.1.4.3.8.2 Suspend Mode
              3. 12.5.1.4.3.8.3 Wakeup request
            9. 12.5.1.4.3.9 Test Modes
              1. 12.5.1.4.3.9.1 Internal Loopback Mode
          4. 12.5.1.4.4  Timestamp Generation
            1. 12.5.1.4.4.1 External Timestamp Counter
          5. 12.5.1.4.5  Timeout Counter
          6. 12.5.1.4.6  ECC Support
            1. 12.5.1.4.6.1 ECC Wrapper
            2. 12.5.1.4.6.2 ECC Aggregator
          7. 12.5.1.4.7  Rx Handling
            1. 12.5.1.4.7.1 Acceptance Filtering
              1. 12.5.1.4.7.1.1 Range Filter
              2. 12.5.1.4.7.1.2 Filter for specific IDs
              3. 12.5.1.4.7.1.3 Classic Bit Mask Filter
              4. 12.5.1.4.7.1.4 Standard Message ID Filtering
              5. 12.5.1.4.7.1.5 Extended Message ID Filtering
            2. 12.5.1.4.7.2 Rx FIFOs
              1. 12.5.1.4.7.2.1 Rx FIFO Blocking Mode
              2. 12.5.1.4.7.2.2 Rx FIFO Overwrite Mode
            3. 12.5.1.4.7.3 Dedicated Rx Buffers
              1. 12.5.1.4.7.3.1 Rx Buffer Handling
            4. 12.5.1.4.7.4 Debug on CAN Support
          8. 12.5.1.4.8  Tx Handling
            1. 12.5.1.4.8.1 Transmit Pause
            2. 12.5.1.4.8.2 Dedicated Tx Buffers
            3. 12.5.1.4.8.3 Tx FIFO
            4. 12.5.1.4.8.4 Tx Queue
            5. 12.5.1.4.8.5 Mixed Dedicated Tx Buffers/Tx FIFO
            6. 12.5.1.4.8.6 Mixed Dedicated Tx Buffers/Tx Queue
            7. 12.5.1.4.8.7 Transmit Cancellation
            8. 12.5.1.4.8.8 Tx Event Handling
          9. 12.5.1.4.9  FIFO Acknowledge Handling
          10. 12.5.1.4.10 Message RAM
            1. 12.5.1.4.10.1 Message RAM Configuration
            2. 12.5.1.4.10.2 Rx Buffer and FIFO Element
            3. 12.5.1.4.10.3 Tx Buffer Element
            4. 12.5.1.4.10.4 Tx Event FIFO Element
            5. 12.5.1.4.10.5 Standard Message ID Filter Element
            6. 12.5.1.4.10.6 Extended Message ID Filter Element
      2. 12.5.2 Enhanced Capture (ECAP) Module
        1. 12.5.2.1 ECAP Overview
          1. 12.5.2.1.1 ECAP Features
          2. 12.5.2.1.2 Unsupported Features
          3.        2562
        2. 12.5.2.2 ECAP Environment
          1. 12.5.2.2.1 ECAP I/O Interface
        3. 12.5.2.3 Integration
        4. 12.5.2.4 ECAP Functional Description
          1. 12.5.2.4.1 Capture and APWM Operating Modes
            1. 12.5.2.4.1.1 ECAP Capture Mode Description
              1. 12.5.2.4.1.1.1 ECAP Event Prescaler
              2. 12.5.2.4.1.1.2 ECAP Edge Polarity Select and Qualifier
              3. 12.5.2.4.1.1.3 ECAP Continuous/One-Shot Control
              4. 12.5.2.4.1.1.4 ECAP 32-Bit Counter and Phase Control
              5. 12.5.2.4.1.1.5 CAP1-CAP4 Registers
              6. 12.5.2.4.1.1.6 ECAP Interrupt Control
              7. 12.5.2.4.1.1.7 ECAP Shadow Load and Lockout Control
            2. 12.5.2.4.1.2 ECAP APWM Mode Operation
          2. 12.5.2.4.2 Summary of ECAP Functional Registers
        5. 12.5.2.5 ECAP Use Cases
          1. 12.5.2.5.1 Absolute Time-Stamp Operation Rising Edge Trigger Example
            1. 12.5.2.5.1.1 Code Snippet for CAP Mode Absolute Time, Rising Edge Trigger
          2. 12.5.2.5.2 Absolute Time-Stamp Operation Rising and Falling Edge Trigger Example
            1. 12.5.2.5.2.1 Code Snippet for CAP Mode Absolute Time, Rising and Falling Edge Trigger
          3. 12.5.2.5.3 Time Difference (Delta) Operation Rising Edge Trigger Example
            1. 12.5.2.5.3.1 Code Snippet for CAP Mode Delta Time, Rising Edge Trigger
          4. 12.5.2.5.4 Time Difference (Delta) Operation Rising and Falling Edge Trigger Example
            1. 12.5.2.5.4.1 Code Snippet for CAP Mode Delta Time, Rising and Falling Edge Triggers
          5. 12.5.2.5.5 Application of the APWM Mode
            1. 12.5.2.5.5.1 Simple PWM Generation (Independent Channel/s) Example
              1. 12.5.2.5.5.1.1 Code Snippet for APWM Mode
            2. 12.5.2.5.5.2 Multichannel PWM Generation with Synchronization Example
              1. 12.5.2.5.5.2.1 Code Snippet for Multichannel PWM Generation with Synchronization
            3. 12.5.2.5.5.3 Multichannel PWM Generation with Phase Control Example
              1. 12.5.2.5.5.3.1 Code Snippet for Multichannel PWM Generation with Phase Control
      3. 12.5.3 Enhanced Pulse Width Modulation (EPWM) Module
        1. 12.5.3.1 EPWM Overview
          1. 12.5.3.1.1 EPWM Features
          2. 12.5.3.1.2 Unsupported Features
          3.        2598
          4. 12.5.3.1.3 Multiple EPWM Module Details
        2. 12.5.3.2 EPWM Environment
        3. 12.5.3.3 Integration
        4. 12.5.3.4 EPWM Functional Description
          1. 12.5.3.4.1  EPWM Submodule Features
            1. 12.5.3.4.1.1 Constant Definitions Used in the EPWM Code Examples
          2. 12.5.3.4.2  EPWM Time-Base (TB) Submodule
            1. 12.5.3.4.2.1 Overview
            2. 12.5.3.4.2.2 Controlling and Monitoring the EPWM Time-Base Submodule
            3. 12.5.3.4.2.3 Calculating PWM Period and Frequency
              1. 12.5.3.4.2.3.1 EPWM Time-Base Period Shadow Register
              2. 12.5.3.4.2.3.2 EPWM Time-Base Counter Synchronization
            4. 12.5.3.4.2.4 Phase Locking the Time-Base Clocks of Multiple EPWM Modules
            5. 12.5.3.4.2.5 EPWM Time-Base Counter Modes and Timing Waveforms
          3. 12.5.3.4.3  EPWM Counter-Compare (CC) Submodule
            1. 12.5.3.4.3.1 Overview
            2. 12.5.3.4.3.2 Controlling and Monitoring the EPWM Counter-Compare Submodule
            3. 12.5.3.4.3.3 Operational Highlights for the EPWM Counter-Compare Submodule
            4. 12.5.3.4.3.4 EPWM Counter-Compare Submodule Timing Waveforms
          4. 12.5.3.4.4  EPWM Action-Qualifier (AQ) Submodule
            1. 12.5.3.4.4.1 Overview
            2. 12.5.3.4.4.2 Controlling and Monitoring the EPWM Action-Qualifier Submodule
            3. 12.5.3.4.4.3 EPWM Action-Qualifier Event Priority
            4. 12.5.3.4.4.4 Waveforms for Common EPWM Configurations
          5. 12.5.3.4.5  EPWM Dead-Band Generator (DB) Submodule
            1. 12.5.3.4.5.1 Overview
            2. 12.5.3.4.5.2 Controlling and Monitoring the EPWM Dead-Band Submodule
            3. 12.5.3.4.5.3 Operational Highlights for the EPWM Dead-Band Generator Submodule
          6. 12.5.3.4.6  EPWM-Chopper (PC) Submodule
            1. 12.5.3.4.6.1 Overview
            2. 12.5.3.4.6.2 2629
            3. 12.5.3.4.6.3 Controlling the EPWM-Chopper Submodule
            4. 12.5.3.4.6.4 Operational Highlights for the EPWM-Chopper Submodule
            5. 12.5.3.4.6.5 EPWM-Chopper Waveforms
              1. 12.5.3.4.6.5.1 EPWM-Chopper One-Shot Pulse
              2. 12.5.3.4.6.5.2 EPWM-Chopper Duty Cycle Control
          7. 12.5.3.4.7  EPWM Trip-Zone (TZ) Submodule
            1. 12.5.3.4.7.1 Overview
            2. 12.5.3.4.7.2 Controlling and Monitoring the EPWM Trip-Zone Submodule
            3. 12.5.3.4.7.3 Operational Highlights for the EPWM Trip-Zone Submodule
            4. 12.5.3.4.7.4 Generating EPWM Trip-Event Interrupts
          8. 12.5.3.4.8  EPWM Event-Trigger (ET) Submodule
            1. 12.5.3.4.8.1 Overview
            2. 12.5.3.4.8.2 Controlling and Monitoring the EPWM Event-Trigger Submodule
            3. 12.5.3.4.8.3 Operational Overview of the EPWM Event-Trigger Submodule
            4. 12.5.3.4.8.4 Operation Overview of the EPWM SOCx Pulse Generator
          9. 12.5.3.4.9  EPWM Functional Register Groups
          10. 12.5.3.4.10 Proper EPWM Interrupt Initialization Procedure
      4. 12.5.4 Enhanced Quadrature Encoder Pulse (EQEP) Module
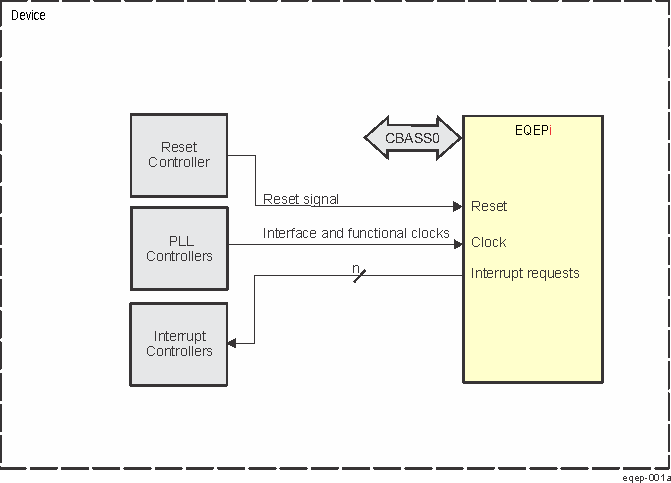
        1. 12.5.4.1 EQEP Overview
          1. 12.5.4.1.1 EQEP Features
          2. 12.5.4.1.2 Unsupported Features
          3.        2651
        2. 12.5.4.2 EQEP Environment
          1. 12.5.4.2.1 EQEP I/O Interface
        3. 12.5.4.3 Integration
        4. 12.5.4.4 EQEP Functional Description
          1. 12.5.4.4.1 EQEP Inputs
          2. 12.5.4.4.2 EQEP Quadrature Decoder Unit (QDU)
            1. 12.5.4.4.2.1 EQEP Position Counter Input Modes
              1. 12.5.4.4.2.1.1 Quadrature Count Mode
              2. 12.5.4.4.2.1.2 EQEP Direction-count Mode
              3. 12.5.4.4.2.1.3 EQEP Up-Count Mode
              4. 12.5.4.4.2.1.4 EQEP Down-Count Mode
            2. 12.5.4.4.2.2 EQEP Input Polarity Selection
            3. 12.5.4.4.2.3 EQEP Position-Compare Sync Output
          3. 12.5.4.4.3 EQEP Position Counter and Control Unit (PCCU)
            1. 12.5.4.4.3.1 EQEP Position Counter Operating Modes
              1. 12.5.4.4.3.1.1 EQEP Position Counter Reset on Index Event (EQEP_QDEC_QEP_CTL[29-28] PCRM] = 0b00)
              2. 12.5.4.4.3.1.2 EQEP Position Counter Reset on Maximum Position (EQEP_QDEC_QEP_CTL[29-28] PCRM = 0b01)
              3. 12.5.4.4.3.1.3 Position Counter Reset on the First Index Event (EQEP_QDEC_QEP_CTL[29-28] PCRM = 0b10)
              4. 12.5.4.4.3.1.4 Position Counter Reset on Unit Time out Event (EQEP_QDEC_QEP_CTL[29-28] PCRM = 0b11)
            2. 12.5.4.4.3.2 EQEP Position Counter Latch
              1. 12.5.4.4.3.2.1 Index Event Latch
              2. 12.5.4.4.3.2.2 EQEP Strobe Event Latch
            3. 12.5.4.4.3.3 EQEP Position Counter Initialization
            4. 12.5.4.4.3.4 EQEP Position-Compare Unit
          4. 12.5.4.4.4 EQEP Edge Capture Unit
          5. 12.5.4.4.5 EQEP Watchdog
          6. 12.5.4.4.6 Unit Timer Base
          7. 12.5.4.4.7 EQEP Interrupt Structure
          8. 12.5.4.4.8 Summary of EQEP Functional Registers
    6. 12.6 Camera Subsystem
      1. 12.6.1 Camera Serial Interface Receiver (CSI_RX_IF)
        1. 12.6.1.1 CSI_RX_IF Overview
          1. 12.6.1.1.1 CSI_RX_IF Features
          2. 12.6.1.1.2 Unsupported Features
          3.        2686
        2. 12.6.1.2 CSI_RX_IF Environment
        3. 12.6.1.3 Integration
        4. 12.6.1.4 CSI_RX_IF Functional Description
          1. 12.6.1.4.1 CSI_RX_IF Block Diagram
          2. 12.6.1.4.2 CSI_RX_IF Hardware and Software Reset
          3. 12.6.1.4.3 CSI_RX_IF Clock Configuration
          4. 12.6.1.4.4 CSI_RX_IF Interrupt Events
          5. 12.6.1.4.5 CSI_RX_IF Data Memory Organization Details
          6. 12.6.1.4.6 CSI_RX_IF PSI_L (DMA) Interface
            1. 12.6.1.4.6.1 PSI_L DMA framing
            2. 12.6.1.4.6.2 PSI_L DMA error handling due to FIFO overflow
          7. 12.6.1.4.7 CSI_RX_IF ECC Protection Support
          8. 12.6.1.4.8 CSI_RX_IF Programming Guide
            1. 12.6.1.4.8.1  Overview
            2. 12.6.1.4.8.2  Controller Configuration
            3. 12.6.1.4.8.3  Power on Configuration
            4. 12.6.1.4.8.4  Stream Start and Stop
            5. 12.6.1.4.8.5  Error Control With Soft Resets
            6. 12.6.1.4.8.6  Stream Error Detected – No Error Bypass Mode
            7. 12.6.1.4.8.7  Stream Error Detected – Error Bypass Mode
            8. 12.6.1.4.8.8  Stream Error Detected – Soft Reset Recovery
            9. 12.6.1.4.8.9  Stream Monitor Configuration
            10. 12.6.1.4.8.10 Stream Monitor Frame Capture Control
            11. 12.6.1.4.8.11 Stream Monitor Timer interrupt
            12. 12.6.1.4.8.12 Stream Monitor Line/Byte Counters Interrupt
            13. 12.6.1.4.8.13 Example Controller Programming Sequence (Single Stream Operation)
            14. 12.6.1.4.8.14 CSI_RX_IF Programming Restrictions
            15. 12.6.1.4.8.15 CSI_RX_IF Real-time operating requirements
      2. 12.6.2 MIPI D-PHY Receiver (DPHY_RX)
        1. 12.6.2.1 DPHY_RX Overview
          1. 12.6.2.1.1 DPHY_RX Features
          2. 12.6.2.1.2 Unsupported Features
          3.        2719
        2. 12.6.2.2 DPHY_RX Environment
        3. 12.6.2.3 Integration
        4. 12.6.2.4 DPHY_RX Functional Description
          1. 12.6.2.4.1 DPHY_RX Programming Guide
            1. 12.6.2.4.1.1 Overview
            2. 12.6.2.4.1.2 Initial Configuration Programming
              1. 12.6.2.4.1.2.1 Start-up Sequence Timing Diagram
            3. 12.6.2.4.1.3 Common Configuration
            4. 12.6.2.4.1.4 Lane Configuration
    7. 12.7 Timer Modules
      1. 12.7.1 Global Timebase Counter (GTC)
        1. 12.7.1.1 Global Timebase Counter (GTC)
          1. 12.7.1.1.1 GTC Overview
            1. 12.7.1.1.1.1 GTC Features
            2. 12.7.1.1.1.2 Unsupported Features
            3.         2735
        2. 12.7.1.2 GTC Functional Description
          1. 12.7.1.2.1 GTC Block Diagram
          2. 12.7.1.2.2 GTC Counter
            1. 12.7.1.2.2.1 Steps to Clear the Counter Value to Zero
          3. 12.7.1.2.3 GTC Register Partitioning
      2. 12.7.2 RTI-Windowed Watchdog Timer (WWDT)
        1. 12.7.2.1 RTI Features
        2. 12.7.2.2 Unsupported Features
        3.       2744
        4. 12.7.2.3 RTI Functional Description
          1. 12.7.2.3.1 RTI Digital Windowed Watchdog
            1. 12.7.2.3.1.1 RTI Debug Mode Behavior
            2. 12.7.2.3.1.2 RTI Low Power Mode Operation
          2. 12.7.2.3.2 RTI Digital Watchdog
          3. 12.7.2.3.3 RTI Counter Operation
      3. 12.7.3 Real-Time Clock (RTC)
        1. 12.7.3.1 RTC Overview
          1. 12.7.3.1.1 RTC Features
          2. 12.7.3.1.2 Unsupported Features
          3.        2755
        2. 12.7.3.2 RTC Integration
        3. 12.7.3.3 RTC Functional Description
          1. 12.7.3.3.1 RTC Block Diagram
            1. 12.7.3.3.1.1 DIG_CORE uARCH
            2. 12.7.3.3.1.2 DIG_ON uARCH
            3. 12.7.3.3.1.3 ISO_LVL uARCH
            4. 12.7.3.3.1.4 DIG_CORE to DIG_ON updates uARCH
          2. 12.7.3.3.2 CPU Interrupt Support
            1. 12.7.3.3.2.1 CPU Interrupts
          3. 12.7.3.3.3 Programming Usage Guide
            1. 12.7.3.3.3.1 No Analog Support
            2. 12.7.3.3.3.2 With Analog Support
              1. 12.7.3.3.3.2.1 MMR Spurious WRT Protection
              2. 12.7.3.3.3.2.2 Crystal Compensation
          4. 12.7.3.3.4 Scratch Registers
          5. 12.7.3.3.5 KS3 Clock Stop Protocol
      4. 12.7.4 Timers
        1. 12.7.4.1 Timers Overview
          1. 12.7.4.1.1 Timers Features
          2. 12.7.4.1.2 Unsupported Features
          3.        2776
        2. 12.7.4.2 Timers Environment
          1. 12.7.4.2.1 Timer External System Interface
        3. 12.7.4.3 Integration
        4. 12.7.4.4 Timers Functional Description
          1. 12.7.4.4.1  Timer Block Diagram
          2. 12.7.4.4.2  Timer Power Management
            1. 12.7.4.4.2.1 Wake-Up Capability
          3. 12.7.4.4.3  Timer Software Reset
          4. 12.7.4.4.4  Timer Interrupts
          5. 12.7.4.4.5  Timer Mode Functionality
            1. 12.7.4.4.5.1 1-ms Tick Generation
          6. 12.7.4.4.6  Timer Capture Mode Functionality
          7. 12.7.4.4.7  Timer Compare Mode Functionality
          8. 12.7.4.4.8  Timer Prescaler Functionality
          9. 12.7.4.4.9  Timer Pulse-Width Modulation
          10. 12.7.4.4.10 Timer Counting Rate
          11. 12.7.4.4.11 Timer Under Emulation
          12. 12.7.4.4.12 Accessing Timer Registers
            1. 12.7.4.4.12.1 Writing to Timer Registers
              1. 12.7.4.4.12.1.1 Write Posting Synchronization Mode
              2. 12.7.4.4.12.1.2 Write Nonposting Synchronization Mode
            2. 12.7.4.4.12.2 Reading From Timer Counter Registers
              1. 12.7.4.4.12.2.1 Read Posted
              2. 12.7.4.4.12.2.2 Read Non-Posted
          13. 12.7.4.4.13 Timer Posted Mode Selection
        5. 12.7.4.5 Timers Low-Level Programming Models
          1. 12.7.4.5.1 Timer Global Initialization
            1. 12.7.4.5.1.1 Main Sequence – Timer Module Global Initialization
          2. 12.7.4.5.2 Timer Operational Mode Configuration
            1. 12.7.4.5.2.1 Timer Mode
              1. 12.7.4.5.2.1.1 Main Sequence – Timer Mode Configuration
            2. 12.7.4.5.2.2 Timer Compare Mode
              1. 12.7.4.5.2.2.1 Main Sequence – Timer Compare Mode Configuration
            3. 12.7.4.5.2.3 Timer Capture Mode
              1. 12.7.4.5.2.3.1 Main Sequence – Timer Capture Mode Configuration
              2. 12.7.4.5.2.3.2 Subsequence – Initialize Capture Mode
              3. 12.7.4.5.2.3.3 Subsequence – Detect Event
            4. 12.7.4.5.2.4 Timer PWM Mode
              1. 12.7.4.5.2.4.1 Main Sequence – Timer PWM Mode Configuration
    8. 12.8 Internal Diagnostics Modules
      1. 12.8.1 Dual Clock Comparator (DCC)
        1. 12.8.1.1 DCC Overview
          1. 12.8.1.1.1 DCC Features
          2. 12.8.1.1.2 Unsupported Features
          3.        2821
        2. 12.8.1.2 DCC Functional Description
          1. 12.8.1.2.1 DCC Counter Operation
          2. 12.8.1.2.2 DCC Low Power Mode Operation
          3. 12.8.1.2.3 DCC Suspend Mode Behavior
          4. 12.8.1.2.4 DCC Single-Shot Mode
          5. 12.8.1.2.5 DCC Continuous mode
            1. 12.8.1.2.5.1 DCC Continue on Error
            2. 12.8.1.2.5.2 DCC Error Count
          6. 12.8.1.2.6 DCC Control and count hand-off across clock domains
          7. 12.8.1.2.7 DCC Error Trajectory record
            1. 12.8.1.2.7.1 DCC FIFO capturing for Errors
            2. 12.8.1.2.7.2 DCC FIFO in continuous capture mode
            3. 12.8.1.2.7.3 DCC FIFO Details
            4. 12.8.1.2.7.4 DCC FIFO Debug mode behavior
          8. 12.8.1.2.8 DCC Count read registers
      2. 12.8.2 Error Signaling Module (ESM)
        1. 12.8.2.1 ESM Overview
          1. 12.8.2.1.1 ESM Features
          2. 12.8.2.1.2 Unsupported Features
          3.        2841
        2. 12.8.2.2 ESM Environment
        3. 12.8.2.3 Integration
        4. 12.8.2.4 ESM Functional Description
          1. 12.8.2.4.1 ESM Interrupt Requests
            1. 12.8.2.4.1.1 ESM Configuration Error Interrupt
            2. 12.8.2.4.1.2 ESM Low Priority Error Interrupt
              1. 12.8.2.4.1.2.1 ESM Low Priority Error Level Event
              2. 12.8.2.4.1.2.2 ESM Low Priority Error Pulse Event
            3. 12.8.2.4.1.3 ESM High Priority Error Interrupt
              1. 12.8.2.4.1.3.1 ESM High Priority Error Level Event
              2. 12.8.2.4.1.3.2 ESM High Priority Error Pulse Event
          2. 12.8.2.4.2 ESM Error Event Inputs
          3. 12.8.2.4.3 ESM Error Pin Output
          4. 12.8.2.4.4 PWM Mode
          5. 12.8.2.4.5 ESM Minimum Time Interval
          6. 12.8.2.4.6 ESM Protection for Registers
          7. 12.8.2.4.7 ESM Clock Stop
      3. 12.8.3 Memory Cyclic Redundancy Check (MCRC) Controller
        1. 12.8.3.1 MCRC Overview
          1. 12.8.3.1.1 MCRC Features
          2. 12.8.3.1.2 Unsupported Features
          3.        2863
        2. 12.8.3.2 MCRC Functional Description
          1. 12.8.3.2.1  MCRC Block Diagram
          2. 12.8.3.2.2  MCRC General Operation
          3. 12.8.3.2.3  MCRC Modes of Operation
            1. 12.8.3.2.3.1 AUTO Mode
            2. 12.8.3.2.3.2 Semi-CPU Mode
            3. 12.8.3.2.3.3 Full-CPU Mode
          4. 12.8.3.2.4  PSA Signature Register
          5. 12.8.3.2.5  PSA Sector Signature Register
          6. 12.8.3.2.6  CRC Value Register
          7. 12.8.3.2.7  Raw Data Register
          8. 12.8.3.2.8  Example DMA Controller Setup
            1. 12.8.3.2.8.1 AUTO Mode Using Hardware Timer Trigger
            2. 12.8.3.2.8.2 AUTO Mode Using Software Trigger
            3. 12.8.3.2.8.3 Semi-CPU Mode Using Hardware Timer Trigger
          9. 12.8.3.2.9  Pattern Count Register
          10. 12.8.3.2.10 Sector Count Register/Current Sector Register
          11. 12.8.3.2.11 Interrupts
            1. 12.8.3.2.11.1 Overrun Interrupt
            2. 12.8.3.2.11.2 Timeout Interrupt
            3. 12.8.3.2.11.3 Underrun Interrupt
            4. 12.8.3.2.11.4 Compression Complete Interrupt
            5. 12.8.3.2.11.5 Interrupt Offset Register
            6. 12.8.3.2.11.6 Error Handling
          12. 12.8.3.2.12 Power Down Mode
          13. 12.8.3.2.13 Emulation
        3. 12.8.3.3 MCRC Programming Examples
          1. 12.8.3.3.1 Example: Auto Mode Using Time Based Event Triggering
            1. 12.8.3.3.1.1 DMA Setup
            2. 12.8.3.3.1.2 Timer Setup
            3. 12.8.3.3.1.3 CRC Setup
          2. 12.8.3.3.2 Example: Auto Mode Without Using Time Based Triggering
            1. 12.8.3.3.2.1 DMA Setup
            2. 12.8.3.3.2.2 CRC Setup
          3. 12.8.3.3.3 Example: Semi-CPU Mode
            1. 12.8.3.3.3.1 DMA Setup
            2. 12.8.3.3.3.2 Timer Setup
            3. 12.8.3.3.3.3 CRC Setup
          4. 12.8.3.3.4 Example: Full-CPU Mode
            1. 12.8.3.3.4.1 CRC Setup
      4. 12.8.4 ECC Aggregator
        1. 12.8.4.1 ECC Aggregator Overview
          1. 12.8.4.1.1 ECC Aggregator Features
          2. 12.8.4.1.2 Unsupported Features
          3.        2908
        2. 12.8.4.2 Integration
        3. 12.8.4.3 ECC Aggregator Functional Description
          1. 12.8.4.3.1 ECC Aggregator Block Diagram
          2. 12.8.4.3.2 ECC Aggregator Register Groups
          3. 12.8.4.3.3 Read Access to the ECC Control and Status Registers
          4. 12.8.4.3.4 Serial Write Operation
          5. 12.8.4.3.5 Interrupts
          6. 12.8.4.3.6 Inject Only Mode
        4. 12.8.4.4 ECC Aggregator Configurations
          1.        2918
          2.        2919
          3.        2920
          4.        2921
          5.        2922
          6.        2923
          7.        2924
          8.        2925
          9.        2926
          10.        2927
          11.        2928
          12.        2929
          13.        2930
          14.        2931
          15.        2932
          16.        2933
          17.        2934
          18.        2935
          19.        2936
          20.        2937
          21.        2938
          22.        2939
          23.        2940
          24.        2941
          25.        2942
          26.        2943
          27.        2944
          28.        2945
          29.        2946
          30.        2947
          31.        2948
    9. 12.9 Display Subsystem (DSS) and Peripherals
      1. 12.9.1 Display Subsystem (DSS)
        1. 12.9.1.1 DSS Overview
          1. 12.9.1.1.1 DSS Features
          2.        2953
          3. 12.9.1.1.2 Unsupported Features
        2. 12.9.1.2 DSS Environment
          1. 12.9.1.2.1 DSS Parallel Interface
            1. 12.9.1.2.1.1 Pixel Data Formats
            2. 12.9.1.2.1.2 Display Timing Diagrams
          2. 12.9.1.2.2 DSS LVDS Interface
        3. 12.9.1.3 Integration
        4. 12.9.1.4 DSS Functional Description
          1. 12.9.1.4.1 DISPC Functional Description
            1. 12.9.1.4.1.1  DISPC Overview
            2. 12.9.1.4.1.2  DISPC Clocks
            3. 12.9.1.4.1.3  DISPC Resets
            4. 12.9.1.4.1.4  DISPC Power Management
            5. 12.9.1.4.1.5  DISPC Interrupt Requests
            6. 12.9.1.4.1.6  DISPC DMA Engine
              1. 12.9.1.4.1.6.1 DISPC DMA Addressing and Bursts
              2. 12.9.1.4.1.6.2 DISPC Read DMA Buffers
              3. 12.9.1.4.1.6.3 DISPC Flip/Mirror Support
              4. 12.9.1.4.1.6.4 DISPC DMA Predecimation
              5. 12.9.1.4.1.6.5 DISPC DMA MFLAG Mechanism
              6. 12.9.1.4.1.6.6 DISPC DMA Priority Requests Control
              7. 12.9.1.4.1.6.7 DISPC DMA Arbitration
              8. 12.9.1.4.1.6.8 DISPC DMA Power Modes
                1. 12.9.1.4.1.6.8.1 DISPC DMA Low Power Mode
                2. 12.9.1.4.1.6.8.2 DISPC DMA Ultra-Low Power Mode
            7. 12.9.1.4.1.7  DISPC Pixel Data Formats
            8. 12.9.1.4.1.8  DISPC Video Pipelines
              1. 12.9.1.4.1.8.1 DISPC VID Replication Logic
              2. 12.9.1.4.1.8.2 DISPC VID VC-1 Range Mapping Unit
              3. 12.9.1.4.1.8.3 DISPC VID Color Look-Up Table (CLUT)
              4. 12.9.1.4.1.8.4 DISPC VID Chrominance Resampling
                1. 12.9.1.4.1.8.4.1 Chrominance Resampling for VID Pipeline
                2. 12.9.1.4.1.8.4.2 Chrominance Resampling for VIDL1 Pipeline
              5. 12.9.1.4.1.8.5 DISPC VID Scaler Unit
              6. 12.9.1.4.1.8.6 DISPC VID Color Space Conversion YUV to RGB
              7. 12.9.1.4.1.8.7 DISPC VID Brightness/Contrast/Saturation/Hue Control
              8. 12.9.1.4.1.8.8 DISPC VID Luma Key Support
            9. 12.9.1.4.1.9  DISPC Overlay Managers
              1. 12.9.1.4.1.9.1 DISPC Overlay Input Selector
              2. 12.9.1.4.1.9.2 DISPC Overlay Mechanism
                1. 12.9.1.4.1.9.2.1 Overlay Alpha Blender
                2. 12.9.1.4.1.9.2.2 Overlay Transparency Color Keys
              3. 12.9.1.4.1.9.3 Overlay 3D Support
              4. 12.9.1.4.1.9.4 Overlay Color Bar Insertion
            10. 12.9.1.4.1.10 DISPC Video Port Outputs
              1. 12.9.1.4.1.10.1 DISPC VP Gamma Correction Unit
              2. 12.9.1.4.1.10.2 DISPC VP Color Phase Rotation Unit
              3. 12.9.1.4.1.10.3 DISPC VP Color Space Conversion - RGB to YUV
              4. 12.9.1.4.1.10.4 DISPC VP BT.656 and BT.1120 Modes
                1. 12.9.1.4.1.10.4.1 DISPC BT Mode Blanking
                2. 12.9.1.4.1.10.4.2 DISPC BT Mode EAV and SAV
              5. 12.9.1.4.1.10.5 DISPC VP Spatial/Temporal Dithering
              6. 12.9.1.4.1.10.6 DISPC VP Multiple Cycle Output Format (TDM)
              7. 12.9.1.4.1.10.7 DISPC VP Timing Generator and Display Panel Settings
            11. 12.9.1.4.1.11 DISPC Safety Features
              1. 12.9.1.4.1.11.1 Safety Check Regions
              2. 12.9.1.4.1.11.2 Safety Signature Generator Using MISR
              3. 12.9.1.4.1.11.3 Safety Checks
              4. 12.9.1.4.1.11.4 Safety Check Limitations
            12. 12.9.1.4.1.12 DISPC Security Management
              1. 12.9.1.4.1.12.1 Security Implementation
              2. 12.9.1.4.1.12.2 Secure Mode Configuration
            13. 12.9.1.4.1.13 DISPC Shadow Registers
          2. 12.9.1.4.2 OLDITX Functional Description
            1. 12.9.1.4.2.1 OLDITX Overview
            2. 12.9.1.4.2.2 OLDITX Clocks
            3. 12.9.1.4.2.3 OLDITX Resets
            4. 12.9.1.4.2.4 OLDITX Input Interface
              1. 12.9.1.4.2.4.1 OLDITX 24-bit RGB Input
              2. 12.9.1.4.2.4.2 OLDITX 18-bit RGB Input
            5. 12.9.1.4.2.5 OLDITX Output Mode Configuration
            6. 12.9.1.4.2.6 OLDITX Loopback Test Mode
      2. 12.9.2 Graphics Processing Unit (GPU)
        1. 12.9.2.1 GPU Registers Description
  15. 13On-Chip Debug
    1. 13.1 On-Chip Debug Overview
    2. 13.2 On-Chip Debug Features
    3.     3031
    4. 13.3 On-Chip Debug Functional Description
      1. 13.3.1  On-Chip Debug Block Diagram
      2. 13.3.2  Device Interfaces
        1. 13.3.2.1 JTAG Interface
        2. 13.3.2.2 Trigger and Debug Boot Mode Interface
        3. 13.3.2.3 Trace Port Interface
      3. 13.3.3  Debug and Boundary Scan Access and Control
      4. 13.3.4  Debug Boot Modes and Boundary Scan Compliance
      5. 13.3.5  Power, Reset, Clock Management
      6. 13.3.6  Debug Cross Triggering
      7. 13.3.7  WKUP_R5F Debug
      8. 13.3.8  SMS0_HSM and MCU_M4F Debug
      9. 13.3.9  A53SS0 Debug
      10. 13.3.10 PRUSS Debug
      11. 13.3.11 SoC Debug and Trace
        1. 13.3.11.1 Software messaging trace
        2. 13.3.11.2 Debug-Aware Peripherals
        3. 13.3.11.3 Traffic Monitoring With Bus Probes
        4. 13.3.11.4 Global timestamping for trace
      12. 13.3.12 Trace Traffic
        1. 13.3.12.1 Trace Sources
        2. 13.3.12.2 Trace Infrasctructure
        3. 13.3.12.3 Trace Sinks
      13. 13.3.13 Application Support
  16. 14Registers
    1. 14.1 System Interconnect Registers
      1. 14.1.1 CBASS Registers
        1. 14.1.1.1    ERR_PID Registers
        2. 14.1.1.2    ERR_DESTINATION_ID Registers
        3. 14.1.1.3    ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.1.4    ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.1.5    ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.1.6    ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.1.7    ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.1.8    ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.1.9    ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.1.10   ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.1.11   ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.1.12   ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.1.13   ERR_EOI Registers
        14. 14.1.1.14   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_CONTROL Registers
        15. 14.1.1.15   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_PERMISSION_0 Registers
        16. 14.1.1.16   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_PERMISSION_1 Registers
        17. 14.1.1.17   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_PERMISSION_2 Registers
        18. 14.1.1.18   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_START_ADDRESS_L Registers
        19. 14.1.1.19   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_START_ADDRESS_H Registers
        20. 14.1.1.20   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_END_ADDRESS_L Registers
        21. 14.1.1.21   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_0_END_ADDRESS_H Registers
        22. 14.1.1.22   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_CONTROL Registers
        23. 14.1.1.23   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_PERMISSION_0 Registers
        24. 14.1.1.24   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_PERMISSION_1 Registers
        25. 14.1.1.25   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_PERMISSION_2 Registers
        26. 14.1.1.26   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_START_ADDRESS_L Registers
        27. 14.1.1.27   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_START_ADDRESS_H Registers
        28. 14.1.1.28   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_END_ADDRESS_L Registers
        29. 14.1.1.29   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_1_END_ADDRESS_H Registers
        30. 14.1.1.30   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_CONTROL Registers
        31. 14.1.1.31   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_PERMISSION_0 Registers
        32. 14.1.1.32   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_PERMISSION_1 Registers
        33. 14.1.1.33   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_PERMISSION_2 Registers
        34. 14.1.1.34   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_START_ADDRESS_L Registers
        35. 14.1.1.35   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_START_ADDRESS_H Registers
        36. 14.1.1.36   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_END_ADDRESS_L Registers
        37. 14.1.1.37   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_2_END_ADDRESS_H Registers
        38. 14.1.1.38   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_CONTROL Registers
        39. 14.1.1.39   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_PERMISSION_0 Registers
        40. 14.1.1.40   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_PERMISSION_1 Registers
        41. 14.1.1.41   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_PERMISSION_2 Registers
        42. 14.1.1.42   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_START_ADDRESS_L Registers
        43. 14.1.1.43   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_START_ADDRESS_H Registers
        44. 14.1.1.44   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_END_ADDRESS_L Registers
        45. 14.1.1.45   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_3_END_ADDRESS_H Registers
        46. 14.1.1.46   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_CONTROL Registers
        47. 14.1.1.47   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_PERMISSION_0 Registers
        48. 14.1.1.48   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_PERMISSION_1 Registers
        49. 14.1.1.49   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_PERMISSION_2 Registers
        50. 14.1.1.50   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_START_ADDRESS_L Registers
        51. 14.1.1.51   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_START_ADDRESS_H Registers
        52. 14.1.1.52   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_END_ADDRESS_L Registers
        53. 14.1.1.53   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_4_END_ADDRESS_H Registers
        54. 14.1.1.54   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_CONTROL Registers
        55. 14.1.1.55   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_PERMISSION_0 Registers
        56. 14.1.1.56   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_PERMISSION_1 Registers
        57. 14.1.1.57   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_PERMISSION_2 Registers
        58. 14.1.1.58   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_START_ADDRESS_L Registers
        59. 14.1.1.59   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_START_ADDRESS_H Registers
        60. 14.1.1.60   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_END_ADDRESS_L Registers
        61. 14.1.1.61   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_5_END_ADDRESS_H Registers
        62. 14.1.1.62   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_CONTROL Registers
        63. 14.1.1.63   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_PERMISSION_0 Registers
        64. 14.1.1.64   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_PERMISSION_1 Registers
        65. 14.1.1.65   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_PERMISSION_2 Registers
        66. 14.1.1.66   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_START_ADDRESS_L Registers
        67. 14.1.1.67   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_START_ADDRESS_H Registers
        68. 14.1.1.68   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_END_ADDRESS_L Registers
        69. 14.1.1.69   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_6_END_ADDRESS_H Registers
        70. 14.1.1.70   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_CONTROL Registers
        71. 14.1.1.71   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_PERMISSION_0 Registers
        72. 14.1.1.72   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_PERMISSION_1 Registers
        73. 14.1.1.73   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_PERMISSION_2 Registers
        74. 14.1.1.74   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_START_ADDRESS_L Registers
        75. 14.1.1.75   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_START_ADDRESS_H Registers
        76. 14.1.1.76   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_END_ADDRESS_L Registers
        77. 14.1.1.77   FW_ISAM62_DDR_WRAP_MAIN_0_DDRSS_FW_REGION_7_END_ADDRESS_H Registers
        78. 14.1.1.78   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_CONTROL Registers
        79. 14.1.1.79   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_PERMISSION_0 Registers
        80. 14.1.1.80   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_PERMISSION_1 Registers
        81. 14.1.1.81   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_PERMISSION_2 Registers
        82. 14.1.1.82   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_START_ADDRESS_L Registers
        83. 14.1.1.83   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_START_ADDRESS_H Registers
        84. 14.1.1.84   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_END_ADDRESS_L Registers
        85. 14.1.1.85   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_0_END_ADDRESS_H Registers
        86. 14.1.1.86   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_CONTROL Registers
        87. 14.1.1.87   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_PERMISSION_0 Registers
        88. 14.1.1.88   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_PERMISSION_1 Registers
        89. 14.1.1.89   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_PERMISSION_2 Registers
        90. 14.1.1.90   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_START_ADDRESS_L Registers
        91. 14.1.1.91   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_START_ADDRESS_H Registers
        92. 14.1.1.92   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_END_ADDRESS_L Registers
        93. 14.1.1.93   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_1_END_ADDRESS_H Registers
        94. 14.1.1.94   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_CONTROL Registers
        95. 14.1.1.95   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_PERMISSION_0 Registers
        96. 14.1.1.96   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_PERMISSION_1 Registers
        97. 14.1.1.97   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_PERMISSION_2 Registers
        98. 14.1.1.98   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_START_ADDRESS_L Registers
        99. 14.1.1.99   FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_START_ADDRESS_H Registers
        100. 14.1.1.100  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_END_ADDRESS_L Registers
        101. 14.1.1.101  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_2_END_ADDRESS_H Registers
        102. 14.1.1.102  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_CONTROL Registers
        103. 14.1.1.103  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_PERMISSION_0 Registers
        104. 14.1.1.104  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_PERMISSION_1 Registers
        105. 14.1.1.105  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_PERMISSION_2 Registers
        106. 14.1.1.106  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_START_ADDRESS_L Registers
        107. 14.1.1.107  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_START_ADDRESS_H Registers
        108. 14.1.1.108  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_END_ADDRESS_L Registers
        109. 14.1.1.109  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_3_END_ADDRESS_H Registers
        110. 14.1.1.110  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_CONTROL Registers
        111. 14.1.1.111  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_PERMISSION_0 Registers
        112. 14.1.1.112  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_PERMISSION_1 Registers
        113. 14.1.1.113  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_PERMISSION_2 Registers
        114. 14.1.1.114  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_START_ADDRESS_L Registers
        115. 14.1.1.115  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_START_ADDRESS_H Registers
        116. 14.1.1.116  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_END_ADDRESS_L Registers
        117. 14.1.1.117  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_4_END_ADDRESS_H Registers
        118. 14.1.1.118  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_CONTROL Registers
        119. 14.1.1.119  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_PERMISSION_0 Registers
        120. 14.1.1.120  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_PERMISSION_1 Registers
        121. 14.1.1.121  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_PERMISSION_2 Registers
        122. 14.1.1.122  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_START_ADDRESS_L Registers
        123. 14.1.1.123  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_START_ADDRESS_H Registers
        124. 14.1.1.124  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_END_ADDRESS_L Registers
        125. 14.1.1.125  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_5_END_ADDRESS_H Registers
        126. 14.1.1.126  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_CONTROL Registers
        127. 14.1.1.127  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_PERMISSION_0 Registers
        128. 14.1.1.128  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_PERMISSION_1 Registers
        129. 14.1.1.129  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_PERMISSION_2 Registers
        130. 14.1.1.130  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_START_ADDRESS_L Registers
        131. 14.1.1.131  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_START_ADDRESS_H Registers
        132. 14.1.1.132  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_END_ADDRESS_L Registers
        133. 14.1.1.133  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_6_END_ADDRESS_H Registers
        134. 14.1.1.134  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_CONTROL Registers
        135. 14.1.1.135  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_PERMISSION_0 Registers
        136. 14.1.1.136  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_PERMISSION_1 Registers
        137. 14.1.1.137  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_PERMISSION_2 Registers
        138. 14.1.1.138  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_START_ADDRESS_L Registers
        139. 14.1.1.139  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_START_ADDRESS_H Registers
        140. 14.1.1.140  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_END_ADDRESS_L Registers
        141. 14.1.1.141  FW_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_ACP_W_FW_REGION_7_END_ADDRESS_H Registers
        142. 14.1.1.142  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_CONTROL Registers
        143. 14.1.1.143  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_PERMISSION_0 Registers
        144. 14.1.1.144  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_PERMISSION_1 Registers
        145. 14.1.1.145  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_PERMISSION_2 Registers
        146. 14.1.1.146  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_START_ADDRESS_L Registers
        147. 14.1.1.147  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_START_ADDRESS_H Registers
        148. 14.1.1.148  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_END_ADDRESS_L Registers
        149. 14.1.1.149  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_0_END_ADDRESS_H Registers
        150. 14.1.1.150  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_CONTROL Registers
        151. 14.1.1.151  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_PERMISSION_0 Registers
        152. 14.1.1.152  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_PERMISSION_1 Registers
        153. 14.1.1.153  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_PERMISSION_2 Registers
        154. 14.1.1.154  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_START_ADDRESS_L Registers
        155. 14.1.1.155  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_START_ADDRESS_H Registers
        156. 14.1.1.156  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_END_ADDRESS_L Registers
        157. 14.1.1.157  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_1_END_ADDRESS_H Registers
        158. 14.1.1.158  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_CONTROL Registers
        159. 14.1.1.159  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_PERMISSION_0 Registers
        160. 14.1.1.160  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_PERMISSION_1 Registers
        161. 14.1.1.161  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_PERMISSION_2 Registers
        162. 14.1.1.162  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_START_ADDRESS_L Registers
        163. 14.1.1.163  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_START_ADDRESS_H Registers
        164. 14.1.1.164  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_END_ADDRESS_L Registers
        165. 14.1.1.165  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_2_END_ADDRESS_H Registers
        166. 14.1.1.166  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_CONTROL Registers
        167. 14.1.1.167  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_PERMISSION_0 Registers
        168. 14.1.1.168  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_PERMISSION_1 Registers
        169. 14.1.1.169  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_PERMISSION_2 Registers
        170. 14.1.1.170  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_START_ADDRESS_L Registers
        171. 14.1.1.171  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_START_ADDRESS_H Registers
        172. 14.1.1.172  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_END_ADDRESS_L Registers
        173. 14.1.1.173  FW_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSP_CFG_FW_REGION_3_END_ADDRESS_H Registers
        174. 14.1.1.174  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_CONTROL Registers
        175. 14.1.1.175  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_PERMISSION_0 Registers
        176. 14.1.1.176  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_PERMISSION_1 Registers
        177. 14.1.1.177  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_PERMISSION_2 Registers
        178. 14.1.1.178  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_L Registers
        179. 14.1.1.179  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_H Registers
        180. 14.1.1.180  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_L Registers
        181. 14.1.1.181  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_H Registers
        182. 14.1.1.182  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_CONTROL Registers
        183. 14.1.1.183  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_PERMISSION_0 Registers
        184. 14.1.1.184  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_PERMISSION_1 Registers
        185. 14.1.1.185  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_PERMISSION_2 Registers
        186. 14.1.1.186  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_L Registers
        187. 14.1.1.187  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_H Registers
        188. 14.1.1.188  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_L Registers
        189. 14.1.1.189  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_H Registers
        190. 14.1.1.190  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_CONTROL Registers
        191. 14.1.1.191  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_PERMISSION_0 Registers
        192. 14.1.1.192  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_PERMISSION_1 Registers
        193. 14.1.1.193  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_PERMISSION_2 Registers
        194. 14.1.1.194  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_L Registers
        195. 14.1.1.195  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_H Registers
        196. 14.1.1.196  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_L Registers
        197. 14.1.1.197  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_H Registers
        198. 14.1.1.198  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_CONTROL Registers
        199. 14.1.1.199  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_PERMISSION_0 Registers
        200. 14.1.1.200  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_PERMISSION_1 Registers
        201. 14.1.1.201  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_PERMISSION_2 Registers
        202. 14.1.1.202  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_L Registers
        203. 14.1.1.203  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_H Registers
        204. 14.1.1.204  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_L Registers
        205. 14.1.1.205  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_H Registers
        206. 14.1.1.206  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_CONTROL Registers
        207. 14.1.1.207  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_PERMISSION_0 Registers
        208. 14.1.1.208  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_PERMISSION_1 Registers
        209. 14.1.1.209  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_PERMISSION_2 Registers
        210. 14.1.1.210  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_L Registers
        211. 14.1.1.211  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_H Registers
        212. 14.1.1.212  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_L Registers
        213. 14.1.1.213  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_H Registers
        214. 14.1.1.214  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_CONTROL Registers
        215. 14.1.1.215  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_PERMISSION_0 Registers
        216. 14.1.1.216  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_PERMISSION_1 Registers
        217. 14.1.1.217  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_PERMISSION_2 Registers
        218. 14.1.1.218  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_L Registers
        219. 14.1.1.219  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_H Registers
        220. 14.1.1.220  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_L Registers
        221. 14.1.1.221  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_H Registers
        222. 14.1.1.222  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_CONTROL Registers
        223. 14.1.1.223  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_PERMISSION_0 Registers
        224. 14.1.1.224  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_PERMISSION_1 Registers
        225. 14.1.1.225  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_PERMISSION_2 Registers
        226. 14.1.1.226  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_L Registers
        227. 14.1.1.227  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_H Registers
        228. 14.1.1.228  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_L Registers
        229. 14.1.1.229  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_H Registers
        230. 14.1.1.230  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_CONTROL Registers
        231. 14.1.1.231  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_PERMISSION_0 Registers
        232. 14.1.1.232  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_PERMISSION_1 Registers
        233. 14.1.1.233  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_PERMISSION_2 Registers
        234. 14.1.1.234  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_L Registers
        235. 14.1.1.235  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_H Registers
        236. 14.1.1.236  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_L Registers
        237. 14.1.1.237  FW_EXPORT_AM62_MAIN_DATA_CBASS_TO_AM62_MAIN_MISC_PERI_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_H Registers
        238. 14.1.1.238  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_CONTROL Registers
        239. 14.1.1.239  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_PERMISSION_0 Registers
        240. 14.1.1.240  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_PERMISSION_1 Registers
        241. 14.1.1.241  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_PERMISSION_2 Registers
        242. 14.1.1.242  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_START_ADDRESS_L Registers
        243. 14.1.1.243  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_START_ADDRESS_H Registers
        244. 14.1.1.244  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_END_ADDRESS_L Registers
        245. 14.1.1.245  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_0_END_ADDRESS_H Registers
        246. 14.1.1.246  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_CONTROL Registers
        247. 14.1.1.247  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_PERMISSION_0 Registers
        248. 14.1.1.248  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_PERMISSION_1 Registers
        249. 14.1.1.249  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_PERMISSION_2 Registers
        250. 14.1.1.250  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_START_ADDRESS_L Registers
        251. 14.1.1.251  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_START_ADDRESS_H Registers
        252. 14.1.1.252  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_END_ADDRESS_L Registers
        253. 14.1.1.253  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_1_END_ADDRESS_H Registers
        254. 14.1.1.254  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_CONTROL Registers
        255. 14.1.1.255  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_PERMISSION_0 Registers
        256. 14.1.1.256  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_PERMISSION_1 Registers
        257. 14.1.1.257  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_PERMISSION_2 Registers
        258. 14.1.1.258  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_START_ADDRESS_L Registers
        259. 14.1.1.259  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_START_ADDRESS_H Registers
        260. 14.1.1.260  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_END_ADDRESS_L Registers
        261. 14.1.1.261  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_2_END_ADDRESS_H Registers
        262. 14.1.1.262  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_CONTROL Registers
        263. 14.1.1.263  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_PERMISSION_0 Registers
        264. 14.1.1.264  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_PERMISSION_1 Registers
        265. 14.1.1.265  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_PERMISSION_2 Registers
        266. 14.1.1.266  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_START_ADDRESS_L Registers
        267. 14.1.1.267  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_START_ADDRESS_H Registers
        268. 14.1.1.268  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_END_ADDRESS_L Registers
        269. 14.1.1.269  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_3_END_ADDRESS_H Registers
        270. 14.1.1.270  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_CONTROL Registers
        271. 14.1.1.271  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_PERMISSION_0 Registers
        272. 14.1.1.272  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_PERMISSION_1 Registers
        273. 14.1.1.273  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_PERMISSION_2 Registers
        274. 14.1.1.274  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_START_ADDRESS_L Registers
        275. 14.1.1.275  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_START_ADDRESS_H Registers
        276. 14.1.1.276  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_END_ADDRESS_L Registers
        277. 14.1.1.277  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_4_END_ADDRESS_H Registers
        278. 14.1.1.278  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_CONTROL Registers
        279. 14.1.1.279  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_PERMISSION_0 Registers
        280. 14.1.1.280  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_PERMISSION_1 Registers
        281. 14.1.1.281  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_PERMISSION_2 Registers
        282. 14.1.1.282  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_START_ADDRESS_L Registers
        283. 14.1.1.283  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_START_ADDRESS_H Registers
        284. 14.1.1.284  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_END_ADDRESS_L Registers
        285. 14.1.1.285  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_5_END_ADDRESS_H Registers
        286. 14.1.1.286  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_CONTROL Registers
        287. 14.1.1.287  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_PERMISSION_0 Registers
        288. 14.1.1.288  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_PERMISSION_1 Registers
        289. 14.1.1.289  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_PERMISSION_2 Registers
        290. 14.1.1.290  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_START_ADDRESS_L Registers
        291. 14.1.1.291  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_START_ADDRESS_H Registers
        292. 14.1.1.292  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_END_ADDRESS_L Registers
        293. 14.1.1.293  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_6_END_ADDRESS_H Registers
        294. 14.1.1.294  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_CONTROL Registers
        295. 14.1.1.295  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_PERMISSION_0 Registers
        296. 14.1.1.296  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_PERMISSION_1 Registers
        297. 14.1.1.297  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_PERMISSION_2 Registers
        298. 14.1.1.298  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_START_ADDRESS_L Registers
        299. 14.1.1.299  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_START_ADDRESS_H Registers
        300. 14.1.1.300  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_END_ADDRESS_L Registers
        301. 14.1.1.301  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_7_END_ADDRESS_H Registers
        302. 14.1.1.302  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_CONTROL Registers
        303. 14.1.1.303  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_PERMISSION_0 Registers
        304. 14.1.1.304  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_PERMISSION_1 Registers
        305. 14.1.1.305  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_PERMISSION_2 Registers
        306. 14.1.1.306  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_START_ADDRESS_L Registers
        307. 14.1.1.307  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_START_ADDRESS_H Registers
        308. 14.1.1.308  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_END_ADDRESS_L Registers
        309. 14.1.1.309  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_8_END_ADDRESS_H Registers
        310. 14.1.1.310  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_CONTROL Registers
        311. 14.1.1.311  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_PERMISSION_0 Registers
        312. 14.1.1.312  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_PERMISSION_1 Registers
        313. 14.1.1.313  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_PERMISSION_2 Registers
        314. 14.1.1.314  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_START_ADDRESS_L Registers
        315. 14.1.1.315  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_START_ADDRESS_H Registers
        316. 14.1.1.316  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_END_ADDRESS_L Registers
        317. 14.1.1.317  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_9_END_ADDRESS_H Registers
        318. 14.1.1.318  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_CONTROL Registers
        319. 14.1.1.319  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_PERMISSION_0 Registers
        320. 14.1.1.320  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_PERMISSION_1 Registers
        321. 14.1.1.321  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_PERMISSION_2 Registers
        322. 14.1.1.322  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_START_ADDRESS_L Registers
        323. 14.1.1.323  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_START_ADDRESS_H Registers
        324. 14.1.1.324  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_END_ADDRESS_L Registers
        325. 14.1.1.325  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_10_END_ADDRESS_H Registers
        326. 14.1.1.326  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_CONTROL Registers
        327. 14.1.1.327  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_PERMISSION_0 Registers
        328. 14.1.1.328  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_PERMISSION_1 Registers
        329. 14.1.1.329  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_PERMISSION_2 Registers
        330. 14.1.1.330  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_START_ADDRESS_L Registers
        331. 14.1.1.331  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_START_ADDRESS_H Registers
        332. 14.1.1.332  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_END_ADDRESS_L Registers
        333. 14.1.1.333  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_11_END_ADDRESS_H Registers
        334. 14.1.1.334  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_CONTROL Registers
        335. 14.1.1.335  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_PERMISSION_0 Registers
        336. 14.1.1.336  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_PERMISSION_1 Registers
        337. 14.1.1.337  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_PERMISSION_2 Registers
        338. 14.1.1.338  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_START_ADDRESS_L Registers
        339. 14.1.1.339  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_START_ADDRESS_H Registers
        340. 14.1.1.340  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_END_ADDRESS_L Registers
        341. 14.1.1.341  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_12_END_ADDRESS_H Registers
        342. 14.1.1.342  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_CONTROL Registers
        343. 14.1.1.343  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_PERMISSION_0 Registers
        344. 14.1.1.344  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_PERMISSION_1 Registers
        345. 14.1.1.345  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_PERMISSION_2 Registers
        346. 14.1.1.346  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_START_ADDRESS_L Registers
        347. 14.1.1.347  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_START_ADDRESS_H Registers
        348. 14.1.1.348  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_END_ADDRESS_L Registers
        349. 14.1.1.349  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_13_END_ADDRESS_H Registers
        350. 14.1.1.350  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_CONTROL Registers
        351. 14.1.1.351  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_PERMISSION_0 Registers
        352. 14.1.1.352  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_PERMISSION_1 Registers
        353. 14.1.1.353  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_PERMISSION_2 Registers
        354. 14.1.1.354  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_START_ADDRESS_L Registers
        355. 14.1.1.355  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_START_ADDRESS_H Registers
        356. 14.1.1.356  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_END_ADDRESS_L Registers
        357. 14.1.1.357  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_14_END_ADDRESS_H Registers
        358. 14.1.1.358  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_CONTROL Registers
        359. 14.1.1.359  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_PERMISSION_0 Registers
        360. 14.1.1.360  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_PERMISSION_1 Registers
        361. 14.1.1.361  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_PERMISSION_2 Registers
        362. 14.1.1.362  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_START_ADDRESS_L Registers
        363. 14.1.1.363  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_START_ADDRESS_H Registers
        364. 14.1.1.364  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_END_ADDRESS_L Registers
        365. 14.1.1.365  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_15_END_ADDRESS_H Registers
        366. 14.1.1.366  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_CONTROL Registers
        367. 14.1.1.367  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_PERMISSION_0 Registers
        368. 14.1.1.368  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_PERMISSION_1 Registers
        369. 14.1.1.369  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_PERMISSION_2 Registers
        370. 14.1.1.370  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_START_ADDRESS_L Registers
        371. 14.1.1.371  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_START_ADDRESS_H Registers
        372. 14.1.1.372  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_END_ADDRESS_L Registers
        373. 14.1.1.373  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_16_END_ADDRESS_H Registers
        374. 14.1.1.374  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_CONTROL Registers
        375. 14.1.1.375  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_PERMISSION_0 Registers
        376. 14.1.1.376  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_PERMISSION_1 Registers
        377. 14.1.1.377  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_PERMISSION_2 Registers
        378. 14.1.1.378  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_START_ADDRESS_L Registers
        379. 14.1.1.379  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_START_ADDRESS_H Registers
        380. 14.1.1.380  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_END_ADDRESS_L Registers
        381. 14.1.1.381  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_17_END_ADDRESS_H Registers
        382. 14.1.1.382  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_CONTROL Registers
        383. 14.1.1.383  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_PERMISSION_0 Registers
        384. 14.1.1.384  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_PERMISSION_1 Registers
        385. 14.1.1.385  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_PERMISSION_2 Registers
        386. 14.1.1.386  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_START_ADDRESS_L Registers
        387. 14.1.1.387  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_START_ADDRESS_H Registers
        388. 14.1.1.388  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_END_ADDRESS_L Registers
        389. 14.1.1.389  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_18_END_ADDRESS_H Registers
        390. 14.1.1.390  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_CONTROL Registers
        391. 14.1.1.391  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_PERMISSION_0 Registers
        392. 14.1.1.392  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_PERMISSION_1 Registers
        393. 14.1.1.393  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_PERMISSION_2 Registers
        394. 14.1.1.394  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_START_ADDRESS_L Registers
        395. 14.1.1.395  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_START_ADDRESS_H Registers
        396. 14.1.1.396  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_END_ADDRESS_L Registers
        397. 14.1.1.397  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_19_END_ADDRESS_H Registers
        398. 14.1.1.398  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_CONTROL Registers
        399. 14.1.1.399  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_PERMISSION_0 Registers
        400. 14.1.1.400  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_PERMISSION_1 Registers
        401. 14.1.1.401  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_PERMISSION_2 Registers
        402. 14.1.1.402  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_START_ADDRESS_L Registers
        403. 14.1.1.403  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_START_ADDRESS_H Registers
        404. 14.1.1.404  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_END_ADDRESS_L Registers
        405. 14.1.1.405  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_20_END_ADDRESS_H Registers
        406. 14.1.1.406  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_CONTROL Registers
        407. 14.1.1.407  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_PERMISSION_0 Registers
        408. 14.1.1.408  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_PERMISSION_1 Registers
        409. 14.1.1.409  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_PERMISSION_2 Registers
        410. 14.1.1.410  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_START_ADDRESS_L Registers
        411. 14.1.1.411  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_START_ADDRESS_H Registers
        412. 14.1.1.412  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_END_ADDRESS_L Registers
        413. 14.1.1.413  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_21_END_ADDRESS_H Registers
        414. 14.1.1.414  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_CONTROL Registers
        415. 14.1.1.415  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_PERMISSION_0 Registers
        416. 14.1.1.416  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_PERMISSION_1 Registers
        417. 14.1.1.417  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_PERMISSION_2 Registers
        418. 14.1.1.418  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_START_ADDRESS_L Registers
        419. 14.1.1.419  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_START_ADDRESS_H Registers
        420. 14.1.1.420  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_END_ADDRESS_L Registers
        421. 14.1.1.421  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_22_END_ADDRESS_H Registers
        422. 14.1.1.422  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_CONTROL Registers
        423. 14.1.1.423  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_PERMISSION_0 Registers
        424. 14.1.1.424  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_PERMISSION_1 Registers
        425. 14.1.1.425  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_PERMISSION_2 Registers
        426. 14.1.1.426  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_START_ADDRESS_L Registers
        427. 14.1.1.427  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_START_ADDRESS_H Registers
        428. 14.1.1.428  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_END_ADDRESS_L Registers
        429. 14.1.1.429  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK2_DMA_CFG_L0_FW_REGION_23_END_ADDRESS_H Registers
        430. 14.1.1.430  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_CONTROL Registers
        431. 14.1.1.431  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_PERMISSION_0 Registers
        432. 14.1.1.432  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_PERMISSION_1 Registers
        433. 14.1.1.433  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_PERMISSION_2 Registers
        434. 14.1.1.434  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_START_ADDRESS_L Registers
        435. 14.1.1.435  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_START_ADDRESS_H Registers
        436. 14.1.1.436  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_END_ADDRESS_L Registers
        437. 14.1.1.437  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_0_END_ADDRESS_H Registers
        438. 14.1.1.438  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_CONTROL Registers
        439. 14.1.1.439  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_PERMISSION_0 Registers
        440. 14.1.1.440  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_PERMISSION_1 Registers
        441. 14.1.1.441  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_PERMISSION_2 Registers
        442. 14.1.1.442  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_START_ADDRESS_L Registers
        443. 14.1.1.443  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_START_ADDRESS_H Registers
        444. 14.1.1.444  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_END_ADDRESS_L Registers
        445. 14.1.1.445  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_1_END_ADDRESS_H Registers
        446. 14.1.1.446  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_CONTROL Registers
        447. 14.1.1.447  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_PERMISSION_0 Registers
        448. 14.1.1.448  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_PERMISSION_1 Registers
        449. 14.1.1.449  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_PERMISSION_2 Registers
        450. 14.1.1.450  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_START_ADDRESS_L Registers
        451. 14.1.1.451  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_START_ADDRESS_H Registers
        452. 14.1.1.452  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_END_ADDRESS_L Registers
        453. 14.1.1.453  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_2_END_ADDRESS_H Registers
        454. 14.1.1.454  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_CONTROL Registers
        455. 14.1.1.455  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_PERMISSION_0 Registers
        456. 14.1.1.456  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_PERMISSION_1 Registers
        457. 14.1.1.457  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_PERMISSION_2 Registers
        458. 14.1.1.458  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_START_ADDRESS_L Registers
        459. 14.1.1.459  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_START_ADDRESS_H Registers
        460. 14.1.1.460  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_END_ADDRESS_L Registers
        461. 14.1.1.461  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_3_END_ADDRESS_H Registers
        462. 14.1.1.462  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_CONTROL Registers
        463. 14.1.1.463  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_PERMISSION_0 Registers
        464. 14.1.1.464  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_PERMISSION_1 Registers
        465. 14.1.1.465  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_PERMISSION_2 Registers
        466. 14.1.1.466  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_START_ADDRESS_L Registers
        467. 14.1.1.467  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_START_ADDRESS_H Registers
        468. 14.1.1.468  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_END_ADDRESS_L Registers
        469. 14.1.1.469  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_4_END_ADDRESS_H Registers
        470. 14.1.1.470  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_CONTROL Registers
        471. 14.1.1.471  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_PERMISSION_0 Registers
        472. 14.1.1.472  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_PERMISSION_1 Registers
        473. 14.1.1.473  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_PERMISSION_2 Registers
        474. 14.1.1.474  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_START_ADDRESS_L Registers
        475. 14.1.1.475  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_START_ADDRESS_H Registers
        476. 14.1.1.476  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_END_ADDRESS_L Registers
        477. 14.1.1.477  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_5_END_ADDRESS_H Registers
        478. 14.1.1.478  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_CONTROL Registers
        479. 14.1.1.479  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_PERMISSION_0 Registers
        480. 14.1.1.480  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_PERMISSION_1 Registers
        481. 14.1.1.481  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_PERMISSION_2 Registers
        482. 14.1.1.482  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_START_ADDRESS_L Registers
        483. 14.1.1.483  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_START_ADDRESS_H Registers
        484. 14.1.1.484  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_END_ADDRESS_L Registers
        485. 14.1.1.485  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_6_END_ADDRESS_H Registers
        486. 14.1.1.486  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_CONTROL Registers
        487. 14.1.1.487  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_PERMISSION_0 Registers
        488. 14.1.1.488  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_PERMISSION_1 Registers
        489. 14.1.1.489  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_PERMISSION_2 Registers
        490. 14.1.1.490  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_START_ADDRESS_L Registers
        491. 14.1.1.491  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_START_ADDRESS_H Registers
        492. 14.1.1.492  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_END_ADDRESS_L Registers
        493. 14.1.1.493  FW_BR_SCRM_64B_CLK2_TO_SCRP_CLK4_CFG_L0_FW_REGION_7_END_ADDRESS_H Registers
        494. 14.1.1.494  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_CONTROL Registers
        495. 14.1.1.495  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_PERMISSION_0 Registers
        496. 14.1.1.496  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_PERMISSION_1 Registers
        497. 14.1.1.497  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_PERMISSION_2 Registers
        498. 14.1.1.498  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_START_ADDRESS_L Registers
        499. 14.1.1.499  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_START_ADDRESS_H Registers
        500. 14.1.1.500  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_END_ADDRESS_L Registers
        501. 14.1.1.501  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_0_END_ADDRESS_H Registers
        502. 14.1.1.502  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_CONTROL Registers
        503. 14.1.1.503  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_PERMISSION_0 Registers
        504. 14.1.1.504  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_PERMISSION_1 Registers
        505. 14.1.1.505  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_PERMISSION_2 Registers
        506. 14.1.1.506  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_START_ADDRESS_L Registers
        507. 14.1.1.507  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_START_ADDRESS_H Registers
        508. 14.1.1.508  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_END_ADDRESS_L Registers
        509. 14.1.1.509  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_1_END_ADDRESS_H Registers
        510. 14.1.1.510  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_CONTROL Registers
        511. 14.1.1.511  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_PERMISSION_0 Registers
        512. 14.1.1.512  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_PERMISSION_1 Registers
        513. 14.1.1.513  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_PERMISSION_2 Registers
        514. 14.1.1.514  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_START_ADDRESS_L Registers
        515. 14.1.1.515  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_START_ADDRESS_H Registers
        516. 14.1.1.516  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_END_ADDRESS_L Registers
        517. 14.1.1.517  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_2_END_ADDRESS_H Registers
        518. 14.1.1.518  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_CONTROL Registers
        519. 14.1.1.519  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_PERMISSION_0 Registers
        520. 14.1.1.520  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_PERMISSION_1 Registers
        521. 14.1.1.521  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_PERMISSION_2 Registers
        522. 14.1.1.522  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_START_ADDRESS_L Registers
        523. 14.1.1.523  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_START_ADDRESS_H Registers
        524. 14.1.1.524  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_END_ADDRESS_L Registers
        525. 14.1.1.525  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_3_END_ADDRESS_H Registers
        526. 14.1.1.526  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_CONTROL Registers
        527. 14.1.1.527  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_PERMISSION_0 Registers
        528. 14.1.1.528  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_PERMISSION_1 Registers
        529. 14.1.1.529  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_PERMISSION_2 Registers
        530. 14.1.1.530  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_START_ADDRESS_L Registers
        531. 14.1.1.531  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_START_ADDRESS_H Registers
        532. 14.1.1.532  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_END_ADDRESS_L Registers
        533. 14.1.1.533  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_4_END_ADDRESS_H Registers
        534. 14.1.1.534  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_CONTROL Registers
        535. 14.1.1.535  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_PERMISSION_0 Registers
        536. 14.1.1.536  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_PERMISSION_1 Registers
        537. 14.1.1.537  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_PERMISSION_2 Registers
        538. 14.1.1.538  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_START_ADDRESS_L Registers
        539. 14.1.1.539  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_START_ADDRESS_H Registers
        540. 14.1.1.540  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_END_ADDRESS_L Registers
        541. 14.1.1.541  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_5_END_ADDRESS_H Registers
        542. 14.1.1.542  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_CONTROL Registers
        543. 14.1.1.543  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_PERMISSION_0 Registers
        544. 14.1.1.544  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_PERMISSION_1 Registers
        545. 14.1.1.545  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_PERMISSION_2 Registers
        546. 14.1.1.546  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_START_ADDRESS_L Registers
        547. 14.1.1.547  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_START_ADDRESS_H Registers
        548. 14.1.1.548  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_END_ADDRESS_L Registers
        549. 14.1.1.549  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_6_END_ADDRESS_H Registers
        550. 14.1.1.550  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_CONTROL Registers
        551. 14.1.1.551  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_PERMISSION_0 Registers
        552. 14.1.1.552  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_PERMISSION_1 Registers
        553. 14.1.1.553  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_PERMISSION_2 Registers
        554. 14.1.1.554  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_START_ADDRESS_L Registers
        555. 14.1.1.555  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_START_ADDRESS_H Registers
        556. 14.1.1.556  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_END_ADDRESS_L Registers
        557. 14.1.1.557  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_7_END_ADDRESS_H Registers
        558. 14.1.1.558  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_CONTROL Registers
        559. 14.1.1.559  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_PERMISSION_0 Registers
        560. 14.1.1.560  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_PERMISSION_1 Registers
        561. 14.1.1.561  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_PERMISSION_2 Registers
        562. 14.1.1.562  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_START_ADDRESS_L Registers
        563. 14.1.1.563  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_START_ADDRESS_H Registers
        564. 14.1.1.564  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_END_ADDRESS_L Registers
        565. 14.1.1.565  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_8_END_ADDRESS_H Registers
        566. 14.1.1.566  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_CONTROL Registers
        567. 14.1.1.567  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_PERMISSION_0 Registers
        568. 14.1.1.568  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_PERMISSION_1 Registers
        569. 14.1.1.569  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_PERMISSION_2 Registers
        570. 14.1.1.570  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_START_ADDRESS_L Registers
        571. 14.1.1.571  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_START_ADDRESS_H Registers
        572. 14.1.1.572  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_END_ADDRESS_L Registers
        573. 14.1.1.573  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_9_END_ADDRESS_H Registers
        574. 14.1.1.574  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_CONTROL Registers
        575. 14.1.1.575  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_PERMISSION_0 Registers
        576. 14.1.1.576  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_PERMISSION_1 Registers
        577. 14.1.1.577  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_PERMISSION_2 Registers
        578. 14.1.1.578  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_START_ADDRESS_L Registers
        579. 14.1.1.579  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_START_ADDRESS_H Registers
        580. 14.1.1.580  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_END_ADDRESS_L Registers
        581. 14.1.1.581  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_10_END_ADDRESS_H Registers
        582. 14.1.1.582  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_CONTROL Registers
        583. 14.1.1.583  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_PERMISSION_0 Registers
        584. 14.1.1.584  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_PERMISSION_1 Registers
        585. 14.1.1.585  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_PERMISSION_2 Registers
        586. 14.1.1.586  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_START_ADDRESS_L Registers
        587. 14.1.1.587  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_START_ADDRESS_H Registers
        588. 14.1.1.588  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_END_ADDRESS_L Registers
        589. 14.1.1.589  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_11_END_ADDRESS_H Registers
        590. 14.1.1.590  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_CONTROL Registers
        591. 14.1.1.591  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_PERMISSION_0 Registers
        592. 14.1.1.592  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_PERMISSION_1 Registers
        593. 14.1.1.593  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_PERMISSION_2 Registers
        594. 14.1.1.594  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_START_ADDRESS_L Registers
        595. 14.1.1.595  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_START_ADDRESS_H Registers
        596. 14.1.1.596  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_END_ADDRESS_L Registers
        597. 14.1.1.597  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_12_END_ADDRESS_H Registers
        598. 14.1.1.598  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_CONTROL Registers
        599. 14.1.1.599  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_PERMISSION_0 Registers
        600. 14.1.1.600  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_PERMISSION_1 Registers
        601. 14.1.1.601  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_PERMISSION_2 Registers
        602. 14.1.1.602  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_START_ADDRESS_L Registers
        603. 14.1.1.603  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_START_ADDRESS_H Registers
        604. 14.1.1.604  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_END_ADDRESS_L Registers
        605. 14.1.1.605  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_13_END_ADDRESS_H Registers
        606. 14.1.1.606  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_CONTROL Registers
        607. 14.1.1.607  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_PERMISSION_0 Registers
        608. 14.1.1.608  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_PERMISSION_1 Registers
        609. 14.1.1.609  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_PERMISSION_2 Registers
        610. 14.1.1.610  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_START_ADDRESS_L Registers
        611. 14.1.1.611  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_START_ADDRESS_H Registers
        612. 14.1.1.612  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_END_ADDRESS_L Registers
        613. 14.1.1.613  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_14_END_ADDRESS_H Registers
        614. 14.1.1.614  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_CONTROL Registers
        615. 14.1.1.615  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_PERMISSION_0 Registers
        616. 14.1.1.616  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_PERMISSION_1 Registers
        617. 14.1.1.617  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_PERMISSION_2 Registers
        618. 14.1.1.618  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_START_ADDRESS_L Registers
        619. 14.1.1.619  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_START_ADDRESS_H Registers
        620. 14.1.1.620  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_END_ADDRESS_L Registers
        621. 14.1.1.621  FW_BR_SCRM_64B_CLK2_TO_SCRP_32_CLK2_MISC_L0_FW_REGION_15_END_ADDRESS_H Registers
        622. 14.1.1.622  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_R_ISC_REGION_0_CONTROL Registers
        623. 14.1.1.623  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_R_ISC_REGION_0_START_ADDRESS_L Registers
        624. 14.1.1.624  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_R_ISC_REGION_0_START_ADDRESS_H Registers
        625. 14.1.1.625  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_R_ISC_REGION_0_END_ADDRESS_L Registers
        626. 14.1.1.626  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_R_ISC_REGION_0_END_ADDRESS_H Registers
        627. 14.1.1.627  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_R_ISC_REGION_DEF_CONTROL Registers
        628. 14.1.1.628  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_W_ISC_REGION_0_CONTROL Registers
        629. 14.1.1.629  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_W_ISC_REGION_0_START_ADDRESS_L Registers
        630. 14.1.1.630  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_W_ISC_REGION_0_START_ADDRESS_H Registers
        631. 14.1.1.631  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_W_ISC_REGION_0_END_ADDRESS_L Registers
        632. 14.1.1.632  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_W_ISC_REGION_0_END_ADDRESS_H Registers
        633. 14.1.1.633  ISC_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_W_ISC_REGION_DEF_CONTROL Registers
        634. 14.1.1.634  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_0_CONTROL Registers
        635. 14.1.1.635  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_0_START_ADDRESS_L Registers
        636. 14.1.1.636  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_0_START_ADDRESS_H Registers
        637. 14.1.1.637  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_0_END_ADDRESS_L Registers
        638. 14.1.1.638  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_0_END_ADDRESS_H Registers
        639. 14.1.1.639  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_1_CONTROL Registers
        640. 14.1.1.640  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_1_START_ADDRESS_L Registers
        641. 14.1.1.641  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_1_START_ADDRESS_H Registers
        642. 14.1.1.642  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_1_END_ADDRESS_L Registers
        643. 14.1.1.643  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_1_END_ADDRESS_H Registers
        644. 14.1.1.644  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_2_CONTROL Registers
        645. 14.1.1.645  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_2_START_ADDRESS_L Registers
        646. 14.1.1.646  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_2_START_ADDRESS_H Registers
        647. 14.1.1.647  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_2_END_ADDRESS_L Registers
        648. 14.1.1.648  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_2_END_ADDRESS_H Registers
        649. 14.1.1.649  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_3_CONTROL Registers
        650. 14.1.1.650  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_3_START_ADDRESS_L Registers
        651. 14.1.1.651  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_3_START_ADDRESS_H Registers
        652. 14.1.1.652  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_3_END_ADDRESS_L Registers
        653. 14.1.1.653  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_3_END_ADDRESS_H Registers
        654. 14.1.1.654  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_4_CONTROL Registers
        655. 14.1.1.655  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_4_START_ADDRESS_L Registers
        656. 14.1.1.656  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_4_START_ADDRESS_H Registers
        657. 14.1.1.657  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_4_END_ADDRESS_L Registers
        658. 14.1.1.658  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_4_END_ADDRESS_H Registers
        659. 14.1.1.659  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_5_CONTROL Registers
        660. 14.1.1.660  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_5_START_ADDRESS_L Registers
        661. 14.1.1.661  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_5_START_ADDRESS_H Registers
        662. 14.1.1.662  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_5_END_ADDRESS_L Registers
        663. 14.1.1.663  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_5_END_ADDRESS_H Registers
        664. 14.1.1.664  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_ISC_REGION_DEF_CONTROL Registers
        665. 14.1.1.665  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_0_CONTROL Registers
        666. 14.1.1.666  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_0_START_ADDRESS_L Registers
        667. 14.1.1.667  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_0_START_ADDRESS_H Registers
        668. 14.1.1.668  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_0_END_ADDRESS_L Registers
        669. 14.1.1.669  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_0_END_ADDRESS_H Registers
        670. 14.1.1.670  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_1_CONTROL Registers
        671. 14.1.1.671  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_1_START_ADDRESS_L Registers
        672. 14.1.1.672  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_1_START_ADDRESS_H Registers
        673. 14.1.1.673  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_1_END_ADDRESS_L Registers
        674. 14.1.1.674  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_1_END_ADDRESS_H Registers
        675. 14.1.1.675  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_2_CONTROL Registers
        676. 14.1.1.676  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_2_START_ADDRESS_L Registers
        677. 14.1.1.677  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_2_START_ADDRESS_H Registers
        678. 14.1.1.678  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_2_END_ADDRESS_L Registers
        679. 14.1.1.679  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_2_END_ADDRESS_H Registers
        680. 14.1.1.680  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_3_CONTROL Registers
        681. 14.1.1.681  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_3_START_ADDRESS_L Registers
        682. 14.1.1.682  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_3_START_ADDRESS_H Registers
        683. 14.1.1.683  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_3_END_ADDRESS_L Registers
        684. 14.1.1.684  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_3_END_ADDRESS_H Registers
        685. 14.1.1.685  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_4_CONTROL Registers
        686. 14.1.1.686  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_4_START_ADDRESS_L Registers
        687. 14.1.1.687  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_4_START_ADDRESS_H Registers
        688. 14.1.1.688  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_4_END_ADDRESS_L Registers
        689. 14.1.1.689  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_4_END_ADDRESS_H Registers
        690. 14.1.1.690  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_5_CONTROL Registers
        691. 14.1.1.691  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_5_START_ADDRESS_L Registers
        692. 14.1.1.692  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_5_START_ADDRESS_H Registers
        693. 14.1.1.693  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_5_END_ADDRESS_L Registers
        694. 14.1.1.694  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_5_END_ADDRESS_H Registers
        695. 14.1.1.695  ISC_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_ISC_REGION_DEF_CONTROL Registers
        696. 14.1.1.696  ISC_IK3_LED2VBUS_MAIN_0_VBUSP_ISC_REGION_0_CONTROL Registers
        697. 14.1.1.697  ISC_IK3_LED2VBUS_MAIN_0_VBUSP_ISC_REGION_0_START_ADDRESS_L Registers
        698. 14.1.1.698  ISC_IK3_LED2VBUS_MAIN_0_VBUSP_ISC_REGION_0_START_ADDRESS_H Registers
        699. 14.1.1.699  ISC_IK3_LED2VBUS_MAIN_0_VBUSP_ISC_REGION_0_END_ADDRESS_L Registers
        700. 14.1.1.700  ISC_IK3_LED2VBUS_MAIN_0_VBUSP_ISC_REGION_0_END_ADDRESS_H Registers
        701. 14.1.1.701  ISC_IK3_LED2VBUS_MAIN_0_VBUSP_ISC_REGION_DEF_CONTROL Registers
        702. 14.1.1.702  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMW_ISC_REGION_0_CONTROL Registers
        703. 14.1.1.703  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMW_ISC_REGION_0_START_ADDRESS_L Registers
        704. 14.1.1.704  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMW_ISC_REGION_0_START_ADDRESS_H Registers
        705. 14.1.1.705  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMW_ISC_REGION_0_END_ADDRESS_L Registers
        706. 14.1.1.706  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMW_ISC_REGION_0_END_ADDRESS_H Registers
        707. 14.1.1.707  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMW_ISC_REGION_DEF_CONTROL Registers
        708. 14.1.1.708  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMR_ISC_REGION_0_CONTROL Registers
        709. 14.1.1.709  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMR_ISC_REGION_0_START_ADDRESS_L Registers
        710. 14.1.1.710  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMR_ISC_REGION_0_START_ADDRESS_H Registers
        711. 14.1.1.711  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMR_ISC_REGION_0_END_ADDRESS_L Registers
        712. 14.1.1.712  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMR_ISC_REGION_0_END_ADDRESS_H Registers
        713. 14.1.1.713  ISC_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMR_ISC_REGION_DEF_CONTROL Registers
        714. 14.1.1.714  ISC_IGIC500SS_1_4_MAIN_0_MEM_WR_VBUSM_ISC_REGION_0_CONTROL Registers
        715. 14.1.1.715  ISC_IGIC500SS_1_4_MAIN_0_MEM_WR_VBUSM_ISC_REGION_0_START_ADDRESS_L Registers
        716. 14.1.1.716  ISC_IGIC500SS_1_4_MAIN_0_MEM_WR_VBUSM_ISC_REGION_0_START_ADDRESS_H Registers
        717. 14.1.1.717  ISC_IGIC500SS_1_4_MAIN_0_MEM_WR_VBUSM_ISC_REGION_0_END_ADDRESS_L Registers
        718. 14.1.1.718  ISC_IGIC500SS_1_4_MAIN_0_MEM_WR_VBUSM_ISC_REGION_0_END_ADDRESS_H Registers
        719. 14.1.1.719  ISC_IGIC500SS_1_4_MAIN_0_MEM_WR_VBUSM_ISC_REGION_DEF_CONTROL Registers
        720. 14.1.1.720  ISC_IGIC500SS_1_4_MAIN_0_MEM_RD_VBUSM_ISC_REGION_0_CONTROL Registers
        721. 14.1.1.721  ISC_IGIC500SS_1_4_MAIN_0_MEM_RD_VBUSM_ISC_REGION_0_START_ADDRESS_L Registers
        722. 14.1.1.722  ISC_IGIC500SS_1_4_MAIN_0_MEM_RD_VBUSM_ISC_REGION_0_START_ADDRESS_H Registers
        723. 14.1.1.723  ISC_IGIC500SS_1_4_MAIN_0_MEM_RD_VBUSM_ISC_REGION_0_END_ADDRESS_L Registers
        724. 14.1.1.724  ISC_IGIC500SS_1_4_MAIN_0_MEM_RD_VBUSM_ISC_REGION_0_END_ADDRESS_H Registers
        725. 14.1.1.725  ISC_IGIC500SS_1_4_MAIN_0_MEM_RD_VBUSM_ISC_REGION_DEF_CONTROL Registers
        726. 14.1.1.726  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_CONTROL Registers
        727. 14.1.1.727  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_START_ADDRESS_L Registers
        728. 14.1.1.728  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_START_ADDRESS_H Registers
        729. 14.1.1.729  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_END_ADDRESS_L Registers
        730. 14.1.1.730  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_END_ADDRESS_H Registers
        731. 14.1.1.731  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_DEF_CONTROL Registers
        732. 14.1.1.732  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_CONTROL Registers
        733. 14.1.1.733  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_START_ADDRESS_L Registers
        734. 14.1.1.734  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_START_ADDRESS_H Registers
        735. 14.1.1.735  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_END_ADDRESS_L Registers
        736. 14.1.1.736  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_END_ADDRESS_H Registers
        737. 14.1.1.737  ISC_IEMMCSD8SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_DEF_CONTROL Registers
        738. 14.1.1.738  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_CONTROL Registers
        739. 14.1.1.739  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_START_ADDRESS_L Registers
        740. 14.1.1.740  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_START_ADDRESS_H Registers
        741. 14.1.1.741  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_END_ADDRESS_L Registers
        742. 14.1.1.742  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_0_END_ADDRESS_H Registers
        743. 14.1.1.743  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_RD_ISC_REGION_DEF_CONTROL Registers
        744. 14.1.1.744  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_CONTROL Registers
        745. 14.1.1.745  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_START_ADDRESS_L Registers
        746. 14.1.1.746  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_START_ADDRESS_H Registers
        747. 14.1.1.747  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_END_ADDRESS_L Registers
        748. 14.1.1.748  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_0_END_ADDRESS_H Registers
        749. 14.1.1.749  ISC_IEMMCSD4SS_MAIN_0_EMMCSDSS_WR_ISC_REGION_DEF_CONTROL Registers
        750. 14.1.1.750  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_WR_ISC_REGION_0_CONTROL Registers
        751. 14.1.1.751  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_WR_ISC_REGION_0_START_ADDRESS_L Registers
        752. 14.1.1.752  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_WR_ISC_REGION_0_START_ADDRESS_H Registers
        753. 14.1.1.753  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_WR_ISC_REGION_0_END_ADDRESS_L Registers
        754. 14.1.1.754  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_WR_ISC_REGION_0_END_ADDRESS_H Registers
        755. 14.1.1.755  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_WR_ISC_REGION_DEF_CONTROL Registers
        756. 14.1.1.756  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_RD_ISC_REGION_0_CONTROL Registers
        757. 14.1.1.757  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_RD_ISC_REGION_0_START_ADDRESS_L Registers
        758. 14.1.1.758  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_RD_ISC_REGION_0_START_ADDRESS_H Registers
        759. 14.1.1.759  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_RD_ISC_REGION_0_END_ADDRESS_L Registers
        760. 14.1.1.760  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_RD_ISC_REGION_0_END_ADDRESS_H Registers
        761. 14.1.1.761  ISC_IEMMCSD4SS_MAIN_1_EMMCSDSS_RD_ISC_REGION_DEF_CONTROL Registers
        762. 14.1.1.762  ISC_IUSB2SS_16FFC_MAIN_0_MSTW0_ISC_REGION_0_CONTROL Registers
        763. 14.1.1.763  ISC_IUSB2SS_16FFC_MAIN_0_MSTW0_ISC_REGION_0_START_ADDRESS_L Registers
        764. 14.1.1.764  ISC_IUSB2SS_16FFC_MAIN_0_MSTW0_ISC_REGION_0_START_ADDRESS_H Registers
        765. 14.1.1.765  ISC_IUSB2SS_16FFC_MAIN_0_MSTW0_ISC_REGION_0_END_ADDRESS_L Registers
        766. 14.1.1.766  ISC_IUSB2SS_16FFC_MAIN_0_MSTW0_ISC_REGION_0_END_ADDRESS_H Registers
        767. 14.1.1.767  ISC_IUSB2SS_16FFC_MAIN_0_MSTW0_ISC_REGION_DEF_CONTROL Registers
        768. 14.1.1.768  ISC_IUSB2SS_16FFC_MAIN_0_MSTR0_ISC_REGION_0_CONTROL Registers
        769. 14.1.1.769  ISC_IUSB2SS_16FFC_MAIN_0_MSTR0_ISC_REGION_0_START_ADDRESS_L Registers
        770. 14.1.1.770  ISC_IUSB2SS_16FFC_MAIN_0_MSTR0_ISC_REGION_0_START_ADDRESS_H Registers
        771. 14.1.1.771  ISC_IUSB2SS_16FFC_MAIN_0_MSTR0_ISC_REGION_0_END_ADDRESS_L Registers
        772. 14.1.1.772  ISC_IUSB2SS_16FFC_MAIN_0_MSTR0_ISC_REGION_0_END_ADDRESS_H Registers
        773. 14.1.1.773  ISC_IUSB2SS_16FFC_MAIN_0_MSTR0_ISC_REGION_DEF_CONTROL Registers
        774. 14.1.1.774  ISC_IUSB2SS_16FFC_MAIN_1_MSTR0_ISC_REGION_0_CONTROL Registers
        775. 14.1.1.775  ISC_IUSB2SS_16FFC_MAIN_1_MSTR0_ISC_REGION_0_START_ADDRESS_L Registers
        776. 14.1.1.776  ISC_IUSB2SS_16FFC_MAIN_1_MSTR0_ISC_REGION_0_START_ADDRESS_H Registers
        777. 14.1.1.777  ISC_IUSB2SS_16FFC_MAIN_1_MSTR0_ISC_REGION_0_END_ADDRESS_L Registers
        778. 14.1.1.778  ISC_IUSB2SS_16FFC_MAIN_1_MSTR0_ISC_REGION_0_END_ADDRESS_H Registers
        779. 14.1.1.779  ISC_IUSB2SS_16FFC_MAIN_1_MSTR0_ISC_REGION_DEF_CONTROL Registers
        780. 14.1.1.780  ISC_IUSB2SS_16FFC_MAIN_1_MSTW0_ISC_REGION_0_CONTROL Registers
        781. 14.1.1.781  ISC_IUSB2SS_16FFC_MAIN_1_MSTW0_ISC_REGION_0_START_ADDRESS_L Registers
        782. 14.1.1.782  ISC_IUSB2SS_16FFC_MAIN_1_MSTW0_ISC_REGION_0_START_ADDRESS_H Registers
        783. 14.1.1.783  ISC_IUSB2SS_16FFC_MAIN_1_MSTW0_ISC_REGION_0_END_ADDRESS_L Registers
        784. 14.1.1.784  ISC_IUSB2SS_16FFC_MAIN_1_MSTW0_ISC_REGION_0_END_ADDRESS_H Registers
        785. 14.1.1.785  ISC_IUSB2SS_16FFC_MAIN_1_MSTW0_ISC_REGION_DEF_CONTROL Registers
        786. 14.1.1.786  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_0_CONTROL Registers
        787. 14.1.1.787  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_0_START_ADDRESS_L Registers
        788. 14.1.1.788  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_0_START_ADDRESS_H Registers
        789. 14.1.1.789  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_0_END_ADDRESS_L Registers
        790. 14.1.1.790  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_0_END_ADDRESS_H Registers
        791. 14.1.1.791  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_1_CONTROL Registers
        792. 14.1.1.792  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_1_START_ADDRESS_L Registers
        793. 14.1.1.793  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_1_START_ADDRESS_H Registers
        794. 14.1.1.794  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_1_END_ADDRESS_L Registers
        795. 14.1.1.795  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_1_END_ADDRESS_H Registers
        796. 14.1.1.796  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_2_CONTROL Registers
        797. 14.1.1.797  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_2_START_ADDRESS_L Registers
        798. 14.1.1.798  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_2_START_ADDRESS_H Registers
        799. 14.1.1.799  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_2_END_ADDRESS_L Registers
        800. 14.1.1.800  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_2_END_ADDRESS_H Registers
        801. 14.1.1.801  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_3_CONTROL Registers
        802. 14.1.1.802  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_3_START_ADDRESS_L Registers
        803. 14.1.1.803  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_3_START_ADDRESS_H Registers
        804. 14.1.1.804  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_3_END_ADDRESS_L Registers
        805. 14.1.1.805  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_3_END_ADDRESS_H Registers
        806. 14.1.1.806  ISC_IK3_DSS_UL_MAIN_0_VBUSM_DMA_ISC_REGION_DEF_CONTROL Registers
        807. 14.1.1.807  ISC_ISA3SS_AM62_MAIN_0_CTXCACH_EXT_DMA_ISC_REGION_0_CONTROL Registers
        808. 14.1.1.808  ISC_ISA3SS_AM62_MAIN_0_CTXCACH_EXT_DMA_ISC_REGION_0_START_ADDRESS_L Registers
        809. 14.1.1.809  ISC_ISA3SS_AM62_MAIN_0_CTXCACH_EXT_DMA_ISC_REGION_0_START_ADDRESS_H Registers
        810. 14.1.1.810  ISC_ISA3SS_AM62_MAIN_0_CTXCACH_EXT_DMA_ISC_REGION_0_END_ADDRESS_L Registers
        811. 14.1.1.811  ISC_ISA3SS_AM62_MAIN_0_CTXCACH_EXT_DMA_ISC_REGION_0_END_ADDRESS_H Registers
        812. 14.1.1.812  ISC_ISA3SS_AM62_MAIN_0_CTXCACH_EXT_DMA_ISC_REGION_DEF_CONTROL Registers
        813. 14.1.1.813  GLB_PID Registers
        814. 14.1.1.814  GLB_DESTINATION_ID Registers
        815. 14.1.1.815  GLB_EXCEPTION_LOGGING_CONTROL Registers
        816. 14.1.1.816  GLB_EXCEPTION_LOGGING_HEADER0 Registers
        817. 14.1.1.817  GLB_EXCEPTION_LOGGING_HEADER1 Registers
        818. 14.1.1.818  GLB_EXCEPTION_LOGGING_DATA0 Registers
        819. 14.1.1.819  GLB_EXCEPTION_LOGGING_DATA1 Registers
        820. 14.1.1.820  GLB_EXCEPTION_LOGGING_DATA2 Registers
        821. 14.1.1.821  GLB_EXCEPTION_LOGGING_DATA3 Registers
        822. 14.1.1.822  GLB_EXCEPTION_PEND_SET Registers
        823. 14.1.1.823  GLB_EXCEPTION_PEND_CLEAR Registers
        824. 14.1.1.824  QOS_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_R_MAP0 Registers
        825. 14.1.1.825  QOS_ISAM62_A53_512KB_WRAP_MAIN_0_A53_QUAD_WRAP_CBA_AXI_W_MAP0 Registers
        826. 14.1.1.826  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_MAP0 Registers
        827. 14.1.1.827  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_MAP1 Registers
        828. 14.1.1.828  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_MAP2 Registers
        829. 14.1.1.829  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_MAP3 Registers
        830. 14.1.1.830  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_MAP4 Registers
        831. 14.1.1.831  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_W_MAP5 Registers
        832. 14.1.1.832  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_MAP0 Registers
        833. 14.1.1.833  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_MAP1 Registers
        834. 14.1.1.834  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_MAP2 Registers
        835. 14.1.1.835  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_MAP3 Registers
        836. 14.1.1.836  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_MAP4 Registers
        837. 14.1.1.837  QOS_IK3_GPU_AXE116M_MAIN_0_K3_GPU_M_VBUSM_R_MAP5 Registers
        838. 14.1.1.838  QOS_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMW_MAP0 Registers
        839. 14.1.1.839  QOS_IDEBUGSS_K3_WRAP_CV0_MAIN_0_VBUSMR_MAP0 Registers
        840. 14.1.1.840  QOS_IGIC500SS_1_4_MAIN_0_MEM_WR_VBUSM_MAP0 Registers
        841. 14.1.1.841  QOS_IGIC500SS_1_4_MAIN_0_MEM_RD_VBUSM_MAP0 Registers
        842. 14.1.1.842  QOS_IEMMCSD8SS_MAIN_0_EMMCSDSS_RD_MAP0 Registers
        843. 14.1.1.843  QOS_IEMMCSD8SS_MAIN_0_EMMCSDSS_WR_MAP0 Registers
        844. 14.1.1.844  QOS_IEMMCSD4SS_MAIN_0_EMMCSDSS_RD_MAP0 Registers
        845. 14.1.1.845  QOS_IEMMCSD4SS_MAIN_0_EMMCSDSS_WR_MAP0 Registers
        846. 14.1.1.846  QOS_IEMMCSD4SS_MAIN_1_EMMCSDSS_WR_MAP0 Registers
        847. 14.1.1.847  QOS_IEMMCSD4SS_MAIN_1_EMMCSDSS_RD_MAP0 Registers
        848. 14.1.1.848  QOS_IUSB2SS_16FFC_MAIN_0_MSTW0_MAP0 Registers
        849. 14.1.1.849  QOS_IUSB2SS_16FFC_MAIN_0_MSTR0_MAP0 Registers
        850. 14.1.1.850  QOS_IUSB2SS_16FFC_MAIN_1_MSTR0_MAP0 Registers
        851. 14.1.1.851  QOS_IUSB2SS_16FFC_MAIN_1_MSTW0_MAP0 Registers
        852. 14.1.1.852  QOS_IK3_DSS_UL_MAIN_0_VBUSM_DMA_MAP0 Registers
        853. 14.1.1.853  QOS_IK3_DSS_UL_MAIN_0_VBUSM_DMA_MAP1 Registers
        854. 14.1.1.854  QOS_IK3_DSS_UL_MAIN_0_VBUSM_DMA_MAP2 Registers
        855. 14.1.1.855  QOS_IK3_DSS_UL_MAIN_0_VBUSM_DMA_MAP3 Registers
        856. 14.1.1.856  QOS_ISA3SS_AM62_MAIN_0_CTXCACH_EXT_DMA_MAP0 Registers
        857. 14.1.1.857  ISC_IBLAZAR_MCU_0_VBUSP_M_ISC_REGION_0_CONTROL Registers
        858. 14.1.1.858  ISC_IBLAZAR_MCU_0_VBUSP_M_ISC_REGION_0_START_ADDRESS_L Registers
        859. 14.1.1.859  ISC_IBLAZAR_MCU_0_VBUSP_M_ISC_REGION_0_START_ADDRESS_H Registers
        860. 14.1.1.860  ISC_IBLAZAR_MCU_0_VBUSP_M_ISC_REGION_0_END_ADDRESS_L Registers
        861. 14.1.1.861  ISC_IBLAZAR_MCU_0_VBUSP_M_ISC_REGION_0_END_ADDRESS_H Registers
        862. 14.1.1.862  ISC_IBLAZAR_MCU_0_VBUSP_M_ISC_REGION_DEF_CONTROL Registers
        863. 14.1.1.863  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_CONTROL Registers
        864. 14.1.1.864  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_PERMISSION_0 Registers
        865. 14.1.1.865  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_PERMISSION_1 Registers
        866. 14.1.1.866  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_PERMISSION_2 Registers
        867. 14.1.1.867  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_START_ADDRESS_L Registers
        868. 14.1.1.868  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_START_ADDRESS_H Registers
        869. 14.1.1.869  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_END_ADDRESS_L Registers
        870. 14.1.1.870  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_0_END_ADDRESS_H Registers
        871. 14.1.1.871  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_CONTROL Registers
        872. 14.1.1.872  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_PERMISSION_0 Registers
        873. 14.1.1.873  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_PERMISSION_1 Registers
        874. 14.1.1.874  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_PERMISSION_2 Registers
        875. 14.1.1.875  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_START_ADDRESS_L Registers
        876. 14.1.1.876  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_START_ADDRESS_H Registers
        877. 14.1.1.877  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_END_ADDRESS_L Registers
        878. 14.1.1.878  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_1_END_ADDRESS_H Registers
        879. 14.1.1.879  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_CONTROL Registers
        880. 14.1.1.880  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_PERMISSION_0 Registers
        881. 14.1.1.881  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_PERMISSION_1 Registers
        882. 14.1.1.882  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_PERMISSION_2 Registers
        883. 14.1.1.883  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_START_ADDRESS_L Registers
        884. 14.1.1.884  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_START_ADDRESS_H Registers
        885. 14.1.1.885  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_END_ADDRESS_L Registers
        886. 14.1.1.886  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_2_END_ADDRESS_H Registers
        887. 14.1.1.887  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_CONTROL Registers
        888. 14.1.1.888  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_PERMISSION_0 Registers
        889. 14.1.1.889  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_PERMISSION_1 Registers
        890. 14.1.1.890  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_PERMISSION_2 Registers
        891. 14.1.1.891  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_START_ADDRESS_L Registers
        892. 14.1.1.892  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_START_ADDRESS_H Registers
        893. 14.1.1.893  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_END_ADDRESS_L Registers
        894. 14.1.1.894  FW_IPULSAR_UL_WKUP_0_CPU0_SLV_FW_REGION_3_END_ADDRESS_H Registers
        895. 14.1.1.895  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_CONTROL Registers
        896. 14.1.1.896  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_PERMISSION_0 Registers
        897. 14.1.1.897  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_PERMISSION_1 Registers
        898. 14.1.1.898  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_PERMISSION_2 Registers
        899. 14.1.1.899  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_L Registers
        900. 14.1.1.900  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_H Registers
        901. 14.1.1.901  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_L Registers
        902. 14.1.1.902  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_H Registers
        903. 14.1.1.903  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_CONTROL Registers
        904. 14.1.1.904  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_PERMISSION_0 Registers
        905. 14.1.1.905  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_PERMISSION_1 Registers
        906. 14.1.1.906  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_PERMISSION_2 Registers
        907. 14.1.1.907  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_L Registers
        908. 14.1.1.908  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_H Registers
        909. 14.1.1.909  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_L Registers
        910. 14.1.1.910  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_H Registers
        911. 14.1.1.911  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_CONTROL Registers
        912. 14.1.1.912  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_PERMISSION_0 Registers
        913. 14.1.1.913  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_PERMISSION_1 Registers
        914. 14.1.1.914  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_PERMISSION_2 Registers
        915. 14.1.1.915  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_L Registers
        916. 14.1.1.916  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_H Registers
        917. 14.1.1.917  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_L Registers
        918. 14.1.1.918  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_H Registers
        919. 14.1.1.919  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_CONTROL Registers
        920. 14.1.1.920  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_PERMISSION_0 Registers
        921. 14.1.1.921  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_PERMISSION_1 Registers
        922. 14.1.1.922  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_PERMISSION_2 Registers
        923. 14.1.1.923  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_L Registers
        924. 14.1.1.924  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_H Registers
        925. 14.1.1.925  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_L Registers
        926. 14.1.1.926  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_H Registers
        927. 14.1.1.927  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_CONTROL Registers
        928. 14.1.1.928  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_PERMISSION_0 Registers
        929. 14.1.1.929  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_PERMISSION_1 Registers
        930. 14.1.1.930  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_PERMISSION_2 Registers
        931. 14.1.1.931  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_L Registers
        932. 14.1.1.932  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_H Registers
        933. 14.1.1.933  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_L Registers
        934. 14.1.1.934  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_H Registers
        935. 14.1.1.935  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_CONTROL Registers
        936. 14.1.1.936  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_PERMISSION_0 Registers
        937. 14.1.1.937  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_PERMISSION_1 Registers
        938. 14.1.1.938  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_PERMISSION_2 Registers
        939. 14.1.1.939  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_L Registers
        940. 14.1.1.940  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_H Registers
        941. 14.1.1.941  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_L Registers
        942. 14.1.1.942  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_H Registers
        943. 14.1.1.943  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_CONTROL Registers
        944. 14.1.1.944  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_PERMISSION_0 Registers
        945. 14.1.1.945  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_PERMISSION_1 Registers
        946. 14.1.1.946  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_PERMISSION_2 Registers
        947. 14.1.1.947  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_L Registers
        948. 14.1.1.948  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_H Registers
        949. 14.1.1.949  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_L Registers
        950. 14.1.1.950  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_H Registers
        951. 14.1.1.951  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_CONTROL Registers
        952. 14.1.1.952  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_PERMISSION_0 Registers
        953. 14.1.1.953  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_PERMISSION_1 Registers
        954. 14.1.1.954  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_PERMISSION_2 Registers
        955. 14.1.1.955  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_L Registers
        956. 14.1.1.956  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_H Registers
        957. 14.1.1.957  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_L Registers
        958. 14.1.1.958  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_H Registers
        959. 14.1.1.959  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_CONTROL Registers
        960. 14.1.1.960  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_PERMISSION_0 Registers
        961. 14.1.1.961  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_PERMISSION_1 Registers
        962. 14.1.1.962  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_PERMISSION_2 Registers
        963. 14.1.1.963  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_START_ADDRESS_L Registers
        964. 14.1.1.964  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_START_ADDRESS_H Registers
        965. 14.1.1.965  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_END_ADDRESS_L Registers
        966. 14.1.1.966  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_8_END_ADDRESS_H Registers
        967. 14.1.1.967  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_CONTROL Registers
        968. 14.1.1.968  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_PERMISSION_0 Registers
        969. 14.1.1.969  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_PERMISSION_1 Registers
        970. 14.1.1.970  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_PERMISSION_2 Registers
        971. 14.1.1.971  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_START_ADDRESS_L Registers
        972. 14.1.1.972  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_START_ADDRESS_H Registers
        973. 14.1.1.973  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_END_ADDRESS_L Registers
        974. 14.1.1.974  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_9_END_ADDRESS_H Registers
        975. 14.1.1.975  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_CONTROL Registers
        976. 14.1.1.976  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_PERMISSION_0 Registers
        977. 14.1.1.977  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_PERMISSION_1 Registers
        978. 14.1.1.978  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_PERMISSION_2 Registers
        979. 14.1.1.979  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_START_ADDRESS_L Registers
        980. 14.1.1.980  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_START_ADDRESS_H Registers
        981. 14.1.1.981  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_END_ADDRESS_L Registers
        982. 14.1.1.982  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_10_END_ADDRESS_H Registers
        983. 14.1.1.983  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_CONTROL Registers
        984. 14.1.1.984  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_PERMISSION_0 Registers
        985. 14.1.1.985  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_PERMISSION_1 Registers
        986. 14.1.1.986  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_PERMISSION_2 Registers
        987. 14.1.1.987  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_START_ADDRESS_L Registers
        988. 14.1.1.988  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_START_ADDRESS_H Registers
        989. 14.1.1.989  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_END_ADDRESS_L Registers
        990. 14.1.1.990  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_11_END_ADDRESS_H Registers
        991. 14.1.1.991  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_CONTROL Registers
        992. 14.1.1.992  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_PERMISSION_0 Registers
        993. 14.1.1.993  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_PERMISSION_1 Registers
        994. 14.1.1.994  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_PERMISSION_2 Registers
        995. 14.1.1.995  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_START_ADDRESS_L Registers
        996. 14.1.1.996  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_START_ADDRESS_H Registers
        997. 14.1.1.997  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_END_ADDRESS_L Registers
        998. 14.1.1.998  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_12_END_ADDRESS_H Registers
        999. 14.1.1.999  FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_CONTROL Registers
        1000. 14.1.1.1000 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_PERMISSION_0 Registers
        1001. 14.1.1.1001 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_PERMISSION_1 Registers
        1002. 14.1.1.1002 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_PERMISSION_2 Registers
        1003. 14.1.1.1003 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_START_ADDRESS_L Registers
        1004. 14.1.1.1004 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_START_ADDRESS_H Registers
        1005. 14.1.1.1005 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_END_ADDRESS_L Registers
        1006. 14.1.1.1006 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_13_END_ADDRESS_H Registers
        1007. 14.1.1.1007 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_CONTROL Registers
        1008. 14.1.1.1008 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_PERMISSION_0 Registers
        1009. 14.1.1.1009 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_PERMISSION_1 Registers
        1010. 14.1.1.1010 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_PERMISSION_2 Registers
        1011. 14.1.1.1011 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_START_ADDRESS_L Registers
        1012. 14.1.1.1012 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_START_ADDRESS_H Registers
        1013. 14.1.1.1013 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_END_ADDRESS_L Registers
        1014. 14.1.1.1014 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_14_END_ADDRESS_H Registers
        1015. 14.1.1.1015 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_CONTROL Registers
        1016. 14.1.1.1016 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_PERMISSION_0 Registers
        1017. 14.1.1.1017 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_PERMISSION_1 Registers
        1018. 14.1.1.1018 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_PERMISSION_2 Registers
        1019. 14.1.1.1019 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_START_ADDRESS_L Registers
        1020. 14.1.1.1020 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_START_ADDRESS_H Registers
        1021. 14.1.1.1021 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_END_ADDRESS_L Registers
        1022. 14.1.1.1022 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_MAIN_INFRA_CBASS_DATA_L0_FW_REGION_15_END_ADDRESS_H Registers
        1023. 14.1.1.1023 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_CONTROL Registers
        1024. 14.1.1.1024 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_PERMISSION_0 Registers
        1025. 14.1.1.1025 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_PERMISSION_1 Registers
        1026. 14.1.1.1026 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_PERMISSION_2 Registers
        1027. 14.1.1.1027 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_START_ADDRESS_L Registers
        1028. 14.1.1.1028 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_START_ADDRESS_H Registers
        1029. 14.1.1.1029 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_END_ADDRESS_L Registers
        1030. 14.1.1.1030 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_0_END_ADDRESS_H Registers
        1031. 14.1.1.1031 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_CONTROL Registers
        1032. 14.1.1.1032 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_PERMISSION_0 Registers
        1033. 14.1.1.1033 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_PERMISSION_1 Registers
        1034. 14.1.1.1034 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_PERMISSION_2 Registers
        1035. 14.1.1.1035 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_START_ADDRESS_L Registers
        1036. 14.1.1.1036 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_START_ADDRESS_H Registers
        1037. 14.1.1.1037 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_END_ADDRESS_L Registers
        1038. 14.1.1.1038 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_1_END_ADDRESS_H Registers
        1039. 14.1.1.1039 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_CONTROL Registers
        1040. 14.1.1.1040 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_PERMISSION_0 Registers
        1041. 14.1.1.1041 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_PERMISSION_1 Registers
        1042. 14.1.1.1042 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_PERMISSION_2 Registers
        1043. 14.1.1.1043 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_START_ADDRESS_L Registers
        1044. 14.1.1.1044 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_START_ADDRESS_H Registers
        1045. 14.1.1.1045 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_END_ADDRESS_L Registers
        1046. 14.1.1.1046 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_2_END_ADDRESS_H Registers
        1047. 14.1.1.1047 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_CONTROL Registers
        1048. 14.1.1.1048 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_PERMISSION_0 Registers
        1049. 14.1.1.1049 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_PERMISSION_1 Registers
        1050. 14.1.1.1050 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_PERMISSION_2 Registers
        1051. 14.1.1.1051 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_START_ADDRESS_L Registers
        1052. 14.1.1.1052 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_START_ADDRESS_H Registers
        1053. 14.1.1.1053 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_END_ADDRESS_L Registers
        1054. 14.1.1.1054 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_3_END_ADDRESS_H Registers
        1055. 14.1.1.1055 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_CONTROL Registers
        1056. 14.1.1.1056 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_PERMISSION_0 Registers
        1057. 14.1.1.1057 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_PERMISSION_1 Registers
        1058. 14.1.1.1058 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_PERMISSION_2 Registers
        1059. 14.1.1.1059 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_START_ADDRESS_L Registers
        1060. 14.1.1.1060 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_START_ADDRESS_H Registers
        1061. 14.1.1.1061 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_END_ADDRESS_L Registers
        1062. 14.1.1.1062 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_4_END_ADDRESS_H Registers
        1063. 14.1.1.1063 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_CONTROL Registers
        1064. 14.1.1.1064 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_PERMISSION_0 Registers
        1065. 14.1.1.1065 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_PERMISSION_1 Registers
        1066. 14.1.1.1066 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_PERMISSION_2 Registers
        1067. 14.1.1.1067 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_START_ADDRESS_L Registers
        1068. 14.1.1.1068 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_START_ADDRESS_H Registers
        1069. 14.1.1.1069 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_END_ADDRESS_L Registers
        1070. 14.1.1.1070 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_5_END_ADDRESS_H Registers
        1071. 14.1.1.1071 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_CONTROL Registers
        1072. 14.1.1.1072 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_PERMISSION_0 Registers
        1073. 14.1.1.1073 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_PERMISSION_1 Registers
        1074. 14.1.1.1074 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_PERMISSION_2 Registers
        1075. 14.1.1.1075 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_START_ADDRESS_L Registers
        1076. 14.1.1.1076 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_START_ADDRESS_H Registers
        1077. 14.1.1.1077 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_END_ADDRESS_L Registers
        1078. 14.1.1.1078 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_6_END_ADDRESS_H Registers
        1079. 14.1.1.1079 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_CONTROL Registers
        1080. 14.1.1.1080 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_PERMISSION_0 Registers
        1081. 14.1.1.1081 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_PERMISSION_1 Registers
        1082. 14.1.1.1082 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_PERMISSION_2 Registers
        1083. 14.1.1.1083 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_START_ADDRESS_L Registers
        1084. 14.1.1.1084 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_START_ADDRESS_H Registers
        1085. 14.1.1.1085 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_END_ADDRESS_L Registers
        1086. 14.1.1.1086 FW_BR_SCRM_DM_CLK1_TO_SCRP_32B_DM_CLK4_L0_FW_REGION_7_END_ADDRESS_H Registers
        1087. 14.1.1.1087 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_CONTROL Registers
        1088. 14.1.1.1088 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_PERMISSION_0 Registers
        1089. 14.1.1.1089 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_PERMISSION_1 Registers
        1090. 14.1.1.1090 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_PERMISSION_2 Registers
        1091. 14.1.1.1091 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_L Registers
        1092. 14.1.1.1092 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_H Registers
        1093. 14.1.1.1093 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_L Registers
        1094. 14.1.1.1094 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_H Registers
        1095. 14.1.1.1095 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_CONTROL Registers
        1096. 14.1.1.1096 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_PERMISSION_0 Registers
        1097. 14.1.1.1097 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_PERMISSION_1 Registers
        1098. 14.1.1.1098 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_PERMISSION_2 Registers
        1099. 14.1.1.1099 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_L Registers
        1100. 14.1.1.1100 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_H Registers
        1101. 14.1.1.1101 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_L Registers
        1102. 14.1.1.1102 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_H Registers
        1103. 14.1.1.1103 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_CONTROL Registers
        1104. 14.1.1.1104 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_PERMISSION_0 Registers
        1105. 14.1.1.1105 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_PERMISSION_1 Registers
        1106. 14.1.1.1106 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_PERMISSION_2 Registers
        1107. 14.1.1.1107 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_L Registers
        1108. 14.1.1.1108 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_H Registers
        1109. 14.1.1.1109 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_L Registers
        1110. 14.1.1.1110 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_H Registers
        1111. 14.1.1.1111 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_CONTROL Registers
        1112. 14.1.1.1112 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_PERMISSION_0 Registers
        1113. 14.1.1.1113 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_PERMISSION_1 Registers
        1114. 14.1.1.1114 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_PERMISSION_2 Registers
        1115. 14.1.1.1115 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_L Registers
        1116. 14.1.1.1116 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_H Registers
        1117. 14.1.1.1117 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_L Registers
        1118. 14.1.1.1118 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_H Registers
        1119. 14.1.1.1119 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_CONTROL Registers
        1120. 14.1.1.1120 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_PERMISSION_0 Registers
        1121. 14.1.1.1121 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_PERMISSION_1 Registers
        1122. 14.1.1.1122 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_PERMISSION_2 Registers
        1123. 14.1.1.1123 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_L Registers
        1124. 14.1.1.1124 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_H Registers
        1125. 14.1.1.1125 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_L Registers
        1126. 14.1.1.1126 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_H Registers
        1127. 14.1.1.1127 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_CONTROL Registers
        1128. 14.1.1.1128 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_PERMISSION_0 Registers
        1129. 14.1.1.1129 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_PERMISSION_1 Registers
        1130. 14.1.1.1130 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_PERMISSION_2 Registers
        1131. 14.1.1.1131 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_L Registers
        1132. 14.1.1.1132 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_H Registers
        1133. 14.1.1.1133 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_L Registers
        1134. 14.1.1.1134 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_H Registers
        1135. 14.1.1.1135 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_CONTROL Registers
        1136. 14.1.1.1136 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_PERMISSION_0 Registers
        1137. 14.1.1.1137 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_PERMISSION_1 Registers
        1138. 14.1.1.1138 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_PERMISSION_2 Registers
        1139. 14.1.1.1139 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_L Registers
        1140. 14.1.1.1140 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_H Registers
        1141. 14.1.1.1141 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_L Registers
        1142. 14.1.1.1142 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_H Registers
        1143. 14.1.1.1143 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_CONTROL Registers
        1144. 14.1.1.1144 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_PERMISSION_0 Registers
        1145. 14.1.1.1145 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_PERMISSION_1 Registers
        1146. 14.1.1.1146 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_PERMISSION_2 Registers
        1147. 14.1.1.1147 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_L Registers
        1148. 14.1.1.1148 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_H Registers
        1149. 14.1.1.1149 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_L Registers
        1150. 14.1.1.1150 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_H Registers
        1151. 14.1.1.1151 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_CONTROL Registers
        1152. 14.1.1.1152 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_PERMISSION_0 Registers
        1153. 14.1.1.1153 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_PERMISSION_1 Registers
        1154. 14.1.1.1154 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_PERMISSION_2 Registers
        1155. 14.1.1.1155 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_START_ADDRESS_L Registers
        1156. 14.1.1.1156 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_START_ADDRESS_H Registers
        1157. 14.1.1.1157 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_END_ADDRESS_L Registers
        1158. 14.1.1.1158 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_8_END_ADDRESS_H Registers
        1159. 14.1.1.1159 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_CONTROL Registers
        1160. 14.1.1.1160 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_PERMISSION_0 Registers
        1161. 14.1.1.1161 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_PERMISSION_1 Registers
        1162. 14.1.1.1162 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_PERMISSION_2 Registers
        1163. 14.1.1.1163 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_START_ADDRESS_L Registers
        1164. 14.1.1.1164 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_START_ADDRESS_H Registers
        1165. 14.1.1.1165 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_END_ADDRESS_L Registers
        1166. 14.1.1.1166 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_9_END_ADDRESS_H Registers
        1167. 14.1.1.1167 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_CONTROL Registers
        1168. 14.1.1.1168 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_PERMISSION_0 Registers
        1169. 14.1.1.1169 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_PERMISSION_1 Registers
        1170. 14.1.1.1170 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_PERMISSION_2 Registers
        1171. 14.1.1.1171 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_START_ADDRESS_L Registers
        1172. 14.1.1.1172 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_START_ADDRESS_H Registers
        1173. 14.1.1.1173 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_END_ADDRESS_L Registers
        1174. 14.1.1.1174 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_10_END_ADDRESS_H Registers
        1175. 14.1.1.1175 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_CONTROL Registers
        1176. 14.1.1.1176 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_PERMISSION_0 Registers
        1177. 14.1.1.1177 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_PERMISSION_1 Registers
        1178. 14.1.1.1178 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_PERMISSION_2 Registers
        1179. 14.1.1.1179 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_START_ADDRESS_L Registers
        1180. 14.1.1.1180 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_START_ADDRESS_H Registers
        1181. 14.1.1.1181 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_END_ADDRESS_L Registers
        1182. 14.1.1.1182 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_11_END_ADDRESS_H Registers
        1183. 14.1.1.1183 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_CONTROL Registers
        1184. 14.1.1.1184 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_PERMISSION_0 Registers
        1185. 14.1.1.1185 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_PERMISSION_1 Registers
        1186. 14.1.1.1186 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_PERMISSION_2 Registers
        1187. 14.1.1.1187 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_START_ADDRESS_L Registers
        1188. 14.1.1.1188 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_START_ADDRESS_H Registers
        1189. 14.1.1.1189 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_END_ADDRESS_L Registers
        1190. 14.1.1.1190 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_12_END_ADDRESS_H Registers
        1191. 14.1.1.1191 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_CONTROL Registers
        1192. 14.1.1.1192 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_PERMISSION_0 Registers
        1193. 14.1.1.1193 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_PERMISSION_1 Registers
        1194. 14.1.1.1194 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_PERMISSION_2 Registers
        1195. 14.1.1.1195 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_START_ADDRESS_L Registers
        1196. 14.1.1.1196 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_START_ADDRESS_H Registers
        1197. 14.1.1.1197 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_END_ADDRESS_L Registers
        1198. 14.1.1.1198 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_13_END_ADDRESS_H Registers
        1199. 14.1.1.1199 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_CONTROL Registers
        1200. 14.1.1.1200 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_PERMISSION_0 Registers
        1201. 14.1.1.1201 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_PERMISSION_1 Registers
        1202. 14.1.1.1202 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_PERMISSION_2 Registers
        1203. 14.1.1.1203 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_START_ADDRESS_L Registers
        1204. 14.1.1.1204 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_START_ADDRESS_H Registers
        1205. 14.1.1.1205 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_END_ADDRESS_L Registers
        1206. 14.1.1.1206 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_14_END_ADDRESS_H Registers
        1207. 14.1.1.1207 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_CONTROL Registers
        1208. 14.1.1.1208 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_PERMISSION_0 Registers
        1209. 14.1.1.1209 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_PERMISSION_1 Registers
        1210. 14.1.1.1210 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_PERMISSION_2 Registers
        1211. 14.1.1.1211 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_START_ADDRESS_L Registers
        1212. 14.1.1.1212 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_START_ADDRESS_H Registers
        1213. 14.1.1.1213 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_END_ADDRESS_L Registers
        1214. 14.1.1.1214 FW_EXPORT_AM62_WKUP_DM_CBASS_TO_AM62_WKUP_SAFE_CBASS_DATA_L0_FW_REGION_15_END_ADDRESS_H Registers
        1215. 14.1.1.1215 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_0_CONTROL Registers
        1216. 14.1.1.1216 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_0_START_ADDRESS_L Registers
        1217. 14.1.1.1217 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_0_START_ADDRESS_H Registers
        1218. 14.1.1.1218 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_0_END_ADDRESS_L Registers
        1219. 14.1.1.1219 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_0_END_ADDRESS_H Registers
        1220. 14.1.1.1220 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_1_CONTROL Registers
        1221. 14.1.1.1221 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_1_START_ADDRESS_L Registers
        1222. 14.1.1.1222 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_1_START_ADDRESS_H Registers
        1223. 14.1.1.1223 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_1_END_ADDRESS_L Registers
        1224. 14.1.1.1224 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_1_END_ADDRESS_H Registers
        1225. 14.1.1.1225 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_2_CONTROL Registers
        1226. 14.1.1.1226 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_2_START_ADDRESS_L Registers
        1227. 14.1.1.1227 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_2_START_ADDRESS_H Registers
        1228. 14.1.1.1228 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_2_END_ADDRESS_L Registers
        1229. 14.1.1.1229 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_2_END_ADDRESS_H Registers
        1230. 14.1.1.1230 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_3_CONTROL Registers
        1231. 14.1.1.1231 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_3_START_ADDRESS_L Registers
        1232. 14.1.1.1232 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_3_START_ADDRESS_H Registers
        1233. 14.1.1.1233 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_3_END_ADDRESS_L Registers
        1234. 14.1.1.1234 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_3_END_ADDRESS_H Registers
        1235. 14.1.1.1235 ISC_IPULSAR_UL_WKUP_0_CPU0_RMST_ISC_REGION_DEF_CONTROL Registers
        1236. 14.1.1.1236 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_0_CONTROL Registers
        1237. 14.1.1.1237 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_0_START_ADDRESS_L Registers
        1238. 14.1.1.1238 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_0_START_ADDRESS_H Registers
        1239. 14.1.1.1239 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_0_END_ADDRESS_L Registers
        1240. 14.1.1.1240 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_0_END_ADDRESS_H Registers
        1241. 14.1.1.1241 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_1_CONTROL Registers
        1242. 14.1.1.1242 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_1_START_ADDRESS_L Registers
        1243. 14.1.1.1243 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_1_START_ADDRESS_H Registers
        1244. 14.1.1.1244 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_1_END_ADDRESS_L Registers
        1245. 14.1.1.1245 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_1_END_ADDRESS_H Registers
        1246. 14.1.1.1246 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_2_CONTROL Registers
        1247. 14.1.1.1247 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_2_START_ADDRESS_L Registers
        1248. 14.1.1.1248 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_2_START_ADDRESS_H Registers
        1249. 14.1.1.1249 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_2_END_ADDRESS_L Registers
        1250. 14.1.1.1250 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_2_END_ADDRESS_H Registers
        1251. 14.1.1.1251 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_3_CONTROL Registers
        1252. 14.1.1.1252 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_3_START_ADDRESS_L Registers
        1253. 14.1.1.1253 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_3_START_ADDRESS_H Registers
        1254. 14.1.1.1254 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_3_END_ADDRESS_L Registers
        1255. 14.1.1.1255 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_3_END_ADDRESS_H Registers
        1256. 14.1.1.1256 ISC_IPULSAR_UL_WKUP_0_CPU0_WMST_ISC_REGION_DEF_CONTROL Registers
        1257. 14.1.1.1257 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_0_CONTROL Registers
        1258. 14.1.1.1258 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_0_START_ADDRESS_L Registers
        1259. 14.1.1.1259 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_0_START_ADDRESS_H Registers
        1260. 14.1.1.1260 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_0_END_ADDRESS_L Registers
        1261. 14.1.1.1261 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_0_END_ADDRESS_H Registers
        1262. 14.1.1.1262 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_1_CONTROL Registers
        1263. 14.1.1.1263 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_1_START_ADDRESS_L Registers
        1264. 14.1.1.1264 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_1_START_ADDRESS_H Registers
        1265. 14.1.1.1265 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_1_END_ADDRESS_L Registers
        1266. 14.1.1.1266 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_1_END_ADDRESS_H Registers
        1267. 14.1.1.1267 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_2_CONTROL Registers
        1268. 14.1.1.1268 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_2_START_ADDRESS_L Registers
        1269. 14.1.1.1269 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_2_START_ADDRESS_H Registers
        1270. 14.1.1.1270 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_2_END_ADDRESS_L Registers
        1271. 14.1.1.1271 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_2_END_ADDRESS_H Registers
        1272. 14.1.1.1272 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_3_CONTROL Registers
        1273. 14.1.1.1273 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_3_START_ADDRESS_L Registers
        1274. 14.1.1.1274 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_3_START_ADDRESS_H Registers
        1275. 14.1.1.1275 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_3_END_ADDRESS_L Registers
        1276. 14.1.1.1276 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_3_END_ADDRESS_H Registers
        1277. 14.1.1.1277 ISC_IPULSAR_UL_WKUP_0_CPU0_PMST_ISC_REGION_DEF_CONTROL Registers
        1278. 14.1.1.1278 QOS_IPULSAR_UL_WKUP_0_CPU0_RMST_MAP0 Registers
        1279. 14.1.1.1279 QOS_IPULSAR_UL_WKUP_0_CPU0_WMST_MAP0 Registers
        1280. 14.1.1.1280 QOS_IPULSAR_UL_WKUP_0_CPU0_PMST_MAP0 Registers
        1281. 14.1.1.1281 Access Table
      2. 14.1.2 CBASS_CENTRAL Registers
        1. 14.1.2.1   ERR_PID Registers
        2. 14.1.2.2   ERR_DESTINATION_ID Registers
        3. 14.1.2.3   ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.2.4   ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.2.5   ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.2.6   ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.2.7   ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.2.8   ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.2.9   ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.2.10  ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.2.11  ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.2.12  ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.2.13  ERR_EOI Registers
        14. 14.1.2.14  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_CONTROL Registers
        15. 14.1.2.15  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_PERMISSION_0 Registers
        16. 14.1.2.16  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_PERMISSION_1 Registers
        17. 14.1.2.17  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_PERMISSION_2 Registers
        18. 14.1.2.18  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_START_ADDRESS_L Registers
        19. 14.1.2.19  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_START_ADDRESS_H Registers
        20. 14.1.2.20  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_END_ADDRESS_L Registers
        21. 14.1.2.21  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_0_END_ADDRESS_H Registers
        22. 14.1.2.22  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_CONTROL Registers
        23. 14.1.2.23  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_PERMISSION_0 Registers
        24. 14.1.2.24  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_PERMISSION_1 Registers
        25. 14.1.2.25  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_PERMISSION_2 Registers
        26. 14.1.2.26  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_START_ADDRESS_L Registers
        27. 14.1.2.27  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_START_ADDRESS_H Registers
        28. 14.1.2.28  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_END_ADDRESS_L Registers
        29. 14.1.2.29  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_1_END_ADDRESS_H Registers
        30. 14.1.2.30  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_CONTROL Registers
        31. 14.1.2.31  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_PERMISSION_0 Registers
        32. 14.1.2.32  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_PERMISSION_1 Registers
        33. 14.1.2.33  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_PERMISSION_2 Registers
        34. 14.1.2.34  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_START_ADDRESS_L Registers
        35. 14.1.2.35  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_START_ADDRESS_H Registers
        36. 14.1.2.36  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_END_ADDRESS_L Registers
        37. 14.1.2.37  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_2_END_ADDRESS_H Registers
        38. 14.1.2.38  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_CONTROL Registers
        39. 14.1.2.39  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_PERMISSION_0 Registers
        40. 14.1.2.40  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_PERMISSION_1 Registers
        41. 14.1.2.41  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_PERMISSION_2 Registers
        42. 14.1.2.42  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_START_ADDRESS_L Registers
        43. 14.1.2.43  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_START_ADDRESS_H Registers
        44. 14.1.2.44  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_END_ADDRESS_L Registers
        45. 14.1.2.45  FW_IPSRAM16KX32E_MAIN_0_RAM_VB_FW_REGION_3_END_ADDRESS_H Registers
        46. 14.1.2.46  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_CONTROL Registers
        47. 14.1.2.47  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_PERMISSION_0 Registers
        48. 14.1.2.48  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_PERMISSION_1 Registers
        49. 14.1.2.49  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_PERMISSION_2 Registers
        50. 14.1.2.50  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_L Registers
        51. 14.1.2.51  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_START_ADDRESS_H Registers
        52. 14.1.2.52  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_L Registers
        53. 14.1.2.53  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_0_END_ADDRESS_H Registers
        54. 14.1.2.54  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_CONTROL Registers
        55. 14.1.2.55  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_PERMISSION_0 Registers
        56. 14.1.2.56  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_PERMISSION_1 Registers
        57. 14.1.2.57  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_PERMISSION_2 Registers
        58. 14.1.2.58  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_L Registers
        59. 14.1.2.59  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_START_ADDRESS_H Registers
        60. 14.1.2.60  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_L Registers
        61. 14.1.2.61  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_1_END_ADDRESS_H Registers
        62. 14.1.2.62  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_CONTROL Registers
        63. 14.1.2.63  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_PERMISSION_0 Registers
        64. 14.1.2.64  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_PERMISSION_1 Registers
        65. 14.1.2.65  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_PERMISSION_2 Registers
        66. 14.1.2.66  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_L Registers
        67. 14.1.2.67  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_START_ADDRESS_H Registers
        68. 14.1.2.68  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_L Registers
        69. 14.1.2.69  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_2_END_ADDRESS_H Registers
        70. 14.1.2.70  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_CONTROL Registers
        71. 14.1.2.71  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_PERMISSION_0 Registers
        72. 14.1.2.72  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_PERMISSION_1 Registers
        73. 14.1.2.73  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_PERMISSION_2 Registers
        74. 14.1.2.74  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_L Registers
        75. 14.1.2.75  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_START_ADDRESS_H Registers
        76. 14.1.2.76  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_L Registers
        77. 14.1.2.77  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_3_END_ADDRESS_H Registers
        78. 14.1.2.78  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_CONTROL Registers
        79. 14.1.2.79  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_PERMISSION_0 Registers
        80. 14.1.2.80  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_PERMISSION_1 Registers
        81. 14.1.2.81  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_PERMISSION_2 Registers
        82. 14.1.2.82  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_L Registers
        83. 14.1.2.83  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_START_ADDRESS_H Registers
        84. 14.1.2.84  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_L Registers
        85. 14.1.2.85  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_4_END_ADDRESS_H Registers
        86. 14.1.2.86  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_CONTROL Registers
        87. 14.1.2.87  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_PERMISSION_0 Registers
        88. 14.1.2.88  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_PERMISSION_1 Registers
        89. 14.1.2.89  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_PERMISSION_2 Registers
        90. 14.1.2.90  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_L Registers
        91. 14.1.2.91  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_START_ADDRESS_H Registers
        92. 14.1.2.92  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_L Registers
        93. 14.1.2.93  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_5_END_ADDRESS_H Registers
        94. 14.1.2.94  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_CONTROL Registers
        95. 14.1.2.95  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_PERMISSION_0 Registers
        96. 14.1.2.96  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_PERMISSION_1 Registers
        97. 14.1.2.97  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_PERMISSION_2 Registers
        98. 14.1.2.98  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_L Registers
        99. 14.1.2.99  FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_START_ADDRESS_H Registers
        100. 14.1.2.100 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_L Registers
        101. 14.1.2.101 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_6_END_ADDRESS_H Registers
        102. 14.1.2.102 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_CONTROL Registers
        103. 14.1.2.103 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_PERMISSION_0 Registers
        104. 14.1.2.104 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_PERMISSION_1 Registers
        105. 14.1.2.105 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_PERMISSION_2 Registers
        106. 14.1.2.106 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_L Registers
        107. 14.1.2.107 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_START_ADDRESS_H Registers
        108. 14.1.2.108 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_L Registers
        109. 14.1.2.109 FW_EXPORT_AM62_MAIN_CENTRAL_CBASS_TO_AM62_MCU_CBASS_DATA_L0_FW_REGION_7_END_ADDRESS_H Registers
        110. 14.1.2.110 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_CONTROL Registers
        111. 14.1.2.111 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_PERMISSION_0 Registers
        112. 14.1.2.112 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_PERMISSION_1 Registers
        113. 14.1.2.113 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_PERMISSION_2 Registers
        114. 14.1.2.114 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_START_ADDRESS_L Registers
        115. 14.1.2.115 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_START_ADDRESS_H Registers
        116. 14.1.2.116 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_END_ADDRESS_L Registers
        117. 14.1.2.117 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_0_END_ADDRESS_H Registers
        118. 14.1.2.118 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_CONTROL Registers
        119. 14.1.2.119 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_PERMISSION_0 Registers
        120. 14.1.2.120 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_PERMISSION_1 Registers
        121. 14.1.2.121 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_PERMISSION_2 Registers
        122. 14.1.2.122 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_START_ADDRESS_L Registers
        123. 14.1.2.123 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_START_ADDRESS_H Registers
        124. 14.1.2.124 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_END_ADDRESS_L Registers
        125. 14.1.2.125 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_1_END_ADDRESS_H Registers
        126. 14.1.2.126 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_CONTROL Registers
        127. 14.1.2.127 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_PERMISSION_0 Registers
        128. 14.1.2.128 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_PERMISSION_1 Registers
        129. 14.1.2.129 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_PERMISSION_2 Registers
        130. 14.1.2.130 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_START_ADDRESS_L Registers
        131. 14.1.2.131 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_START_ADDRESS_H Registers
        132. 14.1.2.132 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_END_ADDRESS_L Registers
        133. 14.1.2.133 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_2_END_ADDRESS_H Registers
        134. 14.1.2.134 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_CONTROL Registers
        135. 14.1.2.135 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_PERMISSION_0 Registers
        136. 14.1.2.136 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_PERMISSION_1 Registers
        137. 14.1.2.137 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_PERMISSION_2 Registers
        138. 14.1.2.138 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_START_ADDRESS_L Registers
        139. 14.1.2.139 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_START_ADDRESS_H Registers
        140. 14.1.2.140 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_END_ADDRESS_L Registers
        141. 14.1.2.141 FW_BR_SCRP_32B_DMSC_HSM_TO_SCRP_HSM_CLK2_L0_FW_REGION_3_END_ADDRESS_H Registers
        142. 14.1.2.142 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP0_ISC_REGION_0_CONTROL Registers
        143. 14.1.2.143 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP0_ISC_REGION_0_START_ADDRESS_L Registers
        144. 14.1.2.144 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP0_ISC_REGION_0_START_ADDRESS_H Registers
        145. 14.1.2.145 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP0_ISC_REGION_0_END_ADDRESS_L Registers
        146. 14.1.2.146 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP0_ISC_REGION_0_END_ADDRESS_H Registers
        147. 14.1.2.147 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP0_ISC_REGION_DEF_CONTROL Registers
        148. 14.1.2.148 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP1_ISC_REGION_0_CONTROL Registers
        149. 14.1.2.149 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP1_ISC_REGION_0_START_ADDRESS_L Registers
        150. 14.1.2.150 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP1_ISC_REGION_0_START_ADDRESS_H Registers
        151. 14.1.2.151 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP1_ISC_REGION_0_END_ADDRESS_L Registers
        152. 14.1.2.152 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP1_ISC_REGION_0_END_ADDRESS_H Registers
        153. 14.1.2.153 ISC_IICSS_M_MAIN_0_PR1_MST_VBUSP1_ISC_REGION_DEF_CONTROL Registers
        154. 14.1.2.154 GLB_PID Registers
        155. 14.1.2.155 GLB_DESTINATION_ID Registers
        156. 14.1.2.156 GLB_EXCEPTION_LOGGING_CONTROL Registers
        157. 14.1.2.157 GLB_EXCEPTION_LOGGING_HEADER0 Registers
        158. 14.1.2.158 GLB_EXCEPTION_LOGGING_HEADER1 Registers
        159. 14.1.2.159 GLB_EXCEPTION_LOGGING_DATA0 Registers
        160. 14.1.2.160 GLB_EXCEPTION_LOGGING_DATA1 Registers
        161. 14.1.2.161 GLB_EXCEPTION_LOGGING_DATA2 Registers
        162. 14.1.2.162 GLB_EXCEPTION_LOGGING_DATA3 Registers
        163. 14.1.2.163 GLB_EXCEPTION_PEND_SET Registers
        164. 14.1.2.164 GLB_EXCEPTION_PEND_CLEAR Registers
        165. 14.1.2.165 QOS_IICSS_M_MAIN_0_PR1_MST_VBUSP0_MAP0 Registers
        166. 14.1.2.166 QOS_IICSS_M_MAIN_0_PR1_MST_VBUSP1_MAP0 Registers
        167. 14.1.2.167 Access Table
      3. 14.1.3 CBASS_DBG Registers
        1. 14.1.3.1  ERR_PID Registers
        2. 14.1.3.2  ERR_DESTINATION_ID Registers
        3. 14.1.3.3  ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.3.4  ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.3.5  ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.3.6  ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.3.7  ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.3.8  ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.3.9  ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.3.10 ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.3.11 ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.3.12 ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.3.13 ERR_EOI Registers
        14. 14.1.3.14 Access Table
      4. 14.1.4 CBASS_FW Registers
        1. 14.1.4.1  ERR_PID Registers
        2. 14.1.4.2  ERR_DESTINATION_ID Registers
        3. 14.1.4.3  ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.4.4  ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.4.5  ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.4.6  ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.4.7  ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.4.8  ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.4.9  ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.4.10 ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.4.11 ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.4.12 ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.4.13 ERR_EOI Registers
        14. 14.1.4.14 Access Table
      5. 14.1.5 CBASS_INFRA Registers
        1. 14.1.5.1  ERR_PID Registers
        2. 14.1.5.2  ERR_DESTINATION_ID Registers
        3. 14.1.5.3  ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.5.4  ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.5.5  ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.5.6  ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.5.7  ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.5.8  ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.5.9  ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.5.10 ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.5.11 ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.5.12 ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.5.13 ERR_EOI Registers
        14. 14.1.5.14 Access Table
      6. 14.1.6 CBASS_IPCSS Registers
        1. 14.1.6.1   ERR_PID Registers
        2. 14.1.6.2   ERR_DESTINATION_ID Registers
        3. 14.1.6.3   ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.6.4   ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.6.5   ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.6.6   ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.6.7   ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.6.8   ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.6.9   ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.6.10  ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.6.11  ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.6.12  ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.6.13  ERR_EOI Registers
        14. 14.1.6.14  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_CONTROL Registers
        15. 14.1.6.15  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_PERMISSION_0 Registers
        16. 14.1.6.16  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_PERMISSION_1 Registers
        17. 14.1.6.17  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_PERMISSION_2 Registers
        18. 14.1.6.18  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_START_ADDRESS_L Registers
        19. 14.1.6.19  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_START_ADDRESS_H Registers
        20. 14.1.6.20  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_END_ADDRESS_L Registers
        21. 14.1.6.21  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_END_ADDRESS_H Registers
        22. 14.1.6.22  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_CONTROL Registers
        23. 14.1.6.23  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_PERMISSION_0 Registers
        24. 14.1.6.24  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_PERMISSION_1 Registers
        25. 14.1.6.25  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_PERMISSION_2 Registers
        26. 14.1.6.26  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_START_ADDRESS_L Registers
        27. 14.1.6.27  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_START_ADDRESS_H Registers
        28. 14.1.6.28  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_END_ADDRESS_L Registers
        29. 14.1.6.29  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_END_ADDRESS_H Registers
        30. 14.1.6.30  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_CONTROL Registers
        31. 14.1.6.31  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_PERMISSION_0 Registers
        32. 14.1.6.32  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_PERMISSION_1 Registers
        33. 14.1.6.33  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_PERMISSION_2 Registers
        34. 14.1.6.34  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_START_ADDRESS_L Registers
        35. 14.1.6.35  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_START_ADDRESS_H Registers
        36. 14.1.6.36  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_END_ADDRESS_L Registers
        37. 14.1.6.37  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_END_ADDRESS_H Registers
        38. 14.1.6.38  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_CONTROL Registers
        39. 14.1.6.39  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_PERMISSION_0 Registers
        40. 14.1.6.40  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_PERMISSION_1 Registers
        41. 14.1.6.41  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_PERMISSION_2 Registers
        42. 14.1.6.42  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_START_ADDRESS_L Registers
        43. 14.1.6.43  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_START_ADDRESS_H Registers
        44. 14.1.6.44  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_END_ADDRESS_L Registers
        45. 14.1.6.45  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_END_ADDRESS_H Registers
        46. 14.1.6.46  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_CONTROL Registers
        47. 14.1.6.47  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_PERMISSION_0 Registers
        48. 14.1.6.48  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_PERMISSION_1 Registers
        49. 14.1.6.49  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_PERMISSION_2 Registers
        50. 14.1.6.50  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_START_ADDRESS_L Registers
        51. 14.1.6.51  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_START_ADDRESS_H Registers
        52. 14.1.6.52  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_END_ADDRESS_L Registers
        53. 14.1.6.53  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_END_ADDRESS_H Registers
        54. 14.1.6.54  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_CONTROL Registers
        55. 14.1.6.55  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_PERMISSION_0 Registers
        56. 14.1.6.56  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_PERMISSION_1 Registers
        57. 14.1.6.57  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_PERMISSION_2 Registers
        58. 14.1.6.58  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_START_ADDRESS_L Registers
        59. 14.1.6.59  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_START_ADDRESS_H Registers
        60. 14.1.6.60  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_END_ADDRESS_L Registers
        61. 14.1.6.61  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_END_ADDRESS_H Registers
        62. 14.1.6.62  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_CONTROL Registers
        63. 14.1.6.63  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_PERMISSION_0 Registers
        64. 14.1.6.64  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_PERMISSION_1 Registers
        65. 14.1.6.65  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_PERMISSION_2 Registers
        66. 14.1.6.66  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_START_ADDRESS_L Registers
        67. 14.1.6.67  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_START_ADDRESS_H Registers
        68. 14.1.6.68  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_END_ADDRESS_L Registers
        69. 14.1.6.69  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_END_ADDRESS_H Registers
        70. 14.1.6.70  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_CONTROL Registers
        71. 14.1.6.71  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_PERMISSION_0 Registers
        72. 14.1.6.72  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_PERMISSION_1 Registers
        73. 14.1.6.73  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_PERMISSION_2 Registers
        74. 14.1.6.74  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_START_ADDRESS_L Registers
        75. 14.1.6.75  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_START_ADDRESS_H Registers
        76. 14.1.6.76  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_END_ADDRESS_L Registers
        77. 14.1.6.77  FW_IDMSS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_END_ADDRESS_H Registers
        78. 14.1.6.78  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_CONTROL Registers
        79. 14.1.6.79  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_PERMISSION_0 Registers
        80. 14.1.6.80  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_PERMISSION_1 Registers
        81. 14.1.6.81  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_PERMISSION_2 Registers
        82. 14.1.6.82  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_START_ADDRESS_L Registers
        83. 14.1.6.83  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_START_ADDRESS_H Registers
        84. 14.1.6.84  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_END_ADDRESS_L Registers
        85. 14.1.6.85  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_0_END_ADDRESS_H Registers
        86. 14.1.6.86  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_CONTROL Registers
        87. 14.1.6.87  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_PERMISSION_0 Registers
        88. 14.1.6.88  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_PERMISSION_1 Registers
        89. 14.1.6.89  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_PERMISSION_2 Registers
        90. 14.1.6.90  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_START_ADDRESS_L Registers
        91. 14.1.6.91  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_START_ADDRESS_H Registers
        92. 14.1.6.92  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_END_ADDRESS_L Registers
        93. 14.1.6.93  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_1_END_ADDRESS_H Registers
        94. 14.1.6.94  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_CONTROL Registers
        95. 14.1.6.95  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_PERMISSION_0 Registers
        96. 14.1.6.96  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_PERMISSION_1 Registers
        97. 14.1.6.97  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_PERMISSION_2 Registers
        98. 14.1.6.98  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_START_ADDRESS_L Registers
        99. 14.1.6.99  FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_START_ADDRESS_H Registers
        100. 14.1.6.100 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_END_ADDRESS_L Registers
        101. 14.1.6.101 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_2_END_ADDRESS_H Registers
        102. 14.1.6.102 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_CONTROL Registers
        103. 14.1.6.103 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_PERMISSION_0 Registers
        104. 14.1.6.104 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_PERMISSION_1 Registers
        105. 14.1.6.105 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_PERMISSION_2 Registers
        106. 14.1.6.106 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_START_ADDRESS_L Registers
        107. 14.1.6.107 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_START_ADDRESS_H Registers
        108. 14.1.6.108 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_END_ADDRESS_L Registers
        109. 14.1.6.109 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_3_END_ADDRESS_H Registers
        110. 14.1.6.110 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_CONTROL Registers
        111. 14.1.6.111 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_PERMISSION_0 Registers
        112. 14.1.6.112 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_PERMISSION_1 Registers
        113. 14.1.6.113 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_PERMISSION_2 Registers
        114. 14.1.6.114 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_START_ADDRESS_L Registers
        115. 14.1.6.115 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_START_ADDRESS_H Registers
        116. 14.1.6.116 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_END_ADDRESS_L Registers
        117. 14.1.6.117 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_4_END_ADDRESS_H Registers
        118. 14.1.6.118 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_CONTROL Registers
        119. 14.1.6.119 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_PERMISSION_0 Registers
        120. 14.1.6.120 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_PERMISSION_1 Registers
        121. 14.1.6.121 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_PERMISSION_2 Registers
        122. 14.1.6.122 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_START_ADDRESS_L Registers
        123. 14.1.6.123 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_START_ADDRESS_H Registers
        124. 14.1.6.124 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_END_ADDRESS_L Registers
        125. 14.1.6.125 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_5_END_ADDRESS_H Registers
        126. 14.1.6.126 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_CONTROL Registers
        127. 14.1.6.127 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_PERMISSION_0 Registers
        128. 14.1.6.128 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_PERMISSION_1 Registers
        129. 14.1.6.129 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_PERMISSION_2 Registers
        130. 14.1.6.130 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_START_ADDRESS_L Registers
        131. 14.1.6.131 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_START_ADDRESS_H Registers
        132. 14.1.6.132 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_END_ADDRESS_L Registers
        133. 14.1.6.133 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_6_END_ADDRESS_H Registers
        134. 14.1.6.134 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_CONTROL Registers
        135. 14.1.6.135 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_PERMISSION_0 Registers
        136. 14.1.6.136 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_PERMISSION_1 Registers
        137. 14.1.6.137 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_PERMISSION_2 Registers
        138. 14.1.6.138 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_START_ADDRESS_L Registers
        139. 14.1.6.139 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_START_ADDRESS_H Registers
        140. 14.1.6.140 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_END_ADDRESS_L Registers
        141. 14.1.6.141 FW_ISA3SS_AM62_MAIN_0_IPCSS_VBM_DST_FW_REGION_7_END_ADDRESS_H Registers
        142. 14.1.6.142 GLB_PID Registers
        143. 14.1.6.143 GLB_DESTINATION_ID Registers
        144. 14.1.6.144 GLB_EXCEPTION_LOGGING_CONTROL Registers
        145. 14.1.6.145 GLB_EXCEPTION_LOGGING_HEADER0 Registers
        146. 14.1.6.146 GLB_EXCEPTION_LOGGING_HEADER1 Registers
        147. 14.1.6.147 GLB_EXCEPTION_LOGGING_DATA0 Registers
        148. 14.1.6.148 GLB_EXCEPTION_LOGGING_DATA1 Registers
        149. 14.1.6.149 GLB_EXCEPTION_LOGGING_DATA2 Registers
        150. 14.1.6.150 GLB_EXCEPTION_LOGGING_DATA3 Registers
        151. 14.1.6.151 GLB_EXCEPTION_PEND_SET Registers
        152. 14.1.6.152 GLB_EXCEPTION_PEND_CLEAR Registers
        153. 14.1.6.153 Access Table
      7. 14.1.7 CBASS_MCASP Registers
        1. 14.1.7.1  ERR_PID Registers
        2. 14.1.7.2  ERR_DESTINATION_ID Registers
        3. 14.1.7.3  ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.7.4  ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.7.5  ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.7.6  ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.7.7  ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.7.8  ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.7.9  ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.7.10 ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.7.11 ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.7.12 ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.7.13 ERR_EOI Registers
        14. 14.1.7.14 Access Table
      8. 14.1.8 CBASS_MISC_PERI Registers
        1. 14.1.8.1  ERR_PID Registers
        2. 14.1.8.2  ERR_DESTINATION_ID Registers
        3. 14.1.8.3  ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.8.4  ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.8.5  ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.8.6  ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.8.7  ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.8.8  ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.8.9  ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.8.10 ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.8.11 ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.8.12 ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.8.13 ERR_EOI Registers
        14. 14.1.8.14 Access Table
      9. 14.1.9 CBASS_SAFE Registers
        1. 14.1.9.1  ERR_PID Registers
        2. 14.1.9.2  ERR_DESTINATION_ID Registers
        3. 14.1.9.3  ERR_EXCEPTION_LOGGING_HEADER0 Registers
        4. 14.1.9.4  ERR_EXCEPTION_LOGGING_HEADER1 Registers
        5. 14.1.9.5  ERR_EXCEPTION_LOGGING_DATA0 Registers
        6. 14.1.9.6  ERR_EXCEPTION_LOGGING_DATA1 Registers
        7. 14.1.9.7  ERR_EXCEPTION_LOGGING_DATA2 Registers
        8. 14.1.9.8  ERR_EXCEPTION_LOGGING_DATA3 Registers
        9. 14.1.9.9  ERR_ERR_INTR_RAW_STAT Registers
        10. 14.1.9.10 ERR_ERR_INTR_ENABLED_STAT Registers
        11. 14.1.9.11 ERR_ERR_INTR_ENABLE_SET Registers
        12. 14.1.9.12 ERR_ERR_INTR_ENABLE_CLR Registers
        13. 14.1.9.13 ERR_EOI Registers
        14. 14.1.9.14 Access Table
    2. 14.2 Device Configuration Registers
      1. 14.2.1 CTRL_MMR Registers
        1. 14.2.1.1 General Purpose Control Registers
          1. 14.2.1.1.1 CTRL_MMR Registers
            1. 14.2.1.1.1.1   CFG0_PID Registers
            2. 14.2.1.1.1.2   CFG0_MMR_CFG1 Registers
            3. 14.2.1.1.1.3   CFG0_LOCK0_KICK0 Registers
            4. 14.2.1.1.1.4   CFG0_LOCK0_KICK1 Registers
            5. 14.2.1.1.1.5   CFG0_INTR_RAW_STATUS Registers
            6. 14.2.1.1.1.6   CFG0_INTR_ENABLED_STATUS_CLEAR Registers
            7. 14.2.1.1.1.7   CFG0_INTR_ENABLE Registers
            8. 14.2.1.1.1.8   CFG0_INTR_ENABLE_CLEAR Registers
            9. 14.2.1.1.1.9   CFG0_EOI Registers
            10. 14.2.1.1.1.10  CFG0_FAULT_ADDRESS Registers
            11. 14.2.1.1.1.11  CFG0_FAULT_TYPE_STATUS Registers
            12. 14.2.1.1.1.12  CFG0_FAULT_ATTR_STATUS Registers
            13. 14.2.1.1.1.13  CFG0_FAULT_CLEAR Registers
            14. 14.2.1.1.1.14  CFG0_CLAIMREG_P0_R0_READONLY Registers
            15. 14.2.1.1.1.15  CFG0_CLAIMREG_P0_R1_READONLY Registers
            16. 14.2.1.1.1.16  CFG0_CLAIMREG_P0_R2_READONLY Registers
            17. 14.2.1.1.1.17  CFG0_CLAIMREG_P0_R3_READONLY Registers
            18. 14.2.1.1.1.18  CFG0_CLAIMREG_P0_R4_READONLY Registers
            19. 14.2.1.1.1.19  CFG0_CLAIMREG_P0_R5_READONLY Registers
            20. 14.2.1.1.1.20  CFG0_CLAIMREG_P0_R6_READONLY Registers
            21. 14.2.1.1.1.21  CFG0_PID_PROXY Registers
            22. 14.2.1.1.1.22  CFG0_MMR_CFG1_PROXY Registers
            23. 14.2.1.1.1.23  CFG0_LOCK0_KICK0_PROXY Registers
            24. 14.2.1.1.1.24  CFG0_LOCK0_KICK1_PROXY Registers
            25. 14.2.1.1.1.25  CFG0_INTR_RAW_STATUS_PROXY Registers
            26. 14.2.1.1.1.26  CFG0_INTR_ENABLED_STATUS_CLEAR_PROXY Registers
            27. 14.2.1.1.1.27  CFG0_INTR_ENABLE_PROXY Registers
            28. 14.2.1.1.1.28  CFG0_INTR_ENABLE_CLEAR_PROXY Registers
            29. 14.2.1.1.1.29  CFG0_EOI_PROXY Registers
            30. 14.2.1.1.1.30  CFG0_FAULT_ADDRESS_PROXY Registers
            31. 14.2.1.1.1.31  CFG0_FAULT_TYPE_STATUS_PROXY Registers
            32. 14.2.1.1.1.32  CFG0_FAULT_ATTR_STATUS_PROXY Registers
            33. 14.2.1.1.1.33  CFG0_FAULT_CLEAR_PROXY Registers
            34. 14.2.1.1.1.34  CFG0_CLAIMREG_P0_R0 Registers
            35. 14.2.1.1.1.35  CFG0_CLAIMREG_P0_R1 Registers
            36. 14.2.1.1.1.36  CFG0_CLAIMREG_P0_R2 Registers
            37. 14.2.1.1.1.37  CFG0_CLAIMREG_P0_R3 Registers
            38. 14.2.1.1.1.38  CFG0_CLAIMREG_P0_R4 Registers
            39. 14.2.1.1.1.39  CFG0_CLAIMREG_P0_R5 Registers
            40. 14.2.1.1.1.40  CFG0_CLAIMREG_P0_R6 Registers
            41. 14.2.1.1.1.41  CFG0_ENET1_CTRL Registers
            42. 14.2.1.1.1.42  CFG0_ENET2_CTRL Registers
            43. 14.2.1.1.1.43  CFG0_ICSSM0_CTRL0 Registers
            44. 14.2.1.1.1.44  CFG0_EPWM_TB_CLKEN Registers
            45. 14.2.1.1.1.45  CFG0_EPWM0_CTRL Registers
            46. 14.2.1.1.1.46  CFG0_EPWM1_CTRL Registers
            47. 14.2.1.1.1.47  CFG0_EPWM2_CTRL Registers
            48. 14.2.1.1.1.48  CFG0_SOCA_SEL Registers
            49. 14.2.1.1.1.49  CFG0_SOCB_SEL Registers
            50. 14.2.1.1.1.50  CFG0_EQEP0_CTRL Registers
            51. 14.2.1.1.1.51  CFG0_EQEP1_CTRL Registers
            52. 14.2.1.1.1.52  CFG0_EQEP2_CTRL Registers
            53. 14.2.1.1.1.53  CFG0_EQEP_STAT Registers
            54. 14.2.1.1.1.54  CFG0_TIMER1_CTRL Registers
            55. 14.2.1.1.1.55  CFG0_TIMER3_CTRL Registers
            56. 14.2.1.1.1.56  CFG0_TIMER5_CTRL Registers
            57. 14.2.1.1.1.57  CFG0_TIMER7_CTRL Registers
            58. 14.2.1.1.1.58  CFG0_EMMC0_STAT Registers
            59. 14.2.1.1.1.59  CFG0_EMMC1_STAT Registers
            60. 14.2.1.1.1.60  CFG0_EMMC2_STAT Registers
            61. 14.2.1.1.1.61  CFG0_FSS_CTRL Registers
            62. 14.2.1.1.1.62  CFG0_DCC_STAT Registers
            63. 14.2.1.1.1.63  CFG0_LOCK1_KICK0 Registers
            64. 14.2.1.1.1.64  CFG0_LOCK1_KICK1 Registers
            65. 14.2.1.1.1.65  CFG0_CLAIMREG_P1_R0_READONLY Registers
            66. 14.2.1.1.1.66  CFG0_CLAIMREG_P1_R1_READONLY Registers
            67. 14.2.1.1.1.67  CFG0_CLAIMREG_P1_R2_READONLY Registers
            68. 14.2.1.1.1.68  CFG0_CLAIMREG_P1_R3_READONLY Registers
            69. 14.2.1.1.1.69  CFG0_CLAIMREG_P1_R4_READONLY Registers
            70. 14.2.1.1.1.70  CFG0_CLAIMREG_P1_R5_READONLY Registers
            71. 14.2.1.1.1.71  CFG0_CLAIMREG_P1_R6_READONLY Registers
            72. 14.2.1.1.1.72  CFG0_CLAIMREG_P1_R7_READONLY Registers
            73. 14.2.1.1.1.73  CFG0_CLAIMREG_P1_R8_READONLY Registers
            74. 14.2.1.1.1.74  CFG0_CLAIMREG_P1_R9_READONLY Registers
            75. 14.2.1.1.1.75  CFG0_CLAIMREG_P1_R10_READONLY Registers
            76. 14.2.1.1.1.76  CFG0_CLAIMREG_P1_R11_READONLY Registers
            77. 14.2.1.1.1.77  CFG0_CLAIMREG_P1_R12_READONLY Registers
            78. 14.2.1.1.1.78  CFG0_CLAIMREG_P1_R13_READONLY Registers
            79. 14.2.1.1.1.79  CFG0_CLAIMREG_P1_R14_READONLY Registers
            80. 14.2.1.1.1.80  CFG0_ENET1_CTRL_PROXY Registers
            81. 14.2.1.1.1.81  CFG0_ENET2_CTRL_PROXY Registers
            82. 14.2.1.1.1.82  CFG0_ICSSM0_CTRL0_PROXY Registers
            83. 14.2.1.1.1.83  CFG0_EPWM_TB_CLKEN_PROXY Registers
            84. 14.2.1.1.1.84  CFG0_EPWM0_CTRL_PROXY Registers
            85. 14.2.1.1.1.85  CFG0_EPWM1_CTRL_PROXY Registers
            86. 14.2.1.1.1.86  CFG0_EPWM2_CTRL_PROXY Registers
            87. 14.2.1.1.1.87  CFG0_SOCA_SEL_PROXY Registers
            88. 14.2.1.1.1.88  CFG0_SOCB_SEL_PROXY Registers
            89. 14.2.1.1.1.89  CFG0_EQEP0_CTRL_PROXY Registers
            90. 14.2.1.1.1.90  CFG0_EQEP1_CTRL_PROXY Registers
            91. 14.2.1.1.1.91  CFG0_EQEP2_CTRL_PROXY Registers
            92. 14.2.1.1.1.92  CFG0_EQEP_STAT_PROXY Registers
            93. 14.2.1.1.1.93  CFG0_TIMER1_CTRL_PROXY Registers
            94. 14.2.1.1.1.94  CFG0_TIMER3_CTRL_PROXY Registers
            95. 14.2.1.1.1.95  CFG0_TIMER5_CTRL_PROXY Registers
            96. 14.2.1.1.1.96  CFG0_TIMER7_CTRL_PROXY Registers
            97. 14.2.1.1.1.97  CFG0_EMMC0_STAT_PROXY Registers
            98. 14.2.1.1.1.98  CFG0_EMMC1_STAT_PROXY Registers
            99. 14.2.1.1.1.99  CFG0_EMMC2_STAT_PROXY Registers
            100. 14.2.1.1.1.100 CFG0_FSS_CTRL_PROXY Registers
            101. 14.2.1.1.1.101 CFG0_DCC_STAT_PROXY Registers
            102. 14.2.1.1.1.102 CFG0_LOCK1_KICK0_PROXY Registers
            103. 14.2.1.1.1.103 CFG0_LOCK1_KICK1_PROXY Registers
            104. 14.2.1.1.1.104 CFG0_CLAIMREG_P1_R0 Registers
            105. 14.2.1.1.1.105 CFG0_CLAIMREG_P1_R1 Registers
            106. 14.2.1.1.1.106 CFG0_CLAIMREG_P1_R2 Registers
            107. 14.2.1.1.1.107 CFG0_CLAIMREG_P1_R3 Registers
            108. 14.2.1.1.1.108 CFG0_CLAIMREG_P1_R4 Registers
            109. 14.2.1.1.1.109 CFG0_CLAIMREG_P1_R5 Registers
            110. 14.2.1.1.1.110 CFG0_CLAIMREG_P1_R6 Registers
            111. 14.2.1.1.1.111 CFG0_CLAIMREG_P1_R7 Registers
            112. 14.2.1.1.1.112 CFG0_CLAIMREG_P1_R8 Registers
            113. 14.2.1.1.1.113 CFG0_CLAIMREG_P1_R9 Registers
            114. 14.2.1.1.1.114 CFG0_CLAIMREG_P1_R10 Registers
            115. 14.2.1.1.1.115 CFG0_CLAIMREG_P1_R11 Registers
            116. 14.2.1.1.1.116 CFG0_CLAIMREG_P1_R12 Registers
            117. 14.2.1.1.1.117 CFG0_CLAIMREG_P1_R13 Registers
            118. 14.2.1.1.1.118 CFG0_CLAIMREG_P1_R14 Registers
            119. 14.2.1.1.1.119 CFG0_OBSCLK0_CTRL Registers
            120. 14.2.1.1.1.120 CFG0_CLKOUT_CTRL Registers
            121. 14.2.1.1.1.121 CFG0_ICSSM0_CLKSEL Registers
            122. 14.2.1.1.1.122 CFG0_MAIN_PLL0_CLKSEL Registers
            123. 14.2.1.1.1.123 CFG0_MAIN_PLL1_CLKSEL Registers
            124. 14.2.1.1.1.124 CFG0_MAIN_PLL2_CLKSEL Registers
            125. 14.2.1.1.1.125 CFG0_MAIN_PLL8_CLKSEL Registers
            126. 14.2.1.1.1.126 CFG0_MAIN_PLL12_CLKSEL Registers
            127. 14.2.1.1.1.127 CFG0_MAIN_PLL16_CLKSEL Registers
            128. 14.2.1.1.1.128 CFG0_MAIN_PLL17_CLKSEL Registers
            129. 14.2.1.1.1.129 CFG0_CPSW_CLKSEL Registers
            130. 14.2.1.1.1.130 CFG0_EMMC0_CLKSEL Registers
            131. 14.2.1.1.1.131 CFG0_EMMC1_CLKSEL Registers
            132. 14.2.1.1.1.132 CFG0_EMMC2_CLKSEL Registers
            133. 14.2.1.1.1.133 CFG0_GPMC_CLKSEL Registers
            134. 14.2.1.1.1.134 CFG0_TIMER0_CLKSEL Registers
            135. 14.2.1.1.1.135 CFG0_TIMER1_CLKSEL Registers
            136. 14.2.1.1.1.136 CFG0_TIMER2_CLKSEL Registers
            137. 14.2.1.1.1.137 CFG0_TIMER3_CLKSEL Registers
            138. 14.2.1.1.1.138 CFG0_TIMER4_CLKSEL Registers
            139. 14.2.1.1.1.139 CFG0_TIMER5_CLKSEL Registers
            140. 14.2.1.1.1.140 CFG0_TIMER6_CLKSEL Registers
            141. 14.2.1.1.1.141 CFG0_TIMER7_CLKSEL Registers
            142. 14.2.1.1.1.142 CFG0_SPI0_CLKSEL Registers
            143. 14.2.1.1.1.143 CFG0_SPI1_CLKSEL Registers
            144. 14.2.1.1.1.144 CFG0_SPI2_CLKSEL Registers
            145. 14.2.1.1.1.145 CFG0_USART0_CLK_CTRL Registers
            146. 14.2.1.1.1.146 CFG0_USART1_CLK_CTRL Registers
            147. 14.2.1.1.1.147 CFG0_USART2_CLK_CTRL Registers
            148. 14.2.1.1.1.148 CFG0_USART3_CLK_CTRL Registers
            149. 14.2.1.1.1.149 CFG0_USART4_CLK_CTRL Registers
            150. 14.2.1.1.1.150 CFG0_USART5_CLK_CTRL Registers
            151. 14.2.1.1.1.151 CFG0_USART6_CLK_CTRL Registers
            152. 14.2.1.1.1.152 CFG0_USART0_CLKSEL Registers
            153. 14.2.1.1.1.153 CFG0_USART1_CLKSEL Registers
            154. 14.2.1.1.1.154 CFG0_USART2_CLKSEL Registers
            155. 14.2.1.1.1.155 CFG0_USART3_CLKSEL Registers
            156. 14.2.1.1.1.156 CFG0_USART4_CLKSEL Registers
            157. 14.2.1.1.1.157 CFG0_USART5_CLKSEL Registers
            158. 14.2.1.1.1.158 CFG0_USART6_CLKSEL Registers
            159. 14.2.1.1.1.159 CFG0_AUDIO_REFCLK0_CTRL Registers
            160. 14.2.1.1.1.160 CFG0_AUDIO_REFCLK1_CTRL Registers
            161. 14.2.1.1.1.161 CFG0_DPI0_CLK_CTRL Registers
            162. 14.2.1.1.1.162 CFG0_DSS_DISPC0_CLKSEL1 Registers
            163. 14.2.1.1.1.163 CFG0_MCASP0_CLKSEL Registers
            164. 14.2.1.1.1.164 CFG0_MCASP1_CLKSEL Registers
            165. 14.2.1.1.1.165 CFG0_MCASP2_CLKSEL Registers
            166. 14.2.1.1.1.166 CFG0_MCASP0_AHCLKSEL Registers
            167. 14.2.1.1.1.167 CFG0_MCASP1_AHCLKSEL Registers
            168. 14.2.1.1.1.168 CFG0_MCASP2_AHCLKSEL Registers
            169. 14.2.1.1.1.169 CFG0_WWD0_CLKSEL Registers
            170. 14.2.1.1.1.170 CFG0_WWD1_CLKSEL Registers
            171. 14.2.1.1.1.171 CFG0_WWD2_CLKSEL Registers
            172. 14.2.1.1.1.172 CFG0_WWD3_CLKSEL Registers
            173. 14.2.1.1.1.173 CFG0_WWD15_CLKSEL Registers
            174. 14.2.1.1.1.174 CFG0_MCAN0_CLKSEL Registers
            175. 14.2.1.1.1.175 CFG0_OSPI0_CLKSEL Registers
            176. 14.2.1.1.1.176 CFG0_OLDI0_DAT0_IO_CTRL Registers
            177. 14.2.1.1.1.177 CFG0_OLDI0_DAT1_IO_CTRL Registers
            178. 14.2.1.1.1.178 CFG0_OLDI0_DAT2_IO_CTRL Registers
            179. 14.2.1.1.1.179 CFG0_OLDI0_DAT3_IO_CTRL Registers
            180. 14.2.1.1.1.180 CFG0_OLDI0_CLK_IO_CTRL Registers
            181. 14.2.1.1.1.181 CFG0_OLDI1_DAT0_IO_CTRL Registers
            182. 14.2.1.1.1.182 CFG0_OLDI1_DAT1_IO_CTRL Registers
            183. 14.2.1.1.1.183 CFG0_OLDI1_DAT2_IO_CTRL Registers
            184. 14.2.1.1.1.184 CFG0_OLDI1_DAT3_IO_CTRL Registers
            185. 14.2.1.1.1.185 CFG0_OLDI1_CLK_IO_CTRL Registers
            186. 14.2.1.1.1.186 CFG0_OLDI_PD_CTRL Registers
            187. 14.2.1.1.1.187 CFG0_OLDI_LB_CTRL Registers
            188. 14.2.1.1.1.188 CFG0_LOCK2_KICK0 Registers
            189. 14.2.1.1.1.189 CFG0_LOCK2_KICK1 Registers
            190. 14.2.1.1.1.190 CFG0_CLAIMREG_P2_R0_READONLY Registers
            191. 14.2.1.1.1.191 CFG0_CLAIMREG_P2_R1_READONLY Registers
            192. 14.2.1.1.1.192 CFG0_CLAIMREG_P2_R2_READONLY Registers
            193. 14.2.1.1.1.193 CFG0_CLAIMREG_P2_R3_READONLY Registers
            194. 14.2.1.1.1.194 CFG0_CLAIMREG_P2_R4_READONLY Registers
            195. 14.2.1.1.1.195 CFG0_CLAIMREG_P2_R5_READONLY Registers
            196. 14.2.1.1.1.196 CFG0_CLAIMREG_P2_R6_READONLY Registers
            197. 14.2.1.1.1.197 CFG0_CLAIMREG_P2_R7_READONLY Registers
            198. 14.2.1.1.1.198 CFG0_CLAIMREG_P2_R8_READONLY Registers
            199. 14.2.1.1.1.199 CFG0_CLAIMREG_P2_R9_READONLY Registers
            200. 14.2.1.1.1.200 CFG0_CLAIMREG_P2_R10_READONLY Registers
            201. 14.2.1.1.1.201 CFG0_CLAIMREG_P2_R11_READONLY Registers
            202. 14.2.1.1.1.202 CFG0_CLAIMREG_P2_R12_READONLY Registers
            203. 14.2.1.1.1.203 CFG0_CLAIMREG_P2_R13_READONLY Registers
            204. 14.2.1.1.1.204 CFG0_CLAIMREG_P2_R14_READONLY Registers
            205. 14.2.1.1.1.205 CFG0_OBSCLK0_CTRL_PROXY Registers
            206. 14.2.1.1.1.206 CFG0_CLKOUT_CTRL_PROXY Registers
            207. 14.2.1.1.1.207 CFG0_ICSSM0_CLKSEL_PROXY Registers
            208. 14.2.1.1.1.208 CFG0_MAIN_PLL0_CLKSEL_PROXY Registers
            209. 14.2.1.1.1.209 CFG0_MAIN_PLL1_CLKSEL_PROXY Registers
            210. 14.2.1.1.1.210 CFG0_MAIN_PLL2_CLKSEL_PROXY Registers
            211. 14.2.1.1.1.211 CFG0_MAIN_PLL8_CLKSEL_PROXY Registers
            212. 14.2.1.1.1.212 CFG0_MAIN_PLL12_CLKSEL_PROXY Registers
            213. 14.2.1.1.1.213 CFG0_MAIN_PLL16_CLKSEL_PROXY Registers
            214. 14.2.1.1.1.214 CFG0_MAIN_PLL17_CLKSEL_PROXY Registers
            215. 14.2.1.1.1.215 CFG0_CPSW_CLKSEL_PROXY Registers
            216. 14.2.1.1.1.216 CFG0_EMMC0_CLKSEL_PROXY Registers
            217. 14.2.1.1.1.217 CFG0_EMMC1_CLKSEL_PROXY Registers
            218. 14.2.1.1.1.218 CFG0_EMMC2_CLKSEL_PROXY Registers
            219. 14.2.1.1.1.219 CFG0_GPMC_CLKSEL_PROXY Registers
            220. 14.2.1.1.1.220 CFG0_TIMER0_CLKSEL_PROXY Registers
            221. 14.2.1.1.1.221 CFG0_TIMER1_CLKSEL_PROXY Registers
            222. 14.2.1.1.1.222 CFG0_TIMER2_CLKSEL_PROXY Registers
            223. 14.2.1.1.1.223 CFG0_TIMER3_CLKSEL_PROXY Registers
            224. 14.2.1.1.1.224 CFG0_TIMER4_CLKSEL_PROXY Registers
            225. 14.2.1.1.1.225 CFG0_TIMER5_CLKSEL_PROXY Registers
            226. 14.2.1.1.1.226 CFG0_TIMER6_CLKSEL_PROXY Registers
            227. 14.2.1.1.1.227 CFG0_TIMER7_CLKSEL_PROXY Registers
            228. 14.2.1.1.1.228 CFG0_SPI0_CLKSEL_PROXY Registers
            229. 14.2.1.1.1.229 CFG0_SPI1_CLKSEL_PROXY Registers
            230. 14.2.1.1.1.230 CFG0_SPI2_CLKSEL_PROXY Registers
            231. 14.2.1.1.1.231 CFG0_USART0_CLK_CTRL_PROXY Registers
            232. 14.2.1.1.1.232 CFG0_USART1_CLK_CTRL_PROXY Registers
            233. 14.2.1.1.1.233 CFG0_USART2_CLK_CTRL_PROXY Registers
            234. 14.2.1.1.1.234 CFG0_USART3_CLK_CTRL_PROXY Registers
            235. 14.2.1.1.1.235 CFG0_USART4_CLK_CTRL_PROXY Registers
            236. 14.2.1.1.1.236 CFG0_USART5_CLK_CTRL_PROXY Registers
            237. 14.2.1.1.1.237 CFG0_USART6_CLK_CTRL_PROXY Registers
            238. 14.2.1.1.1.238 CFG0_USART0_CLKSEL_PROXY Registers
            239. 14.2.1.1.1.239 CFG0_USART1_CLKSEL_PROXY Registers
            240. 14.2.1.1.1.240 CFG0_USART2_CLKSEL_PROXY Registers
            241. 14.2.1.1.1.241 CFG0_USART3_CLKSEL_PROXY Registers
            242. 14.2.1.1.1.242 CFG0_USART4_CLKSEL_PROXY Registers
            243. 14.2.1.1.1.243 CFG0_USART5_CLKSEL_PROXY Registers
            244. 14.2.1.1.1.244 CFG0_USART6_CLKSEL_PROXY Registers
            245. 14.2.1.1.1.245 CFG0_AUDIO_REFCLK0_CTRL_PROXY Registers
            246. 14.2.1.1.1.246 CFG0_AUDIO_REFCLK1_CTRL_PROXY Registers
            247. 14.2.1.1.1.247 CFG0_DPI0_CLK_CTRL_PROXY Registers
            248. 14.2.1.1.1.248 CFG0_DSS_DISPC0_CLKSEL1_PROXY Registers
            249. 14.2.1.1.1.249 CFG0_MCASP0_CLKSEL_PROXY Registers
            250. 14.2.1.1.1.250 CFG0_MCASP1_CLKSEL_PROXY Registers
            251. 14.2.1.1.1.251 CFG0_MCASP2_CLKSEL_PROXY Registers
            252. 14.2.1.1.1.252 CFG0_MCASP0_AHCLKSEL_PROXY Registers
            253. 14.2.1.1.1.253 CFG0_MCASP1_AHCLKSEL_PROXY Registers
            254. 14.2.1.1.1.254 CFG0_MCASP2_AHCLKSEL_PROXY Registers
            255. 14.2.1.1.1.255 CFG0_WWD0_CLKSEL_PROXY Registers
            256. 14.2.1.1.1.256 CFG0_WWD1_CLKSEL_PROXY Registers
            257. 14.2.1.1.1.257 CFG0_WWD2_CLKSEL_PROXY Registers
            258. 14.2.1.1.1.258 CFG0_WWD3_CLKSEL_PROXY Registers
            259. 14.2.1.1.1.259 CFG0_WWD15_CLKSEL_PROXY Registers
            260. 14.2.1.1.1.260 CFG0_MCAN0_CLKSEL_PROXY Registers
            261. 14.2.1.1.1.261 CFG0_OSPI0_CLKSEL_PROXY Registers
            262. 14.2.1.1.1.262 CFG0_OLDI0_DAT0_IO_CTRL_PROXY Registers
            263. 14.2.1.1.1.263 CFG0_OLDI0_DAT1_IO_CTRL_PROXY Registers
            264. 14.2.1.1.1.264 CFG0_OLDI0_DAT2_IO_CTRL_PROXY Registers
            265. 14.2.1.1.1.265 CFG0_OLDI0_DAT3_IO_CTRL_PROXY Registers
            266. 14.2.1.1.1.266 CFG0_OLDI0_CLK_IO_CTRL_PROXY Registers
            267. 14.2.1.1.1.267 CFG0_OLDI1_DAT0_IO_CTRL_PROXY Registers
            268. 14.2.1.1.1.268 CFG0_OLDI1_DAT1_IO_CTRL_PROXY Registers
            269. 14.2.1.1.1.269 CFG0_OLDI1_DAT2_IO_CTRL_PROXY Registers
            270. 14.2.1.1.1.270 CFG0_OLDI1_DAT3_IO_CTRL_PROXY Registers
            271. 14.2.1.1.1.271 CFG0_OLDI1_CLK_IO_CTRL_PROXY Registers
            272. 14.2.1.1.1.272 CFG0_OLDI_PD_CTRL_PROXY Registers
            273. 14.2.1.1.1.273 CFG0_OLDI_LB_CTRL_PROXY Registers
            274. 14.2.1.1.1.274 CFG0_LOCK2_KICK0_PROXY Registers
            275. 14.2.1.1.1.275 CFG0_LOCK2_KICK1_PROXY Registers
            276. 14.2.1.1.1.276 CFG0_CLAIMREG_P2_R0 Registers
            277. 14.2.1.1.1.277 CFG0_CLAIMREG_P2_R1 Registers
            278. 14.2.1.1.1.278 CFG0_CLAIMREG_P2_R2 Registers
            279. 14.2.1.1.1.279 CFG0_CLAIMREG_P2_R3 Registers
            280. 14.2.1.1.1.280 CFG0_CLAIMREG_P2_R4 Registers
            281. 14.2.1.1.1.281 CFG0_CLAIMREG_P2_R5 Registers
            282. 14.2.1.1.1.282 CFG0_CLAIMREG_P2_R6 Registers
            283. 14.2.1.1.1.283 CFG0_CLAIMREG_P2_R7 Registers
            284. 14.2.1.1.1.284 CFG0_CLAIMREG_P2_R8 Registers
            285. 14.2.1.1.1.285 CFG0_CLAIMREG_P2_R9 Registers
            286. 14.2.1.1.1.286 CFG0_CLAIMREG_P2_R10 Registers
            287. 14.2.1.1.1.287 CFG0_CLAIMREG_P2_R11 Registers
            288. 14.2.1.1.1.288 CFG0_CLAIMREG_P2_R12 Registers
            289. 14.2.1.1.1.289 CFG0_CLAIMREG_P2_R13 Registers
            290. 14.2.1.1.1.290 CFG0_CLAIMREG_P2_R14 Registers
            291. 14.2.1.1.1.291 CFG0_MAIN_PLL_TEST_CLKSEL Registers
            292. 14.2.1.1.1.292 CFG0_LOCK4_KICK0 Registers
            293. 14.2.1.1.1.293 CFG0_LOCK4_KICK1 Registers
            294. 14.2.1.1.1.294 CFG0_CLAIMREG_P4_R0_READONLY Registers
            295. 14.2.1.1.1.295 CFG0_CLAIMREG_P4_R1_READONLY Registers
            296. 14.2.1.1.1.296 CFG0_CLAIMREG_P4_R2_READONLY Registers
            297. 14.2.1.1.1.297 CFG0_CLAIMREG_P4_R3_READONLY Registers
            298. 14.2.1.1.1.298 CFG0_CLAIMREG_P4_R4_READONLY Registers
            299. 14.2.1.1.1.299 CFG0_CLAIMREG_P4_R5_READONLY Registers
            300. 14.2.1.1.1.300 CFG0_CLAIMREG_P4_R6_READONLY Registers
            301. 14.2.1.1.1.301 CFG0_CLAIMREG_P4_R7_READONLY Registers
            302. 14.2.1.1.1.302 CFG0_CLAIMREG_P4_R8_READONLY Registers
            303. 14.2.1.1.1.303 CFG0_CLAIMREG_P4_R9_READONLY Registers
            304. 14.2.1.1.1.304 CFG0_CLAIMREG_P4_R10_READONLY Registers
            305. 14.2.1.1.1.305 CFG0_MAIN_PLL_TEST_CLKSEL_PROXY Registers
            306. 14.2.1.1.1.306 CFG0_LOCK4_KICK0_PROXY Registers
            307. 14.2.1.1.1.307 CFG0_LOCK4_KICK1_PROXY Registers
            308. 14.2.1.1.1.308 CFG0_CLAIMREG_P4_R0 Registers
            309. 14.2.1.1.1.309 CFG0_CLAIMREG_P4_R1 Registers
            310. 14.2.1.1.1.310 CFG0_CLAIMREG_P4_R2 Registers
            311. 14.2.1.1.1.311 CFG0_CLAIMREG_P4_R3 Registers
            312. 14.2.1.1.1.312 CFG0_CLAIMREG_P4_R4 Registers
            313. 14.2.1.1.1.313 CFG0_CLAIMREG_P4_R5 Registers
            314. 14.2.1.1.1.314 CFG0_CLAIMREG_P4_R6 Registers
            315. 14.2.1.1.1.315 CFG0_CLAIMREG_P4_R7 Registers
            316. 14.2.1.1.1.316 CFG0_CLAIMREG_P4_R8 Registers
            317. 14.2.1.1.1.317 CFG0_CLAIMREG_P4_R9 Registers
            318. 14.2.1.1.1.318 CFG0_CLAIMREG_P4_R10 Registers
            319. 14.2.1.1.1.319 CFG0_LOCK6_KICK0 Registers
            320. 14.2.1.1.1.320 CFG0_LOCK6_KICK1 Registers
            321. 14.2.1.1.1.321 CFG0_CLAIMREG_P6_R0_READONLY Registers
            322. 14.2.1.1.1.322 CFG0_CLAIMREG_P6_R1_READONLY Registers
            323. 14.2.1.1.1.323 CFG0_CLAIMREG_P6_R2_READONLY Registers
            324. 14.2.1.1.1.324 CFG0_CLAIMREG_P6_R3_READONLY Registers
            325. 14.2.1.1.1.325 CFG0_CLAIMREG_P6_R4_READONLY Registers
            326. 14.2.1.1.1.326 CFG0_CLAIMREG_P6_R5_READONLY Registers
            327. 14.2.1.1.1.327 CFG0_CLAIMREG_P6_R6_READONLY Registers
            328. 14.2.1.1.1.328 CFG0_CLAIMREG_P6_R7_READONLY Registers
            329. 14.2.1.1.1.329 CFG0_CLAIMREG_P6_R8_READONLY Registers
            330. 14.2.1.1.1.330 CFG0_LOCK6_KICK0_PROXY Registers
            331. 14.2.1.1.1.331 CFG0_LOCK6_KICK1_PROXY Registers
            332. 14.2.1.1.1.332 CFG0_CLAIMREG_P6_R0 Registers
            333. 14.2.1.1.1.333 CFG0_CLAIMREG_P6_R1 Registers
            334. 14.2.1.1.1.334 CFG0_CLAIMREG_P6_R2 Registers
            335. 14.2.1.1.1.335 CFG0_CLAIMREG_P6_R3 Registers
            336. 14.2.1.1.1.336 CFG0_CLAIMREG_P6_R4 Registers
            337. 14.2.1.1.1.337 CFG0_CLAIMREG_P6_R5 Registers
            338. 14.2.1.1.1.338 CFG0_CLAIMREG_P6_R6 Registers
            339. 14.2.1.1.1.339 CFG0_CLAIMREG_P6_R7 Registers
            340. 14.2.1.1.1.340 CFG0_CLAIMREG_P6_R8 Registers
            341. 14.2.1.1.1.341 CFG0_IPC_SET0 Registers
            342. 14.2.1.1.1.342 CFG0_IPC_CLR0 Registers
            343. 14.2.1.1.1.343 CFG0_CBA_ERR_STAT Registers
            344. 14.2.1.1.1.344 CFG0_ACCESS_ERR_STAT Registers
            345. 14.2.1.1.1.345 CFG0_IPC_SET0_PROXY Registers
            346. 14.2.1.1.1.346 CFG0_IPC_CLR0_PROXY Registers
            347. 14.2.1.1.1.347 CFG0_CBA_ERR_STAT_PROXY Registers
            348. 14.2.1.1.1.348 CFG0_ACCESS_ERR_STAT_PROXY Registers
            349. 14.2.1.1.1.349 CFG0_MCU_GPIO_CTRL Registers
            350. 14.2.1.1.1.350 CFG0_TEMP_DIODE_TRIM Registers
            351. 14.2.1.1.1.351 CFG0_IO_VOLTAGE_STAT Registers
            352. 14.2.1.1.1.352 CFG0_MCU_TIMER1_CTRL Registers
            353. 14.2.1.1.1.353 CFG0_MCU_TIMER3_CTRL Registers
            354. 14.2.1.1.1.354 CFG0_MCU_I2C0_CTRL Registers
            355. 14.2.1.1.1.355 CFG0_MAIN_MTOG_CTRL Registers
            356. 14.2.1.1.1.356 CFG0_WKUP_MTOG_CTRL Registers
            357. 14.2.1.1.1.357 CFG0_TOG_STAT Registers
            358. 14.2.1.1.1.358 CFG0_MCU_GPIO_CTRL_PROXY Registers
            359. 14.2.1.1.1.359 CFG0_TEMP_DIODE_TRIM_PROXY Registers
            360. 14.2.1.1.1.360 CFG0_IO_VOLTAGE_STAT_PROXY Registers
            361. 14.2.1.1.1.361 CFG0_MCU_TIMER1_CTRL_PROXY Registers
            362. 14.2.1.1.1.362 CFG0_MCU_TIMER3_CTRL_PROXY Registers
            363. 14.2.1.1.1.363 CFG0_MCU_I2C0_CTRL_PROXY Registers
            364. 14.2.1.1.1.364 CFG0_MAIN_MTOG_CTRL_PROXY Registers
            365. 14.2.1.1.1.365 CFG0_WKUP_MTOG_CTRL_PROXY Registers
            366. 14.2.1.1.1.366 CFG0_TOG_STAT_PROXY Registers
            367. 14.2.1.1.1.367 CFG0_MCU_OBSCLK_CTRL Registers
            368. 14.2.1.1.1.368 CFG0_HFOSC0_CTRL Registers
            369. 14.2.1.1.1.369 CFG0_HFOSC0_TRIM Registers
            370. 14.2.1.1.1.370 CFG0_HFOSC0_STAT Registers
            371. 14.2.1.1.1.371 CFG0_RC12M_OSC_TRIM Registers
            372. 14.2.1.1.1.372 CFG0_HFOSC0_CLKOUT_32K_CTRL Registers
            373. 14.2.1.1.1.373 CFG0_LFXOSC_CTRL Registers
            374. 14.2.1.1.1.374 CFG0_LFXOSC_TRIM Registers
            375. 14.2.1.1.1.375 CFG0_MCU_M4FSS_CLKSEL Registers
            376. 14.2.1.1.1.376 CFG0_MCU_M4FSS_SYSTICK Registers
            377. 14.2.1.1.1.377 CFG0_MCU_PLL_CLKSEL Registers
            378. 14.2.1.1.1.378 CFG0_DEVICE_CLKOUT_32K_CTRL Registers
            379. 14.2.1.1.1.379 CFG0_MCU_TIMER0_CLKSEL Registers
            380. 14.2.1.1.1.380 CFG0_MCU_TIMER1_CLKSEL Registers
            381. 14.2.1.1.1.381 CFG0_MCU_TIMER2_CLKSEL Registers
            382. 14.2.1.1.1.382 CFG0_MCU_TIMER3_CLKSEL Registers
            383. 14.2.1.1.1.383 CFG0_MCU_GPIO_CLKSEL Registers
            384. 14.2.1.1.1.384 CFG0_MCU_MCAN0_CLKSEL Registers
            385. 14.2.1.1.1.385 CFG0_MCU_MCAN1_CLKSEL Registers
            386. 14.2.1.1.1.386 CFG0_MCU_SPI0_CLKSEL Registers
            387. 14.2.1.1.1.387 CFG0_MCU_SPI1_CLKSEL Registers
            388. 14.2.1.1.1.388 CFG0_MCU_WWD0_CLKSEL Registers
            389. 14.2.1.1.1.389 CFG0_MCU_OBSCLK_CTRL_PROXY Registers
            390. 14.2.1.1.1.390 CFG0_HFOSC0_CTRL_PROXY Registers
            391. 14.2.1.1.1.391 CFG0_HFOSC0_TRIM_PROXY Registers
            392. 14.2.1.1.1.392 CFG0_HFOSC0_STAT_PROXY Registers
            393. 14.2.1.1.1.393 CFG0_RC12M_OSC_TRIM_PROXY Registers
            394. 14.2.1.1.1.394 CFG0_HFOSC0_CLKOUT_32K_CTRL_PROXY Registers
            395. 14.2.1.1.1.395 CFG0_LFXOSC_CTRL_PROXY Registers
            396. 14.2.1.1.1.396 CFG0_LFXOSC_TRIM_PROXY Registers
            397. 14.2.1.1.1.397 CFG0_MCU_M4FSS_CLKSEL_PROXY Registers
            398. 14.2.1.1.1.398 CFG0_MCU_M4FSS_SYSTICK_PROXY Registers
            399. 14.2.1.1.1.399 CFG0_MCU_PLL_CLKSEL_PROXY Registers
            400. 14.2.1.1.1.400 CFG0_DEVICE_CLKOUT_32K_CTRL_PROXY Registers
            401. 14.2.1.1.1.401 CFG0_MCU_TIMER0_CLKSEL_PROXY Registers
            402. 14.2.1.1.1.402 CFG0_MCU_TIMER1_CLKSEL_PROXY Registers
            403. 14.2.1.1.1.403 CFG0_MCU_TIMER2_CLKSEL_PROXY Registers
            404. 14.2.1.1.1.404 CFG0_MCU_TIMER3_CLKSEL_PROXY Registers
            405. 14.2.1.1.1.405 CFG0_MCU_GPIO_CLKSEL_PROXY Registers
            406. 14.2.1.1.1.406 CFG0_MCU_MCAN0_CLKSEL_PROXY Registers
            407. 14.2.1.1.1.407 CFG0_MCU_MCAN1_CLKSEL_PROXY Registers
            408. 14.2.1.1.1.408 CFG0_MCU_SPI0_CLKSEL_PROXY Registers
            409. 14.2.1.1.1.409 CFG0_MCU_SPI1_CLKSEL_PROXY Registers
            410. 14.2.1.1.1.410 CFG0_MCU_WWD0_CLKSEL_PROXY Registers
            411. 14.2.1.1.1.411 CFG0_MCU_M4FSS0_LBIST_CTRL Registers
            412. 14.2.1.1.1.412 CFG0_MCU_M4FSS0_LBIST_PATCOUNT Registers
            413. 14.2.1.1.1.413 CFG0_MCU_M4FSS0_LBIST_SEED0 Registers
            414. 14.2.1.1.1.414 CFG0_MCU_M4FSS0_LBIST_SEED1 Registers
            415. 14.2.1.1.1.415 CFG0_MCU_M4FSS0_LBIST_SPARE0 Registers
            416. 14.2.1.1.1.416 CFG0_MCU_M4FSS0_LBIST_SPARE1 Registers
            417. 14.2.1.1.1.417 CFG0_MCU_M4FSS0_LBIST_STAT Registers
            418. 14.2.1.1.1.418 CFG0_MCU_M4FSS0_LBIST_MISR Registers
            419. 14.2.1.1.1.419 CFG0_LOCK3_KICK0 Registers
            420. 14.2.1.1.1.420 CFG0_LOCK3_KICK1 Registers
            421. 14.2.1.1.1.421 CFG0_CLAIMREG_P3_R0_READONLY Registers
            422. 14.2.1.1.1.422 CFG0_MCU_M4FSS0_LBIST_CTRL_PROXY Registers
            423. 14.2.1.1.1.423 CFG0_MCU_M4FSS0_LBIST_PATCOUNT_PROXY Registers
            424. 14.2.1.1.1.424 CFG0_MCU_M4FSS0_LBIST_SEED0_PROXY Registers
            425. 14.2.1.1.1.425 CFG0_MCU_M4FSS0_LBIST_SEED1_PROXY Registers
            426. 14.2.1.1.1.426 CFG0_MCU_M4FSS0_LBIST_SPARE0_PROXY Registers
            427. 14.2.1.1.1.427 CFG0_MCU_M4FSS0_LBIST_SPARE1_PROXY Registers
            428. 14.2.1.1.1.428 CFG0_MCU_M4FSS0_LBIST_STAT_PROXY Registers
            429. 14.2.1.1.1.429 CFG0_MCU_M4FSS0_LBIST_MISR_PROXY Registers
            430. 14.2.1.1.1.430 CFG0_LOCK3_KICK0_PROXY Registers
            431. 14.2.1.1.1.431 CFG0_LOCK3_KICK1_PROXY Registers
            432. 14.2.1.1.1.432 CFG0_CLAIMREG_P3_R0 Registers
            433. 14.2.1.1.1.433 CFG0_OLDI_PD_CTRL_TEST_REG Registers
            434. 14.2.1.1.1.434 CFG0_PBIST_EN_TEST_REG Registers
            435. 14.2.1.1.1.435 CFG0_CLAIMREG_P4_R11_READONLY Registers
            436. 14.2.1.1.1.436 CFG0_CLAIMREG_P4_R12_READONLY Registers
            437. 14.2.1.1.1.437 CFG0_CLAIMREG_P4_R13_READONLY Registers
            438. 14.2.1.1.1.438 CFG0_CLAIMREG_P4_R14_READONLY Registers
            439. 14.2.1.1.1.439 CFG0_CLAIMREG_P4_R15_READONLY Registers
            440. 14.2.1.1.1.440 CFG0_CLAIMREG_P4_R16_READONLY Registers
            441. 14.2.1.1.1.441 CFG0_CLAIMREG_P4_R17_READONLY Registers
            442. 14.2.1.1.1.442 CFG0_CLAIMREG_P4_R18_READONLY Registers
            443. 14.2.1.1.1.443 CFG0_CLAIMREG_P4_R19_READONLY Registers
            444. 14.2.1.1.1.444 CFG0_OLDI_PD_CTRL_TEST_REG_PROXY Registers
            445. 14.2.1.1.1.445 CFG0_PBIST_EN_TEST_REG_PROXY Registers
            446. 14.2.1.1.1.446 CFG0_CLAIMREG_P4_R11 Registers
            447. 14.2.1.1.1.447 CFG0_CLAIMREG_P4_R12 Registers
            448. 14.2.1.1.1.448 CFG0_CLAIMREG_P4_R13 Registers
            449. 14.2.1.1.1.449 CFG0_CLAIMREG_P4_R14 Registers
            450. 14.2.1.1.1.450 CFG0_CLAIMREG_P4_R15 Registers
            451. 14.2.1.1.1.451 CFG0_CLAIMREG_P4_R16 Registers
            452. 14.2.1.1.1.452 CFG0_CLAIMREG_P4_R17 Registers
            453. 14.2.1.1.1.453 CFG0_CLAIMREG_P4_R18 Registers
            454. 14.2.1.1.1.454 CFG0_CLAIMREG_P4_R19 Registers
            455. 14.2.1.1.1.455 CFG0_POR_CTRL Registers
            456. 14.2.1.1.1.456 CFG0_POR_STAT Registers
            457. 14.2.1.1.1.457 CFG0_POR_BANDGAP_CTRL Registers
            458. 14.2.1.1.1.458 CFG0_POK_VDDA_MCU_UV_CTRL Registers
            459. 14.2.1.1.1.459 CFG0_POK_VDDA_MCU_OV_CTRL Registers
            460. 14.2.1.1.1.460 CFG0_POK_VDD_CORE_UV_CTRL Registers
            461. 14.2.1.1.1.461 CFG0_POK_VDD_CORE_OV_CTRL Registers
            462. 14.2.1.1.1.462 CFG0_POK_VDDR_CORE_UV_CTRL Registers
            463. 14.2.1.1.1.463 CFG0_POK_VDDR_CORE_OV_CTRL Registers
            464. 14.2.1.1.1.464 CFG0_POK_VMON_CAP_MCU_GENERAL_UV_CTRL Registers
            465. 14.2.1.1.1.465 CFG0_POK_VMON_CAP_MCU_GENERAL_OV_CTRL Registers
            466. 14.2.1.1.1.466 CFG0_POK_VDDSHV_MAIN_1P8_UV_CTRL Registers
            467. 14.2.1.1.1.467 CFG0_POK_VDDSHV_MAIN_1P8_OV_CTRL Registers
            468. 14.2.1.1.1.468 CFG0_POK_VDDSHV_MAIN_3P3_UV_CTRL Registers
            469. 14.2.1.1.1.469 CFG0_POK_VDDSHV_MAIN_3P3_OV_CTRL Registers
            470. 14.2.1.1.1.470 CFG0_POK_VDDS_DDRIO_UV_CTRL Registers
            471. 14.2.1.1.1.471 CFG0_POK_VDDS_DDRIO_OV_CTRL Registers
            472. 14.2.1.1.1.472 CFG0_POK_VDDA_PMIC_IN_CTRL Registers
            473. 14.2.1.1.1.473 CFG0_RST_CTRL Registers
            474. 14.2.1.1.1.474 CFG0_RST_STAT Registers
            475. 14.2.1.1.1.475 CFG0_RST_SRC Registers
            476. 14.2.1.1.1.476 CFG0_RST_MAGIC_WORD Registers
            477. 14.2.1.1.1.477 CFG0_ISO_CTRL Registers
            478. 14.2.1.1.1.478 CFG0_VDD_CORE_GLDTC_CTRL Registers
            479. 14.2.1.1.1.479 CFG0_VDD_CORE_GLDTC_STAT Registers
            480. 14.2.1.1.1.480 CFG0_PRG_PP_0_CTRL Registers
            481. 14.2.1.1.1.481 CFG0_PRG_PP_1_CTRL Registers
            482. 14.2.1.1.1.482 CFG0_CLKGATE_CTRL Registers
            483. 14.2.1.1.1.483 CFG0_LVDS_BANDGAP_CTRL Registers
            484. 14.2.1.1.1.484 CFG0_POR_CTRL_PROXY Registers
            485. 14.2.1.1.1.485 CFG0_POR_STAT_PROXY Registers
            486. 14.2.1.1.1.486 CFG0_POR_BANDGAP_CTRL_PROXY Registers
            487. 14.2.1.1.1.487 CFG0_POK_VDDA_MCU_UV_CTRL_PROXY Registers
            488. 14.2.1.1.1.488 CFG0_POK_VDDA_MCU_OV_CTRL_PROXY Registers
            489. 14.2.1.1.1.489 CFG0_POK_VDD_CORE_UV_CTRL_PROXY Registers
            490. 14.2.1.1.1.490 CFG0_POK_VDD_CORE_OV_CTRL_PROXY Registers
            491. 14.2.1.1.1.491 CFG0_POK_VDDR_CORE_UV_CTRL_PROXY Registers
            492. 14.2.1.1.1.492 CFG0_POK_VDDR_CORE_OV_CTRL_PROXY Registers
            493. 14.2.1.1.1.493 CFG0_POK_VMON_CAP_MCU_GENERAL_UV_CTRL_PROXY Registers
            494. 14.2.1.1.1.494 CFG0_POK_VMON_CAP_MCU_GENERAL_OV_CTRL_PROXY Registers
            495. 14.2.1.1.1.495 CFG0_POK_VDDSHV_MAIN_1P8_UV_CTRL_PROXY Registers
            496. 14.2.1.1.1.496 CFG0_POK_VDDSHV_MAIN_1P8_OV_CTRL_PROXY Registers
            497. 14.2.1.1.1.497 CFG0_POK_VDDSHV_MAIN_3P3_UV_CTRL_PROXY Registers
            498. 14.2.1.1.1.498 CFG0_POK_VDDSHV_MAIN_3P3_OV_CTRL_PROXY Registers
            499. 14.2.1.1.1.499 CFG0_POK_VDDS_DDRIO_UV_CTRL_PROXY Registers
            500. 14.2.1.1.1.500 CFG0_POK_VDDS_DDRIO_OV_CTRL_PROXY Registers
            501. 14.2.1.1.1.501 CFG0_POK_VDDA_PMIC_IN_CTRL_PROXY Registers
            502. 14.2.1.1.1.502 CFG0_RST_CTRL_PROXY Registers
            503. 14.2.1.1.1.503 CFG0_RST_STAT_PROXY Registers
            504. 14.2.1.1.1.504 CFG0_RST_SRC_PROXY Registers
            505. 14.2.1.1.1.505 CFG0_RST_MAGIC_WORD_PROXY Registers
            506. 14.2.1.1.1.506 CFG0_ISO_CTRL_PROXY Registers
            507. 14.2.1.1.1.507 CFG0_VDD_CORE_GLDTC_CTRL_PROXY Registers
            508. 14.2.1.1.1.508 CFG0_VDD_CORE_GLDTC_STAT_PROXY Registers
            509. 14.2.1.1.1.509 CFG0_PRG_PP_0_CTRL_PROXY Registers
            510. 14.2.1.1.1.510 CFG0_PRG_PP_1_CTRL_PROXY Registers
            511. 14.2.1.1.1.511 CFG0_CLKGATE_CTRL_PROXY Registers
            512. 14.2.1.1.1.512 CFG0_LVDS_BANDGAP_CTRL_PROXY Registers
            513. 14.2.1.1.1.513 CFG0_JTAGID Registers
            514. 14.2.1.1.1.514 CFG0_JTAG_USER_ID Registers
            515. 14.2.1.1.1.515 CFG0_MAIN_DEVSTAT Registers
            516. 14.2.1.1.1.516 CFG0_MAIN_BOOTCFG Registers
            517. 14.2.1.1.1.517 CFG0_BOOT_PROGRESS Registers
            518. 14.2.1.1.1.518 CFG0_DEVICE_FEATURE0 Registers
            519. 14.2.1.1.1.519 CFG0_DEVICE_FEATURE1 Registers
            520. 14.2.1.1.1.520 CFG0_DEVICE_FEATURE2 Registers
            521. 14.2.1.1.1.521 CFG0_DEVICE_FEATURE3 Registers
            522. 14.2.1.1.1.522 CFG0_DEVICE_FEATURE6 Registers
            523. 14.2.1.1.1.523 CFG0_MAC_ID0 Registers
            524. 14.2.1.1.1.524 CFG0_MAC_ID1 Registers
            525. 14.2.1.1.1.525 CFG0_USB_DEVICE_ID0 Registers
            526. 14.2.1.1.1.526 CFG0_USB_DEVICE_ID1 Registers
            527. 14.2.1.1.1.527 CFG0_GP_SW0 Registers
            528. 14.2.1.1.1.528 CFG0_GP_SW1 Registers
            529. 14.2.1.1.1.529 CFG0_GP_SW2 Registers
            530. 14.2.1.1.1.530 CFG0_GP_SW3 Registers
            531. 14.2.1.1.1.531 CFG0_JTAGID_PROXY Registers
            532. 14.2.1.1.1.532 CFG0_JTAG_USER_ID_PROXY Registers
            533. 14.2.1.1.1.533 CFG0_MAIN_DEVSTAT_PROXY Registers
            534. 14.2.1.1.1.534 CFG0_MAIN_BOOTCFG_PROXY Registers
            535. 14.2.1.1.1.535 CFG0_BOOT_PROGRESS_PROXY Registers
            536. 14.2.1.1.1.536 CFG0_DEVICE_FEATURE0_PROXY Registers
            537. 14.2.1.1.1.537 CFG0_DEVICE_FEATURE1_PROXY Registers
            538. 14.2.1.1.1.538 CFG0_DEVICE_FEATURE2_PROXY Registers
            539. 14.2.1.1.1.539 CFG0_DEVICE_FEATURE3_PROXY Registers
            540. 14.2.1.1.1.540 CFG0_DEVICE_FEATURE6_PROXY Registers
            541. 14.2.1.1.1.541 CFG0_MAC_ID0_PROXY Registers
            542. 14.2.1.1.1.542 CFG0_MAC_ID1_PROXY Registers
            543. 14.2.1.1.1.543 CFG0_USB_DEVICE_ID0_PROXY Registers
            544. 14.2.1.1.1.544 CFG0_USB_DEVICE_ID1_PROXY Registers
            545. 14.2.1.1.1.545 CFG0_GP_SW0_PROXY Registers
            546. 14.2.1.1.1.546 CFG0_GP_SW1_PROXY Registers
            547. 14.2.1.1.1.547 CFG0_GP_SW2_PROXY Registers
            548. 14.2.1.1.1.548 CFG0_GP_SW3_PROXY Registers
            549. 14.2.1.1.1.549 CFG0_USB0_PHY_CTRL Registers
            550. 14.2.1.1.1.550 CFG0_USB1_PHY_CTRL Registers
            551. 14.2.1.1.1.551 CFG0_SDIO0_CTRL Registers
            552. 14.2.1.1.1.552 CFG0_SDIO1_CTRL Registers
            553. 14.2.1.1.1.553 CFG0_SDIO2_CTRL Registers
            554. 14.2.1.1.1.554 CFG0_WKUP_TIMER1_CTRL Registers
            555. 14.2.1.1.1.555 CFG0_WKUP_I2C0_CTRL Registers
            556. 14.2.1.1.1.556 CFG0_USB0_PHY_CTRL_PROXY Registers
            557. 14.2.1.1.1.557 CFG0_USB1_PHY_CTRL_PROXY Registers
            558. 14.2.1.1.1.558 CFG0_SDIO0_CTRL_PROXY Registers
            559. 14.2.1.1.1.559 CFG0_SDIO1_CTRL_PROXY Registers
            560. 14.2.1.1.1.560 CFG0_SDIO2_CTRL_PROXY Registers
            561. 14.2.1.1.1.561 CFG0_WKUP_TIMER1_CTRL_PROXY Registers
            562. 14.2.1.1.1.562 CFG0_WKUP_I2C0_CTRL_PROXY Registers
            563. 14.2.1.1.1.563 CFG0_WKUP_CLKSEL Registers
            564. 14.2.1.1.1.564 CFG0_WKUP_GTC_CLKSEL Registers
            565. 14.2.1.1.1.565 CFG0_EFUSE_CLKSEL Registers
            566. 14.2.1.1.1.566 CFG0_DDR16SS_PMCTRL Registers
            567. 14.2.1.1.1.567 CFG0_USB0_CLKSEL Registers
            568. 14.2.1.1.1.568 CFG0_USB1_CLKSEL Registers
            569. 14.2.1.1.1.569 CFG0_WKUP_TIMER0_CLKSEL Registers
            570. 14.2.1.1.1.570 CFG0_WKUP_TIMER1_CLKSEL Registers
            571. 14.2.1.1.1.571 CFG0_WKUP_WWD0_CTRL Registers
            572. 14.2.1.1.1.572 CFG0_WKUP_WWD0_CLKSEL Registers
            573. 14.2.1.1.1.573 CFG0_WKUP_RTC_CLKSEL Registers
            574. 14.2.1.1.1.574 CFG0_WKUP_CLKSEL_PROXY Registers
            575. 14.2.1.1.1.575 CFG0_WKUP_GTC_CLKSEL_PROXY Registers
            576. 14.2.1.1.1.576 CFG0_EFUSE_CLKSEL_PROXY Registers
            577. 14.2.1.1.1.577 CFG0_DDR16SS_PMCTRL_PROXY Registers
            578. 14.2.1.1.1.578 CFG0_USB0_CLKSEL_PROXY Registers
            579. 14.2.1.1.1.579 CFG0_USB1_CLKSEL_PROXY Registers
            580. 14.2.1.1.1.580 CFG0_WKUP_TIMER0_CLKSEL_PROXY Registers
            581. 14.2.1.1.1.581 CFG0_WKUP_TIMER1_CLKSEL_PROXY Registers
            582. 14.2.1.1.1.582 CFG0_WKUP_WWD0_CTRL_PROXY Registers
            583. 14.2.1.1.1.583 CFG0_WKUP_WWD0_CLKSEL_PROXY Registers
            584. 14.2.1.1.1.584 CFG0_WKUP_RTC_CLKSEL_PROXY Registers
            585. 14.2.1.1.1.585 CFG0_FUSE_CRC_STAT Registers
            586. 14.2.1.1.1.586 CFG0_CHAIN1_CRC_CALC Registers
            587. 14.2.1.1.1.587 CFG0_CHAIN2_CRC_CALC Registers
            588. 14.2.1.1.1.588 CFG0_CHAIN1_CRC_CALC_RO Registers
            589. 14.2.1.1.1.589 CFG0_CHAIN2_CRC_CALC_RO Registers
            590. 14.2.1.1.1.590 CFG0_PBIST_EN Registers
            591. 14.2.1.1.1.591 CFG0_CLAIMREG_P3_R1_READONLY Registers
            592. 14.2.1.1.1.592 CFG0_CLAIMREG_P3_R2_READONLY Registers
            593. 14.2.1.1.1.593 CFG0_CLAIMREG_P3_R3_READONLY Registers
            594. 14.2.1.1.1.594 CFG0_CLAIMREG_P3_R4_READONLY Registers
            595. 14.2.1.1.1.595 CFG0_CLAIMREG_P3_R5_READONLY Registers
            596. 14.2.1.1.1.596 CFG0_CLAIMREG_P3_R6_READONLY Registers
            597. 14.2.1.1.1.597 CFG0_CLAIMREG_P3_R7_READONLY Registers
            598. 14.2.1.1.1.598 CFG0_CLAIMREG_P3_R8_READONLY Registers
            599. 14.2.1.1.1.599 CFG0_FUSE_CRC_STAT_PROXY Registers
            600. 14.2.1.1.1.600 CFG0_CHAIN1_CRC_CALC_PROXY Registers
            601. 14.2.1.1.1.601 CFG0_CHAIN2_CRC_CALC_PROXY Registers
            602. 14.2.1.1.1.602 CFG0_CHAIN1_CRC_CALC_RO_PROXY Registers
            603. 14.2.1.1.1.603 CFG0_CHAIN2_CRC_CALC_RO_PROXY Registers
            604. 14.2.1.1.1.604 CFG0_PBIST_EN_PROXY Registers
            605. 14.2.1.1.1.605 CFG0_CLAIMREG_P3_R1 Registers
            606. 14.2.1.1.1.606 CFG0_CLAIMREG_P3_R2 Registers
            607. 14.2.1.1.1.607 CFG0_CLAIMREG_P3_R3 Registers
            608. 14.2.1.1.1.608 CFG0_CLAIMREG_P3_R4 Registers
            609. 14.2.1.1.1.609 CFG0_CLAIMREG_P3_R5 Registers
            610. 14.2.1.1.1.610 CFG0_CLAIMREG_P3_R6 Registers
            611. 14.2.1.1.1.611 CFG0_CLAIMREG_P3_R7 Registers
            612. 14.2.1.1.1.612 CFG0_CLAIMREG_P3_R8 Registers
            613. 14.2.1.1.1.613 CFG0_DV_REG32 Registers
            614. 14.2.1.1.1.614 CFG0_DV_REG33 Registers
            615. 14.2.1.1.1.615 CFG0_DV_REG32_PROXY Registers
            616. 14.2.1.1.1.616 CFG0_DV_REG33_PROXY Registers
            617. 14.2.1.1.1.617 CFG0_CHNG_DDR4_FSP_REQ Registers
            618. 14.2.1.1.1.618 CFG0_CHNG_DDR4_FSP_ACK Registers
            619. 14.2.1.1.1.619 CFG0_DDR4_FSP_CLKCHNG_REQ Registers
            620. 14.2.1.1.1.620 CFG0_DDR4_FSP_CLKCHNG_ACK Registers
            621. 14.2.1.1.1.621 CFG0_LOCK5_KICK0 Registers
            622. 14.2.1.1.1.622 CFG0_LOCK5_KICK1 Registers
            623. 14.2.1.1.1.623 CFG0_CLAIMREG_P5_R0_READONLY Registers
            624. 14.2.1.1.1.624 CFG0_CLAIMREG_P5_R1_READONLY Registers
            625. 14.2.1.1.1.625 CFG0_CHNG_DDR4_FSP_REQ_PROXY Registers
            626. 14.2.1.1.1.626 CFG0_CHNG_DDR4_FSP_ACK_PROXY Registers
            627. 14.2.1.1.1.627 CFG0_DDR4_FSP_CLKCHNG_REQ_PROXY Registers
            628. 14.2.1.1.1.628 CFG0_DDR4_FSP_CLKCHNG_ACK_PROXY Registers
            629. 14.2.1.1.1.629 CFG0_LOCK5_KICK0_PROXY Registers
            630. 14.2.1.1.1.630 CFG0_LOCK5_KICK1_PROXY Registers
            631. 14.2.1.1.1.631 CFG0_CLAIMREG_P5_R0 Registers
            632. 14.2.1.1.1.632 CFG0_CLAIMREG_P5_R1 Registers
            633. 14.2.1.1.1.633 CFG0_FW_CTRL_OUT0 Registers
            634. 14.2.1.1.1.634 CFG0_FW_CTRL_OUT0_SET Registers
            635. 14.2.1.1.1.635 CFG0_FW_CTRL_OUT0_CLR Registers
            636. 14.2.1.1.1.636 CFG0_FW_STS_IN0 Registers
            637. 14.2.1.1.1.637 CFG0_FW_CTRL_OUT1 Registers
            638. 14.2.1.1.1.638 CFG0_FW_CTRL_OUT1_SET Registers
            639. 14.2.1.1.1.639 CFG0_FW_CTRL_OUT1_CLR Registers
            640. 14.2.1.1.1.640 CFG0_FW_STS_IN1 Registers
            641. 14.2.1.1.1.641 CFG0_PMCTRL_SYS Registers
            642. 14.2.1.1.1.642 CFG0_PMCTRL_IO_0 Registers
            643. 14.2.1.1.1.643 CFG0_PMCTRL_IO_1 Registers
            644. 14.2.1.1.1.644 CFG0_PMCTRL_MOSC Registers
            645. 14.2.1.1.1.645 CFG0_PM_MISC_STATUS Registers
            646. 14.2.1.1.1.646 CFG0_PMCTRL_IO_GLB Registers
            647. 14.2.1.1.1.647 CFG0_PM_PERMISSION Registers
            648. 14.2.1.1.1.648 CFG0_DEEPSLEEP_CTRL Registers
            649. 14.2.1.1.1.649 CFG0_WKUP0_EN Registers
            650. 14.2.1.1.1.650 CFG0_CANUART_WAKE_CTRL Registers
            651. 14.2.1.1.1.651 CFG0_CANUART_WAKE_STAT0 Registers
            652. 14.2.1.1.1.652 CFG0_CANUART_WAKE_STAT1 Registers
            653. 14.2.1.1.1.653 CFG0_WFI_STATUS Registers
            654. 14.2.1.1.1.654 CFG0_DS_MAGIC_WORD Registers
            655. 14.2.1.1.1.655 CFG0_DS_MAIN Registers
            656. 14.2.1.1.1.656 CFG0_DS_DM_RESET Registers
            657. 14.2.1.1.1.657 CFG0_DS_DDR0_RESET Registers
            658. 14.2.1.1.1.658 CFG0_DS_USB0_RESET Registers
            659. 14.2.1.1.1.659 CFG0_DS_USB1_RESET Registers
            660. 14.2.1.1.1.660 CFG0_DM_CLKSTOP_EN Registers
            661. 14.2.1.1.1.661 CFG0_DM_CLKSTOP_ACK Registers
            662. 14.2.1.1.1.662 CFG0_DM_GRP_CLKSTOP_REQ Registers
            663. 14.2.1.1.1.663 CFG0_DM_GRP_CLKSTOP_ACK Registers
            664. 14.2.1.1.1.664 CFG0_DEVICE_TYPE Registers
            665. 14.2.1.1.1.665 CFG0_CLAIMREG_P6_R9_READONLY Registers
            666. 14.2.1.1.1.666 CFG0_CLAIMREG_P6_R10_READONLY Registers
            667. 14.2.1.1.1.667 CFG0_FW_CTRL_OUT0_PROXY Registers
            668. 14.2.1.1.1.668 CFG0_FW_CTRL_OUT0_SET_PROXY Registers
            669. 14.2.1.1.1.669 CFG0_FW_CTRL_OUT0_CLR_PROXY Registers
            670. 14.2.1.1.1.670 CFG0_FW_STS_IN0_PROXY Registers
            671. 14.2.1.1.1.671 CFG0_FW_CTRL_OUT1_PROXY Registers
            672. 14.2.1.1.1.672 CFG0_FW_CTRL_OUT1_SET_PROXY Registers
            673. 14.2.1.1.1.673 CFG0_FW_CTRL_OUT1_CLR_PROXY Registers
            674. 14.2.1.1.1.674 CFG0_FW_STS_IN1_PROXY Registers
            675. 14.2.1.1.1.675 CFG0_PMCTRL_SYS_PROXY Registers
            676. 14.2.1.1.1.676 CFG0_PMCTRL_IO_0_PROXY Registers
            677. 14.2.1.1.1.677 CFG0_PMCTRL_IO_1_PROXY Registers
            678. 14.2.1.1.1.678 CFG0_PMCTRL_MOSC_PROXY Registers
            679. 14.2.1.1.1.679 CFG0_PM_MISC_STATUS_PROXY Registers
            680. 14.2.1.1.1.680 CFG0_PMCTRL_IO_GLB_PROXY Registers
            681. 14.2.1.1.1.681 CFG0_PM_PERMISSION_PROXY Registers
            682. 14.2.1.1.1.682 CFG0_DEEPSLEEP_CTRL_PROXY Registers
            683. 14.2.1.1.1.683 CFG0_WKUP0_EN_PROXY Registers
            684. 14.2.1.1.1.684 CFG0_CANUART_WAKE_CTRL_PROXY Registers
            685. 14.2.1.1.1.685 CFG0_CANUART_WAKE_STAT0_PROXY Registers
            686. 14.2.1.1.1.686 CFG0_CANUART_WAKE_STAT1_PROXY Registers
            687. 14.2.1.1.1.687 CFG0_WFI_STATUS_PROXY Registers
            688. 14.2.1.1.1.688 CFG0_DS_MAGIC_WORD_PROXY Registers
            689. 14.2.1.1.1.689 CFG0_DS_MAIN_PROXY Registers
            690. 14.2.1.1.1.690 CFG0_DS_DM_RESET_PROXY Registers
            691. 14.2.1.1.1.691 CFG0_DS_DDR0_RESET_PROXY Registers
            692. 14.2.1.1.1.692 CFG0_DS_USB0_RESET_PROXY Registers
            693. 14.2.1.1.1.693 CFG0_DS_USB1_RESET_PROXY Registers
            694. 14.2.1.1.1.694 CFG0_DM_CLKSTOP_EN_PROXY Registers
            695. 14.2.1.1.1.695 CFG0_DM_CLKSTOP_ACK_PROXY Registers
            696. 14.2.1.1.1.696 CFG0_DM_GRP_CLKSTOP_REQ_PROXY Registers
            697. 14.2.1.1.1.697 CFG0_DM_GRP_CLKSTOP_ACK_PROXY Registers
            698. 14.2.1.1.1.698 CFG0_DEVICE_TYPE_PROXY Registers
            699. 14.2.1.1.1.699 CFG0_CLAIMREG_P6_R9 Registers
            700. 14.2.1.1.1.700 CFG0_CLAIMREG_P6_R10 Registers
            701. 14.2.1.1.1.701 CFG0_BACKUP_REG_N Registers
            702. 14.2.1.1.1.702 CFG0_LOCK7_KICK0 Registers
            703. 14.2.1.1.1.703 CFG0_LOCK7_KICK1 Registers
            704. 14.2.1.1.1.704 CFG0_CLAIMREG_P7_R0_READONLY Registers
            705. 14.2.1.1.1.705 CFG0_CLAIMREG_P7_R1_READONLY Registers
            706. 14.2.1.1.1.706 CFG0_CLAIMREG_P7_R2_READONLY Registers
            707. 14.2.1.1.1.707 CFG0_BACKUP_REG_PROXY_N Registers
            708. 14.2.1.1.1.708 CFG0_LOCK7_KICK0_PROXY Registers
            709. 14.2.1.1.1.709 CFG0_LOCK7_KICK1_PROXY Registers
            710. 14.2.1.1.1.710 CFG0_CLAIMREG_P7_R0 Registers
            711. 14.2.1.1.1.711 CFG0_CLAIMREG_P7_R1 Registers
            712. 14.2.1.1.1.712 CFG0_CLAIMREG_P7_R2 Registers
            713. 14.2.1.1.1.713 Access Table
          2. 14.2.1.1.2 MCU_CTRL_MMR Registers
            1. 14.2.1.1.2.1   CFG0_MCU_CTRL_MMR_PID Registers
            2. 14.2.1.1.2.2   CFG0_MCU_CTRL_MMR_MMR_CFG1 Registers
            3. 14.2.1.1.2.3   CFG0_MCU_CTRL_MMR_IPC_SET0 Registers
            4. 14.2.1.1.2.4   CFG0_MCU_CTRL_MMR_IPC_CLR0 Registers
            5. 14.2.1.1.2.5   CFG0_MCU_CTRL_MMR_CBA_ERR_STAT Registers
            6. 14.2.1.1.2.6   CFG0_MCU_CTRL_MMR_ACCESS_ERR_STAT Registers
            7. 14.2.1.1.2.7   CFG0_MCU_CTRL_MMR_LOCK0_KICK0 Registers
            8. 14.2.1.1.2.8   CFG0_MCU_CTRL_MMR_LOCK0_KICK1 Registers
            9. 14.2.1.1.2.9   CFG0_MCU_CTRL_MMR_INTR_RAW_STATUS Registers
            10. 14.2.1.1.2.10  CFG0_MCU_CTRL_MMR_INTR_ENABLED_STATUS_CLEAR Registers
            11. 14.2.1.1.2.11  CFG0_MCU_CTRL_MMR_INTR_ENABLE Registers
            12. 14.2.1.1.2.12  CFG0_MCU_CTRL_MMR_INTR_ENABLE_CLEAR Registers
            13. 14.2.1.1.2.13  CFG0_MCU_CTRL_MMR_EOI Registers
            14. 14.2.1.1.2.14  CFG0_MCU_CTRL_MMR_FAULT_ADDRESS Registers
            15. 14.2.1.1.2.15  CFG0_MCU_CTRL_MMR_FAULT_TYPE_STATUS Registers
            16. 14.2.1.1.2.16  CFG0_MCU_CTRL_MMR_FAULT_ATTR_STATUS Registers
            17. 14.2.1.1.2.17  CFG0_MCU_CTRL_MMR_FAULT_CLEAR Registers
            18. 14.2.1.1.2.18  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R0_READONLY Registers
            19. 14.2.1.1.2.19  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R1_READONLY Registers
            20. 14.2.1.1.2.20  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R2_READONLY Registers
            21. 14.2.1.1.2.21  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R3_READONLY Registers
            22. 14.2.1.1.2.22  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R4_READONLY Registers
            23. 14.2.1.1.2.23  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R5_READONLY Registers
            24. 14.2.1.1.2.24  CFG0_MCU_CTRL_MMR_PID_PROXY Registers
            25. 14.2.1.1.2.25  CFG0_MCU_CTRL_MMR_MMR_CFG1_PROXY Registers
            26. 14.2.1.1.2.26  CFG0_MCU_CTRL_MMR_IPC_SET0_PROXY Registers
            27. 14.2.1.1.2.27  CFG0_MCU_CTRL_MMR_IPC_CLR0_PROXY Registers
            28. 14.2.1.1.2.28  CFG0_MCU_CTRL_MMR_CBA_ERR_STAT_PROXY Registers
            29. 14.2.1.1.2.29  CFG0_MCU_CTRL_MMR_ACCESS_ERR_STAT_PROXY Registers
            30. 14.2.1.1.2.30  CFG0_MCU_CTRL_MMR_LOCK0_KICK0_PROXY Registers
            31. 14.2.1.1.2.31  CFG0_MCU_CTRL_MMR_LOCK0_KICK1_PROXY Registers
            32. 14.2.1.1.2.32  CFG0_MCU_CTRL_MMR_INTR_RAW_STATUS_PROXY Registers
            33. 14.2.1.1.2.33  CFG0_MCU_CTRL_MMR_INTR_ENABLED_STATUS_CLEAR_PROXY Registers
            34. 14.2.1.1.2.34  CFG0_MCU_CTRL_MMR_INTR_ENABLE_PROXY Registers
            35. 14.2.1.1.2.35  CFG0_MCU_CTRL_MMR_INTR_ENABLE_CLEAR_PROXY Registers
            36. 14.2.1.1.2.36  CFG0_MCU_CTRL_MMR_EOI_PROXY Registers
            37. 14.2.1.1.2.37  CFG0_MCU_CTRL_MMR_FAULT_ADDRESS_PROXY Registers
            38. 14.2.1.1.2.38  CFG0_MCU_CTRL_MMR_FAULT_TYPE_STATUS_PROXY Registers
            39. 14.2.1.1.2.39  CFG0_MCU_CTRL_MMR_FAULT_ATTR_STATUS_PROXY Registers
            40. 14.2.1.1.2.40  CFG0_MCU_CTRL_MMR_FAULT_CLEAR_PROXY Registers
            41. 14.2.1.1.2.41  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R0 Registers
            42. 14.2.1.1.2.42  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R1 Registers
            43. 14.2.1.1.2.43  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R2 Registers
            44. 14.2.1.1.2.44  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R3 Registers
            45. 14.2.1.1.2.45  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R4 Registers
            46. 14.2.1.1.2.46  CFG0_MCU_CTRL_MMR_CLAIMREG_P0_R5 Registers
            47. 14.2.1.1.2.47  CFG0_MCU_CTRL_MMR_MCU_GPIO_CTRL Registers
            48. 14.2.1.1.2.48  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG1 Registers
            49. 14.2.1.1.2.49  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG2 Registers
            50. 14.2.1.1.2.50  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG3 Registers
            51. 14.2.1.1.2.51  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG4 Registers
            52. 14.2.1.1.2.52  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG5 Registers
            53. 14.2.1.1.2.53  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG6 Registers
            54. 14.2.1.1.2.54  CFG0_MCU_CTRL_MMR_TEMP_DIODE_TRIM Registers
            55. 14.2.1.1.2.55  CFG0_MCU_CTRL_MMR_IO_VOLTAGE_STAT Registers
            56. 14.2.1.1.2.56  CFG0_MCU_CTRL_MMR_MCU_TIMER1_CTRL Registers
            57. 14.2.1.1.2.57  CFG0_MCU_CTRL_MMR_MCU_TIMER3_CTRL Registers
            58. 14.2.1.1.2.58  CFG0_MCU_CTRL_MMR_MCU_I2C0_CTRL Registers
            59. 14.2.1.1.2.59  CFG0_MCU_CTRL_MMR_MAIN_MTOG_CTRL Registers
            60. 14.2.1.1.2.60  CFG0_MCU_CTRL_MMR_WKUP_MTOG_CTRL Registers
            61. 14.2.1.1.2.61  CFG0_MCU_CTRL_MMR_TOG_STAT Registers
            62. 14.2.1.1.2.62  CFG0_MCU_CTRL_MMR_LOCK1_KICK0 Registers
            63. 14.2.1.1.2.63  CFG0_MCU_CTRL_MMR_LOCK1_KICK1 Registers
            64. 14.2.1.1.2.64  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R0_READONLY Registers
            65. 14.2.1.1.2.65  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R1_READONLY Registers
            66. 14.2.1.1.2.66  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R2_READONLY Registers
            67. 14.2.1.1.2.67  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R3_READONLY Registers
            68. 14.2.1.1.2.68  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R4_READONLY Registers
            69. 14.2.1.1.2.69  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R5_READONLY Registers
            70. 14.2.1.1.2.70  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R6_READONLY Registers
            71. 14.2.1.1.2.71  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R7_READONLY Registers
            72. 14.2.1.1.2.72  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R8_READONLY Registers
            73. 14.2.1.1.2.73  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R9_READONLY Registers
            74. 14.2.1.1.2.74  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R10_READONLY Registers
            75. 14.2.1.1.2.75  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R11_READONLY Registers
            76. 14.2.1.1.2.76  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R12_READONLY Registers
            77. 14.2.1.1.2.77  CFG0_MCU_CTRL_MMR_MCU_GPIO_CTRL_PROXY Registers
            78. 14.2.1.1.2.78  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG1_PROXY Registers
            79. 14.2.1.1.2.79  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG2_PROXY Registers
            80. 14.2.1.1.2.80  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG3_PROXY Registers
            81. 14.2.1.1.2.81  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG4_PROXY Registers
            82. 14.2.1.1.2.82  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG5_PROXY Registers
            83. 14.2.1.1.2.83  CFG0_MCU_CTRL_MMR_DBOUNCE_CFG6_PROXY Registers
            84. 14.2.1.1.2.84  CFG0_MCU_CTRL_MMR_TEMP_DIODE_TRIM_PROXY Registers
            85. 14.2.1.1.2.85  CFG0_MCU_CTRL_MMR_IO_VOLTAGE_STAT_PROXY Registers
            86. 14.2.1.1.2.86  CFG0_MCU_CTRL_MMR_MCU_TIMER1_CTRL_PROXY Registers
            87. 14.2.1.1.2.87  CFG0_MCU_CTRL_MMR_MCU_TIMER3_CTRL_PROXY Registers
            88. 14.2.1.1.2.88  CFG0_MCU_CTRL_MMR_MCU_I2C0_CTRL_PROXY Registers
            89. 14.2.1.1.2.89  CFG0_MCU_CTRL_MMR_MAIN_MTOG_CTRL_PROXY Registers
            90. 14.2.1.1.2.90  CFG0_MCU_CTRL_MMR_WKUP_MTOG_CTRL_PROXY Registers
            91. 14.2.1.1.2.91  CFG0_MCU_CTRL_MMR_TOG_STAT_PROXY Registers
            92. 14.2.1.1.2.92  CFG0_MCU_CTRL_MMR_LOCK1_KICK0_PROXY Registers
            93. 14.2.1.1.2.93  CFG0_MCU_CTRL_MMR_LOCK1_KICK1_PROXY Registers
            94. 14.2.1.1.2.94  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R0 Registers
            95. 14.2.1.1.2.95  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R1 Registers
            96. 14.2.1.1.2.96  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R2 Registers
            97. 14.2.1.1.2.97  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R3 Registers
            98. 14.2.1.1.2.98  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R4 Registers
            99. 14.2.1.1.2.99  CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R5 Registers
            100. 14.2.1.1.2.100 CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R6 Registers
            101. 14.2.1.1.2.101 CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R7 Registers
            102. 14.2.1.1.2.102 CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R8 Registers
            103. 14.2.1.1.2.103 CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R9 Registers
            104. 14.2.1.1.2.104 CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R10 Registers
            105. 14.2.1.1.2.105 CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R11 Registers
            106. 14.2.1.1.2.106 CFG0_MCU_CTRL_MMR_CLAIMREG_P1_R12 Registers
            107. 14.2.1.1.2.107 CFG0_MCU_CTRL_MMR_MCU_OBSCLK_CTRL Registers
            108. 14.2.1.1.2.108 CFG0_MCU_CTRL_MMR_HFOSC0_CTRL Registers
            109. 14.2.1.1.2.109 CFG0_MCU_CTRL_MMR_HFOSC0_TRIM Registers
            110. 14.2.1.1.2.110 CFG0_MCU_CTRL_MMR_HFOSC0_STAT Registers
            111. 14.2.1.1.2.111 CFG0_MCU_CTRL_MMR_RC12M_OSC_TRIM Registers
            112. 14.2.1.1.2.112 CFG0_MCU_CTRL_MMR_HFOSC0_CLKOUT_32K_CTRL Registers
            113. 14.2.1.1.2.113 CFG0_MCU_CTRL_MMR_LFXOSC_CTRL Registers
            114. 14.2.1.1.2.114 CFG0_MCU_CTRL_MMR_LFXOSC_TRIM Registers
            115. 14.2.1.1.2.115 CFG0_MCU_CTRL_MMR_MCU_M4FSS_CLKSEL Registers
            116. 14.2.1.1.2.116 CFG0_MCU_CTRL_MMR_MCU_M4FSS_SYSTICK Registers
            117. 14.2.1.1.2.117 CFG0_MCU_CTRL_MMR_MCU_PLL_CLKSEL Registers
            118. 14.2.1.1.2.118 CFG0_MCU_CTRL_MMR_DEVICE_CLKOUT_32K_CTRL Registers
            119. 14.2.1.1.2.119 CFG0_MCU_CTRL_MMR_MCU_TIMER0_CLKSEL Registers
            120. 14.2.1.1.2.120 CFG0_MCU_CTRL_MMR_MCU_TIMER1_CLKSEL Registers
            121. 14.2.1.1.2.121 CFG0_MCU_CTRL_MMR_MCU_TIMER2_CLKSEL Registers
            122. 14.2.1.1.2.122 CFG0_MCU_CTRL_MMR_MCU_TIMER3_CLKSEL Registers
            123. 14.2.1.1.2.123 CFG0_MCU_CTRL_MMR_MCU_GPIO_CLKSEL Registers
            124. 14.2.1.1.2.124 CFG0_MCU_CTRL_MMR_MCU_MCAN0_CLKSEL Registers
            125. 14.2.1.1.2.125 CFG0_MCU_CTRL_MMR_MCU_MCAN1_CLKSEL Registers
            126. 14.2.1.1.2.126 CFG0_MCU_CTRL_MMR_MCU_SPI0_CLKSEL Registers
            127. 14.2.1.1.2.127 CFG0_MCU_CTRL_MMR_MCU_SPI1_CLKSEL Registers
            128. 14.2.1.1.2.128 CFG0_MCU_CTRL_MMR_MCU_WWD0_CLKSEL Registers
            129. 14.2.1.1.2.129 CFG0_MCU_CTRL_MMR_LOCK2_KICK0 Registers
            130. 14.2.1.1.2.130 CFG0_MCU_CTRL_MMR_LOCK2_KICK1 Registers
            131. 14.2.1.1.2.131 CFG0_MCU_CTRL_MMR_CLAIMREG_P2_R0_READONLY Registers
            132. 14.2.1.1.2.132 CFG0_MCU_CTRL_MMR_CLAIMREG_P2_R1_READONLY Registers
            133. 14.2.1.1.2.133 CFG0_MCU_CTRL_MMR_MCU_OBSCLK_CTRL_PROXY Registers
            134. 14.2.1.1.2.134 CFG0_MCU_CTRL_MMR_HFOSC0_CTRL_PROXY Registers
            135. 14.2.1.1.2.135 CFG0_MCU_CTRL_MMR_HFOSC0_TRIM_PROXY Registers
            136. 14.2.1.1.2.136 CFG0_MCU_CTRL_MMR_HFOSC0_STAT_PROXY Registers
            137. 14.2.1.1.2.137 CFG0_MCU_CTRL_MMR_RC12M_OSC_TRIM_PROXY Registers
            138. 14.2.1.1.2.138 CFG0_MCU_CTRL_MMR_HFOSC0_CLKOUT_32K_CTRL_PROXY Registers
            139. 14.2.1.1.2.139 CFG0_MCU_CTRL_MMR_LFXOSC_CTRL_PROXY Registers
            140. 14.2.1.1.2.140 CFG0_MCU_CTRL_MMR_LFXOSC_TRIM_PROXY Registers
            141. 14.2.1.1.2.141 CFG0_MCU_CTRL_MMR_MCU_M4FSS_CLKSEL_PROXY Registers
            142. 14.2.1.1.2.142 CFG0_MCU_CTRL_MMR_MCU_M4FSS_SYSTICK_PROXY Registers
            143. 14.2.1.1.2.143 CFG0_MCU_CTRL_MMR_MCU_PLL_CLKSEL_PROXY Registers
            144. 14.2.1.1.2.144 CFG0_MCU_CTRL_MMR_DEVICE_CLKOUT_32K_CTRL_PROXY Registers
            145. 14.2.1.1.2.145 CFG0_MCU_CTRL_MMR_MCU_TIMER0_CLKSEL_PROXY Registers
            146. 14.2.1.1.2.146 CFG0_MCU_CTRL_MMR_MCU_TIMER1_CLKSEL_PROXY Registers
            147. 14.2.1.1.2.147 CFG0_MCU_CTRL_MMR_MCU_TIMER2_CLKSEL_PROXY Registers
            148. 14.2.1.1.2.148 CFG0_MCU_CTRL_MMR_MCU_TIMER3_CLKSEL_PROXY Registers
            149. 14.2.1.1.2.149 CFG0_MCU_CTRL_MMR_MCU_GPIO_CLKSEL_PROXY Registers
            150. 14.2.1.1.2.150 CFG0_MCU_CTRL_MMR_MCU_MCAN0_CLKSEL_PROXY Registers
            151. 14.2.1.1.2.151 CFG0_MCU_CTRL_MMR_MCU_MCAN1_CLKSEL_PROXY Registers
            152. 14.2.1.1.2.152 CFG0_MCU_CTRL_MMR_MCU_SPI0_CLKSEL_PROXY Registers
            153. 14.2.1.1.2.153 CFG0_MCU_CTRL_MMR_MCU_SPI1_CLKSEL_PROXY Registers
            154. 14.2.1.1.2.154 CFG0_MCU_CTRL_MMR_MCU_WWD0_CLKSEL_PROXY Registers
            155. 14.2.1.1.2.155 CFG0_MCU_CTRL_MMR_LOCK2_KICK0_PROXY Registers
            156. 14.2.1.1.2.156 CFG0_MCU_CTRL_MMR_LOCK2_KICK1_PROXY Registers
            157. 14.2.1.1.2.157 CFG0_MCU_CTRL_MMR_CLAIMREG_P2_R0 Registers
            158. 14.2.1.1.2.158 CFG0_MCU_CTRL_MMR_CLAIMREG_P2_R1 Registers
            159. 14.2.1.1.2.159 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_CTRL Registers
            160. 14.2.1.1.2.160 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_PATCOUNT Registers
            161. 14.2.1.1.2.161 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SEED0 Registers
            162. 14.2.1.1.2.162 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SEED1 Registers
            163. 14.2.1.1.2.163 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SPARE0 Registers
            164. 14.2.1.1.2.164 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SPARE1 Registers
            165. 14.2.1.1.2.165 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_STAT Registers
            166. 14.2.1.1.2.166 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_MISR Registers
            167. 14.2.1.1.2.167 CFG0_MCU_CTRL_MMR_LOCK3_KICK0 Registers
            168. 14.2.1.1.2.168 CFG0_MCU_CTRL_MMR_LOCK3_KICK1 Registers
            169. 14.2.1.1.2.169 CFG0_MCU_CTRL_MMR_CLAIMREG_P3_R0_READONLY Registers
            170. 14.2.1.1.2.170 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_CTRL_PROXY Registers
            171. 14.2.1.1.2.171 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_PATCOUNT_PROXY Registers
            172. 14.2.1.1.2.172 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SEED0_PROXY Registers
            173. 14.2.1.1.2.173 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SEED1_PROXY Registers
            174. 14.2.1.1.2.174 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SPARE0_PROXY Registers
            175. 14.2.1.1.2.175 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_SPARE1_PROXY Registers
            176. 14.2.1.1.2.176 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_STAT_PROXY Registers
            177. 14.2.1.1.2.177 CFG0_MCU_CTRL_MMR_MCU_M4FSS0_LBIST_MISR_PROXY Registers
            178. 14.2.1.1.2.178 CFG0_MCU_CTRL_MMR_LOCK3_KICK0_PROXY Registers
            179. 14.2.1.1.2.179 CFG0_MCU_CTRL_MMR_LOCK3_KICK1_PROXY Registers
            180. 14.2.1.1.2.180 CFG0_MCU_CTRL_MMR_CLAIMREG_P3_R0 Registers
            181. 14.2.1.1.2.181 CFG0_MCU_CTRL_MMR_DV_REG4 Registers
            182. 14.2.1.1.2.182 CFG0_MCU_CTRL_MMR_DV_REG5 Registers
            183. 14.2.1.1.2.183 CFG0_MCU_CTRL_MMR_OLDI_PD_CTRL_TEST_REG Registers
            184. 14.2.1.1.2.184 CFG0_MCU_CTRL_MMR_PBIST_EN_TEST_REG Registers
            185. 14.2.1.1.2.185 CFG0_MCU_CTRL_MMR_LOCK4_KICK0 Registers
            186. 14.2.1.1.2.186 CFG0_MCU_CTRL_MMR_LOCK4_KICK1 Registers
            187. 14.2.1.1.2.187 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R0_READONLY Registers
            188. 14.2.1.1.2.188 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R1_READONLY Registers
            189. 14.2.1.1.2.189 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R2_READONLY Registers
            190. 14.2.1.1.2.190 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R3_READONLY Registers
            191. 14.2.1.1.2.191 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R4_READONLY Registers
            192. 14.2.1.1.2.192 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R5_READONLY Registers
            193. 14.2.1.1.2.193 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R6_READONLY Registers
            194. 14.2.1.1.2.194 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R7_READONLY Registers
            195. 14.2.1.1.2.195 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R8_READONLY Registers
            196. 14.2.1.1.2.196 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R9_READONLY Registers
            197. 14.2.1.1.2.197 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R10_READONLY Registers
            198. 14.2.1.1.2.198 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R11_READONLY Registers
            199. 14.2.1.1.2.199 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R12_READONLY Registers
            200. 14.2.1.1.2.200 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R13_READONLY Registers
            201. 14.2.1.1.2.201 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R14_READONLY Registers
            202. 14.2.1.1.2.202 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R15_READONLY Registers
            203. 14.2.1.1.2.203 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R16_READONLY Registers
            204. 14.2.1.1.2.204 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R17_READONLY Registers
            205. 14.2.1.1.2.205 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R18_READONLY Registers
            206. 14.2.1.1.2.206 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R19_READONLY Registers
            207. 14.2.1.1.2.207 CFG0_MCU_CTRL_MMR_DV_REG4_PROXY Registers
            208. 14.2.1.1.2.208 CFG0_MCU_CTRL_MMR_DV_REG5_PROXY Registers
            209. 14.2.1.1.2.209 CFG0_MCU_CTRL_MMR_OLDI_PD_CTRL_TEST_REG_PROXY Registers
            210. 14.2.1.1.2.210 CFG0_MCU_CTRL_MMR_PBIST_EN_TEST_REG_PROXY Registers
            211. 14.2.1.1.2.211 CFG0_MCU_CTRL_MMR_LOCK4_KICK0_PROXY Registers
            212. 14.2.1.1.2.212 CFG0_MCU_CTRL_MMR_LOCK4_KICK1_PROXY Registers
            213. 14.2.1.1.2.213 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R0 Registers
            214. 14.2.1.1.2.214 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R1 Registers
            215. 14.2.1.1.2.215 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R2 Registers
            216. 14.2.1.1.2.216 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R3 Registers
            217. 14.2.1.1.2.217 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R4 Registers
            218. 14.2.1.1.2.218 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R5 Registers
            219. 14.2.1.1.2.219 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R6 Registers
            220. 14.2.1.1.2.220 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R7 Registers
            221. 14.2.1.1.2.221 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R8 Registers
            222. 14.2.1.1.2.222 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R9 Registers
            223. 14.2.1.1.2.223 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R10 Registers
            224. 14.2.1.1.2.224 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R11 Registers
            225. 14.2.1.1.2.225 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R12 Registers
            226. 14.2.1.1.2.226 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R13 Registers
            227. 14.2.1.1.2.227 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R14 Registers
            228. 14.2.1.1.2.228 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R15 Registers
            229. 14.2.1.1.2.229 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R16 Registers
            230. 14.2.1.1.2.230 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R17 Registers
            231. 14.2.1.1.2.231 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R18 Registers
            232. 14.2.1.1.2.232 CFG0_MCU_CTRL_MMR_CLAIMREG_P4_R19 Registers
            233. 14.2.1.1.2.233 CFG0_MCU_CTRL_MMR_POR_CTRL Registers
            234. 14.2.1.1.2.234 CFG0_MCU_CTRL_MMR_POR_STAT Registers
            235. 14.2.1.1.2.235 CFG0_MCU_CTRL_MMR_POR_BANDGAP_CTRL Registers
            236. 14.2.1.1.2.236 CFG0_MCU_CTRL_MMR_POK_VDDA_MCU_UV_CTRL Registers
            237. 14.2.1.1.2.237 CFG0_MCU_CTRL_MMR_POK_VDDA_MCU_OV_CTRL Registers
            238. 14.2.1.1.2.238 CFG0_MCU_CTRL_MMR_POK_VDD_CORE_UV_CTRL Registers
            239. 14.2.1.1.2.239 CFG0_MCU_CTRL_MMR_POK_VDD_CORE_OV_CTRL Registers
            240. 14.2.1.1.2.240 CFG0_MCU_CTRL_MMR_POK_VDDR_CORE_UV_CTRL Registers
            241. 14.2.1.1.2.241 CFG0_MCU_CTRL_MMR_POK_VDDR_CORE_OV_CTRL Registers
            242. 14.2.1.1.2.242 CFG0_MCU_CTRL_MMR_POK_VMON_CAP_MCU_GENERAL_UV_CTRL Registers
            243. 14.2.1.1.2.243 CFG0_MCU_CTRL_MMR_POK_VMON_CAP_MCU_GENERAL_OV_CTRL Registers
            244. 14.2.1.1.2.244 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_1P8_UV_CTRL Registers
            245. 14.2.1.1.2.245 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_1P8_OV_CTRL Registers
            246. 14.2.1.1.2.246 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_3P3_UV_CTRL Registers
            247. 14.2.1.1.2.247 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_3P3_OV_CTRL Registers
            248. 14.2.1.1.2.248 CFG0_MCU_CTRL_MMR_POK_VDDS_DDRIO_UV_CTRL Registers
            249. 14.2.1.1.2.249 CFG0_MCU_CTRL_MMR_POK_VDDS_DDRIO_OV_CTRL Registers
            250. 14.2.1.1.2.250 CFG0_MCU_CTRL_MMR_POK_VDDA_PMIC_IN_CTRL Registers
            251. 14.2.1.1.2.251 CFG0_MCU_CTRL_MMR_RST_CTRL Registers
            252. 14.2.1.1.2.252 CFG0_MCU_CTRL_MMR_RST_STAT Registers
            253. 14.2.1.1.2.253 CFG0_MCU_CTRL_MMR_RST_SRC Registers
            254. 14.2.1.1.2.254 CFG0_MCU_CTRL_MMR_RST_MAGIC_WORD Registers
            255. 14.2.1.1.2.255 CFG0_MCU_CTRL_MMR_ISO_CTRL Registers
            256. 14.2.1.1.2.256 CFG0_MCU_CTRL_MMR_VDD_CORE_GLDTC_CTRL Registers
            257. 14.2.1.1.2.257 CFG0_MCU_CTRL_MMR_VDD_CORE_GLDTC_STAT Registers
            258. 14.2.1.1.2.258 CFG0_MCU_CTRL_MMR_PRG_PP_0_CTRL Registers
            259. 14.2.1.1.2.259 CFG0_MCU_CTRL_MMR_PRG_PP_1_CTRL Registers
            260. 14.2.1.1.2.260 CFG0_MCU_CTRL_MMR_CLKGATE_CTRL Registers
            261. 14.2.1.1.2.261 CFG0_MCU_CTRL_MMR_LVDS_BANDGAP_CTRL Registers
            262. 14.2.1.1.2.262 CFG0_MCU_CTRL_MMR_LOCK6_KICK0 Registers
            263. 14.2.1.1.2.263 CFG0_MCU_CTRL_MMR_LOCK6_KICK1 Registers
            264. 14.2.1.1.2.264 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R0_READONLY Registers
            265. 14.2.1.1.2.265 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R1_READONLY Registers
            266. 14.2.1.1.2.266 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R2_READONLY Registers
            267. 14.2.1.1.2.267 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R3_READONLY Registers
            268. 14.2.1.1.2.268 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R4_READONLY Registers
            269. 14.2.1.1.2.269 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R5_READONLY Registers
            270. 14.2.1.1.2.270 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R6_READONLY Registers
            271. 14.2.1.1.2.271 CFG0_MCU_CTRL_MMR_POR_CTRL_PROXY Registers
            272. 14.2.1.1.2.272 CFG0_MCU_CTRL_MMR_POR_STAT_PROXY Registers
            273. 14.2.1.1.2.273 CFG0_MCU_CTRL_MMR_POR_BANDGAP_CTRL_PROXY Registers
            274. 14.2.1.1.2.274 CFG0_MCU_CTRL_MMR_POK_VDDA_MCU_UV_CTRL_PROXY Registers
            275. 14.2.1.1.2.275 CFG0_MCU_CTRL_MMR_POK_VDDA_MCU_OV_CTRL_PROXY Registers
            276. 14.2.1.1.2.276 CFG0_MCU_CTRL_MMR_POK_VDD_CORE_UV_CTRL_PROXY Registers
            277. 14.2.1.1.2.277 CFG0_MCU_CTRL_MMR_POK_VDD_CORE_OV_CTRL_PROXY Registers
            278. 14.2.1.1.2.278 CFG0_MCU_CTRL_MMR_POK_VDDR_CORE_UV_CTRL_PROXY Registers
            279. 14.2.1.1.2.279 CFG0_MCU_CTRL_MMR_POK_VDDR_CORE_OV_CTRL_PROXY Registers
            280. 14.2.1.1.2.280 CFG0_MCU_CTRL_MMR_POK_VMON_CAP_MCU_GENERAL_UV_CTRL_PROXY Registers
            281. 14.2.1.1.2.281 CFG0_MCU_CTRL_MMR_POK_VMON_CAP_MCU_GENERAL_OV_CTRL_PROXY Registers
            282. 14.2.1.1.2.282 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_1P8_UV_CTRL_PROXY Registers
            283. 14.2.1.1.2.283 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_1P8_OV_CTRL_PROXY Registers
            284. 14.2.1.1.2.284 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_3P3_UV_CTRL_PROXY Registers
            285. 14.2.1.1.2.285 CFG0_MCU_CTRL_MMR_POK_VDDSHV_MAIN_3P3_OV_CTRL_PROXY Registers
            286. 14.2.1.1.2.286 CFG0_MCU_CTRL_MMR_POK_VDDS_DDRIO_UV_CTRL_PROXY Registers
            287. 14.2.1.1.2.287 CFG0_MCU_CTRL_MMR_POK_VDDS_DDRIO_OV_CTRL_PROXY Registers
            288. 14.2.1.1.2.288 CFG0_MCU_CTRL_MMR_POK_VDDA_PMIC_IN_CTRL_PROXY Registers
            289. 14.2.1.1.2.289 CFG0_MCU_CTRL_MMR_RST_CTRL_PROXY Registers
            290. 14.2.1.1.2.290 CFG0_MCU_CTRL_MMR_RST_STAT_PROXY Registers
            291. 14.2.1.1.2.291 CFG0_MCU_CTRL_MMR_RST_SRC_PROXY Registers
            292. 14.2.1.1.2.292 CFG0_MCU_CTRL_MMR_RST_MAGIC_WORD_PROXY Registers
            293. 14.2.1.1.2.293 CFG0_MCU_CTRL_MMR_ISO_CTRL_PROXY Registers
            294. 14.2.1.1.2.294 CFG0_MCU_CTRL_MMR_VDD_CORE_GLDTC_CTRL_PROXY Registers
            295. 14.2.1.1.2.295 CFG0_MCU_CTRL_MMR_VDD_CORE_GLDTC_STAT_PROXY Registers
            296. 14.2.1.1.2.296 CFG0_MCU_CTRL_MMR_PRG_PP_0_CTRL_PROXY Registers
            297. 14.2.1.1.2.297 CFG0_MCU_CTRL_MMR_PRG_PP_1_CTRL_PROXY Registers
            298. 14.2.1.1.2.298 CFG0_MCU_CTRL_MMR_CLKGATE_CTRL_PROXY Registers
            299. 14.2.1.1.2.299 CFG0_MCU_CTRL_MMR_LVDS_BANDGAP_CTRL_PROXY Registers
            300. 14.2.1.1.2.300 CFG0_MCU_CTRL_MMR_LOCK6_KICK0_PROXY Registers
            301. 14.2.1.1.2.301 CFG0_MCU_CTRL_MMR_LOCK6_KICK1_PROXY Registers
            302. 14.2.1.1.2.302 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R0 Registers
            303. 14.2.1.1.2.303 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R1 Registers
            304. 14.2.1.1.2.304 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R2 Registers
            305. 14.2.1.1.2.305 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R3 Registers
            306. 14.2.1.1.2.306 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R4 Registers
            307. 14.2.1.1.2.307 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R5 Registers
            308. 14.2.1.1.2.308 CFG0_MCU_CTRL_MMR_CLAIMREG_P6_R6 Registers
            309. 14.2.1.1.2.309 Access Table
          3. 14.2.1.1.3 WKUP_CTRL_MMR Registers
            1. 14.2.1.1.3.1   CFG0_WKUP_CTRL_MMR_PID Registers
            2. 14.2.1.1.3.2   CFG0_WKUP_CTRL_MMR_MMR_CFG1 Registers
            3. 14.2.1.1.3.3   CFG0_WKUP_CTRL_MMR_JTAGID Registers
            4. 14.2.1.1.3.4   CFG0_WKUP_CTRL_MMR_JTAG_USER_ID Registers
            5. 14.2.1.1.3.5   CFG0_WKUP_CTRL_MMR_MAIN_DEVSTAT Registers
            6. 14.2.1.1.3.6   CFG0_WKUP_CTRL_MMR_MAIN_BOOTCFG Registers
            7. 14.2.1.1.3.7   CFG0_WKUP_CTRL_MMR_BOOT_PROGRESS Registers
            8. 14.2.1.1.3.8   CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE0 Registers
            9. 14.2.1.1.3.9   CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE1 Registers
            10. 14.2.1.1.3.10  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE2 Registers
            11. 14.2.1.1.3.11  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE3 Registers
            12. 14.2.1.1.3.12  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE6 Registers
            13. 14.2.1.1.3.13  CFG0_WKUP_CTRL_MMR_MAC_ID0 Registers
            14. 14.2.1.1.3.14  CFG0_WKUP_CTRL_MMR_MAC_ID1 Registers
            15. 14.2.1.1.3.15  CFG0_WKUP_CTRL_MMR_USB_DEVICE_ID0 Registers
            16. 14.2.1.1.3.16  CFG0_WKUP_CTRL_MMR_USB_DEVICE_ID1 Registers
            17. 14.2.1.1.3.17  CFG0_WKUP_CTRL_MMR_GP_SW0 Registers
            18. 14.2.1.1.3.18  CFG0_WKUP_CTRL_MMR_GP_SW1 Registers
            19. 14.2.1.1.3.19  CFG0_WKUP_CTRL_MMR_GP_SW2 Registers
            20. 14.2.1.1.3.20  CFG0_WKUP_CTRL_MMR_GP_SW3 Registers
            21. 14.2.1.1.3.21  CFG0_WKUP_CTRL_MMR_CBA_ERR_STAT Registers
            22. 14.2.1.1.3.22  CFG0_WKUP_CTRL_MMR_ACCESS_ERR_STAT Registers
            23. 14.2.1.1.3.23  CFG0_WKUP_CTRL_MMR_LOCK0_KICK0 Registers
            24. 14.2.1.1.3.24  CFG0_WKUP_CTRL_MMR_LOCK0_KICK1 Registers
            25. 14.2.1.1.3.25  CFG0_WKUP_CTRL_MMR_INTR_RAW_STATUS Registers
            26. 14.2.1.1.3.26  CFG0_WKUP_CTRL_MMR_INTR_ENABLED_STATUS_CLEAR Registers
            27. 14.2.1.1.3.27  CFG0_WKUP_CTRL_MMR_INTR_ENABLE Registers
            28. 14.2.1.1.3.28  CFG0_WKUP_CTRL_MMR_INTR_ENABLE_CLEAR Registers
            29. 14.2.1.1.3.29  CFG0_WKUP_CTRL_MMR_EOI Registers
            30. 14.2.1.1.3.30  CFG0_WKUP_CTRL_MMR_FAULT_ADDRESS Registers
            31. 14.2.1.1.3.31  CFG0_WKUP_CTRL_MMR_FAULT_TYPE_STATUS Registers
            32. 14.2.1.1.3.32  CFG0_WKUP_CTRL_MMR_FAULT_ATTR_STATUS Registers
            33. 14.2.1.1.3.33  CFG0_WKUP_CTRL_MMR_FAULT_CLEAR Registers
            34. 14.2.1.1.3.34  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R0_READONLY Registers
            35. 14.2.1.1.3.35  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R1_READONLY Registers
            36. 14.2.1.1.3.36  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R2_READONLY Registers
            37. 14.2.1.1.3.37  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R3_READONLY Registers
            38. 14.2.1.1.3.38  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R4_READONLY Registers
            39. 14.2.1.1.3.39  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R5_READONLY Registers
            40. 14.2.1.1.3.40  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R6_READONLY Registers
            41. 14.2.1.1.3.41  CFG0_WKUP_CTRL_MMR_PID_PROXY Registers
            42. 14.2.1.1.3.42  CFG0_WKUP_CTRL_MMR_MMR_CFG1_PROXY Registers
            43. 14.2.1.1.3.43  CFG0_WKUP_CTRL_MMR_JTAGID_PROXY Registers
            44. 14.2.1.1.3.44  CFG0_WKUP_CTRL_MMR_JTAG_USER_ID_PROXY Registers
            45. 14.2.1.1.3.45  CFG0_WKUP_CTRL_MMR_MAIN_DEVSTAT_PROXY Registers
            46. 14.2.1.1.3.46  CFG0_WKUP_CTRL_MMR_MAIN_BOOTCFG_PROXY Registers
            47. 14.2.1.1.3.47  CFG0_WKUP_CTRL_MMR_BOOT_PROGRESS_PROXY Registers
            48. 14.2.1.1.3.48  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE0_PROXY Registers
            49. 14.2.1.1.3.49  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE1_PROXY Registers
            50. 14.2.1.1.3.50  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE2_PROXY Registers
            51. 14.2.1.1.3.51  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE3_PROXY Registers
            52. 14.2.1.1.3.52  CFG0_WKUP_CTRL_MMR_DEVICE_FEATURE6_PROXY Registers
            53. 14.2.1.1.3.53  CFG0_WKUP_CTRL_MMR_MAC_ID0_PROXY Registers
            54. 14.2.1.1.3.54  CFG0_WKUP_CTRL_MMR_MAC_ID1_PROXY Registers
            55. 14.2.1.1.3.55  CFG0_WKUP_CTRL_MMR_USB_DEVICE_ID0_PROXY Registers
            56. 14.2.1.1.3.56  CFG0_WKUP_CTRL_MMR_USB_DEVICE_ID1_PROXY Registers
            57. 14.2.1.1.3.57  CFG0_WKUP_CTRL_MMR_GP_SW0_PROXY Registers
            58. 14.2.1.1.3.58  CFG0_WKUP_CTRL_MMR_GP_SW1_PROXY Registers
            59. 14.2.1.1.3.59  CFG0_WKUP_CTRL_MMR_GP_SW2_PROXY Registers
            60. 14.2.1.1.3.60  CFG0_WKUP_CTRL_MMR_GP_SW3_PROXY Registers
            61. 14.2.1.1.3.61  CFG0_WKUP_CTRL_MMR_CBA_ERR_STAT_PROXY Registers
            62. 14.2.1.1.3.62  CFG0_WKUP_CTRL_MMR_ACCESS_ERR_STAT_PROXY Registers
            63. 14.2.1.1.3.63  CFG0_WKUP_CTRL_MMR_LOCK0_KICK0_PROXY Registers
            64. 14.2.1.1.3.64  CFG0_WKUP_CTRL_MMR_LOCK0_KICK1_PROXY Registers
            65. 14.2.1.1.3.65  CFG0_WKUP_CTRL_MMR_INTR_RAW_STATUS_PROXY Registers
            66. 14.2.1.1.3.66  CFG0_WKUP_CTRL_MMR_INTR_ENABLED_STATUS_CLEAR_PROXY Registers
            67. 14.2.1.1.3.67  CFG0_WKUP_CTRL_MMR_INTR_ENABLE_PROXY Registers
            68. 14.2.1.1.3.68  CFG0_WKUP_CTRL_MMR_INTR_ENABLE_CLEAR_PROXY Registers
            69. 14.2.1.1.3.69  CFG0_WKUP_CTRL_MMR_EOI_PROXY Registers
            70. 14.2.1.1.3.70  CFG0_WKUP_CTRL_MMR_FAULT_ADDRESS_PROXY Registers
            71. 14.2.1.1.3.71  CFG0_WKUP_CTRL_MMR_FAULT_TYPE_STATUS_PROXY Registers
            72. 14.2.1.1.3.72  CFG0_WKUP_CTRL_MMR_FAULT_ATTR_STATUS_PROXY Registers
            73. 14.2.1.1.3.73  CFG0_WKUP_CTRL_MMR_FAULT_CLEAR_PROXY Registers
            74. 14.2.1.1.3.74  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R0 Registers
            75. 14.2.1.1.3.75  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R1 Registers
            76. 14.2.1.1.3.76  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R2 Registers
            77. 14.2.1.1.3.77  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R3 Registers
            78. 14.2.1.1.3.78  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R4 Registers
            79. 14.2.1.1.3.79  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R5 Registers
            80. 14.2.1.1.3.80  CFG0_WKUP_CTRL_MMR_CLAIMREG_P0_R6 Registers
            81. 14.2.1.1.3.81  CFG0_WKUP_CTRL_MMR_USB0_PHY_CTRL Registers
            82. 14.2.1.1.3.82  CFG0_WKUP_CTRL_MMR_USB1_PHY_CTRL Registers
            83. 14.2.1.1.3.83  CFG0_WKUP_CTRL_MMR_SDIO0_CTRL Registers
            84. 14.2.1.1.3.84  CFG0_WKUP_CTRL_MMR_SDIO1_CTRL Registers
            85. 14.2.1.1.3.85  CFG0_WKUP_CTRL_MMR_SDIO2_CTRL Registers
            86. 14.2.1.1.3.86  CFG0_WKUP_CTRL_MMR_WKUP_TIMER1_CTRL Registers
            87. 14.2.1.1.3.87  CFG0_WKUP_CTRL_MMR_WKUP_I2C0_CTRL Registers
            88. 14.2.1.1.3.88  CFG0_WKUP_CTRL_MMR_TOG_STAT Registers
            89. 14.2.1.1.3.89  CFG0_WKUP_CTRL_MMR_LOCK1_KICK0 Registers
            90. 14.2.1.1.3.90  CFG0_WKUP_CTRL_MMR_LOCK1_KICK1 Registers
            91. 14.2.1.1.3.91  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R0_READONLY Registers
            92. 14.2.1.1.3.92  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R1_READONLY Registers
            93. 14.2.1.1.3.93  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R2_READONLY Registers
            94. 14.2.1.1.3.94  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R3_READONLY Registers
            95. 14.2.1.1.3.95  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R4_READONLY Registers
            96. 14.2.1.1.3.96  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R5_READONLY Registers
            97. 14.2.1.1.3.97  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R6_READONLY Registers
            98. 14.2.1.1.3.98  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R7_READONLY Registers
            99. 14.2.1.1.3.99  CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R8_READONLY Registers
            100. 14.2.1.1.3.100 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R9_READONLY Registers
            101. 14.2.1.1.3.101 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R10_READONLY Registers
            102. 14.2.1.1.3.102 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R11_READONLY Registers
            103. 14.2.1.1.3.103 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R12_READONLY Registers
            104. 14.2.1.1.3.104 CFG0_WKUP_CTRL_MMR_USB0_PHY_CTRL_PROXY Registers
            105. 14.2.1.1.3.105 CFG0_WKUP_CTRL_MMR_USB1_PHY_CTRL_PROXY Registers
            106. 14.2.1.1.3.106 CFG0_WKUP_CTRL_MMR_SDIO0_CTRL_PROXY Registers
            107. 14.2.1.1.3.107 CFG0_WKUP_CTRL_MMR_SDIO1_CTRL_PROXY Registers
            108. 14.2.1.1.3.108 CFG0_WKUP_CTRL_MMR_SDIO2_CTRL_PROXY Registers
            109. 14.2.1.1.3.109 CFG0_WKUP_CTRL_MMR_WKUP_TIMER1_CTRL_PROXY Registers
            110. 14.2.1.1.3.110 CFG0_WKUP_CTRL_MMR_WKUP_I2C0_CTRL_PROXY Registers
            111. 14.2.1.1.3.111 CFG0_WKUP_CTRL_MMR_TOG_STAT_PROXY Registers
            112. 14.2.1.1.3.112 CFG0_WKUP_CTRL_MMR_LOCK1_KICK0_PROXY Registers
            113. 14.2.1.1.3.113 CFG0_WKUP_CTRL_MMR_LOCK1_KICK1_PROXY Registers
            114. 14.2.1.1.3.114 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R0 Registers
            115. 14.2.1.1.3.115 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R1 Registers
            116. 14.2.1.1.3.116 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R2 Registers
            117. 14.2.1.1.3.117 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R3 Registers
            118. 14.2.1.1.3.118 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R4 Registers
            119. 14.2.1.1.3.119 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R5 Registers
            120. 14.2.1.1.3.120 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R6 Registers
            121. 14.2.1.1.3.121 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R7 Registers
            122. 14.2.1.1.3.122 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R8 Registers
            123. 14.2.1.1.3.123 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R9 Registers
            124. 14.2.1.1.3.124 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R10 Registers
            125. 14.2.1.1.3.125 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R11 Registers
            126. 14.2.1.1.3.126 CFG0_WKUP_CTRL_MMR_CLAIMREG_P1_R12 Registers
            127. 14.2.1.1.3.127 CFG0_WKUP_CTRL_MMR_WKUP_CLKSEL Registers
            128. 14.2.1.1.3.128 CFG0_WKUP_CTRL_MMR_CLKOUT_CTRL Registers
            129. 14.2.1.1.3.129 CFG0_WKUP_CTRL_MMR_WKUP_GTC_CLKSEL Registers
            130. 14.2.1.1.3.130 CFG0_WKUP_CTRL_MMR_EFUSE_CLKSEL Registers
            131. 14.2.1.1.3.131 CFG0_WKUP_CTRL_MMR_DDR16SS_PMCTRL Registers
            132. 14.2.1.1.3.132 CFG0_WKUP_CTRL_MMR_USB0_CLKSEL Registers
            133. 14.2.1.1.3.133 CFG0_WKUP_CTRL_MMR_USB1_CLKSEL Registers
            134. 14.2.1.1.3.134 CFG0_WKUP_CTRL_MMR_WKUP_TIMER0_CLKSEL Registers
            135. 14.2.1.1.3.135 CFG0_WKUP_CTRL_MMR_WKUP_TIMER1_CLKSEL Registers
            136. 14.2.1.1.3.136 CFG0_WKUP_CTRL_MMR_WKUP_WWD0_CTRL Registers
            137. 14.2.1.1.3.137 CFG0_WKUP_CTRL_MMR_WKUP_WWD0_CLKSEL Registers
            138. 14.2.1.1.3.138 CFG0_WKUP_CTRL_MMR_WKUP_RTC_CLKSEL Registers
            139. 14.2.1.1.3.139 CFG0_WKUP_CTRL_MMR_LOCK2_KICK0 Registers
            140. 14.2.1.1.3.140 CFG0_WKUP_CTRL_MMR_LOCK2_KICK1 Registers
            141. 14.2.1.1.3.141 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R0_READONLY Registers
            142. 14.2.1.1.3.142 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R1_READONLY Registers
            143. 14.2.1.1.3.143 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R2_READONLY Registers
            144. 14.2.1.1.3.144 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R3_READONLY Registers
            145. 14.2.1.1.3.145 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R4_READONLY Registers
            146. 14.2.1.1.3.146 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R5_READONLY Registers
            147. 14.2.1.1.3.147 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R6_READONLY Registers
            148. 14.2.1.1.3.148 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R7_READONLY Registers
            149. 14.2.1.1.3.149 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R8_READONLY Registers
            150. 14.2.1.1.3.150 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R9_READONLY Registers
            151. 14.2.1.1.3.151 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R10_READONLY Registers
            152. 14.2.1.1.3.152 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R11_READONLY Registers
            153. 14.2.1.1.3.153 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R12_READONLY Registers
            154. 14.2.1.1.3.154 CFG0_WKUP_CTRL_MMR_WKUP_CLKSEL_PROXY Registers
            155. 14.2.1.1.3.155 CFG0_WKUP_CTRL_MMR_CLKOUT_CTRL_PROXY Registers
            156. 14.2.1.1.3.156 CFG0_WKUP_CTRL_MMR_WKUP_GTC_CLKSEL_PROXY Registers
            157. 14.2.1.1.3.157 CFG0_WKUP_CTRL_MMR_EFUSE_CLKSEL_PROXY Registers
            158. 14.2.1.1.3.158 CFG0_WKUP_CTRL_MMR_DDR16SS_PMCTRL_PROXY Registers
            159. 14.2.1.1.3.159 CFG0_WKUP_CTRL_MMR_USB0_CLKSEL_PROXY Registers
            160. 14.2.1.1.3.160 CFG0_WKUP_CTRL_MMR_USB1_CLKSEL_PROXY Registers
            161. 14.2.1.1.3.161 CFG0_WKUP_CTRL_MMR_WKUP_TIMER0_CLKSEL_PROXY Registers
            162. 14.2.1.1.3.162 CFG0_WKUP_CTRL_MMR_WKUP_TIMER1_CLKSEL_PROXY Registers
            163. 14.2.1.1.3.163 CFG0_WKUP_CTRL_MMR_WKUP_WWD0_CTRL_PROXY Registers
            164. 14.2.1.1.3.164 CFG0_WKUP_CTRL_MMR_WKUP_WWD0_CLKSEL_PROXY Registers
            165. 14.2.1.1.3.165 CFG0_WKUP_CTRL_MMR_WKUP_RTC_CLKSEL_PROXY Registers
            166. 14.2.1.1.3.166 CFG0_WKUP_CTRL_MMR_LOCK2_KICK0_PROXY Registers
            167. 14.2.1.1.3.167 CFG0_WKUP_CTRL_MMR_LOCK2_KICK1_PROXY Registers
            168. 14.2.1.1.3.168 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R0 Registers
            169. 14.2.1.1.3.169 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R1 Registers
            170. 14.2.1.1.3.170 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R2 Registers
            171. 14.2.1.1.3.171 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R3 Registers
            172. 14.2.1.1.3.172 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R4 Registers
            173. 14.2.1.1.3.173 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R5 Registers
            174. 14.2.1.1.3.174 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R6 Registers
            175. 14.2.1.1.3.175 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R7 Registers
            176. 14.2.1.1.3.176 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R8 Registers
            177. 14.2.1.1.3.177 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R9 Registers
            178. 14.2.1.1.3.178 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R10 Registers
            179. 14.2.1.1.3.179 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R11 Registers
            180. 14.2.1.1.3.180 CFG0_WKUP_CTRL_MMR_CLAIMREG_P2_R12 Registers
            181. 14.2.1.1.3.181 CFG0_WKUP_CTRL_MMR_FUSE_CRC_STAT Registers
            182. 14.2.1.1.3.182 CFG0_WKUP_CTRL_MMR_CHAIN1_CRC_CALC Registers
            183. 14.2.1.1.3.183 CFG0_WKUP_CTRL_MMR_CHAIN2_CRC_CALC Registers
            184. 14.2.1.1.3.184 CFG0_WKUP_CTRL_MMR_CHAIN1_CRC_CALC_RO Registers
            185. 14.2.1.1.3.185 CFG0_WKUP_CTRL_MMR_CHAIN2_CRC_CALC_RO Registers
            186. 14.2.1.1.3.186 CFG0_WKUP_CTRL_MMR_PBIST_EN Registers
            187. 14.2.1.1.3.187 CFG0_WKUP_CTRL_MMR_LOCK3_KICK0 Registers
            188. 14.2.1.1.3.188 CFG0_WKUP_CTRL_MMR_LOCK3_KICK1 Registers
            189. 14.2.1.1.3.189 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R0_READONLY Registers
            190. 14.2.1.1.3.190 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R1_READONLY Registers
            191. 14.2.1.1.3.191 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R2_READONLY Registers
            192. 14.2.1.1.3.192 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R3_READONLY Registers
            193. 14.2.1.1.3.193 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R4_READONLY Registers
            194. 14.2.1.1.3.194 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R5_READONLY Registers
            195. 14.2.1.1.3.195 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R6_READONLY Registers
            196. 14.2.1.1.3.196 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R7_READONLY Registers
            197. 14.2.1.1.3.197 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R8_READONLY Registers
            198. 14.2.1.1.3.198 CFG0_WKUP_CTRL_MMR_FUSE_CRC_STAT_PROXY Registers
            199. 14.2.1.1.3.199 CFG0_WKUP_CTRL_MMR_CHAIN1_CRC_CALC_PROXY Registers
            200. 14.2.1.1.3.200 CFG0_WKUP_CTRL_MMR_CHAIN2_CRC_CALC_PROXY Registers
            201. 14.2.1.1.3.201 CFG0_WKUP_CTRL_MMR_CHAIN1_CRC_CALC_RO_PROXY Registers
            202. 14.2.1.1.3.202 CFG0_WKUP_CTRL_MMR_CHAIN2_CRC_CALC_RO_PROXY Registers
            203. 14.2.1.1.3.203 CFG0_WKUP_CTRL_MMR_PBIST_EN_PROXY Registers
            204. 14.2.1.1.3.204 CFG0_WKUP_CTRL_MMR_LOCK3_KICK0_PROXY Registers
            205. 14.2.1.1.3.205 CFG0_WKUP_CTRL_MMR_LOCK3_KICK1_PROXY Registers
            206. 14.2.1.1.3.206 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R0 Registers
            207. 14.2.1.1.3.207 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R1 Registers
            208. 14.2.1.1.3.208 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R2 Registers
            209. 14.2.1.1.3.209 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R3 Registers
            210. 14.2.1.1.3.210 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R4 Registers
            211. 14.2.1.1.3.211 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R5 Registers
            212. 14.2.1.1.3.212 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R6 Registers
            213. 14.2.1.1.3.213 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R7 Registers
            214. 14.2.1.1.3.214 CFG0_WKUP_CTRL_MMR_CLAIMREG_P3_R8 Registers
            215. 14.2.1.1.3.215 CFG0_WKUP_CTRL_MMR_DV_REG32 Registers
            216. 14.2.1.1.3.216 CFG0_WKUP_CTRL_MMR_DV_REG33 Registers
            217. 14.2.1.1.3.217 CFG0_WKUP_CTRL_MMR_LOCK4_KICK0 Registers
            218. 14.2.1.1.3.218 CFG0_WKUP_CTRL_MMR_LOCK4_KICK1 Registers
            219. 14.2.1.1.3.219 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R0_READONLY Registers
            220. 14.2.1.1.3.220 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R1_READONLY Registers
            221. 14.2.1.1.3.221 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R2_READONLY Registers
            222. 14.2.1.1.3.222 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R3_READONLY Registers
            223. 14.2.1.1.3.223 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R4_READONLY Registers
            224. 14.2.1.1.3.224 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R5_READONLY Registers
            225. 14.2.1.1.3.225 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R6_READONLY Registers
            226. 14.2.1.1.3.226 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R7_READONLY Registers
            227. 14.2.1.1.3.227 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R8_READONLY Registers
            228. 14.2.1.1.3.228 CFG0_WKUP_CTRL_MMR_DV_REG32_PROXY Registers
            229. 14.2.1.1.3.229 CFG0_WKUP_CTRL_MMR_DV_REG33_PROXY Registers
            230. 14.2.1.1.3.230 CFG0_WKUP_CTRL_MMR_LOCK4_KICK0_PROXY Registers
            231. 14.2.1.1.3.231 CFG0_WKUP_CTRL_MMR_LOCK4_KICK1_PROXY Registers
            232. 14.2.1.1.3.232 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R0 Registers
            233. 14.2.1.1.3.233 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R1 Registers
            234. 14.2.1.1.3.234 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R2 Registers
            235. 14.2.1.1.3.235 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R3 Registers
            236. 14.2.1.1.3.236 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R4 Registers
            237. 14.2.1.1.3.237 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R5 Registers
            238. 14.2.1.1.3.238 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R6 Registers
            239. 14.2.1.1.3.239 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R7 Registers
            240. 14.2.1.1.3.240 CFG0_WKUP_CTRL_MMR_CLAIMREG_P4_R8 Registers
            241. 14.2.1.1.3.241 CFG0_WKUP_CTRL_MMR_CHNG_DDR4_FSP_REQ Registers
            242. 14.2.1.1.3.242 CFG0_WKUP_CTRL_MMR_CHNG_DDR4_FSP_ACK Registers
            243. 14.2.1.1.3.243 CFG0_WKUP_CTRL_MMR_DDR4_FSP_CLKCHNG_REQ Registers
            244. 14.2.1.1.3.244 CFG0_WKUP_CTRL_MMR_DDR4_FSP_CLKCHNG_ACK Registers
            245. 14.2.1.1.3.245 CFG0_WKUP_CTRL_MMR_LOCK5_KICK0 Registers
            246. 14.2.1.1.3.246 CFG0_WKUP_CTRL_MMR_LOCK5_KICK1 Registers
            247. 14.2.1.1.3.247 CFG0_WKUP_CTRL_MMR_CLAIMREG_P5_R0_READONLY Registers
            248. 14.2.1.1.3.248 CFG0_WKUP_CTRL_MMR_CLAIMREG_P5_R1_READONLY Registers
            249. 14.2.1.1.3.249 CFG0_WKUP_CTRL_MMR_CHNG_DDR4_FSP_REQ_PROXY Registers
            250. 14.2.1.1.3.250 CFG0_WKUP_CTRL_MMR_CHNG_DDR4_FSP_ACK_PROXY Registers
            251. 14.2.1.1.3.251 CFG0_WKUP_CTRL_MMR_DDR4_FSP_CLKCHNG_REQ_PROXY Registers
            252. 14.2.1.1.3.252 CFG0_WKUP_CTRL_MMR_DDR4_FSP_CLKCHNG_ACK_PROXY Registers
            253. 14.2.1.1.3.253 CFG0_WKUP_CTRL_MMR_LOCK5_KICK0_PROXY Registers
            254. 14.2.1.1.3.254 CFG0_WKUP_CTRL_MMR_LOCK5_KICK1_PROXY Registers
            255. 14.2.1.1.3.255 CFG0_WKUP_CTRL_MMR_CLAIMREG_P5_R0 Registers
            256. 14.2.1.1.3.256 CFG0_WKUP_CTRL_MMR_CLAIMREG_P5_R1 Registers
            257. 14.2.1.1.3.257 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT0 Registers
            258. 14.2.1.1.3.258 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT0_SET Registers
            259. 14.2.1.1.3.259 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT0_CLR Registers
            260. 14.2.1.1.3.260 CFG0_WKUP_CTRL_MMR_FW_STS_IN0 Registers
            261. 14.2.1.1.3.261 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT1 Registers
            262. 14.2.1.1.3.262 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT1_SET Registers
            263. 14.2.1.1.3.263 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT1_CLR Registers
            264. 14.2.1.1.3.264 CFG0_WKUP_CTRL_MMR_FW_STS_IN1 Registers
            265. 14.2.1.1.3.265 CFG0_WKUP_CTRL_MMR_PMCTRL_SYS Registers
            266. 14.2.1.1.3.266 CFG0_WKUP_CTRL_MMR_PMCTRL_IO_0 Registers
            267. 14.2.1.1.3.267 CFG0_WKUP_CTRL_MMR_PMCTRL_IO_1 Registers
            268. 14.2.1.1.3.268 CFG0_WKUP_CTRL_MMR_PMCTRL_MOSC Registers
            269. 14.2.1.1.3.269 CFG0_WKUP_CTRL_MMR_PM_MISC_STATUS Registers
            270. 14.2.1.1.3.270 CFG0_WKUP_CTRL_MMR_PMCTRL_IO_GLB Registers
            271. 14.2.1.1.3.271 CFG0_WKUP_CTRL_MMR_PM_PERMISSION Registers
            272. 14.2.1.1.3.272 CFG0_WKUP_CTRL_MMR_DEEPSLEEP_CTRL Registers
            273. 14.2.1.1.3.273 CFG0_WKUP_CTRL_MMR_RST_CTRL Registers
            274. 14.2.1.1.3.274 CFG0_WKUP_CTRL_MMR_RST_STAT Registers
            275. 14.2.1.1.3.275 CFG0_WKUP_CTRL_MMR_RST_SRC Registers
            276. 14.2.1.1.3.276 CFG0_WKUP_CTRL_MMR_RST_MAGIC_WORD Registers
            277. 14.2.1.1.3.277 CFG0_WKUP_CTRL_MMR_WKUP0_EN Registers
            278. 14.2.1.1.3.278 CFG0_WKUP_CTRL_MMR_CLKGATE_CTRL Registers
            279. 14.2.1.1.3.279 CFG0_WKUP_CTRL_MMR_CANUART_WAKE_CTRL Registers
            280. 14.2.1.1.3.280 CFG0_WKUP_CTRL_MMR_CANUART_WAKE_STAT0 Registers
            281. 14.2.1.1.3.281 CFG0_WKUP_CTRL_MMR_CANUART_WAKE_STAT1 Registers
            282. 14.2.1.1.3.282 CFG0_WKUP_CTRL_MMR_WFI_STATUS Registers
            283. 14.2.1.1.3.283 CFG0_WKUP_CTRL_MMR_SLEEP_STATUS Registers
            284. 14.2.1.1.3.284 CFG0_WKUP_CTRL_MMR_DS_MAGIC_WORD Registers
            285. 14.2.1.1.3.285 CFG0_WKUP_CTRL_MMR_DS_MAIN Registers
            286. 14.2.1.1.3.286 CFG0_WKUP_CTRL_MMR_DS_DM_RESET Registers
            287. 14.2.1.1.3.287 CFG0_WKUP_CTRL_MMR_DS_DDR0_RESET Registers
            288. 14.2.1.1.3.288 CFG0_WKUP_CTRL_MMR_DS_USB0_RESET Registers
            289. 14.2.1.1.3.289 CFG0_WKUP_CTRL_MMR_DS_USB1_RESET Registers
            290. 14.2.1.1.3.290 CFG0_WKUP_CTRL_MMR_DM_CLKSTOP_EN Registers
            291. 14.2.1.1.3.291 CFG0_WKUP_CTRL_MMR_DM_CLKSTOP_ACK Registers
            292. 14.2.1.1.3.292 CFG0_WKUP_CTRL_MMR_DM_GRP_CLKSTOP_REQ Registers
            293. 14.2.1.1.3.293 CFG0_WKUP_CTRL_MMR_DM_GRP_CLKSTOP_ACK Registers
            294. 14.2.1.1.3.294 CFG0_WKUP_CTRL_MMR_DEVICE_TYPE Registers
            295. 14.2.1.1.3.295 CFG0_WKUP_CTRL_MMR_LOCK6_KICK0 Registers
            296. 14.2.1.1.3.296 CFG0_WKUP_CTRL_MMR_LOCK6_KICK1 Registers
            297. 14.2.1.1.3.297 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R0_READONLY Registers
            298. 14.2.1.1.3.298 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R1_READONLY Registers
            299. 14.2.1.1.3.299 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R2_READONLY Registers
            300. 14.2.1.1.3.300 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R3_READONLY Registers
            301. 14.2.1.1.3.301 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R4_READONLY Registers
            302. 14.2.1.1.3.302 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R5_READONLY Registers
            303. 14.2.1.1.3.303 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R6_READONLY Registers
            304. 14.2.1.1.3.304 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R7_READONLY Registers
            305. 14.2.1.1.3.305 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R8_READONLY Registers
            306. 14.2.1.1.3.306 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R9_READONLY Registers
            307. 14.2.1.1.3.307 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R10_READONLY Registers
            308. 14.2.1.1.3.308 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT0_PROXY Registers
            309. 14.2.1.1.3.309 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT0_SET_PROXY Registers
            310. 14.2.1.1.3.310 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT0_CLR_PROXY Registers
            311. 14.2.1.1.3.311 CFG0_WKUP_CTRL_MMR_FW_STS_IN0_PROXY Registers
            312. 14.2.1.1.3.312 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT1_PROXY Registers
            313. 14.2.1.1.3.313 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT1_SET_PROXY Registers
            314. 14.2.1.1.3.314 CFG0_WKUP_CTRL_MMR_FW_CTRL_OUT1_CLR_PROXY Registers
            315. 14.2.1.1.3.315 CFG0_WKUP_CTRL_MMR_FW_STS_IN1_PROXY Registers
            316. 14.2.1.1.3.316 CFG0_WKUP_CTRL_MMR_PMCTRL_SYS_PROXY Registers
            317. 14.2.1.1.3.317 CFG0_WKUP_CTRL_MMR_PMCTRL_IO_0_PROXY Registers
            318. 14.2.1.1.3.318 CFG0_WKUP_CTRL_MMR_PMCTRL_IO_1_PROXY Registers
            319. 14.2.1.1.3.319 CFG0_WKUP_CTRL_MMR_PMCTRL_MOSC_PROXY Registers
            320. 14.2.1.1.3.320 CFG0_WKUP_CTRL_MMR_PM_MISC_STATUS_PROXY Registers
            321. 14.2.1.1.3.321 CFG0_WKUP_CTRL_MMR_PMCTRL_IO_GLB_PROXY Registers
            322. 14.2.1.1.3.322 CFG0_WKUP_CTRL_MMR_PM_PERMISSION_PROXY Registers
            323. 14.2.1.1.3.323 CFG0_WKUP_CTRL_MMR_DEEPSLEEP_CTRL_PROXY Registers
            324. 14.2.1.1.3.324 CFG0_WKUP_CTRL_MMR_RST_CTRL_PROXY Registers
            325. 14.2.1.1.3.325 CFG0_WKUP_CTRL_MMR_RST_STAT_PROXY Registers
            326. 14.2.1.1.3.326 CFG0_WKUP_CTRL_MMR_RST_SRC_PROXY Registers
            327. 14.2.1.1.3.327 CFG0_WKUP_CTRL_MMR_RST_MAGIC_WORD_PROXY Registers
            328. 14.2.1.1.3.328 CFG0_WKUP_CTRL_MMR_WKUP0_EN_PROXY Registers
            329. 14.2.1.1.3.329 CFG0_WKUP_CTRL_MMR_CLKGATE_CTRL_PROXY Registers
            330. 14.2.1.1.3.330 CFG0_WKUP_CTRL_MMR_CANUART_WAKE_CTRL_PROXY Registers
            331. 14.2.1.1.3.331 CFG0_WKUP_CTRL_MMR_CANUART_WAKE_STAT0_PROXY Registers
            332. 14.2.1.1.3.332 CFG0_WKUP_CTRL_MMR_CANUART_WAKE_STAT1_PROXY Registers
            333. 14.2.1.1.3.333 CFG0_WKUP_CTRL_MMR_WFI_STATUS_PROXY Registers
            334. 14.2.1.1.3.334 CFG0_WKUP_CTRL_MMR_SLEEP_STATUS_PROXY Registers
            335. 14.2.1.1.3.335 CFG0_WKUP_CTRL_MMR_DS_MAGIC_WORD_PROXY Registers
            336. 14.2.1.1.3.336 CFG0_WKUP_CTRL_MMR_DS_MAIN_PROXY Registers
            337. 14.2.1.1.3.337 CFG0_WKUP_CTRL_MMR_DS_DM_RESET_PROXY Registers
            338. 14.2.1.1.3.338 CFG0_WKUP_CTRL_MMR_DS_DDR0_RESET_PROXY Registers
            339. 14.2.1.1.3.339 CFG0_WKUP_CTRL_MMR_DS_USB0_RESET_PROXY Registers
            340. 14.2.1.1.3.340 CFG0_WKUP_CTRL_MMR_DS_USB1_RESET_PROXY Registers
            341. 14.2.1.1.3.341 CFG0_WKUP_CTRL_MMR_DM_CLKSTOP_EN_PROXY Registers
            342. 14.2.1.1.3.342 CFG0_WKUP_CTRL_MMR_DM_CLKSTOP_ACK_PROXY Registers
            343. 14.2.1.1.3.343 CFG0_WKUP_CTRL_MMR_DM_GRP_CLKSTOP_REQ_PROXY Registers
            344. 14.2.1.1.3.344 CFG0_WKUP_CTRL_MMR_DM_GRP_CLKSTOP_ACK_PROXY Registers
            345. 14.2.1.1.3.345 CFG0_WKUP_CTRL_MMR_DEVICE_TYPE_PROXY Registers
            346. 14.2.1.1.3.346 CFG0_WKUP_CTRL_MMR_LOCK6_KICK0_PROXY Registers
            347. 14.2.1.1.3.347 CFG0_WKUP_CTRL_MMR_LOCK6_KICK1_PROXY Registers
            348. 14.2.1.1.3.348 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R0 Registers
            349. 14.2.1.1.3.349 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R1 Registers
            350. 14.2.1.1.3.350 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R2 Registers
            351. 14.2.1.1.3.351 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R3 Registers
            352. 14.2.1.1.3.352 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R4 Registers
            353. 14.2.1.1.3.353 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R5 Registers
            354. 14.2.1.1.3.354 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R6 Registers
            355. 14.2.1.1.3.355 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R7 Registers
            356. 14.2.1.1.3.356 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R8 Registers
            357. 14.2.1.1.3.357 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R9 Registers
            358. 14.2.1.1.3.358 CFG0_WKUP_CTRL_MMR_CLAIMREG_P6_R10 Registers
            359. 14.2.1.1.3.359 CFG0_WKUP_CTRL_MMR_BACKUP_REG Registers
            360. 14.2.1.1.3.360 CFG0_WKUP_CTRL_MMR_LOCK7_KICK0 Registers
            361. 14.2.1.1.3.361 CFG0_WKUP_CTRL_MMR_LOCK7_KICK1 Registers
            362. 14.2.1.1.3.362 CFG0_WKUP_CTRL_MMR_CLAIMREG_P7_R0_READONLY Registers
            363. 14.2.1.1.3.363 CFG0_WKUP_CTRL_MMR_CLAIMREG_P7_R1_READONLY Registers
            364. 14.2.1.1.3.364 CFG0_WKUP_CTRL_MMR_CLAIMREG_P7_R2_READONLY Registers
            365. 14.2.1.1.3.365 CFG0_WKUP_CTRL_MMR_BACKUP_REG_PROXY Registers
            366. 14.2.1.1.3.366 CFG0_WKUP_CTRL_MMR_LOCK7_KICK0_PROXY Registers
            367. 14.2.1.1.3.367 CFG0_WKUP_CTRL_MMR_LOCK7_KICK1_PROXY Registers
            368. 14.2.1.1.3.368 CFG0_WKUP_CTRL_MMR_CLAIMREG_P7_R0 Registers
            369. 14.2.1.1.3.369 CFG0_WKUP_CTRL_MMR_CLAIMREG_P7_R1 Registers
            370. 14.2.1.1.3.370 CFG0_WKUP_CTRL_MMR_CLAIMREG_P7_R2 Registers
            371. 14.2.1.1.3.371 Access Table
        2. 14.2.1.2 Pad Configuration Registers
          1. 14.2.1.2.1 Pad Configuration Register Functional Description
          2. 14.2.1.2.2 Pad Configuration PADCONFIG Registers
          3. 14.2.1.2.3 Pad Configuration Registers
            1. 14.2.1.2.3.1 PADCFG_CTRL Registers
              1. 14.2.1.2.3.1.1  CFG0_PID Registers
              2. 14.2.1.2.3.1.2  CFG0_MMR_CFG0 Registers
              3. 14.2.1.2.3.1.3  CFG0_MMR_CFG1 Registers
              4. 14.2.1.2.3.1.4  CFG0_LOCK0_KICK0 Registers
              5. 14.2.1.2.3.1.5  CFG0_LOCK0_KICK1 Registers
              6. 14.2.1.2.3.1.6  CFG0_INTR_RAW_STATUS Registers
              7. 14.2.1.2.3.1.7  CFG0_INTR_ENABLED_STATUS_CLEAR Registers
              8. 14.2.1.2.3.1.8  CFG0_INTR_ENABLE Registers
              9. 14.2.1.2.3.1.9  CFG0_INTR_ENABLE_CLEAR Registers
              10. 14.2.1.2.3.1.10 CFG0_EOI Registers
              11. 14.2.1.2.3.1.11 CFG0_FAULT_ADDRESS Registers
              12. 14.2.1.2.3.1.12 CFG0_FAULT_TYPE_STATUS Registers
              13. 14.2.1.2.3.1.13 CFG0_FAULT_ATTR_STATUS Registers
              14. 14.2.1.2.3.1.14 CFG0_FAULT_CLEAR Registers
              15. 14.2.1.2.3.1.15 CFG0_CLAIMREG_P0_R0_READONLY Registers
              16. 14.2.1.2.3.1.16 CFG0_PID_PROXY Registers
              17. 14.2.1.2.3.1.17 CFG0_MMR_CFG0_PROXY Registers
              18. 14.2.1.2.3.1.18 CFG0_MMR_CFG1_PROXY Registers
              19. 14.2.1.2.3.1.19 CFG0_LOCK0_KICK0_PROXY Registers
              20. 14.2.1.2.3.1.20 CFG0_LOCK0_KICK1_PROXY Registers
              21. 14.2.1.2.3.1.21 CFG0_INTR_RAW_STATUS_PROXY Registers
              22. 14.2.1.2.3.1.22 CFG0_INTR_ENABLED_STATUS_CLEAR_PROXY Registers
              23. 14.2.1.2.3.1.23 CFG0_INTR_ENABLE_PROXY Registers
              24. 14.2.1.2.3.1.24 CFG0_INTR_ENABLE_CLEAR_PROXY Registers
              25. 14.2.1.2.3.1.25 CFG0_EOI_PROXY Registers
              26. 14.2.1.2.3.1.26 CFG0_FAULT_ADDRESS_PROXY Registers
              27. 14.2.1.2.3.1.27 CFG0_FAULT_TYPE_STATUS_PROXY Registers
              28. 14.2.1.2.3.1.28 CFG0_FAULT_ATTR_STATUS_PROXY Registers
              29. 14.2.1.2.3.1.29 CFG0_FAULT_CLEAR_PROXY Registers
              30. 14.2.1.2.3.1.30 CFG0_CLAIMREG_P0_R0 Registers
              31. 14.2.1.2.3.1.31 CFG0_LOCK1_KICK0 Registers
              32. 14.2.1.2.3.1.32 CFG0_LOCK1_KICK1 Registers
              33. 14.2.1.2.3.1.33 CFG0_CLAIMREG_P1_R0_READONLY Registers
              34. 14.2.1.2.3.1.34 CFG0_CLAIMREG_P1_R1_READONLY Registers
              35. 14.2.1.2.3.1.35 CFG0_CLAIMREG_P1_R2_READONLY Registers
              36. 14.2.1.2.3.1.36 CFG0_CLAIMREG_P1_R3_READONLY Registers
              37. 14.2.1.2.3.1.37 CFG0_CLAIMREG_P1_R4_READONLY Registers
              38. 14.2.1.2.3.1.38 CFG0_CLAIMREG_P1_R5_READONLY Registers
              39. 14.2.1.2.3.1.39 CFG0_LOCK1_KICK0_PROXY Registers
              40. 14.2.1.2.3.1.40 CFG0_LOCK1_KICK1_PROXY Registers
              41. 14.2.1.2.3.1.41 CFG0_CLAIMREG_P1_R0 Registers
              42. 14.2.1.2.3.1.42 CFG0_CLAIMREG_P1_R1 Registers
              43. 14.2.1.2.3.1.43 CFG0_CLAIMREG_P1_R2 Registers
              44. 14.2.1.2.3.1.44 CFG0_CLAIMREG_P1_R3 Registers
              45. 14.2.1.2.3.1.45 CFG0_CLAIMREG_P1_R4 Registers
              46. 14.2.1.2.3.1.46 CFG0_CLAIMREG_P1_R5 Registers
              47. 14.2.1.2.3.1.47 Access Table
            2. 14.2.1.2.3.2 WKUP_PADCFG_CTRL Registers
              1. 14.2.1.2.3.2.1  CFG0_WKUP_PADCFG_CTRL_PID Registers
              2. 14.2.1.2.3.2.2  CFG0_WKUP_PADCFG_CTRL_MMR_CFG0 Registers
              3. 14.2.1.2.3.2.3  CFG0_WKUP_PADCFG_CTRL_MMR_CFG1 Registers
              4. 14.2.1.2.3.2.4  CFG0_WKUP_PADCFG_CTRL_LOCK0_KICK0 Registers
              5. 14.2.1.2.3.2.5  CFG0_WKUP_PADCFG_CTRL_LOCK0_KICK1 Registers
              6. 14.2.1.2.3.2.6  CFG0_WKUP_PADCFG_CTRL_INTR_RAW_STATUS Registers
              7. 14.2.1.2.3.2.7  CFG0_WKUP_PADCFG_CTRL_INTR_ENABLED_STATUS_CLEAR Registers
              8. 14.2.1.2.3.2.8  CFG0_WKUP_PADCFG_CTRL_INTR_ENABLE Registers
              9. 14.2.1.2.3.2.9  CFG0_WKUP_PADCFG_CTRL_INTR_ENABLE_CLEAR Registers
              10. 14.2.1.2.3.2.10 CFG0_WKUP_PADCFG_CTRL_EOI Registers
              11. 14.2.1.2.3.2.11 CFG0_WKUP_PADCFG_CTRL_FAULT_ADDRESS Registers
              12. 14.2.1.2.3.2.12 CFG0_WKUP_PADCFG_CTRL_FAULT_TYPE_STATUS Registers
              13. 14.2.1.2.3.2.13 CFG0_WKUP_PADCFG_CTRL_FAULT_ATTR_STATUS Registers
              14. 14.2.1.2.3.2.14 CFG0_WKUP_PADCFG_CTRL_FAULT_CLEAR Registers
              15. 14.2.1.2.3.2.15 CFG0_WKUP_PADCFG_CTRL_CLAIMREG_P0_R0_READONLY Registers
              16. 14.2.1.2.3.2.16 CFG0_WKUP_PADCFG_CTRL_PID_PROXY Registers
              17. 14.2.1.2.3.2.17 CFG0_WKUP_PADCFG_CTRL_MMR_CFG0_PROXY Registers
              18. 14.2.1.2.3.2.18 CFG0_WKUP_PADCFG_CTRL_MMR_CFG1_PROXY Registers
              19. 14.2.1.2.3.2.19 CFG0_WKUP_PADCFG_CTRL_LOCK0_KICK0_PROXY Registers
              20. 14.2.1.2.3.2.20 CFG0_WKUP_PADCFG_CTRL_LOCK0_KICK1_PROXY Registers
              21. 14.2.1.2.3.2.21 CFG0_WKUP_PADCFG_CTRL_INTR_RAW_STATUS_PROXY Registers
              22. 14.2.1.2.3.2.22 CFG0_WKUP_PADCFG_CTRL_INTR_ENABLED_STATUS_CLEAR_PROXY Registers
              23. 14.2.1.2.3.2.23 CFG0_WKUP_PADCFG_CTRL_INTR_ENABLE_PROXY Registers
              24. 14.2.1.2.3.2.24 CFG0_WKUP_PADCFG_CTRL_INTR_ENABLE_CLEAR_PROXY Registers
              25. 14.2.1.2.3.2.25 CFG0_WKUP_PADCFG_CTRL_EOI_PROXY Registers
              26. 14.2.1.2.3.2.26 CFG0_WKUP_PADCFG_CTRL_FAULT_ADDRESS_PROXY Registers
              27. 14.2.1.2.3.2.27 CFG0_WKUP_PADCFG_CTRL_FAULT_TYPE_STATUS_PROXY Registers
              28. 14.2.1.2.3.2.28 CFG0_WKUP_PADCFG_CTRL_FAULT_ATTR_STATUS_PROXY Registers
              29. 14.2.1.2.3.2.29 CFG0_WKUP_PADCFG_CTRL_FAULT_CLEAR_PROXY Registers
              30. 14.2.1.2.3.2.30 CFG0_WKUP_PADCFG_CTRL_CLAIMREG_P0_R0 Registers
              31. 14.2.1.2.3.2.31 CFG0_WKUP_PADCFG_CTRL_LOCK1_KICK0 Registers
              32. 14.2.1.2.3.2.32 CFG0_WKUP_PADCFG_CTRL_LOCK1_KICK1 Registers
              33. 14.2.1.2.3.2.33 CFG0_WKUP_PADCFG_CTRL_CLAIMREG_P1_R0_READONLY Registers
              34. 14.2.1.2.3.2.34 CFG0_WKUP_PADCFG_CTRL_CLAIMREG_P1_R1_READONLY Registers
              35. 14.2.1.2.3.2.35 CFG0_WKUP_PADCFG_CTRL_LOCK1_KICK0_PROXY Registers
              36. 14.2.1.2.3.2.36 CFG0_WKUP_PADCFG_CTRL_LOCK1_KICK1_PROXY Registers
              37. 14.2.1.2.3.2.37 CFG0_WKUP_PADCFG_CTRL_CLAIMREG_P1_R0 Registers
              38. 14.2.1.2.3.2.38 CFG0_WKUP_PADCFG_CTRL_CLAIMREG_P1_R1 Registers
              39. 14.2.1.2.3.2.39 Access Table
        3. 14.2.1.3 Kick Protection Registers
        4. 14.2.1.4 Security Control Registers
          1. 14.2.1.4.1 MAIN_SEC_MMR Registers
            1. 14.2.1.4.1.1  CFG2_CLSTR9_CORE0_DBG_CFG Registers
            2. 14.2.1.4.1.2  CFG2_CLSTR9_CORE1_DBG_CFG Registers
            3. 14.2.1.4.1.3  CFG2_CLSTR9_CORE2_DBG_CFG Registers
            4. 14.2.1.4.1.4  CFG2_CLSTR9_CORE3_DBG_CFG Registers
            5. 14.2.1.4.1.5  CFG2_CLSTR16_CORE0_DBG_CFG Registers
            6. 14.2.1.4.1.6  CFG0_PID Registers
            7. 14.2.1.4.1.7  CFG0_CLSTR9_DEF Registers
            8. 14.2.1.4.1.8  CFG0_CLSTR9_CFG Registers
            9. 14.2.1.4.1.9  CFG0_CLSTR9_PMCTRL Registers
            10. 14.2.1.4.1.10 CFG0_CLSTR9_PMSTAT Registers
            11. 14.2.1.4.1.11 CFG0_CLSTR9_CORE0_BOOTVECT_LO Registers
            12. 14.2.1.4.1.12 CFG0_CLSTR9_CORE0_BOOTVECT_HI Registers
            13. 14.2.1.4.1.13 CFG0_CLSTR9_CORE1_BOOTVECT_LO Registers
            14. 14.2.1.4.1.14 CFG0_CLSTR9_CORE1_BOOTVECT_HI Registers
            15. 14.2.1.4.1.15 CFG0_CLSTR9_CORE2_BOOTVECT_LO Registers
            16. 14.2.1.4.1.16 CFG0_CLSTR9_CORE2_BOOTVECT_HI Registers
            17. 14.2.1.4.1.17 CFG0_CLSTR9_CORE3_BOOTVECT_LO Registers
            18. 14.2.1.4.1.18 CFG0_CLSTR9_CORE3_BOOTVECT_HI Registers
            19. 14.2.1.4.1.19 CFG0_CLSTR16_DEF Registers
            20. 14.2.1.4.1.20 CFG0_CLSTR16_CORE0_PMSTAT Registers
            21. 14.2.1.4.1.21 CFG0_GIC_CONFIG Registers
            22. 14.2.1.4.1.22 Access Table
          2. 14.2.1.4.2 WKUP_SEC_MMR Registers
            1. 14.2.1.4.2.1  CFG2_CLSTR28_CORE0_DBG_CFG Registers
            2. 14.2.1.4.2.2  CFG0_PID Registers
            3. 14.2.1.4.2.3  CFG0_CLSTR28_DEF Registers
            4. 14.2.1.4.2.4  CFG0_CLSTR28_CFG Registers
            5. 14.2.1.4.2.5  CFG0_CLSTR28_CORE0_CFG Registers
            6. 14.2.1.4.2.6  CFG0_CLSTR28_CORE0_BOOTVECT_LO Registers
            7. 14.2.1.4.2.7  CFG0_CLSTR28_CORE0_BOOTVECT_HI Registers
            8. 14.2.1.4.2.8  CFG0_CLSTR28_CORE0_PMCTRL Registers
            9. 14.2.1.4.2.9  CFG0_CLSTR28_CORE0_PMSTAT Registers
            10. 14.2.1.4.2.10 Access Table
      2. 14.2.2 Power Registers
        1. 14.2.2.1 PSC Registers
          1. 14.2.2.1.1  _PSC_PID Registers
          2. 14.2.2.1.2  _PSC_GBLCTL Registers
          3. 14.2.2.1.3  _PSC_GBLSTAT Registers
          4. 14.2.2.1.4  _PSC_INTEVAL Registers
          5. 14.2.2.1.5  _PSC_MERRPR_N Registers
          6. 14.2.2.1.6  _PSC_MERRCR_N Registers
          7. 14.2.2.1.7  _PSC_PERRPR Registers
          8. 14.2.2.1.8  _PSC_PERRCR Registers
          9. 14.2.2.1.9  _PSC_EPCPR Registers
          10. 14.2.2.1.10 _PSC_EPCCR Registers
          11. 14.2.2.1.11 _PSC_RAILSTAT Registers
          12. 14.2.2.1.12 _PSC_RAILCTL Registers
          13. 14.2.2.1.13 _PSC_RAILSEL Registers
          14. 14.2.2.1.14 _PSC_PTCMD Registers
          15. 14.2.2.1.15 _PSC_PTSTAT Registers
          16. 14.2.2.1.16 _PSC_PDSTAT_N Registers
          17. 14.2.2.1.17 _PSC_PDCTL_N Registers
          18. 14.2.2.1.18 _PSC_PDCFG_N Registers
          19. 14.2.2.1.19 _PSC_MDCFG_N Registers
          20. 14.2.2.1.20 _PSC_MDSTAT_N Registers
          21. 14.2.2.1.21 _PSC_MDCTL_N Registers
          22. 14.2.2.1.22 Access Table
        2. 14.2.2.2 PSC_FW_0 Registers
          1. 14.2.2.2.1  FW_DST_FWCH_REGION_0_CH_0_CONTROL Registers
          2. 14.2.2.2.2  FW_DST_FWCH_REGION_0_CH_0_PERMISSION_0 Registers
          3. 14.2.2.2.3  FW_DST_FWCH_REGION_0_CH_0_PERMISSION_1 Registers
          4. 14.2.2.2.4  FW_DST_FWCH_REGION_0_CH_0_PERMISSION_2 Registers
          5. 14.2.2.2.5  FW_DST_FWCH_REGION_1_CH_0_CONTROL Registers
          6. 14.2.2.2.6  FW_DST_FWCH_REGION_1_CH_0_PERMISSION_0 Registers
          7. 14.2.2.2.7  FW_DST_FWCH_REGION_1_CH_0_PERMISSION_1 Registers
          8. 14.2.2.2.8  FW_DST_FWCH_REGION_1_CH_0_PERMISSION_2 Registers
          9. 14.2.2.2.9  FW_DST_FWCH_REGION_2_CH_0_CONTROL Registers
          10. 14.2.2.2.10 FW_DST_FWCH_REGION_2_CH_0_PERMISSION_0 Registers
          11. 14.2.2.2.11 FW_DST_FWCH_REGION_2_CH_0_PERMISSION_1 Registers
          12. 14.2.2.2.12 FW_DST_FWCH_REGION_2_CH_0_PERMISSION_2 Registers
          13. 14.2.2.2.13 FW_DST_FWCH_REGION_3_CH_0_CONTROL Registers
          14. 14.2.2.2.14 FW_DST_FWCH_REGION_3_CH_0_PERMISSION_0 Registers
          15. 14.2.2.2.15 FW_DST_FWCH_REGION_3_CH_0_PERMISSION_1 Registers
          16. 14.2.2.2.16 FW_DST_FWCH_REGION_3_CH_0_PERMISSION_2 Registers
          17. 14.2.2.2.17 FW_DST_FWCH_REGION_4_CH_0_CONTROL Registers
          18. 14.2.2.2.18 FW_DST_FWCH_REGION_4_CH_0_PERMISSION_0 Registers
          19. 14.2.2.2.19 FW_DST_FWCH_REGION_4_CH_0_PERMISSION_1 Registers
          20. 14.2.2.2.20 FW_DST_FWCH_REGION_4_CH_0_PERMISSION_2 Registers
          21. 14.2.2.2.21 GLB_PID Registers
          22. 14.2.2.2.22 GLB_DESTINATION_ID Registers
          23. 14.2.2.2.23 GLB_EXCEPTION_LOGGING_CONTROL Registers
          24. 14.2.2.2.24 GLB_EXCEPTION_LOGGING_HEADER0 Registers
          25. 14.2.2.2.25 GLB_EXCEPTION_LOGGING_HEADER1 Registers
          26. 14.2.2.2.26 GLB_EXCEPTION_LOGGING_DATA0 Registers
          27. 14.2.2.2.27 GLB_EXCEPTION_LOGGING_DATA1 Registers
          28. 14.2.2.2.28 GLB_EXCEPTION_LOGGING_DATA2 Registers
          29. 14.2.2.2.29 GLB_EXCEPTION_LOGGING_DATA3 Registers
          30. 14.2.2.2.30 GLB_EXCEPTION_PEND_SET Registers
          31. 14.2.2.2.31 GLB_EXCEPTION_PEND_CLEAR Registers
          32. 14.2.2.2.32 Access Table
        3. 14.2.2.3 VTM Registers
          1. 14.2.2.3.1  MMR_VBUSP_CFG1_VTM_PID Registers
          2. 14.2.2.3.2  MMR_VBUSP_CFG1_VTM_DEVINFO_PWR0 Registers
          3. 14.2.2.3.3  MMR_VBUSP_CFG1_VTM_GT_TH1_INT_RAW_STAT_SET Registers
          4. 14.2.2.3.4  MMR_VBUSP_CFG1_VTM_GT_TH1_INT_EN_STAT_CLR Registers
          5. 14.2.2.3.5  MMR_VBUSP_CFG1_VTM_GT_TH1_INT_EN_SET Registers
          6. 14.2.2.3.6  MMR_VBUSP_CFG1_VTM_GT_TH1_INT_EN_CLR Registers
          7. 14.2.2.3.7  MMR_VBUSP_CFG1_VTM_GT_TH2_INT_RAW_STAT_SET Registers
          8. 14.2.2.3.8  MMR_VBUSP_CFG1_VTM_GT_TH2_INT_EN_STAT_CLR Registers
          9. 14.2.2.3.9  MMR_VBUSP_CFG1_VTM_GT_TH2_INT_EN_SET Registers
          10. 14.2.2.3.10 MMR_VBUSP_CFG1_VTM_GT_TH2_INT_EN_CLR Registers
          11. 14.2.2.3.11 MMR_VBUSP_CFG1_VTM_LT_TH0_INT_RAW_STAT_SET Registers
          12. 14.2.2.3.12 MMR_VBUSP_CFG1_VTM_LT_TH0_INT_EN_STAT_CLR Registers
          13. 14.2.2.3.13 MMR_VBUSP_CFG1_VTM_LT_TH0_INT_EN_SET Registers
          14. 14.2.2.3.14 MMR_VBUSP_CFG1_VTM_LT_TH0_INT_EN_CLR Registers
          15. 14.2.2.3.15 MMR_VBUSP_CFG1_VTM_VD_VTM_VD_DEVINFO_J_J Registers
          16. 14.2.2.3.16 MMR_VBUSP_CFG1_VTM_VD_VTM_VD_OPPVID_J_J Registers
          17. 14.2.2.3.17 MMR_VBUSP_CFG1_VTM_VD_VTM_VD_EVT_STAT_J_J Registers
          18. 14.2.2.3.18 MMR_VBUSP_CFG1_VTM_VD_VTM_VD_EVT_SEL_SET_J_J Registers
          19. 14.2.2.3.19 MMR_VBUSP_CFG1_VTM_VD_VTM_VD_EVT_SEL_CLR_J_J Registers
          20. 14.2.2.3.20 MMR_VBUSP_CFG1_VTM_TMPSENS_VTM_TMPSENS_CTRL_J_J Registers
          21. 14.2.2.3.21 MMR_VBUSP_CFG1_VTM_TMPSENS_VTM_TMPSENS_STAT_J_J Registers
          22. 14.2.2.3.22 MMR_VBUSP_CFG1_VTM_TMPSENS_VTM_TMPSENS_TH_J_J Registers
          23. 14.2.2.3.23 MMR_VBUSP_CFG1_VTM_TMPSENS_VTM_TMPSENS_TH2_J_J Registers
          24. 14.2.2.3.24 MMR_VBUSP_CFG2_VTM_CLK_CTRL Registers
          25. 14.2.2.3.25 MMR_VBUSP_CFG2_VTM_MISC_CTRL Registers
          26. 14.2.2.3.26 MMR_VBUSP_CFG2_VTM_MISC_CTRL2 Registers
          27. 14.2.2.3.27 MMR_VBUSP_CFG2_VTM_SAMPLE_CTRL Registers
          28. 14.2.2.3.28 MMR_VBUSP_CFG2_VTM_TMPSENS_VTM_TMPSENS_CTRL_J_J Registers
          29. 14.2.2.3.29 MMR_VBUSP_CFG2_VTM_TMPSENS_VTM_TMPSENS_TRIM_J_J Registers
          30. 14.2.2.3.30 ECCAGGR_CFG_REV Registers
          31. 14.2.2.3.31 ECCAGGR_CFG_VECTOR Registers
          32. 14.2.2.3.32 ECCAGGR_CFG_STAT Registers
          33. 14.2.2.3.33 ECCAGGR_CFG_RESERVED_SVBUS_N Registers
          34. 14.2.2.3.34 ECCAGGR_CFG_SEC_EOI_REG Registers
          35. 14.2.2.3.35 ECCAGGR_CFG_SEC_STATUS_REG0 Registers
          36. 14.2.2.3.36 ECCAGGR_CFG_SEC_ENABLE_SET_REG0 Registers
          37. 14.2.2.3.37 ECCAGGR_CFG_SEC_ENABLE_CLR_REG0 Registers
          38. 14.2.2.3.38 ECCAGGR_CFG_DED_EOI_REG Registers
          39. 14.2.2.3.39 ECCAGGR_CFG_DED_STATUS_REG0 Registers
          40. 14.2.2.3.40 ECCAGGR_CFG_DED_ENABLE_SET_REG0 Registers
          41. 14.2.2.3.41 ECCAGGR_CFG_DED_ENABLE_CLR_REG0 Registers
          42. 14.2.2.3.42 ECCAGGR_CFG_AGGR_ENABLE_SET Registers
          43. 14.2.2.3.43 ECCAGGR_CFG_AGGR_ENABLE_CLR Registers
          44. 14.2.2.3.44 ECCAGGR_CFG_AGGR_STATUS_SET Registers
          45. 14.2.2.3.45 ECCAGGR_CFG_AGGR_STATUS_CLR Registers
          46. 14.2.2.3.46 Access Table
      3. 14.2.3 Clocking Registers
        1. 14.2.3.1 PLL Registers
          1. 14.2.3.1.1   CFG_PLL0_PID Registers
          2. 14.2.3.1.2   CFG_PLL0_CFG Registers
          3. 14.2.3.1.3   CFG_PLL0_LOCKKEY0 Registers
          4. 14.2.3.1.4   CFG_PLL0_LOCKKEY1 Registers
          5. 14.2.3.1.5   CFG_PLL0_CTRL Registers
          6. 14.2.3.1.6   CFG_PLL0_STAT Registers
          7. 14.2.3.1.7   CFG_PLL0_FREQ_CTRL0 Registers
          8. 14.2.3.1.8   CFG_PLL0_FREQ_CTRL1 Registers
          9. 14.2.3.1.9   CFG_PLL0_DIV_CTRL Registers
          10. 14.2.3.1.10  CFG_PLL0_SS_CTRL Registers
          11. 14.2.3.1.11  CFG_PLL0_SS_SPREAD Registers
          12. 14.2.3.1.12  CFG_PLL0_CAL_CTRL Registers
          13. 14.2.3.1.13  CFG_PLL0_CAL_STAT Registers
          14. 14.2.3.1.14  CFG_PLL0_HSDIV_CTRL0 Registers
          15. 14.2.3.1.15  CFG_PLL0_HSDIV_CTRL1 Registers
          16. 14.2.3.1.16  CFG_PLL0_HSDIV_CTRL2 Registers
          17. 14.2.3.1.17  CFG_PLL0_HSDIV_CTRL3 Registers
          18. 14.2.3.1.18  CFG_PLL0_HSDIV_CTRL4 Registers
          19. 14.2.3.1.19  CFG_PLL0_HSDIV_CTRL5 Registers
          20. 14.2.3.1.20  CFG_PLL0_HSDIV_CTRL6 Registers
          21. 14.2.3.1.21  CFG_PLL0_HSDIV_CTRL7 Registers
          22. 14.2.3.1.22  CFG_PLL0_HSDIV_CTRL8 Registers
          23. 14.2.3.1.23  CFG_PLL0_HSDIV_CTRL9 Registers
          24. 14.2.3.1.24  CFG_PLL1_PID Registers
          25. 14.2.3.1.25  CFG_PLL1_CFG Registers
          26. 14.2.3.1.26  CFG_PLL1_LOCKKEY0 Registers
          27. 14.2.3.1.27  CFG_PLL1_LOCKKEY1 Registers
          28. 14.2.3.1.28  CFG_PLL1_CTRL Registers
          29. 14.2.3.1.29  CFG_PLL1_STAT Registers
          30. 14.2.3.1.30  CFG_PLL1_FREQ_CTRL0 Registers
          31. 14.2.3.1.31  CFG_PLL1_FREQ_CTRL1 Registers
          32. 14.2.3.1.32  CFG_PLL1_DIV_CTRL Registers
          33. 14.2.3.1.33  CFG_PLL1_SS_CTRL Registers
          34. 14.2.3.1.34  CFG_PLL1_SS_SPREAD Registers
          35. 14.2.3.1.35  CFG_PLL1_CAL_CTRL Registers
          36. 14.2.3.1.36  CFG_PLL1_CAL_STAT Registers
          37. 14.2.3.1.37  CFG_PLL1_HSDIV_CTRL0 Registers
          38. 14.2.3.1.38  CFG_PLL1_HSDIV_CTRL1 Registers
          39. 14.2.3.1.39  CFG_PLL1_HSDIV_CTRL2 Registers
          40. 14.2.3.1.40  CFG_PLL1_HSDIV_CTRL3 Registers
          41. 14.2.3.1.41  CFG_PLL1_HSDIV_CTRL4 Registers
          42. 14.2.3.1.42  CFG_PLL1_HSDIV_CTRL5 Registers
          43. 14.2.3.1.43  CFG_PLL1_HSDIV_CTRL6 Registers
          44. 14.2.3.1.44  CFG_PLL2_PID Registers
          45. 14.2.3.1.45  CFG_PLL2_CFG Registers
          46. 14.2.3.1.46  CFG_PLL2_LOCKKEY0 Registers
          47. 14.2.3.1.47  CFG_PLL2_LOCKKEY1 Registers
          48. 14.2.3.1.48  CFG_PLL2_CTRL Registers
          49. 14.2.3.1.49  CFG_PLL2_STAT Registers
          50. 14.2.3.1.50  CFG_PLL2_FREQ_CTRL0 Registers
          51. 14.2.3.1.51  CFG_PLL2_FREQ_CTRL1 Registers
          52. 14.2.3.1.52  CFG_PLL2_DIV_CTRL Registers
          53. 14.2.3.1.53  CFG_PLL2_SS_CTRL Registers
          54. 14.2.3.1.54  CFG_PLL2_SS_SPREAD Registers
          55. 14.2.3.1.55  CFG_PLL2_CAL_CTRL Registers
          56. 14.2.3.1.56  CFG_PLL2_CAL_STAT Registers
          57. 14.2.3.1.57  CFG_PLL2_HSDIV_CTRL0 Registers
          58. 14.2.3.1.58  CFG_PLL2_HSDIV_CTRL1 Registers
          59. 14.2.3.1.59  CFG_PLL2_HSDIV_CTRL2 Registers
          60. 14.2.3.1.60  CFG_PLL2_HSDIV_CTRL3 Registers
          61. 14.2.3.1.61  CFG_PLL2_HSDIV_CTRL4 Registers
          62. 14.2.3.1.62  CFG_PLL2_HSDIV_CTRL5 Registers
          63. 14.2.3.1.63  CFG_PLL2_HSDIV_CTRL6 Registers
          64. 14.2.3.1.64  CFG_PLL2_HSDIV_CTRL7 Registers
          65. 14.2.3.1.65  CFG_PLL2_HSDIV_CTRL8 Registers
          66. 14.2.3.1.66  CFG_PLL2_HSDIV_CTRL9 Registers
          67. 14.2.3.1.67  CFG_PLL8_PID Registers
          68. 14.2.3.1.68  CFG_PLL8_CFG Registers
          69. 14.2.3.1.69  CFG_PLL8_LOCKKEY0 Registers
          70. 14.2.3.1.70  CFG_PLL8_LOCKKEY1 Registers
          71. 14.2.3.1.71  CFG_PLL8_CTRL Registers
          72. 14.2.3.1.72  CFG_PLL8_STAT Registers
          73. 14.2.3.1.73  CFG_PLL8_FREQ_CTRL0 Registers
          74. 14.2.3.1.74  CFG_PLL8_FREQ_CTRL1 Registers
          75. 14.2.3.1.75  CFG_PLL8_DIV_CTRL Registers
          76. 14.2.3.1.76  CFG_PLL8_SS_CTRL Registers
          77. 14.2.3.1.77  CFG_PLL8_SS_SPREAD Registers
          78. 14.2.3.1.78  CFG_PLL8_CAL_CTRL Registers
          79. 14.2.3.1.79  CFG_PLL8_CAL_STAT Registers
          80. 14.2.3.1.80  CFG_PLL8_HSDIV_CTRL0 Registers
          81. 14.2.3.1.81  CFG_PLL12_PID Registers
          82. 14.2.3.1.82  CFG_PLL12_CFG Registers
          83. 14.2.3.1.83  CFG_PLL12_LOCKKEY0 Registers
          84. 14.2.3.1.84  CFG_PLL12_LOCKKEY1 Registers
          85. 14.2.3.1.85  CFG_PLL12_CTRL Registers
          86. 14.2.3.1.86  CFG_PLL12_STAT Registers
          87. 14.2.3.1.87  CFG_PLL12_FREQ_CTRL0 Registers
          88. 14.2.3.1.88  CFG_PLL12_FREQ_CTRL1 Registers
          89. 14.2.3.1.89  CFG_PLL12_DIV_CTRL Registers
          90. 14.2.3.1.90  CFG_PLL12_SS_CTRL Registers
          91. 14.2.3.1.91  CFG_PLL12_SS_SPREAD Registers
          92. 14.2.3.1.92  CFG_PLL12_CAL_CTRL Registers
          93. 14.2.3.1.93  CFG_PLL12_CAL_STAT Registers
          94. 14.2.3.1.94  CFG_PLL12_HSDIV_CTRL0 Registers
          95. 14.2.3.1.95  CFG_PLL15_PID Registers
          96. 14.2.3.1.96  CFG_PLL15_CFG Registers
          97. 14.2.3.1.97  CFG_PLL15_LOCKKEY0 Registers
          98. 14.2.3.1.98  CFG_PLL15_LOCKKEY1 Registers
          99. 14.2.3.1.99  CFG_PLL15_CTRL Registers
          100. 14.2.3.1.100 CFG_PLL15_STAT Registers
          101. 14.2.3.1.101 CFG_PLL15_FREQ_CTRL0 Registers
          102. 14.2.3.1.102 CFG_PLL15_FREQ_CTRL1 Registers
          103. 14.2.3.1.103 CFG_PLL15_DIV_CTRL Registers
          104. 14.2.3.1.104 CFG_PLL15_SS_CTRL Registers
          105. 14.2.3.1.105 CFG_PLL15_SS_SPREAD Registers
          106. 14.2.3.1.106 CFG_PLL15_CAL_CTRL Registers
          107. 14.2.3.1.107 CFG_PLL15_CAL_STAT Registers
          108. 14.2.3.1.108 CFG_PLL15_HSDIV_CTRL0 Registers
          109. 14.2.3.1.109 CFG_PLL15_HSDIV_CTRL1 Registers
          110. 14.2.3.1.110 CFG_PLL16_PID Registers
          111. 14.2.3.1.111 CFG_PLL16_CFG Registers
          112. 14.2.3.1.112 CFG_PLL16_LOCKKEY0 Registers
          113. 14.2.3.1.113 CFG_PLL16_LOCKKEY1 Registers
          114. 14.2.3.1.114 CFG_PLL16_CTRL Registers
          115. 14.2.3.1.115 CFG_PLL16_STAT Registers
          116. 14.2.3.1.116 CFG_PLL16_FREQ_CTRL0 Registers
          117. 14.2.3.1.117 CFG_PLL16_FREQ_CTRL1 Registers
          118. 14.2.3.1.118 CFG_PLL16_DIV_CTRL Registers
          119. 14.2.3.1.119 CFG_PLL16_SS_CTRL Registers
          120. 14.2.3.1.120 CFG_PLL16_SS_SPREAD Registers
          121. 14.2.3.1.121 CFG_PLL16_CAL_CTRL Registers
          122. 14.2.3.1.122 CFG_PLL16_CAL_STAT Registers
          123. 14.2.3.1.123 CFG_PLL16_HSDIV_CTRL0 Registers
          124. 14.2.3.1.124 CFG_PLL17_PID Registers
          125. 14.2.3.1.125 CFG_PLL17_CFG Registers
          126. 14.2.3.1.126 CFG_PLL17_LOCKKEY0 Registers
          127. 14.2.3.1.127 CFG_PLL17_LOCKKEY1 Registers
          128. 14.2.3.1.128 CFG_PLL17_CTRL Registers
          129. 14.2.3.1.129 CFG_PLL17_STAT Registers
          130. 14.2.3.1.130 CFG_PLL17_FREQ_CTRL0 Registers
          131. 14.2.3.1.131 CFG_PLL17_FREQ_CTRL1 Registers
          132. 14.2.3.1.132 CFG_PLL17_DIV_CTRL Registers
          133. 14.2.3.1.133 CFG_PLL17_SS_CTRL Registers
          134. 14.2.3.1.134 CFG_PLL17_SS_SPREAD Registers
          135. 14.2.3.1.135 CFG_PLL17_CAL_CTRL Registers
          136. 14.2.3.1.136 CFG_PLL17_CAL_STAT Registers
          137. 14.2.3.1.137 CFG_PLL17_HSDIV_CTRL0 Registers
          138. 14.2.3.1.138 Access Table
    3. 14.3 Processors and Accelerators Registers
      1. 14.3.1 A53SS Registers
        1. 14.3.1.1 A53SS Registers
          1. 14.3.1.1.1    SS_ECC_AGGR_REV Registers
          2. 14.3.1.1.2    SS_ECC_AGGR_VECTOR Registers
          3. 14.3.1.1.3    SS_ECC_AGGR_STAT Registers
          4. 14.3.1.1.4    SS_ECC_AGGR_RESERVED_SVBUS_N Registers
          5. 14.3.1.1.5    SS_ECC_AGGR_SEC_EOI_REG Registers
          6. 14.3.1.1.6    SS_ECC_AGGR_SEC_STATUS_REG0 Registers
          7. 14.3.1.1.7    SS_ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          8. 14.3.1.1.8    SS_ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          9. 14.3.1.1.9    SS_ECC_AGGR_DED_EOI_REG Registers
          10. 14.3.1.1.10   SS_ECC_AGGR_DED_STATUS_REG0 Registers
          11. 14.3.1.1.11   SS_ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          12. 14.3.1.1.12   SS_ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          13. 14.3.1.1.13   SS_ECC_AGGR_AGGR_ENABLE_SET Registers
          14. 14.3.1.1.14   SS_ECC_AGGR_AGGR_ENABLE_CLR Registers
          15. 14.3.1.1.15   SS_ECC_AGGR_AGGR_STATUS_SET Registers
          16. 14.3.1.1.16   SS_ECC_AGGR_AGGR_STATUS_CLR Registers
          17. 14.3.1.1.17   CORE0_ECC_AGGR_REV Registers
          18. 14.3.1.1.18   CORE0_ECC_AGGR_VECTOR Registers
          19. 14.3.1.1.19   CORE0_ECC_AGGR_STAT Registers
          20. 14.3.1.1.20   CORE0_ECC_AGGR_RESERVED_SVBUS_N Registers
          21. 14.3.1.1.21   CORE0_ECC_AGGR_SEC_EOI_REG Registers
          22. 14.3.1.1.22   CORE0_ECC_AGGR_SEC_STATUS_REG0 Registers
          23. 14.3.1.1.23   CORE0_ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          24. 14.3.1.1.24   CORE0_ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          25. 14.3.1.1.25   CORE0_ECC_AGGR_DED_EOI_REG Registers
          26. 14.3.1.1.26   CORE0_ECC_AGGR_DED_STATUS_REG0 Registers
          27. 14.3.1.1.27   CORE0_ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          28. 14.3.1.1.28   CORE0_ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          29. 14.3.1.1.29   CORE0_ECC_AGGR_AGGR_ENABLE_SET Registers
          30. 14.3.1.1.30   CORE0_ECC_AGGR_AGGR_ENABLE_CLR Registers
          31. 14.3.1.1.31   CORE0_ECC_AGGR_AGGR_STATUS_SET Registers
          32. 14.3.1.1.32   CORE0_ECC_AGGR_AGGR_STATUS_CLR Registers
          33. 14.3.1.1.33   CORE1_ECC_AGGR_REV Registers
          34. 14.3.1.1.34   CORE1_ECC_AGGR_VECTOR Registers
          35. 14.3.1.1.35   CORE1_ECC_AGGR_STAT Registers
          36. 14.3.1.1.36   CORE1_ECC_AGGR_RESERVED_SVBUS_N Registers
          37. 14.3.1.1.37   CORE1_ECC_AGGR_SEC_EOI_REG Registers
          38. 14.3.1.1.38   CORE1_ECC_AGGR_SEC_STATUS_REG0 Registers
          39. 14.3.1.1.39   CORE1_ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          40. 14.3.1.1.40   CORE1_ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          41. 14.3.1.1.41   CORE1_ECC_AGGR_DED_EOI_REG Registers
          42. 14.3.1.1.42   CORE1_ECC_AGGR_DED_STATUS_REG0 Registers
          43. 14.3.1.1.43   CORE1_ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          44. 14.3.1.1.44   CORE1_ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          45. 14.3.1.1.45   CORE1_ECC_AGGR_AGGR_ENABLE_SET Registers
          46. 14.3.1.1.46   CORE1_ECC_AGGR_AGGR_ENABLE_CLR Registers
          47. 14.3.1.1.47   CORE1_ECC_AGGR_AGGR_STATUS_SET Registers
          48. 14.3.1.1.48   CORE1_ECC_AGGR_AGGR_STATUS_CLR Registers
          49. 14.3.1.1.49   CORE2_ECC_AGGR_REV Registers
          50. 14.3.1.1.50   CORE2_ECC_AGGR_VECTOR Registers
          51. 14.3.1.1.51   CORE2_ECC_AGGR_STAT Registers
          52. 14.3.1.1.52   CORE2_ECC_AGGR_RESERVED_SVBUS_N Registers
          53. 14.3.1.1.53   CORE2_ECC_AGGR_SEC_EOI_REG Registers
          54. 14.3.1.1.54   CORE2_ECC_AGGR_SEC_STATUS_REG0 Registers
          55. 14.3.1.1.55   CORE2_ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          56. 14.3.1.1.56   CORE2_ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          57. 14.3.1.1.57   CORE2_ECC_AGGR_DED_EOI_REG Registers
          58. 14.3.1.1.58   CORE2_ECC_AGGR_DED_STATUS_REG0 Registers
          59. 14.3.1.1.59   CORE2_ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          60. 14.3.1.1.60   CORE2_ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          61. 14.3.1.1.61   CORE2_ECC_AGGR_AGGR_ENABLE_SET Registers
          62. 14.3.1.1.62   CORE2_ECC_AGGR_AGGR_ENABLE_CLR Registers
          63. 14.3.1.1.63   CORE2_ECC_AGGR_AGGR_STATUS_SET Registers
          64. 14.3.1.1.64   CORE2_ECC_AGGR_AGGR_STATUS_CLR Registers
          65. 14.3.1.1.65   CORE3_ECC_AGGR_REV Registers
          66. 14.3.1.1.66   CORE3_ECC_AGGR_VECTOR Registers
          67. 14.3.1.1.67   CORE3_ECC_AGGR_STAT Registers
          68. 14.3.1.1.68   CORE3_ECC_AGGR_RESERVED_SVBUS_N Registers
          69. 14.3.1.1.69   CORE3_ECC_AGGR_SEC_EOI_REG Registers
          70. 14.3.1.1.70   CORE3_ECC_AGGR_SEC_STATUS_REG0 Registers
          71. 14.3.1.1.71   CORE3_ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          72. 14.3.1.1.72   CORE3_ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          73. 14.3.1.1.73   CORE3_ECC_AGGR_DED_EOI_REG Registers
          74. 14.3.1.1.74   CORE3_ECC_AGGR_DED_STATUS_REG0 Registers
          75. 14.3.1.1.75   CORE3_ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          76. 14.3.1.1.76   CORE3_ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          77. 14.3.1.1.77   CORE3_ECC_AGGR_AGGR_ENABLE_SET Registers
          78. 14.3.1.1.78   CORE3_ECC_AGGR_AGGR_ENABLE_CLR Registers
          79. 14.3.1.1.79   CORE3_ECC_AGGR_AGGR_STATUS_SET Registers
          80. 14.3.1.1.80   CORE3_ECC_AGGR_AGGR_STATUS_CLR Registers
          81. 14.3.1.1.81   SS_ROM_ROMENTRY0 Registers
          82. 14.3.1.1.82   SS_ROM_ROMENTRY1 Registers
          83. 14.3.1.1.83   SS_ROM_ROMENTRY2 Registers
          84. 14.3.1.1.84   SS_ROM_ROMENTRY3 Registers
          85. 14.3.1.1.85   SS_ROM_ROMENTRY4 Registers
          86. 14.3.1.1.86   SS_ROM_ROMENTRY5 Registers
          87. 14.3.1.1.87   SS_ROM_ROMENTRY6 Registers
          88. 14.3.1.1.88   SS_ROM_ROMENTRY7 Registers
          89. 14.3.1.1.89   SS_ROM_ROMENTRY8 Registers
          90. 14.3.1.1.90   SS_ROM_ROMENTRY9 Registers
          91. 14.3.1.1.91   SS_ROM_ROMENTRY10 Registers
          92. 14.3.1.1.92   SS_ROM_ROMENTRY11 Registers
          93. 14.3.1.1.93   SS_ROM_ROMENTRY12 Registers
          94. 14.3.1.1.94   SS_ROM_ROMENTRY13 Registers
          95. 14.3.1.1.95   SS_ROM_ROMENTRY14 Registers
          96. 14.3.1.1.96   SS_ROM_ROMENTRY15 Registers
          97. 14.3.1.1.97   SS_ROM_ROM_PERIPHID4_VAL Registers
          98. 14.3.1.1.98   SS_ROM_ROM_PERIPHID5_VAL Registers
          99. 14.3.1.1.99   SS_ROM_ROM_PERIPHID6_VAL Registers
          100. 14.3.1.1.100  SS_ROM_ROM_PERIPHID7_VAL Registers
          101. 14.3.1.1.101  SS_ROM_ROM_PERIPHID0_VAL Registers
          102. 14.3.1.1.102  SS_ROM_ROM_PERIPHID1_VAL Registers
          103. 14.3.1.1.103  SS_ROM_ROM_PERIPHID2_VAL Registers
          104. 14.3.1.1.104  SS_ROM_ROM_PERIPHID3_VAL Registers
          105. 14.3.1.1.105  SS_ROM_ROM_COMPONID0_VAL Registers
          106. 14.3.1.1.106  SS_ROM_ROM_COMPONID1_VAL Registers
          107. 14.3.1.1.107  SS_ROM_ROM_COMPONID2_VAL Registers
          108. 14.3.1.1.108  SS_ROM_ROM_COMPONID3_VAL Registers
          109. 14.3.1.1.109  CORE0_DBG_EDESR Registers
          110. 14.3.1.1.110  CORE0_DBG_EDECR Registers
          111. 14.3.1.1.111  CORE0_DBG_EDWAR_31_0 Registers
          112. 14.3.1.1.112  CORE0_DBG_EDWAR_63_32 Registers
          113. 14.3.1.1.113  CORE0_DBG_DBGDTRRX_EL0 Registers
          114. 14.3.1.1.114  CORE0_DBG_EDITR Registers
          115. 14.3.1.1.115  CORE0_DBG_EDSCR Registers
          116. 14.3.1.1.116  CORE0_DBG_DBGDTRTX_EL0 Registers
          117. 14.3.1.1.117  CORE0_DBG_EDRCR Registers
          118. 14.3.1.1.118  CORE0_DBG_EDACR Registers
          119. 14.3.1.1.119  CORE0_DBG_EDECCR Registers
          120. 14.3.1.1.120  CORE0_DBG_EDPCSR_31_0 Registers
          121. 14.3.1.1.121  CORE0_DBG_EDCIDSR Registers
          122. 14.3.1.1.122  CORE0_DBG_EDVIDSR Registers
          123. 14.3.1.1.123  CORE0_DBG_EDPCSR_63_32 Registers
          124. 14.3.1.1.124  CORE0_DBG_OSLAR_EL1 Registers
          125. 14.3.1.1.125  CORE0_DBG_EDPRCR Registers
          126. 14.3.1.1.126  CORE0_DBG_EDPRSR Registers
          127. 14.3.1.1.127  CORE0_DBG_DBGBVR0_EL1_31_0 Registers
          128. 14.3.1.1.128  CORE0_DBG_DBGBVR0_EL1_63_32 Registers
          129. 14.3.1.1.129  CORE0_DBG_DBGBCR0_EL1 Registers
          130. 14.3.1.1.130  CORE0_DBG_DBGBVR1_EL1_31_0 Registers
          131. 14.3.1.1.131  CORE0_DBG_DBGBVR1_EL1_63_32 Registers
          132. 14.3.1.1.132  CORE0_DBG_DBGBCR1_EL1 Registers
          133. 14.3.1.1.133  CORE0_DBG_DBGBVR2_EL1_31_0 Registers
          134. 14.3.1.1.134  CORE0_DBG_DBGBVR2_EL1_63_32 Registers
          135. 14.3.1.1.135  CORE0_DBG_DBGBCR2_EL1 Registers
          136. 14.3.1.1.136  CORE0_DBG_DBGBVR3_EL1_31_0 Registers
          137. 14.3.1.1.137  CORE0_DBG_DBGBVR3_EL1_63_32 Registers
          138. 14.3.1.1.138  CORE0_DBG_DBGBCR3_EL1 Registers
          139. 14.3.1.1.139  CORE0_DBG_DBGBVR4_EL1_31_0 Registers
          140. 14.3.1.1.140  CORE0_DBG_DBGBVR4_EL1_63_32 Registers
          141. 14.3.1.1.141  CORE0_DBG_DBGBCR4_EL1 Registers
          142. 14.3.1.1.142  CORE0_DBG_DBGBVR5_EL1_31_0 Registers
          143. 14.3.1.1.143  CORE0_DBG_DBGBVR5_EL1_63_32 Registers
          144. 14.3.1.1.144  CORE0_DBG_DBGBCR5_EL1 Registers
          145. 14.3.1.1.145  CORE0_DBG_DBGWVR0_EL1_31_0 Registers
          146. 14.3.1.1.146  CORE0_DBG_DBGWVR0_EL1_63_32 Registers
          147. 14.3.1.1.147  CORE0_DBG_DBGWCR0_EL1 Registers
          148. 14.3.1.1.148  CORE0_DBG_DBGWVR1_EL1_31_0 Registers
          149. 14.3.1.1.149  CORE0_DBG_DBGWVR1_EL1_63_32 Registers
          150. 14.3.1.1.150  CORE0_DBG_DBGWCR1_EL1 Registers
          151. 14.3.1.1.151  CORE0_DBG_DBGWVR2_EL1_31_0 Registers
          152. 14.3.1.1.152  CORE0_DBG_DBGWVR2_EL1_63_32 Registers
          153. 14.3.1.1.153  CORE0_DBG_DBGWCR2_EL1 Registers
          154. 14.3.1.1.154  CORE0_DBG_DBGWVR3_EL1_31_0 Registers
          155. 14.3.1.1.155  CORE0_DBG_DBGWVR3_EL1_63_32 Registers
          156. 14.3.1.1.156  CORE0_DBG_DBGWCR3_EL1 Registers
          157. 14.3.1.1.157  CORE0_DBG_MIDR_EL1 Registers
          158. 14.3.1.1.158  CORE0_DBG_ID_AA64PFR0_EL1_31_0 Registers
          159. 14.3.1.1.159  CORE0_DBG_ID_AA64PFR0_EL1_63_32 Registers
          160. 14.3.1.1.160  CORE0_DBG_ID_AA64DFR0_EL1_31_0 Registers
          161. 14.3.1.1.161  CORE0_DBG_ID_AA64DFR0_EL1_63_32 Registers
          162. 14.3.1.1.162  CORE0_DBG_ID_AA64ISAR0_EL1_31_0 Registers
          163. 14.3.1.1.163  CORE0_DBG_ID_AA64ISAR0_EL1_63_32 Registers
          164. 14.3.1.1.164  CORE0_DBG_ID_AA64MMFR0_EL1_31_0 Registers
          165. 14.3.1.1.165  CORE0_DBG_ID_AA64MMFR0_EL1_63_32 Registers
          166. 14.3.1.1.166  CORE0_DBG_ID_AA64PFR1_EL1_31_0 Registers
          167. 14.3.1.1.167  CORE0_DBG_ID_AA64PFR1_EL1_63_32 Registers
          168. 14.3.1.1.168  CORE0_DBG_ID_AA64DFR1_EL1_31_0 Registers
          169. 14.3.1.1.169  CORE0_DBG_ID_AA64DFR1_EL1_63_32 Registers
          170. 14.3.1.1.170  CORE0_DBG_ID_AA64ISAR1_EL1_31_0 Registers
          171. 14.3.1.1.171  CORE0_DBG_ID_AA64ISAR1_EL1_63_32 Registers
          172. 14.3.1.1.172  CORE0_DBG_ID_AA64MMFR1_EL1_31_0 Registers
          173. 14.3.1.1.173  CORE0_DBG_ID_AA64MMFR1_EL1_63_32 Registers
          174. 14.3.1.1.174  CORE0_DBG_EDITCTRL Registers
          175. 14.3.1.1.175  CORE0_DBG_DBGCLAIMSET_EL1 Registers
          176. 14.3.1.1.176  CORE0_DBG_DBGCLAIMCLR_EL1 Registers
          177. 14.3.1.1.177  CORE0_DBG_EDDEVAFF0 Registers
          178. 14.3.1.1.178  CORE0_DBG_EDDEVAFF1 Registers
          179. 14.3.1.1.179  CORE0_DBG_EDLAR Registers
          180. 14.3.1.1.180  CORE0_DBG_EDLSR Registers
          181. 14.3.1.1.181  CORE0_DBG_DBGAUTHSTATUS_EL1 Registers
          182. 14.3.1.1.182  CORE0_DBG_EDDEVARCH Registers
          183. 14.3.1.1.183  CORE0_DBG_EDDEVID2 Registers
          184. 14.3.1.1.184  CORE0_DBG_EDDEVID1 Registers
          185. 14.3.1.1.185  CORE0_DBG_EDDEVID Registers
          186. 14.3.1.1.186  CORE0_DBG_EDDEVTYPE Registers
          187. 14.3.1.1.187  CORE0_DBG_EDPIDR4 Registers
          188. 14.3.1.1.188  CORE0_DBG_EDPIDR0 Registers
          189. 14.3.1.1.189  CORE0_DBG_EDPIDR1 Registers
          190. 14.3.1.1.190  CORE0_DBG_EDPIDR2 Registers
          191. 14.3.1.1.191  CORE0_DBG_EDPIDR3 Registers
          192. 14.3.1.1.192  CORE0_DBG_EDCIDR0 Registers
          193. 14.3.1.1.193  CORE0_DBG_EDCIDR1 Registers
          194. 14.3.1.1.194  CORE0_DBG_EDCIDR2 Registers
          195. 14.3.1.1.195  CORE0_DBG_EDCIDR3 Registers
          196. 14.3.1.1.196  CORE0_CTI_CTICONTROL Registers
          197. 14.3.1.1.197  CORE0_CTI_CTIINTACK Registers
          198. 14.3.1.1.198  CORE0_CTI_CTIAPPSET Registers
          199. 14.3.1.1.199  CORE0_CTI_CTIAPPCLEAR Registers
          200. 14.3.1.1.200  CORE0_CTI_CTIAPPPULSE Registers
          201. 14.3.1.1.201  CORE0_CTI_CTIINEN0 Registers
          202. 14.3.1.1.202  CORE0_CTI_CTIINEN1 Registers
          203. 14.3.1.1.203  CORE0_CTI_CTIINEN2 Registers
          204. 14.3.1.1.204  CORE0_CTI_CTIINEN3 Registers
          205. 14.3.1.1.205  CORE0_CTI_CTIINEN4 Registers
          206. 14.3.1.1.206  CORE0_CTI_CTIINEN5 Registers
          207. 14.3.1.1.207  CORE0_CTI_CTIINEN6 Registers
          208. 14.3.1.1.208  CORE0_CTI_CTIINEN7 Registers
          209. 14.3.1.1.209  CORE0_CTI_CTIOUTEN0 Registers
          210. 14.3.1.1.210  CORE0_CTI_CTIOUTEN1 Registers
          211. 14.3.1.1.211  CORE0_CTI_CTIOUTEN2 Registers
          212. 14.3.1.1.212  CORE0_CTI_CTIOUTEN3 Registers
          213. 14.3.1.1.213  CORE0_CTI_CTIOUTEN4 Registers
          214. 14.3.1.1.214  CORE0_CTI_CTIOUTEN5 Registers
          215. 14.3.1.1.215  CORE0_CTI_CTIOUTEN6 Registers
          216. 14.3.1.1.216  CORE0_CTI_CTIOUTEN7 Registers
          217. 14.3.1.1.217  CORE0_CTI_CTITRIGINSTATUS Registers
          218. 14.3.1.1.218  CORE0_CTI_CTITRIGOUTSTATUS Registers
          219. 14.3.1.1.219  CORE0_CTI_CTICHINSTATUS Registers
          220. 14.3.1.1.220  CORE0_CTI_CTICHOUTSTATUS Registers
          221. 14.3.1.1.221  CORE0_CTI_CTIGATE Registers
          222. 14.3.1.1.222  CORE0_CTI_ASICCTL Registers
          223. 14.3.1.1.223  CORE0_CTI_CTIITCTRL Registers
          224. 14.3.1.1.224  CORE0_CTI_CTICLAIMSET Registers
          225. 14.3.1.1.225  CORE0_CTI_CTICLAIMCLR Registers
          226. 14.3.1.1.226  CORE0_CTI_CTIDEVAFF0 Registers
          227. 14.3.1.1.227  CORE0_CTI_CTIDEVAFF1 Registers
          228. 14.3.1.1.228  CORE0_CTI_CTILAR Registers
          229. 14.3.1.1.229  CORE0_CTI_CTILSR Registers
          230. 14.3.1.1.230  CORE0_CTI_CTIAUTHSTATUS Registers
          231. 14.3.1.1.231  CORE0_CTI_CTIDEVARCH Registers
          232. 14.3.1.1.232  CORE0_CTI_CTIDEVID2 Registers
          233. 14.3.1.1.233  CORE0_CTI_CTIDEVID1 Registers
          234. 14.3.1.1.234  CORE0_CTI_CTIDEVID Registers
          235. 14.3.1.1.235  CORE0_CTI_CTIDEVTYPE Registers
          236. 14.3.1.1.236  CORE0_CTI_CTIPIDR4 Registers
          237. 14.3.1.1.237  CORE0_CTI_CTIPIDR5 Registers
          238. 14.3.1.1.238  CORE0_CTI_CTIPIDR6 Registers
          239. 14.3.1.1.239  CORE0_CTI_CTIPIDR7 Registers
          240. 14.3.1.1.240  CORE0_CTI_CTIPIDR0 Registers
          241. 14.3.1.1.241  CORE0_CTI_CTIPIDR1 Registers
          242. 14.3.1.1.242  CORE0_CTI_CTIPIDR2 Registers
          243. 14.3.1.1.243  CORE0_CTI_CTIPIDR3 Registers
          244. 14.3.1.1.244  CORE0_CTI_CTICIDR0 Registers
          245. 14.3.1.1.245  CORE0_CTI_CTICIDR1 Registers
          246. 14.3.1.1.246  CORE0_CTI_CTICIDR2 Registers
          247. 14.3.1.1.247  CORE0_CTI_CTICIDR3 Registers
          248. 14.3.1.1.248  CORE0_PMU_PMEVCNTR0_EL0 Registers
          249. 14.3.1.1.249  CORE0_PMU_PMEVCNTR1_EL0 Registers
          250. 14.3.1.1.250  CORE0_PMU_PMEVCNTR2_EL0 Registers
          251. 14.3.1.1.251  CORE0_PMU_PMEVCNTR3_EL0 Registers
          252. 14.3.1.1.252  CORE0_PMU_PMEVCNTR4_EL0 Registers
          253. 14.3.1.1.253  CORE0_PMU_PMEVCNTR5_EL0 Registers
          254. 14.3.1.1.254  CORE0_PMU_PMCCNTR_EL0_31_0 Registers
          255. 14.3.1.1.255  CORE0_PMU_PMCCNTR_EL0_63_32 Registers
          256. 14.3.1.1.256  CORE0_PMU_PMEVTYPER0_EL0 Registers
          257. 14.3.1.1.257  CORE0_PMU_PMEVTYPER1_EL0 Registers
          258. 14.3.1.1.258  CORE0_PMU_PMEVTYPER2_EL0 Registers
          259. 14.3.1.1.259  CORE0_PMU_PMEVTYPER3_EL0 Registers
          260. 14.3.1.1.260  CORE0_PMU_PMEVTYPER4_EL0 Registers
          261. 14.3.1.1.261  CORE0_PMU_PMEVTYPER5_EL0 Registers
          262. 14.3.1.1.262  CORE0_PMU_PMCCFILTR_EL0 Registers
          263. 14.3.1.1.263  CORE0_PMU_PMCNTENSET_EL0 Registers
          264. 14.3.1.1.264  CORE0_PMU_PMCNTENCLR_EL0 Registers
          265. 14.3.1.1.265  CORE0_PMU_PMINTENSET_EL1 Registers
          266. 14.3.1.1.266  CORE0_PMU_PMINTENCLR_EL1 Registers
          267. 14.3.1.1.267  CORE0_PMU_PMOVSCLR_EL0 Registers
          268. 14.3.1.1.268  CORE0_PMU_PMSWINC_EL0 Registers
          269. 14.3.1.1.269  CORE0_PMU_PMOVSSET_EL0 Registers
          270. 14.3.1.1.270  CORE0_PMU_PMCFGR Registers
          271. 14.3.1.1.271  CORE0_PMU_PMCR_EL0 Registers
          272. 14.3.1.1.272  CORE0_PMU_PMCEID0_EL0 Registers
          273. 14.3.1.1.273  CORE0_PMU_PMCEID1_EL0 Registers
          274. 14.3.1.1.274  CORE0_PMU_PMITCTRL Registers
          275. 14.3.1.1.275  CORE0_PMU_PMDEVAFF0 Registers
          276. 14.3.1.1.276  CORE0_PMU_PMDEVAFF1 Registers
          277. 14.3.1.1.277  CORE0_PMU_PMLAR Registers
          278. 14.3.1.1.278  CORE0_PMU_PMLSR Registers
          279. 14.3.1.1.279  CORE0_PMU_PMAUTHSTATUS Registers
          280. 14.3.1.1.280  CORE0_PMU_PMDEVARCH Registers
          281. 14.3.1.1.281  CORE0_PMU_PMDEVTYPE Registers
          282. 14.3.1.1.282  CORE0_PMU_PMPIDR4 Registers
          283. 14.3.1.1.283  CORE0_PMU_PMPIDR5 Registers
          284. 14.3.1.1.284  CORE0_PMU_PMPIDR6 Registers
          285. 14.3.1.1.285  CORE0_PMU_PMPIDR7 Registers
          286. 14.3.1.1.286  CORE0_PMU_PMPIDR0 Registers
          287. 14.3.1.1.287  CORE0_PMU_PMPIDR1 Registers
          288. 14.3.1.1.288  CORE0_PMU_PMPIDR2 Registers
          289. 14.3.1.1.289  CORE0_PMU_PMPIDR3 Registers
          290. 14.3.1.1.290  CORE0_PMU_PMCIDR0 Registers
          291. 14.3.1.1.291  CORE0_PMU_PMCIDR1 Registers
          292. 14.3.1.1.292  CORE0_PMU_PMCIDR2 Registers
          293. 14.3.1.1.293  CORE0_PMU_PMCIDR3 Registers
          294. 14.3.1.1.294  CORE0_ETM_TRCPRGCTLR Registers
          295. 14.3.1.1.295  CORE0_ETM_TRCSTATR Registers
          296. 14.3.1.1.296  CORE0_ETM_TRCCONFIGR Registers
          297. 14.3.1.1.297  CORE0_ETM_TRCAUXCTLR Registers
          298. 14.3.1.1.298  CORE0_ETM_TRCEVENTCTL0R Registers
          299. 14.3.1.1.299  CORE0_ETM_TRCEVENTCTL1R Registers
          300. 14.3.1.1.300  CORE0_ETM_TRCSTALLCTLR Registers
          301. 14.3.1.1.301  CORE0_ETM_TRCTSCTLR Registers
          302. 14.3.1.1.302  CORE0_ETM_TRCSYNCPR Registers
          303. 14.3.1.1.303  CORE0_ETM_TRCCCCTLR Registers
          304. 14.3.1.1.304  CORE0_ETM_TRCBBCTLR Registers
          305. 14.3.1.1.305  CORE0_ETM_TRCTRACEIDR Registers
          306. 14.3.1.1.306  CORE0_ETM_TRCVICTLR Registers
          307. 14.3.1.1.307  CORE0_ETM_TRCVIIECTLR Registers
          308. 14.3.1.1.308  CORE0_ETM_TRCVISSCTLR Registers
          309. 14.3.1.1.309  CORE0_ETM_TRCSEQEVR0 Registers
          310. 14.3.1.1.310  CORE0_ETM_TRCSEQEVR1 Registers
          311. 14.3.1.1.311  CORE0_ETM_TRCSEQEVR2 Registers
          312. 14.3.1.1.312  CORE0_ETM_TRCSEQRSTEVR Registers
          313. 14.3.1.1.313  CORE0_ETM_TRCSEQSTR Registers
          314. 14.3.1.1.314  CORE0_ETM_TRCEXTINSELR Registers
          315. 14.3.1.1.315  CORE0_ETM_TRCCNTRLDVR0 Registers
          316. 14.3.1.1.316  CORE0_ETM_TRCCNTRLDVR1 Registers
          317. 14.3.1.1.317  CORE0_ETM_TRCCNTCTLR0 Registers
          318. 14.3.1.1.318  CORE0_ETM_TRCCNTCTLR1 Registers
          319. 14.3.1.1.319  CORE0_ETM_TRCCNTVR0 Registers
          320. 14.3.1.1.320  CORE0_ETM_TRCCNTVR1 Registers
          321. 14.3.1.1.321  CORE0_ETM_TRCIDR8 Registers
          322. 14.3.1.1.322  CORE0_ETM_TRCIDR9 Registers
          323. 14.3.1.1.323  CORE0_ETM_TRCIDR10 Registers
          324. 14.3.1.1.324  CORE0_ETM_TRCIDR11 Registers
          325. 14.3.1.1.325  CORE0_ETM_TRCIDR12 Registers
          326. 14.3.1.1.326  CORE0_ETM_TRCIDR13 Registers
          327. 14.3.1.1.327  CORE0_ETM_TRCIMSPEC0 Registers
          328. 14.3.1.1.328  CORE0_ETM_TRCIDR0 Registers
          329. 14.3.1.1.329  CORE0_ETM_TRCIDR1 Registers
          330. 14.3.1.1.330  CORE0_ETM_TRCIDR2 Registers
          331. 14.3.1.1.331  CORE0_ETM_TRCIDR3 Registers
          332. 14.3.1.1.332  CORE0_ETM_TRCIDR4 Registers
          333. 14.3.1.1.333  CORE0_ETM_TRCIDR5 Registers
          334. 14.3.1.1.334  CORE0_ETM_TRCRSCTLR2 Registers
          335. 14.3.1.1.335  CORE0_ETM_TRCRSCTLR3 Registers
          336. 14.3.1.1.336  CORE0_ETM_TRCRSCTLR4 Registers
          337. 14.3.1.1.337  CORE0_ETM_TRCRSCTLR5 Registers
          338. 14.3.1.1.338  CORE0_ETM_TRCRSCTLR6 Registers
          339. 14.3.1.1.339  CORE0_ETM_TRCRSCTLR7 Registers
          340. 14.3.1.1.340  CORE0_ETM_TRCRSCTLR8 Registers
          341. 14.3.1.1.341  CORE0_ETM_TRCRSCTLR9 Registers
          342. 14.3.1.1.342  CORE0_ETM_TRCRSCTLR10 Registers
          343. 14.3.1.1.343  CORE0_ETM_TRCRSCTLR11 Registers
          344. 14.3.1.1.344  CORE0_ETM_TRCRSCTLR12 Registers
          345. 14.3.1.1.345  CORE0_ETM_TRCRSCTLR13 Registers
          346. 14.3.1.1.346  CORE0_ETM_TRCRSCTLR14 Registers
          347. 14.3.1.1.347  CORE0_ETM_TRCRSCTLR15 Registers
          348. 14.3.1.1.348  CORE0_ETM_TRCSSCCR0 Registers
          349. 14.3.1.1.349  CORE0_ETM_TRCSSCSR0 Registers
          350. 14.3.1.1.350  CORE0_ETM_TRCOSLAR Registers
          351. 14.3.1.1.351  CORE0_ETM_TRCOSLSR Registers
          352. 14.3.1.1.352  CORE0_ETM_TRCPDCR Registers
          353. 14.3.1.1.353  CORE0_ETM_TRCPDSR Registers
          354. 14.3.1.1.354  CORE0_ETM_TRCACVR0_31_0 Registers
          355. 14.3.1.1.355  CORE0_ETM_TRCACVR0_63_32 Registers
          356. 14.3.1.1.356  CORE0_ETM_TRCACVR1_31_0 Registers
          357. 14.3.1.1.357  CORE0_ETM_TRCACVR1_63_32 Registers
          358. 14.3.1.1.358  CORE0_ETM_TRCACVR2_31_0 Registers
          359. 14.3.1.1.359  CORE0_ETM_TRCACVR2_63_32 Registers
          360. 14.3.1.1.360  CORE0_ETM_TRCACVR3_31_0 Registers
          361. 14.3.1.1.361  CORE0_ETM_TRCACVR3_63_32 Registers
          362. 14.3.1.1.362  CORE0_ETM_TRCACVR4_31_0 Registers
          363. 14.3.1.1.363  CORE0_ETM_TRCACVR4_63_32 Registers
          364. 14.3.1.1.364  CORE0_ETM_TRCACVR5_31_0 Registers
          365. 14.3.1.1.365  CORE0_ETM_TRCACVR5_63_32 Registers
          366. 14.3.1.1.366  CORE0_ETM_TRCACVR6_31_0 Registers
          367. 14.3.1.1.367  CORE0_ETM_TRCACVR6_63_32 Registers
          368. 14.3.1.1.368  CORE0_ETM_TRCACVR7_31_0 Registers
          369. 14.3.1.1.369  CORE0_ETM_TRCACVR7_63_32 Registers
          370. 14.3.1.1.370  CORE0_ETM_TRCACATR0 Registers
          371. 14.3.1.1.371  CORE0_ETM_TRCACATR1 Registers
          372. 14.3.1.1.372  CORE0_ETM_TRCACATR2 Registers
          373. 14.3.1.1.373  CORE0_ETM_TRCACATR3 Registers
          374. 14.3.1.1.374  CORE0_ETM_TRCACATR4 Registers
          375. 14.3.1.1.375  CORE0_ETM_TRCACATR5 Registers
          376. 14.3.1.1.376  CORE0_ETM_TRCACATR6 Registers
          377. 14.3.1.1.377  CORE0_ETM_TRCACATR7 Registers
          378. 14.3.1.1.378  CORE0_ETM_TRCCIDCVR0 Registers
          379. 14.3.1.1.379  CORE0_ETM_TRCVMIDCVR0 Registers
          380. 14.3.1.1.380  CORE0_ETM_TRCCIDCCTLR0 Registers
          381. 14.3.1.1.381  CORE0_ETM_TRCITATBIDR Registers
          382. 14.3.1.1.382  CORE0_ETM_TRCITIDATAR Registers
          383. 14.3.1.1.383  CORE0_ETM_TRCITIATBINR Registers
          384. 14.3.1.1.384  CORE0_ETM_TRCITIATBOUTR Registers
          385. 14.3.1.1.385  CORE0_ETM_TRCITCTRL Registers
          386. 14.3.1.1.386  CORE0_ETM_TRCCLAIMSET Registers
          387. 14.3.1.1.387  CORE0_ETM_TRCCLAIMCLR Registers
          388. 14.3.1.1.388  CORE0_ETM_TRCDEVAFF0 Registers
          389. 14.3.1.1.389  CORE0_ETM_TRCDEVAFF1 Registers
          390. 14.3.1.1.390  CORE0_ETM_TRCLAR Registers
          391. 14.3.1.1.391  CORE0_ETM_TRCLSR Registers
          392. 14.3.1.1.392  CORE0_ETM_TRCAUTHSTATUS Registers
          393. 14.3.1.1.393  CORE0_ETM_TRCDEVARCH Registers
          394. 14.3.1.1.394  CORE0_ETM_TRCDEVID Registers
          395. 14.3.1.1.395  CORE0_ETM_TRCDEVTYPE Registers
          396. 14.3.1.1.396  CORE0_ETM_TRCPIDR4 Registers
          397. 14.3.1.1.397  CORE0_ETM_TRCPIDR5 Registers
          398. 14.3.1.1.398  CORE0_ETM_TRCPIDR6 Registers
          399. 14.3.1.1.399  CORE0_ETM_TRCPIDR7 Registers
          400. 14.3.1.1.400  CORE0_ETM_TRCPIDR0 Registers
          401. 14.3.1.1.401  CORE0_ETM_TRCPIDR1 Registers
          402. 14.3.1.1.402  CORE0_ETM_TRCPIDR2 Registers
          403. 14.3.1.1.403  CORE0_ETM_TRCPIDR3 Registers
          404. 14.3.1.1.404  CORE0_ETM_TRCCIDR0 Registers
          405. 14.3.1.1.405  CORE0_ETM_TRCCIDR1 Registers
          406. 14.3.1.1.406  CORE0_ETM_TRCCIDR2 Registers
          407. 14.3.1.1.407  CORE0_ETM_TRCCIDR3 Registers
          408. 14.3.1.1.408  CORE1_DBG_EDESR Registers
          409. 14.3.1.1.409  CORE1_DBG_EDECR Registers
          410. 14.3.1.1.410  CORE1_DBG_EDWAR_31_0 Registers
          411. 14.3.1.1.411  CORE1_DBG_EDWAR_63_32 Registers
          412. 14.3.1.1.412  CORE1_DBG_DBGDTRRX_EL0 Registers
          413. 14.3.1.1.413  CORE1_DBG_EDITR Registers
          414. 14.3.1.1.414  CORE1_DBG_EDSCR Registers
          415. 14.3.1.1.415  CORE1_DBG_DBGDTRTX_EL0 Registers
          416. 14.3.1.1.416  CORE1_DBG_EDRCR Registers
          417. 14.3.1.1.417  CORE1_DBG_EDACR Registers
          418. 14.3.1.1.418  CORE1_DBG_EDECCR Registers
          419. 14.3.1.1.419  CORE1_DBG_EDPCSR_31_0 Registers
          420. 14.3.1.1.420  CORE1_DBG_EDCIDSR Registers
          421. 14.3.1.1.421  CORE1_DBG_EDVIDSR Registers
          422. 14.3.1.1.422  CORE1_DBG_EDPCSR_63_32 Registers
          423. 14.3.1.1.423  CORE1_DBG_OSLAR_EL1 Registers
          424. 14.3.1.1.424  CORE1_DBG_EDPRCR Registers
          425. 14.3.1.1.425  CORE1_DBG_EDPRSR Registers
          426. 14.3.1.1.426  CORE1_DBG_DBGBVR0_EL1_31_0 Registers
          427. 14.3.1.1.427  CORE1_DBG_DBGBVR0_EL1_63_32 Registers
          428. 14.3.1.1.428  CORE1_DBG_DBGBCR0_EL1 Registers
          429. 14.3.1.1.429  CORE1_DBG_DBGBVR1_EL1_31_0 Registers
          430. 14.3.1.1.430  CORE1_DBG_DBGBVR1_EL1_63_32 Registers
          431. 14.3.1.1.431  CORE1_DBG_DBGBCR1_EL1 Registers
          432. 14.3.1.1.432  CORE1_DBG_DBGBVR2_EL1_31_0 Registers
          433. 14.3.1.1.433  CORE1_DBG_DBGBVR2_EL1_63_32 Registers
          434. 14.3.1.1.434  CORE1_DBG_DBGBCR2_EL1 Registers
          435. 14.3.1.1.435  CORE1_DBG_DBGBVR3_EL1_31_0 Registers
          436. 14.3.1.1.436  CORE1_DBG_DBGBVR3_EL1_63_32 Registers
          437. 14.3.1.1.437  CORE1_DBG_DBGBCR3_EL1 Registers
          438. 14.3.1.1.438  CORE1_DBG_DBGBVR4_EL1_31_0 Registers
          439. 14.3.1.1.439  CORE1_DBG_DBGBVR4_EL1_63_32 Registers
          440. 14.3.1.1.440  CORE1_DBG_DBGBCR4_EL1 Registers
          441. 14.3.1.1.441  CORE1_DBG_DBGBVR5_EL1_31_0 Registers
          442. 14.3.1.1.442  CORE1_DBG_DBGBVR5_EL1_63_32 Registers
          443. 14.3.1.1.443  CORE1_DBG_DBGBCR5_EL1 Registers
          444. 14.3.1.1.444  CORE1_DBG_DBGWVR0_EL1_31_0 Registers
          445. 14.3.1.1.445  CORE1_DBG_DBGWVR0_EL1_63_32 Registers
          446. 14.3.1.1.446  CORE1_DBG_DBGWCR0_EL1 Registers
          447. 14.3.1.1.447  CORE1_DBG_DBGWVR1_EL1_31_0 Registers
          448. 14.3.1.1.448  CORE1_DBG_DBGWVR1_EL1_63_32 Registers
          449. 14.3.1.1.449  CORE1_DBG_DBGWCR1_EL1 Registers
          450. 14.3.1.1.450  CORE1_DBG_DBGWVR2_EL1_31_0 Registers
          451. 14.3.1.1.451  CORE1_DBG_DBGWVR2_EL1_63_32 Registers
          452. 14.3.1.1.452  CORE1_DBG_DBGWCR2_EL1 Registers
          453. 14.3.1.1.453  CORE1_DBG_DBGWVR3_EL1_31_0 Registers
          454. 14.3.1.1.454  CORE1_DBG_DBGWVR3_EL1_63_32 Registers
          455. 14.3.1.1.455  CORE1_DBG_DBGWCR3_EL1 Registers
          456. 14.3.1.1.456  CORE1_DBG_MIDR_EL1 Registers
          457. 14.3.1.1.457  CORE1_DBG_ID_AA64PFR0_EL1_31_0 Registers
          458. 14.3.1.1.458  CORE1_DBG_ID_AA64PFR0_EL1_63_32 Registers
          459. 14.3.1.1.459  CORE1_DBG_ID_AA64DFR0_EL1_31_0 Registers
          460. 14.3.1.1.460  CORE1_DBG_ID_AA64DFR0_EL1_63_32 Registers
          461. 14.3.1.1.461  CORE1_DBG_ID_AA64ISAR0_EL1_31_0 Registers
          462. 14.3.1.1.462  CORE1_DBG_ID_AA64ISAR0_EL1_63_32 Registers
          463. 14.3.1.1.463  CORE1_DBG_ID_AA64MMFR0_EL1_31_0 Registers
          464. 14.3.1.1.464  CORE1_DBG_ID_AA64MMFR0_EL1_63_32 Registers
          465. 14.3.1.1.465  CORE1_DBG_ID_AA64PFR1_EL1_31_0 Registers
          466. 14.3.1.1.466  CORE1_DBG_ID_AA64PFR1_EL1_63_32 Registers
          467. 14.3.1.1.467  CORE1_DBG_ID_AA64DFR1_EL1_31_0 Registers
          468. 14.3.1.1.468  CORE1_DBG_ID_AA64DFR1_EL1_63_32 Registers
          469. 14.3.1.1.469  CORE1_DBG_ID_AA64ISAR1_EL1_31_0 Registers
          470. 14.3.1.1.470  CORE1_DBG_ID_AA64ISAR1_EL1_63_32 Registers
          471. 14.3.1.1.471  CORE1_DBG_ID_AA64MMFR1_EL1_31_0 Registers
          472. 14.3.1.1.472  CORE1_DBG_ID_AA64MMFR1_EL1_63_32 Registers
          473. 14.3.1.1.473  CORE1_DBG_EDITCTRL Registers
          474. 14.3.1.1.474  CORE1_DBG_DBGCLAIMSET_EL1 Registers
          475. 14.3.1.1.475  CORE1_DBG_DBGCLAIMCLR_EL1 Registers
          476. 14.3.1.1.476  CORE1_DBG_EDDEVAFF0 Registers
          477. 14.3.1.1.477  CORE1_DBG_EDDEVAFF1 Registers
          478. 14.3.1.1.478  CORE1_DBG_EDLAR Registers
          479. 14.3.1.1.479  CORE1_DBG_EDLSR Registers
          480. 14.3.1.1.480  CORE1_DBG_DBGAUTHSTATUS_EL1 Registers
          481. 14.3.1.1.481  CORE1_DBG_EDDEVARCH Registers
          482. 14.3.1.1.482  CORE1_DBG_EDDEVID2 Registers
          483. 14.3.1.1.483  CORE1_DBG_EDDEVID1 Registers
          484. 14.3.1.1.484  CORE1_DBG_EDDEVID Registers
          485. 14.3.1.1.485  CORE1_DBG_EDDEVTYPE Registers
          486. 14.3.1.1.486  CORE1_DBG_EDPIDR4 Registers
          487. 14.3.1.1.487  CORE1_DBG_EDPIDR0 Registers
          488. 14.3.1.1.488  CORE1_DBG_EDPIDR1 Registers
          489. 14.3.1.1.489  CORE1_DBG_EDPIDR2 Registers
          490. 14.3.1.1.490  CORE1_DBG_EDPIDR3 Registers
          491. 14.3.1.1.491  CORE1_DBG_EDCIDR0 Registers
          492. 14.3.1.1.492  CORE1_DBG_EDCIDR1 Registers
          493. 14.3.1.1.493  CORE1_DBG_EDCIDR2 Registers
          494. 14.3.1.1.494  CORE1_DBG_EDCIDR3 Registers
          495. 14.3.1.1.495  CORE1_PMU_PMEVCNTR0_EL0 Registers
          496. 14.3.1.1.496  CORE1_PMU_PMEVCNTR1_EL0 Registers
          497. 14.3.1.1.497  CORE1_PMU_PMEVCNTR2_EL0 Registers
          498. 14.3.1.1.498  CORE1_PMU_PMEVCNTR3_EL0 Registers
          499. 14.3.1.1.499  CORE1_PMU_PMEVCNTR4_EL0 Registers
          500. 14.3.1.1.500  CORE1_PMU_PMEVCNTR5_EL0 Registers
          501. 14.3.1.1.501  CORE1_PMU_PMCCNTR_EL0_31_0 Registers
          502. 14.3.1.1.502  CORE1_PMU_PMCCNTR_EL0_63_32 Registers
          503. 14.3.1.1.503  CORE1_PMU_PMEVTYPER0_EL0 Registers
          504. 14.3.1.1.504  CORE1_PMU_PMEVTYPER1_EL0 Registers
          505. 14.3.1.1.505  CORE1_PMU_PMEVTYPER2_EL0 Registers
          506. 14.3.1.1.506  CORE1_PMU_PMEVTYPER3_EL0 Registers
          507. 14.3.1.1.507  CORE1_PMU_PMEVTYPER4_EL0 Registers
          508. 14.3.1.1.508  CORE1_PMU_PMEVTYPER5_EL0 Registers
          509. 14.3.1.1.509  CORE1_PMU_PMCCFILTR_EL0 Registers
          510. 14.3.1.1.510  CORE1_PMU_PMCNTENSET_EL0 Registers
          511. 14.3.1.1.511  CORE1_PMU_PMCNTENCLR_EL0 Registers
          512. 14.3.1.1.512  CORE1_PMU_PMINTENSET_EL1 Registers
          513. 14.3.1.1.513  CORE1_PMU_PMINTENCLR_EL1 Registers
          514. 14.3.1.1.514  CORE1_PMU_PMOVSCLR_EL0 Registers
          515. 14.3.1.1.515  CORE1_PMU_PMSWINC_EL0 Registers
          516. 14.3.1.1.516  CORE1_PMU_PMOVSSET_EL0 Registers
          517. 14.3.1.1.517  CORE1_PMU_PMCFGR Registers
          518. 14.3.1.1.518  CORE1_PMU_PMCR_EL0 Registers
          519. 14.3.1.1.519  CORE1_PMU_PMCEID0_EL0 Registers
          520. 14.3.1.1.520  CORE1_PMU_PMCEID1_EL0 Registers
          521. 14.3.1.1.521  CORE1_PMU_PMITCTRL Registers
          522. 14.3.1.1.522  CORE1_PMU_PMDEVAFF0 Registers
          523. 14.3.1.1.523  CORE1_PMU_PMDEVAFF1 Registers
          524. 14.3.1.1.524  CORE1_PMU_PMLAR Registers
          525. 14.3.1.1.525  CORE1_PMU_PMLSR Registers
          526. 14.3.1.1.526  CORE1_PMU_PMAUTHSTATUS Registers
          527. 14.3.1.1.527  CORE1_PMU_PMDEVARCH Registers
          528. 14.3.1.1.528  CORE1_PMU_PMDEVTYPE Registers
          529. 14.3.1.1.529  CORE1_PMU_PMPIDR4 Registers
          530. 14.3.1.1.530  CORE1_PMU_PMPIDR5 Registers
          531. 14.3.1.1.531  CORE1_PMU_PMPIDR6 Registers
          532. 14.3.1.1.532  CORE1_PMU_PMPIDR7 Registers
          533. 14.3.1.1.533  CORE1_PMU_PMPIDR0 Registers
          534. 14.3.1.1.534  CORE1_PMU_PMPIDR1 Registers
          535. 14.3.1.1.535  CORE1_PMU_PMPIDR2 Registers
          536. 14.3.1.1.536  CORE1_PMU_PMPIDR3 Registers
          537. 14.3.1.1.537  CORE1_PMU_PMCIDR0 Registers
          538. 14.3.1.1.538  CORE1_PMU_PMCIDR1 Registers
          539. 14.3.1.1.539  CORE1_PMU_PMCIDR2 Registers
          540. 14.3.1.1.540  CORE1_PMU_PMCIDR3 Registers
          541. 14.3.1.1.541  CORE1_ETM_TRCPRGCTLR Registers
          542. 14.3.1.1.542  CORE1_ETM_TRCSTATR Registers
          543. 14.3.1.1.543  CORE1_ETM_TRCCONFIGR Registers
          544. 14.3.1.1.544  CORE1_ETM_TRCAUXCTLR Registers
          545. 14.3.1.1.545  CORE1_ETM_TRCEVENTCTL0R Registers
          546. 14.3.1.1.546  CORE1_ETM_TRCEVENTCTL1R Registers
          547. 14.3.1.1.547  CORE1_ETM_TRCSTALLCTLR Registers
          548. 14.3.1.1.548  CORE1_ETM_TRCTSCTLR Registers
          549. 14.3.1.1.549  CORE1_ETM_TRCSYNCPR Registers
          550. 14.3.1.1.550  CORE1_ETM_TRCCCCTLR Registers
          551. 14.3.1.1.551  CORE1_ETM_TRCBBCTLR Registers
          552. 14.3.1.1.552  CORE1_ETM_TRCTRACEIDR Registers
          553. 14.3.1.1.553  CORE1_ETM_TRCVICTLR Registers
          554. 14.3.1.1.554  CORE1_ETM_TRCVIIECTLR Registers
          555. 14.3.1.1.555  CORE1_ETM_TRCVISSCTLR Registers
          556. 14.3.1.1.556  CORE1_ETM_TRCSEQEVR0 Registers
          557. 14.3.1.1.557  CORE1_ETM_TRCSEQEVR1 Registers
          558. 14.3.1.1.558  CORE1_ETM_TRCSEQEVR2 Registers
          559. 14.3.1.1.559  CORE1_ETM_TRCSEQRSTEVR Registers
          560. 14.3.1.1.560  CORE1_ETM_TRCSEQSTR Registers
          561. 14.3.1.1.561  CORE1_ETM_TRCEXTINSELR Registers
          562. 14.3.1.1.562  CORE1_ETM_TRCCNTRLDVR0 Registers
          563. 14.3.1.1.563  CORE1_ETM_TRCCNTRLDVR1 Registers
          564. 14.3.1.1.564  CORE1_ETM_TRCCNTCTLR0 Registers
          565. 14.3.1.1.565  CORE1_ETM_TRCCNTCTLR1 Registers
          566. 14.3.1.1.566  CORE1_ETM_TRCCNTVR0 Registers
          567. 14.3.1.1.567  CORE1_ETM_TRCCNTVR1 Registers
          568. 14.3.1.1.568  CORE1_ETM_TRCIDR8 Registers
          569. 14.3.1.1.569  CORE1_ETM_TRCIDR9 Registers
          570. 14.3.1.1.570  CORE1_ETM_TRCIDR10 Registers
          571. 14.3.1.1.571  CORE1_ETM_TRCIDR11 Registers
          572. 14.3.1.1.572  CORE1_ETM_TRCIDR12 Registers
          573. 14.3.1.1.573  CORE1_ETM_TRCIDR13 Registers
          574. 14.3.1.1.574  CORE1_ETM_TRCIMSPEC0 Registers
          575. 14.3.1.1.575  CORE1_ETM_TRCIDR0 Registers
          576. 14.3.1.1.576  CORE1_ETM_TRCIDR1 Registers
          577. 14.3.1.1.577  CORE1_ETM_TRCIDR2 Registers
          578. 14.3.1.1.578  CORE1_ETM_TRCIDR3 Registers
          579. 14.3.1.1.579  CORE1_ETM_TRCIDR4 Registers
          580. 14.3.1.1.580  CORE1_ETM_TRCIDR5 Registers
          581. 14.3.1.1.581  CORE1_ETM_TRCRSCTLR2 Registers
          582. 14.3.1.1.582  CORE1_ETM_TRCRSCTLR3 Registers
          583. 14.3.1.1.583  CORE1_ETM_TRCRSCTLR4 Registers
          584. 14.3.1.1.584  CORE1_ETM_TRCRSCTLR5 Registers
          585. 14.3.1.1.585  CORE1_ETM_TRCRSCTLR6 Registers
          586. 14.3.1.1.586  CORE1_ETM_TRCRSCTLR7 Registers
          587. 14.3.1.1.587  CORE1_ETM_TRCRSCTLR8 Registers
          588. 14.3.1.1.588  CORE1_ETM_TRCRSCTLR9 Registers
          589. 14.3.1.1.589  CORE1_ETM_TRCRSCTLR10 Registers
          590. 14.3.1.1.590  CORE1_ETM_TRCRSCTLR11 Registers
          591. 14.3.1.1.591  CORE1_ETM_TRCRSCTLR12 Registers
          592. 14.3.1.1.592  CORE1_ETM_TRCRSCTLR13 Registers
          593. 14.3.1.1.593  CORE1_ETM_TRCRSCTLR14 Registers
          594. 14.3.1.1.594  CORE1_ETM_TRCRSCTLR15 Registers
          595. 14.3.1.1.595  CORE1_ETM_TRCSSCCR0 Registers
          596. 14.3.1.1.596  CORE1_ETM_TRCSSCSR0 Registers
          597. 14.3.1.1.597  CORE1_ETM_TRCOSLAR Registers
          598. 14.3.1.1.598  CORE1_ETM_TRCOSLSR Registers
          599. 14.3.1.1.599  CORE1_ETM_TRCPDCR Registers
          600. 14.3.1.1.600  CORE1_ETM_TRCPDSR Registers
          601. 14.3.1.1.601  CORE1_ETM_TRCACVR0_31_0 Registers
          602. 14.3.1.1.602  CORE1_ETM_TRCACVR0_63_32 Registers
          603. 14.3.1.1.603  CORE1_ETM_TRCACVR1_31_0 Registers
          604. 14.3.1.1.604  CORE1_ETM_TRCACVR1_63_32 Registers
          605. 14.3.1.1.605  CORE1_ETM_TRCACVR2_31_0 Registers
          606. 14.3.1.1.606  CORE1_ETM_TRCACVR2_63_32 Registers
          607. 14.3.1.1.607  CORE1_ETM_TRCACVR3_31_0 Registers
          608. 14.3.1.1.608  CORE1_ETM_TRCACVR3_63_32 Registers
          609. 14.3.1.1.609  CORE1_ETM_TRCACVR4_31_0 Registers
          610. 14.3.1.1.610  CORE1_ETM_TRCACVR4_63_32 Registers
          611. 14.3.1.1.611  CORE1_ETM_TRCACVR5_31_0 Registers
          612. 14.3.1.1.612  CORE1_ETM_TRCACVR5_63_32 Registers
          613. 14.3.1.1.613  CORE1_ETM_TRCACVR6_31_0 Registers
          614. 14.3.1.1.614  CORE1_ETM_TRCACVR6_63_32 Registers
          615. 14.3.1.1.615  CORE1_ETM_TRCACVR7_31_0 Registers
          616. 14.3.1.1.616  CORE1_ETM_TRCACVR7_63_32 Registers
          617. 14.3.1.1.617  CORE1_ETM_TRCACATR0 Registers
          618. 14.3.1.1.618  CORE1_ETM_TRCACATR1 Registers
          619. 14.3.1.1.619  CORE1_ETM_TRCACATR2 Registers
          620. 14.3.1.1.620  CORE1_ETM_TRCACATR3 Registers
          621. 14.3.1.1.621  CORE1_ETM_TRCACATR4 Registers
          622. 14.3.1.1.622  CORE1_ETM_TRCACATR5 Registers
          623. 14.3.1.1.623  CORE1_ETM_TRCACATR6 Registers
          624. 14.3.1.1.624  CORE1_ETM_TRCACATR7 Registers
          625. 14.3.1.1.625  CORE1_ETM_TRCCIDCVR0 Registers
          626. 14.3.1.1.626  CORE1_ETM_TRCVMIDCVR0 Registers
          627. 14.3.1.1.627  CORE1_ETM_TRCCIDCCTLR0 Registers
          628. 14.3.1.1.628  CORE1_ETM_TRCITATBIDR Registers
          629. 14.3.1.1.629  CORE1_ETM_TRCITIDATAR Registers
          630. 14.3.1.1.630  CORE1_ETM_TRCITIATBINR Registers
          631. 14.3.1.1.631  CORE1_ETM_TRCITIATBOUTR Registers
          632. 14.3.1.1.632  CORE1_ETM_TRCITCTRL Registers
          633. 14.3.1.1.633  CORE1_ETM_TRCCLAIMSET Registers
          634. 14.3.1.1.634  CORE1_ETM_TRCCLAIMCLR Registers
          635. 14.3.1.1.635  CORE1_ETM_TRCDEVAFF0 Registers
          636. 14.3.1.1.636  CORE1_ETM_TRCDEVAFF1 Registers
          637. 14.3.1.1.637  CORE1_ETM_TRCLAR Registers
          638. 14.3.1.1.638  CORE1_ETM_TRCLSR Registers
          639. 14.3.1.1.639  CORE1_ETM_TRCAUTHSTATUS Registers
          640. 14.3.1.1.640  CORE1_ETM_TRCDEVARCH Registers
          641. 14.3.1.1.641  CORE1_ETM_TRCDEVID Registers
          642. 14.3.1.1.642  CORE1_ETM_TRCDEVTYPE Registers
          643. 14.3.1.1.643  CORE1_ETM_TRCPIDR4 Registers
          644. 14.3.1.1.644  CORE1_ETM_TRCPIDR5 Registers
          645. 14.3.1.1.645  CORE1_ETM_TRCPIDR6 Registers
          646. 14.3.1.1.646  CORE1_ETM_TRCPIDR7 Registers
          647. 14.3.1.1.647  CORE1_ETM_TRCPIDR0 Registers
          648. 14.3.1.1.648  CORE1_ETM_TRCPIDR1 Registers
          649. 14.3.1.1.649  CORE1_ETM_TRCPIDR2 Registers
          650. 14.3.1.1.650  CORE1_ETM_TRCPIDR3 Registers
          651. 14.3.1.1.651  CORE1_ETM_TRCCIDR0 Registers
          652. 14.3.1.1.652  CORE1_ETM_TRCCIDR1 Registers
          653. 14.3.1.1.653  CORE1_ETM_TRCCIDR2 Registers
          654. 14.3.1.1.654  CORE1_ETM_TRCCIDR3 Registers
          655. 14.3.1.1.655  CORE1_CTI_CTICONTROL Registers
          656. 14.3.1.1.656  CORE1_CTI_CTIINTACK Registers
          657. 14.3.1.1.657  CORE1_CTI_CTIAPPSET Registers
          658. 14.3.1.1.658  CORE1_CTI_CTIAPPCLEAR Registers
          659. 14.3.1.1.659  CORE1_CTI_CTIAPPPULSE Registers
          660. 14.3.1.1.660  CORE1_CTI_CTIINEN0 Registers
          661. 14.3.1.1.661  CORE1_CTI_CTIINEN1 Registers
          662. 14.3.1.1.662  CORE1_CTI_CTIINEN2 Registers
          663. 14.3.1.1.663  CORE1_CTI_CTIINEN3 Registers
          664. 14.3.1.1.664  CORE1_CTI_CTIINEN4 Registers
          665. 14.3.1.1.665  CORE1_CTI_CTIINEN5 Registers
          666. 14.3.1.1.666  CORE1_CTI_CTIINEN6 Registers
          667. 14.3.1.1.667  CORE1_CTI_CTIINEN7 Registers
          668. 14.3.1.1.668  CORE1_CTI_CTIOUTEN0 Registers
          669. 14.3.1.1.669  CORE1_CTI_CTIOUTEN1 Registers
          670. 14.3.1.1.670  CORE1_CTI_CTIOUTEN2 Registers
          671. 14.3.1.1.671  CORE1_CTI_CTIOUTEN3 Registers
          672. 14.3.1.1.672  CORE1_CTI_CTIOUTEN4 Registers
          673. 14.3.1.1.673  CORE1_CTI_CTIOUTEN5 Registers
          674. 14.3.1.1.674  CORE1_CTI_CTIOUTEN6 Registers
          675. 14.3.1.1.675  CORE1_CTI_CTIOUTEN7 Registers
          676. 14.3.1.1.676  CORE1_CTI_CTITRIGINSTATUS Registers
          677. 14.3.1.1.677  CORE1_CTI_CTITRIGOUTSTATUS Registers
          678. 14.3.1.1.678  CORE1_CTI_CTICHINSTATUS Registers
          679. 14.3.1.1.679  CORE1_CTI_CTICHOUTSTATUS Registers
          680. 14.3.1.1.680  CORE1_CTI_CTIGATE Registers
          681. 14.3.1.1.681  CORE1_CTI_ASICCTL Registers
          682. 14.3.1.1.682  CORE1_CTI_CTIITCTRL Registers
          683. 14.3.1.1.683  CORE1_CTI_CTICLAIMSET Registers
          684. 14.3.1.1.684  CORE1_CTI_CTICLAIMCLR Registers
          685. 14.3.1.1.685  CORE1_CTI_CTIDEVAFF0 Registers
          686. 14.3.1.1.686  CORE1_CTI_CTIDEVAFF1 Registers
          687. 14.3.1.1.687  CORE1_CTI_CTILAR Registers
          688. 14.3.1.1.688  CORE1_CTI_CTILSR Registers
          689. 14.3.1.1.689  CORE1_CTI_CTIAUTHSTATUS Registers
          690. 14.3.1.1.690  CORE1_CTI_CTIDEVARCH Registers
          691. 14.3.1.1.691  CORE1_CTI_CTIDEVID2 Registers
          692. 14.3.1.1.692  CORE1_CTI_CTIDEVID1 Registers
          693. 14.3.1.1.693  CORE1_CTI_CTIDEVID Registers
          694. 14.3.1.1.694  CORE1_CTI_CTIDEVTYPE Registers
          695. 14.3.1.1.695  CORE1_CTI_CTIPIDR4 Registers
          696. 14.3.1.1.696  CORE1_CTI_CTIPIDR5 Registers
          697. 14.3.1.1.697  CORE1_CTI_CTIPIDR6 Registers
          698. 14.3.1.1.698  CORE1_CTI_CTIPIDR7 Registers
          699. 14.3.1.1.699  CORE1_CTI_CTIPIDR0 Registers
          700. 14.3.1.1.700  CORE1_CTI_CTIPIDR1 Registers
          701. 14.3.1.1.701  CORE1_CTI_CTIPIDR2 Registers
          702. 14.3.1.1.702  CORE1_CTI_CTIPIDR3 Registers
          703. 14.3.1.1.703  CORE1_CTI_CTICIDR0 Registers
          704. 14.3.1.1.704  CORE1_CTI_CTICIDR1 Registers
          705. 14.3.1.1.705  CORE1_CTI_CTICIDR2 Registers
          706. 14.3.1.1.706  CORE1_CTI_CTICIDR3 Registers
          707. 14.3.1.1.707  CORE2_DBG_EDESR Registers
          708. 14.3.1.1.708  CORE2_DBG_EDECR Registers
          709. 14.3.1.1.709  CORE2_DBG_EDWAR_31_0 Registers
          710. 14.3.1.1.710  CORE2_DBG_EDWAR_63_32 Registers
          711. 14.3.1.1.711  CORE2_DBG_DBGDTRRX_EL0 Registers
          712. 14.3.1.1.712  CORE2_DBG_EDITR Registers
          713. 14.3.1.1.713  CORE2_DBG_EDSCR Registers
          714. 14.3.1.1.714  CORE2_DBG_DBGDTRTX_EL0 Registers
          715. 14.3.1.1.715  CORE2_DBG_EDRCR Registers
          716. 14.3.1.1.716  CORE2_DBG_EDACR Registers
          717. 14.3.1.1.717  CORE2_DBG_EDECCR Registers
          718. 14.3.1.1.718  CORE2_DBG_EDPCSR_31_0 Registers
          719. 14.3.1.1.719  CORE2_DBG_EDCIDSR Registers
          720. 14.3.1.1.720  CORE2_DBG_EDVIDSR Registers
          721. 14.3.1.1.721  CORE2_DBG_EDPCSR_63_32 Registers
          722. 14.3.1.1.722  CORE2_DBG_OSLAR_EL1 Registers
          723. 14.3.1.1.723  CORE2_DBG_EDPRCR Registers
          724. 14.3.1.1.724  CORE2_DBG_EDPRSR Registers
          725. 14.3.1.1.725  CORE2_DBG_DBGBVR0_EL1_31_0 Registers
          726. 14.3.1.1.726  CORE2_DBG_DBGBVR0_EL1_63_32 Registers
          727. 14.3.1.1.727  CORE2_DBG_DBGBCR0_EL1 Registers
          728. 14.3.1.1.728  CORE2_DBG_DBGBVR1_EL1_31_0 Registers
          729. 14.3.1.1.729  CORE2_DBG_DBGBVR1_EL1_63_32 Registers
          730. 14.3.1.1.730  CORE2_DBG_DBGBCR1_EL1 Registers
          731. 14.3.1.1.731  CORE2_DBG_DBGBVR2_EL1_31_0 Registers
          732. 14.3.1.1.732  CORE2_DBG_DBGBVR2_EL1_63_32 Registers
          733. 14.3.1.1.733  CORE2_DBG_DBGBCR2_EL1 Registers
          734. 14.3.1.1.734  CORE2_DBG_DBGBVR3_EL1_31_0 Registers
          735. 14.3.1.1.735  CORE2_DBG_DBGBVR3_EL1_63_32 Registers
          736. 14.3.1.1.736  CORE2_DBG_DBGBCR3_EL1 Registers
          737. 14.3.1.1.737  CORE2_DBG_DBGBVR4_EL1_31_0 Registers
          738. 14.3.1.1.738  CORE2_DBG_DBGBVR4_EL1_63_32 Registers
          739. 14.3.1.1.739  CORE2_DBG_DBGBCR4_EL1 Registers
          740. 14.3.1.1.740  CORE2_DBG_DBGBVR5_EL1_31_0 Registers
          741. 14.3.1.1.741  CORE2_DBG_DBGBVR5_EL1_63_32 Registers
          742. 14.3.1.1.742  CORE2_DBG_DBGBCR5_EL1 Registers
          743. 14.3.1.1.743  CORE2_DBG_DBGWVR0_EL1_31_0 Registers
          744. 14.3.1.1.744  CORE2_DBG_DBGWVR0_EL1_63_32 Registers
          745. 14.3.1.1.745  CORE2_DBG_DBGWCR0_EL1 Registers
          746. 14.3.1.1.746  CORE2_DBG_DBGWVR1_EL1_31_0 Registers
          747. 14.3.1.1.747  CORE2_DBG_DBGWVR1_EL1_63_32 Registers
          748. 14.3.1.1.748  CORE2_DBG_DBGWCR1_EL1 Registers
          749. 14.3.1.1.749  CORE2_DBG_DBGWVR2_EL1_31_0 Registers
          750. 14.3.1.1.750  CORE2_DBG_DBGWVR2_EL1_63_32 Registers
          751. 14.3.1.1.751  CORE2_DBG_DBGWCR2_EL1 Registers
          752. 14.3.1.1.752  CORE2_DBG_DBGWVR3_EL1_31_0 Registers
          753. 14.3.1.1.753  CORE2_DBG_DBGWVR3_EL1_63_32 Registers
          754. 14.3.1.1.754  CORE2_DBG_DBGWCR3_EL1 Registers
          755. 14.3.1.1.755  CORE2_DBG_MIDR_EL1 Registers
          756. 14.3.1.1.756  CORE2_DBG_ID_AA64PFR0_EL1_31_0 Registers
          757. 14.3.1.1.757  CORE2_DBG_ID_AA64PFR0_EL1_63_32 Registers
          758. 14.3.1.1.758  CORE2_DBG_ID_AA64DFR0_EL1_31_0 Registers
          759. 14.3.1.1.759  CORE2_DBG_ID_AA64DFR0_EL1_63_32 Registers
          760. 14.3.1.1.760  CORE2_DBG_ID_AA64ISAR0_EL1_31_0 Registers
          761. 14.3.1.1.761  CORE2_DBG_ID_AA64ISAR0_EL1_63_32 Registers
          762. 14.3.1.1.762  CORE2_DBG_ID_AA64MMFR0_EL1_31_0 Registers
          763. 14.3.1.1.763  CORE2_DBG_ID_AA64MMFR0_EL1_63_32 Registers
          764. 14.3.1.1.764  CORE2_DBG_ID_AA64PFR1_EL1_31_0 Registers
          765. 14.3.1.1.765  CORE2_DBG_ID_AA64PFR1_EL1_63_32 Registers
          766. 14.3.1.1.766  CORE2_DBG_ID_AA64DFR1_EL1_31_0 Registers
          767. 14.3.1.1.767  CORE2_DBG_ID_AA64DFR1_EL1_63_32 Registers
          768. 14.3.1.1.768  CORE2_DBG_ID_AA64ISAR1_EL1_31_0 Registers
          769. 14.3.1.1.769  CORE2_DBG_ID_AA64ISAR1_EL1_63_32 Registers
          770. 14.3.1.1.770  CORE2_DBG_ID_AA64MMFR1_EL1_31_0 Registers
          771. 14.3.1.1.771  CORE2_DBG_ID_AA64MMFR1_EL1_63_32 Registers
          772. 14.3.1.1.772  CORE2_DBG_EDITCTRL Registers
          773. 14.3.1.1.773  CORE2_DBG_DBGCLAIMSET_EL1 Registers
          774. 14.3.1.1.774  CORE2_DBG_DBGCLAIMCLR_EL1 Registers
          775. 14.3.1.1.775  CORE2_DBG_EDDEVAFF0 Registers
          776. 14.3.1.1.776  CORE2_DBG_EDDEVAFF1 Registers
          777. 14.3.1.1.777  CORE2_DBG_EDLAR Registers
          778. 14.3.1.1.778  CORE2_DBG_EDLSR Registers
          779. 14.3.1.1.779  CORE2_DBG_DBGAUTHSTATUS_EL1 Registers
          780. 14.3.1.1.780  CORE2_DBG_EDDEVARCH Registers
          781. 14.3.1.1.781  CORE2_DBG_EDDEVID2 Registers
          782. 14.3.1.1.782  CORE2_DBG_EDDEVID1 Registers
          783. 14.3.1.1.783  CORE2_DBG_EDDEVID Registers
          784. 14.3.1.1.784  CORE2_DBG_EDDEVTYPE Registers
          785. 14.3.1.1.785  CORE2_DBG_EDPIDR4 Registers
          786. 14.3.1.1.786  CORE2_DBG_EDPIDR0 Registers
          787. 14.3.1.1.787  CORE2_DBG_EDPIDR1 Registers
          788. 14.3.1.1.788  CORE2_DBG_EDPIDR2 Registers
          789. 14.3.1.1.789  CORE2_DBG_EDPIDR3 Registers
          790. 14.3.1.1.790  CORE2_DBG_EDCIDR0 Registers
          791. 14.3.1.1.791  CORE2_DBG_EDCIDR1 Registers
          792. 14.3.1.1.792  CORE2_DBG_EDCIDR2 Registers
          793. 14.3.1.1.793  CORE2_DBG_EDCIDR3 Registers
          794. 14.3.1.1.794  CORE2_PMU_PMEVCNTR0_EL0 Registers
          795. 14.3.1.1.795  CORE2_PMU_PMEVCNTR1_EL0 Registers
          796. 14.3.1.1.796  CORE2_PMU_PMEVCNTR2_EL0 Registers
          797. 14.3.1.1.797  CORE2_PMU_PMEVCNTR3_EL0 Registers
          798. 14.3.1.1.798  CORE2_PMU_PMEVCNTR4_EL0 Registers
          799. 14.3.1.1.799  CORE2_PMU_PMEVCNTR5_EL0 Registers
          800. 14.3.1.1.800  CORE2_PMU_PMCCNTR_EL0_31_0 Registers
          801. 14.3.1.1.801  CORE2_PMU_PMCCNTR_EL0_63_32 Registers
          802. 14.3.1.1.802  CORE2_PMU_PMEVTYPER0_EL0 Registers
          803. 14.3.1.1.803  CORE2_PMU_PMEVTYPER1_EL0 Registers
          804. 14.3.1.1.804  CORE2_PMU_PMEVTYPER2_EL0 Registers
          805. 14.3.1.1.805  CORE2_PMU_PMEVTYPER3_EL0 Registers
          806. 14.3.1.1.806  CORE2_PMU_PMEVTYPER4_EL0 Registers
          807. 14.3.1.1.807  CORE2_PMU_PMEVTYPER5_EL0 Registers
          808. 14.3.1.1.808  CORE2_PMU_PMCCFILTR_EL0 Registers
          809. 14.3.1.1.809  CORE2_PMU_PMCNTENSET_EL0 Registers
          810. 14.3.1.1.810  CORE2_PMU_PMCNTENCLR_EL0 Registers
          811. 14.3.1.1.811  CORE2_PMU_PMINTENSET_EL1 Registers
          812. 14.3.1.1.812  CORE2_PMU_PMINTENCLR_EL1 Registers
          813. 14.3.1.1.813  CORE2_PMU_PMOVSCLR_EL0 Registers
          814. 14.3.1.1.814  CORE2_PMU_PMSWINC_EL0 Registers
          815. 14.3.1.1.815  CORE2_PMU_PMOVSSET_EL0 Registers
          816. 14.3.1.1.816  CORE2_PMU_PMCFGR Registers
          817. 14.3.1.1.817  CORE2_PMU_PMCR_EL0 Registers
          818. 14.3.1.1.818  CORE2_PMU_PMCEID0_EL0 Registers
          819. 14.3.1.1.819  CORE2_PMU_PMCEID1_EL0 Registers
          820. 14.3.1.1.820  CORE2_PMU_PMITCTRL Registers
          821. 14.3.1.1.821  CORE2_PMU_PMDEVAFF0 Registers
          822. 14.3.1.1.822  CORE2_PMU_PMDEVAFF1 Registers
          823. 14.3.1.1.823  CORE2_PMU_PMLAR Registers
          824. 14.3.1.1.824  CORE2_PMU_PMLSR Registers
          825. 14.3.1.1.825  CORE2_PMU_PMAUTHSTATUS Registers
          826. 14.3.1.1.826  CORE2_PMU_PMDEVARCH Registers
          827. 14.3.1.1.827  CORE2_PMU_PMDEVTYPE Registers
          828. 14.3.1.1.828  CORE2_PMU_PMPIDR4 Registers
          829. 14.3.1.1.829  CORE2_PMU_PMPIDR5 Registers
          830. 14.3.1.1.830  CORE2_PMU_PMPIDR6 Registers
          831. 14.3.1.1.831  CORE2_PMU_PMPIDR7 Registers
          832. 14.3.1.1.832  CORE2_PMU_PMPIDR0 Registers
          833. 14.3.1.1.833  CORE2_PMU_PMPIDR1 Registers
          834. 14.3.1.1.834  CORE2_PMU_PMPIDR2 Registers
          835. 14.3.1.1.835  CORE2_PMU_PMPIDR3 Registers
          836. 14.3.1.1.836  CORE2_PMU_PMCIDR0 Registers
          837. 14.3.1.1.837  CORE2_PMU_PMCIDR1 Registers
          838. 14.3.1.1.838  CORE2_PMU_PMCIDR2 Registers
          839. 14.3.1.1.839  CORE2_PMU_PMCIDR3 Registers
          840. 14.3.1.1.840  CORE2_ETM_TRCPRGCTLR Registers
          841. 14.3.1.1.841  CORE2_ETM_TRCSTATR Registers
          842. 14.3.1.1.842  CORE2_ETM_TRCCONFIGR Registers
          843. 14.3.1.1.843  CORE2_ETM_TRCAUXCTLR Registers
          844. 14.3.1.1.844  CORE2_ETM_TRCEVENTCTL0R Registers
          845. 14.3.1.1.845  CORE2_ETM_TRCEVENTCTL1R Registers
          846. 14.3.1.1.846  CORE2_ETM_TRCSTALLCTLR Registers
          847. 14.3.1.1.847  CORE2_ETM_TRCTSCTLR Registers
          848. 14.3.1.1.848  CORE2_ETM_TRCSYNCPR Registers
          849. 14.3.1.1.849  CORE2_ETM_TRCCCCTLR Registers
          850. 14.3.1.1.850  CORE2_ETM_TRCBBCTLR Registers
          851. 14.3.1.1.851  CORE2_ETM_TRCTRACEIDR Registers
          852. 14.3.1.1.852  CORE2_ETM_TRCVICTLR Registers
          853. 14.3.1.1.853  CORE2_ETM_TRCVIIECTLR Registers
          854. 14.3.1.1.854  CORE2_ETM_TRCVISSCTLR Registers
          855. 14.3.1.1.855  CORE2_ETM_TRCSEQEVR0 Registers
          856. 14.3.1.1.856  CORE2_ETM_TRCSEQEVR1 Registers
          857. 14.3.1.1.857  CORE2_ETM_TRCSEQEVR2 Registers
          858. 14.3.1.1.858  CORE2_ETM_TRCSEQRSTEVR Registers
          859. 14.3.1.1.859  CORE2_ETM_TRCSEQSTR Registers
          860. 14.3.1.1.860  CORE2_ETM_TRCEXTINSELR Registers
          861. 14.3.1.1.861  CORE2_ETM_TRCCNTRLDVR0 Registers
          862. 14.3.1.1.862  CORE2_ETM_TRCCNTRLDVR1 Registers
          863. 14.3.1.1.863  CORE2_ETM_TRCCNTCTLR0 Registers
          864. 14.3.1.1.864  CORE2_ETM_TRCCNTCTLR1 Registers
          865. 14.3.1.1.865  CORE2_ETM_TRCCNTVR0 Registers
          866. 14.3.1.1.866  CORE2_ETM_TRCCNTVR1 Registers
          867. 14.3.1.1.867  CORE2_ETM_TRCIDR8 Registers
          868. 14.3.1.1.868  CORE2_ETM_TRCIDR9 Registers
          869. 14.3.1.1.869  CORE2_ETM_TRCIDR10 Registers
          870. 14.3.1.1.870  CORE2_ETM_TRCIDR11 Registers
          871. 14.3.1.1.871  CORE2_ETM_TRCIDR12 Registers
          872. 14.3.1.1.872  CORE2_ETM_TRCIDR13 Registers
          873. 14.3.1.1.873  CORE2_ETM_TRCIMSPEC0 Registers
          874. 14.3.1.1.874  CORE2_ETM_TRCIDR0 Registers
          875. 14.3.1.1.875  CORE2_ETM_TRCIDR1 Registers
          876. 14.3.1.1.876  CORE2_ETM_TRCIDR2 Registers
          877. 14.3.1.1.877  CORE2_ETM_TRCIDR3 Registers
          878. 14.3.1.1.878  CORE2_ETM_TRCIDR4 Registers
          879. 14.3.1.1.879  CORE2_ETM_TRCIDR5 Registers
          880. 14.3.1.1.880  CORE2_ETM_TRCRSCTLR2 Registers
          881. 14.3.1.1.881  CORE2_ETM_TRCRSCTLR3 Registers
          882. 14.3.1.1.882  CORE2_ETM_TRCRSCTLR4 Registers
          883. 14.3.1.1.883  CORE2_ETM_TRCRSCTLR5 Registers
          884. 14.3.1.1.884  CORE2_ETM_TRCRSCTLR6 Registers
          885. 14.3.1.1.885  CORE2_ETM_TRCRSCTLR7 Registers
          886. 14.3.1.1.886  CORE2_ETM_TRCRSCTLR8 Registers
          887. 14.3.1.1.887  CORE2_ETM_TRCRSCTLR9 Registers
          888. 14.3.1.1.888  CORE2_ETM_TRCRSCTLR10 Registers
          889. 14.3.1.1.889  CORE2_ETM_TRCRSCTLR11 Registers
          890. 14.3.1.1.890  CORE2_ETM_TRCRSCTLR12 Registers
          891. 14.3.1.1.891  CORE2_ETM_TRCRSCTLR13 Registers
          892. 14.3.1.1.892  CORE2_ETM_TRCRSCTLR14 Registers
          893. 14.3.1.1.893  CORE2_ETM_TRCRSCTLR15 Registers
          894. 14.3.1.1.894  CORE2_ETM_TRCSSCCR0 Registers
          895. 14.3.1.1.895  CORE2_ETM_TRCSSCSR0 Registers
          896. 14.3.1.1.896  CORE2_ETM_TRCOSLAR Registers
          897. 14.3.1.1.897  CORE2_ETM_TRCOSLSR Registers
          898. 14.3.1.1.898  CORE2_ETM_TRCPDCR Registers
          899. 14.3.1.1.899  CORE2_ETM_TRCPDSR Registers
          900. 14.3.1.1.900  CORE2_ETM_TRCACVR0_31_0 Registers
          901. 14.3.1.1.901  CORE2_ETM_TRCACVR0_63_32 Registers
          902. 14.3.1.1.902  CORE2_ETM_TRCACVR1_31_0 Registers
          903. 14.3.1.1.903  CORE2_ETM_TRCACVR1_63_32 Registers
          904. 14.3.1.1.904  CORE2_ETM_TRCACVR2_31_0 Registers
          905. 14.3.1.1.905  CORE2_ETM_TRCACVR2_63_32 Registers
          906. 14.3.1.1.906  CORE2_ETM_TRCACVR3_31_0 Registers
          907. 14.3.1.1.907  CORE2_ETM_TRCACVR3_63_32 Registers
          908. 14.3.1.1.908  CORE2_ETM_TRCACVR4_31_0 Registers
          909. 14.3.1.1.909  CORE2_ETM_TRCACVR4_63_32 Registers
          910. 14.3.1.1.910  CORE2_ETM_TRCACVR5_31_0 Registers
          911. 14.3.1.1.911  CORE2_ETM_TRCACVR5_63_32 Registers
          912. 14.3.1.1.912  CORE2_ETM_TRCACVR6_31_0 Registers
          913. 14.3.1.1.913  CORE2_ETM_TRCACVR6_63_32 Registers
          914. 14.3.1.1.914  CORE2_ETM_TRCACVR7_31_0 Registers
          915. 14.3.1.1.915  CORE2_ETM_TRCACVR7_63_32 Registers
          916. 14.3.1.1.916  CORE2_ETM_TRCACATR0 Registers
          917. 14.3.1.1.917  CORE2_ETM_TRCACATR1 Registers
          918. 14.3.1.1.918  CORE2_ETM_TRCACATR2 Registers
          919. 14.3.1.1.919  CORE2_ETM_TRCACATR3 Registers
          920. 14.3.1.1.920  CORE2_ETM_TRCACATR4 Registers
          921. 14.3.1.1.921  CORE2_ETM_TRCACATR5 Registers
          922. 14.3.1.1.922  CORE2_ETM_TRCACATR6 Registers
          923. 14.3.1.1.923  CORE2_ETM_TRCACATR7 Registers
          924. 14.3.1.1.924  CORE2_ETM_TRCCIDCVR0 Registers
          925. 14.3.1.1.925  CORE2_ETM_TRCVMIDCVR0 Registers
          926. 14.3.1.1.926  CORE2_ETM_TRCCIDCCTLR0 Registers
          927. 14.3.1.1.927  CORE2_ETM_TRCITATBIDR Registers
          928. 14.3.1.1.928  CORE2_ETM_TRCITIDATAR Registers
          929. 14.3.1.1.929  CORE2_ETM_TRCITIATBINR Registers
          930. 14.3.1.1.930  CORE2_ETM_TRCITIATBOUTR Registers
          931. 14.3.1.1.931  CORE2_ETM_TRCITCTRL Registers
          932. 14.3.1.1.932  CORE2_ETM_TRCCLAIMSET Registers
          933. 14.3.1.1.933  CORE2_ETM_TRCCLAIMCLR Registers
          934. 14.3.1.1.934  CORE2_ETM_TRCDEVAFF0 Registers
          935. 14.3.1.1.935  CORE2_ETM_TRCDEVAFF1 Registers
          936. 14.3.1.1.936  CORE2_ETM_TRCLAR Registers
          937. 14.3.1.1.937  CORE2_ETM_TRCLSR Registers
          938. 14.3.1.1.938  CORE2_ETM_TRCAUTHSTATUS Registers
          939. 14.3.1.1.939  CORE2_ETM_TRCDEVARCH Registers
          940. 14.3.1.1.940  CORE2_ETM_TRCDEVID Registers
          941. 14.3.1.1.941  CORE2_ETM_TRCDEVTYPE Registers
          942. 14.3.1.1.942  CORE2_ETM_TRCPIDR4 Registers
          943. 14.3.1.1.943  CORE2_ETM_TRCPIDR5 Registers
          944. 14.3.1.1.944  CORE2_ETM_TRCPIDR6 Registers
          945. 14.3.1.1.945  CORE2_ETM_TRCPIDR7 Registers
          946. 14.3.1.1.946  CORE2_ETM_TRCPIDR0 Registers
          947. 14.3.1.1.947  CORE2_ETM_TRCPIDR1 Registers
          948. 14.3.1.1.948  CORE2_ETM_TRCPIDR2 Registers
          949. 14.3.1.1.949  CORE2_ETM_TRCPIDR3 Registers
          950. 14.3.1.1.950  CORE2_ETM_TRCCIDR0 Registers
          951. 14.3.1.1.951  CORE2_ETM_TRCCIDR1 Registers
          952. 14.3.1.1.952  CORE2_ETM_TRCCIDR2 Registers
          953. 14.3.1.1.953  CORE2_ETM_TRCCIDR3 Registers
          954. 14.3.1.1.954  CORE2_CTI_CTICONTROL Registers
          955. 14.3.1.1.955  CORE2_CTI_CTIINTACK Registers
          956. 14.3.1.1.956  CORE2_CTI_CTIAPPSET Registers
          957. 14.3.1.1.957  CORE2_CTI_CTIAPPCLEAR Registers
          958. 14.3.1.1.958  CORE2_CTI_CTIAPPPULSE Registers
          959. 14.3.1.1.959  CORE2_CTI_CTIINEN0 Registers
          960. 14.3.1.1.960  CORE2_CTI_CTIINEN1 Registers
          961. 14.3.1.1.961  CORE2_CTI_CTIINEN2 Registers
          962. 14.3.1.1.962  CORE2_CTI_CTIINEN3 Registers
          963. 14.3.1.1.963  CORE2_CTI_CTIINEN4 Registers
          964. 14.3.1.1.964  CORE2_CTI_CTIINEN5 Registers
          965. 14.3.1.1.965  CORE2_CTI_CTIINEN6 Registers
          966. 14.3.1.1.966  CORE2_CTI_CTIINEN7 Registers
          967. 14.3.1.1.967  CORE2_CTI_CTIOUTEN0 Registers
          968. 14.3.1.1.968  CORE2_CTI_CTIOUTEN1 Registers
          969. 14.3.1.1.969  CORE2_CTI_CTIOUTEN2 Registers
          970. 14.3.1.1.970  CORE2_CTI_CTIOUTEN3 Registers
          971. 14.3.1.1.971  CORE2_CTI_CTIOUTEN4 Registers
          972. 14.3.1.1.972  CORE2_CTI_CTIOUTEN5 Registers
          973. 14.3.1.1.973  CORE2_CTI_CTIOUTEN6 Registers
          974. 14.3.1.1.974  CORE2_CTI_CTIOUTEN7 Registers
          975. 14.3.1.1.975  CORE2_CTI_CTITRIGINSTATUS Registers
          976. 14.3.1.1.976  CORE2_CTI_CTITRIGOUTSTATUS Registers
          977. 14.3.1.1.977  CORE2_CTI_CTICHINSTATUS Registers
          978. 14.3.1.1.978  CORE2_CTI_CTICHOUTSTATUS Registers
          979. 14.3.1.1.979  CORE2_CTI_CTIGATE Registers
          980. 14.3.1.1.980  CORE2_CTI_ASICCTL Registers
          981. 14.3.1.1.981  CORE2_CTI_CTIITCTRL Registers
          982. 14.3.1.1.982  CORE2_CTI_CTICLAIMSET Registers
          983. 14.3.1.1.983  CORE2_CTI_CTICLAIMCLR Registers
          984. 14.3.1.1.984  CORE2_CTI_CTIDEVAFF0 Registers
          985. 14.3.1.1.985  CORE2_CTI_CTIDEVAFF1 Registers
          986. 14.3.1.1.986  CORE2_CTI_CTILAR Registers
          987. 14.3.1.1.987  CORE2_CTI_CTILSR Registers
          988. 14.3.1.1.988  CORE2_CTI_CTIAUTHSTATUS Registers
          989. 14.3.1.1.989  CORE2_CTI_CTIDEVARCH Registers
          990. 14.3.1.1.990  CORE2_CTI_CTIDEVID2 Registers
          991. 14.3.1.1.991  CORE2_CTI_CTIDEVID1 Registers
          992. 14.3.1.1.992  CORE2_CTI_CTIDEVID Registers
          993. 14.3.1.1.993  CORE2_CTI_CTIDEVTYPE Registers
          994. 14.3.1.1.994  CORE2_CTI_CTIPIDR4 Registers
          995. 14.3.1.1.995  CORE2_CTI_CTIPIDR5 Registers
          996. 14.3.1.1.996  CORE2_CTI_CTIPIDR6 Registers
          997. 14.3.1.1.997  CORE2_CTI_CTIPIDR7 Registers
          998. 14.3.1.1.998  CORE2_CTI_CTIPIDR0 Registers
          999. 14.3.1.1.999  CORE2_CTI_CTIPIDR1 Registers
          1000. 14.3.1.1.1000 CORE2_CTI_CTIPIDR2 Registers
          1001. 14.3.1.1.1001 CORE2_CTI_CTIPIDR3 Registers
          1002. 14.3.1.1.1002 CORE2_CTI_CTICIDR0 Registers
          1003. 14.3.1.1.1003 CORE2_CTI_CTICIDR1 Registers
          1004. 14.3.1.1.1004 CORE2_CTI_CTICIDR2 Registers
          1005. 14.3.1.1.1005 CORE2_CTI_CTICIDR3 Registers
          1006. 14.3.1.1.1006 CORE3_DBG_EDESR Registers
          1007. 14.3.1.1.1007 CORE3_DBG_EDECR Registers
          1008. 14.3.1.1.1008 CORE3_DBG_EDWAR_31_0 Registers
          1009. 14.3.1.1.1009 CORE3_DBG_EDWAR_63_32 Registers
          1010. 14.3.1.1.1010 CORE3_DBG_DBGDTRRX_EL0 Registers
          1011. 14.3.1.1.1011 CORE3_DBG_EDITR Registers
          1012. 14.3.1.1.1012 CORE3_DBG_EDSCR Registers
          1013. 14.3.1.1.1013 CORE3_DBG_DBGDTRTX_EL0 Registers
          1014. 14.3.1.1.1014 CORE3_DBG_EDRCR Registers
          1015. 14.3.1.1.1015 CORE3_DBG_EDACR Registers
          1016. 14.3.1.1.1016 CORE3_DBG_EDECCR Registers
          1017. 14.3.1.1.1017 CORE3_DBG_EDPCSR_31_0 Registers
          1018. 14.3.1.1.1018 CORE3_DBG_EDCIDSR Registers
          1019. 14.3.1.1.1019 CORE3_DBG_EDVIDSR Registers
          1020. 14.3.1.1.1020 CORE3_DBG_EDPCSR_63_32 Registers
          1021. 14.3.1.1.1021 CORE3_DBG_OSLAR_EL1 Registers
          1022. 14.3.1.1.1022 CORE3_DBG_EDPRCR Registers
          1023. 14.3.1.1.1023 CORE3_DBG_EDPRSR Registers
          1024. 14.3.1.1.1024 CORE3_DBG_DBGBVR0_EL1_31_0 Registers
          1025. 14.3.1.1.1025 CORE3_DBG_DBGBVR0_EL1_63_32 Registers
          1026. 14.3.1.1.1026 CORE3_DBG_DBGBCR0_EL1 Registers
          1027. 14.3.1.1.1027 CORE3_DBG_DBGBVR1_EL1_31_0 Registers
          1028. 14.3.1.1.1028 CORE3_DBG_DBGBVR1_EL1_63_32 Registers
          1029. 14.3.1.1.1029 CORE3_DBG_DBGBCR1_EL1 Registers
          1030. 14.3.1.1.1030 CORE3_DBG_DBGBVR2_EL1_31_0 Registers
          1031. 14.3.1.1.1031 CORE3_DBG_DBGBVR2_EL1_63_32 Registers
          1032. 14.3.1.1.1032 CORE3_DBG_DBGBCR2_EL1 Registers
          1033. 14.3.1.1.1033 CORE3_DBG_DBGBVR3_EL1_31_0 Registers
          1034. 14.3.1.1.1034 CORE3_DBG_DBGBVR3_EL1_63_32 Registers
          1035. 14.3.1.1.1035 CORE3_DBG_DBGBCR3_EL1 Registers
          1036. 14.3.1.1.1036 CORE3_DBG_DBGBVR4_EL1_31_0 Registers
          1037. 14.3.1.1.1037 CORE3_DBG_DBGBVR4_EL1_63_32 Registers
          1038. 14.3.1.1.1038 CORE3_DBG_DBGBCR4_EL1 Registers
          1039. 14.3.1.1.1039 CORE3_DBG_DBGBVR5_EL1_31_0 Registers
          1040. 14.3.1.1.1040 CORE3_DBG_DBGBVR5_EL1_63_32 Registers
          1041. 14.3.1.1.1041 CORE3_DBG_DBGBCR5_EL1 Registers
          1042. 14.3.1.1.1042 CORE3_DBG_DBGWVR0_EL1_31_0 Registers
          1043. 14.3.1.1.1043 CORE3_DBG_DBGWVR0_EL1_63_32 Registers
          1044. 14.3.1.1.1044 CORE3_DBG_DBGWCR0_EL1 Registers
          1045. 14.3.1.1.1045 CORE3_DBG_DBGWVR1_EL1_31_0 Registers
          1046. 14.3.1.1.1046 CORE3_DBG_DBGWVR1_EL1_63_32 Registers
          1047. 14.3.1.1.1047 CORE3_DBG_DBGWCR1_EL1 Registers
          1048. 14.3.1.1.1048 CORE3_DBG_DBGWVR2_EL1_31_0 Registers
          1049. 14.3.1.1.1049 CORE3_DBG_DBGWVR2_EL1_63_32 Registers
          1050. 14.3.1.1.1050 CORE3_DBG_DBGWCR2_EL1 Registers
          1051. 14.3.1.1.1051 CORE3_DBG_DBGWVR3_EL1_31_0 Registers
          1052. 14.3.1.1.1052 CORE3_DBG_DBGWVR3_EL1_63_32 Registers
          1053. 14.3.1.1.1053 CORE3_DBG_DBGWCR3_EL1 Registers
          1054. 14.3.1.1.1054 CORE3_DBG_MIDR_EL1 Registers
          1055. 14.3.1.1.1055 CORE3_DBG_ID_AA64PFR0_EL1_31_0 Registers
          1056. 14.3.1.1.1056 CORE3_DBG_ID_AA64PFR0_EL1_63_32 Registers
          1057. 14.3.1.1.1057 CORE3_DBG_ID_AA64DFR0_EL1_31_0 Registers
          1058. 14.3.1.1.1058 CORE3_DBG_ID_AA64DFR0_EL1_63_32 Registers
          1059. 14.3.1.1.1059 CORE3_DBG_ID_AA64ISAR0_EL1_31_0 Registers
          1060. 14.3.1.1.1060 CORE3_DBG_ID_AA64ISAR0_EL1_63_32 Registers
          1061. 14.3.1.1.1061 CORE3_DBG_ID_AA64MMFR0_EL1_31_0 Registers
          1062. 14.3.1.1.1062 CORE3_DBG_ID_AA64MMFR0_EL1_63_32 Registers
          1063. 14.3.1.1.1063 CORE3_DBG_ID_AA64PFR1_EL1_31_0 Registers
          1064. 14.3.1.1.1064 CORE3_DBG_ID_AA64PFR1_EL1_63_32 Registers
          1065. 14.3.1.1.1065 CORE3_DBG_ID_AA64DFR1_EL1_31_0 Registers
          1066. 14.3.1.1.1066 CORE3_DBG_ID_AA64DFR1_EL1_63_32 Registers
          1067. 14.3.1.1.1067 CORE3_DBG_ID_AA64ISAR1_EL1_31_0 Registers
          1068. 14.3.1.1.1068 CORE3_DBG_ID_AA64ISAR1_EL1_63_32 Registers
          1069. 14.3.1.1.1069 CORE3_DBG_ID_AA64MMFR1_EL1_31_0 Registers
          1070. 14.3.1.1.1070 CORE3_DBG_ID_AA64MMFR1_EL1_63_32 Registers
          1071. 14.3.1.1.1071 CORE3_DBG_EDITCTRL Registers
          1072. 14.3.1.1.1072 CORE3_DBG_DBGCLAIMSET_EL1 Registers
          1073. 14.3.1.1.1073 CORE3_DBG_DBGCLAIMCLR_EL1 Registers
          1074. 14.3.1.1.1074 CORE3_DBG_EDDEVAFF0 Registers
          1075. 14.3.1.1.1075 CORE3_DBG_EDDEVAFF1 Registers
          1076. 14.3.1.1.1076 CORE3_DBG_EDLAR Registers
          1077. 14.3.1.1.1077 CORE3_DBG_EDLSR Registers
          1078. 14.3.1.1.1078 CORE3_DBG_DBGAUTHSTATUS_EL1 Registers
          1079. 14.3.1.1.1079 CORE3_DBG_EDDEVARCH Registers
          1080. 14.3.1.1.1080 CORE3_DBG_EDDEVID2 Registers
          1081. 14.3.1.1.1081 CORE3_DBG_EDDEVID1 Registers
          1082. 14.3.1.1.1082 CORE3_DBG_EDDEVID Registers
          1083. 14.3.1.1.1083 CORE3_DBG_EDDEVTYPE Registers
          1084. 14.3.1.1.1084 CORE3_DBG_EDPIDR4 Registers
          1085. 14.3.1.1.1085 CORE3_DBG_EDPIDR0 Registers
          1086. 14.3.1.1.1086 CORE3_DBG_EDPIDR1 Registers
          1087. 14.3.1.1.1087 CORE3_DBG_EDPIDR2 Registers
          1088. 14.3.1.1.1088 CORE3_DBG_EDPIDR3 Registers
          1089. 14.3.1.1.1089 CORE3_DBG_EDCIDR0 Registers
          1090. 14.3.1.1.1090 CORE3_DBG_EDCIDR1 Registers
          1091. 14.3.1.1.1091 CORE3_DBG_EDCIDR2 Registers
          1092. 14.3.1.1.1092 CORE3_DBG_EDCIDR3 Registers
          1093. 14.3.1.1.1093 CORE3_PMU_PMEVCNTR0_EL0 Registers
          1094. 14.3.1.1.1094 CORE3_PMU_PMEVCNTR1_EL0 Registers
          1095. 14.3.1.1.1095 CORE3_PMU_PMEVCNTR2_EL0 Registers
          1096. 14.3.1.1.1096 CORE3_PMU_PMEVCNTR3_EL0 Registers
          1097. 14.3.1.1.1097 CORE3_PMU_PMEVCNTR4_EL0 Registers
          1098. 14.3.1.1.1098 CORE3_PMU_PMEVCNTR5_EL0 Registers
          1099. 14.3.1.1.1099 CORE3_PMU_PMCCNTR_EL0_31_0 Registers
          1100. 14.3.1.1.1100 CORE3_PMU_PMCCNTR_EL0_63_32 Registers
          1101. 14.3.1.1.1101 CORE3_PMU_PMEVTYPER0_EL0 Registers
          1102. 14.3.1.1.1102 CORE3_PMU_PMEVTYPER1_EL0 Registers
          1103. 14.3.1.1.1103 CORE3_PMU_PMEVTYPER2_EL0 Registers
          1104. 14.3.1.1.1104 CORE3_PMU_PMEVTYPER3_EL0 Registers
          1105. 14.3.1.1.1105 CORE3_PMU_PMEVTYPER4_EL0 Registers
          1106. 14.3.1.1.1106 CORE3_PMU_PMEVTYPER5_EL0 Registers
          1107. 14.3.1.1.1107 CORE3_PMU_PMCCFILTR_EL0 Registers
          1108. 14.3.1.1.1108 CORE3_PMU_PMCNTENSET_EL0 Registers
          1109. 14.3.1.1.1109 CORE3_PMU_PMCNTENCLR_EL0 Registers
          1110. 14.3.1.1.1110 CORE3_PMU_PMINTENSET_EL1 Registers
          1111. 14.3.1.1.1111 CORE3_PMU_PMINTENCLR_EL1 Registers
          1112. 14.3.1.1.1112 CORE3_PMU_PMOVSCLR_EL0 Registers
          1113. 14.3.1.1.1113 CORE3_PMU_PMSWINC_EL0 Registers
          1114. 14.3.1.1.1114 CORE3_PMU_PMOVSSET_EL0 Registers
          1115. 14.3.1.1.1115 CORE3_PMU_PMCFGR Registers
          1116. 14.3.1.1.1116 CORE3_PMU_PMCR_EL0 Registers
          1117. 14.3.1.1.1117 CORE3_PMU_PMCEID0_EL0 Registers
          1118. 14.3.1.1.1118 CORE3_PMU_PMCEID1_EL0 Registers
          1119. 14.3.1.1.1119 CORE3_PMU_PMITCTRL Registers
          1120. 14.3.1.1.1120 CORE3_PMU_PMDEVAFF0 Registers
          1121. 14.3.1.1.1121 CORE3_PMU_PMDEVAFF1 Registers
          1122. 14.3.1.1.1122 CORE3_PMU_PMLAR Registers
          1123. 14.3.1.1.1123 CORE3_PMU_PMLSR Registers
          1124. 14.3.1.1.1124 CORE3_PMU_PMAUTHSTATUS Registers
          1125. 14.3.1.1.1125 CORE3_PMU_PMDEVARCH Registers
          1126. 14.3.1.1.1126 CORE3_PMU_PMDEVTYPE Registers
          1127. 14.3.1.1.1127 CORE3_PMU_PMPIDR4 Registers
          1128. 14.3.1.1.1128 CORE3_PMU_PMPIDR5 Registers
          1129. 14.3.1.1.1129 CORE3_PMU_PMPIDR6 Registers
          1130. 14.3.1.1.1130 CORE3_PMU_PMPIDR7 Registers
          1131. 14.3.1.1.1131 CORE3_PMU_PMPIDR0 Registers
          1132. 14.3.1.1.1132 CORE3_PMU_PMPIDR1 Registers
          1133. 14.3.1.1.1133 CORE3_PMU_PMPIDR2 Registers
          1134. 14.3.1.1.1134 CORE3_PMU_PMPIDR3 Registers
          1135. 14.3.1.1.1135 CORE3_PMU_PMCIDR0 Registers
          1136. 14.3.1.1.1136 CORE3_PMU_PMCIDR1 Registers
          1137. 14.3.1.1.1137 CORE3_PMU_PMCIDR2 Registers
          1138. 14.3.1.1.1138 CORE3_PMU_PMCIDR3 Registers
          1139. 14.3.1.1.1139 CORE3_ETM_TRCPRGCTLR Registers
          1140. 14.3.1.1.1140 CORE3_ETM_TRCSTATR Registers
          1141. 14.3.1.1.1141 CORE3_ETM_TRCCONFIGR Registers
          1142. 14.3.1.1.1142 CORE3_ETM_TRCAUXCTLR Registers
          1143. 14.3.1.1.1143 CORE3_ETM_TRCEVENTCTL0R Registers
          1144. 14.3.1.1.1144 CORE3_ETM_TRCEVENTCTL1R Registers
          1145. 14.3.1.1.1145 CORE3_ETM_TRCSTALLCTLR Registers
          1146. 14.3.1.1.1146 CORE3_ETM_TRCTSCTLR Registers
          1147. 14.3.1.1.1147 CORE3_ETM_TRCSYNCPR Registers
          1148. 14.3.1.1.1148 CORE3_ETM_TRCCCCTLR Registers
          1149. 14.3.1.1.1149 CORE3_ETM_TRCBBCTLR Registers
          1150. 14.3.1.1.1150 CORE3_ETM_TRCTRACEIDR Registers
          1151. 14.3.1.1.1151 CORE3_ETM_TRCVICTLR Registers
          1152. 14.3.1.1.1152 CORE3_ETM_TRCVIIECTLR Registers
          1153. 14.3.1.1.1153 CORE3_ETM_TRCVISSCTLR Registers
          1154. 14.3.1.1.1154 CORE3_ETM_TRCSEQEVR0 Registers
          1155. 14.3.1.1.1155 CORE3_ETM_TRCSEQEVR1 Registers
          1156. 14.3.1.1.1156 CORE3_ETM_TRCSEQEVR2 Registers
          1157. 14.3.1.1.1157 CORE3_ETM_TRCSEQRSTEVR Registers
          1158. 14.3.1.1.1158 CORE3_ETM_TRCSEQSTR Registers
          1159. 14.3.1.1.1159 CORE3_ETM_TRCEXTINSELR Registers
          1160. 14.3.1.1.1160 CORE3_ETM_TRCCNTRLDVR0 Registers
          1161. 14.3.1.1.1161 CORE3_ETM_TRCCNTRLDVR1 Registers
          1162. 14.3.1.1.1162 CORE3_ETM_TRCCNTCTLR0 Registers
          1163. 14.3.1.1.1163 CORE3_ETM_TRCCNTCTLR1 Registers
          1164. 14.3.1.1.1164 CORE3_ETM_TRCCNTVR0 Registers
          1165. 14.3.1.1.1165 CORE3_ETM_TRCCNTVR1 Registers
          1166. 14.3.1.1.1166 CORE3_ETM_TRCIDR8 Registers
          1167. 14.3.1.1.1167 CORE3_ETM_TRCIDR9 Registers
          1168. 14.3.1.1.1168 CORE3_ETM_TRCIDR10 Registers
          1169. 14.3.1.1.1169 CORE3_ETM_TRCIDR11 Registers
          1170. 14.3.1.1.1170 CORE3_ETM_TRCIDR12 Registers
          1171. 14.3.1.1.1171 CORE3_ETM_TRCIDR13 Registers
          1172. 14.3.1.1.1172 CORE3_ETM_TRCIMSPEC0 Registers
          1173. 14.3.1.1.1173 CORE3_ETM_TRCIDR0 Registers
          1174. 14.3.1.1.1174 CORE3_ETM_TRCIDR1 Registers
          1175. 14.3.1.1.1175 CORE3_ETM_TRCIDR2 Registers
          1176. 14.3.1.1.1176 CORE3_ETM_TRCIDR3 Registers
          1177. 14.3.1.1.1177 CORE3_ETM_TRCIDR4 Registers
          1178. 14.3.1.1.1178 CORE3_ETM_TRCIDR5 Registers
          1179. 14.3.1.1.1179 CORE3_ETM_TRCRSCTLR2 Registers
          1180. 14.3.1.1.1180 CORE3_ETM_TRCRSCTLR3 Registers
          1181. 14.3.1.1.1181 CORE3_ETM_TRCRSCTLR4 Registers
          1182. 14.3.1.1.1182 CORE3_ETM_TRCRSCTLR5 Registers
          1183. 14.3.1.1.1183 CORE3_ETM_TRCRSCTLR6 Registers
          1184. 14.3.1.1.1184 CORE3_ETM_TRCRSCTLR7 Registers
          1185. 14.3.1.1.1185 CORE3_ETM_TRCRSCTLR8 Registers
          1186. 14.3.1.1.1186 CORE3_ETM_TRCRSCTLR9 Registers
          1187. 14.3.1.1.1187 CORE3_ETM_TRCRSCTLR10 Registers
          1188. 14.3.1.1.1188 CORE3_ETM_TRCRSCTLR11 Registers
          1189. 14.3.1.1.1189 CORE3_ETM_TRCRSCTLR12 Registers
          1190. 14.3.1.1.1190 CORE3_ETM_TRCRSCTLR13 Registers
          1191. 14.3.1.1.1191 CORE3_ETM_TRCRSCTLR14 Registers
          1192. 14.3.1.1.1192 CORE3_ETM_TRCRSCTLR15 Registers
          1193. 14.3.1.1.1193 CORE3_ETM_TRCSSCCR0 Registers
          1194. 14.3.1.1.1194 CORE3_ETM_TRCSSCSR0 Registers
          1195. 14.3.1.1.1195 CORE3_ETM_TRCOSLAR Registers
          1196. 14.3.1.1.1196 CORE3_ETM_TRCOSLSR Registers
          1197. 14.3.1.1.1197 CORE3_ETM_TRCPDCR Registers
          1198. 14.3.1.1.1198 CORE3_ETM_TRCPDSR Registers
          1199. 14.3.1.1.1199 CORE3_ETM_TRCACVR0_31_0 Registers
          1200. 14.3.1.1.1200 CORE3_ETM_TRCACVR0_63_32 Registers
          1201. 14.3.1.1.1201 CORE3_ETM_TRCACVR1_31_0 Registers
          1202. 14.3.1.1.1202 CORE3_ETM_TRCACVR1_63_32 Registers
          1203. 14.3.1.1.1203 CORE3_ETM_TRCACVR2_31_0 Registers
          1204. 14.3.1.1.1204 CORE3_ETM_TRCACVR2_63_32 Registers
          1205. 14.3.1.1.1205 CORE3_ETM_TRCACVR3_31_0 Registers
          1206. 14.3.1.1.1206 CORE3_ETM_TRCACVR3_63_32 Registers
          1207. 14.3.1.1.1207 CORE3_ETM_TRCACVR4_31_0 Registers
          1208. 14.3.1.1.1208 CORE3_ETM_TRCACVR4_63_32 Registers
          1209. 14.3.1.1.1209 CORE3_ETM_TRCACVR5_31_0 Registers
          1210. 14.3.1.1.1210 CORE3_ETM_TRCACVR5_63_32 Registers
          1211. 14.3.1.1.1211 CORE3_ETM_TRCACVR6_31_0 Registers
          1212. 14.3.1.1.1212 CORE3_ETM_TRCACVR6_63_32 Registers
          1213. 14.3.1.1.1213 CORE3_ETM_TRCACVR7_31_0 Registers
          1214. 14.3.1.1.1214 CORE3_ETM_TRCACVR7_63_32 Registers
          1215. 14.3.1.1.1215 CORE3_ETM_TRCACATR0 Registers
          1216. 14.3.1.1.1216 CORE3_ETM_TRCACATR1 Registers
          1217. 14.3.1.1.1217 CORE3_ETM_TRCACATR2 Registers
          1218. 14.3.1.1.1218 CORE3_ETM_TRCACATR3 Registers
          1219. 14.3.1.1.1219 CORE3_ETM_TRCACATR4 Registers
          1220. 14.3.1.1.1220 CORE3_ETM_TRCACATR5 Registers
          1221. 14.3.1.1.1221 CORE3_ETM_TRCACATR6 Registers
          1222. 14.3.1.1.1222 CORE3_ETM_TRCACATR7 Registers
          1223. 14.3.1.1.1223 CORE3_ETM_TRCCIDCVR0 Registers
          1224. 14.3.1.1.1224 CORE3_ETM_TRCVMIDCVR0 Registers
          1225. 14.3.1.1.1225 CORE3_ETM_TRCCIDCCTLR0 Registers
          1226. 14.3.1.1.1226 CORE3_ETM_TRCITATBIDR Registers
          1227. 14.3.1.1.1227 CORE3_ETM_TRCITIDATAR Registers
          1228. 14.3.1.1.1228 CORE3_ETM_TRCITIATBINR Registers
          1229. 14.3.1.1.1229 CORE3_ETM_TRCITIATBOUTR Registers
          1230. 14.3.1.1.1230 CORE3_ETM_TRCITCTRL Registers
          1231. 14.3.1.1.1231 CORE3_ETM_TRCCLAIMSET Registers
          1232. 14.3.1.1.1232 CORE3_ETM_TRCCLAIMCLR Registers
          1233. 14.3.1.1.1233 CORE3_ETM_TRCDEVAFF0 Registers
          1234. 14.3.1.1.1234 CORE3_ETM_TRCDEVAFF1 Registers
          1235. 14.3.1.1.1235 CORE3_ETM_TRCLAR Registers
          1236. 14.3.1.1.1236 CORE3_ETM_TRCLSR Registers
          1237. 14.3.1.1.1237 CORE3_ETM_TRCAUTHSTATUS Registers
          1238. 14.3.1.1.1238 CORE3_ETM_TRCDEVARCH Registers
          1239. 14.3.1.1.1239 CORE3_ETM_TRCDEVID Registers
          1240. 14.3.1.1.1240 CORE3_ETM_TRCDEVTYPE Registers
          1241. 14.3.1.1.1241 CORE3_ETM_TRCPIDR4 Registers
          1242. 14.3.1.1.1242 CORE3_ETM_TRCPIDR5 Registers
          1243. 14.3.1.1.1243 CORE3_ETM_TRCPIDR6 Registers
          1244. 14.3.1.1.1244 CORE3_ETM_TRCPIDR7 Registers
          1245. 14.3.1.1.1245 CORE3_ETM_TRCPIDR0 Registers
          1246. 14.3.1.1.1246 CORE3_ETM_TRCPIDR1 Registers
          1247. 14.3.1.1.1247 CORE3_ETM_TRCPIDR2 Registers
          1248. 14.3.1.1.1248 CORE3_ETM_TRCPIDR3 Registers
          1249. 14.3.1.1.1249 CORE3_ETM_TRCCIDR0 Registers
          1250. 14.3.1.1.1250 CORE3_ETM_TRCCIDR1 Registers
          1251. 14.3.1.1.1251 CORE3_ETM_TRCCIDR2 Registers
          1252. 14.3.1.1.1252 CORE3_ETM_TRCCIDR3 Registers
          1253. 14.3.1.1.1253 CORE3_CTI_CTICONTROL Registers
          1254. 14.3.1.1.1254 CORE3_CTI_CTIINTACK Registers
          1255. 14.3.1.1.1255 CORE3_CTI_CTIAPPSET Registers
          1256. 14.3.1.1.1256 CORE3_CTI_CTIAPPCLEAR Registers
          1257. 14.3.1.1.1257 CORE3_CTI_CTIAPPPULSE Registers
          1258. 14.3.1.1.1258 CORE3_CTI_CTIINEN0 Registers
          1259. 14.3.1.1.1259 CORE3_CTI_CTIINEN1 Registers
          1260. 14.3.1.1.1260 CORE3_CTI_CTIINEN2 Registers
          1261. 14.3.1.1.1261 CORE3_CTI_CTIINEN3 Registers
          1262. 14.3.1.1.1262 CORE3_CTI_CTIINEN4 Registers
          1263. 14.3.1.1.1263 CORE3_CTI_CTIINEN5 Registers
          1264. 14.3.1.1.1264 CORE3_CTI_CTIINEN6 Registers
          1265. 14.3.1.1.1265 CORE3_CTI_CTIINEN7 Registers
          1266. 14.3.1.1.1266 CORE3_CTI_CTIOUTEN0 Registers
          1267. 14.3.1.1.1267 CORE3_CTI_CTIOUTEN1 Registers
          1268. 14.3.1.1.1268 CORE3_CTI_CTIOUTEN2 Registers
          1269. 14.3.1.1.1269 CORE3_CTI_CTIOUTEN3 Registers
          1270. 14.3.1.1.1270 CORE3_CTI_CTIOUTEN4 Registers
          1271. 14.3.1.1.1271 CORE3_CTI_CTIOUTEN5 Registers
          1272. 14.3.1.1.1272 CORE3_CTI_CTIOUTEN6 Registers
          1273. 14.3.1.1.1273 CORE3_CTI_CTIOUTEN7 Registers
          1274. 14.3.1.1.1274 CORE3_CTI_CTITRIGINSTATUS Registers
          1275. 14.3.1.1.1275 CORE3_CTI_CTITRIGOUTSTATUS Registers
          1276. 14.3.1.1.1276 CORE3_CTI_CTICHINSTATUS Registers
          1277. 14.3.1.1.1277 CORE3_CTI_CTICHOUTSTATUS Registers
          1278. 14.3.1.1.1278 CORE3_CTI_CTIGATE Registers
          1279. 14.3.1.1.1279 CORE3_CTI_ASICCTL Registers
          1280. 14.3.1.1.1280 CORE3_CTI_CTIITCTRL Registers
          1281. 14.3.1.1.1281 CORE3_CTI_CTICLAIMSET Registers
          1282. 14.3.1.1.1282 CORE3_CTI_CTICLAIMCLR Registers
          1283. 14.3.1.1.1283 CORE3_CTI_CTIDEVAFF0 Registers
          1284. 14.3.1.1.1284 CORE3_CTI_CTIDEVAFF1 Registers
          1285. 14.3.1.1.1285 CORE3_CTI_CTILAR Registers
          1286. 14.3.1.1.1286 CORE3_CTI_CTILSR Registers
          1287. 14.3.1.1.1287 CORE3_CTI_CTIAUTHSTATUS Registers
          1288. 14.3.1.1.1288 CORE3_CTI_CTIDEVARCH Registers
          1289. 14.3.1.1.1289 CORE3_CTI_CTIDEVID2 Registers
          1290. 14.3.1.1.1290 CORE3_CTI_CTIDEVID1 Registers
          1291. 14.3.1.1.1291 CORE3_CTI_CTIDEVID Registers
          1292. 14.3.1.1.1292 CORE3_CTI_CTIDEVTYPE Registers
          1293. 14.3.1.1.1293 CORE3_CTI_CTIPIDR4 Registers
          1294. 14.3.1.1.1294 CORE3_CTI_CTIPIDR5 Registers
          1295. 14.3.1.1.1295 CORE3_CTI_CTIPIDR6 Registers
          1296. 14.3.1.1.1296 CORE3_CTI_CTIPIDR7 Registers
          1297. 14.3.1.1.1297 CORE3_CTI_CTIPIDR0 Registers
          1298. 14.3.1.1.1298 CORE3_CTI_CTIPIDR1 Registers
          1299. 14.3.1.1.1299 CORE3_CTI_CTIPIDR2 Registers
          1300. 14.3.1.1.1300 CORE3_CTI_CTIPIDR3 Registers
          1301. 14.3.1.1.1301 CORE3_CTI_CTICIDR0 Registers
          1302. 14.3.1.1.1302 CORE3_CTI_CTICIDR1 Registers
          1303. 14.3.1.1.1303 CORE3_CTI_CTICIDR2 Registers
          1304. 14.3.1.1.1304 CORE3_CTI_CTICIDR3 Registers
          1305. 14.3.1.1.1305 Access Table
        2. 14.3.1.2 A53_RS_BW_LIMITER Registers
          1. 14.3.1.2.1  REGS_PID Registers
          2. 14.3.1.2.2  REGS_CTRL Registers
          3. 14.3.1.2.3  REGS_RD_BW_CIR Registers
          4. 14.3.1.2.4  REGS_RD_BW_PIR Registers
          5. 14.3.1.2.5  REGS_RD_BW_BURST_OFFSET Registers
          6. 14.3.1.2.6  REGS_RD_BW_INFO Registers
          7. 14.3.1.2.7  REGS_RD_BW_STATS Registers
          8. 14.3.1.2.8  REGS_RD_BW_STATS_THRSHLD Registers
          9. 14.3.1.2.9  REGS_RD_BW_WINDOWS_CNT Registers
          10. 14.3.1.2.10 REGS_RD_BW_STATS_CIR Registers
          11. 14.3.1.2.11 REGS_RD_BW_STATS_PIR Registers
          12. 14.3.1.2.12 REGS_RD_BW_THRSHLD_CNT Registers
          13. 14.3.1.2.13 REGS_RD_BYTES_MAX Registers
          14. 14.3.1.2.14 REGS_RD_TXN Registers
          15. 14.3.1.2.15 REGS_RD_TXN_INFO Registers
          16. 14.3.1.2.16 REGS_RD_TXN_STATS Registers
          17. 14.3.1.2.17 REGS_RD_TXN_STATS_THRSHLD Registers
          18. 14.3.1.2.18 REGS_RD_TXN_WINDOWS_CNT Registers
          19. 14.3.1.2.19 REGS_RD_TXN_LIMIT_CNT Registers
          20. 14.3.1.2.20 REGS_RD_TXN_THRESHOLD_CNT Registers
          21. 14.3.1.2.21 REGS_RD_TXN_LIMIT_TOTAL Registers
          22. 14.3.1.2.22 REGS_RD_TXN_THRESHOLD_TOTAL Registers
          23. 14.3.1.2.23 REGS_RD_TXN_MAX Registers
          24. 14.3.1.2.24 Access Table
        3. 14.3.1.3 A53_WS_BW_LIMITER Registers
          1. 14.3.1.3.1  REGS_PID Registers
          2. 14.3.1.3.2  REGS_CTRL Registers
          3. 14.3.1.3.3  REGS_WR_BW_CIR Registers
          4. 14.3.1.3.4  REGS_WR_BW_PIR Registers
          5. 14.3.1.3.5  REGS_WR_BW_BURST_OFFSET Registers
          6. 14.3.1.3.6  REGS_WR_BW_INFO Registers
          7. 14.3.1.3.7  REGS_WR_BW_STATS Registers
          8. 14.3.1.3.8  REGS_WR_BW_STATS_THRSHLD Registers
          9. 14.3.1.3.9  REGS_WR_BW_WINDOWS_CNT Registers
          10. 14.3.1.3.10 REGS_WR_BW_STATS_CIR Registers
          11. 14.3.1.3.11 REGS_WR_BW_STATS_PIR Registers
          12. 14.3.1.3.12 REGS_WR_BW_THRSHLD_CNT Registers
          13. 14.3.1.3.13 REGS_WR_BYTES_MAX Registers
          14. 14.3.1.3.14 REGS_WR_TXN Registers
          15. 14.3.1.3.15 REGS_WR_TXN_INFO Registers
          16. 14.3.1.3.16 REGS_WR_TXN_STATS Registers
          17. 14.3.1.3.17 REGS_WR_TXN_STATS_THRSHLD Registers
          18. 14.3.1.3.18 REGS_WR_TXN_WINDOWS_CNT Registers
          19. 14.3.1.3.19 REGS_WR_TXN_LIMIT_CNT Registers
          20. 14.3.1.3.20 REGS_WR_TXN_THRESHOLD_CNT Registers
          21. 14.3.1.3.21 REGS_WR_TXN_LIMIT_TOTAL Registers
          22. 14.3.1.3.22 REGS_WR_TXN_THRESHOLD_TOTAL Registers
          23. 14.3.1.3.23 REGS_WR_TXN_MAX Registers
          24. 14.3.1.3.24 Access Table
        4. 14.3.1.4 COMPUTE_CLUSTER_PBIST_0 Registers
          1. 14.3.1.4.1  PBIST_RF0L Registers
          2. 14.3.1.4.2  PBIST_RF1L Registers
          3. 14.3.1.4.3  PBIST_RF2L Registers
          4. 14.3.1.4.4  PBIST_RF3L Registers
          5. 14.3.1.4.5  PBIST_RF4L Registers
          6. 14.3.1.4.6  PBIST_RF5L Registers
          7. 14.3.1.4.7  PBIST_RF6L Registers
          8. 14.3.1.4.8  PBIST_RF7L Registers
          9. 14.3.1.4.9  PBIST_RF8L Registers
          10. 14.3.1.4.10 PBIST_RF9L Registers
          11. 14.3.1.4.11 PBIST_RF10L Registers
          12. 14.3.1.4.12 PBIST_RF11L Registers
          13. 14.3.1.4.13 PBIST_RF12L Registers
          14. 14.3.1.4.14 PBIST_RF13L Registers
          15. 14.3.1.4.15 PBIST_RF14L Registers
          16. 14.3.1.4.16 PBIST_RF15L Registers
          17. 14.3.1.4.17 PBIST_RF0U Registers
          18. 14.3.1.4.18 PBIST_RF1U Registers
          19. 14.3.1.4.19 PBIST_RF2U Registers
          20. 14.3.1.4.20 PBIST_RF3U Registers
          21. 14.3.1.4.21 PBIST_RF4U Registers
          22. 14.3.1.4.22 PBIST_RF5U Registers
          23. 14.3.1.4.23 PBIST_RF6U Registers
          24. 14.3.1.4.24 PBIST_RF7U Registers
          25. 14.3.1.4.25 PBIST_RF8U Registers
          26. 14.3.1.4.26 PBIST_RF9U Registers
          27. 14.3.1.4.27 PBIST_RF10U Registers
          28. 14.3.1.4.28 PBIST_RF11U Registers
          29. 14.3.1.4.29 PBIST_RF12U Registers
          30. 14.3.1.4.30 PBIST_RF13U Registers
          31. 14.3.1.4.31 PBIST_RF14U Registers
          32. 14.3.1.4.32 PBIST_RF15U Registers
          33. 14.3.1.4.33 PBIST_A0 Registers
          34. 14.3.1.4.34 PBIST_A1 Registers
          35. 14.3.1.4.35 PBIST_A2 Registers
          36. 14.3.1.4.36 PBIST_A3 Registers
          37. 14.3.1.4.37 PBIST_L0 Registers
          38. 14.3.1.4.38 PBIST_L1 Registers
          39. 14.3.1.4.39 PBIST_L2 Registers
          40. 14.3.1.4.40 PBIST_L3 Registers
          41. 14.3.1.4.41 PBIST_D Registers
          42. 14.3.1.4.42 PBIST_E Registers
          43. 14.3.1.4.43 PBIST_CA0 Registers
          44. 14.3.1.4.44 PBIST_CA1 Registers
          45. 14.3.1.4.45 PBIST_CA2 Registers
          46. 14.3.1.4.46 PBIST_CA3 Registers
          47. 14.3.1.4.47 PBIST_CL0 Registers
          48. 14.3.1.4.48 PBIST_CL1 Registers
          49. 14.3.1.4.49 PBIST_CL2 Registers
          50. 14.3.1.4.50 PBIST_CL3 Registers
          51. 14.3.1.4.51 PBIST_I0 Registers
          52. 14.3.1.4.52 PBIST_I1 Registers
          53. 14.3.1.4.53 PBIST_I2 Registers
          54. 14.3.1.4.54 PBIST_I3 Registers
          55. 14.3.1.4.55 PBIST_RAMT Registers
          56. 14.3.1.4.56 PBIST_DLR Registers
          57. 14.3.1.4.57 PBIST_CMS Registers
          58. 14.3.1.4.58 PBIST_STR Registers
          59. 14.3.1.4.59 PBIST_SCR Registers
          60. 14.3.1.4.60 PBIST_CSR Registers
          61. 14.3.1.4.61 PBIST_FDLY Registers
          62. 14.3.1.4.62 PBIST_PACT Registers
          63. 14.3.1.4.63 PBIST_PID Registers
          64. 14.3.1.4.64 PBIST_OVER Registers
          65. 14.3.1.4.65 PBIST_FSRF Registers
          66. 14.3.1.4.66 PBIST_FSRC Registers
          67. 14.3.1.4.67 PBIST_FSRA Registers
          68. 14.3.1.4.68 PBIST_FSRDL0 Registers
          69. 14.3.1.4.69 PBIST_FSRDL1 Registers
          70. 14.3.1.4.70 PBIST_MARGIN_MODE Registers
          71. 14.3.1.4.71 PBIST_WRENZ Registers
          72. 14.3.1.4.72 PBIST_PAGE_PGS Registers
          73. 14.3.1.4.73 PBIST_ROM Registers
          74. 14.3.1.4.74 PBIST_ALGO Registers
          75. 14.3.1.4.75 PBIST_RINFO Registers
          76. 14.3.1.4.76 Access Table
      2. 14.3.2 M4FSS Registers
        1. 14.3.2.1 M4FSS_DRAM_0 Registers
          1. 14.3.2.1.1 DRAM_RAM_REG_N Registers
          2. 14.3.2.1.2 Access Table
        2. 14.3.2.2 M4FSS_IRAM_0 Registers
          1. 14.3.2.2.1 IRAM_RAM_REG_N Registers
          2. 14.3.2.2.2 Access Table
        3. 14.3.2.3 M4FSS_RAT_0 Registers
          1. 14.3.2.3.1  RAT_PID Registers
          2. 14.3.2.3.2  RAT_CONFIG Registers
          3. 14.3.2.3.3  RAT_DESTINATION_ID Registers
          4. 14.3.2.3.4  RAT_EXCEPTION_LOGGING_CONTROL Registers
          5. 14.3.2.3.5  RAT_EXCEPTION_LOGGING_HEADER0 Registers
          6. 14.3.2.3.6  RAT_EXCEPTION_LOGGING_HEADER1 Registers
          7. 14.3.2.3.7  RAT_EXCEPTION_LOGGING_DATA0 Registers
          8. 14.3.2.3.8  RAT_EXCEPTION_LOGGING_DATA1 Registers
          9. 14.3.2.3.9  RAT_EXCEPTION_LOGGING_DATA2 Registers
          10. 14.3.2.3.10 RAT_EXCEPTION_LOGGING_DATA3 Registers
          11. 14.3.2.3.11 RAT_EXCEPTION_PEND_SET Registers
          12. 14.3.2.3.12 RAT_EXCEPTION_PEND_CLEAR Registers
          13. 14.3.2.3.13 RAT_EXCEPTION_ENABLE_SET Registers
          14. 14.3.2.3.14 RAT_EXCEPTION_ENABLE_CLEAR Registers
          15. 14.3.2.3.15 RAT_EOI_REG Registers
          16. 14.3.2.3.16 RAT_REGION_REGION_CTRL_J_J Registers
          17. 14.3.2.3.17 RAT_REGION_REGION_BASE_J_J Registers
          18. 14.3.2.3.18 RAT_REGION_REGION_TRANS_L_J_J Registers
          19. 14.3.2.3.19 RAT_REGION_REGION_TRANS_U_J_J Registers
          20. 14.3.2.3.20 Access Table
      3. 14.3.3 R5FSS Registers
        1. 14.3.3.1 R5FSS_COMMON0 Registers
          1. 14.3.3.1.1  EVNT_BUS_VBUSP_MMRS_DISABLE_CR Registers
          2. 14.3.3.1.2  EVNT_BUS_VBUSP_MMRS_PULSAR_CPU0_EVNT_BUS_SB_ERR_CNT_STATUS Registers
          3. 14.3.3.1.3  EVNT_BUS_VBUSP_MMRS_PULSAR_CPU1_EVNT_BUS_SB_ERR_CNT_STATUS Registers
          4. 14.3.3.1.4  EVNT_BUS_VBUSP_MMRS_PULSAR_CPU0_EVNT_BUS_MB_ERR_CNT_STATUS Registers
          5. 14.3.3.1.5  EVNT_BUS_VBUSP_MMRS_PULSAR_CPU1_EVNT_BUS_MB_ERR_CNT_STATUS Registers
          6. 14.3.3.1.6  EVNT_BUS_VBUSP_MMRS_PULSAR_EVNT_BUS_ESM_STATUS Registers
          7. 14.3.3.1.7  EVNT_BUS_VBUSP_MMRS_PULSAR_EVNT_BUS_ESM_SET Registers
          8. 14.3.3.1.8  EVNT_BUS_VBUSP_MMRS_PULSAR_EVNT_BUS_ESM_CLR Registers
          9. 14.3.3.1.9  EVNT_BUS_VBUSP_MMRS_PULSAR_EVNT_BUS_MASK_ESM_SET Registers
          10. 14.3.3.1.10 EVNT_BUS_VBUSP_MMRS_PULSAR_EVNT_BUS_MASK_ESM_CLR Registers
          11. 14.3.3.1.11 EVNT_BUS_VBUSP_MMRS_PULSAR_EVT_BUS_REVID Registers
          12. 14.3.3.1.12 CORE0_ECC_AGGR_REV Registers
          13. 14.3.3.1.13 CORE0_ECC_AGGR_VECTOR Registers
          14. 14.3.3.1.14 CORE0_ECC_AGGR_STAT Registers
          15. 14.3.3.1.15 CORE0_ECC_AGGR_RESERVED_SVBUS_N Registers
          16. 14.3.3.1.16 CORE0_ECC_AGGR_SEC_EOI_REG Registers
          17. 14.3.3.1.17 CORE0_ECC_AGGR_SEC_STATUS_REG0 Registers
          18. 14.3.3.1.18 CORE0_ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          19. 14.3.3.1.19 CORE0_ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          20. 14.3.3.1.20 CORE0_ECC_AGGR_DED_EOI_REG Registers
          21. 14.3.3.1.21 CORE0_ECC_AGGR_DED_STATUS_REG0 Registers
          22. 14.3.3.1.22 CORE0_ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          23. 14.3.3.1.23 CORE0_ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          24. 14.3.3.1.24 CORE0_ECC_AGGR_AGGR_ENABLE_SET Registers
          25. 14.3.3.1.25 CORE0_ECC_AGGR_AGGR_ENABLE_CLR Registers
          26. 14.3.3.1.26 CORE0_ECC_AGGR_AGGR_STATUS_SET Registers
          27. 14.3.3.1.27 CORE0_ECC_AGGR_AGGR_STATUS_CLR Registers
          28. 14.3.3.1.28 Access Table
      4. 14.3.4 VIM Registers
        1. 14.3.4.1  Revision Register (Base Address + 0x00)
        2. 14.3.4.2  Info Register (Base Address + 0x04)
        3. 14.3.4.3  Prioritized IRQ (Base Address + 0x08)
        4. 14.3.4.4  Prioritized FIQ (Base Address + 0x0C)
        5. 14.3.4.5  IRQ Group Status (Base Address + 0x10)
        6. 14.3.4.6  FIQ Group Status (Base Address + 0x14)
        7. 14.3.4.7  IRQ Vector Address (Base Address + 0x18)
        8. 14.3.4.8  FIQ Vector Address (Base Address + 0x1C)
        9. 14.3.4.9  Active IRQ (Base Address + 0x20)
        10. 14.3.4.10 Active FIQ (Base Address + 0x24)
        11. 14.3.4.11 IRQ Priority Mask Register (Base Address + 0x28)
        12. 14.3.4.12 FIQ Priority Mask Register (Base Address + 0x2C)
        13. 14.3.4.13 DED Vector Address (Base Address + 0x30)
        14. 14.3.4.14 Group M Interrupt Raw Status/Set Register (Base Address + 0x400 + M*0x20 + 0x00)
        15. 14.3.4.15 Group M Interrupt Enabled Status/Clear Register (Base Address + 0x400 + M*0x20 + 0x04)
        16. 14.3.4.16 Group M Interrupt Enabled Set Register (Base Address + 0x400 + M*0x20 + 0x08)
        17. 14.3.4.17 Group M Interrupt Enabled Clear Register (Base Address + 0x400 + M*0x20 + 0x0C)
        18. 14.3.4.18 Group M Interrupt IRQ Enabled Status/Clear Register (Base Address + 0x400 + M*0x20 + 0x10)
        19. 14.3.4.19 Group M Interrupt FIQ Enabled Status/Clear Register (Base Address + 0x400 + M*0x20 + 0x14)
        20. 14.3.4.20 Group M Interrupt Map Register (Base Address + 0x400 + M*0x20 + 0x18)
        21. 14.3.4.21 Group M Type Map Register (Base Address + 0x400 + M*0x20 + 0x1C)
        22. 14.3.4.22 Interrupt Q Priority Register (Base Address + 0x1000 + Q*0x4)
        23. 14.3.4.23 Interrupt Q Vector Register (Base Address + 0x2000 + Q*0x4)
      5. 14.3.5 PRUSS Registers
        1. 14.3.5.1 ICSSM Registers
          1. 14.3.5.1.1   DRAM0_SLV_RAM_RAM_REG_N Registers
          2. 14.3.5.1.2   DRAM1_SLV_RAM_RAM_REG_N Registers
          3. 14.3.5.1.3   RAT_SLICE0_CFG_PID Registers
          4. 14.3.5.1.4   RAT_SLICE0_CFG_CONFIG Registers
          5. 14.3.5.1.5   RAT_SLICE0_CFG_DESTINATION_ID Registers
          6. 14.3.5.1.6   RAT_SLICE0_CFG_EXCEPTION_LOGGING_CONTROL Registers
          7. 14.3.5.1.7   RAT_SLICE0_CFG_EXCEPTION_LOGGING_HEADER0 Registers
          8. 14.3.5.1.8   RAT_SLICE0_CFG_EXCEPTION_LOGGING_HEADER1 Registers
          9. 14.3.5.1.9   RAT_SLICE0_CFG_EXCEPTION_LOGGING_DATA0 Registers
          10. 14.3.5.1.10  RAT_SLICE0_CFG_EXCEPTION_LOGGING_DATA1 Registers
          11. 14.3.5.1.11  RAT_SLICE0_CFG_EXCEPTION_LOGGING_DATA2 Registers
          12. 14.3.5.1.12  RAT_SLICE0_CFG_EXCEPTION_LOGGING_DATA3 Registers
          13. 14.3.5.1.13  RAT_SLICE0_CFG_EXCEPTION_PEND_SET Registers
          14. 14.3.5.1.14  RAT_SLICE0_CFG_EXCEPTION_PEND_CLEAR Registers
          15. 14.3.5.1.15  RAT_SLICE0_CFG_EXCEPTION_ENABLE_SET Registers
          16. 14.3.5.1.16  RAT_SLICE0_CFG_EXCEPTION_ENABLE_CLEAR Registers
          17. 14.3.5.1.17  RAT_SLICE0_CFG_EOI_REG Registers
          18. 14.3.5.1.18  RAT_SLICE0_CFG_REGION_REGION_CTRL_J_J Registers
          19. 14.3.5.1.19  RAT_SLICE0_CFG_REGION_REGION_BASE_J_J Registers
          20. 14.3.5.1.20  RAT_SLICE0_CFG_REGION_REGION_TRANS_L_J_J Registers
          21. 14.3.5.1.21  RAT_SLICE0_CFG_REGION_REGION_TRANS_U_J_J Registers
          22. 14.3.5.1.22  RAT_SLICE1_CFG_PID Registers
          23. 14.3.5.1.23  RAT_SLICE1_CFG_CONFIG Registers
          24. 14.3.5.1.24  RAT_SLICE1_CFG_DESTINATION_ID Registers
          25. 14.3.5.1.25  RAT_SLICE1_CFG_EXCEPTION_LOGGING_CONTROL Registers
          26. 14.3.5.1.26  RAT_SLICE1_CFG_EXCEPTION_LOGGING_HEADER0 Registers
          27. 14.3.5.1.27  RAT_SLICE1_CFG_EXCEPTION_LOGGING_HEADER1 Registers
          28. 14.3.5.1.28  RAT_SLICE1_CFG_EXCEPTION_LOGGING_DATA0 Registers
          29. 14.3.5.1.29  RAT_SLICE1_CFG_EXCEPTION_LOGGING_DATA1 Registers
          30. 14.3.5.1.30  RAT_SLICE1_CFG_EXCEPTION_LOGGING_DATA2 Registers
          31. 14.3.5.1.31  RAT_SLICE1_CFG_EXCEPTION_LOGGING_DATA3 Registers
          32. 14.3.5.1.32  RAT_SLICE1_CFG_EXCEPTION_PEND_SET Registers
          33. 14.3.5.1.33  RAT_SLICE1_CFG_EXCEPTION_PEND_CLEAR Registers
          34. 14.3.5.1.34  RAT_SLICE1_CFG_EXCEPTION_ENABLE_SET Registers
          35. 14.3.5.1.35  RAT_SLICE1_CFG_EXCEPTION_ENABLE_CLEAR Registers
          36. 14.3.5.1.36  RAT_SLICE1_CFG_EOI_REG Registers
          37. 14.3.5.1.37  RAT_SLICE1_CFG_REGION_REGION_CTRL_J_J Registers
          38. 14.3.5.1.38  RAT_SLICE1_CFG_REGION_REGION_BASE_J_J Registers
          39. 14.3.5.1.39  RAT_SLICE1_CFG_REGION_REGION_TRANS_L_J_J Registers
          40. 14.3.5.1.40  RAT_SLICE1_CFG_REGION_REGION_TRANS_U_J_J Registers
          41. 14.3.5.1.41  RAM_SLV_RAM_RAM_REG_N Registers
          42. 14.3.5.1.42  PR1_ICSS_INTC_INTC_SLV_REVISION_REG Registers
          43. 14.3.5.1.43  PR1_ICSS_INTC_INTC_SLV_CONTROL_REG Registers
          44. 14.3.5.1.44  PR1_ICSS_INTC_INTC_SLV_GLOBAL_ENABLE_HINT_REG Registers
          45. 14.3.5.1.45  PR1_ICSS_INTC_INTC_SLV_GLB_NEST_LEVEL_REG Registers
          46. 14.3.5.1.46  PR1_ICSS_INTC_INTC_SLV_STATUS_SET_INDEX_REG Registers
          47. 14.3.5.1.47  PR1_ICSS_INTC_INTC_SLV_STATUS_CLR_INDEX_REG Registers
          48. 14.3.5.1.48  PR1_ICSS_INTC_INTC_SLV_ENABLE_SET_INDEX_REG Registers
          49. 14.3.5.1.49  PR1_ICSS_INTC_INTC_SLV_ENABLE_CLR_INDEX_REG Registers
          50. 14.3.5.1.50  PR1_ICSS_INTC_INTC_SLV_HINT_ENABLE_SET_INDEX_REG Registers
          51. 14.3.5.1.51  PR1_ICSS_INTC_INTC_SLV_HINT_ENABLE_CLR_INDEX_REG Registers
          52. 14.3.5.1.52  PR1_ICSS_INTC_INTC_SLV_GLB_PRI_INTR_REG Registers
          53. 14.3.5.1.53  PR1_ICSS_INTC_INTC_SLV_RAW_STATUS_REG0 Registers
          54. 14.3.5.1.54  PR1_ICSS_INTC_INTC_SLV_RAW_STATUS_REG1 Registers
          55. 14.3.5.1.55  PR1_ICSS_INTC_INTC_SLV_ENA_STATUS_REG0 Registers
          56. 14.3.5.1.56  PR1_ICSS_INTC_INTC_SLV_ENA_STATUS_REG1 Registers
          57. 14.3.5.1.57  PR1_ICSS_INTC_INTC_SLV_ENABLE_REG0 Registers
          58. 14.3.5.1.58  PR1_ICSS_INTC_INTC_SLV_ENABLE_REG1 Registers
          59. 14.3.5.1.59  PR1_ICSS_INTC_INTC_SLV_ENABLE_CLR_REG0 Registers
          60. 14.3.5.1.60  PR1_ICSS_INTC_INTC_SLV_ENABLE_CLR_REG1 Registers
          61. 14.3.5.1.61  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG0 Registers
          62. 14.3.5.1.62  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG1 Registers
          63. 14.3.5.1.63  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG2 Registers
          64. 14.3.5.1.64  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG3 Registers
          65. 14.3.5.1.65  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG4 Registers
          66. 14.3.5.1.66  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG5 Registers
          67. 14.3.5.1.67  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG6 Registers
          68. 14.3.5.1.68  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG7 Registers
          69. 14.3.5.1.69  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG8 Registers
          70. 14.3.5.1.70  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG9 Registers
          71. 14.3.5.1.71  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG10 Registers
          72. 14.3.5.1.72  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG11 Registers
          73. 14.3.5.1.73  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG12 Registers
          74. 14.3.5.1.74  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG13 Registers
          75. 14.3.5.1.75  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG14 Registers
          76. 14.3.5.1.76  PR1_ICSS_INTC_INTC_SLV_CH_MAP_REG15 Registers
          77. 14.3.5.1.77  PR1_ICSS_INTC_INTC_SLV_HINT_MAP_REG0 Registers
          78. 14.3.5.1.78  PR1_ICSS_INTC_INTC_SLV_HINT_MAP_REG1 Registers
          79. 14.3.5.1.79  PR1_ICSS_INTC_INTC_SLV_HINT_MAP_REG2 Registers
          80. 14.3.5.1.80  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG0 Registers
          81. 14.3.5.1.81  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG1 Registers
          82. 14.3.5.1.82  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG2 Registers
          83. 14.3.5.1.83  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG3 Registers
          84. 14.3.5.1.84  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG4 Registers
          85. 14.3.5.1.85  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG5 Registers
          86. 14.3.5.1.86  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG6 Registers
          87. 14.3.5.1.87  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG7 Registers
          88. 14.3.5.1.88  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG8 Registers
          89. 14.3.5.1.89  PR1_ICSS_INTC_INTC_SLV_PRI_HINT_REG9 Registers
          90. 14.3.5.1.90  PR1_ICSS_INTC_INTC_SLV_POLARITY_REG0 Registers
          91. 14.3.5.1.91  PR1_ICSS_INTC_INTC_SLV_POLARITY_REG1 Registers
          92. 14.3.5.1.92  PR1_ICSS_INTC_INTC_SLV_TYPE_REG0 Registers
          93. 14.3.5.1.93  PR1_ICSS_INTC_INTC_SLV_TYPE_REG1 Registers
          94. 14.3.5.1.94  PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG0 Registers
          95. 14.3.5.1.95  PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG1 Registers
          96. 14.3.5.1.96  PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG2 Registers
          97. 14.3.5.1.97  PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG3 Registers
          98. 14.3.5.1.98  PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG4 Registers
          99. 14.3.5.1.99  PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG5 Registers
          100. 14.3.5.1.100 PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG6 Registers
          101. 14.3.5.1.101 PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG7 Registers
          102. 14.3.5.1.102 PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG8 Registers
          103. 14.3.5.1.103 PR1_ICSS_INTC_INTC_SLV_NEST_LEVEL_REG9 Registers
          104. 14.3.5.1.104 PR1_ICSS_INTC_INTC_SLV_ENABLE_HINT_REG0 Registers
          105. 14.3.5.1.105 PR1_PROT_SLV_UNLOCK_KEY Registers
          106. 14.3.5.1.106 PR1_PROT_SLV_CFG Registers
          107. 14.3.5.1.107 PR1_CFG_SLV_PID_REG Registers
          108. 14.3.5.1.108 PR1_CFG_SLV_HWDIS_REG Registers
          109. 14.3.5.1.109 PR1_CFG_SLV_GPCFG0_REG Registers
          110. 14.3.5.1.110 PR1_CFG_SLV_GPCFG1_REG Registers
          111. 14.3.5.1.111 PR1_CFG_SLV_CGR_REG Registers
          112. 14.3.5.1.112 PR1_CFG_SLV_GPECFG0_REG Registers
          113. 14.3.5.1.113 PR1_CFG_SLV_GPECFG1_REG Registers
          114. 14.3.5.1.114 PR1_CFG_SLV_RESET_ISO_REG Registers
          115. 14.3.5.1.115 PR1_CFG_SLV_MII_RT_REG Registers
          116. 14.3.5.1.116 PR1_CFG_SLV_IEPCLK_REG Registers
          117. 14.3.5.1.117 PR1_CFG_SLV_SPP_REG Registers
          118. 14.3.5.1.118 PR1_CFG_SLV_SPIN_CFG_REG Registers
          119. 14.3.5.1.119 PR1_CFG_SLV_CORE_SYNC_REG Registers
          120. 14.3.5.1.120 PR1_CFG_SLV_SA_MX_REG Registers
          121. 14.3.5.1.121 PR1_CFG_SLV_PRU0_SD_CLK_DIV_REG Registers
          122. 14.3.5.1.122 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG0 Registers
          123. 14.3.5.1.123 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG0 Registers
          124. 14.3.5.1.124 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG1 Registers
          125. 14.3.5.1.125 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG1 Registers
          126. 14.3.5.1.126 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG2 Registers
          127. 14.3.5.1.127 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG2 Registers
          128. 14.3.5.1.128 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG3 Registers
          129. 14.3.5.1.129 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG3 Registers
          130. 14.3.5.1.130 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG4 Registers
          131. 14.3.5.1.131 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG4 Registers
          132. 14.3.5.1.132 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG5 Registers
          133. 14.3.5.1.133 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG5 Registers
          134. 14.3.5.1.134 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG6 Registers
          135. 14.3.5.1.135 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG6 Registers
          136. 14.3.5.1.136 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG7 Registers
          137. 14.3.5.1.137 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG7 Registers
          138. 14.3.5.1.138 PR1_CFG_SLV_PRU0_SD_CLK_SEL_REG8 Registers
          139. 14.3.5.1.139 PR1_CFG_SLV_PRU0_SD_SAMPLE_SIZE_REG8 Registers
          140. 14.3.5.1.140 PR1_CFG_SLV_PRU1_SD_CLK_DIV_REG Registers
          141. 14.3.5.1.141 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG0 Registers
          142. 14.3.5.1.142 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG0 Registers
          143. 14.3.5.1.143 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG1 Registers
          144. 14.3.5.1.144 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG1 Registers
          145. 14.3.5.1.145 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG2 Registers
          146. 14.3.5.1.146 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG2 Registers
          147. 14.3.5.1.147 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG3 Registers
          148. 14.3.5.1.148 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG3 Registers
          149. 14.3.5.1.149 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG4 Registers
          150. 14.3.5.1.150 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG4 Registers
          151. 14.3.5.1.151 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG5 Registers
          152. 14.3.5.1.152 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG5 Registers
          153. 14.3.5.1.153 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG6 Registers
          154. 14.3.5.1.154 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG6 Registers
          155. 14.3.5.1.155 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG7 Registers
          156. 14.3.5.1.156 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG7 Registers
          157. 14.3.5.1.157 PR1_CFG_SLV_PRU1_SD_CLK_SEL_REG8 Registers
          158. 14.3.5.1.158 PR1_CFG_SLV_PRU1_SD_SAMPLE_SIZE_REG8 Registers
          159. 14.3.5.1.159 PR1_CFG_SLV_PRU0_ED_RX_CFG_REG Registers
          160. 14.3.5.1.160 PR1_CFG_SLV_PRU0_ED_TX_CFG_REG Registers
          161. 14.3.5.1.161 PR1_CFG_SLV_PRU0_ED_CH0_CFG0_REG Registers
          162. 14.3.5.1.162 PR1_CFG_SLV_PRU0_ED_CH0_CFG1_REG Registers
          163. 14.3.5.1.163 PR1_CFG_SLV_PRU0_ED_CH1_CFG0_REG Registers
          164. 14.3.5.1.164 PR1_CFG_SLV_PRU0_ED_CH1_CFG1_REG Registers
          165. 14.3.5.1.165 PR1_CFG_SLV_PRU0_ED_CH2_CFG0_REG Registers
          166. 14.3.5.1.166 PR1_CFG_SLV_PRU0_ED_CH2_CFG1_REG Registers
          167. 14.3.5.1.167 PR1_CFG_SLV_PRU1_ED_RX_CFG_REG Registers
          168. 14.3.5.1.168 PR1_CFG_SLV_PRU1_ED_TX_CFG_REG Registers
          169. 14.3.5.1.169 PR1_CFG_SLV_PRU1_ED_CH0_CFG0_REG Registers
          170. 14.3.5.1.170 PR1_CFG_SLV_PRU1_ED_CH0_CFG1_REG Registers
          171. 14.3.5.1.171 PR1_CFG_SLV_PRU1_ED_CH1_CFG0_REG Registers
          172. 14.3.5.1.172 PR1_CFG_SLV_PRU1_ED_CH1_CFG1_REG Registers
          173. 14.3.5.1.173 PR1_CFG_SLV_PRU1_ED_CH2_CFG0_REG Registers
          174. 14.3.5.1.174 PR1_CFG_SLV_PRU1_ED_CH2_CFG1_REG Registers
          175. 14.3.5.1.175 PR1_CFG_SLV_RTU0_POKE_EN0_REG Registers
          176. 14.3.5.1.176 PR1_CFG_SLV_RTU1_POKE_EN0_REG Registers
          177. 14.3.5.1.177 PR1_CFG_SLV_PWM0 Registers
          178. 14.3.5.1.178 PR1_CFG_SLV_PWM1 Registers
          179. 14.3.5.1.179 PR1_CFG_SLV_PWM2 Registers
          180. 14.3.5.1.180 PR1_CFG_SLV_PWM3 Registers
          181. 14.3.5.1.181 PR1_CFG_SLV_PWM0_0 Registers
          182. 14.3.5.1.182 PR1_CFG_SLV_PWM0_1 Registers
          183. 14.3.5.1.183 PR1_CFG_SLV_PWM0_2 Registers
          184. 14.3.5.1.184 PR1_CFG_SLV_PWM1_0 Registers
          185. 14.3.5.1.185 PR1_CFG_SLV_PWM1_1 Registers
          186. 14.3.5.1.186 PR1_CFG_SLV_PWM1_2 Registers
          187. 14.3.5.1.187 PR1_CFG_SLV_PWM2_0 Registers
          188. 14.3.5.1.188 PR1_CFG_SLV_PWM2_1 Registers
          189. 14.3.5.1.189 PR1_CFG_SLV_PWM2_2 Registers
          190. 14.3.5.1.190 PR1_CFG_SLV_PWM3_0 Registers
          191. 14.3.5.1.191 PR1_CFG_SLV_PWM3_1 Registers
          192. 14.3.5.1.192 PR1_CFG_SLV_PWM3_2 Registers
          193. 14.3.5.1.193 PR1_CFG_SLV_SPIN_LOCK0 Registers
          194. 14.3.5.1.194 PR1_CFG_SLV_SPIN_LOCK1 Registers
          195. 14.3.5.1.195 PR1_CFG_SLV_PA_STAT_PDSP_CFG0 Registers
          196. 14.3.5.1.196 PR1_CFG_SLV_PA_STAT_PDSP_STAT0 Registers
          197. 14.3.5.1.197 PR1_CFG_SLV_PA_STAT_PDSP_CFG1 Registers
          198. 14.3.5.1.198 PR1_CFG_SLV_PA_STAT_PDSP_STAT1 Registers
          199. 14.3.5.1.199 PR1_CFG_SLV_PA_STAT_PDSP_CFG2 Registers
          200. 14.3.5.1.200 PR1_CFG_SLV_PA_STAT_PDSP_STAT2 Registers
          201. 14.3.5.1.201 PR1_CFG_SLV_PA_STAT_PDSP_CFG3 Registers
          202. 14.3.5.1.202 PR1_CFG_SLV_PA_STAT_PDSP_STAT3 Registers
          203. 14.3.5.1.203 PR1_ICSS_UART_UART_SLV_RBR_TBR Registers
          204. 14.3.5.1.204 PR1_ICSS_UART_UART_SLV_INT_EN Registers
          205. 14.3.5.1.205 PR1_ICSS_UART_UART_SLV_INT_FIFO Registers
          206. 14.3.5.1.206 PR1_ICSS_UART_UART_SLV_LCTR Registers
          207. 14.3.5.1.207 PR1_ICSS_UART_UART_SLV_MCTR Registers
          208. 14.3.5.1.208 PR1_ICSS_UART_UART_SLV_LSR1 Registers
          209. 14.3.5.1.209 PR1_ICSS_UART_UART_SLV_MSR Registers
          210. 14.3.5.1.210 PR1_ICSS_UART_UART_SLV_SCRATCH Registers
          211. 14.3.5.1.211 PR1_ICSS_UART_UART_SLV_DIVLSB Registers
          212. 14.3.5.1.212 PR1_ICSS_UART_UART_SLV_DIVMSB Registers
          213. 14.3.5.1.213 PR1_ICSS_UART_UART_SLV_PID Registers
          214. 14.3.5.1.214 PR1_ICSS_UART_UART_SLV_PWR Registers
          215. 14.3.5.1.215 PR1_ICSS_UART_UART_SLV_MODE Registers
          216. 14.3.5.1.216 IEP0_GLOBAL_CFG_REG Registers
          217. 14.3.5.1.217 IEP0_GLOBAL_STATUS_REG Registers
          218. 14.3.5.1.218 IEP0_COMPEN_REG Registers
          219. 14.3.5.1.219 IEP0_SLOW_COMPEN_REG Registers
          220. 14.3.5.1.220 IEP0_COUNT_REG0 Registers
          221. 14.3.5.1.221 IEP0_COUNT_REG1 Registers
          222. 14.3.5.1.222 IEP0_CAP_CFG_REG Registers
          223. 14.3.5.1.223 IEP0_CAP_STATUS_REG Registers
          224. 14.3.5.1.224 IEP0_CAPR0_REG0 Registers
          225. 14.3.5.1.225 IEP0_CAPR0_REG1 Registers
          226. 14.3.5.1.226 IEP0_CAPR1_REG0 Registers
          227. 14.3.5.1.227 IEP0_CAPR1_REG1 Registers
          228. 14.3.5.1.228 IEP0_CAPR2_REG0 Registers
          229. 14.3.5.1.229 IEP0_CAPR2_REG1 Registers
          230. 14.3.5.1.230 IEP0_CAPR3_REG0 Registers
          231. 14.3.5.1.231 IEP0_CAPR3_REG1 Registers
          232. 14.3.5.1.232 IEP0_CAPR4_REG0 Registers
          233. 14.3.5.1.233 IEP0_CAPR4_REG1 Registers
          234. 14.3.5.1.234 IEP0_CAPR5_REG0 Registers
          235. 14.3.5.1.235 IEP0_CAPR5_REG1 Registers
          236. 14.3.5.1.236 IEP0_CAPR6_REG0 Registers
          237. 14.3.5.1.237 IEP0_CAPR6_REG1 Registers
          238. 14.3.5.1.238 IEP0_CAPF6_REG0 Registers
          239. 14.3.5.1.239 IEP0_CAPF6_REG1 Registers
          240. 14.3.5.1.240 IEP0_CAPR7_REG0 Registers
          241. 14.3.5.1.241 IEP0_CAPR7_REG1 Registers
          242. 14.3.5.1.242 IEP0_CAPF7_REG0 Registers
          243. 14.3.5.1.243 IEP0_CAPF7_REG1 Registers
          244. 14.3.5.1.244 IEP0_CMP_CFG_REG Registers
          245. 14.3.5.1.245 IEP0_CMP_STATUS_REG Registers
          246. 14.3.5.1.246 IEP0_CMP0_REG0 Registers
          247. 14.3.5.1.247 IEP0_CMP0_REG1 Registers
          248. 14.3.5.1.248 IEP0_CMP1_REG0 Registers
          249. 14.3.5.1.249 IEP0_CMP1_REG1 Registers
          250. 14.3.5.1.250 IEP0_CMP2_REG0 Registers
          251. 14.3.5.1.251 IEP0_CMP2_REG1 Registers
          252. 14.3.5.1.252 IEP0_CMP3_REG0 Registers
          253. 14.3.5.1.253 IEP0_CMP3_REG1 Registers
          254. 14.3.5.1.254 IEP0_CMP4_REG0 Registers
          255. 14.3.5.1.255 IEP0_CMP4_REG1 Registers
          256. 14.3.5.1.256 IEP0_CMP5_REG0 Registers
          257. 14.3.5.1.257 IEP0_CMP5_REG1 Registers
          258. 14.3.5.1.258 IEP0_CMP6_REG0 Registers
          259. 14.3.5.1.259 IEP0_CMP6_REG1 Registers
          260. 14.3.5.1.260 IEP0_CMP7_REG0 Registers
          261. 14.3.5.1.261 IEP0_CMP7_REG1 Registers
          262. 14.3.5.1.262 IEP0_RXIPG0_REG Registers
          263. 14.3.5.1.263 IEP0_RXIPG1_REG Registers
          264. 14.3.5.1.264 IEP0_CMP8_REG0 Registers
          265. 14.3.5.1.265 IEP0_CMP8_REG1 Registers
          266. 14.3.5.1.266 IEP0_CMP9_REG0 Registers
          267. 14.3.5.1.267 IEP0_CMP9_REG1 Registers
          268. 14.3.5.1.268 IEP0_CMP10_REG0 Registers
          269. 14.3.5.1.269 IEP0_CMP10_REG1 Registers
          270. 14.3.5.1.270 IEP0_CMP11_REG0 Registers
          271. 14.3.5.1.271 IEP0_CMP11_REG1 Registers
          272. 14.3.5.1.272 IEP0_CMP12_REG0 Registers
          273. 14.3.5.1.273 IEP0_CMP12_REG1 Registers
          274. 14.3.5.1.274 IEP0_CMP13_REG0 Registers
          275. 14.3.5.1.275 IEP0_CMP13_REG1 Registers
          276. 14.3.5.1.276 IEP0_CMP14_REG0 Registers
          277. 14.3.5.1.277 IEP0_CMP14_REG1 Registers
          278. 14.3.5.1.278 IEP0_CMP15_REG0 Registers
          279. 14.3.5.1.279 IEP0_CMP15_REG1 Registers
          280. 14.3.5.1.280 IEP0_COUNT_RESET_VAL_REG0 Registers
          281. 14.3.5.1.281 IEP0_COUNT_RESET_VAL_REG1 Registers
          282. 14.3.5.1.282 IEP0_PWM_REG Registers
          283. 14.3.5.1.283 IEP0_CAPR0_BI_REG0 Registers
          284. 14.3.5.1.284 IEP0_CAPR0_BI_REG1 Registers
          285. 14.3.5.1.285 IEP0_CAPR1_BI_REG0 Registers
          286. 14.3.5.1.286 IEP0_CAPR1_BI_REG1 Registers
          287. 14.3.5.1.287 IEP0_CAPR2_BI_REG0 Registers
          288. 14.3.5.1.288 IEP0_CAPR2_BI_REG1 Registers
          289. 14.3.5.1.289 IEP0_CAPR3_BI_REG0 Registers
          290. 14.3.5.1.290 IEP0_CAPR3_BI_REG1 Registers
          291. 14.3.5.1.291 IEP0_CAPR4_BI_REG0 Registers
          292. 14.3.5.1.292 IEP0_CAPR4_BI_REG1 Registers
          293. 14.3.5.1.293 IEP0_CAPR5_BI_REG0 Registers
          294. 14.3.5.1.294 IEP0_CAPR5_BI_REG1 Registers
          295. 14.3.5.1.295 IEP0_CAPR6_BI_REG0 Registers
          296. 14.3.5.1.296 IEP0_CAPR6_BI_REG1 Registers
          297. 14.3.5.1.297 IEP0_CAPF6_BI_REG0 Registers
          298. 14.3.5.1.298 IEP0_CAPF6_BI_REG1 Registers
          299. 14.3.5.1.299 IEP0_CAPR7_BI_REG0 Registers
          300. 14.3.5.1.300 IEP0_CAPR7_BI_REG1 Registers
          301. 14.3.5.1.301 IEP0_CAPF7_BI_REG0 Registers
          302. 14.3.5.1.302 IEP0_CAPF7_BI_REG1 Registers
          303. 14.3.5.1.303 IEP0_SYNC_CTRL_REG Registers
          304. 14.3.5.1.304 IEP0_SYNC_FIRST_STAT_REG Registers
          305. 14.3.5.1.305 IEP0_SYNC0_STAT_REG Registers
          306. 14.3.5.1.306 IEP0_SYNC1_STAT_REG Registers
          307. 14.3.5.1.307 IEP0_SYNC_PWIDTH_REG Registers
          308. 14.3.5.1.308 IEP0_SYNC0_PERIOD_REG Registers
          309. 14.3.5.1.309 IEP0_SYNC1_DELAY_REG Registers
          310. 14.3.5.1.310 IEP0_SYNC_START_REG Registers
          311. 14.3.5.1.311 IEP0_WD_PREDIV_REG Registers
          312. 14.3.5.1.312 IEP0_PDI_WD_TIM_REG Registers
          313. 14.3.5.1.313 IEP0_PD_WD_TIM_REG Registers
          314. 14.3.5.1.314 IEP0_WD_STATUS_REG Registers
          315. 14.3.5.1.315 IEP0_WD_EXP_CNT_REG Registers
          316. 14.3.5.1.316 IEP0_WD_CTRL_REG Registers
          317. 14.3.5.1.317 IEP0_DIGIO_CTRL_REG Registers
          318. 14.3.5.1.318 IEP0_DIGIO_STATUS_REG Registers
          319. 14.3.5.1.319 IEP0_DIGIO_DATA_IN_REG Registers
          320. 14.3.5.1.320 IEP0_DIGIO_DATA_IN_RAW_REG Registers
          321. 14.3.5.1.321 IEP0_DIGIO_DATA_OUT_REG Registers
          322. 14.3.5.1.322 IEP0_DIGIO_DATA_OUT_EN_REG Registers
          323. 14.3.5.1.323 IEP0_DIGIO_EXP_REG Registers
          324. 14.3.5.1.324 PR1_ICSS_ECAP0_ECAP_SLV_TSCNT Registers
          325. 14.3.5.1.325 PR1_ICSS_ECAP0_ECAP_SLV_CNTPHS Registers
          326. 14.3.5.1.326 PR1_ICSS_ECAP0_ECAP_SLV_CAP1 Registers
          327. 14.3.5.1.327 PR1_ICSS_ECAP0_ECAP_SLV_CAP2 Registers
          328. 14.3.5.1.328 PR1_ICSS_ECAP0_ECAP_SLV_CAP3 Registers
          329. 14.3.5.1.329 PR1_ICSS_ECAP0_ECAP_SLV_CAP4 Registers
          330. 14.3.5.1.330 PR1_ICSS_ECAP0_ECAP_SLV_ECCTL2_ECCTL1 Registers
          331. 14.3.5.1.331 PR1_ICSS_ECAP0_ECAP_SLV_ECFLG_ECEINT Registers
          332. 14.3.5.1.332 PR1_ICSS_ECAP0_ECAP_SLV_ECCLR Registers
          333. 14.3.5.1.333 PR1_ICSS_ECAP0_ECAP_SLV_ECFRC Registers
          334. 14.3.5.1.334 PR1_ICSS_ECAP0_ECAP_SLV_PID Registers
          335. 14.3.5.1.335 PR1_MII_RT_PR1_MII_RT_CFG_RXCFG0 Registers
          336. 14.3.5.1.336 PR1_MII_RT_PR1_MII_RT_CFG_RXCFG1 Registers
          337. 14.3.5.1.337 PR1_MII_RT_PR1_MII_RT_CFG_TXCFG0 Registers
          338. 14.3.5.1.338 PR1_MII_RT_PR1_MII_RT_CFG_TXCFG1 Registers
          339. 14.3.5.1.339 PR1_MII_RT_PR1_MII_RT_CFG_TX_CRC0 Registers
          340. 14.3.5.1.340 PR1_MII_RT_PR1_MII_RT_CFG_TX_CRC1 Registers
          341. 14.3.5.1.341 PR1_MII_RT_PR1_MII_RT_CFG_TX_IPG0 Registers
          342. 14.3.5.1.342 PR1_MII_RT_PR1_MII_RT_CFG_TX_IPG1 Registers
          343. 14.3.5.1.343 PR1_MII_RT_PR1_MII_RT_CFG_PRS0 Registers
          344. 14.3.5.1.344 PR1_MII_RT_PR1_MII_RT_CFG_PRS1 Registers
          345. 14.3.5.1.345 PR1_MII_RT_PR1_MII_RT_CFG_RX_FRMS0 Registers
          346. 14.3.5.1.346 PR1_MII_RT_PR1_MII_RT_CFG_RX_FRMS1 Registers
          347. 14.3.5.1.347 PR1_MII_RT_PR1_MII_RT_CFG_RX_PCNT0 Registers
          348. 14.3.5.1.348 PR1_MII_RT_PR1_MII_RT_CFG_RX_PCNT1 Registers
          349. 14.3.5.1.349 PR1_MII_RT_PR1_MII_RT_CFG_RX_ERR0 Registers
          350. 14.3.5.1.350 PR1_MII_RT_PR1_MII_RT_CFG_RX_ERR1 Registers
          351. 14.3.5.1.351 PR1_MII_RT_PR1_MII_RT_CFG_RX_FIFO_LEVEL0 Registers
          352. 14.3.5.1.352 PR1_MII_RT_PR1_MII_RT_CFG_RX_FIFO_LEVEL1 Registers
          353. 14.3.5.1.353 PR1_MII_RT_PR1_MII_RT_CFG_TX_FIFO_LEVEL0 Registers
          354. 14.3.5.1.354 PR1_MII_RT_PR1_MII_RT_CFG_TX_FIFO_LEVEL1 Registers
          355. 14.3.5.1.355 PR1_MDIO_V1P7_MDIO_MDIO_VERSION_REG Registers
          356. 14.3.5.1.356 PR1_MDIO_V1P7_MDIO_CONTROL_REG Registers
          357. 14.3.5.1.357 PR1_MDIO_V1P7_MDIO_ALIVE_REG Registers
          358. 14.3.5.1.358 PR1_MDIO_V1P7_MDIO_LINK_REG Registers
          359. 14.3.5.1.359 PR1_MDIO_V1P7_MDIO_LINK_INT_RAW_REG Registers
          360. 14.3.5.1.360 PR1_MDIO_V1P7_MDIO_LINK_INT_MASKED_REG Registers
          361. 14.3.5.1.361 PR1_MDIO_V1P7_MDIO_LINK_INT_MASK_SET_REG Registers
          362. 14.3.5.1.362 PR1_MDIO_V1P7_MDIO_LINK_INT_MASK_CLEAR_REG Registers
          363. 14.3.5.1.363 PR1_MDIO_V1P7_MDIO_USER_INT_RAW_REG Registers
          364. 14.3.5.1.364 PR1_MDIO_V1P7_MDIO_USER_INT_MASKED_REG Registers
          365. 14.3.5.1.365 PR1_MDIO_V1P7_MDIO_USER_INT_MASK_SET_REG Registers
          366. 14.3.5.1.366 PR1_MDIO_V1P7_MDIO_USER_INT_MASK_CLEAR_REG Registers
          367. 14.3.5.1.367 PR1_MDIO_V1P7_MDIO_MANUAL_IF_REG Registers
          368. 14.3.5.1.368 PR1_MDIO_V1P7_MDIO_POLL_REG Registers
          369. 14.3.5.1.369 PR1_MDIO_V1P7_MDIO_POLL_EN_REG Registers
          370. 14.3.5.1.370 PR1_MDIO_V1P7_MDIO_CLAUS45_REG Registers
          371. 14.3.5.1.371 PR1_MDIO_V1P7_MDIO_USER_ADDR0_REG Registers
          372. 14.3.5.1.372 PR1_MDIO_V1P7_MDIO_USER_ADDR1_REG Registers
          373. 14.3.5.1.373 PR1_MDIO_V1P7_MDIO_USER_GROUP_USER_GROUP_USER_ACCESS_REG_J_J Registers
          374. 14.3.5.1.374 PR1_MDIO_V1P7_MDIO_USER_GROUP_USER_GROUP_USER_PHY_SEL_REG_J_J Registers
          375. 14.3.5.1.375 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_ICSS_G_CFG Registers
          376. 14.3.5.1.376 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_PREEMPT_CFG Registers
          377. 14.3.5.1.377 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_SMDT1S_CFG Registers
          378. 14.3.5.1.378 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_SMDT1C_CFG Registers
          379. 14.3.5.1.379 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_POOL_PTR_CFG Registers
          380. 14.3.5.1.380 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_TX_EARLY_EOF Registers
          381. 14.3.5.1.381 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_FRAG_CNT_CFG Registers
          382. 14.3.5.1.382 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE0 Registers
          383. 14.3.5.1.383 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE1 Registers
          384. 14.3.5.1.384 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE2 Registers
          385. 14.3.5.1.385 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE3 Registers
          386. 14.3.5.1.386 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE4 Registers
          387. 14.3.5.1.387 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE5 Registers
          388. 14.3.5.1.388 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE6 Registers
          389. 14.3.5.1.389 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE7 Registers
          390. 14.3.5.1.390 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE8 Registers
          391. 14.3.5.1.391 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE9 Registers
          392. 14.3.5.1.392 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE10 Registers
          393. 14.3.5.1.393 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE11 Registers
          394. 14.3.5.1.394 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE12 Registers
          395. 14.3.5.1.395 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE13 Registers
          396. 14.3.5.1.396 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE14 Registers
          397. 14.3.5.1.397 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE15 Registers
          398. 14.3.5.1.398 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE16 Registers
          399. 14.3.5.1.399 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE17 Registers
          400. 14.3.5.1.400 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE18 Registers
          401. 14.3.5.1.401 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE19 Registers
          402. 14.3.5.1.402 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE20 Registers
          403. 14.3.5.1.403 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE21 Registers
          404. 14.3.5.1.404 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE22 Registers
          405. 14.3.5.1.405 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE23 Registers
          406. 14.3.5.1.406 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE24 Registers
          407. 14.3.5.1.407 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE25 Registers
          408. 14.3.5.1.408 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE26 Registers
          409. 14.3.5.1.409 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE27 Registers
          410. 14.3.5.1.410 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE28 Registers
          411. 14.3.5.1.411 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE29 Registers
          412. 14.3.5.1.412 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE30 Registers
          413. 14.3.5.1.413 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE31 Registers
          414. 14.3.5.1.414 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK0 Registers
          415. 14.3.5.1.415 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK1 Registers
          416. 14.3.5.1.416 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK2 Registers
          417. 14.3.5.1.417 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK3 Registers
          418. 14.3.5.1.418 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK4 Registers
          419. 14.3.5.1.419 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK5 Registers
          420. 14.3.5.1.420 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK6 Registers
          421. 14.3.5.1.421 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK7 Registers
          422. 14.3.5.1.422 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK8 Registers
          423. 14.3.5.1.423 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK9 Registers
          424. 14.3.5.1.424 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK10 Registers
          425. 14.3.5.1.425 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK11 Registers
          426. 14.3.5.1.426 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK12 Registers
          427. 14.3.5.1.427 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK13 Registers
          428. 14.3.5.1.428 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK14 Registers
          429. 14.3.5.1.429 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_PEEK15 Registers
          430. 14.3.5.1.430 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT0 Registers
          431. 14.3.5.1.431 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT1 Registers
          432. 14.3.5.1.432 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT2 Registers
          433. 14.3.5.1.433 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT3 Registers
          434. 14.3.5.1.434 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT4 Registers
          435. 14.3.5.1.435 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT5 Registers
          436. 14.3.5.1.436 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT6 Registers
          437. 14.3.5.1.437 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT7 Registers
          438. 14.3.5.1.438 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT8 Registers
          439. 14.3.5.1.439 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT9 Registers
          440. 14.3.5.1.440 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT10 Registers
          441. 14.3.5.1.441 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT11 Registers
          442. 14.3.5.1.442 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT12 Registers
          443. 14.3.5.1.443 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT13 Registers
          444. 14.3.5.1.444 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT14 Registers
          445. 14.3.5.1.445 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT15 Registers
          446. 14.3.5.1.446 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT16 Registers
          447. 14.3.5.1.447 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT17 Registers
          448. 14.3.5.1.448 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT18 Registers
          449. 14.3.5.1.449 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT19 Registers
          450. 14.3.5.1.450 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT20 Registers
          451. 14.3.5.1.451 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT21 Registers
          452. 14.3.5.1.452 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT22 Registers
          453. 14.3.5.1.453 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT23 Registers
          454. 14.3.5.1.454 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT24 Registers
          455. 14.3.5.1.455 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT25 Registers
          456. 14.3.5.1.456 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT26 Registers
          457. 14.3.5.1.457 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT27 Registers
          458. 14.3.5.1.458 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT28 Registers
          459. 14.3.5.1.459 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT29 Registers
          460. 14.3.5.1.460 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT30 Registers
          461. 14.3.5.1.461 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_CNT31 Registers
          462. 14.3.5.1.462 PR1_MII_RT_PR1_MII_RT_G_CFG_REGS_G_QUEUE_RESET Registers
          463. 14.3.5.1.463 ECC_AGGR_REV Registers
          464. 14.3.5.1.464 ECC_AGGR_VECTOR Registers
          465. 14.3.5.1.465 ECC_AGGR_STAT Registers
          466. 14.3.5.1.466 ECC_AGGR_RESERVED_SVBUS_N Registers
          467. 14.3.5.1.467 ECC_AGGR_SEC_EOI_REG Registers
          468. 14.3.5.1.468 ECC_AGGR_SEC_STATUS_REG0 Registers
          469. 14.3.5.1.469 ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          470. 14.3.5.1.470 ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          471. 14.3.5.1.471 ECC_AGGR_DED_EOI_REG Registers
          472. 14.3.5.1.472 ECC_AGGR_DED_STATUS_REG0 Registers
          473. 14.3.5.1.473 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          474. 14.3.5.1.474 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          475. 14.3.5.1.475 ECC_AGGR_AGGR_ENABLE_SET Registers
          476. 14.3.5.1.476 ECC_AGGR_AGGR_ENABLE_CLR Registers
          477. 14.3.5.1.477 ECC_AGGR_AGGR_STATUS_SET Registers
          478. 14.3.5.1.478 ECC_AGGR_AGGR_STATUS_CLR Registers
          479. 14.3.5.1.479 Access Table
      6. 14.3.6 GPU Registers
        1. 14.3.6.1 Graphics Processing Unit (GPU)
          1. 14.3.6.1.1 GPU Registers Description
        2. 14.3.6.2 GPU_WS_BW_LIMITER Registers
          1. 14.3.6.2.1  REGS_PID Registers
          2. 14.3.6.2.2  REGS_CTRL Registers
          3. 14.3.6.2.3  REGS_WR_BW_CIR Registers
          4. 14.3.6.2.4  REGS_WR_BW_PIR Registers
          5. 14.3.6.2.5  REGS_WR_BW_BURST_OFFSET Registers
          6. 14.3.6.2.6  REGS_WR_BW_INFO Registers
          7. 14.3.6.2.7  REGS_WR_BW_STATS Registers
          8. 14.3.6.2.8  REGS_WR_BW_STATS_THRSHLD Registers
          9. 14.3.6.2.9  REGS_WR_BW_WINDOWS_CNT Registers
          10. 14.3.6.2.10 REGS_WR_BW_STATS_CIR Registers
          11. 14.3.6.2.11 REGS_WR_BW_STATS_PIR Registers
          12. 14.3.6.2.12 REGS_WR_BW_THRSHLD_CNT Registers
          13. 14.3.6.2.13 REGS_WR_BYTES_MAX Registers
          14. 14.3.6.2.14 REGS_WR_TXN Registers
          15. 14.3.6.2.15 REGS_WR_TXN_INFO Registers
          16. 14.3.6.2.16 REGS_WR_TXN_STATS Registers
          17. 14.3.6.2.17 REGS_WR_TXN_STATS_THRSHLD Registers
          18. 14.3.6.2.18 REGS_WR_TXN_WINDOWS_CNT Registers
          19. 14.3.6.2.19 REGS_WR_TXN_LIMIT_CNT Registers
          20. 14.3.6.2.20 REGS_WR_TXN_THRESHOLD_CNT Registers
          21. 14.3.6.2.21 REGS_WR_TXN_LIMIT_TOTAL Registers
          22. 14.3.6.2.22 REGS_WR_TXN_THRESHOLD_TOTAL Registers
          23. 14.3.6.2.23 REGS_WR_TXN_MAX Registers
          24. 14.3.6.2.24 Access Table
        3. 14.3.6.3 GPU_RS_BW_LIMITER Registers
          1. 14.3.6.3.1  REGS_PID Registers
          2. 14.3.6.3.2  REGS_CTRL Registers
          3. 14.3.6.3.3  REGS_RD_BW_CIR Registers
          4. 14.3.6.3.4  REGS_RD_BW_PIR Registers
          5. 14.3.6.3.5  REGS_RD_BW_BURST_OFFSET Registers
          6. 14.3.6.3.6  REGS_RD_BW_INFO Registers
          7. 14.3.6.3.7  REGS_RD_BW_STATS Registers
          8. 14.3.6.3.8  REGS_RD_BW_STATS_THRSHLD Registers
          9. 14.3.6.3.9  REGS_RD_BW_WINDOWS_CNT Registers
          10. 14.3.6.3.10 REGS_RD_BW_STATS_CIR Registers
          11. 14.3.6.3.11 REGS_RD_BW_STATS_PIR Registers
          12. 14.3.6.3.12 REGS_RD_BW_THRSHLD_CNT Registers
          13. 14.3.6.3.13 REGS_RD_BYTES_MAX Registers
          14. 14.3.6.3.14 REGS_RD_TXN Registers
          15. 14.3.6.3.15 REGS_RD_TXN_INFO Registers
          16. 14.3.6.3.16 REGS_RD_TXN_STATS Registers
          17. 14.3.6.3.17 REGS_RD_TXN_STATS_THRSHLD Registers
          18. 14.3.6.3.18 REGS_RD_TXN_WINDOWS_CNT Registers
          19. 14.3.6.3.19 REGS_RD_TXN_LIMIT_CNT Registers
          20. 14.3.6.3.20 REGS_RD_TXN_THRESHOLD_CNT Registers
          21. 14.3.6.3.21 REGS_RD_TXN_LIMIT_TOTAL Registers
          22. 14.3.6.3.22 REGS_RD_TXN_THRESHOLD_TOTAL Registers
          23. 14.3.6.3.23 REGS_RD_TXN_MAX Registers
          24. 14.3.6.3.24 Access Table
    4. 14.4 Interprocessor Communication Registers
      1. 14.4.1 MAILBOX_CLUSTER_0 Registers
        1. 14.4.1.1  REGS0_REVISION Registers
        2. 14.4.1.2  REGS0_SYSCONFIG Registers
        3. 14.4.1.3  REGS0_MESSAGE_N Registers
        4. 14.4.1.4  REGS0_FIFO_STATUS_N Registers
        5. 14.4.1.5  REGS0_MSG_STATUS_N Registers
        6. 14.4.1.6  REGS0_IRQ_EOI Registers
        7. 14.4.1.7  REGS0_USERS_USERS_IRQ_STATUS_RAW_J_J Registers
        8. 14.4.1.8  REGS0_USERS_USERS_IRQ_STATUS_CLR_J_J Registers
        9. 14.4.1.9  REGS0_USERS_USERS_IRQ_ENABLE_SET_J_J Registers
        10. 14.4.1.10 REGS0_USERS_USERS_IRQ_ENABLE_CLR_J_J Registers
        11. 14.4.1.11 Access Table
      2. 14.4.2 SPINLOCK Registers
        1. 14.4.2.1 _SPINLOCK_REVISION Registers
        2. 14.4.2.2 _SPINLOCK_SYSCONFIG Registers
        3. 14.4.2.3 _SPINLOCK_SYSTATUS Registers
        4. 14.4.2.4 _SPINLOCK_LOCK_REG_N Registers
        5. 14.4.2.5 Access Table
    5. 14.5 Memory Controller Registers
      1. 14.5.1 ROM Registers
        1. 14.5.1.1 _ROM_ROM_REG_N Registers
        2. 14.5.1.2 Access Table
      2. 14.5.2 PSRAMECC Registers
        1. 14.5.2.1  RAM_RAM_REG_N Registers
        2. 14.5.2.2  ECC_AGGR_REV Registers
        3. 14.5.2.3  ECC_AGGR_VECTOR Registers
        4. 14.5.2.4  ECC_AGGR_STAT Registers
        5. 14.5.2.5  ECC_AGGR_RESERVED_SVBUS_N Registers
        6. 14.5.2.6  ECC_AGGR_SEC_EOI_REG Registers
        7. 14.5.2.7  ECC_AGGR_SEC_STATUS_REG0 Registers
        8. 14.5.2.8  ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
        9. 14.5.2.9  ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
        10. 14.5.2.10 ECC_AGGR_DED_EOI_REG Registers
        11. 14.5.2.11 ECC_AGGR_DED_STATUS_REG0 Registers
        12. 14.5.2.12 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
        13. 14.5.2.13 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
        14. 14.5.2.14 ECC_AGGR_AGGR_ENABLE_SET Registers
        15. 14.5.2.15 ECC_AGGR_AGGR_ENABLE_CLR Registers
        16. 14.5.2.16 ECC_AGGR_AGGR_STATUS_SET Registers
        17. 14.5.2.17 ECC_AGGR_AGGR_STATUS_CLR Registers
        18. 14.5.2.18 Access Table
      3. 14.5.3 PSRAMECC_16K Registers
        1. 14.5.3.1  ECC_AGGR_REV Registers
        2. 14.5.3.2  ECC_AGGR_VECTOR Registers
        3. 14.5.3.3  ECC_AGGR_STAT Registers
        4. 14.5.3.4  ECC_AGGR_RESERVED_SVBUS_N Registers
        5. 14.5.3.5  ECC_AGGR_SEC_EOI_REG Registers
        6. 14.5.3.6  ECC_AGGR_SEC_STATUS_REG0 Registers
        7. 14.5.3.7  ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
        8. 14.5.3.8  ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
        9. 14.5.3.9  ECC_AGGR_DED_EOI_REG Registers
        10. 14.5.3.10 ECC_AGGR_DED_STATUS_REG0 Registers
        11. 14.5.3.11 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
        12. 14.5.3.12 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
        13. 14.5.3.13 ECC_AGGR_AGGR_ENABLE_SET Registers
        14. 14.5.3.14 ECC_AGGR_AGGR_ENABLE_CLR Registers
        15. 14.5.3.15 ECC_AGGR_AGGR_STATUS_SET Registers
        16. 14.5.3.16 ECC_AGGR_AGGR_STATUS_CLR Registers
        17. 14.5.3.17 RAM_RAM_REG_N Registers
        18. 14.5.3.18 Access Table
      4. 14.5.4 DDR16SS Registers
        1. 14.5.4.1    REGS_SS_CFG_SSCFG_SS_ID_REV_REG Registers
        2. 14.5.4.2    REGS_SS_CFG_SSCFG_SS_CTL_REG Registers
        3. 14.5.4.3    REGS_SS_CFG_SSCFG_V2A_CTL_REG Registers
        4. 14.5.4.4    REGS_SS_CFG_SSCFG_V2A_R1_MAT_REG Registers
        5. 14.5.4.5    REGS_SS_CFG_SSCFG_V2A_R2_MAT_REG Registers
        6. 14.5.4.6    REGS_SS_CFG_SSCFG_V2A_R3_MAT_REG Registers
        7. 14.5.4.7    REGS_SS_CFG_SSCFG_V2A_DEF_PRI_MAP_REG Registers
        8. 14.5.4.8    REGS_SS_CFG_SSCFG_V2A_R1_PRI_MAP_REG Registers
        9. 14.5.4.9    REGS_SS_CFG_SSCFG_V2A_R2_PRI_MAP_REG Registers
        10. 14.5.4.10   REGS_SS_CFG_SSCFG_V2A_R3_PRI_MAP_REG Registers
        11. 14.5.4.11   REGS_SS_CFG_SSCFG_V2A_OLD_CMD_PR_REG Registers
        12. 14.5.4.12   REGS_SS_CFG_SSCFG_V2A_AERR_LOG1_REG Registers
        13. 14.5.4.13   REGS_SS_CFG_SSCFG_V2A_AERR_LOG2_REG Registers
        14. 14.5.4.14   REGS_SS_CFG_SSCFG_V2A_BUS_TO Registers
        15. 14.5.4.15   REGS_SS_CFG_SSCFG_V2A_INT_RAW_REG Registers
        16. 14.5.4.16   REGS_SS_CFG_SSCFG_V2A_INT_STAT_REG Registers
        17. 14.5.4.17   REGS_SS_CFG_SSCFG_V2A_INT_SET_REG Registers
        18. 14.5.4.18   REGS_SS_CFG_SSCFG_V2A_INT_CLR_REG Registers
        19. 14.5.4.19   REGS_SS_CFG_SSCFG_V2A_EOI_REG Registers
        20. 14.5.4.20   REGS_SS_CFG_SSCFG_PERF_CNT_SEL_REG Registers
        21. 14.5.4.21   REGS_SS_CFG_SSCFG_PERF_CNT1_REG Registers
        22. 14.5.4.22   REGS_SS_CFG_SSCFG_PERF_CNT2_REG Registers
        23. 14.5.4.23   REGS_SS_CFG_SSCFG_PERF_CNT3_REG Registers
        24. 14.5.4.24   REGS_SS_CFG_SSCFG_PERF_CNT4_REG Registers
        25. 14.5.4.25   REGS_SS_CFG_SSCFG_ECC_CTRL_REG Registers
        26. 14.5.4.26   REGS_SS_CFG_SSCFG_ECC_RID_INDX_REG Registers
        27. 14.5.4.27   REGS_SS_CFG_SSCFG_ECC_RID_VAL_REG Registers
        28. 14.5.4.28   REGS_SS_CFG_SSCFG_ECC_R0_STR_ADDR_REG Registers
        29. 14.5.4.29   REGS_SS_CFG_SSCFG_ECC_R0_END_ADDR_REG Registers
        30. 14.5.4.30   REGS_SS_CFG_SSCFG_ECC_R1_STR_ADDR_REG Registers
        31. 14.5.4.31   REGS_SS_CFG_SSCFG_ECC_R1_END_ADDR_REG Registers
        32. 14.5.4.32   REGS_SS_CFG_SSCFG_ECC_R2_STR_ADDR_REG Registers
        33. 14.5.4.33   REGS_SS_CFG_SSCFG_ECC_R2_END_ADDR_REG Registers
        34. 14.5.4.34   REGS_SS_CFG_SSCFG_ECC_1B_ERR_CNT_REG Registers
        35. 14.5.4.35   REGS_SS_CFG_SSCFG_ECC_1B_ERR_THRSH_REG Registers
        36. 14.5.4.36   REGS_SS_CFG_SSCFG_ECC_1B_ERR_ADR_LOG_REG Registers
        37. 14.5.4.37   REGS_SS_CFG_SSCFG_ECC_1B_ERR_MSK_LOG_REG Registers
        38. 14.5.4.38   REGS_SS_CFG_SSCFG_ECC_2B_ERR_ADR_LOG_REG Registers
        39. 14.5.4.39   REGS_SS_CFG_SSCFG_ECC_2B_ERR_MSK_LOG_REG Registers
        40. 14.5.4.40   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL1_REG Registers
        41. 14.5.4.41   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL2_REG Registers
        42. 14.5.4.42   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL3_REG Registers
        43. 14.5.4.43   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL4_REG Registers
        44. 14.5.4.44   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL5_REG Registers
        45. 14.5.4.45   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL6_REG Registers
        46. 14.5.4.46   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL7_REG Registers
        47. 14.5.4.47   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL8_REG Registers
        48. 14.5.4.48   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL9_REG Registers
        49. 14.5.4.49   REGS_SS_CFG_SSCFG_PHY_TEST_CTRL10_REG Registers
        50. 14.5.4.50   REGS_SS_CFG_SSCFG_PHY_TEST_STAT1_REG Registers
        51. 14.5.4.51   REGS_SS_CFG_SSCFG_PHY_TEST_STAT2_REG Registers
        52. 14.5.4.52   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_0 Registers
        53. 14.5.4.53   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_1 Registers
        54. 14.5.4.54   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_2 Registers
        55. 14.5.4.55   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_3 Registers
        56. 14.5.4.56   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_4 Registers
        57. 14.5.4.57   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_5 Registers
        58. 14.5.4.58   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_6 Registers
        59. 14.5.4.59   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_7 Registers
        60. 14.5.4.60   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_8 Registers
        61. 14.5.4.61   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_9 Registers
        62. 14.5.4.62   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_10 Registers
        63. 14.5.4.63   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_11 Registers
        64. 14.5.4.64   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_12 Registers
        65. 14.5.4.65   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_13 Registers
        66. 14.5.4.66   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_14 Registers
        67. 14.5.4.67   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_15 Registers
        68. 14.5.4.68   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_16 Registers
        69. 14.5.4.69   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_17 Registers
        70. 14.5.4.70   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_18 Registers
        71. 14.5.4.71   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_19 Registers
        72. 14.5.4.72   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_20 Registers
        73. 14.5.4.73   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_21 Registers
        74. 14.5.4.74   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_22 Registers
        75. 14.5.4.75   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_23 Registers
        76. 14.5.4.76   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_24 Registers
        77. 14.5.4.77   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_25 Registers
        78. 14.5.4.78   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_26 Registers
        79. 14.5.4.79   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_27 Registers
        80. 14.5.4.80   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_28 Registers
        81. 14.5.4.81   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_29 Registers
        82. 14.5.4.82   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_30 Registers
        83. 14.5.4.83   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_31 Registers
        84. 14.5.4.84   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_32 Registers
        85. 14.5.4.85   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_33 Registers
        86. 14.5.4.86   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_34 Registers
        87. 14.5.4.87   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_35 Registers
        88. 14.5.4.88   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_36 Registers
        89. 14.5.4.89   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_37 Registers
        90. 14.5.4.90   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_38 Registers
        91. 14.5.4.91   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_39 Registers
        92. 14.5.4.92   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_40 Registers
        93. 14.5.4.93   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_41 Registers
        94. 14.5.4.94   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_42 Registers
        95. 14.5.4.95   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_43 Registers
        96. 14.5.4.96   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_44 Registers
        97. 14.5.4.97   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_45 Registers
        98. 14.5.4.98   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_46 Registers
        99. 14.5.4.99   CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_47 Registers
        100. 14.5.4.100  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_48 Registers
        101. 14.5.4.101  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_49 Registers
        102. 14.5.4.102  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_50 Registers
        103. 14.5.4.103  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_51 Registers
        104. 14.5.4.104  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_52 Registers
        105. 14.5.4.105  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_53 Registers
        106. 14.5.4.106  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_54 Registers
        107. 14.5.4.107  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_55 Registers
        108. 14.5.4.108  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_56 Registers
        109. 14.5.4.109  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_57 Registers
        110. 14.5.4.110  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_58 Registers
        111. 14.5.4.111  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_59 Registers
        112. 14.5.4.112  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_60 Registers
        113. 14.5.4.113  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_61 Registers
        114. 14.5.4.114  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_62 Registers
        115. 14.5.4.115  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_63 Registers
        116. 14.5.4.116  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_64 Registers
        117. 14.5.4.117  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_65 Registers
        118. 14.5.4.118  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_66 Registers
        119. 14.5.4.119  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_67 Registers
        120. 14.5.4.120  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_68 Registers
        121. 14.5.4.121  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_69 Registers
        122. 14.5.4.122  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_70 Registers
        123. 14.5.4.123  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_71 Registers
        124. 14.5.4.124  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_72 Registers
        125. 14.5.4.125  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_73 Registers
        126. 14.5.4.126  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_74 Registers
        127. 14.5.4.127  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_75 Registers
        128. 14.5.4.128  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_76 Registers
        129. 14.5.4.129  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_77 Registers
        130. 14.5.4.130  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_78 Registers
        131. 14.5.4.131  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_79 Registers
        132. 14.5.4.132  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_80 Registers
        133. 14.5.4.133  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_81 Registers
        134. 14.5.4.134  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_82 Registers
        135. 14.5.4.135  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_83 Registers
        136. 14.5.4.136  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_84 Registers
        137. 14.5.4.137  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_85 Registers
        138. 14.5.4.138  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_86 Registers
        139. 14.5.4.139  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_87 Registers
        140. 14.5.4.140  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_88 Registers
        141. 14.5.4.141  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_89 Registers
        142. 14.5.4.142  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_90 Registers
        143. 14.5.4.143  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_91 Registers
        144. 14.5.4.144  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_92 Registers
        145. 14.5.4.145  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_93 Registers
        146. 14.5.4.146  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_94 Registers
        147. 14.5.4.147  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_95 Registers
        148. 14.5.4.148  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_96 Registers
        149. 14.5.4.149  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_97 Registers
        150. 14.5.4.150  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_98 Registers
        151. 14.5.4.151  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_99 Registers
        152. 14.5.4.152  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_100 Registers
        153. 14.5.4.153  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_101 Registers
        154. 14.5.4.154  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_102 Registers
        155. 14.5.4.155  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_103 Registers
        156. 14.5.4.156  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_104 Registers
        157. 14.5.4.157  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_105 Registers
        158. 14.5.4.158  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_106 Registers
        159. 14.5.4.159  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_107 Registers
        160. 14.5.4.160  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_108 Registers
        161. 14.5.4.161  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_109 Registers
        162. 14.5.4.162  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_110 Registers
        163. 14.5.4.163  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_111 Registers
        164. 14.5.4.164  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_112 Registers
        165. 14.5.4.165  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_113 Registers
        166. 14.5.4.166  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_114 Registers
        167. 14.5.4.167  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_115 Registers
        168. 14.5.4.168  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_116 Registers
        169. 14.5.4.169  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_117 Registers
        170. 14.5.4.170  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_118 Registers
        171. 14.5.4.171  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_119 Registers
        172. 14.5.4.172  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_120 Registers
        173. 14.5.4.173  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_121 Registers
        174. 14.5.4.174  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_122 Registers
        175. 14.5.4.175  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_123 Registers
        176. 14.5.4.176  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_124 Registers
        177. 14.5.4.177  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_125 Registers
        178. 14.5.4.178  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_126 Registers
        179. 14.5.4.179  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_127 Registers
        180. 14.5.4.180  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_128 Registers
        181. 14.5.4.181  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_129 Registers
        182. 14.5.4.182  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_130 Registers
        183. 14.5.4.183  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_131 Registers
        184. 14.5.4.184  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_132 Registers
        185. 14.5.4.185  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_133 Registers
        186. 14.5.4.186  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_134 Registers
        187. 14.5.4.187  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_135 Registers
        188. 14.5.4.188  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_136 Registers
        189. 14.5.4.189  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_137 Registers
        190. 14.5.4.190  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_138 Registers
        191. 14.5.4.191  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_139 Registers
        192. 14.5.4.192  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_140 Registers
        193. 14.5.4.193  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_141 Registers
        194. 14.5.4.194  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_142 Registers
        195. 14.5.4.195  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_143 Registers
        196. 14.5.4.196  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_144 Registers
        197. 14.5.4.197  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_145 Registers
        198. 14.5.4.198  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_146 Registers
        199. 14.5.4.199  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_147 Registers
        200. 14.5.4.200  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_148 Registers
        201. 14.5.4.201  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_149 Registers
        202. 14.5.4.202  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_150 Registers
        203. 14.5.4.203  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_151 Registers
        204. 14.5.4.204  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_152 Registers
        205. 14.5.4.205  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_153 Registers
        206. 14.5.4.206  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_154 Registers
        207. 14.5.4.207  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_155 Registers
        208. 14.5.4.208  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_156 Registers
        209. 14.5.4.209  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_157 Registers
        210. 14.5.4.210  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_158 Registers
        211. 14.5.4.211  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_159 Registers
        212. 14.5.4.212  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_160 Registers
        213. 14.5.4.213  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_161 Registers
        214. 14.5.4.214  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_162 Registers
        215. 14.5.4.215  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_163 Registers
        216. 14.5.4.216  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_164 Registers
        217. 14.5.4.217  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_165 Registers
        218. 14.5.4.218  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_166 Registers
        219. 14.5.4.219  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_167 Registers
        220. 14.5.4.220  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_168 Registers
        221. 14.5.4.221  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_169 Registers
        222. 14.5.4.222  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_170 Registers
        223. 14.5.4.223  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_171 Registers
        224. 14.5.4.224  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_172 Registers
        225. 14.5.4.225  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_173 Registers
        226. 14.5.4.226  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_174 Registers
        227. 14.5.4.227  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_175 Registers
        228. 14.5.4.228  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_176 Registers
        229. 14.5.4.229  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_177 Registers
        230. 14.5.4.230  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_178 Registers
        231. 14.5.4.231  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_179 Registers
        232. 14.5.4.232  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_180 Registers
        233. 14.5.4.233  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_181 Registers
        234. 14.5.4.234  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_182 Registers
        235. 14.5.4.235  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_183 Registers
        236. 14.5.4.236  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_184 Registers
        237. 14.5.4.237  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_185 Registers
        238. 14.5.4.238  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_186 Registers
        239. 14.5.4.239  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_187 Registers
        240. 14.5.4.240  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_188 Registers
        241. 14.5.4.241  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_189 Registers
        242. 14.5.4.242  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_190 Registers
        243. 14.5.4.243  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_191 Registers
        244. 14.5.4.244  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_192 Registers
        245. 14.5.4.245  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_193 Registers
        246. 14.5.4.246  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_194 Registers
        247. 14.5.4.247  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_195 Registers
        248. 14.5.4.248  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_196 Registers
        249. 14.5.4.249  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_197 Registers
        250. 14.5.4.250  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_198 Registers
        251. 14.5.4.251  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_199 Registers
        252. 14.5.4.252  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_200 Registers
        253. 14.5.4.253  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_201 Registers
        254. 14.5.4.254  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_202 Registers
        255. 14.5.4.255  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_203 Registers
        256. 14.5.4.256  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_204 Registers
        257. 14.5.4.257  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_205 Registers
        258. 14.5.4.258  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_206 Registers
        259. 14.5.4.259  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_207 Registers
        260. 14.5.4.260  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_208 Registers
        261. 14.5.4.261  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_209 Registers
        262. 14.5.4.262  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_210 Registers
        263. 14.5.4.263  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_211 Registers
        264. 14.5.4.264  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_212 Registers
        265. 14.5.4.265  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_213 Registers
        266. 14.5.4.266  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_214 Registers
        267. 14.5.4.267  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_215 Registers
        268. 14.5.4.268  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_216 Registers
        269. 14.5.4.269  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_217 Registers
        270. 14.5.4.270  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_218 Registers
        271. 14.5.4.271  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_219 Registers
        272. 14.5.4.272  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_220 Registers
        273. 14.5.4.273  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_221 Registers
        274. 14.5.4.274  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_222 Registers
        275. 14.5.4.275  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_223 Registers
        276. 14.5.4.276  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_224 Registers
        277. 14.5.4.277  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_225 Registers
        278. 14.5.4.278  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_226 Registers
        279. 14.5.4.279  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_227 Registers
        280. 14.5.4.280  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_228 Registers
        281. 14.5.4.281  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_229 Registers
        282. 14.5.4.282  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_230 Registers
        283. 14.5.4.283  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_231 Registers
        284. 14.5.4.284  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_232 Registers
        285. 14.5.4.285  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_233 Registers
        286. 14.5.4.286  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_234 Registers
        287. 14.5.4.287  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_235 Registers
        288. 14.5.4.288  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_236 Registers
        289. 14.5.4.289  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_237 Registers
        290. 14.5.4.290  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_238 Registers
        291. 14.5.4.291  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_239 Registers
        292. 14.5.4.292  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_240 Registers
        293. 14.5.4.293  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_241 Registers
        294. 14.5.4.294  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_242 Registers
        295. 14.5.4.295  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_243 Registers
        296. 14.5.4.296  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_244 Registers
        297. 14.5.4.297  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_245 Registers
        298. 14.5.4.298  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_246 Registers
        299. 14.5.4.299  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_247 Registers
        300. 14.5.4.300  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_248 Registers
        301. 14.5.4.301  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_249 Registers
        302. 14.5.4.302  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_250 Registers
        303. 14.5.4.303  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_251 Registers
        304. 14.5.4.304  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_252 Registers
        305. 14.5.4.305  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_253 Registers
        306. 14.5.4.306  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_254 Registers
        307. 14.5.4.307  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_255 Registers
        308. 14.5.4.308  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_256 Registers
        309. 14.5.4.309  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_257 Registers
        310. 14.5.4.310  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_258 Registers
        311. 14.5.4.311  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_259 Registers
        312. 14.5.4.312  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_260 Registers
        313. 14.5.4.313  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_261 Registers
        314. 14.5.4.314  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_262 Registers
        315. 14.5.4.315  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_263 Registers
        316. 14.5.4.316  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_264 Registers
        317. 14.5.4.317  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_265 Registers
        318. 14.5.4.318  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_266 Registers
        319. 14.5.4.319  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_267 Registers
        320. 14.5.4.320  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_268 Registers
        321. 14.5.4.321  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_269 Registers
        322. 14.5.4.322  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_270 Registers
        323. 14.5.4.323  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_271 Registers
        324. 14.5.4.324  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_272 Registers
        325. 14.5.4.325  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_273 Registers
        326. 14.5.4.326  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_274 Registers
        327. 14.5.4.327  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_275 Registers
        328. 14.5.4.328  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_276 Registers
        329. 14.5.4.329  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_277 Registers
        330. 14.5.4.330  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_278 Registers
        331. 14.5.4.331  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_279 Registers
        332. 14.5.4.332  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_280 Registers
        333. 14.5.4.333  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_281 Registers
        334. 14.5.4.334  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_282 Registers
        335. 14.5.4.335  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_283 Registers
        336. 14.5.4.336  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_284 Registers
        337. 14.5.4.337  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_285 Registers
        338. 14.5.4.338  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_286 Registers
        339. 14.5.4.339  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_287 Registers
        340. 14.5.4.340  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_288 Registers
        341. 14.5.4.341  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_289 Registers
        342. 14.5.4.342  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_290 Registers
        343. 14.5.4.343  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_291 Registers
        344. 14.5.4.344  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_292 Registers
        345. 14.5.4.345  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_293 Registers
        346. 14.5.4.346  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_294 Registers
        347. 14.5.4.347  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_295 Registers
        348. 14.5.4.348  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_296 Registers
        349. 14.5.4.349  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_297 Registers
        350. 14.5.4.350  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_298 Registers
        351. 14.5.4.351  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_299 Registers
        352. 14.5.4.352  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_300 Registers
        353. 14.5.4.353  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_301 Registers
        354. 14.5.4.354  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_302 Registers
        355. 14.5.4.355  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_303 Registers
        356. 14.5.4.356  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_304 Registers
        357. 14.5.4.357  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_305 Registers
        358. 14.5.4.358  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_306 Registers
        359. 14.5.4.359  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_307 Registers
        360. 14.5.4.360  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_308 Registers
        361. 14.5.4.361  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_309 Registers
        362. 14.5.4.362  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_310 Registers
        363. 14.5.4.363  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_311 Registers
        364. 14.5.4.364  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_312 Registers
        365. 14.5.4.365  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_313 Registers
        366. 14.5.4.366  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_314 Registers
        367. 14.5.4.367  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_315 Registers
        368. 14.5.4.368  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_316 Registers
        369. 14.5.4.369  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_317 Registers
        370. 14.5.4.370  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_318 Registers
        371. 14.5.4.371  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_319 Registers
        372. 14.5.4.372  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_320 Registers
        373. 14.5.4.373  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_321 Registers
        374. 14.5.4.374  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_322 Registers
        375. 14.5.4.375  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_323 Registers
        376. 14.5.4.376  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_324 Registers
        377. 14.5.4.377  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_325 Registers
        378. 14.5.4.378  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_326 Registers
        379. 14.5.4.379  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_327 Registers
        380. 14.5.4.380  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_328 Registers
        381. 14.5.4.381  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_329 Registers
        382. 14.5.4.382  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_330 Registers
        383. 14.5.4.383  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_331 Registers
        384. 14.5.4.384  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_332 Registers
        385. 14.5.4.385  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_333 Registers
        386. 14.5.4.386  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_334 Registers
        387. 14.5.4.387  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_335 Registers
        388. 14.5.4.388  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_336 Registers
        389. 14.5.4.389  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_337 Registers
        390. 14.5.4.390  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_338 Registers
        391. 14.5.4.391  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_339 Registers
        392. 14.5.4.392  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_340 Registers
        393. 14.5.4.393  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_341 Registers
        394. 14.5.4.394  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_342 Registers
        395. 14.5.4.395  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_343 Registers
        396. 14.5.4.396  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_344 Registers
        397. 14.5.4.397  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_345 Registers
        398. 14.5.4.398  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_346 Registers
        399. 14.5.4.399  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_347 Registers
        400. 14.5.4.400  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_348 Registers
        401. 14.5.4.401  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_349 Registers
        402. 14.5.4.402  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_350 Registers
        403. 14.5.4.403  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_351 Registers
        404. 14.5.4.404  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_352 Registers
        405. 14.5.4.405  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_353 Registers
        406. 14.5.4.406  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_354 Registers
        407. 14.5.4.407  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_355 Registers
        408. 14.5.4.408  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_356 Registers
        409. 14.5.4.409  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_357 Registers
        410. 14.5.4.410  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_358 Registers
        411. 14.5.4.411  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_359 Registers
        412. 14.5.4.412  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_360 Registers
        413. 14.5.4.413  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_361 Registers
        414. 14.5.4.414  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_362 Registers
        415. 14.5.4.415  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_363 Registers
        416. 14.5.4.416  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_364 Registers
        417. 14.5.4.417  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_365 Registers
        418. 14.5.4.418  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_366 Registers
        419. 14.5.4.419  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_367 Registers
        420. 14.5.4.420  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_368 Registers
        421. 14.5.4.421  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_369 Registers
        422. 14.5.4.422  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_370 Registers
        423. 14.5.4.423  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_371 Registers
        424. 14.5.4.424  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_372 Registers
        425. 14.5.4.425  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_373 Registers
        426. 14.5.4.426  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_374 Registers
        427. 14.5.4.427  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_375 Registers
        428. 14.5.4.428  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_376 Registers
        429. 14.5.4.429  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_377 Registers
        430. 14.5.4.430  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_378 Registers
        431. 14.5.4.431  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_379 Registers
        432. 14.5.4.432  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_380 Registers
        433. 14.5.4.433  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_381 Registers
        434. 14.5.4.434  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_382 Registers
        435. 14.5.4.435  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_383 Registers
        436. 14.5.4.436  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_384 Registers
        437. 14.5.4.437  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_385 Registers
        438. 14.5.4.438  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_386 Registers
        439. 14.5.4.439  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_387 Registers
        440. 14.5.4.440  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_388 Registers
        441. 14.5.4.441  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_389 Registers
        442. 14.5.4.442  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_390 Registers
        443. 14.5.4.443  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_391 Registers
        444. 14.5.4.444  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_392 Registers
        445. 14.5.4.445  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_393 Registers
        446. 14.5.4.446  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_394 Registers
        447. 14.5.4.447  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_395 Registers
        448. 14.5.4.448  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_396 Registers
        449. 14.5.4.449  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_397 Registers
        450. 14.5.4.450  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_398 Registers
        451. 14.5.4.451  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_399 Registers
        452. 14.5.4.452  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_400 Registers
        453. 14.5.4.453  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_401 Registers
        454. 14.5.4.454  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_402 Registers
        455. 14.5.4.455  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_403 Registers
        456. 14.5.4.456  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_404 Registers
        457. 14.5.4.457  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_405 Registers
        458. 14.5.4.458  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_406 Registers
        459. 14.5.4.459  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_407 Registers
        460. 14.5.4.460  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_408 Registers
        461. 14.5.4.461  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_409 Registers
        462. 14.5.4.462  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_410 Registers
        463. 14.5.4.463  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_411 Registers
        464. 14.5.4.464  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_412 Registers
        465. 14.5.4.465  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_413 Registers
        466. 14.5.4.466  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_414 Registers
        467. 14.5.4.467  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_415 Registers
        468. 14.5.4.468  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_416 Registers
        469. 14.5.4.469  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_417 Registers
        470. 14.5.4.470  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_418 Registers
        471. 14.5.4.471  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_419 Registers
        472. 14.5.4.472  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_420 Registers
        473. 14.5.4.473  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_421 Registers
        474. 14.5.4.474  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_CTL_422 Registers
        475. 14.5.4.475  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_0 Registers
        476. 14.5.4.476  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_1 Registers
        477. 14.5.4.477  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_2 Registers
        478. 14.5.4.478  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_3 Registers
        479. 14.5.4.479  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_4 Registers
        480. 14.5.4.480  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_5 Registers
        481. 14.5.4.481  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_6 Registers
        482. 14.5.4.482  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_7 Registers
        483. 14.5.4.483  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_8 Registers
        484. 14.5.4.484  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_9 Registers
        485. 14.5.4.485  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_10 Registers
        486. 14.5.4.486  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_11 Registers
        487. 14.5.4.487  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_12 Registers
        488. 14.5.4.488  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_13 Registers
        489. 14.5.4.489  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_14 Registers
        490. 14.5.4.490  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_15 Registers
        491. 14.5.4.491  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_16 Registers
        492. 14.5.4.492  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_17 Registers
        493. 14.5.4.493  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_18 Registers
        494. 14.5.4.494  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_19 Registers
        495. 14.5.4.495  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_20 Registers
        496. 14.5.4.496  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_21 Registers
        497. 14.5.4.497  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_22 Registers
        498. 14.5.4.498  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_23 Registers
        499. 14.5.4.499  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_24 Registers
        500. 14.5.4.500  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_25 Registers
        501. 14.5.4.501  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_26 Registers
        502. 14.5.4.502  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_27 Registers
        503. 14.5.4.503  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_28 Registers
        504. 14.5.4.504  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_29 Registers
        505. 14.5.4.505  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_30 Registers
        506. 14.5.4.506  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_31 Registers
        507. 14.5.4.507  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_32 Registers
        508. 14.5.4.508  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_33 Registers
        509. 14.5.4.509  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_34 Registers
        510. 14.5.4.510  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_35 Registers
        511. 14.5.4.511  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_36 Registers
        512. 14.5.4.512  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_37 Registers
        513. 14.5.4.513  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_38 Registers
        514. 14.5.4.514  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_39 Registers
        515. 14.5.4.515  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_40 Registers
        516. 14.5.4.516  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_41 Registers
        517. 14.5.4.517  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_42 Registers
        518. 14.5.4.518  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_43 Registers
        519. 14.5.4.519  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_44 Registers
        520. 14.5.4.520  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_45 Registers
        521. 14.5.4.521  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_46 Registers
        522. 14.5.4.522  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_47 Registers
        523. 14.5.4.523  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_48 Registers
        524. 14.5.4.524  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_49 Registers
        525. 14.5.4.525  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_50 Registers
        526. 14.5.4.526  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_51 Registers
        527. 14.5.4.527  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_52 Registers
        528. 14.5.4.528  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_53 Registers
        529. 14.5.4.529  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_54 Registers
        530. 14.5.4.530  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_55 Registers
        531. 14.5.4.531  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_56 Registers
        532. 14.5.4.532  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_57 Registers
        533. 14.5.4.533  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_58 Registers
        534. 14.5.4.534  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_59 Registers
        535. 14.5.4.535  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_60 Registers
        536. 14.5.4.536  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_61 Registers
        537. 14.5.4.537  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_62 Registers
        538. 14.5.4.538  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_63 Registers
        539. 14.5.4.539  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_64 Registers
        540. 14.5.4.540  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_65 Registers
        541. 14.5.4.541  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_66 Registers
        542. 14.5.4.542  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_67 Registers
        543. 14.5.4.543  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_68 Registers
        544. 14.5.4.544  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_69 Registers
        545. 14.5.4.545  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_70 Registers
        546. 14.5.4.546  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_71 Registers
        547. 14.5.4.547  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_72 Registers
        548. 14.5.4.548  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_73 Registers
        549. 14.5.4.549  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_74 Registers
        550. 14.5.4.550  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_75 Registers
        551. 14.5.4.551  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_76 Registers
        552. 14.5.4.552  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_77 Registers
        553. 14.5.4.553  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_78 Registers
        554. 14.5.4.554  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_79 Registers
        555. 14.5.4.555  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_80 Registers
        556. 14.5.4.556  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_81 Registers
        557. 14.5.4.557  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_82 Registers
        558. 14.5.4.558  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_83 Registers
        559. 14.5.4.559  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_84 Registers
        560. 14.5.4.560  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_85 Registers
        561. 14.5.4.561  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_86 Registers
        562. 14.5.4.562  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_87 Registers
        563. 14.5.4.563  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_88 Registers
        564. 14.5.4.564  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_89 Registers
        565. 14.5.4.565  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_90 Registers
        566. 14.5.4.566  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_91 Registers
        567. 14.5.4.567  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_92 Registers
        568. 14.5.4.568  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_93 Registers
        569. 14.5.4.569  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_94 Registers
        570. 14.5.4.570  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_95 Registers
        571. 14.5.4.571  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_96 Registers
        572. 14.5.4.572  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_97 Registers
        573. 14.5.4.573  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_98 Registers
        574. 14.5.4.574  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_99 Registers
        575. 14.5.4.575  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_100 Registers
        576. 14.5.4.576  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_101 Registers
        577. 14.5.4.577  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_102 Registers
        578. 14.5.4.578  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_103 Registers
        579. 14.5.4.579  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_104 Registers
        580. 14.5.4.580  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_105 Registers
        581. 14.5.4.581  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_106 Registers
        582. 14.5.4.582  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_107 Registers
        583. 14.5.4.583  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_108 Registers
        584. 14.5.4.584  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_109 Registers
        585. 14.5.4.585  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_110 Registers
        586. 14.5.4.586  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_111 Registers
        587. 14.5.4.587  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_112 Registers
        588. 14.5.4.588  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_113 Registers
        589. 14.5.4.589  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_114 Registers
        590. 14.5.4.590  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_115 Registers
        591. 14.5.4.591  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_116 Registers
        592. 14.5.4.592  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_117 Registers
        593. 14.5.4.593  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_118 Registers
        594. 14.5.4.594  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_119 Registers
        595. 14.5.4.595  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_120 Registers
        596. 14.5.4.596  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_121 Registers
        597. 14.5.4.597  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_122 Registers
        598. 14.5.4.598  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_123 Registers
        599. 14.5.4.599  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_124 Registers
        600. 14.5.4.600  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_125 Registers
        601. 14.5.4.601  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_126 Registers
        602. 14.5.4.602  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_127 Registers
        603. 14.5.4.603  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_128 Registers
        604. 14.5.4.604  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_129 Registers
        605. 14.5.4.605  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_130 Registers
        606. 14.5.4.606  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_131 Registers
        607. 14.5.4.607  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_132 Registers
        608. 14.5.4.608  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_133 Registers
        609. 14.5.4.609  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_134 Registers
        610. 14.5.4.610  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_135 Registers
        611. 14.5.4.611  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_136 Registers
        612. 14.5.4.612  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_137 Registers
        613. 14.5.4.613  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_138 Registers
        614. 14.5.4.614  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_139 Registers
        615. 14.5.4.615  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_140 Registers
        616. 14.5.4.616  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_141 Registers
        617. 14.5.4.617  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_142 Registers
        618. 14.5.4.618  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_143 Registers
        619. 14.5.4.619  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_144 Registers
        620. 14.5.4.620  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_145 Registers
        621. 14.5.4.621  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_146 Registers
        622. 14.5.4.622  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_147 Registers
        623. 14.5.4.623  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_148 Registers
        624. 14.5.4.624  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_149 Registers
        625. 14.5.4.625  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_150 Registers
        626. 14.5.4.626  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_151 Registers
        627. 14.5.4.627  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_152 Registers
        628. 14.5.4.628  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_153 Registers
        629. 14.5.4.629  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_154 Registers
        630. 14.5.4.630  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_155 Registers
        631. 14.5.4.631  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_156 Registers
        632. 14.5.4.632  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_157 Registers
        633. 14.5.4.633  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_158 Registers
        634. 14.5.4.634  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_159 Registers
        635. 14.5.4.635  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_160 Registers
        636. 14.5.4.636  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_161 Registers
        637. 14.5.4.637  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_162 Registers
        638. 14.5.4.638  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_163 Registers
        639. 14.5.4.639  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_164 Registers
        640. 14.5.4.640  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_165 Registers
        641. 14.5.4.641  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_166 Registers
        642. 14.5.4.642  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_167 Registers
        643. 14.5.4.643  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_168 Registers
        644. 14.5.4.644  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_169 Registers
        645. 14.5.4.645  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_170 Registers
        646. 14.5.4.646  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_171 Registers
        647. 14.5.4.647  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_172 Registers
        648. 14.5.4.648  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_173 Registers
        649. 14.5.4.649  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_174 Registers
        650. 14.5.4.650  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_175 Registers
        651. 14.5.4.651  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_176 Registers
        652. 14.5.4.652  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_177 Registers
        653. 14.5.4.653  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_178 Registers
        654. 14.5.4.654  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_179 Registers
        655. 14.5.4.655  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_180 Registers
        656. 14.5.4.656  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_181 Registers
        657. 14.5.4.657  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_182 Registers
        658. 14.5.4.658  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_183 Registers
        659. 14.5.4.659  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_184 Registers
        660. 14.5.4.660  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_185 Registers
        661. 14.5.4.661  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_186 Registers
        662. 14.5.4.662  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_187 Registers
        663. 14.5.4.663  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_188 Registers
        664. 14.5.4.664  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_189 Registers
        665. 14.5.4.665  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_190 Registers
        666. 14.5.4.666  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_191 Registers
        667. 14.5.4.667  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_192 Registers
        668. 14.5.4.668  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_193 Registers
        669. 14.5.4.669  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_194 Registers
        670. 14.5.4.670  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_195 Registers
        671. 14.5.4.671  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_196 Registers
        672. 14.5.4.672  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_197 Registers
        673. 14.5.4.673  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_198 Registers
        674. 14.5.4.674  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_199 Registers
        675. 14.5.4.675  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_200 Registers
        676. 14.5.4.676  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_201 Registers
        677. 14.5.4.677  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_202 Registers
        678. 14.5.4.678  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_203 Registers
        679. 14.5.4.679  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_204 Registers
        680. 14.5.4.680  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_205 Registers
        681. 14.5.4.681  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_206 Registers
        682. 14.5.4.682  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_207 Registers
        683. 14.5.4.683  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_208 Registers
        684. 14.5.4.684  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_209 Registers
        685. 14.5.4.685  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_210 Registers
        686. 14.5.4.686  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_211 Registers
        687. 14.5.4.687  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_212 Registers
        688. 14.5.4.688  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_213 Registers
        689. 14.5.4.689  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_214 Registers
        690. 14.5.4.690  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_215 Registers
        691. 14.5.4.691  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_216 Registers
        692. 14.5.4.692  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_217 Registers
        693. 14.5.4.693  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_218 Registers
        694. 14.5.4.694  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_219 Registers
        695. 14.5.4.695  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_220 Registers
        696. 14.5.4.696  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_221 Registers
        697. 14.5.4.697  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_222 Registers
        698. 14.5.4.698  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_223 Registers
        699. 14.5.4.699  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_224 Registers
        700. 14.5.4.700  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_225 Registers
        701. 14.5.4.701  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_226 Registers
        702. 14.5.4.702  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_227 Registers
        703. 14.5.4.703  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_228 Registers
        704. 14.5.4.704  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_229 Registers
        705. 14.5.4.705  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_230 Registers
        706. 14.5.4.706  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_231 Registers
        707. 14.5.4.707  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_232 Registers
        708. 14.5.4.708  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_233 Registers
        709. 14.5.4.709  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_234 Registers
        710. 14.5.4.710  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_235 Registers
        711. 14.5.4.711  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_236 Registers
        712. 14.5.4.712  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_237 Registers
        713. 14.5.4.713  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_238 Registers
        714. 14.5.4.714  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_239 Registers
        715. 14.5.4.715  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_240 Registers
        716. 14.5.4.716  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_241 Registers
        717. 14.5.4.717  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_242 Registers
        718. 14.5.4.718  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_243 Registers
        719. 14.5.4.719  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_244 Registers
        720. 14.5.4.720  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_245 Registers
        721. 14.5.4.721  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_246 Registers
        722. 14.5.4.722  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_247 Registers
        723. 14.5.4.723  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_248 Registers
        724. 14.5.4.724  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_249 Registers
        725. 14.5.4.725  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_250 Registers
        726. 14.5.4.726  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_251 Registers
        727. 14.5.4.727  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_252 Registers
        728. 14.5.4.728  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_253 Registers
        729. 14.5.4.729  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_254 Registers
        730. 14.5.4.730  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_255 Registers
        731. 14.5.4.731  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_256 Registers
        732. 14.5.4.732  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_257 Registers
        733. 14.5.4.733  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_258 Registers
        734. 14.5.4.734  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_259 Registers
        735. 14.5.4.735  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_260 Registers
        736. 14.5.4.736  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_261 Registers
        737. 14.5.4.737  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_262 Registers
        738. 14.5.4.738  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_263 Registers
        739. 14.5.4.739  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_264 Registers
        740. 14.5.4.740  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_265 Registers
        741. 14.5.4.741  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_266 Registers
        742. 14.5.4.742  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_267 Registers
        743. 14.5.4.743  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_268 Registers
        744. 14.5.4.744  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_269 Registers
        745. 14.5.4.745  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_270 Registers
        746. 14.5.4.746  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_271 Registers
        747. 14.5.4.747  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_272 Registers
        748. 14.5.4.748  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_273 Registers
        749. 14.5.4.749  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_274 Registers
        750. 14.5.4.750  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_275 Registers
        751. 14.5.4.751  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_276 Registers
        752. 14.5.4.752  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_277 Registers
        753. 14.5.4.753  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_278 Registers
        754. 14.5.4.754  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_279 Registers
        755. 14.5.4.755  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_280 Registers
        756. 14.5.4.756  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_281 Registers
        757. 14.5.4.757  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_282 Registers
        758. 14.5.4.758  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_283 Registers
        759. 14.5.4.759  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_284 Registers
        760. 14.5.4.760  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_285 Registers
        761. 14.5.4.761  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_286 Registers
        762. 14.5.4.762  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_287 Registers
        763. 14.5.4.763  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_288 Registers
        764. 14.5.4.764  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_289 Registers
        765. 14.5.4.765  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_290 Registers
        766. 14.5.4.766  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_291 Registers
        767. 14.5.4.767  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_292 Registers
        768. 14.5.4.768  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_293 Registers
        769. 14.5.4.769  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_294 Registers
        770. 14.5.4.770  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_295 Registers
        771. 14.5.4.771  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_296 Registers
        772. 14.5.4.772  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_297 Registers
        773. 14.5.4.773  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_298 Registers
        774. 14.5.4.774  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_299 Registers
        775. 14.5.4.775  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_300 Registers
        776. 14.5.4.776  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_301 Registers
        777. 14.5.4.777  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_302 Registers
        778. 14.5.4.778  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_303 Registers
        779. 14.5.4.779  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_304 Registers
        780. 14.5.4.780  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_305 Registers
        781. 14.5.4.781  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_306 Registers
        782. 14.5.4.782  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_307 Registers
        783. 14.5.4.783  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_308 Registers
        784. 14.5.4.784  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_309 Registers
        785. 14.5.4.785  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_310 Registers
        786. 14.5.4.786  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_311 Registers
        787. 14.5.4.787  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_312 Registers
        788. 14.5.4.788  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_313 Registers
        789. 14.5.4.789  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_314 Registers
        790. 14.5.4.790  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_315 Registers
        791. 14.5.4.791  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_316 Registers
        792. 14.5.4.792  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_317 Registers
        793. 14.5.4.793  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_318 Registers
        794. 14.5.4.794  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_319 Registers
        795. 14.5.4.795  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_320 Registers
        796. 14.5.4.796  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_321 Registers
        797. 14.5.4.797  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_322 Registers
        798. 14.5.4.798  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_323 Registers
        799. 14.5.4.799  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_324 Registers
        800. 14.5.4.800  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_325 Registers
        801. 14.5.4.801  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_326 Registers
        802. 14.5.4.802  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_327 Registers
        803. 14.5.4.803  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_328 Registers
        804. 14.5.4.804  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_329 Registers
        805. 14.5.4.805  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_330 Registers
        806. 14.5.4.806  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_331 Registers
        807. 14.5.4.807  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_332 Registers
        808. 14.5.4.808  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_333 Registers
        809. 14.5.4.809  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_334 Registers
        810. 14.5.4.810  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_335 Registers
        811. 14.5.4.811  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_336 Registers
        812. 14.5.4.812  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_337 Registers
        813. 14.5.4.813  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_338 Registers
        814. 14.5.4.814  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_339 Registers
        815. 14.5.4.815  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_340 Registers
        816. 14.5.4.816  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_341 Registers
        817. 14.5.4.817  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_342 Registers
        818. 14.5.4.818  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_343 Registers
        819. 14.5.4.819  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PI_344 Registers
        820. 14.5.4.820  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_0 Registers
        821. 14.5.4.821  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1 Registers
        822. 14.5.4.822  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_2 Registers
        823. 14.5.4.823  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_3 Registers
        824. 14.5.4.824  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_4 Registers
        825. 14.5.4.825  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_5 Registers
        826. 14.5.4.826  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_6 Registers
        827. 14.5.4.827  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_7 Registers
        828. 14.5.4.828  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_8 Registers
        829. 14.5.4.829  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_9 Registers
        830. 14.5.4.830  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_10 Registers
        831. 14.5.4.831  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_11 Registers
        832. 14.5.4.832  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_12 Registers
        833. 14.5.4.833  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_13 Registers
        834. 14.5.4.834  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_14 Registers
        835. 14.5.4.835  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_15 Registers
        836. 14.5.4.836  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_16 Registers
        837. 14.5.4.837  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_17 Registers
        838. 14.5.4.838  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_18 Registers
        839. 14.5.4.839  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_19 Registers
        840. 14.5.4.840  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_20 Registers
        841. 14.5.4.841  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_21 Registers
        842. 14.5.4.842  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_22 Registers
        843. 14.5.4.843  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_23 Registers
        844. 14.5.4.844  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_24 Registers
        845. 14.5.4.845  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_25 Registers
        846. 14.5.4.846  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_26 Registers
        847. 14.5.4.847  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_27 Registers
        848. 14.5.4.848  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_28 Registers
        849. 14.5.4.849  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_29 Registers
        850. 14.5.4.850  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_30 Registers
        851. 14.5.4.851  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_31 Registers
        852. 14.5.4.852  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_32 Registers
        853. 14.5.4.853  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_33 Registers
        854. 14.5.4.854  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_34 Registers
        855. 14.5.4.855  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_35 Registers
        856. 14.5.4.856  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_36 Registers
        857. 14.5.4.857  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_37 Registers
        858. 14.5.4.858  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_38 Registers
        859. 14.5.4.859  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_39 Registers
        860. 14.5.4.860  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_40 Registers
        861. 14.5.4.861  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_41 Registers
        862. 14.5.4.862  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_42 Registers
        863. 14.5.4.863  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_43 Registers
        864. 14.5.4.864  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_44 Registers
        865. 14.5.4.865  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_45 Registers
        866. 14.5.4.866  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_46 Registers
        867. 14.5.4.867  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_47 Registers
        868. 14.5.4.868  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_48 Registers
        869. 14.5.4.869  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_49 Registers
        870. 14.5.4.870  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_50 Registers
        871. 14.5.4.871  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_51 Registers
        872. 14.5.4.872  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_52 Registers
        873. 14.5.4.873  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_53 Registers
        874. 14.5.4.874  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_54 Registers
        875. 14.5.4.875  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_55 Registers
        876. 14.5.4.876  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_56 Registers
        877. 14.5.4.877  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_57 Registers
        878. 14.5.4.878  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_58 Registers
        879. 14.5.4.879  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_59 Registers
        880. 14.5.4.880  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_60 Registers
        881. 14.5.4.881  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_61 Registers
        882. 14.5.4.882  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_62 Registers
        883. 14.5.4.883  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_63 Registers
        884. 14.5.4.884  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_64 Registers
        885. 14.5.4.885  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_65 Registers
        886. 14.5.4.886  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_66 Registers
        887. 14.5.4.887  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_67 Registers
        888. 14.5.4.888  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_68 Registers
        889. 14.5.4.889  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_69 Registers
        890. 14.5.4.890  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_70 Registers
        891. 14.5.4.891  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_71 Registers
        892. 14.5.4.892  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_72 Registers
        893. 14.5.4.893  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_73 Registers
        894. 14.5.4.894  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_74 Registers
        895. 14.5.4.895  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_75 Registers
        896. 14.5.4.896  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_76 Registers
        897. 14.5.4.897  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_77 Registers
        898. 14.5.4.898  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_78 Registers
        899. 14.5.4.899  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_79 Registers
        900. 14.5.4.900  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_80 Registers
        901. 14.5.4.901  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_81 Registers
        902. 14.5.4.902  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_82 Registers
        903. 14.5.4.903  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_83 Registers
        904. 14.5.4.904  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_84 Registers
        905. 14.5.4.905  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_85 Registers
        906. 14.5.4.906  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_86 Registers
        907. 14.5.4.907  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_87 Registers
        908. 14.5.4.908  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_88 Registers
        909. 14.5.4.909  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_89 Registers
        910. 14.5.4.910  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_90 Registers
        911. 14.5.4.911  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_91 Registers
        912. 14.5.4.912  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_92 Registers
        913. 14.5.4.913  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_93 Registers
        914. 14.5.4.914  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_94 Registers
        915. 14.5.4.915  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_95 Registers
        916. 14.5.4.916  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_96 Registers
        917. 14.5.4.917  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_97 Registers
        918. 14.5.4.918  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_98 Registers
        919. 14.5.4.919  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_99 Registers
        920. 14.5.4.920  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_100 Registers
        921. 14.5.4.921  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_101 Registers
        922. 14.5.4.922  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_102 Registers
        923. 14.5.4.923  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_103 Registers
        924. 14.5.4.924  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_104 Registers
        925. 14.5.4.925  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_105 Registers
        926. 14.5.4.926  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_106 Registers
        927. 14.5.4.927  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_107 Registers
        928. 14.5.4.928  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_108 Registers
        929. 14.5.4.929  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_109 Registers
        930. 14.5.4.930  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_110 Registers
        931. 14.5.4.931  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_111 Registers
        932. 14.5.4.932  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_112 Registers
        933. 14.5.4.933  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_113 Registers
        934. 14.5.4.934  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_114 Registers
        935. 14.5.4.935  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_115 Registers
        936. 14.5.4.936  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_116 Registers
        937. 14.5.4.937  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_117 Registers
        938. 14.5.4.938  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_118 Registers
        939. 14.5.4.939  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_119 Registers
        940. 14.5.4.940  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_120 Registers
        941. 14.5.4.941  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_121 Registers
        942. 14.5.4.942  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_122 Registers
        943. 14.5.4.943  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_123 Registers
        944. 14.5.4.944  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_124 Registers
        945. 14.5.4.945  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_125 Registers
        946. 14.5.4.946  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_256 Registers
        947. 14.5.4.947  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_257 Registers
        948. 14.5.4.948  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_258 Registers
        949. 14.5.4.949  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_259 Registers
        950. 14.5.4.950  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_260 Registers
        951. 14.5.4.951  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_261 Registers
        952. 14.5.4.952  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_262 Registers
        953. 14.5.4.953  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_263 Registers
        954. 14.5.4.954  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_264 Registers
        955. 14.5.4.955  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_265 Registers
        956. 14.5.4.956  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_266 Registers
        957. 14.5.4.957  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_267 Registers
        958. 14.5.4.958  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_268 Registers
        959. 14.5.4.959  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_269 Registers
        960. 14.5.4.960  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_270 Registers
        961. 14.5.4.961  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_271 Registers
        962. 14.5.4.962  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_272 Registers
        963. 14.5.4.963  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_273 Registers
        964. 14.5.4.964  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_274 Registers
        965. 14.5.4.965  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_275 Registers
        966. 14.5.4.966  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_276 Registers
        967. 14.5.4.967  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_277 Registers
        968. 14.5.4.968  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_278 Registers
        969. 14.5.4.969  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_279 Registers
        970. 14.5.4.970  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_280 Registers
        971. 14.5.4.971  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_281 Registers
        972. 14.5.4.972  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_282 Registers
        973. 14.5.4.973  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_283 Registers
        974. 14.5.4.974  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_284 Registers
        975. 14.5.4.975  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_285 Registers
        976. 14.5.4.976  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_286 Registers
        977. 14.5.4.977  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_287 Registers
        978. 14.5.4.978  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_288 Registers
        979. 14.5.4.979  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_289 Registers
        980. 14.5.4.980  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_290 Registers
        981. 14.5.4.981  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_291 Registers
        982. 14.5.4.982  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_292 Registers
        983. 14.5.4.983  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_293 Registers
        984. 14.5.4.984  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_294 Registers
        985. 14.5.4.985  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_295 Registers
        986. 14.5.4.986  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_296 Registers
        987. 14.5.4.987  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_297 Registers
        988. 14.5.4.988  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_298 Registers
        989. 14.5.4.989  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_299 Registers
        990. 14.5.4.990  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_300 Registers
        991. 14.5.4.991  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_301 Registers
        992. 14.5.4.992  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_302 Registers
        993. 14.5.4.993  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_303 Registers
        994. 14.5.4.994  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_304 Registers
        995. 14.5.4.995  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_305 Registers
        996. 14.5.4.996  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_306 Registers
        997. 14.5.4.997  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_307 Registers
        998. 14.5.4.998  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_308 Registers
        999. 14.5.4.999  CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_309 Registers
        1000. 14.5.4.1000 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_310 Registers
        1001. 14.5.4.1001 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_311 Registers
        1002. 14.5.4.1002 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_312 Registers
        1003. 14.5.4.1003 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_313 Registers
        1004. 14.5.4.1004 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_314 Registers
        1005. 14.5.4.1005 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_315 Registers
        1006. 14.5.4.1006 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_316 Registers
        1007. 14.5.4.1007 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_317 Registers
        1008. 14.5.4.1008 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_318 Registers
        1009. 14.5.4.1009 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_319 Registers
        1010. 14.5.4.1010 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_320 Registers
        1011. 14.5.4.1011 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_321 Registers
        1012. 14.5.4.1012 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_322 Registers
        1013. 14.5.4.1013 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_323 Registers
        1014. 14.5.4.1014 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_324 Registers
        1015. 14.5.4.1015 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_325 Registers
        1016. 14.5.4.1016 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_326 Registers
        1017. 14.5.4.1017 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_327 Registers
        1018. 14.5.4.1018 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_328 Registers
        1019. 14.5.4.1019 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_329 Registers
        1020. 14.5.4.1020 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_330 Registers
        1021. 14.5.4.1021 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_331 Registers
        1022. 14.5.4.1022 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_332 Registers
        1023. 14.5.4.1023 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_333 Registers
        1024. 14.5.4.1024 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_334 Registers
        1025. 14.5.4.1025 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_335 Registers
        1026. 14.5.4.1026 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_336 Registers
        1027. 14.5.4.1027 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_337 Registers
        1028. 14.5.4.1028 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_338 Registers
        1029. 14.5.4.1029 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_339 Registers
        1030. 14.5.4.1030 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_340 Registers
        1031. 14.5.4.1031 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_341 Registers
        1032. 14.5.4.1032 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_342 Registers
        1033. 14.5.4.1033 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_343 Registers
        1034. 14.5.4.1034 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_344 Registers
        1035. 14.5.4.1035 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_345 Registers
        1036. 14.5.4.1036 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_346 Registers
        1037. 14.5.4.1037 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_347 Registers
        1038. 14.5.4.1038 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_348 Registers
        1039. 14.5.4.1039 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_349 Registers
        1040. 14.5.4.1040 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_350 Registers
        1041. 14.5.4.1041 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_351 Registers
        1042. 14.5.4.1042 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_352 Registers
        1043. 14.5.4.1043 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_353 Registers
        1044. 14.5.4.1044 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_354 Registers
        1045. 14.5.4.1045 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_355 Registers
        1046. 14.5.4.1046 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_356 Registers
        1047. 14.5.4.1047 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_357 Registers
        1048. 14.5.4.1048 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_358 Registers
        1049. 14.5.4.1049 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_359 Registers
        1050. 14.5.4.1050 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_360 Registers
        1051. 14.5.4.1051 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_361 Registers
        1052. 14.5.4.1052 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_362 Registers
        1053. 14.5.4.1053 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_363 Registers
        1054. 14.5.4.1054 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_364 Registers
        1055. 14.5.4.1055 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_365 Registers
        1056. 14.5.4.1056 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_366 Registers
        1057. 14.5.4.1057 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_367 Registers
        1058. 14.5.4.1058 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_368 Registers
        1059. 14.5.4.1059 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_369 Registers
        1060. 14.5.4.1060 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_370 Registers
        1061. 14.5.4.1061 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_371 Registers
        1062. 14.5.4.1062 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_372 Registers
        1063. 14.5.4.1063 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_373 Registers
        1064. 14.5.4.1064 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_374 Registers
        1065. 14.5.4.1065 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_375 Registers
        1066. 14.5.4.1066 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_376 Registers
        1067. 14.5.4.1067 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_377 Registers
        1068. 14.5.4.1068 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_378 Registers
        1069. 14.5.4.1069 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_379 Registers
        1070. 14.5.4.1070 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_380 Registers
        1071. 14.5.4.1071 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_381 Registers
        1072. 14.5.4.1072 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_512 Registers
        1073. 14.5.4.1073 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_513 Registers
        1074. 14.5.4.1074 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_514 Registers
        1075. 14.5.4.1075 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_515 Registers
        1076. 14.5.4.1076 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_516 Registers
        1077. 14.5.4.1077 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_517 Registers
        1078. 14.5.4.1078 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_518 Registers
        1079. 14.5.4.1079 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_519 Registers
        1080. 14.5.4.1080 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_520 Registers
        1081. 14.5.4.1081 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_521 Registers
        1082. 14.5.4.1082 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_522 Registers
        1083. 14.5.4.1083 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_523 Registers
        1084. 14.5.4.1084 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_524 Registers
        1085. 14.5.4.1085 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_525 Registers
        1086. 14.5.4.1086 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_526 Registers
        1087. 14.5.4.1087 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_527 Registers
        1088. 14.5.4.1088 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_528 Registers
        1089. 14.5.4.1089 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_529 Registers
        1090. 14.5.4.1090 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_530 Registers
        1091. 14.5.4.1091 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_531 Registers
        1092. 14.5.4.1092 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_532 Registers
        1093. 14.5.4.1093 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_533 Registers
        1094. 14.5.4.1094 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_534 Registers
        1095. 14.5.4.1095 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_535 Registers
        1096. 14.5.4.1096 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_536 Registers
        1097. 14.5.4.1097 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_537 Registers
        1098. 14.5.4.1098 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_538 Registers
        1099. 14.5.4.1099 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_539 Registers
        1100. 14.5.4.1100 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_540 Registers
        1101. 14.5.4.1101 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_541 Registers
        1102. 14.5.4.1102 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_542 Registers
        1103. 14.5.4.1103 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_543 Registers
        1104. 14.5.4.1104 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_544 Registers
        1105. 14.5.4.1105 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_545 Registers
        1106. 14.5.4.1106 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_546 Registers
        1107. 14.5.4.1107 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_547 Registers
        1108. 14.5.4.1108 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_548 Registers
        1109. 14.5.4.1109 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_549 Registers
        1110. 14.5.4.1110 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_550 Registers
        1111. 14.5.4.1111 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_551 Registers
        1112. 14.5.4.1112 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_552 Registers
        1113. 14.5.4.1113 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_553 Registers
        1114. 14.5.4.1114 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_554 Registers
        1115. 14.5.4.1115 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_768 Registers
        1116. 14.5.4.1116 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_769 Registers
        1117. 14.5.4.1117 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_770 Registers
        1118. 14.5.4.1118 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_771 Registers
        1119. 14.5.4.1119 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_772 Registers
        1120. 14.5.4.1120 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_773 Registers
        1121. 14.5.4.1121 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_774 Registers
        1122. 14.5.4.1122 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_775 Registers
        1123. 14.5.4.1123 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_776 Registers
        1124. 14.5.4.1124 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_777 Registers
        1125. 14.5.4.1125 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_778 Registers
        1126. 14.5.4.1126 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_779 Registers
        1127. 14.5.4.1127 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_780 Registers
        1128. 14.5.4.1128 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_781 Registers
        1129. 14.5.4.1129 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_782 Registers
        1130. 14.5.4.1130 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_783 Registers
        1131. 14.5.4.1131 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_784 Registers
        1132. 14.5.4.1132 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_785 Registers
        1133. 14.5.4.1133 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_786 Registers
        1134. 14.5.4.1134 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_787 Registers
        1135. 14.5.4.1135 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_788 Registers
        1136. 14.5.4.1136 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_789 Registers
        1137. 14.5.4.1137 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_790 Registers
        1138. 14.5.4.1138 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_791 Registers
        1139. 14.5.4.1139 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_792 Registers
        1140. 14.5.4.1140 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_793 Registers
        1141. 14.5.4.1141 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_794 Registers
        1142. 14.5.4.1142 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_795 Registers
        1143. 14.5.4.1143 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_796 Registers
        1144. 14.5.4.1144 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_797 Registers
        1145. 14.5.4.1145 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_798 Registers
        1146. 14.5.4.1146 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_799 Registers
        1147. 14.5.4.1147 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_800 Registers
        1148. 14.5.4.1148 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_801 Registers
        1149. 14.5.4.1149 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_802 Registers
        1150. 14.5.4.1150 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_803 Registers
        1151. 14.5.4.1151 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_804 Registers
        1152. 14.5.4.1152 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_805 Registers
        1153. 14.5.4.1153 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_806 Registers
        1154. 14.5.4.1154 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_807 Registers
        1155. 14.5.4.1155 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_808 Registers
        1156. 14.5.4.1156 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_809 Registers
        1157. 14.5.4.1157 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_810 Registers
        1158. 14.5.4.1158 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1024 Registers
        1159. 14.5.4.1159 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1025 Registers
        1160. 14.5.4.1160 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1026 Registers
        1161. 14.5.4.1161 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1027 Registers
        1162. 14.5.4.1162 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1028 Registers
        1163. 14.5.4.1163 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1029 Registers
        1164. 14.5.4.1164 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1030 Registers
        1165. 14.5.4.1165 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1031 Registers
        1166. 14.5.4.1166 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1032 Registers
        1167. 14.5.4.1167 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1033 Registers
        1168. 14.5.4.1168 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1034 Registers
        1169. 14.5.4.1169 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1035 Registers
        1170. 14.5.4.1170 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1036 Registers
        1171. 14.5.4.1171 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1037 Registers
        1172. 14.5.4.1172 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1038 Registers
        1173. 14.5.4.1173 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1039 Registers
        1174. 14.5.4.1174 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1040 Registers
        1175. 14.5.4.1175 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1041 Registers
        1176. 14.5.4.1176 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1042 Registers
        1177. 14.5.4.1177 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1043 Registers
        1178. 14.5.4.1178 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1044 Registers
        1179. 14.5.4.1179 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1045 Registers
        1180. 14.5.4.1180 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1046 Registers
        1181. 14.5.4.1181 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1047 Registers
        1182. 14.5.4.1182 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1048 Registers
        1183. 14.5.4.1183 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1049 Registers
        1184. 14.5.4.1184 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1050 Registers
        1185. 14.5.4.1185 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1051 Registers
        1186. 14.5.4.1186 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1052 Registers
        1187. 14.5.4.1187 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1053 Registers
        1188. 14.5.4.1188 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1054 Registers
        1189. 14.5.4.1189 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1055 Registers
        1190. 14.5.4.1190 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1056 Registers
        1191. 14.5.4.1191 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1057 Registers
        1192. 14.5.4.1192 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1058 Registers
        1193. 14.5.4.1193 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1059 Registers
        1194. 14.5.4.1194 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1060 Registers
        1195. 14.5.4.1195 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1061 Registers
        1196. 14.5.4.1196 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1062 Registers
        1197. 14.5.4.1197 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1063 Registers
        1198. 14.5.4.1198 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1064 Registers
        1199. 14.5.4.1199 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1065 Registers
        1200. 14.5.4.1200 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1066 Registers
        1201. 14.5.4.1201 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1280 Registers
        1202. 14.5.4.1202 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1281 Registers
        1203. 14.5.4.1203 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1282 Registers
        1204. 14.5.4.1204 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1283 Registers
        1205. 14.5.4.1205 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1284 Registers
        1206. 14.5.4.1206 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1285 Registers
        1207. 14.5.4.1207 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1286 Registers
        1208. 14.5.4.1208 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1287 Registers
        1209. 14.5.4.1209 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1288 Registers
        1210. 14.5.4.1210 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1289 Registers
        1211. 14.5.4.1211 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1290 Registers
        1212. 14.5.4.1212 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1291 Registers
        1213. 14.5.4.1213 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1292 Registers
        1214. 14.5.4.1214 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1293 Registers
        1215. 14.5.4.1215 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1294 Registers
        1216. 14.5.4.1216 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1295 Registers
        1217. 14.5.4.1217 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1296 Registers
        1218. 14.5.4.1218 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1297 Registers
        1219. 14.5.4.1219 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1298 Registers
        1220. 14.5.4.1220 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1299 Registers
        1221. 14.5.4.1221 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1300 Registers
        1222. 14.5.4.1222 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1301 Registers
        1223. 14.5.4.1223 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1302 Registers
        1224. 14.5.4.1224 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1303 Registers
        1225. 14.5.4.1225 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1304 Registers
        1226. 14.5.4.1226 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1305 Registers
        1227. 14.5.4.1227 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1306 Registers
        1228. 14.5.4.1228 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1307 Registers
        1229. 14.5.4.1229 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1308 Registers
        1230. 14.5.4.1230 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1309 Registers
        1231. 14.5.4.1231 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1310 Registers
        1232. 14.5.4.1232 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1311 Registers
        1233. 14.5.4.1233 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1312 Registers
        1234. 14.5.4.1234 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1313 Registers
        1235. 14.5.4.1235 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1314 Registers
        1236. 14.5.4.1236 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1315 Registers
        1237. 14.5.4.1237 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1316 Registers
        1238. 14.5.4.1238 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1317 Registers
        1239. 14.5.4.1239 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1318 Registers
        1240. 14.5.4.1240 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1319 Registers
        1241. 14.5.4.1241 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1320 Registers
        1242. 14.5.4.1242 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1321 Registers
        1243. 14.5.4.1243 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1322 Registers
        1244. 14.5.4.1244 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1323 Registers
        1245. 14.5.4.1245 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1324 Registers
        1246. 14.5.4.1246 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1325 Registers
        1247. 14.5.4.1247 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1326 Registers
        1248. 14.5.4.1248 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1327 Registers
        1249. 14.5.4.1249 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1328 Registers
        1250. 14.5.4.1250 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1329 Registers
        1251. 14.5.4.1251 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1330 Registers
        1252. 14.5.4.1252 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1331 Registers
        1253. 14.5.4.1253 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1332 Registers
        1254. 14.5.4.1254 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1333 Registers
        1255. 14.5.4.1255 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1334 Registers
        1256. 14.5.4.1256 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1335 Registers
        1257. 14.5.4.1257 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1336 Registers
        1258. 14.5.4.1258 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1337 Registers
        1259. 14.5.4.1259 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1338 Registers
        1260. 14.5.4.1260 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1339 Registers
        1261. 14.5.4.1261 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1340 Registers
        1262. 14.5.4.1262 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1341 Registers
        1263. 14.5.4.1263 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1342 Registers
        1264. 14.5.4.1264 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1343 Registers
        1265. 14.5.4.1265 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1344 Registers
        1266. 14.5.4.1266 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1345 Registers
        1267. 14.5.4.1267 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1346 Registers
        1268. 14.5.4.1268 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1347 Registers
        1269. 14.5.4.1269 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1348 Registers
        1270. 14.5.4.1270 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1349 Registers
        1271. 14.5.4.1271 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1350 Registers
        1272. 14.5.4.1272 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1351 Registers
        1273. 14.5.4.1273 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1352 Registers
        1274. 14.5.4.1274 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1353 Registers
        1275. 14.5.4.1275 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1354 Registers
        1276. 14.5.4.1276 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1355 Registers
        1277. 14.5.4.1277 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1356 Registers
        1278. 14.5.4.1278 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1357 Registers
        1279. 14.5.4.1279 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1358 Registers
        1280. 14.5.4.1280 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1359 Registers
        1281. 14.5.4.1281 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1360 Registers
        1282. 14.5.4.1282 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1361 Registers
        1283. 14.5.4.1283 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1362 Registers
        1284. 14.5.4.1284 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1363 Registers
        1285. 14.5.4.1285 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1364 Registers
        1286. 14.5.4.1286 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1365 Registers
        1287. 14.5.4.1287 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1366 Registers
        1288. 14.5.4.1288 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1367 Registers
        1289. 14.5.4.1289 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1368 Registers
        1290. 14.5.4.1290 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1369 Registers
        1291. 14.5.4.1291 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1370 Registers
        1292. 14.5.4.1292 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1371 Registers
        1293. 14.5.4.1293 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1372 Registers
        1294. 14.5.4.1294 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1373 Registers
        1295. 14.5.4.1295 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1374 Registers
        1296. 14.5.4.1296 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1375 Registers
        1297. 14.5.4.1297 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1376 Registers
        1298. 14.5.4.1298 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1377 Registers
        1299. 14.5.4.1299 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1378 Registers
        1300. 14.5.4.1300 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1379 Registers
        1301. 14.5.4.1301 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1380 Registers
        1302. 14.5.4.1302 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1381 Registers
        1303. 14.5.4.1303 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1382 Registers
        1304. 14.5.4.1304 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1383 Registers
        1305. 14.5.4.1305 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1384 Registers
        1306. 14.5.4.1306 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1385 Registers
        1307. 14.5.4.1307 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1386 Registers
        1308. 14.5.4.1308 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1387 Registers
        1309. 14.5.4.1309 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1388 Registers
        1310. 14.5.4.1310 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1389 Registers
        1311. 14.5.4.1311 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1390 Registers
        1312. 14.5.4.1312 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1391 Registers
        1313. 14.5.4.1313 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1392 Registers
        1314. 14.5.4.1314 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1393 Registers
        1315. 14.5.4.1315 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1394 Registers
        1316. 14.5.4.1316 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1395 Registers
        1317. 14.5.4.1317 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1396 Registers
        1318. 14.5.4.1318 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1397 Registers
        1319. 14.5.4.1319 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1398 Registers
        1320. 14.5.4.1320 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1399 Registers
        1321. 14.5.4.1321 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1400 Registers
        1322. 14.5.4.1322 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1401 Registers
        1323. 14.5.4.1323 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1402 Registers
        1324. 14.5.4.1324 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1403 Registers
        1325. 14.5.4.1325 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1404 Registers
        1326. 14.5.4.1326 CTLPHY_WRAP_CTL_CFG_CTLCFG_DENALI_PHY_1405 Registers
        1327. 14.5.4.1327 Access Table
    6. 14.6 Interrupt Router Registers
      1. 14.6.1 GICSS Registers
        1. 14.6.1.1   GIC_TRANSLATER_TRANSLATER__1_GITS_TRANSLATER Registers
        2. 14.6.1.2   GIC_DISTRIBUTOR__1_GICD_CTLR Registers
        3. 14.6.1.3   GIC_DISTRIBUTOR__3_GICD_TYPER Registers
        4. 14.6.1.4   GIC_DISTRIBUTOR__4_GICD_IIDR Registers
        5. 14.6.1.5   GIC_DISTRIBUTOR__5_GICD_SETSPI_NSR Registers
        6. 14.6.1.6   GIC_DISTRIBUTOR__6_GICD_CLRSPI_NSR Registers
        7. 14.6.1.7   GIC_DISTRIBUTOR__7_GICD_SETSPI_SR Registers
        8. 14.6.1.8   GIC_DISTRIBUTOR__8_GICD_CLRSPI_SR Registers
        9. 14.6.1.9   GIC_DISTRIBUTOR__9_GICD_IGROUPR0 Registers
        10. 14.6.1.10  GIC_DISTRIBUTOR__10_GICD_IGROUPR1 Registers
        11. 14.6.1.11  GIC_DISTRIBUTOR__10_GICD_IGROUPR2 Registers
        12. 14.6.1.12  GIC_DISTRIBUTOR__10_GICD_IGROUPR3 Registers
        13. 14.6.1.13  GIC_DISTRIBUTOR__10_GICD_IGROUPR4 Registers
        14. 14.6.1.14  GIC_DISTRIBUTOR__10_GICD_IGROUPR5 Registers
        15. 14.6.1.15  GIC_DISTRIBUTOR__10_GICD_IGROUPR6 Registers
        16. 14.6.1.16  GIC_DISTRIBUTOR__10_GICD_IGROUPR7 Registers
        17. 14.6.1.17  GIC_DISTRIBUTOR__10_GICD_IGROUPR8 Registers
        18. 14.6.1.18  GIC_DISTRIBUTOR__12_GICD_ISENABLER1 Registers
        19. 14.6.1.19  GIC_DISTRIBUTOR__12_GICD_ISENABLER2 Registers
        20. 14.6.1.20  GIC_DISTRIBUTOR__12_GICD_ISENABLER3 Registers
        21. 14.6.1.21  GIC_DISTRIBUTOR__12_GICD_ISENABLER4 Registers
        22. 14.6.1.22  GIC_DISTRIBUTOR__12_GICD_ISENABLER5 Registers
        23. 14.6.1.23  GIC_DISTRIBUTOR__12_GICD_ISENABLER6 Registers
        24. 14.6.1.24  GIC_DISTRIBUTOR__12_GICD_ISENABLER7 Registers
        25. 14.6.1.25  GIC_DISTRIBUTOR__12_GICD_ISENABLER8 Registers
        26. 14.6.1.26  GIC_DISTRIBUTOR__14_GICD_ICENABLER1 Registers
        27. 14.6.1.27  GIC_DISTRIBUTOR__14_GICD_ICENABLER2 Registers
        28. 14.6.1.28  GIC_DISTRIBUTOR__14_GICD_ICENABLER3 Registers
        29. 14.6.1.29  GIC_DISTRIBUTOR__14_GICD_ICENABLER4 Registers
        30. 14.6.1.30  GIC_DISTRIBUTOR__14_GICD_ICENABLER5 Registers
        31. 14.6.1.31  GIC_DISTRIBUTOR__14_GICD_ICENABLER6 Registers
        32. 14.6.1.32  GIC_DISTRIBUTOR__14_GICD_ICENABLER7 Registers
        33. 14.6.1.33  GIC_DISTRIBUTOR__14_GICD_ICENABLER8 Registers
        34. 14.6.1.34  GIC_DISTRIBUTOR__16_GICD_ISPENDR1 Registers
        35. 14.6.1.35  GIC_DISTRIBUTOR__16_GICD_ISPENDR2 Registers
        36. 14.6.1.36  GIC_DISTRIBUTOR__16_GICD_ISPENDR3 Registers
        37. 14.6.1.37  GIC_DISTRIBUTOR__16_GICD_ISPENDR4 Registers
        38. 14.6.1.38  GIC_DISTRIBUTOR__16_GICD_ISPENDR5 Registers
        39. 14.6.1.39  GIC_DISTRIBUTOR__16_GICD_ISPENDR6 Registers
        40. 14.6.1.40  GIC_DISTRIBUTOR__16_GICD_ISPENDR7 Registers
        41. 14.6.1.41  GIC_DISTRIBUTOR__16_GICD_ISPENDR8 Registers
        42. 14.6.1.42  GIC_DISTRIBUTOR__18_GICD_ICPENDR1 Registers
        43. 14.6.1.43  GIC_DISTRIBUTOR__18_GICD_ICPENDR2 Registers
        44. 14.6.1.44  GIC_DISTRIBUTOR__18_GICD_ICPENDR3 Registers
        45. 14.6.1.45  GIC_DISTRIBUTOR__18_GICD_ICPENDR4 Registers
        46. 14.6.1.46  GIC_DISTRIBUTOR__18_GICD_ICPENDR5 Registers
        47. 14.6.1.47  GIC_DISTRIBUTOR__18_GICD_ICPENDR6 Registers
        48. 14.6.1.48  GIC_DISTRIBUTOR__18_GICD_ICPENDR7 Registers
        49. 14.6.1.49  GIC_DISTRIBUTOR__18_GICD_ICPENDR8 Registers
        50. 14.6.1.50  GIC_DISTRIBUTOR__20_GICD_ISACTIVER1 Registers
        51. 14.6.1.51  GIC_DISTRIBUTOR__20_GICD_ISACTIVER2 Registers
        52. 14.6.1.52  GIC_DISTRIBUTOR__20_GICD_ISACTIVER3 Registers
        53. 14.6.1.53  GIC_DISTRIBUTOR__20_GICD_ISACTIVER4 Registers
        54. 14.6.1.54  GIC_DISTRIBUTOR__20_GICD_ISACTIVER5 Registers
        55. 14.6.1.55  GIC_DISTRIBUTOR__20_GICD_ISACTIVER6 Registers
        56. 14.6.1.56  GIC_DISTRIBUTOR__20_GICD_ISACTIVER7 Registers
        57. 14.6.1.57  GIC_DISTRIBUTOR__20_GICD_ISACTIVER8 Registers
        58. 14.6.1.58  GIC_DISTRIBUTOR__22_GICD_ICACTIVER1 Registers
        59. 14.6.1.59  GIC_DISTRIBUTOR__22_GICD_ICACTIVER2 Registers
        60. 14.6.1.60  GIC_DISTRIBUTOR__22_GICD_ICACTIVER3 Registers
        61. 14.6.1.61  GIC_DISTRIBUTOR__22_GICD_ICACTIVER4 Registers
        62. 14.6.1.62  GIC_DISTRIBUTOR__22_GICD_ICACTIVER5 Registers
        63. 14.6.1.63  GIC_DISTRIBUTOR__22_GICD_ICACTIVER6 Registers
        64. 14.6.1.64  GIC_DISTRIBUTOR__22_GICD_ICACTIVER7 Registers
        65. 14.6.1.65  GIC_DISTRIBUTOR__22_GICD_ICACTIVER8 Registers
        66. 14.6.1.66  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR8 Registers
        67. 14.6.1.67  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR9 Registers
        68. 14.6.1.68  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR10 Registers
        69. 14.6.1.69  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR11 Registers
        70. 14.6.1.70  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR12 Registers
        71. 14.6.1.71  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR13 Registers
        72. 14.6.1.72  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR14 Registers
        73. 14.6.1.73  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR15 Registers
        74. 14.6.1.74  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR16 Registers
        75. 14.6.1.75  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR17 Registers
        76. 14.6.1.76  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR18 Registers
        77. 14.6.1.77  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR19 Registers
        78. 14.6.1.78  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR20 Registers
        79. 14.6.1.79  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR21 Registers
        80. 14.6.1.80  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR22 Registers
        81. 14.6.1.81  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR23 Registers
        82. 14.6.1.82  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR24 Registers
        83. 14.6.1.83  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR25 Registers
        84. 14.6.1.84  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR26 Registers
        85. 14.6.1.85  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR27 Registers
        86. 14.6.1.86  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR28 Registers
        87. 14.6.1.87  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR29 Registers
        88. 14.6.1.88  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR30 Registers
        89. 14.6.1.89  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR31 Registers
        90. 14.6.1.90  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR32 Registers
        91. 14.6.1.91  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR33 Registers
        92. 14.6.1.92  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR34 Registers
        93. 14.6.1.93  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR35 Registers
        94. 14.6.1.94  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR36 Registers
        95. 14.6.1.95  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR37 Registers
        96. 14.6.1.96  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR38 Registers
        97. 14.6.1.97  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR39 Registers
        98. 14.6.1.98  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR40 Registers
        99. 14.6.1.99  GIC_DISTRIBUTOR__24_GICD_IPRIORITYR41 Registers
        100. 14.6.1.100 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR42 Registers
        101. 14.6.1.101 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR43 Registers
        102. 14.6.1.102 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR44 Registers
        103. 14.6.1.103 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR45 Registers
        104. 14.6.1.104 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR46 Registers
        105. 14.6.1.105 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR47 Registers
        106. 14.6.1.106 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR48 Registers
        107. 14.6.1.107 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR49 Registers
        108. 14.6.1.108 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR50 Registers
        109. 14.6.1.109 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR51 Registers
        110. 14.6.1.110 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR52 Registers
        111. 14.6.1.111 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR53 Registers
        112. 14.6.1.112 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR54 Registers
        113. 14.6.1.113 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR55 Registers
        114. 14.6.1.114 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR56 Registers
        115. 14.6.1.115 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR57 Registers
        116. 14.6.1.116 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR58 Registers
        117. 14.6.1.117 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR59 Registers
        118. 14.6.1.118 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR60 Registers
        119. 14.6.1.119 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR61 Registers
        120. 14.6.1.120 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR62 Registers
        121. 14.6.1.121 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR63 Registers
        122. 14.6.1.122 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR64 Registers
        123. 14.6.1.123 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR65 Registers
        124. 14.6.1.124 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR66 Registers
        125. 14.6.1.125 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR67 Registers
        126. 14.6.1.126 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR68 Registers
        127. 14.6.1.127 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR69 Registers
        128. 14.6.1.128 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR70 Registers
        129. 14.6.1.129 GIC_DISTRIBUTOR__24_GICD_IPRIORITYR71 Registers
        130. 14.6.1.130 GIC_DISTRIBUTOR__26_GICD_ITARGETSR8 Registers
        131. 14.6.1.131 GIC_DISTRIBUTOR__26_GICD_ITARGETSR9 Registers
        132. 14.6.1.132 GIC_DISTRIBUTOR__26_GICD_ITARGETSR10 Registers
        133. 14.6.1.133 GIC_DISTRIBUTOR__26_GICD_ITARGETSR11 Registers
        134. 14.6.1.134 GIC_DISTRIBUTOR__26_GICD_ITARGETSR12 Registers
        135. 14.6.1.135 GIC_DISTRIBUTOR__26_GICD_ITARGETSR13 Registers
        136. 14.6.1.136 GIC_DISTRIBUTOR__26_GICD_ITARGETSR14 Registers
        137. 14.6.1.137 GIC_DISTRIBUTOR__26_GICD_ITARGETSR15 Registers
        138. 14.6.1.138 GIC_DISTRIBUTOR__26_GICD_ITARGETSR16 Registers
        139. 14.6.1.139 GIC_DISTRIBUTOR__26_GICD_ITARGETSR17 Registers
        140. 14.6.1.140 GIC_DISTRIBUTOR__26_GICD_ITARGETSR18 Registers
        141. 14.6.1.141 GIC_DISTRIBUTOR__26_GICD_ITARGETSR19 Registers
        142. 14.6.1.142 GIC_DISTRIBUTOR__26_GICD_ITARGETSR20 Registers
        143. 14.6.1.143 GIC_DISTRIBUTOR__26_GICD_ITARGETSR21 Registers
        144. 14.6.1.144 GIC_DISTRIBUTOR__26_GICD_ITARGETSR22 Registers
        145. 14.6.1.145 GIC_DISTRIBUTOR__26_GICD_ITARGETSR23 Registers
        146. 14.6.1.146 GIC_DISTRIBUTOR__26_GICD_ITARGETSR24 Registers
        147. 14.6.1.147 GIC_DISTRIBUTOR__26_GICD_ITARGETSR25 Registers
        148. 14.6.1.148 GIC_DISTRIBUTOR__26_GICD_ITARGETSR26 Registers
        149. 14.6.1.149 GIC_DISTRIBUTOR__26_GICD_ITARGETSR27 Registers
        150. 14.6.1.150 GIC_DISTRIBUTOR__26_GICD_ITARGETSR28 Registers
        151. 14.6.1.151 GIC_DISTRIBUTOR__26_GICD_ITARGETSR29 Registers
        152. 14.6.1.152 GIC_DISTRIBUTOR__26_GICD_ITARGETSR30 Registers
        153. 14.6.1.153 GIC_DISTRIBUTOR__26_GICD_ITARGETSR31 Registers
        154. 14.6.1.154 GIC_DISTRIBUTOR__26_GICD_ITARGETSR32 Registers
        155. 14.6.1.155 GIC_DISTRIBUTOR__26_GICD_ITARGETSR33 Registers
        156. 14.6.1.156 GIC_DISTRIBUTOR__26_GICD_ITARGETSR34 Registers
        157. 14.6.1.157 GIC_DISTRIBUTOR__26_GICD_ITARGETSR35 Registers
        158. 14.6.1.158 GIC_DISTRIBUTOR__26_GICD_ITARGETSR36 Registers
        159. 14.6.1.159 GIC_DISTRIBUTOR__26_GICD_ITARGETSR37 Registers
        160. 14.6.1.160 GIC_DISTRIBUTOR__26_GICD_ITARGETSR38 Registers
        161. 14.6.1.161 GIC_DISTRIBUTOR__26_GICD_ITARGETSR39 Registers
        162. 14.6.1.162 GIC_DISTRIBUTOR__26_GICD_ITARGETSR40 Registers
        163. 14.6.1.163 GIC_DISTRIBUTOR__26_GICD_ITARGETSR41 Registers
        164. 14.6.1.164 GIC_DISTRIBUTOR__26_GICD_ITARGETSR42 Registers
        165. 14.6.1.165 GIC_DISTRIBUTOR__26_GICD_ITARGETSR43 Registers
        166. 14.6.1.166 GIC_DISTRIBUTOR__26_GICD_ITARGETSR44 Registers
        167. 14.6.1.167 GIC_DISTRIBUTOR__26_GICD_ITARGETSR45 Registers
        168. 14.6.1.168 GIC_DISTRIBUTOR__26_GICD_ITARGETSR46 Registers
        169. 14.6.1.169 GIC_DISTRIBUTOR__26_GICD_ITARGETSR47 Registers
        170. 14.6.1.170 GIC_DISTRIBUTOR__26_GICD_ITARGETSR48 Registers
        171. 14.6.1.171 GIC_DISTRIBUTOR__26_GICD_ITARGETSR49 Registers
        172. 14.6.1.172 GIC_DISTRIBUTOR__26_GICD_ITARGETSR50 Registers
        173. 14.6.1.173 GIC_DISTRIBUTOR__26_GICD_ITARGETSR51 Registers
        174. 14.6.1.174 GIC_DISTRIBUTOR__26_GICD_ITARGETSR52 Registers
        175. 14.6.1.175 GIC_DISTRIBUTOR__26_GICD_ITARGETSR53 Registers
        176. 14.6.1.176 GIC_DISTRIBUTOR__26_GICD_ITARGETSR54 Registers
        177. 14.6.1.177 GIC_DISTRIBUTOR__26_GICD_ITARGETSR55 Registers
        178. 14.6.1.178 GIC_DISTRIBUTOR__26_GICD_ITARGETSR56 Registers
        179. 14.6.1.179 GIC_DISTRIBUTOR__26_GICD_ITARGETSR57 Registers
        180. 14.6.1.180 GIC_DISTRIBUTOR__26_GICD_ITARGETSR58 Registers
        181. 14.6.1.181 GIC_DISTRIBUTOR__26_GICD_ITARGETSR59 Registers
        182. 14.6.1.182 GIC_DISTRIBUTOR__26_GICD_ITARGETSR60 Registers
        183. 14.6.1.183 GIC_DISTRIBUTOR__26_GICD_ITARGETSR61 Registers
        184. 14.6.1.184 GIC_DISTRIBUTOR__26_GICD_ITARGETSR62 Registers
        185. 14.6.1.185 GIC_DISTRIBUTOR__26_GICD_ITARGETSR63 Registers
        186. 14.6.1.186 GIC_DISTRIBUTOR__26_GICD_ITARGETSR64 Registers
        187. 14.6.1.187 GIC_DISTRIBUTOR__26_GICD_ITARGETSR65 Registers
        188. 14.6.1.188 GIC_DISTRIBUTOR__26_GICD_ITARGETSR66 Registers
        189. 14.6.1.189 GIC_DISTRIBUTOR__26_GICD_ITARGETSR67 Registers
        190. 14.6.1.190 GIC_DISTRIBUTOR__26_GICD_ITARGETSR68 Registers
        191. 14.6.1.191 GIC_DISTRIBUTOR__26_GICD_ITARGETSR69 Registers
        192. 14.6.1.192 GIC_DISTRIBUTOR__26_GICD_ITARGETSR70 Registers
        193. 14.6.1.193 GIC_DISTRIBUTOR__26_GICD_ITARGETSR71 Registers
        194. 14.6.1.194 GIC_DISTRIBUTOR__29_GICD_ICFGR2 Registers
        195. 14.6.1.195 GIC_DISTRIBUTOR__29_GICD_ICFGR3 Registers
        196. 14.6.1.196 GIC_DISTRIBUTOR__29_GICD_ICFGR4 Registers
        197. 14.6.1.197 GIC_DISTRIBUTOR__29_GICD_ICFGR5 Registers
        198. 14.6.1.198 GIC_DISTRIBUTOR__29_GICD_ICFGR6 Registers
        199. 14.6.1.199 GIC_DISTRIBUTOR__29_GICD_ICFGR7 Registers
        200. 14.6.1.200 GIC_DISTRIBUTOR__29_GICD_ICFGR8 Registers
        201. 14.6.1.201 GIC_DISTRIBUTOR__29_GICD_ICFGR9 Registers
        202. 14.6.1.202 GIC_DISTRIBUTOR__29_GICD_ICFGR10 Registers
        203. 14.6.1.203 GIC_DISTRIBUTOR__29_GICD_ICFGR11 Registers
        204. 14.6.1.204 GIC_DISTRIBUTOR__29_GICD_ICFGR12 Registers
        205. 14.6.1.205 GIC_DISTRIBUTOR__29_GICD_ICFGR13 Registers
        206. 14.6.1.206 GIC_DISTRIBUTOR__29_GICD_ICFGR14 Registers
        207. 14.6.1.207 GIC_DISTRIBUTOR__29_GICD_ICFGR15 Registers
        208. 14.6.1.208 GIC_DISTRIBUTOR__29_GICD_ICFGR16 Registers
        209. 14.6.1.209 GIC_DISTRIBUTOR__29_GICD_ICFGR17 Registers
        210. 14.6.1.210 GIC_DISTRIBUTOR__30_GICD_IGRPMODR0 Registers
        211. 14.6.1.211 GIC_DISTRIBUTOR__31_GICD_IGRPMODR1 Registers
        212. 14.6.1.212 GIC_DISTRIBUTOR__31_GICD_IGRPMODR2 Registers
        213. 14.6.1.213 GIC_DISTRIBUTOR__31_GICD_IGRPMODR3 Registers
        214. 14.6.1.214 GIC_DISTRIBUTOR__31_GICD_IGRPMODR4 Registers
        215. 14.6.1.215 GIC_DISTRIBUTOR__31_GICD_IGRPMODR5 Registers
        216. 14.6.1.216 GIC_DISTRIBUTOR__31_GICD_IGRPMODR6 Registers
        217. 14.6.1.217 GIC_DISTRIBUTOR__31_GICD_IGRPMODR7 Registers
        218. 14.6.1.218 GIC_DISTRIBUTOR__31_GICD_IGRPMODR8 Registers
        219. 14.6.1.219 GIC_DISTRIBUTOR__32_GICD_NSACR0 Registers
        220. 14.6.1.220 GIC_DISTRIBUTOR__32_GICD_NSACR1 Registers
        221. 14.6.1.221 GIC_DISTRIBUTOR__33_GICD_NSACR2 Registers
        222. 14.6.1.222 GIC_DISTRIBUTOR__33_GICD_NSACR3 Registers
        223. 14.6.1.223 GIC_DISTRIBUTOR__33_GICD_NSACR4 Registers
        224. 14.6.1.224 GIC_DISTRIBUTOR__33_GICD_NSACR5 Registers
        225. 14.6.1.225 GIC_DISTRIBUTOR__33_GICD_NSACR6 Registers
        226. 14.6.1.226 GIC_DISTRIBUTOR__33_GICD_NSACR7 Registers
        227. 14.6.1.227 GIC_DISTRIBUTOR__33_GICD_NSACR8 Registers
        228. 14.6.1.228 GIC_DISTRIBUTOR__33_GICD_NSACR9 Registers
        229. 14.6.1.229 GIC_DISTRIBUTOR__33_GICD_NSACR10 Registers
        230. 14.6.1.230 GIC_DISTRIBUTOR__33_GICD_NSACR11 Registers
        231. 14.6.1.231 GIC_DISTRIBUTOR__33_GICD_NSACR12 Registers
        232. 14.6.1.232 GIC_DISTRIBUTOR__33_GICD_NSACR13 Registers
        233. 14.6.1.233 GIC_DISTRIBUTOR__33_GICD_NSACR14 Registers
        234. 14.6.1.234 GIC_DISTRIBUTOR__33_GICD_NSACR15 Registers
        235. 14.6.1.235 GIC_DISTRIBUTOR__33_GICD_NSACR16 Registers
        236. 14.6.1.236 GIC_DISTRIBUTOR__33_GICD_NSACR17 Registers
        237. 14.6.1.237 GIC_DISTRIBUTOR__37_GICD_IROUTER32_LOWER Registers
        238. 14.6.1.238 GIC_DISTRIBUTOR__37_GICD_IROUTER32_UPPER Registers
        239. 14.6.1.239 GIC_DISTRIBUTOR__37_GICD_IROUTER33_LOWER Registers
        240. 14.6.1.240 GIC_DISTRIBUTOR__37_GICD_IROUTER33_UPPER Registers
        241. 14.6.1.241 GIC_DISTRIBUTOR__37_GICD_IROUTER34_LOWER Registers
        242. 14.6.1.242 GIC_DISTRIBUTOR__37_GICD_IROUTER34_UPPER Registers
        243. 14.6.1.243 GIC_DISTRIBUTOR__37_GICD_IROUTER35_LOWER Registers
        244. 14.6.1.244 GIC_DISTRIBUTOR__37_GICD_IROUTER35_UPPER Registers
        245. 14.6.1.245 GIC_DISTRIBUTOR__37_GICD_IROUTER36_LOWER Registers
        246. 14.6.1.246 GIC_DISTRIBUTOR__37_GICD_IROUTER36_UPPER Registers
        247. 14.6.1.247 GIC_DISTRIBUTOR__37_GICD_IROUTER37_LOWER Registers
        248. 14.6.1.248 GIC_DISTRIBUTOR__37_GICD_IROUTER37_UPPER Registers
        249. 14.6.1.249 GIC_DISTRIBUTOR__37_GICD_IROUTER38_LOWER Registers
        250. 14.6.1.250 GIC_DISTRIBUTOR__37_GICD_IROUTER38_UPPER Registers
        251. 14.6.1.251 GIC_DISTRIBUTOR__37_GICD_IROUTER39_LOWER Registers
        252. 14.6.1.252 GIC_DISTRIBUTOR__37_GICD_IROUTER39_UPPER Registers
        253. 14.6.1.253 GIC_DISTRIBUTOR__37_GICD_IROUTER40_LOWER Registers
        254. 14.6.1.254 GIC_DISTRIBUTOR__37_GICD_IROUTER40_UPPER Registers
        255. 14.6.1.255 GIC_DISTRIBUTOR__37_GICD_IROUTER41_LOWER Registers
        256. 14.6.1.256 GIC_DISTRIBUTOR__37_GICD_IROUTER41_UPPER Registers
        257. 14.6.1.257 GIC_DISTRIBUTOR__37_GICD_IROUTER42_LOWER Registers
        258. 14.6.1.258 GIC_DISTRIBUTOR__37_GICD_IROUTER42_UPPER Registers
        259. 14.6.1.259 GIC_DISTRIBUTOR__37_GICD_IROUTER43_LOWER Registers
        260. 14.6.1.260 GIC_DISTRIBUTOR__37_GICD_IROUTER43_UPPER Registers
        261. 14.6.1.261 GIC_DISTRIBUTOR__37_GICD_IROUTER44_LOWER Registers
        262. 14.6.1.262 GIC_DISTRIBUTOR__37_GICD_IROUTER44_UPPER Registers
        263. 14.6.1.263 GIC_DISTRIBUTOR__37_GICD_IROUTER45_LOWER Registers
        264. 14.6.1.264 GIC_DISTRIBUTOR__37_GICD_IROUTER45_UPPER Registers
        265. 14.6.1.265 GIC_DISTRIBUTOR__37_GICD_IROUTER46_LOWER Registers
        266. 14.6.1.266 GIC_DISTRIBUTOR__37_GICD_IROUTER46_UPPER Registers
        267. 14.6.1.267 GIC_DISTRIBUTOR__37_GICD_IROUTER47_LOWER Registers
        268. 14.6.1.268 GIC_DISTRIBUTOR__37_GICD_IROUTER47_UPPER Registers
        269. 14.6.1.269 GIC_DISTRIBUTOR__37_GICD_IROUTER48_LOWER Registers
        270. 14.6.1.270 GIC_DISTRIBUTOR__37_GICD_IROUTER48_UPPER Registers
        271. 14.6.1.271 GIC_DISTRIBUTOR__37_GICD_IROUTER49_LOWER Registers
        272. 14.6.1.272 GIC_DISTRIBUTOR__37_GICD_IROUTER49_UPPER Registers
        273. 14.6.1.273 GIC_DISTRIBUTOR__37_GICD_IROUTER50_LOWER Registers
        274. 14.6.1.274 GIC_DISTRIBUTOR__37_GICD_IROUTER50_UPPER Registers
        275. 14.6.1.275 GIC_DISTRIBUTOR__37_GICD_IROUTER51_LOWER Registers
        276. 14.6.1.276 GIC_DISTRIBUTOR__37_GICD_IROUTER51_UPPER Registers
        277. 14.6.1.277 GIC_DISTRIBUTOR__37_GICD_IROUTER52_LOWER Registers
        278. 14.6.1.278 GIC_DISTRIBUTOR__37_GICD_IROUTER52_UPPER Registers
        279. 14.6.1.279 GIC_DISTRIBUTOR__37_GICD_IROUTER53_LOWER Registers
        280. 14.6.1.280 GIC_DISTRIBUTOR__37_GICD_IROUTER53_UPPER Registers
        281. 14.6.1.281 GIC_DISTRIBUTOR__37_GICD_IROUTER54_LOWER Registers
        282. 14.6.1.282 GIC_DISTRIBUTOR__37_GICD_IROUTER54_UPPER Registers
        283. 14.6.1.283 GIC_DISTRIBUTOR__37_GICD_IROUTER55_LOWER Registers
        284. 14.6.1.284 GIC_DISTRIBUTOR__37_GICD_IROUTER55_UPPER Registers
        285. 14.6.1.285 GIC_DISTRIBUTOR__37_GICD_IROUTER56_LOWER Registers
        286. 14.6.1.286 GIC_DISTRIBUTOR__37_GICD_IROUTER56_UPPER Registers
        287. 14.6.1.287 GIC_DISTRIBUTOR__37_GICD_IROUTER57_LOWER Registers
        288. 14.6.1.288 GIC_DISTRIBUTOR__37_GICD_IROUTER57_UPPER Registers
        289. 14.6.1.289 GIC_DISTRIBUTOR__37_GICD_IROUTER58_LOWER Registers
        290. 14.6.1.290 GIC_DISTRIBUTOR__37_GICD_IROUTER58_UPPER Registers
        291. 14.6.1.291 GIC_DISTRIBUTOR__37_GICD_IROUTER59_LOWER Registers
        292. 14.6.1.292 GIC_DISTRIBUTOR__37_GICD_IROUTER59_UPPER Registers
        293. 14.6.1.293 GIC_DISTRIBUTOR__37_GICD_IROUTER60_LOWER Registers
        294. 14.6.1.294 GIC_DISTRIBUTOR__37_GICD_IROUTER60_UPPER Registers
        295. 14.6.1.295 GIC_DISTRIBUTOR__37_GICD_IROUTER61_LOWER Registers
        296. 14.6.1.296 GIC_DISTRIBUTOR__37_GICD_IROUTER61_UPPER Registers
        297. 14.6.1.297 GIC_DISTRIBUTOR__37_GICD_IROUTER62_LOWER Registers
        298. 14.6.1.298 GIC_DISTRIBUTOR__37_GICD_IROUTER62_UPPER Registers
        299. 14.6.1.299 GIC_DISTRIBUTOR__37_GICD_IROUTER63_LOWER Registers
        300. 14.6.1.300 GIC_DISTRIBUTOR__37_GICD_IROUTER63_UPPER Registers
        301. 14.6.1.301 GIC_DISTRIBUTOR__37_GICD_IROUTER64_LOWER Registers
        302. 14.6.1.302 GIC_DISTRIBUTOR__37_GICD_IROUTER64_UPPER Registers
        303. 14.6.1.303 GIC_DISTRIBUTOR__37_GICD_IROUTER65_LOWER Registers
        304. 14.6.1.304 GIC_DISTRIBUTOR__37_GICD_IROUTER65_UPPER Registers
        305. 14.6.1.305 GIC_DISTRIBUTOR__37_GICD_IROUTER66_LOWER Registers
        306. 14.6.1.306 GIC_DISTRIBUTOR__37_GICD_IROUTER66_UPPER Registers
        307. 14.6.1.307 GIC_DISTRIBUTOR__37_GICD_IROUTER67_LOWER Registers
        308. 14.6.1.308 GIC_DISTRIBUTOR__37_GICD_IROUTER67_UPPER Registers
        309. 14.6.1.309 GIC_DISTRIBUTOR__37_GICD_IROUTER68_LOWER Registers
        310. 14.6.1.310 GIC_DISTRIBUTOR__37_GICD_IROUTER68_UPPER Registers
        311. 14.6.1.311 GIC_DISTRIBUTOR__37_GICD_IROUTER69_LOWER Registers
        312. 14.6.1.312 GIC_DISTRIBUTOR__37_GICD_IROUTER69_UPPER Registers
        313. 14.6.1.313 GIC_DISTRIBUTOR__37_GICD_IROUTER70_LOWER Registers
        314. 14.6.1.314 GIC_DISTRIBUTOR__37_GICD_IROUTER70_UPPER Registers
        315. 14.6.1.315 GIC_DISTRIBUTOR__37_GICD_IROUTER71_LOWER Registers
        316. 14.6.1.316 GIC_DISTRIBUTOR__37_GICD_IROUTER71_UPPER Registers
        317. 14.6.1.317 GIC_DISTRIBUTOR__37_GICD_IROUTER72_LOWER Registers
        318. 14.6.1.318 GIC_DISTRIBUTOR__37_GICD_IROUTER72_UPPER Registers
        319. 14.6.1.319 GIC_DISTRIBUTOR__37_GICD_IROUTER73_LOWER Registers
        320. 14.6.1.320 GIC_DISTRIBUTOR__37_GICD_IROUTER73_UPPER Registers
        321. 14.6.1.321 GIC_DISTRIBUTOR__37_GICD_IROUTER74_LOWER Registers
        322. 14.6.1.322 GIC_DISTRIBUTOR__37_GICD_IROUTER74_UPPER Registers
        323. 14.6.1.323 GIC_DISTRIBUTOR__37_GICD_IROUTER75_LOWER Registers
        324. 14.6.1.324 GIC_DISTRIBUTOR__37_GICD_IROUTER75_UPPER Registers
        325. 14.6.1.325 GIC_DISTRIBUTOR__37_GICD_IROUTER76_LOWER Registers
        326. 14.6.1.326 GIC_DISTRIBUTOR__37_GICD_IROUTER76_UPPER Registers
        327. 14.6.1.327 GIC_DISTRIBUTOR__37_GICD_IROUTER77_LOWER Registers
        328. 14.6.1.328 GIC_DISTRIBUTOR__37_GICD_IROUTER77_UPPER Registers
        329. 14.6.1.329 GIC_DISTRIBUTOR__37_GICD_IROUTER78_LOWER Registers
        330. 14.6.1.330 GIC_DISTRIBUTOR__37_GICD_IROUTER78_UPPER Registers
        331. 14.6.1.331 GIC_DISTRIBUTOR__37_GICD_IROUTER79_LOWER Registers
        332. 14.6.1.332 GIC_DISTRIBUTOR__37_GICD_IROUTER79_UPPER Registers
        333. 14.6.1.333 GIC_DISTRIBUTOR__37_GICD_IROUTER80_LOWER Registers
        334. 14.6.1.334 GIC_DISTRIBUTOR__37_GICD_IROUTER80_UPPER Registers
        335. 14.6.1.335 GIC_DISTRIBUTOR__37_GICD_IROUTER81_LOWER Registers
        336. 14.6.1.336 GIC_DISTRIBUTOR__37_GICD_IROUTER81_UPPER Registers
        337. 14.6.1.337 GIC_DISTRIBUTOR__37_GICD_IROUTER82_LOWER Registers
        338. 14.6.1.338 GIC_DISTRIBUTOR__37_GICD_IROUTER82_UPPER Registers
        339. 14.6.1.339 GIC_DISTRIBUTOR__37_GICD_IROUTER83_LOWER Registers
        340. 14.6.1.340 GIC_DISTRIBUTOR__37_GICD_IROUTER83_UPPER Registers
        341. 14.6.1.341 GIC_DISTRIBUTOR__37_GICD_IROUTER84_LOWER Registers
        342. 14.6.1.342 GIC_DISTRIBUTOR__37_GICD_IROUTER84_UPPER Registers
        343. 14.6.1.343 GIC_DISTRIBUTOR__37_GICD_IROUTER85_LOWER Registers
        344. 14.6.1.344 GIC_DISTRIBUTOR__37_GICD_IROUTER85_UPPER Registers
        345. 14.6.1.345 GIC_DISTRIBUTOR__37_GICD_IROUTER86_LOWER Registers
        346. 14.6.1.346 GIC_DISTRIBUTOR__37_GICD_IROUTER86_UPPER Registers
        347. 14.6.1.347 GIC_DISTRIBUTOR__37_GICD_IROUTER87_LOWER Registers
        348. 14.6.1.348 GIC_DISTRIBUTOR__37_GICD_IROUTER87_UPPER Registers
        349. 14.6.1.349 GIC_DISTRIBUTOR__37_GICD_IROUTER88_LOWER Registers
        350. 14.6.1.350 GIC_DISTRIBUTOR__37_GICD_IROUTER88_UPPER Registers
        351. 14.6.1.351 GIC_DISTRIBUTOR__37_GICD_IROUTER89_LOWER Registers
        352. 14.6.1.352 GIC_DISTRIBUTOR__37_GICD_IROUTER89_UPPER Registers
        353. 14.6.1.353 GIC_DISTRIBUTOR__37_GICD_IROUTER90_LOWER Registers
        354. 14.6.1.354 GIC_DISTRIBUTOR__37_GICD_IROUTER90_UPPER Registers
        355. 14.6.1.355 GIC_DISTRIBUTOR__37_GICD_IROUTER91_LOWER Registers
        356. 14.6.1.356 GIC_DISTRIBUTOR__37_GICD_IROUTER91_UPPER Registers
        357. 14.6.1.357 GIC_DISTRIBUTOR__37_GICD_IROUTER92_LOWER Registers
        358. 14.6.1.358 GIC_DISTRIBUTOR__37_GICD_IROUTER92_UPPER Registers
        359. 14.6.1.359 GIC_DISTRIBUTOR__37_GICD_IROUTER93_LOWER Registers
        360. 14.6.1.360 GIC_DISTRIBUTOR__37_GICD_IROUTER93_UPPER Registers
        361. 14.6.1.361 GIC_DISTRIBUTOR__37_GICD_IROUTER94_LOWER Registers
        362. 14.6.1.362 GIC_DISTRIBUTOR__37_GICD_IROUTER94_UPPER Registers
        363. 14.6.1.363 GIC_DISTRIBUTOR__37_GICD_IROUTER95_LOWER Registers
        364. 14.6.1.364 GIC_DISTRIBUTOR__37_GICD_IROUTER95_UPPER Registers
        365. 14.6.1.365 GIC_DISTRIBUTOR__37_GICD_IROUTER96_LOWER Registers
        366. 14.6.1.366 GIC_DISTRIBUTOR__37_GICD_IROUTER96_UPPER Registers
        367. 14.6.1.367 GIC_DISTRIBUTOR__37_GICD_IROUTER97_LOWER Registers
        368. 14.6.1.368 GIC_DISTRIBUTOR__37_GICD_IROUTER97_UPPER Registers
        369. 14.6.1.369 GIC_DISTRIBUTOR__37_GICD_IROUTER98_LOWER Registers
        370. 14.6.1.370 GIC_DISTRIBUTOR__37_GICD_IROUTER98_UPPER Registers
        371. 14.6.1.371 GIC_DISTRIBUTOR__37_GICD_IROUTER99_LOWER Registers
        372. 14.6.1.372 GIC_DISTRIBUTOR__37_GICD_IROUTER99_UPPER Registers
        373. 14.6.1.373 GIC_DISTRIBUTOR__37_GICD_IROUTER100_LOWER Registers
        374. 14.6.1.374 GIC_DISTRIBUTOR__37_GICD_IROUTER100_UPPER Registers
        375. 14.6.1.375 GIC_DISTRIBUTOR__37_GICD_IROUTER101_LOWER Registers
        376. 14.6.1.376 GIC_DISTRIBUTOR__37_GICD_IROUTER101_UPPER Registers
        377. 14.6.1.377 GIC_DISTRIBUTOR__37_GICD_IROUTER102_LOWER Registers
        378. 14.6.1.378 GIC_DISTRIBUTOR__37_GICD_IROUTER102_UPPER Registers
        379. 14.6.1.379 GIC_DISTRIBUTOR__37_GICD_IROUTER103_LOWER Registers
        380. 14.6.1.380 GIC_DISTRIBUTOR__37_GICD_IROUTER103_UPPER Registers
        381. 14.6.1.381 GIC_DISTRIBUTOR__37_GICD_IROUTER104_LOWER Registers
        382. 14.6.1.382 GIC_DISTRIBUTOR__37_GICD_IROUTER104_UPPER Registers
        383. 14.6.1.383 GIC_DISTRIBUTOR__37_GICD_IROUTER105_LOWER Registers
        384. 14.6.1.384 GIC_DISTRIBUTOR__37_GICD_IROUTER105_UPPER Registers
        385. 14.6.1.385 GIC_DISTRIBUTOR__37_GICD_IROUTER106_LOWER Registers
        386. 14.6.1.386 GIC_DISTRIBUTOR__37_GICD_IROUTER106_UPPER Registers
        387. 14.6.1.387 GIC_DISTRIBUTOR__37_GICD_IROUTER107_LOWER Registers
        388. 14.6.1.388 GIC_DISTRIBUTOR__37_GICD_IROUTER107_UPPER Registers
        389. 14.6.1.389 GIC_DISTRIBUTOR__37_GICD_IROUTER108_LOWER Registers
        390. 14.6.1.390 GIC_DISTRIBUTOR__37_GICD_IROUTER108_UPPER Registers
        391. 14.6.1.391 GIC_DISTRIBUTOR__37_GICD_IROUTER109_LOWER Registers
        392. 14.6.1.392 GIC_DISTRIBUTOR__37_GICD_IROUTER109_UPPER Registers
        393. 14.6.1.393 GIC_DISTRIBUTOR__37_GICD_IROUTER110_LOWER Registers
        394. 14.6.1.394 GIC_DISTRIBUTOR__37_GICD_IROUTER110_UPPER Registers
        395. 14.6.1.395 GIC_DISTRIBUTOR__37_GICD_IROUTER111_LOWER Registers
        396. 14.6.1.396 GIC_DISTRIBUTOR__37_GICD_IROUTER111_UPPER Registers
        397. 14.6.1.397 GIC_DISTRIBUTOR__37_GICD_IROUTER112_LOWER Registers
        398. 14.6.1.398 GIC_DISTRIBUTOR__37_GICD_IROUTER112_UPPER Registers
        399. 14.6.1.399 GIC_DISTRIBUTOR__37_GICD_IROUTER113_LOWER Registers
        400. 14.6.1.400 GIC_DISTRIBUTOR__37_GICD_IROUTER113_UPPER Registers
        401. 14.6.1.401 GIC_DISTRIBUTOR__37_GICD_IROUTER114_LOWER Registers
        402. 14.6.1.402 GIC_DISTRIBUTOR__37_GICD_IROUTER114_UPPER Registers
        403. 14.6.1.403 GIC_DISTRIBUTOR__37_GICD_IROUTER115_LOWER Registers
        404. 14.6.1.404 GIC_DISTRIBUTOR__37_GICD_IROUTER115_UPPER Registers
        405. 14.6.1.405 GIC_DISTRIBUTOR__37_GICD_IROUTER116_LOWER Registers
        406. 14.6.1.406 GIC_DISTRIBUTOR__37_GICD_IROUTER116_UPPER Registers
        407. 14.6.1.407 GIC_DISTRIBUTOR__37_GICD_IROUTER117_LOWER Registers
        408. 14.6.1.408 GIC_DISTRIBUTOR__37_GICD_IROUTER117_UPPER Registers
        409. 14.6.1.409 GIC_DISTRIBUTOR__37_GICD_IROUTER118_LOWER Registers
        410. 14.6.1.410 GIC_DISTRIBUTOR__37_GICD_IROUTER118_UPPER Registers
        411. 14.6.1.411 GIC_DISTRIBUTOR__37_GICD_IROUTER119_LOWER Registers
        412. 14.6.1.412 GIC_DISTRIBUTOR__37_GICD_IROUTER119_UPPER Registers
        413. 14.6.1.413 GIC_DISTRIBUTOR__37_GICD_IROUTER120_LOWER Registers
        414. 14.6.1.414 GIC_DISTRIBUTOR__37_GICD_IROUTER120_UPPER Registers
        415. 14.6.1.415 GIC_DISTRIBUTOR__37_GICD_IROUTER121_LOWER Registers
        416. 14.6.1.416 GIC_DISTRIBUTOR__37_GICD_IROUTER121_UPPER Registers
        417. 14.6.1.417 GIC_DISTRIBUTOR__37_GICD_IROUTER122_LOWER Registers
        418. 14.6.1.418 GIC_DISTRIBUTOR__37_GICD_IROUTER122_UPPER Registers
        419. 14.6.1.419 GIC_DISTRIBUTOR__37_GICD_IROUTER123_LOWER Registers
        420. 14.6.1.420 GIC_DISTRIBUTOR__37_GICD_IROUTER123_UPPER Registers
        421. 14.6.1.421 GIC_DISTRIBUTOR__37_GICD_IROUTER124_LOWER Registers
        422. 14.6.1.422 GIC_DISTRIBUTOR__37_GICD_IROUTER124_UPPER Registers
        423. 14.6.1.423 GIC_DISTRIBUTOR__37_GICD_IROUTER125_LOWER Registers
        424. 14.6.1.424 GIC_DISTRIBUTOR__37_GICD_IROUTER125_UPPER Registers
        425. 14.6.1.425 GIC_DISTRIBUTOR__37_GICD_IROUTER126_LOWER Registers
        426. 14.6.1.426 GIC_DISTRIBUTOR__37_GICD_IROUTER126_UPPER Registers
        427. 14.6.1.427 GIC_DISTRIBUTOR__37_GICD_IROUTER127_LOWER Registers
        428. 14.6.1.428 GIC_DISTRIBUTOR__37_GICD_IROUTER127_UPPER Registers
        429. 14.6.1.429 GIC_DISTRIBUTOR__37_GICD_IROUTER128_LOWER Registers
        430. 14.6.1.430 GIC_DISTRIBUTOR__37_GICD_IROUTER128_UPPER Registers
        431. 14.6.1.431 GIC_DISTRIBUTOR__37_GICD_IROUTER129_LOWER Registers
        432. 14.6.1.432 GIC_DISTRIBUTOR__37_GICD_IROUTER129_UPPER Registers
        433. 14.6.1.433 GIC_DISTRIBUTOR__37_GICD_IROUTER130_LOWER Registers
        434. 14.6.1.434 GIC_DISTRIBUTOR__37_GICD_IROUTER130_UPPER Registers
        435. 14.6.1.435 GIC_DISTRIBUTOR__37_GICD_IROUTER131_LOWER Registers
        436. 14.6.1.436 GIC_DISTRIBUTOR__37_GICD_IROUTER131_UPPER Registers
        437. 14.6.1.437 GIC_DISTRIBUTOR__37_GICD_IROUTER132_LOWER Registers
        438. 14.6.1.438 GIC_DISTRIBUTOR__37_GICD_IROUTER132_UPPER Registers
        439. 14.6.1.439 GIC_DISTRIBUTOR__37_GICD_IROUTER133_LOWER Registers
        440. 14.6.1.440 GIC_DISTRIBUTOR__37_GICD_IROUTER133_UPPER Registers
        441. 14.6.1.441 GIC_DISTRIBUTOR__37_GICD_IROUTER134_LOWER Registers
        442. 14.6.1.442 GIC_DISTRIBUTOR__37_GICD_IROUTER134_UPPER Registers
        443. 14.6.1.443 GIC_DISTRIBUTOR__37_GICD_IROUTER135_LOWER Registers
        444. 14.6.1.444 GIC_DISTRIBUTOR__37_GICD_IROUTER135_UPPER Registers
        445. 14.6.1.445 GIC_DISTRIBUTOR__37_GICD_IROUTER136_LOWER Registers
        446. 14.6.1.446 GIC_DISTRIBUTOR__37_GICD_IROUTER136_UPPER Registers
        447. 14.6.1.447 GIC_DISTRIBUTOR__37_GICD_IROUTER137_LOWER Registers
        448. 14.6.1.448 GIC_DISTRIBUTOR__37_GICD_IROUTER137_UPPER Registers
        449. 14.6.1.449 GIC_DISTRIBUTOR__37_GICD_IROUTER138_LOWER Registers
        450. 14.6.1.450 GIC_DISTRIBUTOR__37_GICD_IROUTER138_UPPER Registers
        451. 14.6.1.451 GIC_DISTRIBUTOR__37_GICD_IROUTER139_LOWER Registers
        452. 14.6.1.452 GIC_DISTRIBUTOR__37_GICD_IROUTER139_UPPER Registers
        453. 14.6.1.453 GIC_DISTRIBUTOR__37_GICD_IROUTER140_LOWER Registers
        454. 14.6.1.454 GIC_DISTRIBUTOR__37_GICD_IROUTER140_UPPER Registers
        455. 14.6.1.455 GIC_DISTRIBUTOR__37_GICD_IROUTER141_LOWER Registers
        456. 14.6.1.456 GIC_DISTRIBUTOR__37_GICD_IROUTER141_UPPER Registers
        457. 14.6.1.457 GIC_DISTRIBUTOR__37_GICD_IROUTER142_LOWER Registers
        458. 14.6.1.458 GIC_DISTRIBUTOR__37_GICD_IROUTER142_UPPER Registers
        459. 14.6.1.459 GIC_DISTRIBUTOR__37_GICD_IROUTER143_LOWER Registers
        460. 14.6.1.460 GIC_DISTRIBUTOR__37_GICD_IROUTER143_UPPER Registers
        461. 14.6.1.461 GIC_DISTRIBUTOR__37_GICD_IROUTER144_LOWER Registers
        462. 14.6.1.462 GIC_DISTRIBUTOR__37_GICD_IROUTER144_UPPER Registers
        463. 14.6.1.463 GIC_DISTRIBUTOR__37_GICD_IROUTER145_LOWER Registers
        464. 14.6.1.464 GIC_DISTRIBUTOR__37_GICD_IROUTER145_UPPER Registers
        465. 14.6.1.465 GIC_DISTRIBUTOR__37_GICD_IROUTER146_LOWER Registers
        466. 14.6.1.466 GIC_DISTRIBUTOR__37_GICD_IROUTER146_UPPER Registers
        467. 14.6.1.467 GIC_DISTRIBUTOR__37_GICD_IROUTER147_LOWER Registers
        468. 14.6.1.468 GIC_DISTRIBUTOR__37_GICD_IROUTER147_UPPER Registers
        469. 14.6.1.469 GIC_DISTRIBUTOR__37_GICD_IROUTER148_LOWER Registers
        470. 14.6.1.470 GIC_DISTRIBUTOR__37_GICD_IROUTER148_UPPER Registers
        471. 14.6.1.471 GIC_DISTRIBUTOR__37_GICD_IROUTER149_LOWER Registers
        472. 14.6.1.472 GIC_DISTRIBUTOR__37_GICD_IROUTER149_UPPER Registers
        473. 14.6.1.473 GIC_DISTRIBUTOR__37_GICD_IROUTER150_LOWER Registers
        474. 14.6.1.474 GIC_DISTRIBUTOR__37_GICD_IROUTER150_UPPER Registers
        475. 14.6.1.475 GIC_DISTRIBUTOR__37_GICD_IROUTER151_LOWER Registers
        476. 14.6.1.476 GIC_DISTRIBUTOR__37_GICD_IROUTER151_UPPER Registers
        477. 14.6.1.477 GIC_DISTRIBUTOR__37_GICD_IROUTER152_LOWER Registers
        478. 14.6.1.478 GIC_DISTRIBUTOR__37_GICD_IROUTER152_UPPER Registers
        479. 14.6.1.479 GIC_DISTRIBUTOR__37_GICD_IROUTER153_LOWER Registers
        480. 14.6.1.480 GIC_DISTRIBUTOR__37_GICD_IROUTER153_UPPER Registers
        481. 14.6.1.481 GIC_DISTRIBUTOR__37_GICD_IROUTER154_LOWER Registers
        482. 14.6.1.482 GIC_DISTRIBUTOR__37_GICD_IROUTER154_UPPER Registers
        483. 14.6.1.483 GIC_DISTRIBUTOR__37_GICD_IROUTER155_LOWER Registers
        484. 14.6.1.484 GIC_DISTRIBUTOR__37_GICD_IROUTER155_UPPER Registers
        485. 14.6.1.485 GIC_DISTRIBUTOR__37_GICD_IROUTER156_LOWER Registers
        486. 14.6.1.486 GIC_DISTRIBUTOR__37_GICD_IROUTER156_UPPER Registers
        487. 14.6.1.487 GIC_DISTRIBUTOR__37_GICD_IROUTER157_LOWER Registers
        488. 14.6.1.488 GIC_DISTRIBUTOR__37_GICD_IROUTER157_UPPER Registers
        489. 14.6.1.489 GIC_DISTRIBUTOR__37_GICD_IROUTER158_LOWER Registers
        490. 14.6.1.490 GIC_DISTRIBUTOR__37_GICD_IROUTER158_UPPER Registers
        491. 14.6.1.491 GIC_DISTRIBUTOR__37_GICD_IROUTER159_LOWER Registers
        492. 14.6.1.492 GIC_DISTRIBUTOR__37_GICD_IROUTER159_UPPER Registers
        493. 14.6.1.493 GIC_DISTRIBUTOR__37_GICD_IROUTER160_LOWER Registers
        494. 14.6.1.494 GIC_DISTRIBUTOR__37_GICD_IROUTER160_UPPER Registers
        495. 14.6.1.495 GIC_DISTRIBUTOR__37_GICD_IROUTER161_LOWER Registers
        496. 14.6.1.496 GIC_DISTRIBUTOR__37_GICD_IROUTER161_UPPER Registers
        497. 14.6.1.497 GIC_DISTRIBUTOR__37_GICD_IROUTER162_LOWER Registers
        498. 14.6.1.498 GIC_DISTRIBUTOR__37_GICD_IROUTER162_UPPER Registers
        499. 14.6.1.499 GIC_DISTRIBUTOR__37_GICD_IROUTER163_LOWER Registers
        500. 14.6.1.500 GIC_DISTRIBUTOR__37_GICD_IROUTER163_UPPER Registers
        501. 14.6.1.501 GIC_DISTRIBUTOR__37_GICD_IROUTER164_LOWER Registers
        502. 14.6.1.502 GIC_DISTRIBUTOR__37_GICD_IROUTER164_UPPER Registers
        503. 14.6.1.503 GIC_DISTRIBUTOR__37_GICD_IROUTER165_LOWER Registers
        504. 14.6.1.504 GIC_DISTRIBUTOR__37_GICD_IROUTER165_UPPER Registers
        505. 14.6.1.505 GIC_DISTRIBUTOR__37_GICD_IROUTER166_LOWER Registers
        506. 14.6.1.506 GIC_DISTRIBUTOR__37_GICD_IROUTER166_UPPER Registers
        507. 14.6.1.507 GIC_DISTRIBUTOR__37_GICD_IROUTER167_LOWER Registers
        508. 14.6.1.508 GIC_DISTRIBUTOR__37_GICD_IROUTER167_UPPER Registers
        509. 14.6.1.509 GIC_DISTRIBUTOR__37_GICD_IROUTER168_LOWER Registers
        510. 14.6.1.510 GIC_DISTRIBUTOR__37_GICD_IROUTER168_UPPER Registers
        511. 14.6.1.511 GIC_DISTRIBUTOR__37_GICD_IROUTER169_LOWER Registers
        512. 14.6.1.512 GIC_DISTRIBUTOR__37_GICD_IROUTER169_UPPER Registers
        513. 14.6.1.513 GIC_DISTRIBUTOR__37_GICD_IROUTER170_LOWER Registers
        514. 14.6.1.514 GIC_DISTRIBUTOR__37_GICD_IROUTER170_UPPER Registers
        515. 14.6.1.515 GIC_DISTRIBUTOR__37_GICD_IROUTER171_LOWER Registers
        516. 14.6.1.516 GIC_DISTRIBUTOR__37_GICD_IROUTER171_UPPER Registers
        517. 14.6.1.517 GIC_DISTRIBUTOR__37_GICD_IROUTER172_LOWER Registers
        518. 14.6.1.518 GIC_DISTRIBUTOR__37_GICD_IROUTER172_UPPER Registers
        519. 14.6.1.519 GIC_DISTRIBUTOR__37_GICD_IROUTER173_LOWER Registers
        520. 14.6.1.520 GIC_DISTRIBUTOR__37_GICD_IROUTER173_UPPER Registers
        521. 14.6.1.521 GIC_DISTRIBUTOR__37_GICD_IROUTER174_LOWER Registers
        522. 14.6.1.522 GIC_DISTRIBUTOR__37_GICD_IROUTER174_UPPER Registers
        523. 14.6.1.523 GIC_DISTRIBUTOR__37_GICD_IROUTER175_LOWER Registers
        524. 14.6.1.524 GIC_DISTRIBUTOR__37_GICD_IROUTER175_UPPER Registers
        525. 14.6.1.525 GIC_DISTRIBUTOR__37_GICD_IROUTER176_LOWER Registers
        526. 14.6.1.526 GIC_DISTRIBUTOR__37_GICD_IROUTER176_UPPER Registers
        527. 14.6.1.527 GIC_DISTRIBUTOR__37_GICD_IROUTER177_LOWER Registers
        528. 14.6.1.528 GIC_DISTRIBUTOR__37_GICD_IROUTER177_UPPER Registers
        529. 14.6.1.529 GIC_DISTRIBUTOR__37_GICD_IROUTER178_LOWER Registers
        530. 14.6.1.530 GIC_DISTRIBUTOR__37_GICD_IROUTER178_UPPER Registers
        531. 14.6.1.531 GIC_DISTRIBUTOR__37_GICD_IROUTER179_LOWER Registers
        532. 14.6.1.532 GIC_DISTRIBUTOR__37_GICD_IROUTER179_UPPER Registers
        533. 14.6.1.533 GIC_DISTRIBUTOR__37_GICD_IROUTER180_LOWER Registers
        534. 14.6.1.534 GIC_DISTRIBUTOR__37_GICD_IROUTER180_UPPER Registers
        535. 14.6.1.535 GIC_DISTRIBUTOR__37_GICD_IROUTER181_LOWER Registers
        536. 14.6.1.536 GIC_DISTRIBUTOR__37_GICD_IROUTER181_UPPER Registers
        537. 14.6.1.537 GIC_DISTRIBUTOR__37_GICD_IROUTER182_LOWER Registers
        538. 14.6.1.538 GIC_DISTRIBUTOR__37_GICD_IROUTER182_UPPER Registers
        539. 14.6.1.539 GIC_DISTRIBUTOR__37_GICD_IROUTER183_LOWER Registers
        540. 14.6.1.540 GIC_DISTRIBUTOR__37_GICD_IROUTER183_UPPER Registers
        541. 14.6.1.541 GIC_DISTRIBUTOR__37_GICD_IROUTER184_LOWER Registers
        542. 14.6.1.542 GIC_DISTRIBUTOR__37_GICD_IROUTER184_UPPER Registers
        543. 14.6.1.543 GIC_DISTRIBUTOR__37_GICD_IROUTER185_LOWER Registers
        544. 14.6.1.544 GIC_DISTRIBUTOR__37_GICD_IROUTER185_UPPER Registers
        545. 14.6.1.545 GIC_DISTRIBUTOR__37_GICD_IROUTER186_LOWER Registers
        546. 14.6.1.546 GIC_DISTRIBUTOR__37_GICD_IROUTER186_UPPER Registers
        547. 14.6.1.547 GIC_DISTRIBUTOR__37_GICD_IROUTER187_LOWER Registers
        548. 14.6.1.548 GIC_DISTRIBUTOR__37_GICD_IROUTER187_UPPER Registers
        549. 14.6.1.549 GIC_DISTRIBUTOR__37_GICD_IROUTER188_LOWER Registers
        550. 14.6.1.550 GIC_DISTRIBUTOR__37_GICD_IROUTER188_UPPER Registers
        551. 14.6.1.551 GIC_DISTRIBUTOR__37_GICD_IROUTER189_LOWER Registers
        552. 14.6.1.552 GIC_DISTRIBUTOR__37_GICD_IROUTER189_UPPER Registers
        553. 14.6.1.553 GIC_DISTRIBUTOR__37_GICD_IROUTER190_LOWER Registers
        554. 14.6.1.554 GIC_DISTRIBUTOR__37_GICD_IROUTER190_UPPER Registers
        555. 14.6.1.555 GIC_DISTRIBUTOR__37_GICD_IROUTER191_LOWER Registers
        556. 14.6.1.556 GIC_DISTRIBUTOR__37_GICD_IROUTER191_UPPER Registers
        557. 14.6.1.557 GIC_DISTRIBUTOR__37_GICD_IROUTER192_LOWER Registers
        558. 14.6.1.558 GIC_DISTRIBUTOR__37_GICD_IROUTER192_UPPER Registers
        559. 14.6.1.559 GIC_DISTRIBUTOR__37_GICD_IROUTER193_LOWER Registers
        560. 14.6.1.560 GIC_DISTRIBUTOR__37_GICD_IROUTER193_UPPER Registers
        561. 14.6.1.561 GIC_DISTRIBUTOR__37_GICD_IROUTER194_LOWER Registers
        562. 14.6.1.562 GIC_DISTRIBUTOR__37_GICD_IROUTER194_UPPER Registers
        563. 14.6.1.563 GIC_DISTRIBUTOR__37_GICD_IROUTER195_LOWER Registers
        564. 14.6.1.564 GIC_DISTRIBUTOR__37_GICD_IROUTER195_UPPER Registers
        565. 14.6.1.565 GIC_DISTRIBUTOR__37_GICD_IROUTER196_LOWER Registers
        566. 14.6.1.566 GIC_DISTRIBUTOR__37_GICD_IROUTER196_UPPER Registers
        567. 14.6.1.567 GIC_DISTRIBUTOR__37_GICD_IROUTER197_LOWER Registers
        568. 14.6.1.568 GIC_DISTRIBUTOR__37_GICD_IROUTER197_UPPER Registers
        569. 14.6.1.569 GIC_DISTRIBUTOR__37_GICD_IROUTER198_LOWER Registers
        570. 14.6.1.570 GIC_DISTRIBUTOR__37_GICD_IROUTER198_UPPER Registers
        571. 14.6.1.571 GIC_DISTRIBUTOR__37_GICD_IROUTER199_LOWER Registers
        572. 14.6.1.572 GIC_DISTRIBUTOR__37_GICD_IROUTER199_UPPER Registers
        573. 14.6.1.573 GIC_DISTRIBUTOR__37_GICD_IROUTER200_LOWER Registers
        574. 14.6.1.574 GIC_DISTRIBUTOR__37_GICD_IROUTER200_UPPER Registers
        575. 14.6.1.575 GIC_DISTRIBUTOR__37_GICD_IROUTER201_LOWER Registers
        576. 14.6.1.576 GIC_DISTRIBUTOR__37_GICD_IROUTER201_UPPER Registers
        577. 14.6.1.577 GIC_DISTRIBUTOR__37_GICD_IROUTER202_LOWER Registers
        578. 14.6.1.578 GIC_DISTRIBUTOR__37_GICD_IROUTER202_UPPER Registers
        579. 14.6.1.579 GIC_DISTRIBUTOR__37_GICD_IROUTER203_LOWER Registers
        580. 14.6.1.580 GIC_DISTRIBUTOR__37_GICD_IROUTER203_UPPER Registers
        581. 14.6.1.581 GIC_DISTRIBUTOR__37_GICD_IROUTER204_LOWER Registers
        582. 14.6.1.582 GIC_DISTRIBUTOR__37_GICD_IROUTER204_UPPER Registers
        583. 14.6.1.583 GIC_DISTRIBUTOR__37_GICD_IROUTER205_LOWER Registers
        584. 14.6.1.584 GIC_DISTRIBUTOR__37_GICD_IROUTER205_UPPER Registers
        585. 14.6.1.585 GIC_DISTRIBUTOR__37_GICD_IROUTER206_LOWER Registers
        586. 14.6.1.586 GIC_DISTRIBUTOR__37_GICD_IROUTER206_UPPER Registers
        587. 14.6.1.587 GIC_DISTRIBUTOR__37_GICD_IROUTER207_LOWER Registers
        588. 14.6.1.588 GIC_DISTRIBUTOR__37_GICD_IROUTER207_UPPER Registers
        589. 14.6.1.589 GIC_DISTRIBUTOR__37_GICD_IROUTER208_LOWER Registers
        590. 14.6.1.590 GIC_DISTRIBUTOR__37_GICD_IROUTER208_UPPER Registers
        591. 14.6.1.591 GIC_DISTRIBUTOR__37_GICD_IROUTER209_LOWER Registers
        592. 14.6.1.592 GIC_DISTRIBUTOR__37_GICD_IROUTER209_UPPER Registers
        593. 14.6.1.593 GIC_DISTRIBUTOR__37_GICD_IROUTER210_LOWER Registers
        594. 14.6.1.594 GIC_DISTRIBUTOR__37_GICD_IROUTER210_UPPER Registers
        595. 14.6.1.595 GIC_DISTRIBUTOR__37_GICD_IROUTER211_LOWER Registers
        596. 14.6.1.596 GIC_DISTRIBUTOR__37_GICD_IROUTER211_UPPER Registers
        597. 14.6.1.597 GIC_DISTRIBUTOR__37_GICD_IROUTER212_LOWER Registers
        598. 14.6.1.598 GIC_DISTRIBUTOR__37_GICD_IROUTER212_UPPER Registers
        599. 14.6.1.599 GIC_DISTRIBUTOR__37_GICD_IROUTER213_LOWER Registers
        600. 14.6.1.600 GIC_DISTRIBUTOR__37_GICD_IROUTER213_UPPER Registers
        601. 14.6.1.601 GIC_DISTRIBUTOR__37_GICD_IROUTER214_LOWER Registers
        602. 14.6.1.602 GIC_DISTRIBUTOR__37_GICD_IROUTER214_UPPER Registers
        603. 14.6.1.603 GIC_DISTRIBUTOR__37_GICD_IROUTER215_LOWER Registers
        604. 14.6.1.604 GIC_DISTRIBUTOR__37_GICD_IROUTER215_UPPER Registers
        605. 14.6.1.605 GIC_DISTRIBUTOR__37_GICD_IROUTER216_LOWER Registers
        606. 14.6.1.606 GIC_DISTRIBUTOR__37_GICD_IROUTER216_UPPER Registers
        607. 14.6.1.607 GIC_DISTRIBUTOR__37_GICD_IROUTER217_LOWER Registers
        608. 14.6.1.608 GIC_DISTRIBUTOR__37_GICD_IROUTER217_UPPER Registers
        609. 14.6.1.609 GIC_DISTRIBUTOR__37_GICD_IROUTER218_LOWER Registers
        610. 14.6.1.610 GIC_DISTRIBUTOR__37_GICD_IROUTER218_UPPER Registers
        611. 14.6.1.611 GIC_DISTRIBUTOR__37_GICD_IROUTER219_LOWER Registers
        612. 14.6.1.612 GIC_DISTRIBUTOR__37_GICD_IROUTER219_UPPER Registers
        613. 14.6.1.613 GIC_DISTRIBUTOR__37_GICD_IROUTER220_LOWER Registers
        614. 14.6.1.614 GIC_DISTRIBUTOR__37_GICD_IROUTER220_UPPER Registers
        615. 14.6.1.615 GIC_DISTRIBUTOR__37_GICD_IROUTER221_LOWER Registers
        616. 14.6.1.616 GIC_DISTRIBUTOR__37_GICD_IROUTER221_UPPER Registers
        617. 14.6.1.617 GIC_DISTRIBUTOR__37_GICD_IROUTER222_LOWER Registers
        618. 14.6.1.618 GIC_DISTRIBUTOR__37_GICD_IROUTER222_UPPER Registers
        619. 14.6.1.619 GIC_DISTRIBUTOR__37_GICD_IROUTER223_LOWER Registers
        620. 14.6.1.620 GIC_DISTRIBUTOR__37_GICD_IROUTER223_UPPER Registers
        621. 14.6.1.621 GIC_DISTRIBUTOR__37_GICD_IROUTER224_LOWER Registers
        622. 14.6.1.622 GIC_DISTRIBUTOR__37_GICD_IROUTER224_UPPER Registers
        623. 14.6.1.623 GIC_DISTRIBUTOR__37_GICD_IROUTER225_LOWER Registers
        624. 14.6.1.624 GIC_DISTRIBUTOR__37_GICD_IROUTER225_UPPER Registers
        625. 14.6.1.625 GIC_DISTRIBUTOR__37_GICD_IROUTER226_LOWER Registers
        626. 14.6.1.626 GIC_DISTRIBUTOR__37_GICD_IROUTER226_UPPER Registers
        627. 14.6.1.627 GIC_DISTRIBUTOR__37_GICD_IROUTER227_LOWER Registers
        628. 14.6.1.628 GIC_DISTRIBUTOR__37_GICD_IROUTER227_UPPER Registers
        629. 14.6.1.629 GIC_DISTRIBUTOR__37_GICD_IROUTER228_LOWER Registers
        630. 14.6.1.630 GIC_DISTRIBUTOR__37_GICD_IROUTER228_UPPER Registers
        631. 14.6.1.631 GIC_DISTRIBUTOR__37_GICD_IROUTER229_LOWER Registers
        632. 14.6.1.632 GIC_DISTRIBUTOR__37_GICD_IROUTER229_UPPER Registers
        633. 14.6.1.633 GIC_DISTRIBUTOR__37_GICD_IROUTER230_LOWER Registers
        634. 14.6.1.634 GIC_DISTRIBUTOR__37_GICD_IROUTER230_UPPER Registers
        635. 14.6.1.635 GIC_DISTRIBUTOR__37_GICD_IROUTER231_LOWER Registers
        636. 14.6.1.636 GIC_DISTRIBUTOR__37_GICD_IROUTER231_UPPER Registers
        637. 14.6.1.637 GIC_DISTRIBUTOR__37_GICD_IROUTER232_LOWER Registers
        638. 14.6.1.638 GIC_DISTRIBUTOR__37_GICD_IROUTER232_UPPER Registers
        639. 14.6.1.639 GIC_DISTRIBUTOR__37_GICD_IROUTER233_LOWER Registers
        640. 14.6.1.640 GIC_DISTRIBUTOR__37_GICD_IROUTER233_UPPER Registers
        641. 14.6.1.641 GIC_DISTRIBUTOR__37_GICD_IROUTER234_LOWER Registers
        642. 14.6.1.642 GIC_DISTRIBUTOR__37_GICD_IROUTER234_UPPER Registers
        643. 14.6.1.643 GIC_DISTRIBUTOR__37_GICD_IROUTER235_LOWER Registers
        644. 14.6.1.644 GIC_DISTRIBUTOR__37_GICD_IROUTER235_UPPER Registers
        645. 14.6.1.645 GIC_DISTRIBUTOR__37_GICD_IROUTER236_LOWER Registers
        646. 14.6.1.646 GIC_DISTRIBUTOR__37_GICD_IROUTER236_UPPER Registers
        647. 14.6.1.647 GIC_DISTRIBUTOR__37_GICD_IROUTER237_LOWER Registers
        648. 14.6.1.648 GIC_DISTRIBUTOR__37_GICD_IROUTER237_UPPER Registers
        649. 14.6.1.649 GIC_DISTRIBUTOR__37_GICD_IROUTER238_LOWER Registers
        650. 14.6.1.650 GIC_DISTRIBUTOR__37_GICD_IROUTER238_UPPER Registers
        651. 14.6.1.651 GIC_DISTRIBUTOR__37_GICD_IROUTER239_LOWER Registers
        652. 14.6.1.652 GIC_DISTRIBUTOR__37_GICD_IROUTER239_UPPER Registers
        653. 14.6.1.653 GIC_DISTRIBUTOR__37_GICD_IROUTER240_LOWER Registers
        654. 14.6.1.654 GIC_DISTRIBUTOR__37_GICD_IROUTER240_UPPER Registers
        655. 14.6.1.655 GIC_DISTRIBUTOR__37_GICD_IROUTER241_LOWER Registers
        656. 14.6.1.656 GIC_DISTRIBUTOR__37_GICD_IROUTER241_UPPER Registers
        657. 14.6.1.657 GIC_DISTRIBUTOR__37_GICD_IROUTER242_LOWER Registers
        658. 14.6.1.658 GIC_DISTRIBUTOR__37_GICD_IROUTER242_UPPER Registers
        659. 14.6.1.659 GIC_DISTRIBUTOR__37_GICD_IROUTER243_LOWER Registers
        660. 14.6.1.660 GIC_DISTRIBUTOR__37_GICD_IROUTER243_UPPER Registers
        661. 14.6.1.661 GIC_DISTRIBUTOR__37_GICD_IROUTER244_LOWER Registers
        662. 14.6.1.662 GIC_DISTRIBUTOR__37_GICD_IROUTER244_UPPER Registers
        663. 14.6.1.663 GIC_DISTRIBUTOR__37_GICD_IROUTER245_LOWER Registers
        664. 14.6.1.664 GIC_DISTRIBUTOR__37_GICD_IROUTER245_UPPER Registers
        665. 14.6.1.665 GIC_DISTRIBUTOR__37_GICD_IROUTER246_LOWER Registers
        666. 14.6.1.666 GIC_DISTRIBUTOR__37_GICD_IROUTER246_UPPER Registers
        667. 14.6.1.667 GIC_DISTRIBUTOR__37_GICD_IROUTER247_LOWER Registers
        668. 14.6.1.668 GIC_DISTRIBUTOR__37_GICD_IROUTER247_UPPER Registers
        669. 14.6.1.669 GIC_DISTRIBUTOR__37_GICD_IROUTER248_LOWER Registers
        670. 14.6.1.670 GIC_DISTRIBUTOR__37_GICD_IROUTER248_UPPER Registers
        671. 14.6.1.671 GIC_DISTRIBUTOR__37_GICD_IROUTER249_LOWER Registers
        672. 14.6.1.672 GIC_DISTRIBUTOR__37_GICD_IROUTER249_UPPER Registers
        673. 14.6.1.673 GIC_DISTRIBUTOR__37_GICD_IROUTER250_LOWER Registers
        674. 14.6.1.674 GIC_DISTRIBUTOR__37_GICD_IROUTER250_UPPER Registers
        675. 14.6.1.675 GIC_DISTRIBUTOR__37_GICD_IROUTER251_LOWER Registers
        676. 14.6.1.676 GIC_DISTRIBUTOR__37_GICD_IROUTER251_UPPER Registers
        677. 14.6.1.677 GIC_DISTRIBUTOR__37_GICD_IROUTER252_LOWER Registers
        678. 14.6.1.678 GIC_DISTRIBUTOR__37_GICD_IROUTER252_UPPER Registers
        679. 14.6.1.679 GIC_DISTRIBUTOR__37_GICD_IROUTER253_LOWER Registers
        680. 14.6.1.680 GIC_DISTRIBUTOR__37_GICD_IROUTER253_UPPER Registers
        681. 14.6.1.681 GIC_DISTRIBUTOR__37_GICD_IROUTER254_LOWER Registers
        682. 14.6.1.682 GIC_DISTRIBUTOR__37_GICD_IROUTER254_UPPER Registers
        683. 14.6.1.683 GIC_DISTRIBUTOR__37_GICD_IROUTER255_LOWER Registers
        684. 14.6.1.684 GIC_DISTRIBUTOR__37_GICD_IROUTER255_UPPER Registers
        685. 14.6.1.685 GIC_DISTRIBUTOR__37_GICD_IROUTER256_LOWER Registers
        686. 14.6.1.686 GIC_DISTRIBUTOR__37_GICD_IROUTER256_UPPER Registers
        687. 14.6.1.687 GIC_DISTRIBUTOR__37_GICD_IROUTER257_LOWER Registers
        688. 14.6.1.688 GIC_DISTRIBUTOR__37_GICD_IROUTER257_UPPER Registers
        689. 14.6.1.689 GIC_DISTRIBUTOR__37_GICD_IROUTER258_LOWER Registers
        690. 14.6.1.690 GIC_DISTRIBUTOR__37_GICD_IROUTER258_UPPER Registers
        691. 14.6.1.691 GIC_DISTRIBUTOR__37_GICD_IROUTER259_LOWER Registers
        692. 14.6.1.692 GIC_DISTRIBUTOR__37_GICD_IROUTER259_UPPER Registers
        693. 14.6.1.693 GIC_DISTRIBUTOR__37_GICD_IROUTER260_LOWER Registers
        694. 14.6.1.694 GIC_DISTRIBUTOR__37_GICD_IROUTER260_UPPER Registers
        695. 14.6.1.695 GIC_DISTRIBUTOR__37_GICD_IROUTER261_LOWER Registers
        696. 14.6.1.696 GIC_DISTRIBUTOR__37_GICD_IROUTER261_UPPER Registers
        697. 14.6.1.697 GIC_DISTRIBUTOR__37_GICD_IROUTER262_LOWER Registers
        698. 14.6.1.698 GIC_DISTRIBUTOR__37_GICD_IROUTER262_UPPER Registers
        699. 14.6.1.699 GIC_DISTRIBUTOR__37_GICD_IROUTER263_LOWER Registers
        700. 14.6.1.700 GIC_DISTRIBUTOR__37_GICD_IROUTER263_UPPER Registers
        701. 14.6.1.701 GIC_DISTRIBUTOR__37_GICD_IROUTER264_LOWER Registers
        702. 14.6.1.702 GIC_DISTRIBUTOR__37_GICD_IROUTER264_UPPER Registers
        703. 14.6.1.703 GIC_DISTRIBUTOR__37_GICD_IROUTER265_LOWER Registers
        704. 14.6.1.704 GIC_DISTRIBUTOR__37_GICD_IROUTER265_UPPER Registers
        705. 14.6.1.705 GIC_DISTRIBUTOR__37_GICD_IROUTER266_LOWER Registers
        706. 14.6.1.706 GIC_DISTRIBUTOR__37_GICD_IROUTER266_UPPER Registers
        707. 14.6.1.707 GIC_DISTRIBUTOR__37_GICD_IROUTER267_LOWER Registers
        708. 14.6.1.708 GIC_DISTRIBUTOR__37_GICD_IROUTER267_UPPER Registers
        709. 14.6.1.709 GIC_DISTRIBUTOR__37_GICD_IROUTER268_LOWER Registers
        710. 14.6.1.710 GIC_DISTRIBUTOR__37_GICD_IROUTER268_UPPER Registers
        711. 14.6.1.711 GIC_DISTRIBUTOR__37_GICD_IROUTER269_LOWER Registers
        712. 14.6.1.712 GIC_DISTRIBUTOR__37_GICD_IROUTER269_UPPER Registers
        713. 14.6.1.713 GIC_DISTRIBUTOR__37_GICD_IROUTER270_LOWER Registers
        714. 14.6.1.714 GIC_DISTRIBUTOR__37_GICD_IROUTER270_UPPER Registers
        715. 14.6.1.715 GIC_DISTRIBUTOR__37_GICD_IROUTER271_LOWER Registers
        716. 14.6.1.716 GIC_DISTRIBUTOR__37_GICD_IROUTER271_UPPER Registers
        717. 14.6.1.717 GIC_DISTRIBUTOR__37_GICD_IROUTER272_LOWER Registers
        718. 14.6.1.718 GIC_DISTRIBUTOR__37_GICD_IROUTER272_UPPER Registers
        719. 14.6.1.719 GIC_DISTRIBUTOR__37_GICD_IROUTER273_LOWER Registers
        720. 14.6.1.720 GIC_DISTRIBUTOR__37_GICD_IROUTER273_UPPER Registers
        721. 14.6.1.721 GIC_DISTRIBUTOR__37_GICD_IROUTER274_LOWER Registers
        722. 14.6.1.722 GIC_DISTRIBUTOR__37_GICD_IROUTER274_UPPER Registers
        723. 14.6.1.723 GIC_DISTRIBUTOR__37_GICD_IROUTER275_LOWER Registers
        724. 14.6.1.724 GIC_DISTRIBUTOR__37_GICD_IROUTER275_UPPER Registers
        725. 14.6.1.725 GIC_DISTRIBUTOR__37_GICD_IROUTER276_LOWER Registers
        726. 14.6.1.726 GIC_DISTRIBUTOR__37_GICD_IROUTER276_UPPER Registers
        727. 14.6.1.727 GIC_DISTRIBUTOR__37_GICD_IROUTER277_LOWER Registers
        728. 14.6.1.728 GIC_DISTRIBUTOR__37_GICD_IROUTER277_UPPER Registers
        729. 14.6.1.729 GIC_DISTRIBUTOR__37_GICD_IROUTER278_LOWER Registers
        730. 14.6.1.730 GIC_DISTRIBUTOR__37_GICD_IROUTER278_UPPER Registers
        731. 14.6.1.731 GIC_DISTRIBUTOR__37_GICD_IROUTER279_LOWER Registers
        732. 14.6.1.732 GIC_DISTRIBUTOR__37_GICD_IROUTER279_UPPER Registers
        733. 14.6.1.733 GIC_DISTRIBUTOR__37_GICD_IROUTER280_LOWER Registers
        734. 14.6.1.734 GIC_DISTRIBUTOR__37_GICD_IROUTER280_UPPER Registers
        735. 14.6.1.735 GIC_DISTRIBUTOR__37_GICD_IROUTER281_LOWER Registers
        736. 14.6.1.736 GIC_DISTRIBUTOR__37_GICD_IROUTER281_UPPER Registers
        737. 14.6.1.737 GIC_DISTRIBUTOR__37_GICD_IROUTER282_LOWER Registers
        738. 14.6.1.738 GIC_DISTRIBUTOR__37_GICD_IROUTER282_UPPER Registers
        739. 14.6.1.739 GIC_DISTRIBUTOR__37_GICD_IROUTER283_LOWER Registers
        740. 14.6.1.740 GIC_DISTRIBUTOR__37_GICD_IROUTER283_UPPER Registers
        741. 14.6.1.741 GIC_DISTRIBUTOR__37_GICD_IROUTER284_LOWER Registers
        742. 14.6.1.742 GIC_DISTRIBUTOR__37_GICD_IROUTER284_UPPER Registers
        743. 14.6.1.743 GIC_DISTRIBUTOR__37_GICD_IROUTER285_LOWER Registers
        744. 14.6.1.744 GIC_DISTRIBUTOR__37_GICD_IROUTER285_UPPER Registers
        745. 14.6.1.745 GIC_DISTRIBUTOR__37_GICD_IROUTER286_LOWER Registers
        746. 14.6.1.746 GIC_DISTRIBUTOR__37_GICD_IROUTER286_UPPER Registers
        747. 14.6.1.747 GIC_DISTRIBUTOR__37_GICD_IROUTER287_LOWER Registers
        748. 14.6.1.748 GIC_DISTRIBUTOR__37_GICD_IROUTER287_UPPER Registers
        749. 14.6.1.749 GIC_DISTRIBUTOR__38_GICD_ESTATUSR Registers
        750. 14.6.1.750 GIC_DISTRIBUTOR__39_GICD_ERRTESTR Registers
        751. 14.6.1.751 GIC_DISTRIBUTOR__40_GICD_SPISR0 Registers
        752. 14.6.1.752 GIC_DISTRIBUTOR__40_GICD_SPISR1 Registers
        753. 14.6.1.753 GIC_DISTRIBUTOR__40_GICD_SPISR2 Registers
        754. 14.6.1.754 GIC_DISTRIBUTOR__40_GICD_SPISR3 Registers
        755. 14.6.1.755 GIC_DISTRIBUTOR__40_GICD_SPISR4 Registers
        756. 14.6.1.756 GIC_DISTRIBUTOR__40_GICD_SPISR5 Registers
        757. 14.6.1.757 GIC_DISTRIBUTOR__40_GICD_SPISR6 Registers
        758. 14.6.1.758 GIC_DISTRIBUTOR__40_GICD_SPISR7 Registers
        759. 14.6.1.759 GIC_DISTRIBUTOR__41_GICD_PIDR4 Registers
        760. 14.6.1.760 GIC_DISTRIBUTOR__42_GICD_PIDR5 Registers
        761. 14.6.1.761 GIC_DISTRIBUTOR__43_GICD_PIDR6 Registers
        762. 14.6.1.762 GIC_DISTRIBUTOR__44_GICD_PIDR7 Registers
        763. 14.6.1.763 GIC_DISTRIBUTOR__45_GICD_PIDR0 Registers
        764. 14.6.1.764 GIC_DISTRIBUTOR__46_GICD_PIDR1 Registers
        765. 14.6.1.765 GIC_DISTRIBUTOR__47_GICD_PIDR2 Registers
        766. 14.6.1.766 GIC_DISTRIBUTOR__48_GICD_PIDR3 Registers
        767. 14.6.1.767 GIC_DISTRIBUTOR__49_GICD_CIDR0 Registers
        768. 14.6.1.768 GIC_DISTRIBUTOR__50_GICD_CIDR1 Registers
        769. 14.6.1.769 GIC_DISTRIBUTOR__51_GICD_CIDR2 Registers
        770. 14.6.1.770 GIC_DISTRIBUTOR__52_GICD_CIDR3 Registers
        771. 14.6.1.771 GIC_MESSAGE_BASED_SPIS__1_GICD_SETSPI_NSR Registers
        772. 14.6.1.772 GIC_MESSAGE_BASED_SPIS__2_GICD_CLRSPI_NSR Registers
        773. 14.6.1.773 GIC_MESSAGE_BASED_SPIS__3_GICD_SETSPI_SR Registers
        774. 14.6.1.774 GIC_MESSAGE_BASED_SPIS__4_GICD_CLRSPI_SR Registers
        775. 14.6.1.775 GIC_ITS__1_GITS_CTLR Registers
        776. 14.6.1.776 GIC_ITS__2_GITS_IIDR Registers
        777. 14.6.1.777 GIC_ITS__3_GITS_TYPER_LOWER Registers
        778. 14.6.1.778 GIC_ITS__4_GITS_TYPER_UPPER Registers
        779. 14.6.1.779 GIC_ITS__5_GITS_CBASER_LOWER Registers
        780. 14.6.1.780 GIC_ITS__6_GITS_CBASER_UPPER Registers
        781. 14.6.1.781 GIC_ITS__7_GITS_CWRITER_LOWER Registers
        782. 14.6.1.782 GIC_ITS__8_GITS_CWRITER_UPPER Registers
        783. 14.6.1.783 GIC_ITS__9_GITS_CREADR_LOWER Registers
        784. 14.6.1.784 GIC_ITS__10_GITS_CREADR_UPPER Registers
        785. 14.6.1.785 GIC_ITS__11_GITS_BASER0_LOWER Registers
        786. 14.6.1.786 GIC_ITS__12_GITS_BASER0_UPPER Registers
        787. 14.6.1.787 GIC_ITS__13_GITS_TRKCTLR Registers
        788. 14.6.1.788 GIC_ITS__14_GITS_TRKR Registers
        789. 14.6.1.789 GIC_ITS__15_GITS_TRKDIDR Registers
        790. 14.6.1.790 GIC_ITS__16_GITS_TRKPIDR Registers
        791. 14.6.1.791 GIC_ITS__17_GITS_TRKVIDR Registers
        792. 14.6.1.792 GIC_ITS__18_GITS_TRKTGTR Registers
        793. 14.6.1.793 GIC_ITS__19_GITS_TRKICR Registers
        794. 14.6.1.794 GIC_ITS__20_GITS_TRKLCR Registers
        795. 14.6.1.795 GIC_ITS__21_GITS_PIDR4 Registers
        796. 14.6.1.796 GIC_ITS__22_GITS_PIDR5 Registers
        797. 14.6.1.797 GIC_ITS__23_GITS_PIDR6 Registers
        798. 14.6.1.798 GIC_ITS__24_GITS_PIDR7 Registers
        799. 14.6.1.799 GIC_ITS__25_GITS_PIDR0 Registers
        800. 14.6.1.800 GIC_ITS__26_GITS_PIDR1 Registers
        801. 14.6.1.801 GIC_ITS__27_GITS_PIDR2 Registers
        802. 14.6.1.802 GIC_ITS__28_GITS_PIDR3 Registers
        803. 14.6.1.803 GIC_ITS__29_GITS_CIDR0 Registers
        804. 14.6.1.804 GIC_ITS__30_GITS_CIDR1 Registers
        805. 14.6.1.805 GIC_ITS__31_GITS_CIDR2 Registers
        806. 14.6.1.806 GIC_ITS__32_GITS_CIDR3 Registers
        807. 14.6.1.807 GIC_REDISTRIBUTOR_CONTROL_LPI_0__2_GICR_CTLR Registers
        808. 14.6.1.808 GIC_REDISTRIBUTOR_CONTROL_LPI_0__3_GICR_IIDR Registers
        809. 14.6.1.809 GIC_REDISTRIBUTOR_CONTROL_LPI_0__4_GICR_TYPER_LOWER Registers
        810. 14.6.1.810 GIC_REDISTRIBUTOR_CONTROL_LPI_0__5_GICR_TYPER_UPPER Registers
        811. 14.6.1.811 GIC_REDISTRIBUTOR_CONTROL_LPI_0__6_GICR_WAKER Registers
        812. 14.6.1.812 GIC_REDISTRIBUTOR_CONTROL_LPI_0__7_GICR_PROPBASER_LOWER Registers
        813. 14.6.1.813 GIC_REDISTRIBUTOR_CONTROL_LPI_0__8_GICR_PROPBASER_UPPER Registers
        814. 14.6.1.814 GIC_REDISTRIBUTOR_CONTROL_LPI_0__9_GICR_PENDBASER_LOWER Registers
        815. 14.6.1.815 GIC_REDISTRIBUTOR_CONTROL_LPI_0__10_GICR_PENDBASER_UPPER Registers
        816. 14.6.1.816 GIC_REDISTRIBUTOR_CONTROL_LPI_0__11_GICR_PIDR4 Registers
        817. 14.6.1.817 GIC_REDISTRIBUTOR_CONTROL_LPI_0__12_GICR_PIDR5 Registers
        818. 14.6.1.818 GIC_REDISTRIBUTOR_CONTROL_LPI_0__13_GICR_PIDR6 Registers
        819. 14.6.1.819 GIC_REDISTRIBUTOR_CONTROL_LPI_0__14_GICR_PIDR7 Registers
        820. 14.6.1.820 GIC_REDISTRIBUTOR_CONTROL_LPI_0__15_GICR_PIDR0 Registers
        821. 14.6.1.821 GIC_REDISTRIBUTOR_CONTROL_LPI_0__16_GICR_PIDR1 Registers
        822. 14.6.1.822 GIC_REDISTRIBUTOR_CONTROL_LPI_0__17_GICR_PIDR2 Registers
        823. 14.6.1.823 GIC_REDISTRIBUTOR_CONTROL_LPI_0__18_GICR_PIDR3 Registers
        824. 14.6.1.824 GIC_REDISTRIBUTOR_CONTROL_LPI_0__19_GICR_CIDR0 Registers
        825. 14.6.1.825 GIC_REDISTRIBUTOR_CONTROL_LPI_0__20_GICR_CIDR1 Registers
        826. 14.6.1.826 GIC_REDISTRIBUTOR_CONTROL_LPI_0__21_GICR_CIDR2 Registers
        827. 14.6.1.827 GIC_REDISTRIBUTOR_CONTROL_LPI_0__22_GICR_CIDR3 Registers
        828. 14.6.1.828 GIC_REDISTRIBUTOR_SGI_PPI_0__1_GICR_IGROUPR0 Registers
        829. 14.6.1.829 GIC_REDISTRIBUTOR_SGI_PPI_0__2_GICR_ISENABLER0 Registers
        830. 14.6.1.830 GIC_REDISTRIBUTOR_SGI_PPI_0__3_GICR_ICENABLER0 Registers
        831. 14.6.1.831 GIC_REDISTRIBUTOR_SGI_PPI_0__4_GICR_ISPENDR0 Registers
        832. 14.6.1.832 GIC_REDISTRIBUTOR_SGI_PPI_0__5_GICR_ICPENDR0 Registers
        833. 14.6.1.833 GIC_REDISTRIBUTOR_SGI_PPI_0__6_GICR_ISACTIVER0 Registers
        834. 14.6.1.834 GIC_REDISTRIBUTOR_SGI_PPI_0__7_GICR_ICACTIVER0 Registers
        835. 14.6.1.835 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR0 Registers
        836. 14.6.1.836 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR1 Registers
        837. 14.6.1.837 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR2 Registers
        838. 14.6.1.838 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR3 Registers
        839. 14.6.1.839 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR4 Registers
        840. 14.6.1.840 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR5 Registers
        841. 14.6.1.841 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR6 Registers
        842. 14.6.1.842 GIC_REDISTRIBUTOR_SGI_PPI_0__8_GICR_IPRIORITYR7 Registers
        843. 14.6.1.843 GIC_REDISTRIBUTOR_SGI_PPI_0__9_GICR_ICFGR0 Registers
        844. 14.6.1.844 GIC_REDISTRIBUTOR_SGI_PPI_0__10_GICR_ICFGR1 Registers
        845. 14.6.1.845 GIC_REDISTRIBUTOR_SGI_PPI_0__11_GICR_IGRPMODR0 Registers
        846. 14.6.1.846 GIC_REDISTRIBUTOR_SGI_PPI_0__12_GICR_NSACR Registers
        847. 14.6.1.847 GIC_REDISTRIBUTOR_SGI_PPI_0__13_GICR_MISCSTATUSR Registers
        848. 14.6.1.848 GIC_REDISTRIBUTOR_SGI_PPI_0__14_GICR_PPISR Registers
        849. 14.6.1.849 GIC_REDISTRIBUTOR_CONTROL_LPI_1__2_GICR_CTLR Registers
        850. 14.6.1.850 GIC_REDISTRIBUTOR_CONTROL_LPI_1__3_GICR_IIDR Registers
        851. 14.6.1.851 GIC_REDISTRIBUTOR_CONTROL_LPI_1__4_GICR_TYPER_LOWER Registers
        852. 14.6.1.852 GIC_REDISTRIBUTOR_CONTROL_LPI_1__5_GICR_TYPER_UPPER Registers
        853. 14.6.1.853 GIC_REDISTRIBUTOR_CONTROL_LPI_1__6_GICR_WAKER Registers
        854. 14.6.1.854 GIC_REDISTRIBUTOR_CONTROL_LPI_1__7_GICR_PROPBASER_LOWER Registers
        855. 14.6.1.855 GIC_REDISTRIBUTOR_CONTROL_LPI_1__8_GICR_PROPBASER_UPPER Registers
        856. 14.6.1.856 GIC_REDISTRIBUTOR_CONTROL_LPI_1__9_GICR_PENDBASER_LOWER Registers
        857. 14.6.1.857 GIC_REDISTRIBUTOR_CONTROL_LPI_1__10_GICR_PENDBASER_UPPER Registers
        858. 14.6.1.858 GIC_REDISTRIBUTOR_CONTROL_LPI_1__11_GICR_PIDR4 Registers
        859. 14.6.1.859 GIC_REDISTRIBUTOR_CONTROL_LPI_1__12_GICR_PIDR5 Registers
        860. 14.6.1.860 GIC_REDISTRIBUTOR_CONTROL_LPI_1__13_GICR_PIDR6 Registers
        861. 14.6.1.861 GIC_REDISTRIBUTOR_CONTROL_LPI_1__14_GICR_PIDR7 Registers
        862. 14.6.1.862 GIC_REDISTRIBUTOR_CONTROL_LPI_1__15_GICR_PIDR0 Registers
        863. 14.6.1.863 GIC_REDISTRIBUTOR_CONTROL_LPI_1__16_GICR_PIDR1 Registers
        864. 14.6.1.864 GIC_REDISTRIBUTOR_CONTROL_LPI_1__17_GICR_PIDR2 Registers
        865. 14.6.1.865 GIC_REDISTRIBUTOR_CONTROL_LPI_1__18_GICR_PIDR3 Registers
        866. 14.6.1.866 GIC_REDISTRIBUTOR_CONTROL_LPI_1__19_GICR_CIDR0 Registers
        867. 14.6.1.867 GIC_REDISTRIBUTOR_CONTROL_LPI_1__20_GICR_CIDR1 Registers
        868. 14.6.1.868 GIC_REDISTRIBUTOR_CONTROL_LPI_1__21_GICR_CIDR2 Registers
        869. 14.6.1.869 GIC_REDISTRIBUTOR_CONTROL_LPI_1__22_GICR_CIDR3 Registers
        870. 14.6.1.870 GIC_REDISTRIBUTOR_SGI_PPI_1__1_GICR_IGROUPR0 Registers
        871. 14.6.1.871 GIC_REDISTRIBUTOR_SGI_PPI_1__2_GICR_ISENABLER0 Registers
        872. 14.6.1.872 GIC_REDISTRIBUTOR_SGI_PPI_1__3_GICR_ICENABLER0 Registers
        873. 14.6.1.873 GIC_REDISTRIBUTOR_SGI_PPI_1__4_GICR_ISPENDR0 Registers
        874. 14.6.1.874 GIC_REDISTRIBUTOR_SGI_PPI_1__5_GICR_ICPENDR0 Registers
        875. 14.6.1.875 GIC_REDISTRIBUTOR_SGI_PPI_1__6_GICR_ISACTIVER0 Registers
        876. 14.6.1.876 GIC_REDISTRIBUTOR_SGI_PPI_1__7_GICR_ICACTIVER0 Registers
        877. 14.6.1.877 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR0 Registers
        878. 14.6.1.878 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR1 Registers
        879. 14.6.1.879 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR2 Registers
        880. 14.6.1.880 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR3 Registers
        881. 14.6.1.881 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR4 Registers
        882. 14.6.1.882 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR5 Registers
        883. 14.6.1.883 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR6 Registers
        884. 14.6.1.884 GIC_REDISTRIBUTOR_SGI_PPI_1__8_GICR_IPRIORITYR7 Registers
        885. 14.6.1.885 GIC_REDISTRIBUTOR_SGI_PPI_1__9_GICR_ICFGR0 Registers
        886. 14.6.1.886 GIC_REDISTRIBUTOR_SGI_PPI_1__10_GICR_ICFGR1 Registers
        887. 14.6.1.887 GIC_REDISTRIBUTOR_SGI_PPI_1__11_GICR_IGRPMODR0 Registers
        888. 14.6.1.888 GIC_REDISTRIBUTOR_SGI_PPI_1__12_GICR_NSACR Registers
        889. 14.6.1.889 GIC_REDISTRIBUTOR_SGI_PPI_1__13_GICR_MISCSTATUSR Registers
        890. 14.6.1.890 GIC_REDISTRIBUTOR_SGI_PPI_1__14_GICR_PPISR Registers
        891. 14.6.1.891 REGS_REV Registers
        892. 14.6.1.892 REGS_VECTOR Registers
        893. 14.6.1.893 REGS_STAT Registers
        894. 14.6.1.894 REGS_RESERVED_SVBUS_N Registers
        895. 14.6.1.895 REGS_SEC_EOI_REG Registers
        896. 14.6.1.896 REGS_SEC_STATUS_REG0 Registers
        897. 14.6.1.897 REGS_SEC_ENABLE_SET_REG0 Registers
        898. 14.6.1.898 REGS_SEC_ENABLE_CLR_REG0 Registers
        899. 14.6.1.899 REGS_DED_EOI_REG Registers
        900. 14.6.1.900 REGS_DED_STATUS_REG0 Registers
        901. 14.6.1.901 REGS_DED_ENABLE_SET_REG0 Registers
        902. 14.6.1.902 REGS_DED_ENABLE_CLR_REG0 Registers
        903. 14.6.1.903 REGS_AGGR_ENABLE_SET Registers
        904. 14.6.1.904 REGS_AGGR_ENABLE_CLR Registers
        905. 14.6.1.905 REGS_AGGR_STATUS_SET Registers
        906. 14.6.1.906 REGS_AGGR_STATUS_CLR Registers
        907. 14.6.1.907 Access Table
      2. 14.6.2 MAIN_GPIOMUX_INTROUTER Registers
        1. 14.6.2.1 INTR_ROUTER_CFG_PID Registers
        2. 14.6.2.2 INTR_ROUTER_CFG_MUXCNTL_N Registers
        3. 14.6.2.3 Access Table
      3. 14.6.3 MCU_GPIOMUX_INTROUTER Registers
        1. 14.6.3.1 INTR_ROUTER_CFG_PID Registers
        2. 14.6.3.2 INTR_ROUTER_CFG_MUXCNTL_N Registers
        3. 14.6.3.3 Access Table
      4. 14.6.4 CMP_EVENT_INTROUTER Registers
        1. 14.6.4.1 INTR_ROUTER_CFG_PID Registers
        2. 14.6.4.2 INTR_ROUTER_CFG_MUXCNTL_N Registers
        3. 14.6.4.3 Access Table
      5. 14.6.5 TIMESYNC_EVENT_ROUTER Registers
        1. 14.6.5.1 INTR_ROUTER_CFG_PID Registers
        2. 14.6.5.2 INTR_ROUTER_CFG_MUXCNTL_N Registers
        3. 14.6.5.3 Access Table
    7. 14.7 DMA Controller Registers
      1. 14.7.1 DMASS_BCDMA_0 Registers
        1. 14.7.1.1  BCDMA_CRED_CRED_CRED_CRED_J_J Registers
        2. 14.7.1.2  BCDMA_BCHAN_BCHAN_BCHAN_CFG_J_J Registers
        3. 14.7.1.3  BCDMA_BCHAN_BCHAN_BCHAN_PRI_CTRL_J_J Registers
        4. 14.7.1.4  BCDMA_BCHAN_BCHAN_BCHAN_TST_SCHED_J_J Registers
        5. 14.7.1.5  BCDMA_TCHAN_TCHAN_TCHAN_TCFG_J_J Registers
        6. 14.7.1.6  BCDMA_TCHAN_TCHAN_TCHAN_TPRI_CTRL_J_J Registers
        7. 14.7.1.7  BCDMA_TCHAN_TCHAN_TCHAN_THREAD_J_J Registers
        8. 14.7.1.8  BCDMA_TCHAN_TCHAN_TCHAN_TFIFO_DEPTH_J_J Registers
        9. 14.7.1.9  BCDMA_TCHAN_TCHAN_TCHAN_TST_SCHED_J_J Registers
        10. 14.7.1.10 BCDMA_RCHAN_RCHAN_RCHAN_RCFG_J_J Registers
        11. 14.7.1.11 BCDMA_RCHAN_RCHAN_RCHAN_RPRI_CTRL_J_J Registers
        12. 14.7.1.12 BCDMA_RCHAN_RCHAN_RCHAN_THREAD_J_J Registers
        13. 14.7.1.13 BCDMA_RCHAN_RCHAN_RCHAN_RST_SCHED_J_J Registers
        14. 14.7.1.14 BCDMA_GCFG_REVISION Registers
        15. 14.7.1.15 BCDMA_GCFG_PERF_CTRL Registers
        16. 14.7.1.16 BCDMA_GCFG_EMU_CTRL Registers
        17. 14.7.1.17 BCDMA_GCFG_PSIL_TO Registers
        18. 14.7.1.18 BCDMA_GCFG_CAP0 Registers
        19. 14.7.1.19 BCDMA_GCFG_CAP1 Registers
        20. 14.7.1.20 BCDMA_GCFG_CAP2 Registers
        21. 14.7.1.21 BCDMA_GCFG_CAP3 Registers
        22. 14.7.1.22 BCDMA_GCFG_CAP4 Registers
        23. 14.7.1.23 BCDMA_GCFG_PM0 Registers
        24. 14.7.1.24 BCDMA_GCFG_PM1 Registers
        25. 14.7.1.25 BCDMA_GCFG_DBGADDR Registers
        26. 14.7.1.26 BCDMA_GCFG_DBGDATA Registers
        27. 14.7.1.27 BCDMA_RING_RING_RING_BA_LO_J_J Registers
        28. 14.7.1.28 BCDMA_RING_RING_RING_BA_HI_J_J Registers
        29. 14.7.1.29 BCDMA_RING_RING_RING_SIZE_J_J Registers
        30. 14.7.1.30 BCDMA_RCHANRT_RCHANRT_RCHANRT_CTL_J_J Registers
        31. 14.7.1.31 BCDMA_RCHANRT_RCHANRT_RCHANRT_SWTRIG_J_J Registers
        32. 14.7.1.32 BCDMA_RCHANRT_RCHANRT_RCHANRT_STATUS0_J_J Registers
        33. 14.7.1.33 BCDMA_RCHANRT_RCHANRT_RCHANRT_STATUS1_J_J Registers
        34. 14.7.1.34 BCDMA_RCHANRT_RCHANRT_RCHANRT_STDATA_J_J_N Registers
        35. 14.7.1.35 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER0_J_J Registers
        36. 14.7.1.36 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER1_J_J Registers
        37. 14.7.1.37 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER2_J_J Registers
        38. 14.7.1.38 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER3_J_J Registers
        39. 14.7.1.39 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER4_J_J Registers
        40. 14.7.1.40 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER5_J_J Registers
        41. 14.7.1.41 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER6_J_J Registers
        42. 14.7.1.42 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER7_J_J Registers
        43. 14.7.1.43 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER8_J_J Registers
        44. 14.7.1.44 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER9_J_J Registers
        45. 14.7.1.45 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER10_J_J Registers
        46. 14.7.1.46 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER11_J_J Registers
        47. 14.7.1.47 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER12_J_J Registers
        48. 14.7.1.48 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER13_J_J Registers
        49. 14.7.1.49 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER14_J_J Registers
        50. 14.7.1.50 BCDMA_RCHANRT_RCHANRT_RCHANRT_PEER15_J_J Registers
        51. 14.7.1.51 BCDMA_RCHANRT_RCHANRT_RCHANRT_PCNT_J_J Registers
        52. 14.7.1.52 BCDMA_RCHANRT_RCHANRT_RCHANRT_BCNT_J_J Registers
        53. 14.7.1.53 BCDMA_RCHANRT_RCHANRT_RCHANRT_SBCNT_J_J Registers
        54. 14.7.1.54 BCDMA_TCHANRT_TCHANRT_TCHANRT_CTL_J_J Registers
        55. 14.7.1.55 BCDMA_TCHANRT_TCHANRT_TCHANRT_SWTRIG_J_J Registers
        56. 14.7.1.56 BCDMA_TCHANRT_TCHANRT_TCHANRT_STATUS0_J_J Registers
        57. 14.7.1.57 BCDMA_TCHANRT_TCHANRT_TCHANRT_STATUS1_J_J Registers
        58. 14.7.1.58 BCDMA_TCHANRT_TCHANRT_TCHANRT_STDATA_J_J_N Registers
        59. 14.7.1.59 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER0_J_J Registers
        60. 14.7.1.60 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER1_J_J Registers
        61. 14.7.1.61 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER2_J_J Registers
        62. 14.7.1.62 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER3_J_J Registers
        63. 14.7.1.63 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER4_J_J Registers
        64. 14.7.1.64 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER5_J_J Registers
        65. 14.7.1.65 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER6_J_J Registers
        66. 14.7.1.66 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER7_J_J Registers
        67. 14.7.1.67 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER8_J_J Registers
        68. 14.7.1.68 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER9_J_J Registers
        69. 14.7.1.69 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER10_J_J Registers
        70. 14.7.1.70 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER11_J_J Registers
        71. 14.7.1.71 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER12_J_J Registers
        72. 14.7.1.72 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER13_J_J Registers
        73. 14.7.1.73 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER14_J_J Registers
        74. 14.7.1.74 BCDMA_TCHANRT_TCHANRT_TCHANRT_PEER15_J_J Registers
        75. 14.7.1.75 BCDMA_TCHANRT_TCHANRT_TCHANRT_PCNT_J_J Registers
        76. 14.7.1.76 BCDMA_TCHANRT_TCHANRT_TCHANRT_BCNT_J_J Registers
        77. 14.7.1.77 BCDMA_TCHANRT_TCHANRT_TCHANRT_SBCNT_J_J Registers
        78. 14.7.1.78 BCDMA_RINGRT_RINGRT_RINGRT_FDB_J_J Registers
        79. 14.7.1.79 BCDMA_RINGRT_RINGRT_RINGRT_FOCC_J_J Registers
        80. 14.7.1.80 BCDMA_RINGRT_RINGRT_RINGRT_RDB_J_J Registers
        81. 14.7.1.81 BCDMA_RINGRT_RINGRT_RINGRT_ROCC_J_J Registers
        82. 14.7.1.82 BCDMA_BCHANRT_CHANRT_CHANRT_CTL_J_J Registers
        83. 14.7.1.83 BCDMA_BCHANRT_CHANRT_CHANRT_SWTRIG_J_J Registers
        84. 14.7.1.84 BCDMA_BCHANRT_CHANRT_CHANRT_STATUS0_J_J Registers
        85. 14.7.1.85 BCDMA_BCHANRT_CHANRT_CHANRT_STATUS1_J_J Registers
        86. 14.7.1.86 BCDMA_BCHANRT_CHANRT_CHANRT_STATUS2_J_J Registers
        87. 14.7.1.87 BCDMA_BCHANRT_CHANRT_CHANRT_STATUS3_J_J Registers
        88. 14.7.1.88 BCDMA_BCHANRT_CHANRT_CHANRT_STDATA_J_J_N Registers
        89. 14.7.1.89 BCDMA_BCHANRT_CHANRT_CHANRT_STDATAW_J_J_N Registers
        90. 14.7.1.90 BCDMA_BCHANRT_CHANRT_CHANRT_PCNT_J_J Registers
        91. 14.7.1.91 BCDMA_BCHANRT_CHANRT_CHANRT_BCNT_J_J Registers
        92. 14.7.1.92 BCDMA_BCHANRT_CHANRT_CHANRT_SBCNT_J_J Registers
        93. 14.7.1.93 Access Table
      2. 14.7.2 DMASS_INTAGGR_0 Registers
        1. 14.7.2.1  INTAGGR_INTR_VINT_VINT_ENABLE_SET_J_J Registers
        2. 14.7.2.2  INTAGGR_INTR_VINT_VINT_ENABLE_CLEAR_J_J Registers
        3. 14.7.2.3  INTAGGR_INTR_VINT_VINT_STATUS_SET_J_J Registers
        4. 14.7.2.4  INTAGGR_INTR_VINT_VINT_STATUS_CLEAR_J_J Registers
        5. 14.7.2.5  INTAGGR_INTR_VINT_VINT_STATUSM_J_J Registers
        6. 14.7.2.6  INTAGGR_IMAP_ENTRY_ENTRY_IMAP_J_J Registers
        7. 14.7.2.7  INTAGGR_CFG_REVISION Registers
        8. 14.7.2.8  INTAGGR_CFG_INTCAP Registers
        9. 14.7.2.9  INTAGGR_CFG_AUXCAP Registers
        10. 14.7.2.10 INTAGGR_L2G_LEVI_LEVI_MAP_J_J Registers
        11. 14.7.2.11 INTAGGR_UNMAP_UENTRY0_UENTRY0_MAP_J_J Registers
        12. 14.7.2.12 INTAGGR_UNMAP_UENTRY1_UENTRY1_MAP_J_J Registers
        13. 14.7.2.13 INTAGGR_UNMAP_UENTRY2_UENTRY2_MAP_J_J Registers
        14. 14.7.2.14 INTAGGR_UNMAP_UENTRY3_UENTRY3_MAP_J_J Registers
        15. 14.7.2.15 INTAGGR_UNMAP_UENTRY4_UENTRY4_MAP_J_J Registers
        16. 14.7.2.16 INTAGGR_UNMAP_UENTRY5_UENTRY5_MAP Registers
        17. 14.7.2.17 INTAGGR_UNMAP_UENTRY6_UENTRY6_MAP_J_J Registers
        18. 14.7.2.18 INTAGGR_UNMAP_UENTRY7_UENTRY7_MAP_J_J Registers
        19. 14.7.2.19 INTAGGR_UNMAP_UENTRY8_UENTRY8_MAP_J_J Registers
        20. 14.7.2.20 INTAGGR_UNMAP_UENTRY9_UENTRY9_MAP_J_J Registers
        21. 14.7.2.21 INTAGGR_UNMAP_UENTRY10_UENTRY10_MAP_J_J Registers
        22. 14.7.2.22 INTAGGR_UNMAP_UENTRY11_UENTRY11_MAP_J_J Registers
        23. 14.7.2.23 INTAGGR_UNMAP_UENTRY12_UENTRY12_MAP_J_J Registers
        24. 14.7.2.24 INTAGGR_UNMAP_UENTRY13_UENTRY13_MAP_J_J Registers
        25. 14.7.2.25 INTAGGR_UNMAP_UENTRY14_UENTRY14_MAP_J_J Registers
        26. 14.7.2.26 INTAGGR_MCAST_GEVI_GEVI_MCMAP_J_J Registers
        27. 14.7.2.27 INTAGGR_GCNTCFG_GEVI_GEVI_MAP_J_J Registers
        28. 14.7.2.28 INTAGGR_GCNTRTI_GEVI_GEVI_COUNT_J_J Registers
        29. 14.7.2.29 Access Table
      3. 14.7.3 DMASS_PKTDMA_0 Registers
        1. 14.7.3.1  PKTDMA_CRED_CRED_CRED_CRED_J_J Registers
        2. 14.7.3.2  PKTDMA_RFLOW_RFLOW_RFLOW_RFA_J_J Registers
        3. 14.7.3.3  PKTDMA_TCHAN_TCHAN_TCHAN_TCFG_J_J Registers
        4. 14.7.3.4  PKTDMA_TCHAN_TCHAN_TCHAN_TPRI_CTRL_J_J Registers
        5. 14.7.3.5  PKTDMA_TCHAN_TCHAN_TCHAN_THREAD_J_J Registers
        6. 14.7.3.6  PKTDMA_TCHAN_TCHAN_TCHAN_TFIFO_DEPTH_J_J Registers
        7. 14.7.3.7  PKTDMA_TCHAN_TCHAN_TCHAN_TST_SCHED_J_J Registers
        8. 14.7.3.8  PKTDMA_RCHAN_RCHAN_RCHAN_RCFG_J_J Registers
        9. 14.7.3.9  PKTDMA_RCHAN_RCHAN_RCHAN_RPRI_CTRL_J_J Registers
        10. 14.7.3.10 PKTDMA_RCHAN_RCHAN_RCHAN_THREAD_J_J Registers
        11. 14.7.3.11 PKTDMA_RCHAN_RCHAN_RCHAN_RST_SCHED_J_J Registers
        12. 14.7.3.12 PKTDMA_GCFG_REVISION Registers
        13. 14.7.3.13 PKTDMA_GCFG_PERF_CTRL Registers
        14. 14.7.3.14 PKTDMA_GCFG_EMU_CTRL Registers
        15. 14.7.3.15 PKTDMA_GCFG_PSIL_TO Registers
        16. 14.7.3.16 PKTDMA_GCFG_CAP0 Registers
        17. 14.7.3.17 PKTDMA_GCFG_CAP1 Registers
        18. 14.7.3.18 PKTDMA_GCFG_CAP2 Registers
        19. 14.7.3.19 PKTDMA_GCFG_CAP3 Registers
        20. 14.7.3.20 PKTDMA_GCFG_CAP4 Registers
        21. 14.7.3.21 PKTDMA_GCFG_PM0 Registers
        22. 14.7.3.22 PKTDMA_GCFG_PM1 Registers
        23. 14.7.3.23 PKTDMA_GCFG_DBGADDR Registers
        24. 14.7.3.24 PKTDMA_GCFG_DBGDATA Registers
        25. 14.7.3.25 PKTDMA_GCFG_RFLOWFWSTAT Registers
        26. 14.7.3.26 PKTDMA_RING_RING_RING_BA_LO_J_J Registers
        27. 14.7.3.27 PKTDMA_RING_RING_RING_BA_HI_J_J Registers
        28. 14.7.3.28 PKTDMA_RING_RING_RING_SIZE_J_J Registers
        29. 14.7.3.29 PKTDMA_RCHANRT_RCHANRT_RCHANRT_CTL_J_J Registers
        30. 14.7.3.30 PKTDMA_RCHANRT_RCHANRT_RCHANRT_STATUS0_J_J Registers
        31. 14.7.3.31 PKTDMA_RCHANRT_RCHANRT_RCHANRT_STATUS1_J_J Registers
        32. 14.7.3.32 PKTDMA_RCHANRT_RCHANRT_RCHANRT_STDATA_J_J_N Registers
        33. 14.7.3.33 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER0_J_J Registers
        34. 14.7.3.34 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER1_J_J Registers
        35. 14.7.3.35 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER2_J_J Registers
        36. 14.7.3.36 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER3_J_J Registers
        37. 14.7.3.37 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER4_J_J Registers
        38. 14.7.3.38 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER5_J_J Registers
        39. 14.7.3.39 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER6_J_J Registers
        40. 14.7.3.40 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER7_J_J Registers
        41. 14.7.3.41 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER8_J_J Registers
        42. 14.7.3.42 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER9_J_J Registers
        43. 14.7.3.43 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER10_J_J Registers
        44. 14.7.3.44 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER11_J_J Registers
        45. 14.7.3.45 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER12_J_J Registers
        46. 14.7.3.46 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER13_J_J Registers
        47. 14.7.3.47 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER14_J_J Registers
        48. 14.7.3.48 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PEER15_J_J Registers
        49. 14.7.3.49 PKTDMA_RCHANRT_RCHANRT_RCHANRT_PCNT_J_J Registers
        50. 14.7.3.50 PKTDMA_RCHANRT_RCHANRT_RCHANRT_DCNT_J_J Registers
        51. 14.7.3.51 PKTDMA_RCHANRT_RCHANRT_RCHANRT_BCNT_J_J Registers
        52. 14.7.3.52 PKTDMA_RCHANRT_RCHANRT_RCHANRT_SBCNT_J_J Registers
        53. 14.7.3.53 PKTDMA_TCHANRT_TCHANRT_TCHANRT_CTL_J_J Registers
        54. 14.7.3.54 PKTDMA_TCHANRT_TCHANRT_TCHANRT_STATUS0_J_J Registers
        55. 14.7.3.55 PKTDMA_TCHANRT_TCHANRT_TCHANRT_STATUS1_J_J Registers
        56. 14.7.3.56 PKTDMA_TCHANRT_TCHANRT_TCHANRT_STDATA_J_J_N Registers
        57. 14.7.3.57 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER0_J_J Registers
        58. 14.7.3.58 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER1_J_J Registers
        59. 14.7.3.59 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER2_J_J Registers
        60. 14.7.3.60 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER3_J_J Registers
        61. 14.7.3.61 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER4_J_J Registers
        62. 14.7.3.62 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER5_J_J Registers
        63. 14.7.3.63 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER6_J_J Registers
        64. 14.7.3.64 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER7_J_J Registers
        65. 14.7.3.65 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER8_J_J Registers
        66. 14.7.3.66 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER9_J_J Registers
        67. 14.7.3.67 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER10_J_J Registers
        68. 14.7.3.68 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER11_J_J Registers
        69. 14.7.3.69 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER12_J_J Registers
        70. 14.7.3.70 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER13_J_J Registers
        71. 14.7.3.71 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER14_J_J Registers
        72. 14.7.3.72 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PEER15_J_J Registers
        73. 14.7.3.73 PKTDMA_TCHANRT_TCHANRT_TCHANRT_PCNT_J_J Registers
        74. 14.7.3.74 PKTDMA_TCHANRT_TCHANRT_TCHANRT_BCNT_J_J Registers
        75. 14.7.3.75 PKTDMA_TCHANRT_TCHANRT_TCHANRT_SBCNT_J_J Registers
        76. 14.7.3.76 PKTDMA_RINGRT_RINGRT_RINGRT_FDB_J_J Registers
        77. 14.7.3.77 PKTDMA_RINGRT_RINGRT_RINGRT_FOCC_J_J Registers
        78. 14.7.3.78 PKTDMA_RINGRT_RINGRT_RINGRT_RDB_J_J Registers
        79. 14.7.3.79 PKTDMA_RINGRT_RINGRT_RINGRT_ROCC_J_J Registers
        80. 14.7.3.80 Access Table
      4. 14.7.4 DMASS_PSILCFG_0 Registers
        1. 14.7.4.1 PSILCFG_PROXY_REVISION Registers
        2. 14.7.4.2 PSILCFG_PROXY_PSIL_TO Registers
        3. 14.7.4.3 PSILCFG_PROXY_CMDA Registers
        4. 14.7.4.4 PSILCFG_PROXY_CMDB Registers
        5. 14.7.4.5 PSILCFG_PROXY_WDATA Registers
        6. 14.7.4.6 PSILCFG_PROXY_RDATA Registers
        7. 14.7.4.7 Access Table
      5. 14.7.5 DMASS_PSILSS_0 Registers
        1. 14.7.5.1  PSILSS_MMRS_PID Registers
        2. 14.7.5.2  PSILSS_MMRS_CONFIG Registers
        3. 14.7.5.3  PSILSS_MMRS_EVENT Registers
        4. 14.7.5.4  PSILSS_MMRS_LINK Registers
        5. 14.7.5.5  PSILSS_MMRS_DOWN Registers
        6. 14.7.5.6  ETLSW_MMRS_PID Registers
        7. 14.7.5.7  ETLSW_MMRS_CONFIG Registers
        8. 14.7.5.8  ETLSW_MMRS_EVENT Registers
        9. 14.7.5.9  ETLSW_MMRS_LINK Registers
        10. 14.7.5.10 ETLSW_MMRS_DOWN Registers
        11. 14.7.5.11 Access Table
      6. 14.7.6 DMASS_RINGACC_0 Registers
        1. 14.7.6.1  RINGACC_GCFG_REVISION Registers
        2. 14.7.6.2  RINGACC_GCFG_TRACE_CTL Registers
        3. 14.7.6.3  RINGACC_GCFG_OVRFLOW Registers
        4. 14.7.6.4  RINGACC_GCFG_ERROR_EVT Registers
        5. 14.7.6.5  RINGACC_GCFG_ERROR_LOG Registers
        6. 14.7.6.6  RINGACC_RT_RINGRT_RINGRT_DB_J_J Registers
        7. 14.7.6.7  RINGACC_RT_RINGRT_RINGRT_OCC_J_J Registers
        8. 14.7.6.8  RINGACC_RT_RINGRT_RINGRT_INDX_J_J Registers
        9. 14.7.6.9  RINGACC_RT_RINGRT_RINGRT_HWOCC_J_J Registers
        10. 14.7.6.10 RINGACC_RT_RINGRT_RINGRT_HWINDX_J_J Registers
        11. 14.7.6.11 RINGACC_CFG_RING_RING_BA_LO_J_J Registers
        12. 14.7.6.12 RINGACC_CFG_RING_RING_BA_HI_J_J Registers
        13. 14.7.6.13 RINGACC_CFG_RING_RING_SIZE_J_J Registers
        14. 14.7.6.14 RINGACC_CFG_RING_RING_EVENT_J_J Registers
        15. 14.7.6.15 RINGACC_CFG_RING_RING_ORDERID_J_J Registers
        16. 14.7.6.16 Access Table
      7. 14.7.7 DMASS_SEC_PROXY_0 Registers
        1. 14.7.7.1  SEC_PROXY_MMRS_PID Registers
        2. 14.7.7.2  SEC_PROXY_MMRS_CONFIG Registers
        3. 14.7.7.3  SEC_PROXY_MMRS_GLB_EVT Registers
        4. 14.7.7.4  SEC_PROXY_SCFG_BUFFER_L Registers
        5. 14.7.7.5  SEC_PROXY_SCFG_BUFFER_H Registers
        6. 14.7.7.6  SEC_PROXY_SCFG_TARGET_L Registers
        7. 14.7.7.7  SEC_PROXY_SCFG_TARGET_H Registers
        8. 14.7.7.8  SEC_PROXY_SCFG_ORDERID Registers
        9. 14.7.7.9  SEC_PROXY_SCFG_THREAD_THREAD_CTL_J_J Registers
        10. 14.7.7.10 SEC_PROXY_SCFG_THREAD_THREAD_EVT_MAP_J_J Registers
        11. 14.7.7.11 SEC_PROXY_SCFG_THREAD_THREAD_DST_J_J Registers
        12. 14.7.7.12 SEC_PROXY_RT_THREAD_THREAD_STATUS_J_J Registers
        13. 14.7.7.13 SEC_PROXY_RT_THREAD_THREAD_THR_J_J Registers
        14. 14.7.7.14 SEC_PROXY_SRC_TARGET_DATA_THREAD_THREAD_DATA_J_J Registers
        15. 14.7.7.15 SEC_PROXY_SRC_TARGET_DATA_THREAD_THREAD_MESSAGE_J_J_N Registers
        16. 14.7.7.16 Access Table
      8. 14.7.8 PDMA Registers
        1. 14.7.8.1  _PDMA_REV Registers
        2. 14.7.8.2  _PDMA_VECTOR Registers
        3. 14.7.8.3  _PDMA_STAT Registers
        4. 14.7.8.4  _PDMA_RESERVED_SVBUS_N Registers
        5. 14.7.8.5  _PDMA_SEC_EOI_REG Registers
        6. 14.7.8.6  _PDMA_SEC_STATUS_REG0 Registers
        7. 14.7.8.7  _PDMA_SEC_ENABLE_SET_REG0 Registers
        8. 14.7.8.8  _PDMA_SEC_ENABLE_CLR_REG0 Registers
        9. 14.7.8.9  _PDMA_DED_EOI_REG Registers
        10. 14.7.8.10 _PDMA_DED_STATUS_REG0 Registers
        11. 14.7.8.11 _PDMA_DED_ENABLE_SET_REG0 Registers
        12. 14.7.8.12 _PDMA_DED_ENABLE_CLR_REG0 Registers
        13. 14.7.8.13 _PDMA_AGGR_ENABLE_SET Registers
        14. 14.7.8.14 _PDMA_AGGR_ENABLE_CLR Registers
        15. 14.7.8.15 _PDMA_AGGR_STATUS_SET Registers
        16. 14.7.8.16 _PDMA_AGGR_STATUS_CLR Registers
        17. 14.7.8.17 Access Table
    8. 14.8 Peripherals Registers
      1. 14.8.1 Audio Registers
        1. 14.8.1.1 MCASP Registers
          1. 14.8.1.1.1   CFG_PID Registers
          2. 14.8.1.1.2   CFG_PWRIDLESYSCONFIG Registers
          3. 14.8.1.1.3   CFG_PFUNC Registers
          4. 14.8.1.1.4   CFG_PDIR Registers
          5. 14.8.1.1.5   CFG_PDOUT Registers
          6. 14.8.1.1.6   CFG_PDIN Registers
          7. 14.8.1.1.7   CFG_PDCLR Registers
          8. 14.8.1.1.8   CFG_GBLCTL Registers
          9. 14.8.1.1.9   CFG_AMUTE Registers
          10. 14.8.1.1.10  CFG_DLBCTL Registers
          11. 14.8.1.1.11  CFG_DITCTL Registers
          12. 14.8.1.1.12  CFG_RGBLCTL Registers
          13. 14.8.1.1.13  CFG_RMASK Registers
          14. 14.8.1.1.14  CFG_RFMT Registers
          15. 14.8.1.1.15  CFG_AFSRCTL Registers
          16. 14.8.1.1.16  CFG_ACLKRCTL Registers
          17. 14.8.1.1.17  CFG_AHCLKRCTL Registers
          18. 14.8.1.1.18  CFG_RTDM Registers
          19. 14.8.1.1.19  CFG_RINTCTL Registers
          20. 14.8.1.1.20  CFG_RSTAT Registers
          21. 14.8.1.1.21  CFG_RSLOT Registers
          22. 14.8.1.1.22  CFG_RCLKCHK Registers
          23. 14.8.1.1.23  CFG_PIDTCTL Registers
          24. 14.8.1.1.24  CFG_XGBLCTL Registers
          25. 14.8.1.1.25  CFG_XMASK Registers
          26. 14.8.1.1.26  CFG_XFMT Registers
          27. 14.8.1.1.27  CFG_AFSXCTL Registers
          28. 14.8.1.1.28  CFG_ACLKXCTL Registers
          29. 14.8.1.1.29  CFG_AHCLKXCTL Registers
          30. 14.8.1.1.30  CFG_XTDM Registers
          31. 14.8.1.1.31  CFG_XINTCTL Registers
          32. 14.8.1.1.32  CFG_XSTAT Registers
          33. 14.8.1.1.33  CFG_XSLOT Registers
          34. 14.8.1.1.34  CFG_XCLKCHK Registers
          35. 14.8.1.1.35  CFG_XEVTCTL Registers
          36. 14.8.1.1.36  CFG_DITCSRA0 Registers
          37. 14.8.1.1.37  CFG_DITCSRA1 Registers
          38. 14.8.1.1.38  CFG_DITCSRA2 Registers
          39. 14.8.1.1.39  CFG_DITCSRA3 Registers
          40. 14.8.1.1.40  CFG_DITCSRA4 Registers
          41. 14.8.1.1.41  CFG_DITCSRA5 Registers
          42. 14.8.1.1.42  CFG_DITCSRB0 Registers
          43. 14.8.1.1.43  CFG_DITCSRB1 Registers
          44. 14.8.1.1.44  CFG_DITCSRB2 Registers
          45. 14.8.1.1.45  CFG_DITCSRB3 Registers
          46. 14.8.1.1.46  CFG_DITCSRB4 Registers
          47. 14.8.1.1.47  CFG_DITCSRB5 Registers
          48. 14.8.1.1.48  CFG_DITUDRA0 Registers
          49. 14.8.1.1.49  CFG_DITUDRA1 Registers
          50. 14.8.1.1.50  CFG_DITUDRA2 Registers
          51. 14.8.1.1.51  CFG_DITUDRA3 Registers
          52. 14.8.1.1.52  CFG_DITUDRA4 Registers
          53. 14.8.1.1.53  CFG_DITUDRA5 Registers
          54. 14.8.1.1.54  CFG_DITUDRB0 Registers
          55. 14.8.1.1.55  CFG_DITUDRB1 Registers
          56. 14.8.1.1.56  CFG_DITUDRB2 Registers
          57. 14.8.1.1.57  CFG_DITUDRB3 Registers
          58. 14.8.1.1.58  CFG_DITUDRB4 Registers
          59. 14.8.1.1.59  CFG_DITUDRB5 Registers
          60. 14.8.1.1.60  CFG_SRCTL0 Registers
          61. 14.8.1.1.61  CFG_SRCTL1 Registers
          62. 14.8.1.1.62  CFG_SRCTL2 Registers
          63. 14.8.1.1.63  CFG_SRCTL3 Registers
          64. 14.8.1.1.64  CFG_SRCTL4 Registers
          65. 14.8.1.1.65  CFG_SRCTL5 Registers
          66. 14.8.1.1.66  CFG_SRCTL6 Registers
          67. 14.8.1.1.67  CFG_SRCTL7 Registers
          68. 14.8.1.1.68  CFG_SRCTL8 Registers
          69. 14.8.1.1.69  CFG_SRCTL9 Registers
          70. 14.8.1.1.70  CFG_SRCTL10 Registers
          71. 14.8.1.1.71  CFG_SRCTL11 Registers
          72. 14.8.1.1.72  CFG_SRCTL12 Registers
          73. 14.8.1.1.73  CFG_SRCTL13 Registers
          74. 14.8.1.1.74  CFG_SRCTL14 Registers
          75. 14.8.1.1.75  CFG_SRCTL15 Registers
          76. 14.8.1.1.76  CFG_XBUF0 Registers
          77. 14.8.1.1.77  CFG_XBUF1 Registers
          78. 14.8.1.1.78  CFG_XBUF2 Registers
          79. 14.8.1.1.79  CFG_XBUF3 Registers
          80. 14.8.1.1.80  CFG_XBUF4 Registers
          81. 14.8.1.1.81  CFG_XBUF5 Registers
          82. 14.8.1.1.82  CFG_XBUF6 Registers
          83. 14.8.1.1.83  CFG_XBUF7 Registers
          84. 14.8.1.1.84  CFG_XBUF8 Registers
          85. 14.8.1.1.85  CFG_XBUF9 Registers
          86. 14.8.1.1.86  CFG_XBUF10 Registers
          87. 14.8.1.1.87  CFG_XBUF11 Registers
          88. 14.8.1.1.88  CFG_XBUF12 Registers
          89. 14.8.1.1.89  CFG_XBUF13 Registers
          90. 14.8.1.1.90  CFG_XBUF14 Registers
          91. 14.8.1.1.91  CFG_XBUF15 Registers
          92. 14.8.1.1.92  CFG_RBUF0 Registers
          93. 14.8.1.1.93  CFG_RBUF1 Registers
          94. 14.8.1.1.94  CFG_RBUF2 Registers
          95. 14.8.1.1.95  CFG_RBUF3 Registers
          96. 14.8.1.1.96  CFG_RBUF4 Registers
          97. 14.8.1.1.97  CFG_RBUF5 Registers
          98. 14.8.1.1.98  CFG_RBUF6 Registers
          99. 14.8.1.1.99  CFG_RBUF7 Registers
          100. 14.8.1.1.100 CFG_RBUF8 Registers
          101. 14.8.1.1.101 CFG_RBUF9 Registers
          102. 14.8.1.1.102 CFG_RBUF10 Registers
          103. 14.8.1.1.103 CFG_RBUF11 Registers
          104. 14.8.1.1.104 CFG_RBUF12 Registers
          105. 14.8.1.1.105 CFG_RBUF13 Registers
          106. 14.8.1.1.106 CFG_RBUF14 Registers
          107. 14.8.1.1.107 CFG_RBUF15 Registers
          108. 14.8.1.1.108 CFG_WFIFOCTL Registers
          109. 14.8.1.1.109 CFG_WFIFOSTS Registers
          110. 14.8.1.1.110 CFG_RFIFOCTL Registers
          111. 14.8.1.1.111 CFG_RFIFOSTS Registers
          112. 14.8.1.1.112 Access Table
      2. 14.8.2 General Connectivity Registers
        1. 14.8.2.1 GPIO Registers
          1. 14.8.2.1.1  _GPIO_PID Registers
          2. 14.8.2.1.2  _GPIO_PCR Registers
          3. 14.8.2.1.3  _GPIO_BINTEN Registers
          4. 14.8.2.1.4  _GPIO_DIR01 Registers
          5. 14.8.2.1.5  _GPIO_OUT_DATA01 Registers
          6. 14.8.2.1.6  _GPIO_SET_DATA01 Registers
          7. 14.8.2.1.7  _GPIO_CLR_DATA01 Registers
          8. 14.8.2.1.8  _GPIO_IN_DATA01 Registers
          9. 14.8.2.1.9  _GPIO_SET_RIS_TRIG01 Registers
          10. 14.8.2.1.10 _GPIO_CLR_RIS_TRIG01 Registers
          11. 14.8.2.1.11 _GPIO_SET_FAL_TRIG01 Registers
          12. 14.8.2.1.12 _GPIO_CLR_FAL_TRIG01 Registers
          13. 14.8.2.1.13 _GPIO_INTSTAT01 Registers
          14. 14.8.2.1.14 _GPIO_DIR23 Registers
          15. 14.8.2.1.15 _GPIO_OUT_DATA23 Registers
          16. 14.8.2.1.16 _GPIO_SET_DATA23 Registers
          17. 14.8.2.1.17 _GPIO_CLR_DATA23 Registers
          18. 14.8.2.1.18 _GPIO_IN_DATA23 Registers
          19. 14.8.2.1.19 _GPIO_SET_RIS_TRIG23 Registers
          20. 14.8.2.1.20 _GPIO_CLR_RIS_TRIG23 Registers
          21. 14.8.2.1.21 _GPIO_SET_FAL_TRIG23 Registers
          22. 14.8.2.1.22 _GPIO_CLR_FAL_TRIG23 Registers
          23. 14.8.2.1.23 _GPIO_INTSTAT23 Registers
          24. 14.8.2.1.24 _GPIO_DIR45 Registers
          25. 14.8.2.1.25 _GPIO_OUT_DATA45 Registers
          26. 14.8.2.1.26 _GPIO_SET_DATA45 Registers
          27. 14.8.2.1.27 _GPIO_CLR_DATA45 Registers
          28. 14.8.2.1.28 _GPIO_IN_DATA45 Registers
          29. 14.8.2.1.29 _GPIO_SET_RIS_TRIG45 Registers
          30. 14.8.2.1.30 _GPIO_CLR_RIS_TRIG45 Registers
          31. 14.8.2.1.31 _GPIO_SET_FAL_TRIG45 Registers
          32. 14.8.2.1.32 _GPIO_CLR_FAL_TRIG45 Registers
          33. 14.8.2.1.33 _GPIO_INTSTAT45 Registers
          34. 14.8.2.1.34 _GPIO_DIR67 Registers
          35. 14.8.2.1.35 _GPIO_OUT_DATA67 Registers
          36. 14.8.2.1.36 _GPIO_SET_DATA67 Registers
          37. 14.8.2.1.37 _GPIO_CLR_DATA67 Registers
          38. 14.8.2.1.38 _GPIO_IN_DATA67 Registers
          39. 14.8.2.1.39 _GPIO_SET_RIS_TRIG67 Registers
          40. 14.8.2.1.40 _GPIO_CLR_RIS_TRIG67 Registers
          41. 14.8.2.1.41 _GPIO_SET_FAL_TRIG67 Registers
          42. 14.8.2.1.42 _GPIO_CLR_FAL_TRIG67 Registers
          43. 14.8.2.1.43 _GPIO_INTSTAT67 Registers
          44. 14.8.2.1.44 _GPIO_DIR8 Registers
          45. 14.8.2.1.45 _GPIO_OUT_DATA8 Registers
          46. 14.8.2.1.46 _GPIO_SET_DATA8 Registers
          47. 14.8.2.1.47 _GPIO_CLR_DATA8 Registers
          48. 14.8.2.1.48 _GPIO_IN_DATA8 Registers
          49. 14.8.2.1.49 _GPIO_SET_RIS_TRIG8 Registers
          50. 14.8.2.1.50 _GPIO_CLR_RIS_TRIG8 Registers
          51. 14.8.2.1.51 _GPIO_SET_FAL_TRIG8 Registers
          52. 14.8.2.1.52 _GPIO_CLR_FAL_TRIG8 Registers
          53. 14.8.2.1.53 _GPIO_INTSTAT8 Registers
          54. 14.8.2.1.54 Access Table
        2. 14.8.2.2 I2C Registers
          1. 14.8.2.2.1  CFG_I2C_REVNB_LO Registers
          2. 14.8.2.2.2  CFG_I2C_REVNB_HI Registers
          3. 14.8.2.2.3  CFG_I2C_SYSC Registers
          4. 14.8.2.2.4  CFG_I2C_EOI Registers
          5. 14.8.2.2.5  CFG_I2C_IRQSTATUS_RAW Registers
          6. 14.8.2.2.6  CFG_I2C_IRQSTATUS Registers
          7. 14.8.2.2.7  CFG_I2C_IRQENABLE_SET Registers
          8. 14.8.2.2.8  CFG_I2C_IRQENABLE_CLR Registers
          9. 14.8.2.2.9  CFG_I2C_WE Registers
          10. 14.8.2.2.10 CFG_I2C_DMARXENABLE_SET Registers
          11. 14.8.2.2.11 CFG_I2C_DMATXENABLE_SET Registers
          12. 14.8.2.2.12 CFG_I2C_DMARXENABLE_CLR Registers
          13. 14.8.2.2.13 CFG_I2C_DMATXENABLE_CLR Registers
          14. 14.8.2.2.14 CFG_I2C_DMARXWAKE_EN Registers
          15. 14.8.2.2.15 CFG_I2C_DMATXWAKE_EN Registers
          16. 14.8.2.2.16 CFG_I2C_IE Registers
          17. 14.8.2.2.17 CFG_I2C_STAT Registers
          18. 14.8.2.2.18 CFG_I2C_SYSS Registers
          19. 14.8.2.2.19 CFG_I2C_BUF Registers
          20. 14.8.2.2.20 CFG_I2C_CNT Registers
          21. 14.8.2.2.21 CFG_I2C_DATA Registers
          22. 14.8.2.2.22 CFG_I2C_CON Registers
          23. 14.8.2.2.23 CFG_I2C_OA Registers
          24. 14.8.2.2.24 CFG_I2C_SA Registers
          25. 14.8.2.2.25 CFG_I2C_PSC Registers
          26. 14.8.2.2.26 CFG_I2C_SCLL Registers
          27. 14.8.2.2.27 CFG_I2C_SCLH Registers
          28. 14.8.2.2.28 CFG_I2C_SYSTEST Registers
          29. 14.8.2.2.29 CFG_I2C_BUFSTAT Registers
          30. 14.8.2.2.30 CFG_I2C_OA1 Registers
          31. 14.8.2.2.31 CFG_I2C_OA2 Registers
          32. 14.8.2.2.32 CFG_I2C_OA3 Registers
          33. 14.8.2.2.33 CFG_I2C_ACTOA Registers
          34. 14.8.2.2.34 CFG_I2C_SBLOCK Registers
          35. 14.8.2.2.35 Access Table
        3. 14.8.2.3 MCSPI Registers
          1. 14.8.2.3.1  CFG_HL_REV Registers
          2. 14.8.2.3.2  CFG_HL_HWINFO Registers
          3. 14.8.2.3.3  CFG_HL_SYSCONFIG Registers
          4. 14.8.2.3.4  CFG_REVISION Registers
          5. 14.8.2.3.5  CFG_SYSCONFIG Registers
          6. 14.8.2.3.6  CFG_SYSSTATUS Registers
          7. 14.8.2.3.7  CFG_IRQSTATUS Registers
          8. 14.8.2.3.8  CFG_IRQENABLE Registers
          9. 14.8.2.3.9  CFG_WAKEUPENABLE Registers
          10. 14.8.2.3.10 CFG_SYST Registers
          11. 14.8.2.3.11 CFG_MODULCTRL Registers
          12. 14.8.2.3.12 CFG_CH0CONF Registers
          13. 14.8.2.3.13 CFG_CH0STAT Registers
          14. 14.8.2.3.14 CFG_CH0CTRL Registers
          15. 14.8.2.3.15 CFG_TX0 Registers
          16. 14.8.2.3.16 CFG_RX0 Registers
          17. 14.8.2.3.17 CFG_CH1CONF Registers
          18. 14.8.2.3.18 CFG_CH1STAT Registers
          19. 14.8.2.3.19 CFG_CH1CTRL Registers
          20. 14.8.2.3.20 CFG_TX1 Registers
          21. 14.8.2.3.21 CFG_RX1 Registers
          22. 14.8.2.3.22 CFG_CH2CONF Registers
          23. 14.8.2.3.23 CFG_CH2STAT Registers
          24. 14.8.2.3.24 CFG_CH2CTRL Registers
          25. 14.8.2.3.25 CFG_TX2 Registers
          26. 14.8.2.3.26 CFG_RX2 Registers
          27. 14.8.2.3.27 CFG_CH3CONF Registers
          28. 14.8.2.3.28 CFG_CH3STAT Registers
          29. 14.8.2.3.29 CFG_CH3CTRL Registers
          30. 14.8.2.3.30 CFG_TX3 Registers
          31. 14.8.2.3.31 CFG_RX3 Registers
          32. 14.8.2.3.32 CFG_XFERLEVEL Registers
          33. 14.8.2.3.33 CFG_DAFTX Registers
          34. 14.8.2.3.34 CFG_DAFRX Registers
          35. 14.8.2.3.35 Access Table
        4. 14.8.2.4 UART Registers
          1. 14.8.2.4.1  _UART_DLL Registers
          2. 14.8.2.4.2  _UART_RHR Registers
          3. 14.8.2.4.3  _UART_THR Registers
          4. 14.8.2.4.4  _UART_DLH Registers
          5. 14.8.2.4.5  _UART_IER_CIR Registers
          6. 14.8.2.4.6  _UART_IER_IRDA Registers
          7. 14.8.2.4.7  _UART_IER_UART Registers
          8. 14.8.2.4.8  _UART_EFR Registers
          9. 14.8.2.4.9  _UART_FCR Registers
          10. 14.8.2.4.10 _UART_IIR_CIR Registers
          11. 14.8.2.4.11 _UART_IIR_IRDA Registers
          12. 14.8.2.4.12 _UART_IIR_UART Registers
          13. 14.8.2.4.13 _UART_LCR Registers
          14. 14.8.2.4.14 _UART_MCR Registers
          15. 14.8.2.4.15 _UART_XON1_ADDR1 Registers
          16. 14.8.2.4.16 _UART_LSR_CIR Registers
          17. 14.8.2.4.17 _UART_LSR_IRDA Registers
          18. 14.8.2.4.18 _UART_LSR_UART Registers
          19. 14.8.2.4.19 _UART_XON2_ADDR2 Registers
          20. 14.8.2.4.20 _UART_MSR Registers
          21. 14.8.2.4.21 _UART_TCR Registers
          22. 14.8.2.4.22 _UART_XOFF1 Registers
          23. 14.8.2.4.23 _UART_SPR Registers
          24. 14.8.2.4.24 _UART_TLR Registers
          25. 14.8.2.4.25 _UART_XOFF2 Registers
          26. 14.8.2.4.26 _UART_MDR1 Registers
          27. 14.8.2.4.27 _UART_MDR2 Registers
          28. 14.8.2.4.28 _UART_SFLSR Registers
          29. 14.8.2.4.29 _UART_TXFLL Registers
          30. 14.8.2.4.30 _UART_RESUME Registers
          31. 14.8.2.4.31 _UART_TXFLH Registers
          32. 14.8.2.4.32 _UART_RXFLL Registers
          33. 14.8.2.4.33 _UART_SFREGL Registers
          34. 14.8.2.4.34 _UART_RXFLH Registers
          35. 14.8.2.4.35 _UART_SFREGH Registers
          36. 14.8.2.4.36 _UART_BLR Registers
          37. 14.8.2.4.37 _UART_UASR Registers
          38. 14.8.2.4.38 _UART_ACREG Registers
          39. 14.8.2.4.39 _UART_SCR Registers
          40. 14.8.2.4.40 _UART_SSR Registers
          41. 14.8.2.4.41 _UART_EBLR Registers
          42. 14.8.2.4.42 _UART_MVR Registers
          43. 14.8.2.4.43 _UART_SYSC Registers
          44. 14.8.2.4.44 _UART_SYSS Registers
          45. 14.8.2.4.45 _UART_WER Registers
          46. 14.8.2.4.46 _UART_CFPS Registers
          47. 14.8.2.4.47 _UART_RXFIFO_LVL Registers
          48. 14.8.2.4.48 _UART_TXFIFO_LVL Registers
          49. 14.8.2.4.49 _UART_IER2 Registers
          50. 14.8.2.4.50 _UART_ISR2 Registers
          51. 14.8.2.4.51 _UART_FREQ_SEL Registers
          52. 14.8.2.4.52 _UART_ABAUD_1ST_CHAR Registers
          53. 14.8.2.4.53 _UART_BAUD_2ND_CHAR Registers
          54. 14.8.2.4.54 _UART_MDR3 Registers
          55. 14.8.2.4.55 _UART_TX_DMA_THRESHOLD Registers
          56. 14.8.2.4.56 _UART_MDR4 Registers
          57. 14.8.2.4.57 _UART_EFR2 Registers
          58. 14.8.2.4.58 _UART_ECR Registers
          59. 14.8.2.4.59 _UART_TIMEGUARD Registers
          60. 14.8.2.4.60 _UART_TIMEOUTL Registers
          61. 14.8.2.4.61 _UART_TIMEOUTH Registers
          62. 14.8.2.4.62 _UART_SCCR Registers
          63. 14.8.2.4.63 _UART_ERHR Registers
          64. 14.8.2.4.64 _UART_ETHR Registers
          65. 14.8.2.4.65 _UART_MAR Registers
          66. 14.8.2.4.66 _UART_MMR Registers
          67. 14.8.2.4.67 _UART_MBR Registers
          68. 14.8.2.4.68 Access Table
      3. 14.8.3 High-speed Serial Interfaces Registers
        1. 14.8.3.1 CPSW Registers
          1. 14.8.3.1.1   ECC_ECC_ECC_REV Registers
          2. 14.8.3.1.2   ECC_ECC_ECC_VECTOR Registers
          3. 14.8.3.1.3   ECC_ECC_ECC_STAT Registers
          4. 14.8.3.1.4   ECC_ECC_ECC_RESERVED_SVBUS_N Registers
          5. 14.8.3.1.5   ECC_ECC_ECC_SEC_EOI_REG Registers
          6. 14.8.3.1.6   ECC_ECC_ECC_SEC_STATUS_REG0 Registers
          7. 14.8.3.1.7   ECC_ECC_ECC_SEC_ENABLE_SET_REG0 Registers
          8. 14.8.3.1.8   ECC_ECC_ECC_SEC_ENABLE_CLR_REG0 Registers
          9. 14.8.3.1.9   ECC_ECC_ECC_DED_EOI_REG Registers
          10. 14.8.3.1.10  ECC_ECC_ECC_DED_STATUS_REG0 Registers
          11. 14.8.3.1.11  ECC_ECC_ECC_DED_ENABLE_SET_REG0 Registers
          12. 14.8.3.1.12  ECC_ECC_ECC_DED_ENABLE_CLR_REG0 Registers
          13. 14.8.3.1.13  ECC_ECC_ECC_AGGR_ENABLE_SET Registers
          14. 14.8.3.1.14  ECC_ECC_ECC_AGGR_ENABLE_CLR Registers
          15. 14.8.3.1.15  ECC_ECC_ECC_AGGR_STATUS_SET Registers
          16. 14.8.3.1.16  ECC_ECC_ECC_AGGR_STATUS_CLR Registers
          17. 14.8.3.1.17  NUSS_CPSW_NUSS_IDVER_REG Registers
          18. 14.8.3.1.18  NUSS_SYNCE_COUNT_REG Registers
          19. 14.8.3.1.19  NUSS_SYNCE_MUX_REG Registers
          20. 14.8.3.1.20  NUSS_CONTROL_REG Registers
          21. 14.8.3.1.21  NUSS_SGMII_NON_FIBER_MODE_REG Registers
          22. 14.8.3.1.22  NUSS_SERDES_RESET_ISO_REG Registers
          23. 14.8.3.1.23  NUSS_SUBSSYSTEM_STATUS_REG Registers
          24. 14.8.3.1.24  NUSS_SUBSYSTEM_CONFIG_REG Registers
          25. 14.8.3.1.25  NUSS_RGMII1_STATUS_REG Registers
          26. 14.8.3.1.26  NUSS_RGMII2_STATUS_REG Registers
          27. 14.8.3.1.27  NUSS_CPSGMII_CPSGMII_SGMII_IDVER_REG_J_J Registers
          28. 14.8.3.1.28  NUSS_CPSGMII_CPSGMII_SOFT_RESET_REG_J_J Registers
          29. 14.8.3.1.29  NUSS_CPSGMII_CPSGMII_CONTROL_REG_J_J Registers
          30. 14.8.3.1.30  NUSS_CPSGMII_CPSGMII_STATUS_REG_J_J Registers
          31. 14.8.3.1.31  NUSS_CPSGMII_CPSGMII_MR_ADV_ABILITY_REG_J_J Registers
          32. 14.8.3.1.32  NUSS_CPSGMII_CPSGMII_MR_NP_TX_REG_J_J Registers
          33. 14.8.3.1.33  NUSS_CPSGMII_CPSGMII_MR_LP_ADV_ABILITY_REG_J_J Registers
          34. 14.8.3.1.34  NUSS_CPSGMII_CPSGMII_MR_LP_NP_RX_REG_J_J Registers
          35. 14.8.3.1.35  NUSS_CPSGMII_CPSGMII_DIAG_CLEAR_REG_J_J Registers
          36. 14.8.3.1.36  NUSS_CPSGMII_CPSGMII_DIAG_CONTROL_REG_J_J Registers
          37. 14.8.3.1.37  NUSS_CPSGMII_CPSGMII_DIAG_STATUS_REG_J_J Registers
          38. 14.8.3.1.38  NUSS_MDIO_MDIO_MDIO_VERSION_REG Registers
          39. 14.8.3.1.39  NUSS_MDIO_MDIO_CONTROL_REG Registers
          40. 14.8.3.1.40  NUSS_MDIO_MDIO_ALIVE_REG Registers
          41. 14.8.3.1.41  NUSS_MDIO_MDIO_LINK_REG Registers
          42. 14.8.3.1.42  NUSS_MDIO_MDIO_LINK_INT_RAW_REG Registers
          43. 14.8.3.1.43  NUSS_MDIO_MDIO_LINK_INT_MASKED_REG Registers
          44. 14.8.3.1.44  NUSS_MDIO_MDIO_LINK_INT_MASK_SET_REG Registers
          45. 14.8.3.1.45  NUSS_MDIO_MDIO_LINK_INT_MASK_CLEAR_REG Registers
          46. 14.8.3.1.46  NUSS_MDIO_MDIO_USER_INT_RAW_REG Registers
          47. 14.8.3.1.47  NUSS_MDIO_MDIO_USER_INT_MASKED_REG Registers
          48. 14.8.3.1.48  NUSS_MDIO_MDIO_USER_INT_MASK_SET_REG Registers
          49. 14.8.3.1.49  NUSS_MDIO_MDIO_USER_INT_MASK_CLEAR_REG Registers
          50. 14.8.3.1.50  NUSS_MDIO_MDIO_MANUAL_IF_REG Registers
          51. 14.8.3.1.51  NUSS_MDIO_MDIO_POLL_REG Registers
          52. 14.8.3.1.52  NUSS_MDIO_MDIO_POLL_EN_REG Registers
          53. 14.8.3.1.53  NUSS_MDIO_MDIO_CLAUS45_REG Registers
          54. 14.8.3.1.54  NUSS_MDIO_MDIO_USER_ADDR0_REG Registers
          55. 14.8.3.1.55  NUSS_MDIO_MDIO_USER_ADDR1_REG Registers
          56. 14.8.3.1.56  NUSS_INTD_INTD_REVISION Registers
          57. 14.8.3.1.57  NUSS_INTD_INTD_EOI_REG Registers
          58. 14.8.3.1.58  NUSS_INTD_INTD_INTR_VECTOR_REG Registers
          59. 14.8.3.1.59  NUSS_INTD_INTD_ENABLE_REG_OUT_PULSE_0 Registers
          60. 14.8.3.1.60  NUSS_INTD_INTD_ENABLE_CLR_REG_OUT_PULSE_0 Registers
          61. 14.8.3.1.61  NUSS_INTD_INTD_STATUS_REG_OUT_PULSE_0 Registers
          62. 14.8.3.1.62  NUSS_INTD_INTD_INTR_VECTOR_REG_OUT_PULSE Registers
          63. 14.8.3.1.63  NUSS_CPSW_NU_CPSW_NU_CPSW_ID_VER_REG Registers
          64. 14.8.3.1.64  NUSS_CPSW_NU_CPSW_NU_CONTROL_REG Registers
          65. 14.8.3.1.65  NUSS_CPSW_NU_CPSW_NU_EM_CONTROL_REG Registers
          66. 14.8.3.1.66  NUSS_CPSW_NU_CPSW_NU_STAT_PORT_EN_REG Registers
          67. 14.8.3.1.67  NUSS_CPSW_NU_CPSW_NU_PTYPE_REG Registers
          68. 14.8.3.1.68  NUSS_CPSW_NU_CPSW_NU_SOFT_IDLE_REG Registers
          69. 14.8.3.1.69  NUSS_CPSW_NU_CPSW_NU_THRU_RATE_REG Registers
          70. 14.8.3.1.70  NUSS_CPSW_NU_CPSW_NU_GAP_THRESH_REG Registers
          71. 14.8.3.1.71  NUSS_CPSW_NU_CPSW_NU_EEE_PRESCALE_REG Registers
          72. 14.8.3.1.72  NUSS_CPSW_NU_CPSW_NU_TX_G_OFLOW_THRESH_SET_REG Registers
          73. 14.8.3.1.73  NUSS_CPSW_NU_CPSW_NU_TX_G_OFLOW_THRESH_CLR_REG Registers
          74. 14.8.3.1.74  NUSS_CPSW_NU_CPSW_NU_TX_G_BUF_THRESH_SET_L_REG Registers
          75. 14.8.3.1.75  NUSS_CPSW_NU_CPSW_NU_TX_G_BUF_THRESH_SET_H_REG Registers
          76. 14.8.3.1.76  NUSS_CPSW_NU_CPSW_NU_TX_G_BUF_THRESH_CLR_L_REG Registers
          77. 14.8.3.1.77  NUSS_CPSW_NU_CPSW_NU_TX_G_BUF_THRESH_CLR_H_REG Registers
          78. 14.8.3.1.78  NUSS_CPSW_NU_CPSW_NU_VLAN_LTYPE_REG Registers
          79. 14.8.3.1.79  NUSS_CPSW_NU_CPSW_NU_EST_TS_DOMAIN_REG Registers
          80. 14.8.3.1.80  NUSS_CPSW_NU_CPSW_NU_CUT_THRESHOLD_REG Registers
          81. 14.8.3.1.81  NUSS_CPSW_NU_CPSW_NU_FREQUENCY_REG Registers
          82. 14.8.3.1.82  NUSS_CPSW_NU_CPSW_NU_IET_HOLD_CNT_LD_VAL_REG Registers
          83. 14.8.3.1.83  NUSS_CPSW_NU_CPSW_NU_TX_PRI0_MAXLEN_REG Registers
          84. 14.8.3.1.84  NUSS_CPSW_NU_CPSW_NU_TX_PRI1_MAXLEN_REG Registers
          85. 14.8.3.1.85  NUSS_CPSW_NU_CPSW_NU_TX_PRI2_MAXLEN_REG Registers
          86. 14.8.3.1.86  NUSS_CPSW_NU_CPSW_NU_TX_PRI3_MAXLEN_REG Registers
          87. 14.8.3.1.87  NUSS_CPSW_NU_CPSW_NU_TX_PRI4_MAXLEN_REG Registers
          88. 14.8.3.1.88  NUSS_CPSW_NU_CPSW_NU_TX_PRI5_MAXLEN_REG Registers
          89. 14.8.3.1.89  NUSS_CPSW_NU_CPSW_NU_TX_PRI6_MAXLEN_REG Registers
          90. 14.8.3.1.90  NUSS_CPSW_NU_CPSW_NU_TX_PRI7_MAXLEN_REG Registers
          91. 14.8.3.1.91  NUSS_MDIO_MDIO_USER_GROUP_USER_ACCESS_REG_J Registers
          92. 14.8.3.1.92  NUSS_MDIO_MDIO_USER_GROUP_USER_PHY_SEL_REG_J Registers
          93. 14.8.3.1.93  NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_CONTROL_REG Registers
          94. 14.8.3.1.94  NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_FLOW_ID_OFFSET_REG Registers
          95. 14.8.3.1.95  NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_BLK_CNT_REG Registers
          96. 14.8.3.1.96  NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_PORT_VLAN_REG Registers
          97. 14.8.3.1.97  NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_PRI_MAP_REG Registers
          98. 14.8.3.1.98  NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_PRI_CTL_REG Registers
          99. 14.8.3.1.99  NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_RX_PRI_MAP_REG Registers
          100. 14.8.3.1.100 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_RX_MAXLEN_REG Registers
          101. 14.8.3.1.101 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_BLKS_PRI_REG Registers
          102. 14.8.3.1.102 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_IDLE2LPI_REG Registers
          103. 14.8.3.1.103 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_LPI2WAKE_REG Registers
          104. 14.8.3.1.104 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_EEE_STATUS_REG Registers
          105. 14.8.3.1.105 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_FIFO_STATUS_REG Registers
          106. 14.8.3.1.106 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_RX_DSCP_MAP_REG_N Registers
          107. 14.8.3.1.107 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_PRI_CIR_REG_N Registers
          108. 14.8.3.1.108 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_PRI_EIR_REG_N Registers
          109. 14.8.3.1.109 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_D_THRESH_SET_L_REG Registers
          110. 14.8.3.1.110 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_D_THRESH_SET_H_REG Registers
          111. 14.8.3.1.111 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_D_THRESH_CLR_L_REG Registers
          112. 14.8.3.1.112 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_D_THRESH_CLR_H_REG Registers
          113. 14.8.3.1.113 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_G_BUF_THRESH_SET_L_REG Registers
          114. 14.8.3.1.114 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_G_BUF_THRESH_SET_H_REG Registers
          115. 14.8.3.1.115 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_G_BUF_THRESH_CLR_L_REG Registers
          116. 14.8.3.1.116 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_TX_G_BUF_THRESH_CLR_H_REG Registers
          117. 14.8.3.1.117 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_SRC_ID_A_REG Registers
          118. 14.8.3.1.118 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_SRC_ID_B_REG Registers
          119. 14.8.3.1.119 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_CPPI_P0_HOST_BLKS_PRI_REG Registers
          120. 14.8.3.1.120 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_RESERVED_REG Registers
          121. 14.8.3.1.121 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_CONTROL_REG Registers
          122. 14.8.3.1.122 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAX_BLKS_REG Registers
          123. 14.8.3.1.123 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_BLK_CNT_REG Registers
          124. 14.8.3.1.124 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_PORT_VLAN_REG Registers
          125. 14.8.3.1.125 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_PRI_MAP_REG Registers
          126. 14.8.3.1.126 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_PRI_CTL_REG Registers
          127. 14.8.3.1.127 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_RX_PRI_MAP_REG Registers
          128. 14.8.3.1.128 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_RX_MAXLEN_REG Registers
          129. 14.8.3.1.129 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_BLKS_PRI_REG Registers
          130. 14.8.3.1.130 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_IDLE2LPI_REG Registers
          131. 14.8.3.1.131 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_LPI2WAKE_REG Registers
          132. 14.8.3.1.132 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_EEE_STATUS_REG Registers
          133. 14.8.3.1.133 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_IET_CONTROL_REG Registers
          134. 14.8.3.1.134 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_IET_STATUS_REG Registers
          135. 14.8.3.1.135 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_IET_VERIFY_REG Registers
          136. 14.8.3.1.136 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_FIFO_STATUS_REG Registers
          137. 14.8.3.1.137 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_EST_CONTROL_REG Registers
          138. 14.8.3.1.138 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_RX_DSCP_MAP_REG_N Registers
          139. 14.8.3.1.139 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_PRI_CIR_REG_N Registers
          140. 14.8.3.1.140 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_PRI_EIR_REG_N Registers
          141. 14.8.3.1.141 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_D_THRESH_SET_L_REG Registers
          142. 14.8.3.1.142 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_D_THRESH_SET_H_REG Registers
          143. 14.8.3.1.143 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_D_THRESH_CLR_L_REG Registers
          144. 14.8.3.1.144 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_D_THRESH_CLR_H_REG Registers
          145. 14.8.3.1.145 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_G_BUF_THRESH_SET_L_REG Registers
          146. 14.8.3.1.146 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_G_BUF_THRESH_SET_H_REG Registers
          147. 14.8.3.1.147 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_G_BUF_THRESH_CLR_L_REG Registers
          148. 14.8.3.1.148 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_G_BUF_THRESH_CLR_H_REG Registers
          149. 14.8.3.1.149 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_D_OFLOW_ADDVAL_L_REG Registers
          150. 14.8.3.1.150 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TX_D_OFLOW_ADDVAL_H_REG Registers
          151. 14.8.3.1.151 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_SA_L_REG Registers
          152. 14.8.3.1.152 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_SA_H_REG Registers
          153. 14.8.3.1.153 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TS_CTL_REG Registers
          154. 14.8.3.1.154 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TS_SEQ_LTYPE_REG Registers
          155. 14.8.3.1.155 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TS_VLAN_LTYPE_REG Registers
          156. 14.8.3.1.156 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TS_CTL_LTYPE2_REG Registers
          157. 14.8.3.1.157 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_TS_CTL2_REG Registers
          158. 14.8.3.1.158 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_CONTROL_REG Registers
          159. 14.8.3.1.159 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_STATUS_REG Registers
          160. 14.8.3.1.160 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_SOFT_RESET_REG Registers
          161. 14.8.3.1.161 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_BOFFTEST_REG Registers
          162. 14.8.3.1.162 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_RX_PAUSETIMER_REG Registers
          163. 14.8.3.1.163 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_RXN_PAUSETIMER_REG_N Registers
          164. 14.8.3.1.164 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_TX_PAUSETIMER_REG Registers
          165. 14.8.3.1.165 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_TXN_PAUSETIMER_REG_N Registers
          166. 14.8.3.1.166 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_EMCONTROL_REG Registers
          167. 14.8.3.1.167 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_TX_GAP_REG Registers
          168. 14.8.3.1.168 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_MAC_PORT_CONFIG Registers
          169. 14.8.3.1.169 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_INTERVLAN_OPX_POINTER_REG Registers
          170. 14.8.3.1.170 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_INTERVLAN_OPX_A_REG Registers
          171. 14.8.3.1.171 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_INTERVLAN_OPX_B_REG Registers
          172. 14.8.3.1.172 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_INTERVLAN_OPX_C_REG Registers
          173. 14.8.3.1.173 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_INTERVLAN_OPX_D_REG Registers
          174. 14.8.3.1.174 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_CUT_THRU_REG Registers
          175. 14.8.3.1.175 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_0_PN_PORT_SPEED_REG Registers
          176. 14.8.3.1.176 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_RESERVED_REG Registers
          177. 14.8.3.1.177 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_CONTROL_REG Registers
          178. 14.8.3.1.178 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAX_BLKS_REG Registers
          179. 14.8.3.1.179 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_BLK_CNT_REG Registers
          180. 14.8.3.1.180 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_PORT_VLAN_REG Registers
          181. 14.8.3.1.181 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_PRI_MAP_REG Registers
          182. 14.8.3.1.182 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_PRI_CTL_REG Registers
          183. 14.8.3.1.183 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_RX_PRI_MAP_REG Registers
          184. 14.8.3.1.184 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_RX_MAXLEN_REG Registers
          185. 14.8.3.1.185 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_BLKS_PRI_REG Registers
          186. 14.8.3.1.186 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_IDLE2LPI_REG Registers
          187. 14.8.3.1.187 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_LPI2WAKE_REG Registers
          188. 14.8.3.1.188 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_EEE_STATUS_REG Registers
          189. 14.8.3.1.189 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_IET_CONTROL_REG Registers
          190. 14.8.3.1.190 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_IET_STATUS_REG Registers
          191. 14.8.3.1.191 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_IET_VERIFY_REG Registers
          192. 14.8.3.1.192 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_FIFO_STATUS_REG Registers
          193. 14.8.3.1.193 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_EST_CONTROL_REG Registers
          194. 14.8.3.1.194 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_RX_DSCP_MAP_REG_N Registers
          195. 14.8.3.1.195 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_PRI_CIR_REG_N Registers
          196. 14.8.3.1.196 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_PRI_EIR_REG_N Registers
          197. 14.8.3.1.197 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_D_THRESH_SET_L_REG Registers
          198. 14.8.3.1.198 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_D_THRESH_SET_H_REG Registers
          199. 14.8.3.1.199 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_D_THRESH_CLR_L_REG Registers
          200. 14.8.3.1.200 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_D_THRESH_CLR_H_REG Registers
          201. 14.8.3.1.201 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_G_BUF_THRESH_SET_L_REG Registers
          202. 14.8.3.1.202 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_G_BUF_THRESH_SET_H_REG Registers
          203. 14.8.3.1.203 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_G_BUF_THRESH_CLR_L_REG Registers
          204. 14.8.3.1.204 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_G_BUF_THRESH_CLR_H_REG Registers
          205. 14.8.3.1.205 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_D_OFLOW_ADDVAL_L_REG Registers
          206. 14.8.3.1.206 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TX_D_OFLOW_ADDVAL_H_REG Registers
          207. 14.8.3.1.207 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_SA_L_REG Registers
          208. 14.8.3.1.208 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_SA_H_REG Registers
          209. 14.8.3.1.209 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TS_CTL_REG Registers
          210. 14.8.3.1.210 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TS_SEQ_LTYPE_REG Registers
          211. 14.8.3.1.211 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TS_VLAN_LTYPE_REG Registers
          212. 14.8.3.1.212 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TS_CTL_LTYPE2_REG Registers
          213. 14.8.3.1.213 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_TS_CTL2_REG Registers
          214. 14.8.3.1.214 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_CONTROL_REG Registers
          215. 14.8.3.1.215 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_STATUS_REG Registers
          216. 14.8.3.1.216 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_SOFT_RESET_REG Registers
          217. 14.8.3.1.217 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_BOFFTEST_REG Registers
          218. 14.8.3.1.218 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_RX_PAUSETIMER_REG Registers
          219. 14.8.3.1.219 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_RXN_PAUSETIMER_REG_N Registers
          220. 14.8.3.1.220 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_TX_PAUSETIMER_REG Registers
          221. 14.8.3.1.221 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_TXN_PAUSETIMER_REG_N Registers
          222. 14.8.3.1.222 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_EMCONTROL_REG Registers
          223. 14.8.3.1.223 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_TX_GAP_REG Registers
          224. 14.8.3.1.224 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_MAC_PORT_CONFIG Registers
          225. 14.8.3.1.225 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_INTERVLAN_OPX_POINTER_REG Registers
          226. 14.8.3.1.226 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_INTERVLAN_OPX_A_REG Registers
          227. 14.8.3.1.227 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_INTERVLAN_OPX_B_REG Registers
          228. 14.8.3.1.228 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_INTERVLAN_OPX_C_REG Registers
          229. 14.8.3.1.229 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_INTERVLAN_OPX_D_REG Registers
          230. 14.8.3.1.230 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_CUT_THRU_REG Registers
          231. 14.8.3.1.231 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_ETH_MAC_1_PN_PORT_SPEED_REG Registers
          232. 14.8.3.1.232 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_EST_FETCH_LOC_N Registers
          233. 14.8.3.1.233 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXGOODFRAMES_J Registers
          234. 14.8.3.1.234 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXBROADCASTFRAMES_J Registers
          235. 14.8.3.1.235 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXMULTICASTFRAMES_J Registers
          236. 14.8.3.1.236 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXPAUSEFRAMES_J Registers
          237. 14.8.3.1.237 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXCRCERRORS_J Registers
          238. 14.8.3.1.238 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXALIGNCODEERRORS_J Registers
          239. 14.8.3.1.239 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXOVERSIZEDFRAMES_J Registers
          240. 14.8.3.1.240 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXJABBERFRAMES_J Registers
          241. 14.8.3.1.241 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXUNDERSIZEDFRAMES_J Registers
          242. 14.8.3.1.242 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXFRAGMENTS_J Registers
          243. 14.8.3.1.243 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_DROP_J Registers
          244. 14.8.3.1.244 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_OVERRUN_DROP_J Registers
          245. 14.8.3.1.245 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXOCTETS_J Registers
          246. 14.8.3.1.246 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXGOODFRAMES_J Registers
          247. 14.8.3.1.247 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXBROADCASTFRAMES_J Registers
          248. 14.8.3.1.248 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXMULTICASTFRAMES_J Registers
          249. 14.8.3.1.249 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXPAUSEFRAMES_J Registers
          250. 14.8.3.1.250 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXDEFERREDFRAMES_J Registers
          251. 14.8.3.1.251 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXCOLLISIONFRAMES_J Registers
          252. 14.8.3.1.252 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXSINGLECOLLFRAMES_J Registers
          253. 14.8.3.1.253 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXMULTCOLLFRAMES_J Registers
          254. 14.8.3.1.254 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXEXCESSIVECOLLISIONS_J Registers
          255. 14.8.3.1.255 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXLATECOLLISIONS_J Registers
          256. 14.8.3.1.256 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RXIPGERROR_J Registers
          257. 14.8.3.1.257 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXCARRIERSENSEERRORS_J Registers
          258. 14.8.3.1.258 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TXOCTETS_J Registers
          259. 14.8.3.1.259 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_OCTETFRAMES64_J Registers
          260. 14.8.3.1.260 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_OCTETFRAMES65T127_J Registers
          261. 14.8.3.1.261 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_OCTETFRAMES128T255_J Registers
          262. 14.8.3.1.262 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_OCTETFRAMES256T511_J Registers
          263. 14.8.3.1.263 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_OCTETFRAMES512T1023_J Registers
          264. 14.8.3.1.264 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_OCTETFRAMES1024TUP_J Registers
          265. 14.8.3.1.265 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_NETOCTETS_J Registers
          266. 14.8.3.1.266 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RX_BOTTOM_OF_FIFO_DROP_J Registers
          267. 14.8.3.1.267 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_PORTMASK_DROP_J Registers
          268. 14.8.3.1.268 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_RX_TOP_OF_FIFO_DROP_J Registers
          269. 14.8.3.1.269 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_RATE_LIMIT_DROP_J Registers
          270. 14.8.3.1.270 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_VID_INGRESS_DROP_J Registers
          271. 14.8.3.1.271 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_DA_EQ_SA_DROP_J Registers
          272. 14.8.3.1.272 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_BLOCK_DROP_J Registers
          273. 14.8.3.1.273 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_SECURE_DROP_J Registers
          274. 14.8.3.1.274 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_AUTH_DROP_J Registers
          275. 14.8.3.1.275 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_UNKN_UNI_J Registers
          276. 14.8.3.1.276 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_UNKN_UNI_BCNT_J Registers
          277. 14.8.3.1.277 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_UNKN_MLT_J Registers
          278. 14.8.3.1.278 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_UNKN_MLT_BCNT_J Registers
          279. 14.8.3.1.279 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_UNKN_BRD_J Registers
          280. 14.8.3.1.280 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_UNKN_BRD_BCNT_J Registers
          281. 14.8.3.1.281 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_POL_MATCH_J Registers
          282. 14.8.3.1.282 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_POL_MATCH_RED_J Registers
          283. 14.8.3.1.283 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_POL_MATCH_YELLOW_J Registers
          284. 14.8.3.1.284 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_MULT_SA_DROP_J Registers
          285. 14.8.3.1.285 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_DUAL_VLAN_DROP_J Registers
          286. 14.8.3.1.286 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_LEN_ERROR_DROP_J Registers
          287. 14.8.3.1.287 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_IP_NEXT_HDR_DROP_J Registers
          288. 14.8.3.1.288 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ALE_IPV4_FRAG_DROP_J Registers
          289. 14.8.3.1.289 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_IET_RX_ASSEMBLY_ERROR_REG_J Registers
          290. 14.8.3.1.290 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_IET_RX_ASSEMBLY_OK_REG_J Registers
          291. 14.8.3.1.291 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_IET_RX_SMD_ERROR_REG_J Registers
          292. 14.8.3.1.292 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_IET_RX_FRAG_REG_J Registers
          293. 14.8.3.1.293 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_IET_TX_HOLD_REG_J Registers
          294. 14.8.3.1.294 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_IET_TX_FRAG_REG_J Registers
          295. 14.8.3.1.295 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_TX_MEMORY_PROTECT_ERROR_J Registers
          296. 14.8.3.1.296 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ENET_PN_TX_PRI_REG_J_N Registers
          297. 14.8.3.1.297 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ENET_PN_TX_PRI_BCNT_REG_J_N Registers
          298. 14.8.3.1.298 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ENET_PN_TX_PRI_DROP_REG_J_N Registers
          299. 14.8.3.1.299 NUSS_CPSW_NU_CPSW_NU_CPSW_NU_STAT_ENET_PN_TX_PRI_DROP_BCNT_REG_J_N Registers
          300. 14.8.3.1.300 NUSS_CPSW_NU_CPSW_NU_CPTS_IDVER_REG Registers
          301. 14.8.3.1.301 NUSS_CPSW_NU_CPSW_NU_CPTS_CONTROL_REG Registers
          302. 14.8.3.1.302 NUSS_CPSW_NU_CPSW_NU_CPTS_RFTCLK_SEL_REG Registers
          303. 14.8.3.1.303 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_PUSH_REG Registers
          304. 14.8.3.1.304 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_LOAD_VAL_REG Registers
          305. 14.8.3.1.305 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_LOAD_EN_REG Registers
          306. 14.8.3.1.306 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_COMP_VAL_REG Registers
          307. 14.8.3.1.307 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_COMP_LEN_REG Registers
          308. 14.8.3.1.308 NUSS_CPSW_NU_CPSW_NU_CPTS_INTSTAT_RAW_REG Registers
          309. 14.8.3.1.309 NUSS_CPSW_NU_CPSW_NU_CPTS_INTSTAT_MASKED_REG Registers
          310. 14.8.3.1.310 NUSS_CPSW_NU_CPSW_NU_CPTS_INT_ENABLE_REG Registers
          311. 14.8.3.1.311 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_COMP_NUDGE_REG Registers
          312. 14.8.3.1.312 NUSS_CPSW_NU_CPSW_NU_CPTS_EVENT_POP_REG Registers
          313. 14.8.3.1.313 NUSS_CPSW_NU_CPSW_NU_CPTS_EVENT_0_REG Registers
          314. 14.8.3.1.314 NUSS_CPSW_NU_CPSW_NU_CPTS_EVENT_1_REG Registers
          315. 14.8.3.1.315 NUSS_CPSW_NU_CPSW_NU_CPTS_EVENT_2_REG Registers
          316. 14.8.3.1.316 NUSS_CPSW_NU_CPSW_NU_CPTS_EVENT_3_REG Registers
          317. 14.8.3.1.317 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_LOAD_HIGH_VAL_REG Registers
          318. 14.8.3.1.318 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_COMP_HIGH_VAL_REG Registers
          319. 14.8.3.1.319 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ADD_VAL_REG Registers
          320. 14.8.3.1.320 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_PPM_LOW_VAL_REG Registers
          321. 14.8.3.1.321 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_PPM_HIGH_VAL_REG Registers
          322. 14.8.3.1.322 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_NUDGE_VAL_REG Registers
          323. 14.8.3.1.323 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_CONFIG Registers
          324. 14.8.3.1.324 NUSS_CPSW_NU_CPSW_NU_ALE_MOD_VER Registers
          325. 14.8.3.1.325 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_STATUS Registers
          326. 14.8.3.1.326 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_CONTROL Registers
          327. 14.8.3.1.327 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_CTRL2 Registers
          328. 14.8.3.1.328 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_PRESCALE Registers
          329. 14.8.3.1.329 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_AGING_CTRL Registers
          330. 14.8.3.1.330 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_NXT_HDR Registers
          331. 14.8.3.1.331 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_TBLCTL Registers
          332. 14.8.3.1.332 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_TBLW2 Registers
          333. 14.8.3.1.333 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_TBLW1 Registers
          334. 14.8.3.1.334 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_TBLW0 Registers
          335. 14.8.3.1.335 NUSS_CPSW_NU_CPSW_NU_ALE_I0_ALE_PORTCTL0_N Registers
          336. 14.8.3.1.336 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_UVLAN_MEMBER Registers
          337. 14.8.3.1.337 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_UVLAN_URCAST Registers
          338. 14.8.3.1.338 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_UVLAN_RMCAST Registers
          339. 14.8.3.1.339 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_UVLAN_UNTAG Registers
          340. 14.8.3.1.340 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_FAST_LUT Registers
          341. 14.8.3.1.341 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_STAT_DIAG Registers
          342. 14.8.3.1.342 NUSS_CPSW_NU_CPSW_NU_ALE_ALE_OAM_LB_CTRL Registers
          343. 14.8.3.1.343 NUSS_CPSW_NU_CPSW_NU_ALE_EGRESSOP Registers
          344. 14.8.3.1.344 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECFG0 Registers
          345. 14.8.3.1.345 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECFG1 Registers
          346. 14.8.3.1.346 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECFG2 Registers
          347. 14.8.3.1.347 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECFG3 Registers
          348. 14.8.3.1.348 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECFG4 Registers
          349. 14.8.3.1.349 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECFG6 Registers
          350. 14.8.3.1.350 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECFG7 Registers
          351. 14.8.3.1.351 NUSS_CPSW_NU_CPSW_NU_ALE_POLICETBLCTL Registers
          352. 14.8.3.1.352 NUSS_CPSW_NU_CPSW_NU_ALE_POLICECONTROL Registers
          353. 14.8.3.1.353 NUSS_CPSW_NU_CPSW_NU_ALE_POLICETESTCTL Registers
          354. 14.8.3.1.354 NUSS_CPSW_NU_CPSW_NU_ALE_POLICEHSTAT Registers
          355. 14.8.3.1.355 NUSS_CPSW_NU_CPSW_NU_ALE_THREADMAPDEF Registers
          356. 14.8.3.1.356 NUSS_CPSW_NU_CPSW_NU_ALE_THREADMAPCTL Registers
          357. 14.8.3.1.357 NUSS_CPSW_NU_CPSW_NU_ALE_THREADMAPVAL Registers
          358. 14.8.3.1.358 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_GENF_COMP_LOW_REG_J Registers
          359. 14.8.3.1.359 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_GENF_COMP_HIGH_REG_J Registers
          360. 14.8.3.1.360 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_GENF_CONTROL_REG_J Registers
          361. 14.8.3.1.361 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_GENF_LENGTH_REG_J Registers
          362. 14.8.3.1.362 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_GENF_PPM_LOW_REG_J Registers
          363. 14.8.3.1.363 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_GENF_PPM_HIGH_REG_J Registers
          364. 14.8.3.1.364 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_GENF_NUDGE_REG_J Registers
          365. 14.8.3.1.365 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ESTF_COMP_LOW_REG_J Registers
          366. 14.8.3.1.366 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ESTF_COMP_HIGH_REG_J Registers
          367. 14.8.3.1.367 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ESTF_CONTROL_REG_J Registers
          368. 14.8.3.1.368 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ESTF_LENGTH_REG_J Registers
          369. 14.8.3.1.369 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ESTF_PPM_LOW_REG_J Registers
          370. 14.8.3.1.370 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ESTF_PPM_HIGH_REG_J Registers
          371. 14.8.3.1.371 NUSS_CPSW_NU_CPSW_NU_CPTS_TS_ESTF_NUDGE_REG_J Registers
          372. 14.8.3.1.372 Access Table
        2. 14.8.3.2 USB Registers
          1. 14.8.3.2.1   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_TRACE_CTRL Registers
          2. 14.8.3.2.2   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB0_W0_J_J Registers
          3. 14.8.3.2.3   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB0_W1_J_J Registers
          4. 14.8.3.2.4   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB0_W2_J_J Registers
          5. 14.8.3.2.5   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB0_W3_J_J Registers
          6. 14.8.3.2.6   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB1_W0_J_J Registers
          7. 14.8.3.2.7   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB1_W1_J_J Registers
          8. 14.8.3.2.8   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB1_W2_J_J Registers
          9. 14.8.3.2.9   DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB1_W3_J_J Registers
          10. 14.8.3.2.10  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB2_W0_J_J Registers
          11. 14.8.3.2.11  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB2_W1_J_J Registers
          12. 14.8.3.2.12  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB2_W2_J_J Registers
          13. 14.8.3.2.13  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB2_W3_J_J Registers
          14. 14.8.3.2.14  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB3_W0_J_J Registers
          15. 14.8.3.2.15  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB3_W1_J_J Registers
          16. 14.8.3.2.16  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB3_W2_J_J Registers
          17. 14.8.3.2.17  DEBUG_TRACE_MMR_TRACE_VBUSP_USB2SS_DEBUG_TRACE_EP_EP_TRB3_W3_J_J Registers
          18. 14.8.3.2.18  MMR_MMRVBP_USB2SS_CFG_REVISION Registers
          19. 14.8.3.2.19  MMR_MMRVBP_USB2SS_CFG_OVERCURRENT_CONTROL Registers
          20. 14.8.3.2.20  MMR_MMRVBP_USB2SS_CFG_PHY_CONFIG Registers
          21. 14.8.3.2.21  MMR_MMRVBP_USB2SS_CFG_PHY_TEST Registers
          22. 14.8.3.2.22  MMR_MMRVBP_USB2SS_CFG_CORE_STAT Registers
          23. 14.8.3.2.23  MMR_MMRVBP_USB2SS_CFG_HOST_VBUS_CTRL Registers
          24. 14.8.3.2.24  MMR_MMRVBP_USB2SS_CFG_MODE_CONTROL Registers
          25. 14.8.3.2.25  MMR_MMRVBP_USB2SS_CFG_WAKEUP_CONFIG Registers
          26. 14.8.3.2.26  MMR_MMRVBP_USB2SS_CFG_WAKEUP_STAT Registers
          27. 14.8.3.2.27  MMR_MMRVBP_USB2SS_CFG_OVERRIDE_CONFIG Registers
          28. 14.8.3.2.28  MMR_MMRVBP_USB2SS_CFG_IRQ_MISC_STATUS_RAW Registers
          29. 14.8.3.2.29  MMR_MMRVBP_USB2SS_CFG_IRQ_MISC_STATUS Registers
          30. 14.8.3.2.30  MMR_MMRVBP_USB2SS_CFG_IRQ_MISC_ENABLE_SET Registers
          31. 14.8.3.2.31  MMR_MMRVBP_USB2SS_CFG_IRQ_MISC_ENABLE_CLR Registers
          32. 14.8.3.2.32  MMR_MMRVBP_USB2SS_CFG_IRQ_MISC_EOI Registers
          33. 14.8.3.2.33  MMR_MMRVBP_USB2SS_CFG_INTR_TEST Registers
          34. 14.8.3.2.34  MMR_MMRVBP_USB2SS_CFG_VBUS_FILTER Registers
          35. 14.8.3.2.35  MMR_MMRVBP_USB2SS_CFG_VBUS_STAT Registers
          36. 14.8.3.2.36  MMR_MMRVBP_USB2SS_CFG_DEBUG_CFG Registers
          37. 14.8.3.2.37  MMR_MMRVBP_USB2SS_CFG_DEBUG_DATA Registers
          38. 14.8.3.2.38  MMR_MMRVBP_USB2SS_CFG_HOST_HUB_CTRL Registers
          39. 14.8.3.2.39  PHY2_AFE_TX_REG0 Registers
          40. 14.8.3.2.40  PHY2_AFE_TX_REG1 Registers
          41. 14.8.3.2.41  PHY2_AFE_TX_REG2 Registers
          42. 14.8.3.2.42  PHY2_AFE_TX_REG3 Registers
          43. 14.8.3.2.43  PHY2_AFE_TX_REG4 Registers
          44. 14.8.3.2.44  PHY2_AFE_TX_REG5 Registers
          45. 14.8.3.2.45  PHY2_AFE_TX_REG6 Registers
          46. 14.8.3.2.46  PHY2_AFE_TX_REG7 Registers
          47. 14.8.3.2.47  PHY2_AFE_TX_REG8 Registers
          48. 14.8.3.2.48  PHY2_AFE_TX_REG9 Registers
          49. 14.8.3.2.49  PHY2_AFE_TX_REG10 Registers
          50. 14.8.3.2.50  PHY2_AFE_TX_REG11 Registers
          51. 14.8.3.2.51  PHY2_AFE_TX_REG12 Registers
          52. 14.8.3.2.52  PHY2_AFE_RX_REG0 Registers
          53. 14.8.3.2.53  PHY2_AFE_RX_REG1 Registers
          54. 14.8.3.2.54  PHY2_AFE_RX_REG2 Registers
          55. 14.8.3.2.55  PHY2_AFE_RX_REG3 Registers
          56. 14.8.3.2.56  PHY2_AFE_RX_REG4 Registers
          57. 14.8.3.2.57  PHY2_AFE_RX_REG5 Registers
          58. 14.8.3.2.58  PHY2_AFE_RX_REG6 Registers
          59. 14.8.3.2.59  PHY2_AFE_TX_REG13 Registers
          60. 14.8.3.2.60  PHY2_AFE_TX_REG14 Registers
          61. 14.8.3.2.61  PHY2_AFE_RX_REG7 Registers
          62. 14.8.3.2.62  PHY2_AFE_RX_REG8 Registers
          63. 14.8.3.2.63  PHY2_AFE_UNUSED_REG0 Registers
          64. 14.8.3.2.64  PHY2_AFE_UNUSED_REG1 Registers
          65. 14.8.3.2.65  PHY2_AFE_BG_REG0 Registers
          66. 14.8.3.2.66  PHY2_AFE_BG_REG1 Registers
          67. 14.8.3.2.67  PHY2_AFE_BG_REG2 Registers
          68. 14.8.3.2.68  PHY2_AFE_BG_REG3 Registers
          69. 14.8.3.2.69  PHY2_AFE_CALIB_REG0 Registers
          70. 14.8.3.2.70  PHY2_AFE_BC_REG0 Registers
          71. 14.8.3.2.71  PHY2_AFE_BC_REG1 Registers
          72. 14.8.3.2.72  PHY2_AFE_BC_REG2 Registers
          73. 14.8.3.2.73  PHY2_AFE_BC_REG3 Registers
          74. 14.8.3.2.74  PHY2_AFE_BC_REG4 Registers
          75. 14.8.3.2.75  PHY2_AFE_BC_REG5 Registers
          76. 14.8.3.2.76  PHY2_AFE_BC_REG6 Registers
          77. 14.8.3.2.77  PHY2_AFE_PLL_REG0 Registers
          78. 14.8.3.2.78  PHY2_AFE_PLL_REG1 Registers
          79. 14.8.3.2.79  PHY2_AFE_PLL_REG2 Registers
          80. 14.8.3.2.80  PHY2_AFE_PLL_REG3 Registers
          81. 14.8.3.2.81  PHY2_AFE_PLL_REG4 Registers
          82. 14.8.3.2.82  PHY2_AFE_PLL_REG5 Registers
          83. 14.8.3.2.83  PHY2_AFE_BG_REG4 Registers
          84. 14.8.3.2.84  PHY2_AFE_CALIB_REG1 Registers
          85. 14.8.3.2.85  PHY2_AFE_BC_REG7 Registers
          86. 14.8.3.2.86  PHY2_AFE_PLL_REG6 Registers
          87. 14.8.3.2.87  PHY2_AFE_UNUSED_REG2 Registers
          88. 14.8.3.2.88  PHY2_AFE_UNUSED_REG3 Registers
          89. 14.8.3.2.89  PHY2_PLL_REG0 Registers
          90. 14.8.3.2.90  PHY2_PLL_REG1 Registers
          91. 14.8.3.2.91  PHY2_PLL_REG2 Registers
          92. 14.8.3.2.92  PHY2_PLL_REG3 Registers
          93. 14.8.3.2.93  PHY2_PLL_REG4 Registers
          94. 14.8.3.2.94  PHY2_PLL_REG5 Registers
          95. 14.8.3.2.95  PHY2_PLL_REG6 Registers
          96. 14.8.3.2.96  PHY2_PLL_REG7 Registers
          97. 14.8.3.2.97  PHY2_PLL_REG8 Registers
          98. 14.8.3.2.98  PHY2_PLL_REG9 Registers
          99. 14.8.3.2.99  PHY2_PLL_REG10 Registers
          100. 14.8.3.2.100 PHY2_PLL_REG11 Registers
          101. 14.8.3.2.101 PHY2_PLL_REG12 Registers
          102. 14.8.3.2.102 PHY2_PLL_REG13 Registers
          103. 14.8.3.2.103 PHY2_PLL_REG14 Registers
          104. 14.8.3.2.104 PHY2_PLL_UNUSED_REG0 Registers
          105. 14.8.3.2.105 PHY2_PLL_UNUSED_REG1 Registers
          106. 14.8.3.2.106 PHY2_PLL_REG15 Registers
          107. 14.8.3.2.107 PHY2_PLL_REG16 Registers
          108. 14.8.3.2.108 PHY2_PLL_UNUSED_REG2 Registers
          109. 14.8.3.2.109 PHY2_CALIB_REG0 Registers
          110. 14.8.3.2.110 PHY2_CALIB_REG1 Registers
          111. 14.8.3.2.111 PHY2_BC_REG0 Registers
          112. 14.8.3.2.112 PHY2_BC_REG1 Registers
          113. 14.8.3.2.113 PHY2_BC_REG2 Registers
          114. 14.8.3.2.114 PHY2_BC_REG3 Registers
          115. 14.8.3.2.115 PHY2_BC_REG4 Registers
          116. 14.8.3.2.116 PHY2_BC_REG5 Registers
          117. 14.8.3.2.117 PHY2_BC_REG6 Registers
          118. 14.8.3.2.118 PHY2_BC_REG7 Registers
          119. 14.8.3.2.119 PHY2_TED_REG0 Registers
          120. 14.8.3.2.120 PHY2_TED_REG1 Registers
          121. 14.8.3.2.121 PHY2_TED_REG2 Registers
          122. 14.8.3.2.122 PHY2_CALIB_REG2 Registers
          123. 14.8.3.2.123 PHY2_CALIB_REG3 Registers
          124. 14.8.3.2.124 PHY2_BC_REG8 Registers
          125. 14.8.3.2.125 PHY2_BC_REG9 Registers
          126. 14.8.3.2.126 PHY2_BC_REG10 Registers
          127. 14.8.3.2.127 PHY2_BC_REG11 Registers
          128. 14.8.3.2.128 PHY2_BC_REG12 Registers
          129. 14.8.3.2.129 PHY2_TED_REG3 Registers
          130. 14.8.3.2.130 PHY2_TED_REG4 Registers
          131. 14.8.3.2.131 PHY2_DIG_UNUSED_REG0 Registers
          132. 14.8.3.2.132 PHY2_DIG_UNUSED_REG1 Registers
          133. 14.8.3.2.133 PHY2_DIG_UNUSED_REG2 Registers
          134. 14.8.3.2.134 PHY2_DIG_UNUSED_REG3 Registers
          135. 14.8.3.2.135 PHY2_INTERRUPT_REG1 Registers
          136. 14.8.3.2.136 PHY2_INTERRUPT_REG2 Registers
          137. 14.8.3.2.137 PHY2_RX_REG0 Registers
          138. 14.8.3.2.138 PHY2_RX_REG1 Registers
          139. 14.8.3.2.139 PHY2_TX_REG0 Registers
          140. 14.8.3.2.140 PHY2_TX_REG1 Registers
          141. 14.8.3.2.141 PHY2_CDR_REG0 Registers
          142. 14.8.3.2.142 PHY2_CDR_REG1 Registers
          143. 14.8.3.2.143 PHY2_CDR_REG2 Registers
          144. 14.8.3.2.144 PHY2_CDR_REG3 Registers
          145. 14.8.3.2.145 PHY2_CDR_REG4 Registers
          146. 14.8.3.2.146 PHY2_CDR_REG5 Registers
          147. 14.8.3.2.147 PHY2_CDR_REG6 Registers
          148. 14.8.3.2.148 PHY2_CDR_REG7 Registers
          149. 14.8.3.2.149 PHY2_CDR_REG8 Registers
          150. 14.8.3.2.150 PHY2_RX_REG2 Registers
          151. 14.8.3.2.151 PHY2_RX_REG3 Registers
          152. 14.8.3.2.152 PHY2_RX_REG4 Registers
          153. 14.8.3.2.153 PHY2_RX_REG5 Registers
          154. 14.8.3.2.154 PHY2_RX_REG6 Registers
          155. 14.8.3.2.155 PHY2_RX_REG7 Registers
          156. 14.8.3.2.156 PHY2_TX_REG2 Registers
          157. 14.8.3.2.157 PHY2_TX_REG3 Registers
          158. 14.8.3.2.158 PHY2_TX_REG4 Registers
          159. 14.8.3.2.159 PHY2_CDR_REG9 Registers
          160. 14.8.3.2.160 PHY2_CDR_REG10 Registers
          161. 14.8.3.2.161 PHY2_CDR_REG11 Registers
          162. 14.8.3.2.162 PHY2_CDR_RE12 Registers
          163. 14.8.3.2.163 PHY2_DIG_TXRX_UNUSED_REG0 Registers
          164. 14.8.3.2.164 PHY2_DIG_TXRX_UNUSED_REG1 Registers
          165. 14.8.3.2.165 PHY2_DIG_TXRX_UNUSED_REG2 Registers
          166. 14.8.3.2.166 PHY2_DIG_TXRX_UNUSED_REG3 Registers
          167. 14.8.3.2.167 PHY2_UTMI_REG0 Registers
          168. 14.8.3.2.168 PHY2_UTMI_REG1 Registers
          169. 14.8.3.2.169 PHY2_UTMI_REG2 Registers
          170. 14.8.3.2.170 PHY2_UTMI_REG3 Registers
          171. 14.8.3.2.171 PHY2_UTMI_REG4 Registers
          172. 14.8.3.2.172 PHY2_UTMI_REG5 Registers
          173. 14.8.3.2.173 PHY2_UTMI_REG6 Registers
          174. 14.8.3.2.174 PHY2_UTMI_REG7 Registers
          175. 14.8.3.2.175 PHY2_UTMI_REG8 Registers
          176. 14.8.3.2.176 PHY2_UTMI_REG9 Registers
          177. 14.8.3.2.177 PHY2_UTMI_REG10 Registers
          178. 14.8.3.2.178 PHY2_UTMI_REG11 Registers
          179. 14.8.3.2.179 PHY2_UTMI_REG12 Registers
          180. 14.8.3.2.180 PHY2_UTMI_REG13 Registers
          181. 14.8.3.2.181 PHY2_UTMI_REG14 Registers
          182. 14.8.3.2.182 PHY2_UTMI_REG15 Registers
          183. 14.8.3.2.183 PHY2_UTMI_REG16 Registers
          184. 14.8.3.2.184 PHY2_UTMI_REG17 Registers
          185. 14.8.3.2.185 PHY2_UTMI_REG18 Registers
          186. 14.8.3.2.186 PHY2_UTMI_REG19 Registers
          187. 14.8.3.2.187 PHY2_UTMI_REG20 Registers
          188. 14.8.3.2.188 PHY2_UTMI_REG21 Registers
          189. 14.8.3.2.189 PHY2_UTMI_REG22 Registers
          190. 14.8.3.2.190 PHY2_UTMI_REG23 Registers
          191. 14.8.3.2.191 PHY2_UTMI_REG24 Registers
          192. 14.8.3.2.192 PHY2_UTMI_REG25 Registers
          193. 14.8.3.2.193 PHY2_UTMI_REG26 Registers
          194. 14.8.3.2.194 PHY2_UTMI_REG27 Registers
          195. 14.8.3.2.195 PHY2_UTMI_REG28 Registers
          196. 14.8.3.2.196 PHY2_UTMI_REG29 Registers
          197. 14.8.3.2.197 PHY2_UTMI_REG30 Registers
          198. 14.8.3.2.198 PHY2_UTMI_UNUSED_REG0 Registers
          199. 14.8.3.2.199 PHY2_UTMI_UNUSED_REG1 Registers
          200. 14.8.3.2.200 PHY2_UTMI_UNUSED_REG2 Registers
          201. 14.8.3.2.201 PHY2_UTMI_UNUSED_REG3 Registers
          202. 14.8.3.2.202 PHY2_UTMI_REG31 Registers
          203. 14.8.3.2.203 PHY2_UTMI_REG32 Registers
          204. 14.8.3.2.204 PHY2_UTMI_REG33 Registers
          205. 14.8.3.2.205 PHY2_UTMI_REG34 Registers
          206. 14.8.3.2.206 PHY2_UTMI_REG35 Registers
          207. 14.8.3.2.207 PHY2_UTMI_REG36 Registers
          208. 14.8.3.2.208 PHY2_UTMI_REG37 Registers
          209. 14.8.3.2.209 PHY2_UTMI_REG38 Registers
          210. 14.8.3.2.210 PHY2_UTMI_REG39 Registers
          211. 14.8.3.2.211 PHY2_UTMI_REG40 Registers
          212. 14.8.3.2.212 PHY2_UTMI_REG41 Registers
          213. 14.8.3.2.213 PHY2_UTMI_REG42 Registers
          214. 14.8.3.2.214 PHY2_UTMI_REG43 Registers
          215. 14.8.3.2.215 PHY2_UTMI_REG44 Registers
          216. 14.8.3.2.216 PHY2_UTMI_REG45 Registers
          217. 14.8.3.2.217 PHY2_UTMI_REG46 Registers
          218. 14.8.3.2.218 PHY2_UTMI_REG47 Registers
          219. 14.8.3.2.219 PHY2_UTMI_REG48 Registers
          220. 14.8.3.2.220 PHY2_UTMI_REG49 Registers
          221. 14.8.3.2.221 PHY2_UTMI_REG50 Registers
          222. 14.8.3.2.222 PHY2_UTMI_REG51 Registers
          223. 14.8.3.2.223 PHY2_UTMI_REG52 Registers
          224. 14.8.3.2.224 PHY2_UTMI_REG53 Registers
          225. 14.8.3.2.225 PHY2_UTMI_REG54 Registers
          226. 14.8.3.2.226 PHY2_UTMI_REG55 Registers
          227. 14.8.3.2.227 PHY2_UTMI_REG56 Registers
          228. 14.8.3.2.228 PHY2_UTMI_REG57 Registers
          229. 14.8.3.2.229 PHY2_UTMI_REG58 Registers
          230. 14.8.3.2.230 PHY2_UTMI_REG59 Registers
          231. 14.8.3.2.231 PHY2_UTMI_UNUSED_REG6 Registers
          232. 14.8.3.2.232 PHY2_UTMI_UNUSED_REG7 Registers
          233. 14.8.3.2.233 ECC_AGGR_REV Registers
          234. 14.8.3.2.234 ECC_AGGR_VECTOR Registers
          235. 14.8.3.2.235 ECC_AGGR_STAT Registers
          236. 14.8.3.2.236 ECC_AGGR_RESERVED_SVBUS_N Registers
          237. 14.8.3.2.237 ECC_AGGR_SEC_EOI_REG Registers
          238. 14.8.3.2.238 ECC_AGGR_SEC_STATUS_REG0 Registers
          239. 14.8.3.2.239 ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          240. 14.8.3.2.240 ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          241. 14.8.3.2.241 ECC_AGGR_DED_EOI_REG Registers
          242. 14.8.3.2.242 ECC_AGGR_DED_STATUS_REG0 Registers
          243. 14.8.3.2.243 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          244. 14.8.3.2.244 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          245. 14.8.3.2.245 ECC_AGGR_AGGR_ENABLE_SET Registers
          246. 14.8.3.2.246 ECC_AGGR_AGGR_ENABLE_CLR Registers
          247. 14.8.3.2.247 ECC_AGGR_AGGR_STATUS_SET Registers
          248. 14.8.3.2.248 ECC_AGGR_AGGR_STATUS_CLR Registers
          249. 14.8.3.2.249 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_CAPLENGTH Registers
          250. 14.8.3.2.250 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_HCSPARAMS1 Registers
          251. 14.8.3.2.251 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_HCSPARAMS2 Registers
          252. 14.8.3.2.252 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_HCSPARAMS3 Registers
          253. 14.8.3.2.253 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_HCCPARAMS1 Registers
          254. 14.8.3.2.254 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_DBOFF Registers
          255. 14.8.3.2.255 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_RTSOFF Registers
          256. 14.8.3.2.256 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_CAP_HCCPARAMS2 Registers
          257. 14.8.3.2.257 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_USBCMD Registers
          258. 14.8.3.2.258 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_USBSTS Registers
          259. 14.8.3.2.259 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_PAGESIZE Registers
          260. 14.8.3.2.260 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_DNCTRL Registers
          261. 14.8.3.2.261 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_CRCR_LO Registers
          262. 14.8.3.2.262 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_CRCR_HI Registers
          263. 14.8.3.2.263 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_DCBAAP_LO Registers
          264. 14.8.3.2.264 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_DCBAAP_HI Registers
          265. 14.8.3.2.265 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_OPER_CONFIG Registers
          266. 14.8.3.2.266 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_PORT_XHCI_PORT_20_XHCI_PORT_20_PORTSC_20 Registers
          267. 14.8.3.2.267 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_PORT_XHCI_PORT_20_XHCI_PORT_20_PORTPMSC_20 Registers
          268. 14.8.3.2.268 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_PORT_XHCI_PORT_20_XHCI_PORT_20_PORTLI_20 Registers
          269. 14.8.3.2.269 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_PORT_XHCI_PORT_20_XHCI_PORT_20_PORTHLPMC_20 Registers
          270. 14.8.3.2.270 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_PORT_XHCI_PORT_30_XHCI_PORT_30_PORTPMSC_30 Registers
          271. 14.8.3.2.271 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_PORT_XHCI_PORT_30_XHCI_PORT_30_PORTLI_30 Registers
          272. 14.8.3.2.272 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_PORT_XHCI_PORT_30_XHCI_PORT_30_PORTHLPMC_30 Registers
          273. 14.8.3.2.273 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_RUNTIME_MFINDEX Registers
          274. 14.8.3.2.274 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_RUNTIME_RSVDZ Registers
          275. 14.8.3.2.275 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_IMAN_J_J Registers
          276. 14.8.3.2.276 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_IMOD_J_J Registers
          277. 14.8.3.2.277 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_ERSTSZ_J_J Registers
          278. 14.8.3.2.278 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_RSVDP_J_J Registers
          279. 14.8.3.2.279 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_ERSTBA_LO_J_J Registers
          280. 14.8.3.2.280 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_ERSTBA_HI_J_J Registers
          281. 14.8.3.2.281 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_ERDP_LO_J_J Registers
          282. 14.8.3.2.282 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_INTR_XHCI_INTR_XHCI_INTR_ERDP_HI_J_J Registers
          283. 14.8.3.2.283 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DB_XHCI_DB_XHCI_DB_DB_J_J Registers
          284. 14.8.3.2.284 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_EXTCAP_USBLEGSUP Registers
          285. 14.8.3.2.285 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_EXTCAP_USBLEGCTLSTS Registers
          286. 14.8.3.2.286 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP2_SUPTPRT2_DW0 Registers
          287. 14.8.3.2.287 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP2_SUPTPRT2_DW1 Registers
          288. 14.8.3.2.288 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP2_SUPTPRT2_DW2 Registers
          289. 14.8.3.2.289 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP2_SUPTPRT2_DW3 Registers
          290. 14.8.3.2.290 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP3_SUPTPRT3_DW0 Registers
          291. 14.8.3.2.291 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP3_SUPTPRT3_DW1 Registers
          292. 14.8.3.2.292 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP3_SUPTPRT3_DW2 Registers
          293. 14.8.3.2.293 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_SUPPRTCAP3_SUPTPRT3_DW3 Registers
          294. 14.8.3.2.294 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GSBUSCFG0 Registers
          295. 14.8.3.2.295 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GSBUSCFG1 Registers
          296. 14.8.3.2.296 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXTHRCFG Registers
          297. 14.8.3.2.297 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GRXTHRCFG Registers
          298. 14.8.3.2.298 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GCTL Registers
          299. 14.8.3.2.299 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPMSTS Registers
          300. 14.8.3.2.300 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GSTS Registers
          301. 14.8.3.2.301 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GUCTL1 Registers
          302. 14.8.3.2.302 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GSNPSID Registers
          303. 14.8.3.2.303 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GGPIO Registers
          304. 14.8.3.2.304 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GUID Registers
          305. 14.8.3.2.305 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GUCTL Registers
          306. 14.8.3.2.306 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GBUSERRADDRLO Registers
          307. 14.8.3.2.307 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GBUSERRADDRHI Registers
          308. 14.8.3.2.308 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPRTBIMAPLO Registers
          309. 14.8.3.2.309 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPRTBIMAPHI Registers
          310. 14.8.3.2.310 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS0 Registers
          311. 14.8.3.2.311 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS1 Registers
          312. 14.8.3.2.312 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS2 Registers
          313. 14.8.3.2.313 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS3 Registers
          314. 14.8.3.2.314 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS4 Registers
          315. 14.8.3.2.315 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS5 Registers
          316. 14.8.3.2.316 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS6 Registers
          317. 14.8.3.2.317 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS7 Registers
          318. 14.8.3.2.318 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGFIFOSPACE Registers
          319. 14.8.3.2.319 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGLTSSM Registers
          320. 14.8.3.2.320 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGLNMCC Registers
          321. 14.8.3.2.321 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGBMU Registers
          322. 14.8.3.2.322 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGLSPMUX_HST Registers
          323. 14.8.3.2.323 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGLSP Registers
          324. 14.8.3.2.324 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGEPINFO0 Registers
          325. 14.8.3.2.325 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDBGEPINFO1 Registers
          326. 14.8.3.2.326 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPRTBIMAP_HSLO Registers
          327. 14.8.3.2.327 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPRTBIMAP_HSHI Registers
          328. 14.8.3.2.328 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPRTBIMAP_FSLO Registers
          329. 14.8.3.2.329 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPRTBIMAP_FSHI Registers
          330. 14.8.3.2.330 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_RESERVED Registers
          331. 14.8.3.2.331 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GUCTL2 Registers
          332. 14.8.3.2.332 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GHWPARAMS8 Registers
          333. 14.8.3.2.333 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GUCTL3 Registers
          334. 14.8.3.2.334 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFOPRIDEV Registers
          335. 14.8.3.2.335 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFOPRIHST Registers
          336. 14.8.3.2.336 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GRXFIFOPRIHST Registers
          337. 14.8.3.2.337 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GDMAHLRATIO Registers
          338. 14.8.3.2.338 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GFLADJ Registers
          339. 14.8.3.2.339 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPHY_GPHY_GUSB2PHYCFG Registers
          340. 14.8.3.2.340 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GI2C_GI2C_GUSB2I2CCTL Registers
          341. 14.8.3.2.341 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GULPI_GULPI_GUSB2PHYACC_ULPI Registers
          342. 14.8.3.2.342 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GPIPE_GPIPE_GUSB3PIPECTL Registers
          343. 14.8.3.2.343 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ0 Registers
          344. 14.8.3.2.344 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ1 Registers
          345. 14.8.3.2.345 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ2 Registers
          346. 14.8.3.2.346 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ3 Registers
          347. 14.8.3.2.347 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ4 Registers
          348. 14.8.3.2.348 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ5 Registers
          349. 14.8.3.2.349 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ6 Registers
          350. 14.8.3.2.350 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ7 Registers
          351. 14.8.3.2.351 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ8 Registers
          352. 14.8.3.2.352 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ9 Registers
          353. 14.8.3.2.353 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ10 Registers
          354. 14.8.3.2.354 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ11 Registers
          355. 14.8.3.2.355 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ12 Registers
          356. 14.8.3.2.356 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ13 Registers
          357. 14.8.3.2.357 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ14 Registers
          358. 14.8.3.2.358 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GTXFIFO_GTXFIFO_GTXFIFOSIZ15 Registers
          359. 14.8.3.2.359 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GRXFIFO_GRXFIFO_GRXFIFOSIZ0 Registers
          360. 14.8.3.2.360 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GRXFIFO_GRXFIFO_GRXFIFOSIZ1 Registers
          361. 14.8.3.2.361 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GRXFIFO_GRXFIFO_GRXFIFOSIZ2 Registers
          362. 14.8.3.2.362 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GEVNT_GEVNT_GEVNTADRLO_J_J Registers
          363. 14.8.3.2.363 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GEVNT_GEVNT_GEVNTADRHI_J_J Registers
          364. 14.8.3.2.364 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GEVNT_GEVNT_GEVNTSIZ_J_J Registers
          365. 14.8.3.2.365 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GEVNT_GEVNT_GEVNTCOUNT_J_J Registers
          366. 14.8.3.2.366 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_GBL_GRHB_GRHB_GUSB2RHBCTL Registers
          367. 14.8.3.2.367 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DCFG Registers
          368. 14.8.3.2.368 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DCTL Registers
          369. 14.8.3.2.369 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DEVTEN Registers
          370. 14.8.3.2.370 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DSTS Registers
          371. 14.8.3.2.371 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DGCMDPAR Registers
          372. 14.8.3.2.372 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DGCMD Registers
          373. 14.8.3.2.373 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DALEPENA Registers
          374. 14.8.3.2.374 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DEV_RESERVED_DEV_RESERVED_RSVD_J_J Registers
          375. 14.8.3.2.375 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DEPCMDPAR_EP_DEPCMDPAR_EP_DEPCMDPAR2_J_J Registers
          376. 14.8.3.2.376 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DEPCMDPAR_EP_DEPCMDPAR_EP_DEPCMDPAR1_J_J Registers
          377. 14.8.3.2.377 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DEPCMDPAR_EP_DEPCMDPAR_EP_DEPCMDPAR0_J_J Registers
          378. 14.8.3.2.378 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DEPCMDPAR_EP_DEPCMDPAR_EP_DEPCMD_J_J Registers
          379. 14.8.3.2.379 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEV_DEV_INTR_DEV_INTR_DEV_IMOD_J_J Registers
          380. 14.8.3.2.380 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_LINK_LINK_LINK_LU1LFPSRXTIM Registers
          381. 14.8.3.2.381 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_LINK_LINK_LINK_LINK_SETTINGS Registers
          382. 14.8.3.2.382 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_LINK_LINK_LINK_LLUCTL Registers
          383. 14.8.3.2.383 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_LINK_LINK_LINK_LPTMDPDELAY Registers
          384. 14.8.3.2.384 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEBUG_DEBUG_DEBUG_U3RHBDBG Registers
          385. 14.8.3.2.385 VBP2AHB_WRAP_CONTROLLER_VBP_USB3_CORE_DEBUG_RAM0_RAM0_N Registers
          386. 14.8.3.2.386 Access Table
      4. 14.8.4 Memory Interfaces Registers
        1. 14.8.4.1 FSS Registers
          1. 14.8.4.1.1 CFG_REVISION Registers
          2. 14.8.4.1.2 Access Table
        2. 14.8.4.2 FSS_FSAS_0 Registers
          1. 14.8.4.2.1   FSAS_CFG_REVISION Registers
          2. 14.8.4.2.2   FSAS_CFG_SYSCONFIG Registers
          3. 14.8.4.2.3   FSAS_CFG_FRAG_ADR Registers
          4. 14.8.4.2.4   FSAS_CFG_FRAG_CTL Registers
          5. 14.8.4.2.5   FSAS_CFG_IRQ_IRQ_EOI Registers
          6. 14.8.4.2.6   FSAS_CFG_IRQ_IRQ_STATUS_RAW Registers
          7. 14.8.4.2.7   FSAS_CFG_IRQ_IRQ_STATUS Registers
          8. 14.8.4.2.8   FSAS_CFG_IRQ_IRQ_ENABLE_SET Registers
          9. 14.8.4.2.9   FSAS_CFG_IRQ_IRQ_ENABLE_CLR Registers
          10. 14.8.4.2.10  FSAS_CFG_ECC_REGCTRL_ECC_REGCTRL_ECC_RGSTRT_J_J Registers
          11. 14.8.4.2.11  FSAS_CFG_ECC_REGCTRL_ECC_REGCTRL_ECC_RGSIZ_J_J Registers
          12. 14.8.4.2.12  FSAS_CFG_ERR_ERR_ECC_BLOCK_ADR Registers
          13. 14.8.4.2.13  FSAS_CFG_ERR_ERR_ECC_TYPE Registers
          14. 14.8.4.2.14  FSAS_CFG_ERR_ERR_WRT_TYPE Registers
          15. 14.8.4.2.15  OTFA_CFG_REVID Registers
          16. 14.8.4.2.16  OTFA_CFG_SCFG Registers
          17. 14.8.4.2.17  OTFA_CFG_ISR Registers
          18. 14.8.4.2.18  OTFA_CFG_IS Registers
          19. 14.8.4.2.19  OTFA_CFG_IES Registers
          20. 14.8.4.2.20  OTFA_CFG_IEC Registers
          21. 14.8.4.2.21  OTFA_CFG_CCFG Registers
          22. 14.8.4.2.22  OTFA_CFG_CSTATUS Registers
          23. 14.8.4.2.23  OTFA_CFG_RGCFG0 Registers
          24. 14.8.4.2.24  OTFA_CFG_RGMACST0 Registers
          25. 14.8.4.2.25  OTFA_CFG_RGST0 Registers
          26. 14.8.4.2.26  OTFA_CFG_RGSI0 Registers
          27. 14.8.4.2.27  OTFA_CFG_RKEYE00 Registers
          28. 14.8.4.2.28  OTFA_CFG_RKEYE01 Registers
          29. 14.8.4.2.29  OTFA_CFG_RKEYE02 Registers
          30. 14.8.4.2.30  OTFA_CFG_RKEYE03 Registers
          31. 14.8.4.2.31  OTFA_CFG_RKEYE04 Registers
          32. 14.8.4.2.32  OTFA_CFG_RKEYE05 Registers
          33. 14.8.4.2.33  OTFA_CFG_RKEYE06 Registers
          34. 14.8.4.2.34  OTFA_CFG_RKEYE07 Registers
          35. 14.8.4.2.35  OTFA_CFG_RKEYEP00 Registers
          36. 14.8.4.2.36  OTFA_CFG_RKEYEP01 Registers
          37. 14.8.4.2.37  OTFA_CFG_RKEYEP02 Registers
          38. 14.8.4.2.38  OTFA_CFG_RKEYEP03 Registers
          39. 14.8.4.2.39  OTFA_CFG_RKEYEP04 Registers
          40. 14.8.4.2.40  OTFA_CFG_RKEYEP05 Registers
          41. 14.8.4.2.41  OTFA_CFG_RKEYEP06 Registers
          42. 14.8.4.2.42  OTFA_CFG_RKEYEP07 Registers
          43. 14.8.4.2.43  OTFA_CFG_RKEYA00 Registers
          44. 14.8.4.2.44  OTFA_CFG_RKEYA01 Registers
          45. 14.8.4.2.45  OTFA_CFG_RKEYA02 Registers
          46. 14.8.4.2.46  OTFA_CFG_RKEYA03 Registers
          47. 14.8.4.2.47  OTFA_CFG_RKEYAP00 Registers
          48. 14.8.4.2.48  OTFA_CFG_RKEYAP01 Registers
          49. 14.8.4.2.49  OTFA_CFG_RKEYAP02 Registers
          50. 14.8.4.2.50  OTFA_CFG_RKEYAP03 Registers
          51. 14.8.4.2.51  OTFA_CFG_RIV00 Registers
          52. 14.8.4.2.52  OTFA_CFG_RIV01 Registers
          53. 14.8.4.2.53  OTFA_CFG_RIV02 Registers
          54. 14.8.4.2.54  OTFA_CFG_RIV03 Registers
          55. 14.8.4.2.55  OTFA_CFG_RGCFG1 Registers
          56. 14.8.4.2.56  OTFA_CFG_RGMACST1 Registers
          57. 14.8.4.2.57  OTFA_CFG_RGST1 Registers
          58. 14.8.4.2.58  OTFA_CFG_RGSI1 Registers
          59. 14.8.4.2.59  OTFA_CFG_RKEYE10 Registers
          60. 14.8.4.2.60  OTFA_CFG_RKEYE11 Registers
          61. 14.8.4.2.61  OTFA_CFG_RKEYE12 Registers
          62. 14.8.4.2.62  OTFA_CFG_RKEYE13 Registers
          63. 14.8.4.2.63  OTFA_CFG_RKEYE14 Registers
          64. 14.8.4.2.64  OTFA_CFG_RKEYE15 Registers
          65. 14.8.4.2.65  OTFA_CFG_RKEYE16 Registers
          66. 14.8.4.2.66  OTFA_CFG_RKEYE17 Registers
          67. 14.8.4.2.67  OTFA_CFG_RKEYEP10 Registers
          68. 14.8.4.2.68  OTFA_CFG_RKEYEP11 Registers
          69. 14.8.4.2.69  OTFA_CFG_RKEYEP12 Registers
          70. 14.8.4.2.70  OTFA_CFG_RKEYEP13 Registers
          71. 14.8.4.2.71  OTFA_CFG_RKEYEP14 Registers
          72. 14.8.4.2.72  OTFA_CFG_RKEYEP15 Registers
          73. 14.8.4.2.73  OTFA_CFG_RKEYEP16 Registers
          74. 14.8.4.2.74  OTFA_CFG_RKEYEP17 Registers
          75. 14.8.4.2.75  OTFA_CFG_RKEYA10 Registers
          76. 14.8.4.2.76  OTFA_CFG_RKEYA11 Registers
          77. 14.8.4.2.77  OTFA_CFG_RKEYA12 Registers
          78. 14.8.4.2.78  OTFA_CFG_RKEYA13 Registers
          79. 14.8.4.2.79  OTFA_CFG_RKEYAP10 Registers
          80. 14.8.4.2.80  OTFA_CFG_RKEYAP11 Registers
          81. 14.8.4.2.81  OTFA_CFG_RKEYAP12 Registers
          82. 14.8.4.2.82  OTFA_CFG_RKEYAP13 Registers
          83. 14.8.4.2.83  OTFA_CFG_RIV10 Registers
          84. 14.8.4.2.84  OTFA_CFG_RIV11 Registers
          85. 14.8.4.2.85  OTFA_CFG_RIV12 Registers
          86. 14.8.4.2.86  OTFA_CFG_RIV13 Registers
          87. 14.8.4.2.87  OTFA_CFG_RGCFG2 Registers
          88. 14.8.4.2.88  OTFA_CFG_RGMACST2 Registers
          89. 14.8.4.2.89  OTFA_CFG_RGST2 Registers
          90. 14.8.4.2.90  OTFA_CFG_RGSI2 Registers
          91. 14.8.4.2.91  OTFA_CFG_RKEYE20 Registers
          92. 14.8.4.2.92  OTFA_CFG_RKEYE21 Registers
          93. 14.8.4.2.93  OTFA_CFG_RKEYE22 Registers
          94. 14.8.4.2.94  OTFA_CFG_RKEYE23 Registers
          95. 14.8.4.2.95  OTFA_CFG_RKEYE24 Registers
          96. 14.8.4.2.96  OTFA_CFG_RKEYE25 Registers
          97. 14.8.4.2.97  OTFA_CFG_RKEYE26 Registers
          98. 14.8.4.2.98  OTFA_CFG_RKEYE27 Registers
          99. 14.8.4.2.99  OTFA_CFG_RKEYEP20 Registers
          100. 14.8.4.2.100 OTFA_CFG_RKEYEP21 Registers
          101. 14.8.4.2.101 OTFA_CFG_RKEYEP22 Registers
          102. 14.8.4.2.102 OTFA_CFG_RKEYEP23 Registers
          103. 14.8.4.2.103 OTFA_CFG_RKEYEP24 Registers
          104. 14.8.4.2.104 OTFA_CFG_RKEYEP25 Registers
          105. 14.8.4.2.105 OTFA_CFG_RKEYEP26 Registers
          106. 14.8.4.2.106 OTFA_CFG_RKEYEP27 Registers
          107. 14.8.4.2.107 OTFA_CFG_RKEYA20 Registers
          108. 14.8.4.2.108 OTFA_CFG_RKEYA21 Registers
          109. 14.8.4.2.109 OTFA_CFG_RKEYA22 Registers
          110. 14.8.4.2.110 OTFA_CFG_RKEYA23 Registers
          111. 14.8.4.2.111 OTFA_CFG_RKEYAP20 Registers
          112. 14.8.4.2.112 OTFA_CFG_RKEYAP21 Registers
          113. 14.8.4.2.113 OTFA_CFG_RKEYAP22 Registers
          114. 14.8.4.2.114 OTFA_CFG_RKEYAP23 Registers
          115. 14.8.4.2.115 OTFA_CFG_RIV20 Registers
          116. 14.8.4.2.116 OTFA_CFG_RIV21 Registers
          117. 14.8.4.2.117 OTFA_CFG_RIV22 Registers
          118. 14.8.4.2.118 OTFA_CFG_RIV23 Registers
          119. 14.8.4.2.119 OTFA_CFG_RGCFG3 Registers
          120. 14.8.4.2.120 OTFA_CFG_RGMACST3 Registers
          121. 14.8.4.2.121 OTFA_CFG_RGST3 Registers
          122. 14.8.4.2.122 OTFA_CFG_RGSI3 Registers
          123. 14.8.4.2.123 OTFA_CFG_RKEYE30 Registers
          124. 14.8.4.2.124 OTFA_CFG_RKEYE31 Registers
          125. 14.8.4.2.125 OTFA_CFG_RKEYE32 Registers
          126. 14.8.4.2.126 OTFA_CFG_RKEYE33 Registers
          127. 14.8.4.2.127 OTFA_CFG_RKEYE34 Registers
          128. 14.8.4.2.128 OTFA_CFG_RKEYE35 Registers
          129. 14.8.4.2.129 OTFA_CFG_RKEYE36 Registers
          130. 14.8.4.2.130 OTFA_CFG_RKEYE37 Registers
          131. 14.8.4.2.131 OTFA_CFG_RKEYEP30 Registers
          132. 14.8.4.2.132 OTFA_CFG_RKEYEP31 Registers
          133. 14.8.4.2.133 OTFA_CFG_RKEYEP32 Registers
          134. 14.8.4.2.134 OTFA_CFG_RKEYEP33 Registers
          135. 14.8.4.2.135 OTFA_CFG_RKEYEP34 Registers
          136. 14.8.4.2.136 OTFA_CFG_RKEYEP35 Registers
          137. 14.8.4.2.137 OTFA_CFG_RKEYEP36 Registers
          138. 14.8.4.2.138 OTFA_CFG_RKEYEP37 Registers
          139. 14.8.4.2.139 OTFA_CFG_RKEYA30 Registers
          140. 14.8.4.2.140 OTFA_CFG_RKEYA31 Registers
          141. 14.8.4.2.141 OTFA_CFG_RKEYA32 Registers
          142. 14.8.4.2.142 OTFA_CFG_RKEYA33 Registers
          143. 14.8.4.2.143 OTFA_CFG_RKEYAP30 Registers
          144. 14.8.4.2.144 OTFA_CFG_RKEYAP31 Registers
          145. 14.8.4.2.145 OTFA_CFG_RKEYAP32 Registers
          146. 14.8.4.2.146 OTFA_CFG_RKEYAP33 Registers
          147. 14.8.4.2.147 OTFA_CFG_RIV30 Registers
          148. 14.8.4.2.148 OTFA_CFG_RIV31 Registers
          149. 14.8.4.2.149 OTFA_CFG_RIV32 Registers
          150. 14.8.4.2.150 OTFA_CFG_RIV33 Registers
          151. 14.8.4.2.151 OTFA_CFG_IRQADDINFO0 Registers
          152. 14.8.4.2.152 OTFA_CFG_IRQADDINFO1 Registers
          153. 14.8.4.2.153 OTFA_CFG_MACCACHEINFO Registers
          154. 14.8.4.2.154 OTFA_CFG_RMWRMCNT Registers
          155. 14.8.4.2.155 DAT_REG1_HPB_DATA_MEM_N Registers
          156. 14.8.4.2.156 DAT_REG0_HPB_DATA_MEM_N Registers
          157. 14.8.4.2.157 DAT_REG3_HPB_DATA_MEM_N Registers
          158. 14.8.4.2.158 Access Table
        3. 14.8.4.3 FSS_OSPI_0 Registers
          1. 14.8.4.3.1  OSPI0_ECC_AGGR_REV Registers
          2. 14.8.4.3.2  OSPI0_ECC_AGGR_VECTOR Registers
          3. 14.8.4.3.3  OSPI0_ECC_AGGR_STAT Registers
          4. 14.8.4.3.4  OSPI0_ECC_AGGR_RESERVED_SVBUS_N Registers
          5. 14.8.4.3.5  OSPI0_ECC_AGGR_SEC_EOI_REG Registers
          6. 14.8.4.3.6  OSPI0_ECC_AGGR_SEC_STATUS_REG0 Registers
          7. 14.8.4.3.7  OSPI0_ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          8. 14.8.4.3.8  OSPI0_ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          9. 14.8.4.3.9  OSPI0_ECC_AGGR_DED_EOI_REG Registers
          10. 14.8.4.3.10 OSPI0_ECC_AGGR_DED_STATUS_REG0 Registers
          11. 14.8.4.3.11 OSPI0_ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          12. 14.8.4.3.12 OSPI0_ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          13. 14.8.4.3.13 OSPI0_ECC_AGGR_AGGR_ENABLE_SET Registers
          14. 14.8.4.3.14 OSPI0_ECC_AGGR_AGGR_ENABLE_CLR Registers
          15. 14.8.4.3.15 OSPI0_ECC_AGGR_AGGR_STATUS_SET Registers
          16. 14.8.4.3.16 OSPI0_ECC_AGGR_AGGR_STATUS_CLR Registers
          17. 14.8.4.3.17 OSPI0_CTRL_CONFIG_REG Registers
          18. 14.8.4.3.18 OSPI0_CTRL_DEV_INSTR_RD_CONFIG_REG Registers
          19. 14.8.4.3.19 OSPI0_CTRL_DEV_INSTR_WR_CONFIG_REG Registers
          20. 14.8.4.3.20 OSPI0_CTRL_DEV_DELAY_REG Registers
          21. 14.8.4.3.21 OSPI0_CTRL_RD_DATA_CAPTURE_REG Registers
          22. 14.8.4.3.22 OSPI0_CTRL_DEV_SIZE_CONFIG_REG Registers
          23. 14.8.4.3.23 OSPI0_CTRL_SRAM_PARTITION_CFG_REG Registers
          24. 14.8.4.3.24 OSPI0_CTRL_IND_AHB_ADDR_TRIGGER_REG Registers
          25. 14.8.4.3.25 OSPI0_CTRL_DMA_PERIPH_CONFIG_REG Registers
          26. 14.8.4.3.26 OSPI0_CTRL_REMAP_ADDR_REG Registers
          27. 14.8.4.3.27 OSPI0_CTRL_MODE_BIT_CONFIG_REG Registers
          28. 14.8.4.3.28 OSPI0_CTRL_SRAM_FILL_REG Registers
          29. 14.8.4.3.29 OSPI0_CTRL_TX_THRESH_REG Registers
          30. 14.8.4.3.30 OSPI0_CTRL_RX_THRESH_REG Registers
          31. 14.8.4.3.31 OSPI0_CTRL_WRITE_COMPLETION_CTRL_REG Registers
          32. 14.8.4.3.32 OSPI0_CTRL_NO_OF_POLLS_BEF_EXP_REG Registers
          33. 14.8.4.3.33 OSPI0_CTRL_IRQ_STATUS_REG Registers
          34. 14.8.4.3.34 OSPI0_CTRL_IRQ_MASK_REG Registers
          35. 14.8.4.3.35 OSPI0_CTRL_LOWER_WR_PROT_REG Registers
          36. 14.8.4.3.36 OSPI0_CTRL_UPPER_WR_PROT_REG Registers
          37. 14.8.4.3.37 OSPI0_CTRL_WR_PROT_CTRL_REG Registers
          38. 14.8.4.3.38 OSPI0_CTRL_INDIRECT_READ_XFER_CTRL_REG Registers
          39. 14.8.4.3.39 OSPI0_CTRL_INDIRECT_READ_XFER_WATERMARK_REG Registers
          40. 14.8.4.3.40 OSPI0_CTRL_INDIRECT_READ_XFER_START_REG Registers
          41. 14.8.4.3.41 OSPI0_CTRL_INDIRECT_READ_XFER_NUM_BYTES_REG Registers
          42. 14.8.4.3.42 OSPI0_CTRL_INDIRECT_WRITE_XFER_CTRL_REG Registers
          43. 14.8.4.3.43 OSPI0_CTRL_INDIRECT_WRITE_XFER_WATERMARK_REG Registers
          44. 14.8.4.3.44 OSPI0_CTRL_INDIRECT_WRITE_XFER_START_REG Registers
          45. 14.8.4.3.45 OSPI0_CTRL_INDIRECT_WRITE_XFER_NUM_BYTES_REG Registers
          46. 14.8.4.3.46 OSPI0_CTRL_INDIRECT_TRIGGER_ADDR_RANGE_REG Registers
          47. 14.8.4.3.47 OSPI0_CTRL_FLASH_COMMAND_CTRL_MEM_REG Registers
          48. 14.8.4.3.48 OSPI0_CTRL_FLASH_CMD_CTRL_REG Registers
          49. 14.8.4.3.49 OSPI0_CTRL_FLASH_CMD_ADDR_REG Registers
          50. 14.8.4.3.50 OSPI0_CTRL_FLASH_RD_DATA_LOWER_REG Registers
          51. 14.8.4.3.51 OSPI0_CTRL_FLASH_RD_DATA_UPPER_REG Registers
          52. 14.8.4.3.52 OSPI0_CTRL_FLASH_WR_DATA_LOWER_REG Registers
          53. 14.8.4.3.53 OSPI0_CTRL_FLASH_WR_DATA_UPPER_REG Registers
          54. 14.8.4.3.54 OSPI0_CTRL_POLLING_FLASH_STATUS_REG Registers
          55. 14.8.4.3.55 OSPI0_CTRL_PHY_CONFIGURATION_REG Registers
          56. 14.8.4.3.56 OSPI0_CTRL_PHY_MASTER_CONTROL_REG Registers
          57. 14.8.4.3.57 OSPI0_CTRL_DLL_OBSERVABLE_LOWER_REG Registers
          58. 14.8.4.3.58 OSPI0_CTRL_DLL_OBSERVABLE_UPPER_REG Registers
          59. 14.8.4.3.59 OSPI0_CTRL_OPCODE_EXT_LOWER_REG Registers
          60. 14.8.4.3.60 OSPI0_CTRL_OPCODE_EXT_UPPER_REG Registers
          61. 14.8.4.3.61 OSPI0_CTRL_MODULE_ID_REG Registers
          62. 14.8.4.3.62 OSPI0_SS_CFG_PID Registers
          63. 14.8.4.3.63 OSPI0_SS_CFG_CTRL Registers
          64. 14.8.4.3.64 OSPI0_SS_CFG_STAT Registers
          65. 14.8.4.3.65 OSPI0_SS_CFG_EOI Registers
          66. 14.8.4.3.66 Access Table
        4. 14.8.4.4 GPMC Registers
          1. 14.8.4.4.1  CFG_GPMC_REVISION Registers
          2. 14.8.4.4.2  CFG_GPMC_SYSCONFIG Registers
          3. 14.8.4.4.3  CFG_GPMC_SYSSTATUS Registers
          4. 14.8.4.4.4  CFG_GPMC_IRQSTATUS Registers
          5. 14.8.4.4.5  CFG_GPMC_IRQENABLE Registers
          6. 14.8.4.4.6  CFG_GPMC_TIMEOUT_CONTROL Registers
          7. 14.8.4.4.7  CFG_GPMC_ERR_ADDRESS Registers
          8. 14.8.4.4.8  CFG_GPMC_ERR_TYPE Registers
          9. 14.8.4.4.9  CFG_GPMC_CONFIG Registers
          10. 14.8.4.4.10 CFG_GPMC_STATUS Registers
          11. 14.8.4.4.11 CFG_GPMC_PREFETCH_CONFIG1 Registers
          12. 14.8.4.4.12 CFG_GPMC_PREFETCH_CONFIG2 Registers
          13. 14.8.4.4.13 CFG_GPMC_PREFETCH_CONTROL Registers
          14. 14.8.4.4.14 CFG_GPMC_PREFETCH_STATUS Registers
          15. 14.8.4.4.15 CFG_GPMC_ECC_CONFIG Registers
          16. 14.8.4.4.16 CFG_GPMC_ECC_CONTROL Registers
          17. 14.8.4.4.17 CFG_GPMC_ECC_SIZE_CONFIG Registers
          18. 14.8.4.4.18 CFG_GPMC_ECC_RESULT_N Registers
          19. 14.8.4.4.19 CFG_GPMC_BCH_SWDATA Registers
          20. 14.8.4.4.20 CFG_CS_CS_GPMC_CONFIG1_J_J Registers
          21. 14.8.4.4.21 CFG_CS_CS_GPMC_CONFIG2_J_J Registers
          22. 14.8.4.4.22 CFG_CS_CS_GPMC_CONFIG3_J_J Registers
          23. 14.8.4.4.23 CFG_CS_CS_GPMC_CONFIG4_J_J Registers
          24. 14.8.4.4.24 CFG_CS_CS_GPMC_CONFIG5_J_J Registers
          25. 14.8.4.4.25 CFG_CS_CS_GPMC_CONFIG6_J_J Registers
          26. 14.8.4.4.26 CFG_CS_CS_GPMC_CONFIG7_J_J Registers
          27. 14.8.4.4.27 CFG_CS_CS_GPMC_NAND_COMMAND_J_J Registers
          28. 14.8.4.4.28 CFG_CS_CS_GPMC_NAND_ADDRESS_J_J Registers
          29. 14.8.4.4.29 CFG_CS_CS_GPMC_NAND_DATA_J_J Registers
          30. 14.8.4.4.30 CFG_CSEL_CSEL_GPMC_BCH_RESULT_0_J_J Registers
          31. 14.8.4.4.31 CFG_CSEL_CSEL_GPMC_BCH_RESULT_1_J_J Registers
          32. 14.8.4.4.32 CFG_CSEL_CSEL_GPMC_BCH_RESULT_2_J_J Registers
          33. 14.8.4.4.33 CFG_CSEL_CSEL_GPMC_BCH_RESULT_3_J_J Registers
          34. 14.8.4.4.34 CFG_CHIPSEL_CHIPSEL_GPMC_BCH_RESULT_4_J_J Registers
          35. 14.8.4.4.35 CFG_CHIPSEL_CHIPSEL_GPMC_BCH_RESULT_5_J_J Registers
          36. 14.8.4.4.36 CFG_CHIPSEL_CHIPSEL_GPMC_BCH_RESULT_6_J_J Registers
          37. 14.8.4.4.37 Access Table
        5. 14.8.4.5 ELM Registers
          1. 14.8.4.5.1  _ELM_ELM_REVISION Registers
          2. 14.8.4.5.2  _ELM_ELM_SYSCONFIG Registers
          3. 14.8.4.5.3  _ELM_ELM_SYSSTATUS Registers
          4. 14.8.4.5.4  _ELM_ELM_IRQSTATUS Registers
          5. 14.8.4.5.5  _ELM_ELM_IRQENABLE Registers
          6. 14.8.4.5.6  _ELM_ELM_LOCATION_CONFIG Registers
          7. 14.8.4.5.7  _ELM_ELM_PAGE_CTRL Registers
          8. 14.8.4.5.8  _ELM_POLY_POLY_ELM_SYNDROME_FRAGMENT_0_J_J Registers
          9. 14.8.4.5.9  _ELM_POLY_POLY_ELM_SYNDROME_FRAGMENT_1_J_J Registers
          10. 14.8.4.5.10 _ELM_POLY_POLY_ELM_SYNDROME_FRAGMENT_2_J_J Registers
          11. 14.8.4.5.11 _ELM_POLY_POLY_ELM_SYNDROME_FRAGMENT_3_J_J Registers
          12. 14.8.4.5.12 _ELM_POLY_POLY_ELM_SYNDROME_FRAGMENT_4_J_J Registers
          13. 14.8.4.5.13 _ELM_POLY_POLY_ELM_SYNDROME_FRAGMENT_5_J_J Registers
          14. 14.8.4.5.14 _ELM_POLY_POLY_ELM_SYNDROME_FRAGMENT_6_J_J Registers
          15. 14.8.4.5.15 _ELM_POLY_POLY_ELM_LOCATION_STATUS_J_J Registers
          16. 14.8.4.5.16 _ELM_POLY_POLY_ELM_ERROR_LOCATION_0_J_J Registers
          17. 14.8.4.5.17 _ELM_POLY_POLY_ELM_ERROR_LOCATION_1_J_J Registers
          18. 14.8.4.5.18 _ELM_POLY_POLY_ELM_ERROR_LOCATION_2_J_J Registers
          19. 14.8.4.5.19 _ELM_POLY_POLY_ELM_ERROR_LOCATION_3_J_J Registers
          20. 14.8.4.5.20 _ELM_POLY_POLY_ELM_ERROR_LOCATION_4_J_J Registers
          21. 14.8.4.5.21 _ELM_POLY_POLY_ELM_ERROR_LOCATION_5_J_J Registers
          22. 14.8.4.5.22 _ELM_POLY_POLY_ELM_ERROR_LOCATION_6_J_J Registers
          23. 14.8.4.5.23 _ELM_POLY_POLY_ELM_ERROR_LOCATION_7_J_J Registers
          24. 14.8.4.5.24 _ELM_POLY_POLY_ELM_ERROR_LOCATION_8_J_J Registers
          25. 14.8.4.5.25 _ELM_POLY_POLY_ELM_ERROR_LOCATION_9_J_J Registers
          26. 14.8.4.5.26 _ELM_POLY_POLY_ELM_ERROR_LOCATION_10_J_J Registers
          27. 14.8.4.5.27 _ELM_POLY_POLY_ELM_ERROR_LOCATION_11_J_J Registers
          28. 14.8.4.5.28 _ELM_POLY_POLY_ELM_ERROR_LOCATION_12_J_J Registers
          29. 14.8.4.5.29 _ELM_POLY_POLY_ELM_ERROR_LOCATION_13_J_J Registers
          30. 14.8.4.5.30 _ELM_POLY_POLY_ELM_ERROR_LOCATION_14_J_J Registers
          31. 14.8.4.5.31 _ELM_POLY_POLY_ELM_ERROR_LOCATION_15_J_J Registers
          32. 14.8.4.5.32 Access Table
        6. 14.8.4.6 MMCSD Registers
          1. 14.8.4.6.1   ECC_AGGR_RXMEM_REV Registers
          2. 14.8.4.6.2   ECC_AGGR_RXMEM_VECTOR Registers
          3. 14.8.4.6.3   ECC_AGGR_RXMEM_STAT Registers
          4. 14.8.4.6.4   ECC_AGGR_RXMEM_RESERVED_SVBUS_N Registers
          5. 14.8.4.6.5   ECC_AGGR_RXMEM_SEC_EOI_REG Registers
          6. 14.8.4.6.6   ECC_AGGR_RXMEM_SEC_STATUS_REG0 Registers
          7. 14.8.4.6.7   ECC_AGGR_RXMEM_SEC_ENABLE_SET_REG0 Registers
          8. 14.8.4.6.8   ECC_AGGR_RXMEM_SEC_ENABLE_CLR_REG0 Registers
          9. 14.8.4.6.9   ECC_AGGR_RXMEM_DED_EOI_REG Registers
          10. 14.8.4.6.10  ECC_AGGR_RXMEM_DED_STATUS_REG0 Registers
          11. 14.8.4.6.11  ECC_AGGR_RXMEM_DED_ENABLE_SET_REG0 Registers
          12. 14.8.4.6.12  ECC_AGGR_RXMEM_DED_ENABLE_CLR_REG0 Registers
          13. 14.8.4.6.13  ECC_AGGR_RXMEM_AGGR_ENABLE_SET Registers
          14. 14.8.4.6.14  ECC_AGGR_RXMEM_AGGR_ENABLE_CLR Registers
          15. 14.8.4.6.15  ECC_AGGR_RXMEM_AGGR_STATUS_SET Registers
          16. 14.8.4.6.16  ECC_AGGR_RXMEM_AGGR_STATUS_CLR Registers
          17. 14.8.4.6.17  ECC_AGGR_TXMEM_REV Registers
          18. 14.8.4.6.18  ECC_AGGR_TXMEM_VECTOR Registers
          19. 14.8.4.6.19  ECC_AGGR_TXMEM_STAT Registers
          20. 14.8.4.6.20  ECC_AGGR_TXMEM_RESERVED_SVBUS_N Registers
          21. 14.8.4.6.21  ECC_AGGR_TXMEM_SEC_EOI_REG Registers
          22. 14.8.4.6.22  ECC_AGGR_TXMEM_SEC_STATUS_REG0 Registers
          23. 14.8.4.6.23  ECC_AGGR_TXMEM_SEC_ENABLE_SET_REG0 Registers
          24. 14.8.4.6.24  ECC_AGGR_TXMEM_SEC_ENABLE_CLR_REG0 Registers
          25. 14.8.4.6.25  ECC_AGGR_TXMEM_DED_EOI_REG Registers
          26. 14.8.4.6.26  ECC_AGGR_TXMEM_DED_STATUS_REG0 Registers
          27. 14.8.4.6.27  ECC_AGGR_TXMEM_DED_ENABLE_SET_REG0 Registers
          28. 14.8.4.6.28  ECC_AGGR_TXMEM_DED_ENABLE_CLR_REG0 Registers
          29. 14.8.4.6.29  ECC_AGGR_TXMEM_AGGR_ENABLE_SET Registers
          30. 14.8.4.6.30  ECC_AGGR_TXMEM_AGGR_ENABLE_CLR Registers
          31. 14.8.4.6.31  ECC_AGGR_TXMEM_AGGR_STATUS_SET Registers
          32. 14.8.4.6.32  ECC_AGGR_TXMEM_AGGR_STATUS_CLR Registers
          33. 14.8.4.6.33  CTL_CFG_SDMA_SYS_ADDR_LO Registers
          34. 14.8.4.6.34  CTL_CFG_SDMA_SYS_ADDR_HI Registers
          35. 14.8.4.6.35  CTL_CFG_BLOCK_SIZE Registers
          36. 14.8.4.6.36  CTL_CFG_BLOCK_COUNT Registers
          37. 14.8.4.6.37  CTL_CFG_ARGUMENT1_LO Registers
          38. 14.8.4.6.38  CTL_CFG_ARGUMENT1_HI Registers
          39. 14.8.4.6.39  CTL_CFG_TRANSFER_MODE Registers
          40. 14.8.4.6.40  CTL_CFG_COMMAND Registers
          41. 14.8.4.6.41  CTL_CFG_RESPONSE_N Registers
          42. 14.8.4.6.42  CTL_CFG_DATA_PORT Registers
          43. 14.8.4.6.43  CTL_CFG_PRESENTSTATE Registers
          44. 14.8.4.6.44  CTL_CFG_HOST_CONTROL1 Registers
          45. 14.8.4.6.45  CTL_CFG_POWER_CONTROL Registers
          46. 14.8.4.6.46  CTL_CFG_BLOCK_GAP_CONTROL Registers
          47. 14.8.4.6.47  CTL_CFG_WAKEUP_CONTROL Registers
          48. 14.8.4.6.48  CTL_CFG_CLOCK_CONTROL Registers
          49. 14.8.4.6.49  CTL_CFG_TIMEOUT_CONTROL Registers
          50. 14.8.4.6.50  CTL_CFG_SOFTWARE_RESET Registers
          51. 14.8.4.6.51  CTL_CFG_NORMAL_INTR_STS Registers
          52. 14.8.4.6.52  CTL_CFG_ERROR_INTR_STS Registers
          53. 14.8.4.6.53  CTL_CFG_NORMAL_INTR_STS_ENA Registers
          54. 14.8.4.6.54  CTL_CFG_ERROR_INTR_STS_ENA Registers
          55. 14.8.4.6.55  CTL_CFG_NORMAL_INTR_SIG_ENA Registers
          56. 14.8.4.6.56  CTL_CFG_ERROR_INTR_SIG_ENA Registers
          57. 14.8.4.6.57  CTL_CFG_AUTOCMD_ERR_STS Registers
          58. 14.8.4.6.58  CTL_CFG_HOST_CONTROL2 Registers
          59. 14.8.4.6.59  CTL_CFG_CAPABILITIES Registers
          60. 14.8.4.6.60  CTL_CFG_MAX_CURRENT_CAP Registers
          61. 14.8.4.6.61  CTL_CFG_FORCE_EVNT_ACMD_ERR_STS Registers
          62. 14.8.4.6.62  CTL_CFG_FORCE_EVNT_ERR_INT_STS Registers
          63. 14.8.4.6.63  CTL_CFG_ADMA_ERR_STATUS Registers
          64. 14.8.4.6.64  CTL_CFG_ADMA_SYS_ADDRESS Registers
          65. 14.8.4.6.65  CTL_CFG_PRESET_VALUE0 Registers
          66. 14.8.4.6.66  CTL_CFG_PRESET_VALUE1 Registers
          67. 14.8.4.6.67  CTL_CFG_PRESET_VALUE2 Registers
          68. 14.8.4.6.68  CTL_CFG_PRESET_VALUE3 Registers
          69. 14.8.4.6.69  CTL_CFG_PRESET_VALUE4 Registers
          70. 14.8.4.6.70  CTL_CFG_PRESET_VALUE5 Registers
          71. 14.8.4.6.71  CTL_CFG_PRESET_VALUE6 Registers
          72. 14.8.4.6.72  CTL_CFG_PRESET_VALUE7 Registers
          73. 14.8.4.6.73  CTL_CFG_PRESET_VALUE8 Registers
          74. 14.8.4.6.74  CTL_CFG_PRESET_VALUE10 Registers
          75. 14.8.4.6.75  CTL_CFG_ADMA3_DESC_ADDRESS Registers
          76. 14.8.4.6.76  CTL_CFG_UHS2_BLOCK_SIZE Registers
          77. 14.8.4.6.77  CTL_CFG_UHS2_BLOCK_COUNT Registers
          78. 14.8.4.6.78  CTL_CFG_UHS2_COMMAND_PKT_N Registers
          79. 14.8.4.6.79  CTL_CFG_UHS2_XFER_MODE Registers
          80. 14.8.4.6.80  CTL_CFG_UHS2_COMMAND Registers
          81. 14.8.4.6.81  CTL_CFG_UHS2_RESPONSE_N Registers
          82. 14.8.4.6.82  CTL_CFG_UHS2_MESSAGE_SELECT Registers
          83. 14.8.4.6.83  CTL_CFG_UHS2_MESSAGE Registers
          84. 14.8.4.6.84  CTL_CFG_UHS2_DEVICE_INTR_STATUS Registers
          85. 14.8.4.6.85  CTL_CFG_UHS2_DEVICE_SELECT Registers
          86. 14.8.4.6.86  CTL_CFG_UHS2_DEVICE_INT_CODE Registers
          87. 14.8.4.6.87  CTL_CFG_UHS2_SOFTWARE_RESET Registers
          88. 14.8.4.6.88  CTL_CFG_UHS2_TIMER_CONTROL Registers
          89. 14.8.4.6.89  CTL_CFG_UHS2_ERR_INTR_STS Registers
          90. 14.8.4.6.90  CTL_CFG_UHS2_ERR_INTR_STS_ENA Registers
          91. 14.8.4.6.91  CTL_CFG_UHS2_ERR_INTR_SIG_ENA Registers
          92. 14.8.4.6.92  CTL_CFG_UHS2_SETTINGS_PTR Registers
          93. 14.8.4.6.93  CTL_CFG_UHS2_CAPABILITIES_PTR Registers
          94. 14.8.4.6.94  CTL_CFG_UHS2_TEST_PTR Registers
          95. 14.8.4.6.95  CTL_CFG_SHARED_BUS_CTRL_PTR Registers
          96. 14.8.4.6.96  CTL_CFG_VENDOR_SPECFIC_PTR Registers
          97. 14.8.4.6.97  CTL_CFG_BOOT_TIMEOUT_CONTROL Registers
          98. 14.8.4.6.98  CTL_CFG_VENDOR_REGISTER Registers
          99. 14.8.4.6.99  CTL_CFG_SLOT_INT_STS Registers
          100. 14.8.4.6.100 CTL_CFG_HOST_CONTROLLER_VER Registers
          101. 14.8.4.6.101 CTL_CFG_UHS2_GEN_SETTINGS Registers
          102. 14.8.4.6.102 CTL_CFG_UHS2_PHY_SETTINGS Registers
          103. 14.8.4.6.103 CTL_CFG_UHS2_LNK_TRN_SETTINGS Registers
          104. 14.8.4.6.104 CTL_CFG_UHS2_GEN_CAP Registers
          105. 14.8.4.6.105 CTL_CFG_UHS2_PHY_CAP Registers
          106. 14.8.4.6.106 CTL_CFG_UHS2_LNK_TRN_CAP Registers
          107. 14.8.4.6.107 CTL_CFG_FORCE_UHSII_ERR_INT_STS Registers
          108. 14.8.4.6.108 CTL_CFG_CQ_VERSION Registers
          109. 14.8.4.6.109 CTL_CFG_CQ_CAPABILITIES Registers
          110. 14.8.4.6.110 CTL_CFG_CQ_CONFIG Registers
          111. 14.8.4.6.111 CTL_CFG_CQ_CONTROL Registers
          112. 14.8.4.6.112 CTL_CFG_CQ_INTR_STS Registers
          113. 14.8.4.6.113 CTL_CFG_CQ_INTR_STS_ENA Registers
          114. 14.8.4.6.114 CTL_CFG_CQ_INTR_SIG_ENA Registers
          115. 14.8.4.6.115 CTL_CFG_CQ_INTR_COALESCING Registers
          116. 14.8.4.6.116 CTL_CFG_CQ_TDL_BASE_ADDR Registers
          117. 14.8.4.6.117 CTL_CFG_CQ_TDL_BASE_ADDR_UPBITS Registers
          118. 14.8.4.6.118 CTL_CFG_CQ_TASK_DOOR_BELL Registers
          119. 14.8.4.6.119 CTL_CFG_CQ_TASK_COMP_NOTIF Registers
          120. 14.8.4.6.120 CTL_CFG_CQ_DEV_QUEUE_STATUS Registers
          121. 14.8.4.6.121 CTL_CFG_CQ_DEV_PENDING_TASKS Registers
          122. 14.8.4.6.122 CTL_CFG_CQ_TASK_CLEAR Registers
          123. 14.8.4.6.123 CTL_CFG_CQ_SEND_STS_CONFIG1 Registers
          124. 14.8.4.6.124 CTL_CFG_CQ_SEND_STS_CONFIG2 Registers
          125. 14.8.4.6.125 CTL_CFG_CQ_DCMD_RESPONSE Registers
          126. 14.8.4.6.126 CTL_CFG_CQ_RESP_ERR_MASK Registers
          127. 14.8.4.6.127 CTL_CFG_CQ_TASK_ERR_INFO Registers
          128. 14.8.4.6.128 CTL_CFG_CQ_CMD_RESP_INDEX Registers
          129. 14.8.4.6.129 CTL_CFG_CQ_CMD_RESP_ARG Registers
          130. 14.8.4.6.130 CTL_CFG_CQ_ERROR_TASK_ID Registers
          131. 14.8.4.6.131 SS_CFG_SS_ID_REV_REG Registers
          132. 14.8.4.6.132 SS_CFG_CTL_CFG_1_REG Registers
          133. 14.8.4.6.133 SS_CFG_CTL_CFG_2_REG Registers
          134. 14.8.4.6.134 SS_CFG_CTL_CFG_3_REG Registers
          135. 14.8.4.6.135 SS_CFG_CTL_CFG_4_REG Registers
          136. 14.8.4.6.136 SS_CFG_CTL_CFG_5_REG Registers
          137. 14.8.4.6.137 SS_CFG_CTL_CFG_6_REG Registers
          138. 14.8.4.6.138 SS_CFG_CTL_CFG_7_REG Registers
          139. 14.8.4.6.139 SS_CFG_CTL_CFG_8_REG Registers
          140. 14.8.4.6.140 SS_CFG_CTL_CFG_9_REG Registers
          141. 14.8.4.6.141 SS_CFG_CTL_CFG_10_REG Registers
          142. 14.8.4.6.142 SS_CFG_CTL_CFG_11_REG Registers
          143. 14.8.4.6.143 SS_CFG_CTL_CFG_12_REG Registers
          144. 14.8.4.6.144 SS_CFG_CTL_CFG_13_REG Registers
          145. 14.8.4.6.145 SS_CFG_CTL_CFG_14_REG Registers
          146. 14.8.4.6.146 SS_CFG_CTL_STAT_1_REG Registers
          147. 14.8.4.6.147 SS_CFG_CTL_STAT_2_REG Registers
          148. 14.8.4.6.148 SS_CFG_CTL_STAT_3_REG Registers
          149. 14.8.4.6.149 SS_CFG_CTL_STAT_4_REG Registers
          150. 14.8.4.6.150 SS_CFG_CTL_STAT_5_REG Registers
          151. 14.8.4.6.151 SS_CFG_CTL_STAT_6_REG Registers
          152. 14.8.4.6.152 SS_CFG_PHY_CTRL_1_REG Registers
          153. 14.8.4.6.153 SS_CFG_PHY_CTRL_2_REG Registers
          154. 14.8.4.6.154 SS_CFG_PHY_CTRL_3_REG Registers
          155. 14.8.4.6.155 SS_CFG_PHY_CTRL_4_REG Registers
          156. 14.8.4.6.156 SS_CFG_PHY_CTRL_5_REG Registers
          157. 14.8.4.6.157 SS_CFG_PHY_CTRL_6_REG Registers
          158. 14.8.4.6.158 SS_CFG_PHY_STAT_1_REG Registers
          159. 14.8.4.6.159 SS_CFG_PHY_STAT_2_REG Registers
          160. 14.8.4.6.160 Access Table
      5. 14.8.5 Industrial and Control Interfaces Registers
        1. 14.8.5.1 MCAN Registers
          1. 14.8.5.1.1  SS_MCANSS_PID Registers
          2. 14.8.5.1.2  SS_MCANSS_CTRL Registers
          3. 14.8.5.1.3  SS_MCANSS_STAT Registers
          4. 14.8.5.1.4  SS_MCANSS_ICS Registers
          5. 14.8.5.1.5  SS_MCANSS_IRS Registers
          6. 14.8.5.1.6  SS_MCANSS_IECS Registers
          7. 14.8.5.1.7  SS_MCANSS_IE Registers
          8. 14.8.5.1.8  SS_MCANSS_IES Registers
          9. 14.8.5.1.9  SS_MCANSS_EOI Registers
          10. 14.8.5.1.10 SS_MCANSS_EXT_TS_PRESCALER Registers
          11. 14.8.5.1.11 SS_MCANSS_EXT_TS_UNSERVICED_INTR_CNTR Registers
          12. 14.8.5.1.12 CFG_CREL Registers
          13. 14.8.5.1.13 CFG_ENDN Registers
          14. 14.8.5.1.14 CFG_CUST Registers
          15. 14.8.5.1.15 CFG_DBTP Registers
          16. 14.8.5.1.16 CFG_TEST Registers
          17. 14.8.5.1.17 CFG_RWD Registers
          18. 14.8.5.1.18 CFG_CCCR Registers
          19. 14.8.5.1.19 CFG_NBTP Registers
          20. 14.8.5.1.20 CFG_TSCC Registers
          21. 14.8.5.1.21 CFG_TSCV Registers
          22. 14.8.5.1.22 CFG_TOCC Registers
          23. 14.8.5.1.23 CFG_TOCV Registers
          24. 14.8.5.1.24 CFG_RESERVED00 Registers
          25. 14.8.5.1.25 CFG_RESERVED11 Registers
          26. 14.8.5.1.26 CFG_RESERVED22 Registers
          27. 14.8.5.1.27 CFG_RESERVED33 Registers
          28. 14.8.5.1.28 CFG_ECR Registers
          29. 14.8.5.1.29 CFG_PSR Registers
          30. 14.8.5.1.30 CFG_TDCR Registers
          31. 14.8.5.1.31 CFG_RESERVED44 Registers
          32. 14.8.5.1.32 CFG_IR Registers
          33. 14.8.5.1.33 CFG_IE Registers
          34. 14.8.5.1.34 CFG_ILS Registers
          35. 14.8.5.1.35 CFG_ILE Registers
          36. 14.8.5.1.36 CFG_RESERVED55 Registers
          37. 14.8.5.1.37 CFG_RESERVED66 Registers
          38. 14.8.5.1.38 CFG_RESERVED77 Registers
          39. 14.8.5.1.39 CFG_RESERVED88 Registers
          40. 14.8.5.1.40 CFG_RESERVED99 Registers
          41. 14.8.5.1.41 CFG_RESERVED1010 Registers
          42. 14.8.5.1.42 CFG_RESERVED1111 Registers
          43. 14.8.5.1.43 CFG_RESERVED1212 Registers
          44. 14.8.5.1.44 CFG_GFC Registers
          45. 14.8.5.1.45 CFG_SIDFC Registers
          46. 14.8.5.1.46 CFG_XIDFC Registers
          47. 14.8.5.1.47 CFG_RESERVED1313 Registers
          48. 14.8.5.1.48 CFG_XIDAM Registers
          49. 14.8.5.1.49 CFG_HPMS Registers
          50. 14.8.5.1.50 CFG_NDAT1 Registers
          51. 14.8.5.1.51 CFG_NDAT2 Registers
          52. 14.8.5.1.52 CFG_RXF0C Registers
          53. 14.8.5.1.53 CFG_RXF0S Registers
          54. 14.8.5.1.54 CFG_RXF0A Registers
          55. 14.8.5.1.55 CFG_RXBC Registers
          56. 14.8.5.1.56 CFG_RXF1C Registers
          57. 14.8.5.1.57 CFG_RXF1S Registers
          58. 14.8.5.1.58 CFG_RXF1A Registers
          59. 14.8.5.1.59 CFG_RXESC Registers
          60. 14.8.5.1.60 CFG_TXBC Registers
          61. 14.8.5.1.61 CFG_TXFQS Registers
          62. 14.8.5.1.62 CFG_TXESC Registers
          63. 14.8.5.1.63 CFG_TXBRP Registers
          64. 14.8.5.1.64 CFG_TXBAR Registers
          65. 14.8.5.1.65 CFG_TXBCR Registers
          66. 14.8.5.1.66 CFG_TXBTO Registers
          67. 14.8.5.1.67 CFG_TXBCF Registers
          68. 14.8.5.1.68 CFG_TXBTIE Registers
          69. 14.8.5.1.69 CFG_TXBCIE Registers
          70. 14.8.5.1.70 CFG_RESERVED1414 Registers
          71. 14.8.5.1.71 CFG_RESERVED1515 Registers
          72. 14.8.5.1.72 CFG_TXEFC Registers
          73. 14.8.5.1.73 CFG_TXEFS Registers
          74. 14.8.5.1.74 CFG_TXEFA Registers
          75. 14.8.5.1.75 CFG_RESERVED1616 Registers
          76. 14.8.5.1.76 CFG_RESERVUPPER256_N Registers
          77. 14.8.5.1.77 MSGMEM_RAM_RAM_REG_N Registers
          78. 14.8.5.1.78 ECC_AGGR_REV Registers
          79. 14.8.5.1.79 ECC_AGGR_VECTOR Registers
          80. 14.8.5.1.80 ECC_AGGR_STAT Registers
          81. 14.8.5.1.81 ECC_AGGR_RESERVED_SVBUS_N Registers
          82. 14.8.5.1.82 ECC_AGGR_SEC_EOI_REG Registers
          83. 14.8.5.1.83 ECC_AGGR_SEC_STATUS_REG0 Registers
          84. 14.8.5.1.84 ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
          85. 14.8.5.1.85 ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
          86. 14.8.5.1.86 ECC_AGGR_DED_EOI_REG Registers
          87. 14.8.5.1.87 ECC_AGGR_DED_STATUS_REG0 Registers
          88. 14.8.5.1.88 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
          89. 14.8.5.1.89 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
          90. 14.8.5.1.90 ECC_AGGR_AGGR_ENABLE_SET Registers
          91. 14.8.5.1.91 ECC_AGGR_AGGR_ENABLE_CLR Registers
          92. 14.8.5.1.92 ECC_AGGR_AGGR_STATUS_SET Registers
          93. 14.8.5.1.93 ECC_AGGR_AGGR_STATUS_CLR Registers
          94. 14.8.5.1.94 Access Table
        2. 14.8.5.2 ECAP Registers
          1. 14.8.5.2.1  CTL_STS_TSCNT Registers
          2. 14.8.5.2.2  CTL_STS_CNTPHS Registers
          3. 14.8.5.2.3  CTL_STS_CAP1 Registers
          4. 14.8.5.2.4  CTL_STS_CAP2 Registers
          5. 14.8.5.2.5  CTL_STS_CAP3 Registers
          6. 14.8.5.2.6  CTL_STS_CAP4 Registers
          7. 14.8.5.2.7  CTL_STS_ECCTL Registers
          8. 14.8.5.2.8  CTL_STS_ECINT_EN_FLG Registers
          9. 14.8.5.2.9  CTL_STS_ECINT_CLR_FRC Registers
          10. 14.8.5.2.10 CTL_STS_PID Registers
          11. 14.8.5.2.11 Access Table
        3. 14.8.5.3 EPWM Registers
          1. 14.8.5.3.1  EPWM_TBCTL Registers
          2. 14.8.5.3.2  EPWM_TBSTS Registers
          3. 14.8.5.3.3  EPWM_TBPHSHR Registers
          4. 14.8.5.3.4  EPWM_TBPHS Registers
          5. 14.8.5.3.5  EPWM_TBCNT Registers
          6. 14.8.5.3.6  EPWM_TBPRD Registers
          7. 14.8.5.3.7  EPWM_CMPCTL Registers
          8. 14.8.5.3.8  EPWM_CMPAHR Registers
          9. 14.8.5.3.9  EPWM_CMPA Registers
          10. 14.8.5.3.10 EPWM_CMPB Registers
          11. 14.8.5.3.11 EPWM_AQCTLA Registers
          12. 14.8.5.3.12 EPWM_AQCTLB Registers
          13. 14.8.5.3.13 EPWM_AQSFRC Registers
          14. 14.8.5.3.14 EPWM_AQCSFRC Registers
          15. 14.8.5.3.15 EPWM_DBCTL Registers
          16. 14.8.5.3.16 EPWM_DBRED Registers
          17. 14.8.5.3.17 EPWM_DBFED Registers
          18. 14.8.5.3.18 EPWM_TZSEL Registers
          19. 14.8.5.3.19 EPWM_TZCTL Registers
          20. 14.8.5.3.20 EPWM_TZEINT Registers
          21. 14.8.5.3.21 EPWM_TZFLG Registers
          22. 14.8.5.3.22 EPWM_TZCLR Registers
          23. 14.8.5.3.23 EPWM_TZFRC Registers
          24. 14.8.5.3.24 EPWM_ETSEL Registers
          25. 14.8.5.3.25 EPWM_ETPS Registers
          26. 14.8.5.3.26 EPWM_ETFLG Registers
          27. 14.8.5.3.27 EPWM_ETCLR Registers
          28. 14.8.5.3.28 EPWM_ETFRC Registers
          29. 14.8.5.3.29 EPWM_PCCTL Registers
          30. 14.8.5.3.30 EPWM_PID Registers
          31. 14.8.5.3.31 Access Table
        4. 14.8.5.4 EQEP Registers
          1. 14.8.5.4.1  REG_QPOSCNT Registers
          2. 14.8.5.4.2  REG_QPOSINIT Registers
          3. 14.8.5.4.3  REG_QPOSMAX Registers
          4. 14.8.5.4.4  REG_QPOSCMP Registers
          5. 14.8.5.4.5  REG_QPOSILAT Registers
          6. 14.8.5.4.6  REG_QPOSSLAT Registers
          7. 14.8.5.4.7  REG_QPOSLAT Registers
          8. 14.8.5.4.8  REG_QUTMR Registers
          9. 14.8.5.4.9  REG_QUPRD Registers
          10. 14.8.5.4.10 REG_QWDTMR Registers
          11. 14.8.5.4.11 REG_QWDPRD Registers
          12. 14.8.5.4.12 REG_QDECCTL_TYPE2 Registers
          13. 14.8.5.4.13 REG_QEPCTL Registers
          14. 14.8.5.4.14 REG_QCAPCTL Registers
          15. 14.8.5.4.15 REG_QPOSCTL Registers
          16. 14.8.5.4.16 REG_QEINT_TYPE1 Registers
          17. 14.8.5.4.17 REG_QFLG_TYPE1 Registers
          18. 14.8.5.4.18 REG_QCLR_TYPE1 Registers
          19. 14.8.5.4.19 REG_QFRC_TYPE1 Registers
          20. 14.8.5.4.20 REG_QEPSTS_TYPE1 Registers
          21. 14.8.5.4.21 REG_QCTMR Registers
          22. 14.8.5.4.22 REG_QCPRD Registers
          23. 14.8.5.4.23 REG_QCTMRLAT Registers
          24. 14.8.5.4.24 REG_QCPRDLAT Registers
          25. 14.8.5.4.25 REG_RESERVED_N Registers
          26. 14.8.5.4.26 REG_PID Registers
          27. 14.8.5.4.27 REG_REV_TYPE2 Registers
          28. 14.8.5.4.28 REG_QEPSTROBESEL Registers
          29. 14.8.5.4.29 REG_QMACTRL Registers
          30. 14.8.5.4.30 REG_QEPSRCSEL Registers
          31. 14.8.5.4.31 Access Table
      6. 14.8.6 Camera Subsystem Registers
        1. 14.8.6.1 csi_rx_if Registers
          1. 14.8.6.1.1   ECC_AGGR_CFG_REV Registers
          2. 14.8.6.1.2   ECC_AGGR_CFG_VECTOR Registers
          3. 14.8.6.1.3   ECC_AGGR_CFG_STAT Registers
          4. 14.8.6.1.4   ECC_AGGR_CFG_RESERVED_SVBUS_N Registers
          5. 14.8.6.1.5   ECC_AGGR_CFG_SEC_EOI_REG Registers
          6. 14.8.6.1.6   ECC_AGGR_CFG_SEC_STATUS_REG0 Registers
          7. 14.8.6.1.7   ECC_AGGR_CFG_SEC_ENABLE_SET_REG0 Registers
          8. 14.8.6.1.8   ECC_AGGR_CFG_SEC_ENABLE_CLR_REG0 Registers
          9. 14.8.6.1.9   ECC_AGGR_CFG_DED_EOI_REG Registers
          10. 14.8.6.1.10  ECC_AGGR_CFG_DED_STATUS_REG0 Registers
          11. 14.8.6.1.11  ECC_AGGR_CFG_DED_ENABLE_SET_REG0 Registers
          12. 14.8.6.1.12  ECC_AGGR_CFG_DED_ENABLE_CLR_REG0 Registers
          13. 14.8.6.1.13  ECC_AGGR_CFG_AGGR_ENABLE_SET Registers
          14. 14.8.6.1.14  ECC_AGGR_CFG_AGGR_ENABLE_CLR Registers
          15. 14.8.6.1.15  ECC_AGGR_CFG_AGGR_STATUS_SET Registers
          16. 14.8.6.1.16  ECC_AGGR_CFG_AGGR_STATUS_CLR Registers
          17. 14.8.6.1.17  CP_INTD_CFG_INTD_CFG_REVISION Registers
          18. 14.8.6.1.18  CP_INTD_CFG_INTD_CFG_EOI_REG Registers
          19. 14.8.6.1.19  CP_INTD_CFG_INTD_CFG_INTR_VECTOR_REG Registers
          20. 14.8.6.1.20  CP_INTD_CFG_INTD_CFG_ENABLE_REG_LEVEL_0 Registers
          21. 14.8.6.1.21  CP_INTD_CFG_INTD_CFG_ENABLE_REG_PULSE_0 Registers
          22. 14.8.6.1.22  CP_INTD_CFG_INTD_CFG_ENABLE_CLR_REG_LEVEL_0 Registers
          23. 14.8.6.1.23  CP_INTD_CFG_INTD_CFG_ENABLE_CLR_REG_PULSE_0 Registers
          24. 14.8.6.1.24  CP_INTD_CFG_INTD_CFG_STATUS_REG_LEVEL_0 Registers
          25. 14.8.6.1.25  CP_INTD_CFG_INTD_CFG_STATUS_REG_PULSE_0 Registers
          26. 14.8.6.1.26  CP_INTD_CFG_INTD_CFG_STATUS_CLR_REG_LEVEL_0 Registers
          27. 14.8.6.1.27  CP_INTD_CFG_INTD_CFG_STATUS_CLR_REG_PULSE_0 Registers
          28. 14.8.6.1.28  CP_INTD_CFG_INTD_CFG_INTR_VECTOR_REG_LEVEL Registers
          29. 14.8.6.1.29  CP_INTD_CFG_INTD_CFG_INTR_VECTOR_REG_PULSE Registers
          30. 14.8.6.1.30  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_DEVICE_CONFIG Registers
          31. 14.8.6.1.31  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_SOFT_RESET Registers
          32. 14.8.6.1.32  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STATIC_CFG Registers
          33. 14.8.6.1.33  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ERROR_BYPASS_CFG Registers
          34. 14.8.6.1.34  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_MONITOR_IRQS Registers
          35. 14.8.6.1.35  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_MONITOR_IRQS_MASK_CFG Registers
          36. 14.8.6.1.36  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_INFO_IRQS Registers
          37. 14.8.6.1.37  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_INFO_IRQS_MASK_CFG Registers
          38. 14.8.6.1.38  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ERROR_IRQS Registers
          39. 14.8.6.1.39  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ERROR_IRQS_MASK_CFG Registers
          40. 14.8.6.1.40  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_DPHY_LANE_CONTROL Registers
          41. 14.8.6.1.41  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_DPHY_STATUS Registers
          42. 14.8.6.1.42  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_DPHY_ERR_STATUS_IRQ Registers
          43. 14.8.6.1.43  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_DPHY_ERR_IRQ_MASK_CFG Registers
          44. 14.8.6.1.44  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_INTEGRATION_DEBUG Registers
          45. 14.8.6.1.45  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ERROR_DEBUG Registers
          46. 14.8.6.1.46  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_TEST_GENERIC Registers
          47. 14.8.6.1.47  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_CTRL Registers
          48. 14.8.6.1.48  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_STATUS Registers
          49. 14.8.6.1.49  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_DATA_CFG Registers
          50. 14.8.6.1.50  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_CFG Registers
          51. 14.8.6.1.51  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_MONITOR_CTRL Registers
          52. 14.8.6.1.52  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_MONITOR_FRAME Registers
          53. 14.8.6.1.53  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_MONITOR_LB Registers
          54. 14.8.6.1.54  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_TIMER Registers
          55. 14.8.6.1.55  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_FCC_CFG Registers
          56. 14.8.6.1.56  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_FCC_CTRL Registers
          57. 14.8.6.1.57  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM0_FIFO_FILL_LVL Registers
          58. 14.8.6.1.58  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_CTRL Registers
          59. 14.8.6.1.59  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_STATUS Registers
          60. 14.8.6.1.60  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_DATA_CFG Registers
          61. 14.8.6.1.61  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_CFG Registers
          62. 14.8.6.1.62  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_MONITOR_CTRL Registers
          63. 14.8.6.1.63  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_MONITOR_FRAME Registers
          64. 14.8.6.1.64  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_MONITOR_LB Registers
          65. 14.8.6.1.65  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_TIMER Registers
          66. 14.8.6.1.66  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_FCC_CFG Registers
          67. 14.8.6.1.67  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_FCC_CTRL Registers
          68. 14.8.6.1.68  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM1_FIFO_FILL_LVL Registers
          69. 14.8.6.1.69  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_CTRL Registers
          70. 14.8.6.1.70  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_STATUS Registers
          71. 14.8.6.1.71  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_DATA_CFG Registers
          72. 14.8.6.1.72  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_CFG Registers
          73. 14.8.6.1.73  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_MONITOR_CTRL Registers
          74. 14.8.6.1.74  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_MONITOR_FRAME Registers
          75. 14.8.6.1.75  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_MONITOR_LB Registers
          76. 14.8.6.1.76  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_TIMER Registers
          77. 14.8.6.1.77  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_FCC_CFG Registers
          78. 14.8.6.1.78  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_FCC_CTRL Registers
          79. 14.8.6.1.79  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM2_FIFO_FILL_LVL Registers
          80. 14.8.6.1.80  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_CTRL Registers
          81. 14.8.6.1.81  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_STATUS Registers
          82. 14.8.6.1.82  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_DATA_CFG Registers
          83. 14.8.6.1.83  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_CFG Registers
          84. 14.8.6.1.84  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_MONITOR_CTRL Registers
          85. 14.8.6.1.85  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_MONITOR_FRAME Registers
          86. 14.8.6.1.86  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_MONITOR_LB Registers
          87. 14.8.6.1.87  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_TIMER Registers
          88. 14.8.6.1.88  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_FCC_CFG Registers
          89. 14.8.6.1.89  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_FCC_CTRL Registers
          90. 14.8.6.1.90  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_STREAM3_FIFO_FILL_LVL Registers
          91. 14.8.6.1.91  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_INT_STATUS Registers
          92. 14.8.6.1.92  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_INT_RAW_STATUS Registers
          93. 14.8.6.1.93  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_INT_MASK Registers
          94. 14.8.6.1.94  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_INT_TEST Registers
          95. 14.8.6.1.95  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_FATAL_NONFATAL_SELECT Registers
          96. 14.8.6.1.96  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_SRAM_CORR_FAULT_STATUS Registers
          97. 14.8.6.1.97  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_SRAM_UNCORR_FAULT_STATUS Registers
          98. 14.8.6.1.98  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_SRAM_FAULT_STATS Registers
          99. 14.8.6.1.99  VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_TRANS_TO_CTRL Registers
          100. 14.8.6.1.100 VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_TRANS_TO_FAULT_MASK Registers
          101. 14.8.6.1.101 VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_TRANS_TO_FAULT_STATUS Registers
          102. 14.8.6.1.102 VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_PROTOCOL_FAULT_MASK Registers
          103. 14.8.6.1.103 VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ASF_PROTOCOL_FAULT_STATUS Registers
          104. 14.8.6.1.104 VBUS2APB_WRAP_VBUSP_APB_CSI2RX_ID_PROD_VER Registers
          105. 14.8.6.1.105 RX_SHIM_VBUSP_MMR_CSI2RXIF_CSIRX_ID Registers
          106. 14.8.6.1.106 RX_SHIM_VBUSP_MMR_CSI2RXIF_VP0 Registers
          107. 14.8.6.1.107 RX_SHIM_VBUSP_MMR_CSI2RXIF_VP1 Registers
          108. 14.8.6.1.108 RX_SHIM_VBUSP_MMR_CSI2RXIF_CNTL Registers
          109. 14.8.6.1.109 RX_SHIM_VBUSP_MMR_CSI2RXIF_CNTX_CNTL_CNTX_CNTL_DMACNTX_J_J Registers
          110. 14.8.6.1.110 RX_SHIM_VBUSP_MMR_CSI2RXIF_CNTX_CNTL_CNTX_CNTL_PSI_CFG0_J_J Registers
          111. 14.8.6.1.111 RX_SHIM_VBUSP_MMR_CSI2RXIF_CNTX_CNTL_CNTX_CNTL_PSI_CFG1_J_J Registers
          112. 14.8.6.1.112 Access Table
        2. 14.8.6.2 DPHY_RX Registers
          1. 14.8.6.2.1  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_CMN0_CMN_DIG_TBIT2 Registers
          2. 14.8.6.2.2  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_CMN0_CMN_DIG_TBIT10 Registers
          3. 14.8.6.2.3  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_CMN0_CMN_DIG_TBIT13 Registers
          4. 14.8.6.2.4  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_CMN0_CMN_DIG_TBIT14 Registers
          5. 14.8.6.2.5  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_PCS_TX_DIG_TBIT0 Registers
          6. 14.8.6.2.6  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_PCS_TX_DIG_TBIT1 Registers
          7. 14.8.6.2.7  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_PCS_TX_DIG_TBIT2 Registers
          8. 14.8.6.2.8  VBUS2APB_WRAP_VBUSP_K3_DPHY_RX_PCS_TX_DIG_TBIT3 Registers
          9. 14.8.6.2.9  MMR_SLV_K3_DPHY_WRAP_LANE Registers
          10. 14.8.6.2.10 Access Table
      7. 14.8.7 Timer Modules Registers
        1. 14.8.7.1 GTC Registers
          1. 14.8.7.1.1  GTC_CFG0_PID Registers
          2. 14.8.7.1.2  GTC_CFG0_GTC_PID Registers
          3. 14.8.7.1.3  GTC_CFG0_PUSHEVT Registers
          4. 14.8.7.1.4  GTC_CFG1_CNTCR Registers
          5. 14.8.7.1.5  GTC_CFG1_CNTSR Registers
          6. 14.8.7.1.6  GTC_CFG1_CNTCV_LO Registers
          7. 14.8.7.1.7  GTC_CFG1_CNTCV_HI Registers
          8. 14.8.7.1.8  GTC_CFG1_CNTFID0 Registers
          9. 14.8.7.1.9  GTC_CFG1_CNTFID1 Registers
          10. 14.8.7.1.10 GTC_CFG2_CNTCVS_LO Registers
          11. 14.8.7.1.11 GTC_CFG2_CNTCVS_HI Registers
          12. 14.8.7.1.12 GTC_CFG3_CNTTIDR Registers
          13. 14.8.7.1.13 Access Table
        2. 14.8.7.2 RTI Registers
          1. 14.8.7.2.1  CFG_GCTRL Registers
          2. 14.8.7.2.2  CFG_TBCTRL Registers
          3. 14.8.7.2.3  CFG_CAPCTRL Registers
          4. 14.8.7.2.4  CFG_COMPCTRL Registers
          5. 14.8.7.2.5  CFG_FRC0 Registers
          6. 14.8.7.2.6  CFG_UC0 Registers
          7. 14.8.7.2.7  CFG_CPUC0 Registers
          8. 14.8.7.2.8  CFG_CAFRC0 Registers
          9. 14.8.7.2.9  CFG_CAUC0 Registers
          10. 14.8.7.2.10 CFG_FRC1 Registers
          11. 14.8.7.2.11 CFG_UC1 Registers
          12. 14.8.7.2.12 CFG_CPUC1 Registers
          13. 14.8.7.2.13 CFG_CAFRC1 Registers
          14. 14.8.7.2.14 CFG_CAUC1 Registers
          15. 14.8.7.2.15 CFG_COMP0 Registers
          16. 14.8.7.2.16 CFG_UDCP0 Registers
          17. 14.8.7.2.17 CFG_COMP1 Registers
          18. 14.8.7.2.18 CFG_UDCP1 Registers
          19. 14.8.7.2.19 CFG_COMP2 Registers
          20. 14.8.7.2.20 CFG_UDCP2 Registers
          21. 14.8.7.2.21 CFG_COMP3 Registers
          22. 14.8.7.2.22 CFG_UDCP3 Registers
          23. 14.8.7.2.23 CFG_TBLCOMP Registers
          24. 14.8.7.2.24 CFG_TBHCOMP Registers
          25. 14.8.7.2.25 CFG_SETINT Registers
          26. 14.8.7.2.26 CFG_CLEARINT Registers
          27. 14.8.7.2.27 CFG_INTFLAG Registers
          28. 14.8.7.2.28 CFG_DWDCTRL Registers
          29. 14.8.7.2.29 CFG_DWDPRLD Registers
          30. 14.8.7.2.30 CFG_WDSTATUS Registers
          31. 14.8.7.2.31 CFG_WDKEY Registers
          32. 14.8.7.2.32 CFG_DWDCNTR Registers
          33. 14.8.7.2.33 CFG_WWDRXNCTRL Registers
          34. 14.8.7.2.34 CFG_WWDSIZECTRL Registers
          35. 14.8.7.2.35 CFG_INTCLRENABLE Registers
          36. 14.8.7.2.36 CFG_COMP0CLR Registers
          37. 14.8.7.2.37 CFG_COMP1CLR Registers
          38. 14.8.7.2.38 CFG_COMP2CLR Registers
          39. 14.8.7.2.39 CFG_COMP3CLR Registers
          40. 14.8.7.2.40 Access Table
        3. 14.8.7.3 rtcss Registers
          1. 14.8.7.3.1  RTC_RTC_RTC_MOD_VER Registers
          2. 14.8.7.3.2  RTC_RTC_RTC_SUB_S_CNT Registers
          3. 14.8.7.3.3  RTC_RTC_RTC_S_CNT_LSW Registers
          4. 14.8.7.3.4  RTC_RTC_RTC_S_CNT_MSW Registers
          5. 14.8.7.3.5  RTC_RTC_RTC_COMP Registers
          6. 14.8.7.3.6  RTC_RTC_RTC_OFF_ON_S_CNT_LSW Registers
          7. 14.8.7.3.7  RTC_RTC_RTC_OFF_ON_S_CNT_MSW Registers
          8. 14.8.7.3.8  RTC_RTC_RTC_ON_OFF_S_CNT_LSW Registers
          9. 14.8.7.3.9  RTC_RTC_RTC_ON_OFF_S_CNT_MSW Registers
          10. 14.8.7.3.10 RTC_RTC_RTC_DEBOUNCE Registers
          11. 14.8.7.3.11 RTC_RTC_RTC_ANALOG Registers
          12. 14.8.7.3.12 RTC_RTC_RTC_SCRATCH0_N Registers
          13. 14.8.7.3.13 RTC_RTC_RTC_GENRAL_CTL Registers
          14. 14.8.7.3.14 RTC_RTC_RTC_IRQSTATUS_RAW_SYS Registers
          15. 14.8.7.3.15 RTC_RTC_RTC_IRQSTATUS_SYS Registers
          16. 14.8.7.3.16 RTC_RTC_RTC_IRQENABLE_SET_SYS Registers
          17. 14.8.7.3.17 RTC_RTC_RTC_IRQENABLE_CLR_SYS Registers
          18. 14.8.7.3.18 RTC_RTC_RTC_SYNCPEND Registers
          19. 14.8.7.3.19 RTC_RTC_RTC_KICK0 Registers
          20. 14.8.7.3.20 RTC_RTC_RTC_KICK1 Registers
          21. 14.8.7.3.21 Access Table
        4. 14.8.7.4 TIMER Registers
          1. 14.8.7.4.1  CFG_TIDR Registers
          2. 14.8.7.4.2  CFG_TIOCP_CFG Registers
          3. 14.8.7.4.3  CFG_IRQ_EOI Registers
          4. 14.8.7.4.4  CFG_IRQSTATUS_RAW Registers
          5. 14.8.7.4.5  CFG_IRQSTATUS Registers
          6. 14.8.7.4.6  CFG_IRQSTATUS_SET Registers
          7. 14.8.7.4.7  CFG_IRQSTATUS_CLR Registers
          8. 14.8.7.4.8  CFG_IRQWAKEEN Registers
          9. 14.8.7.4.9  CFG_TCLR Registers
          10. 14.8.7.4.10 CFG_TCRR Registers
          11. 14.8.7.4.11 CFG_TLDR Registers
          12. 14.8.7.4.12 CFG_TTGR Registers
          13. 14.8.7.4.13 CFG_TWPS Registers
          14. 14.8.7.4.14 CFG_TMAR Registers
          15. 14.8.7.4.15 CFG_TCAR1 Registers
          16. 14.8.7.4.16 CFG_TSICR Registers
          17. 14.8.7.4.17 CFG_TCAR2 Registers
          18. 14.8.7.4.18 CFG_TPIR Registers
          19. 14.8.7.4.19 CFG_TNIR Registers
          20. 14.8.7.4.20 CFG_TCVR Registers
          21. 14.8.7.4.21 CFG_TOCR Registers
          22. 14.8.7.4.22 CFG_TOWR Registers
          23. 14.8.7.4.23 Access Table
      8. 14.8.8 Internal Diagnostics Modules Registers
        1. 14.8.8.1 DCC Registers
          1. 14.8.8.1.1  _DCC_DCCGCTRL Registers
          2. 14.8.8.1.2  _DCC_DCCREV Registers
          3. 14.8.8.1.3  _DCC_DCCCNTSEED0 Registers
          4. 14.8.8.1.4  _DCC_DCCVALIDSEED0 Registers
          5. 14.8.8.1.5  _DCC_DCCCNTSEED1 Registers
          6. 14.8.8.1.6  _DCC_DCCSTATUS Registers
          7. 14.8.8.1.7  _DCC_DCCCNT0 Registers
          8. 14.8.8.1.8  _DCC_DCCVALID0 Registers
          9. 14.8.8.1.9  _DCC_DCCCNT1 Registers
          10. 14.8.8.1.10 _DCC_DCCCLKSRC1 Registers
          11. 14.8.8.1.11 _DCC_DCCCLKSRC0 Registers
          12. 14.8.8.1.12 _DCC_DCCGCTRL2 Registers
          13. 14.8.8.1.13 _DCC_DCCSTATUS2 Registers
          14. 14.8.8.1.14 _DCC_DCCERRCNT Registers
          15. 14.8.8.1.15 Access Table
        2. 14.8.8.2 ESM Registers
          1. 14.8.8.2.1  CFG_PID Registers
          2. 14.8.8.2.2  CFG_INFO Registers
          3. 14.8.8.2.3  CFG_EN Registers
          4. 14.8.8.2.4  CFG_SFT_RST Registers
          5. 14.8.8.2.5  CFG_ERR_RAW Registers
          6. 14.8.8.2.6  CFG_ERR_STS Registers
          7. 14.8.8.2.7  CFG_ERR_EN_SET Registers
          8. 14.8.8.2.8  CFG_ERR_EN_CLR Registers
          9. 14.8.8.2.9  CFG_LOW_PRI Registers
          10. 14.8.8.2.10 CFG_HI_PRI Registers
          11. 14.8.8.2.11 CFG_LOW Registers
          12. 14.8.8.2.12 CFG_HI Registers
          13. 14.8.8.2.13 CFG_EOI Registers
          14. 14.8.8.2.14 CFG_PIN_CTRL Registers
          15. 14.8.8.2.15 CFG_PIN_STS Registers
          16. 14.8.8.2.16 CFG_PIN_CNTR Registers
          17. 14.8.8.2.17 CFG_PIN_CNTR_PRE Registers
          18. 14.8.8.2.18 CFG_PWMH_PIN_CNTR Registers
          19. 14.8.8.2.19 CFG_PWMH_PIN_CNTR_PRE Registers
          20. 14.8.8.2.20 CFG_PWML_PIN_CNTR Registers
          21. 14.8.8.2.21 CFG_PWML_PIN_CNTR_PRE Registers
          22. 14.8.8.2.22 CFG_ERR_GRP_ERR_GRP_RAW_J_J Registers
          23. 14.8.8.2.23 CFG_ERR_GRP_ERR_GRP_STS_J_J Registers
          24. 14.8.8.2.24 CFG_ERR_GRP_ERR_GRP_INTR_EN_SET_J_J Registers
          25. 14.8.8.2.25 CFG_ERR_GRP_ERR_GRP_INTR_EN_CLR_J_J Registers
          26. 14.8.8.2.26 CFG_ERR_GRP_ERR_GRP_INT_PRIO_J_J Registers
          27. 14.8.8.2.27 CFG_ERR_GRP_ERR_GRP_PIN_EN_SET_J_J Registers
          28. 14.8.8.2.28 CFG_ERR_GRP_ERR_GRP_PIN_EN_CLR_J_J Registers
          29. 14.8.8.2.29 Access Table
        3. 14.8.8.3 MCRC64 Registers
          1. 14.8.8.3.1  REGS_MCRC64_MCRC64_CRC_CTRL0 Registers
          2. 14.8.8.3.2  REGS_MCRC64_MCRC64_CRC_CTRL1 Registers
          3. 14.8.8.3.3  REGS_MCRC64_MCRC64_CRC_CTRL2 Registers
          4. 14.8.8.3.4  REGS_MCRC64_MCRC64_CRC_INTS Registers
          5. 14.8.8.3.5  REGS_MCRC64_MCRC64_CRC_INTR Registers
          6. 14.8.8.3.6  REGS_MCRC64_MCRC64_CRC_STATUS Registers
          7. 14.8.8.3.7  REGS_MCRC64_MCRC64_CRC_INT_OFFSET_REG Registers
          8. 14.8.8.3.8  REGS_MCRC64_MCRC64_CRC_BUSY Registers
          9. 14.8.8.3.9  REGS_MCRC64_MCRC64_CRC_PCOUNT_REG1 Registers
          10. 14.8.8.3.10 REGS_MCRC64_MCRC64_CRC_SCOUNT_REG1 Registers
          11. 14.8.8.3.11 REGS_MCRC64_MCRC64_CRC_CURSEC_REG1 Registers
          12. 14.8.8.3.12 REGS_MCRC64_MCRC64_CRC_WDTOPLD1 Registers
          13. 14.8.8.3.13 REGS_MCRC64_MCRC64_CRC_BCTOPLD1 Registers
          14. 14.8.8.3.14 REGS_MCRC64_MCRC64_PSA_SIGREGL1 Registers
          15. 14.8.8.3.15 REGS_MCRC64_MCRC64_PSA_SIGREGH1 Registers
          16. 14.8.8.3.16 REGS_MCRC64_MCRC64_CRC_REGL1 Registers
          17. 14.8.8.3.17 REGS_MCRC64_MCRC64_CRC_REGH1 Registers
          18. 14.8.8.3.18 REGS_MCRC64_MCRC64_PSA_SECSIGREGL1 Registers
          19. 14.8.8.3.19 REGS_MCRC64_MCRC64_PSA_SECSIGREGH1 Registers
          20. 14.8.8.3.20 REGS_MCRC64_MCRC64_RAW_DATAREGL1 Registers
          21. 14.8.8.3.21 REGS_MCRC64_MCRC64_RAW_DATAREGH1 Registers
          22. 14.8.8.3.22 REGS_MCRC64_MCRC64_CRC_PCOUNT_REG2 Registers
          23. 14.8.8.3.23 REGS_MCRC64_MCRC64_CRC_SCOUNT_REG2 Registers
          24. 14.8.8.3.24 REGS_MCRC64_MCRC64_CRC_CURSEC_REG2 Registers
          25. 14.8.8.3.25 REGS_MCRC64_MCRC64_CRC_WDTOPLD2 Registers
          26. 14.8.8.3.26 REGS_MCRC64_MCRC64_CRC_BCTOPLD2 Registers
          27. 14.8.8.3.27 REGS_MCRC64_MCRC64_PSA_SIGREGL2 Registers
          28. 14.8.8.3.28 REGS_MCRC64_MCRC64_PSA_SIGREGH2 Registers
          29. 14.8.8.3.29 REGS_MCRC64_MCRC64_CRC_REGL2 Registers
          30. 14.8.8.3.30 REGS_MCRC64_MCRC64_CRC_REGH2 Registers
          31. 14.8.8.3.31 REGS_MCRC64_MCRC64_PSA_SECSIGREGL2 Registers
          32. 14.8.8.3.32 REGS_MCRC64_MCRC64_PSA_SECSIGREGH2 Registers
          33. 14.8.8.3.33 REGS_MCRC64_MCRC64_RAW_DATAREGL2 Registers
          34. 14.8.8.3.34 REGS_MCRC64_MCRC64_RAW_DATAREGH2 Registers
          35. 14.8.8.3.35 REGS_MCRC64_MCRC64_CRC_PCOUNT_REG3 Registers
          36. 14.8.8.3.36 REGS_MCRC64_MCRC64_CRC_SCOUNT_REG3 Registers
          37. 14.8.8.3.37 REGS_MCRC64_MCRC64_CRC_CURSEC_REG3 Registers
          38. 14.8.8.3.38 REGS_MCRC64_MCRC64_CRC_WDTOPLD3 Registers
          39. 14.8.8.3.39 REGS_MCRC64_MCRC64_CRC_BCTOPLD3 Registers
          40. 14.8.8.3.40 REGS_MCRC64_MCRC64_PSA_SIGREGL3 Registers
          41. 14.8.8.3.41 REGS_MCRC64_MCRC64_PSA_SIGREGH3 Registers
          42. 14.8.8.3.42 REGS_MCRC64_MCRC64_CRC_REGL3 Registers
          43. 14.8.8.3.43 REGS_MCRC64_MCRC64_CRC_REGH3 Registers
          44. 14.8.8.3.44 REGS_MCRC64_MCRC64_PSA_SECSIGREGL3 Registers
          45. 14.8.8.3.45 REGS_MCRC64_MCRC64_PSA_SECSIGREGH3 Registers
          46. 14.8.8.3.46 REGS_MCRC64_MCRC64_RAW_DATAREGL3 Registers
          47. 14.8.8.3.47 REGS_MCRC64_MCRC64_RAW_DATAREGH3 Registers
          48. 14.8.8.3.48 REGS_MCRC64_MCRC64_CRC_PCOUNT_REG4 Registers
          49. 14.8.8.3.49 REGS_MCRC64_MCRC64_CRC_SCOUNT_REG4 Registers
          50. 14.8.8.3.50 REGS_MCRC64_MCRC64_CRC_CURSEC_REG4 Registers
          51. 14.8.8.3.51 REGS_MCRC64_MCRC64_CRC_WDTOPLD4 Registers
          52. 14.8.8.3.52 REGS_MCRC64_MCRC64_CRC_BCTOPLD4 Registers
          53. 14.8.8.3.53 REGS_MCRC64_MCRC64_PSA_SIGREGL4 Registers
          54. 14.8.8.3.54 REGS_MCRC64_MCRC64_PSA_SIGREGH4 Registers
          55. 14.8.8.3.55 REGS_MCRC64_MCRC64_CRC_REGL4 Registers
          56. 14.8.8.3.56 REGS_MCRC64_MCRC64_CRC_REGH4 Registers
          57. 14.8.8.3.57 REGS_MCRC64_MCRC64_PSA_SECSIGREGL4 Registers
          58. 14.8.8.3.58 REGS_MCRC64_MCRC64_PSA_SECSIGREGH4 Registers
          59. 14.8.8.3.59 REGS_MCRC64_MCRC64_RAW_DATAREGL4 Registers
          60. 14.8.8.3.60 REGS_MCRC64_MCRC64_RAW_DATAREGH4 Registers
          61. 14.8.8.3.61 REGS_MCRC64_MCRC64_MCRC_BUS_SEL Registers
          62. 14.8.8.3.62 REGS_MCRC64_MCRC64_I0_PSA_SIGREG1_CPY_N Registers
          63. 14.8.8.3.63 REGS_MCRC64_MCRC64_I0_PSA_SIGREG2_CPY_N Registers
          64. 14.8.8.3.64 REGS_MCRC64_MCRC64_I0_PSA_SIGREG3_CPY_N Registers
          65. 14.8.8.3.65 REGS_MCRC64_MCRC64_I0_PSA_SIGREG4_CPY_N Registers
          66. 14.8.8.3.66 Access Table
        4. 14.8.8.4 ECC Aggregator Registers
          1. 14.8.8.4.1 ECC_AGGR Registers
            1. 14.8.8.4.1.1  ECC_AGGR_REV Registers
            2. 14.8.8.4.1.2  ECC_AGGR_VECTOR Registers
            3. 14.8.8.4.1.3  ECC_AGGR_STAT Registers
            4. 14.8.8.4.1.4  ECC_AGGR_RESERVED_SVBUS_N Registers
            5. 14.8.8.4.1.5  ECC_AGGR_SEC_EOI_REG Registers
            6. 14.8.8.4.1.6  ECC_AGGR_SEC_STATUS_REG0 Registers
            7. 14.8.8.4.1.7  ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
            8. 14.8.8.4.1.8  ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
            9. 14.8.8.4.1.9  ECC_AGGR_DED_EOI_REG Registers
            10. 14.8.8.4.1.10 ECC_AGGR_DED_STATUS_REG0 Registers
            11. 14.8.8.4.1.11 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
            12. 14.8.8.4.1.12 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
            13. 14.8.8.4.1.13 ECC_AGGR_AGGR_ENABLE_SET Registers
            14. 14.8.8.4.1.14 ECC_AGGR_AGGR_ENABLE_CLR Registers
            15. 14.8.8.4.1.15 ECC_AGGR_AGGR_STATUS_SET Registers
            16. 14.8.8.4.1.16 ECC_AGGR_AGGR_STATUS_CLR Registers
            17. 14.8.8.4.1.17 ECC_AGGR_SEC_STATUS_REG1 Registers
            18. 14.8.8.4.1.18 ECC_AGGR_SEC_ENABLE_SET_REG1 Registers
            19. 14.8.8.4.1.19 ECC_AGGR_SEC_ENABLE_CLR_REG1 Registers
            20. 14.8.8.4.1.20 ECC_AGGR_DED_STATUS_REG1 Registers
            21. 14.8.8.4.1.21 ECC_AGGR_DED_ENABLE_SET_REG1 Registers
            22. 14.8.8.4.1.22 ECC_AGGR_DED_ENABLE_CLR_REG1 Registers
            23. 14.8.8.4.1.23 Access Table
          2. 14.8.8.4.2 DMASS_ECC_AGGR_0 Registers
            1. 14.8.8.4.2.1  ECCAGGR_REV Registers
            2. 14.8.8.4.2.2  ECCAGGR_VECTOR Registers
            3. 14.8.8.4.2.3  ECCAGGR_STAT Registers
            4. 14.8.8.4.2.4  ECCAGGR_RESERVED_SVBUS_N Registers
            5. 14.8.8.4.2.5  ECCAGGR_SEC_EOI_REG Registers
            6. 14.8.8.4.2.6  ECCAGGR_SEC_STATUS_REG0 Registers
            7. 14.8.8.4.2.7  ECCAGGR_SEC_ENABLE_SET_REG0 Registers
            8. 14.8.8.4.2.8  ECCAGGR_SEC_ENABLE_CLR_REG0 Registers
            9. 14.8.8.4.2.9  ECCAGGR_DED_EOI_REG Registers
            10. 14.8.8.4.2.10 ECCAGGR_DED_STATUS_REG0 Registers
            11. 14.8.8.4.2.11 ECCAGGR_DED_ENABLE_SET_REG0 Registers
            12. 14.8.8.4.2.12 ECCAGGR_DED_ENABLE_CLR_REG0 Registers
            13. 14.8.8.4.2.13 ECCAGGR_AGGR_ENABLE_SET Registers
            14. 14.8.8.4.2.14 ECCAGGR_AGGR_ENABLE_CLR Registers
            15. 14.8.8.4.2.15 ECCAGGR_AGGR_STATUS_SET Registers
            16. 14.8.8.4.2.16 ECCAGGR_AGGR_STATUS_CLR Registers
            17. 14.8.8.4.2.17 Access Table
          3. 14.8.8.4.3 M4FSS_ECC_AGGR_0 Registers
            1. 14.8.8.4.3.1  ECC_AGGR_REV Registers
            2. 14.8.8.4.3.2  ECC_AGGR_VECTOR Registers
            3. 14.8.8.4.3.3  ECC_AGGR_STAT Registers
            4. 14.8.8.4.3.4  ECC_AGGR_RESERVED_SVBUS_N Registers
            5. 14.8.8.4.3.5  ECC_AGGR_SEC_EOI_REG Registers
            6. 14.8.8.4.3.6  ECC_AGGR_SEC_STATUS_REG0 Registers
            7. 14.8.8.4.3.7  ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
            8. 14.8.8.4.3.8  ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
            9. 14.8.8.4.3.9  ECC_AGGR_DED_EOI_REG Registers
            10. 14.8.8.4.3.10 ECC_AGGR_DED_STATUS_REG0 Registers
            11. 14.8.8.4.3.11 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
            12. 14.8.8.4.3.12 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
            13. 14.8.8.4.3.13 ECC_AGGR_AGGR_ENABLE_SET Registers
            14. 14.8.8.4.3.14 ECC_AGGR_AGGR_ENABLE_CLR Registers
            15. 14.8.8.4.3.15 ECC_AGGR_AGGR_STATUS_SET Registers
            16. 14.8.8.4.3.16 ECC_AGGR_AGGR_STATUS_CLR Registers
            17. 14.8.8.4.3.17 Access Table
          4. 14.8.8.4.4 PSC_ECC_AGGR_0 Registers
            1. 14.8.8.4.4.1  REGS_REV Registers
            2. 14.8.8.4.4.2  REGS_VECTOR Registers
            3. 14.8.8.4.4.3  REGS_STAT Registers
            4. 14.8.8.4.4.4  REGS_RESERVED_SVBUS_N Registers
            5. 14.8.8.4.4.5  REGS_SEC_EOI_REG Registers
            6. 14.8.8.4.4.6  REGS_SEC_STATUS_REG0 Registers
            7. 14.8.8.4.4.7  REGS_SEC_ENABLE_SET_REG0 Registers
            8. 14.8.8.4.4.8  REGS_SEC_ENABLE_CLR_REG0 Registers
            9. 14.8.8.4.4.9  REGS_DED_EOI_REG Registers
            10. 14.8.8.4.4.10 REGS_DED_STATUS_REG0 Registers
            11. 14.8.8.4.4.11 REGS_DED_ENABLE_SET_REG0 Registers
            12. 14.8.8.4.4.12 REGS_DED_ENABLE_CLR_REG0 Registers
            13. 14.8.8.4.4.13 REGS_AGGR_ENABLE_SET Registers
            14. 14.8.8.4.4.14 REGS_AGGR_ENABLE_CLR Registers
            15. 14.8.8.4.4.15 REGS_AGGR_STATUS_SET Registers
            16. 14.8.8.4.4.16 REGS_AGGR_STATUS_CLR Registers
            17. 14.8.8.4.4.17 Access Table
          5. 14.8.8.4.5 SAFE_ECC_AGGR Registers
            1. 14.8.8.4.5.1  ECC_AGGR_REV Registers
            2. 14.8.8.4.5.2  ECC_AGGR_VECTOR Registers
            3. 14.8.8.4.5.3  ECC_AGGR_STAT Registers
            4. 14.8.8.4.5.4  ECC_AGGR_RESERVED_SVBUS_N Registers
            5. 14.8.8.4.5.5  ECC_AGGR_SEC_EOI_REG Registers
            6. 14.8.8.4.5.6  ECC_AGGR_SEC_STATUS_REG0 Registers
            7. 14.8.8.4.5.7  ECC_AGGR_SEC_ENABLE_SET_REG0 Registers
            8. 14.8.8.4.5.8  ECC_AGGR_SEC_ENABLE_CLR_REG0 Registers
            9. 14.8.8.4.5.9  ECC_AGGR_DED_EOI_REG Registers
            10. 14.8.8.4.5.10 ECC_AGGR_DED_STATUS_REG0 Registers
            11. 14.8.8.4.5.11 ECC_AGGR_DED_ENABLE_SET_REG0 Registers
            12. 14.8.8.4.5.12 ECC_AGGR_DED_ENABLE_CLR_REG0 Registers
            13. 14.8.8.4.5.13 ECC_AGGR_AGGR_ENABLE_SET Registers
            14. 14.8.8.4.5.14 ECC_AGGR_AGGR_ENABLE_CLR Registers
            15. 14.8.8.4.5.15 ECC_AGGR_AGGR_STATUS_SET Registers
            16. 14.8.8.4.5.16 ECC_AGGR_AGGR_STATUS_CLR Registers
            17. 14.8.8.4.5.17 Access Table
      9. 14.8.9 Display Subsystem Registers
        1. 14.8.9.1 DSS Registers
          1. 14.8.9.1.1   COMMON_DSS_REVISION Registers
          2. 14.8.9.1.2   COMMON_DSS_SYSCONFIG Registers
          3. 14.8.9.1.3   COMMON_DSS_SYSSTATUS Registers
          4. 14.8.9.1.4   COMMON_DISPC_IRQ_EOI Registers
          5. 14.8.9.1.5   COMMON_DISPC_IRQSTATUS_RAW Registers
          6. 14.8.9.1.6   COMMON_DISPC_IRQSTATUS Registers
          7. 14.8.9.1.7   COMMON_DISPC_IRQENABLE_SET Registers
          8. 14.8.9.1.8   COMMON_DISPC_IRQENABLE_CLR Registers
          9. 14.8.9.1.9   COMMON_VID_IRQENABLE_0 Registers
          10. 14.8.9.1.10  COMMON_VID_IRQENABLE_1 Registers
          11. 14.8.9.1.11  COMMON_VID_IRQSTATUS_0 Registers
          12. 14.8.9.1.12  COMMON_VID_IRQSTATUS_1 Registers
          13. 14.8.9.1.13  COMMON_VP_IRQENABLE_0 Registers
          14. 14.8.9.1.14  COMMON_VP_IRQENABLE_1 Registers
          15. 14.8.9.1.15  COMMON_VP_IRQSTATUS_0 Registers
          16. 14.8.9.1.16  COMMON_VP_IRQSTATUS_1 Registers
          17. 14.8.9.1.17  COMMON_DISPC_GLOBAL_MFLAG_ATTRIBUTE Registers
          18. 14.8.9.1.18  COMMON_DISPC_GLOBAL_OUTPUT_ENABLE Registers
          19. 14.8.9.1.19  COMMON_DISPC_GLOBAL_BUFFER Registers
          20. 14.8.9.1.20  COMMON_DSS_CBA_CFG Registers
          21. 14.8.9.1.21  COMMON_DISPC_DBG_CONTROL Registers
          22. 14.8.9.1.22  COMMON_DISPC_DBG_STATUS Registers
          23. 14.8.9.1.23  COMMON_DISPC_CLKGATING_DISABLE Registers
          24. 14.8.9.1.24  COMMON_DISPC_SECURE_DISABLE Registers
          25. 14.8.9.1.25  COMMON1_DISPC_IRQ_EOI Registers
          26. 14.8.9.1.26  COMMON1_DISPC_IRQSTATUS_RAW Registers
          27. 14.8.9.1.27  COMMON1_DISPC_IRQSTATUS Registers
          28. 14.8.9.1.28  COMMON1_DISPC_IRQENABLE_SET Registers
          29. 14.8.9.1.29  COMMON1_DISPC_IRQENABLE_CLR Registers
          30. 14.8.9.1.30  COMMON1_VID_IRQENABLE_0 Registers
          31. 14.8.9.1.31  COMMON1_VID_IRQENABLE_1 Registers
          32. 14.8.9.1.32  COMMON1_DISPC_SECURE Registers
          33. 14.8.9.1.33  COMMON1_VID_IRQSTATUS_0 Registers
          34. 14.8.9.1.34  COMMON1_VID_IRQSTATUS_1 Registers
          35. 14.8.9.1.35  COMMON1_VP_IRQENABLE_0 Registers
          36. 14.8.9.1.36  COMMON1_VP_IRQENABLE_1 Registers
          37. 14.8.9.1.37  COMMON1_VP_IRQSTATUS_0 Registers
          38. 14.8.9.1.38  COMMON1_VP_IRQSTATUS_1 Registers
          39. 14.8.9.1.39  VIDL1_ATTRIBUTES Registers
          40. 14.8.9.1.40  VIDL1_ATTRIBUTES2 Registers
          41. 14.8.9.1.41  VIDL1_BA_0 Registers
          42. 14.8.9.1.42  VIDL1_BA_1 Registers
          43. 14.8.9.1.43  VIDL1_BA_UV_0 Registers
          44. 14.8.9.1.44  VIDL1_BA_UV_1 Registers
          45. 14.8.9.1.45  VIDL1_BUF_SIZE_STATUS Registers
          46. 14.8.9.1.46  VIDL1_BUF_THRESHOLD Registers
          47. 14.8.9.1.47  VIDL1_CSC_COEF0 Registers
          48. 14.8.9.1.48  VIDL1_CSC_COEF1 Registers
          49. 14.8.9.1.49  VIDL1_CSC_COEF2 Registers
          50. 14.8.9.1.50  VIDL1_CSC_COEF3 Registers
          51. 14.8.9.1.51  VIDL1_CSC_COEF4 Registers
          52. 14.8.9.1.52  VIDL1_CSC_COEF5 Registers
          53. 14.8.9.1.53  VIDL1_CSC_COEF6 Registers
          54. 14.8.9.1.54  VIDL1_GLOBAL_ALPHA Registers
          55. 14.8.9.1.55  VIDL1_MFLAG_THRESHOLD Registers
          56. 14.8.9.1.56  VIDL1_PICTURE_SIZE Registers
          57. 14.8.9.1.57  VIDL1_PIXEL_INC Registers
          58. 14.8.9.1.58  VIDL1_PRELOAD Registers
          59. 14.8.9.1.59  VIDL1_ROW_INC Registers
          60. 14.8.9.1.60  VIDL1_BA_EXT_0 Registers
          61. 14.8.9.1.61  VIDL1_BA_EXT_1 Registers
          62. 14.8.9.1.62  VIDL1_BA_UV_EXT_0 Registers
          63. 14.8.9.1.63  VIDL1_BA_UV_EXT_1 Registers
          64. 14.8.9.1.64  VIDL1_CSC_COEF7 Registers
          65. 14.8.9.1.65  VIDL1_ROW_INC_UV Registers
          66. 14.8.9.1.66  VIDL1_CLUT_0 Registers
          67. 14.8.9.1.67  VIDL1_CLUT_1 Registers
          68. 14.8.9.1.68  VIDL1_CLUT_2 Registers
          69. 14.8.9.1.69  VIDL1_CLUT_3 Registers
          70. 14.8.9.1.70  VIDL1_CLUT_4 Registers
          71. 14.8.9.1.71  VIDL1_CLUT_5 Registers
          72. 14.8.9.1.72  VIDL1_CLUT_6 Registers
          73. 14.8.9.1.73  VIDL1_CLUT_7 Registers
          74. 14.8.9.1.74  VIDL1_CLUT_8 Registers
          75. 14.8.9.1.75  VIDL1_CLUT_9 Registers
          76. 14.8.9.1.76  VIDL1_CLUT_10 Registers
          77. 14.8.9.1.77  VIDL1_CLUT_11 Registers
          78. 14.8.9.1.78  VIDL1_CLUT_12 Registers
          79. 14.8.9.1.79  VIDL1_CLUT_13 Registers
          80. 14.8.9.1.80  VIDL1_CLUT_14 Registers
          81. 14.8.9.1.81  VIDL1_CLUT_15 Registers
          82. 14.8.9.1.82  VIDL1_SAFETY_ATTRIBUTES Registers
          83. 14.8.9.1.83  VIDL1_SAFETY_CAPT_SIGNATURE Registers
          84. 14.8.9.1.84  VIDL1_SAFETY_POSITION Registers
          85. 14.8.9.1.85  VIDL1_SAFETY_REF_SIGNATURE Registers
          86. 14.8.9.1.86  VIDL1_SAFETY_SIZE Registers
          87. 14.8.9.1.87  VIDL1_SAFETY_LFSR_SEED Registers
          88. 14.8.9.1.88  VIDL1_LUMAKEY Registers
          89. 14.8.9.1.89  VID_ACCUH_0 Registers
          90. 14.8.9.1.90  VID_ACCUH_1 Registers
          91. 14.8.9.1.91  VID_ACCUH2_0 Registers
          92. 14.8.9.1.92  VID_ACCUH2_1 Registers
          93. 14.8.9.1.93  VID_ACCUV_0 Registers
          94. 14.8.9.1.94  VID_ACCUV_1 Registers
          95. 14.8.9.1.95  VID_ACCUV2_0 Registers
          96. 14.8.9.1.96  VID_ACCUV2_1 Registers
          97. 14.8.9.1.97  VID_ATTRIBUTES Registers
          98. 14.8.9.1.98  VID_ATTRIBUTES2 Registers
          99. 14.8.9.1.99  VID_BA_0 Registers
          100. 14.8.9.1.100 VID_BA_1 Registers
          101. 14.8.9.1.101 VID_BA_UV_0 Registers
          102. 14.8.9.1.102 VID_BA_UV_1 Registers
          103. 14.8.9.1.103 VID_BUF_SIZE_STATUS Registers
          104. 14.8.9.1.104 VID_BUF_THRESHOLD Registers
          105. 14.8.9.1.105 VID_CSC_COEF0 Registers
          106. 14.8.9.1.106 VID_CSC_COEF1 Registers
          107. 14.8.9.1.107 VID_CSC_COEF2 Registers
          108. 14.8.9.1.108 VID_CSC_COEF3 Registers
          109. 14.8.9.1.109 VID_CSC_COEF4 Registers
          110. 14.8.9.1.110 VID_CSC_COEF5 Registers
          111. 14.8.9.1.111 VID_CSC_COEF6 Registers
          112. 14.8.9.1.112 VID_FIRH Registers
          113. 14.8.9.1.113 VID_FIRH2 Registers
          114. 14.8.9.1.114 VID_FIRV Registers
          115. 14.8.9.1.115 VID_FIRV2 Registers
          116. 14.8.9.1.116 VID_FIR_COEF_H0_0 Registers
          117. 14.8.9.1.117 VID_FIR_COEF_H0_1 Registers
          118. 14.8.9.1.118 VID_FIR_COEF_H0_2 Registers
          119. 14.8.9.1.119 VID_FIR_COEF_H0_3 Registers
          120. 14.8.9.1.120 VID_FIR_COEF_H0_4 Registers
          121. 14.8.9.1.121 VID_FIR_COEF_H0_5 Registers
          122. 14.8.9.1.122 VID_FIR_COEF_H0_6 Registers
          123. 14.8.9.1.123 VID_FIR_COEF_H0_7 Registers
          124. 14.8.9.1.124 VID_FIR_COEF_H0_8 Registers
          125. 14.8.9.1.125 VID_FIR_COEF_H0_C_0 Registers
          126. 14.8.9.1.126 VID_FIR_COEF_H0_C_1 Registers
          127. 14.8.9.1.127 VID_FIR_COEF_H0_C_2 Registers
          128. 14.8.9.1.128 VID_FIR_COEF_H0_C_3 Registers
          129. 14.8.9.1.129 VID_FIR_COEF_H0_C_4 Registers
          130. 14.8.9.1.130 VID_FIR_COEF_H0_C_5 Registers
          131. 14.8.9.1.131 VID_FIR_COEF_H0_C_6 Registers
          132. 14.8.9.1.132 VID_FIR_COEF_H0_C_7 Registers
          133. 14.8.9.1.133 VID_FIR_COEF_H0_C_8 Registers
          134. 14.8.9.1.134 VID_FIR_COEF_H12_0 Registers
          135. 14.8.9.1.135 VID_FIR_COEF_H12_1 Registers
          136. 14.8.9.1.136 VID_FIR_COEF_H12_2 Registers
          137. 14.8.9.1.137 VID_FIR_COEF_H12_3 Registers
          138. 14.8.9.1.138 VID_FIR_COEF_H12_4 Registers
          139. 14.8.9.1.139 VID_FIR_COEF_H12_5 Registers
          140. 14.8.9.1.140 VID_FIR_COEF_H12_6 Registers
          141. 14.8.9.1.141 VID_FIR_COEF_H12_7 Registers
          142. 14.8.9.1.142 VID_FIR_COEF_H12_8 Registers
          143. 14.8.9.1.143 VID_FIR_COEF_H12_9 Registers
          144. 14.8.9.1.144 VID_FIR_COEF_H12_10 Registers
          145. 14.8.9.1.145 VID_FIR_COEF_H12_11 Registers
          146. 14.8.9.1.146 VID_FIR_COEF_H12_12 Registers
          147. 14.8.9.1.147 VID_FIR_COEF_H12_13 Registers
          148. 14.8.9.1.148 VID_FIR_COEF_H12_14 Registers
          149. 14.8.9.1.149 VID_FIR_COEF_H12_15 Registers
          150. 14.8.9.1.150 VID_FIR_COEF_H12_C_0 Registers
          151. 14.8.9.1.151 VID_FIR_COEF_H12_C_1 Registers
          152. 14.8.9.1.152 VID_FIR_COEF_H12_C_2 Registers
          153. 14.8.9.1.153 VID_FIR_COEF_H12_C_3 Registers
          154. 14.8.9.1.154 VID_FIR_COEF_H12_C_4 Registers
          155. 14.8.9.1.155 VID_FIR_COEF_H12_C_5 Registers
          156. 14.8.9.1.156 VID_FIR_COEF_H12_C_6 Registers
          157. 14.8.9.1.157 VID_FIR_COEF_H12_C_7 Registers
          158. 14.8.9.1.158 VID_FIR_COEF_H12_C_8 Registers
          159. 14.8.9.1.159 VID_FIR_COEF_H12_C_9 Registers
          160. 14.8.9.1.160 VID_FIR_COEF_H12_C_10 Registers
          161. 14.8.9.1.161 VID_FIR_COEF_H12_C_11 Registers
          162. 14.8.9.1.162 VID_FIR_COEF_H12_C_12 Registers
          163. 14.8.9.1.163 VID_FIR_COEF_H12_C_13 Registers
          164. 14.8.9.1.164 VID_FIR_COEF_H12_C_14 Registers
          165. 14.8.9.1.165 VID_FIR_COEF_H12_C_15 Registers
          166. 14.8.9.1.166 VID_FIR_COEF_V0_0 Registers
          167. 14.8.9.1.167 VID_FIR_COEF_V0_1 Registers
          168. 14.8.9.1.168 VID_FIR_COEF_V0_2 Registers
          169. 14.8.9.1.169 VID_FIR_COEF_V0_3 Registers
          170. 14.8.9.1.170 VID_FIR_COEF_V0_4 Registers
          171. 14.8.9.1.171 VID_FIR_COEF_V0_5 Registers
          172. 14.8.9.1.172 VID_FIR_COEF_V0_6 Registers
          173. 14.8.9.1.173 VID_FIR_COEF_V0_7 Registers
          174. 14.8.9.1.174 VID_FIR_COEF_V0_8 Registers
          175. 14.8.9.1.175 VID_FIR_COEF_V0_C_0 Registers
          176. 14.8.9.1.176 VID_FIR_COEF_V0_C_1 Registers
          177. 14.8.9.1.177 VID_FIR_COEF_V0_C_2 Registers
          178. 14.8.9.1.178 VID_FIR_COEF_V0_C_3 Registers
          179. 14.8.9.1.179 VID_FIR_COEF_V0_C_4 Registers
          180. 14.8.9.1.180 VID_FIR_COEF_V0_C_5 Registers
          181. 14.8.9.1.181 VID_FIR_COEF_V0_C_6 Registers
          182. 14.8.9.1.182 VID_FIR_COEF_V0_C_7 Registers
          183. 14.8.9.1.183 VID_FIR_COEF_V0_C_8 Registers
          184. 14.8.9.1.184 VID_FIR_COEF_V12_0 Registers
          185. 14.8.9.1.185 VID_FIR_COEF_V12_1 Registers
          186. 14.8.9.1.186 VID_FIR_COEF_V12_2 Registers
          187. 14.8.9.1.187 VID_FIR_COEF_V12_3 Registers
          188. 14.8.9.1.188 VID_FIR_COEF_V12_4 Registers
          189. 14.8.9.1.189 VID_FIR_COEF_V12_5 Registers
          190. 14.8.9.1.190 VID_FIR_COEF_V12_6 Registers
          191. 14.8.9.1.191 VID_FIR_COEF_V12_7 Registers
          192. 14.8.9.1.192 VID_FIR_COEF_V12_8 Registers
          193. 14.8.9.1.193 VID_FIR_COEF_V12_9 Registers
          194. 14.8.9.1.194 VID_FIR_COEF_V12_10 Registers
          195. 14.8.9.1.195 VID_FIR_COEF_V12_11 Registers
          196. 14.8.9.1.196 VID_FIR_COEF_V12_12 Registers
          197. 14.8.9.1.197 VID_FIR_COEF_V12_13 Registers
          198. 14.8.9.1.198 VID_FIR_COEF_V12_14 Registers
          199. 14.8.9.1.199 VID_FIR_COEF_V12_15 Registers
          200. 14.8.9.1.200 VID_FIR_COEF_V12_C_0 Registers
          201. 14.8.9.1.201 VID_FIR_COEF_V12_C_1 Registers
          202. 14.8.9.1.202 VID_FIR_COEF_V12_C_2 Registers
          203. 14.8.9.1.203 VID_FIR_COEF_V12_C_3 Registers
          204. 14.8.9.1.204 VID_FIR_COEF_V12_C_4 Registers
          205. 14.8.9.1.205 VID_FIR_COEF_V12_C_5 Registers
          206. 14.8.9.1.206 VID_FIR_COEF_V12_C_6 Registers
          207. 14.8.9.1.207 VID_FIR_COEF_V12_C_7 Registers
          208. 14.8.9.1.208 VID_FIR_COEF_V12_C_8 Registers
          209. 14.8.9.1.209 VID_FIR_COEF_V12_C_9 Registers
          210. 14.8.9.1.210 VID_FIR_COEF_V12_C_10 Registers
          211. 14.8.9.1.211 VID_FIR_COEF_V12_C_11 Registers
          212. 14.8.9.1.212 VID_FIR_COEF_V12_C_12 Registers
          213. 14.8.9.1.213 VID_FIR_COEF_V12_C_13 Registers
          214. 14.8.9.1.214 VID_FIR_COEF_V12_C_14 Registers
          215. 14.8.9.1.215 VID_FIR_COEF_V12_C_15 Registers
          216. 14.8.9.1.216 VID_GLOBAL_ALPHA Registers
          217. 14.8.9.1.217 VID_MFLAG_THRESHOLD Registers
          218. 14.8.9.1.218 VID_PICTURE_SIZE Registers
          219. 14.8.9.1.219 VID_PIXEL_INC Registers
          220. 14.8.9.1.220 VID_PRELOAD Registers
          221. 14.8.9.1.221 VID_ROW_INC Registers
          222. 14.8.9.1.222 VID_SIZE Registers
          223. 14.8.9.1.223 VID_BA_EXT_0 Registers
          224. 14.8.9.1.224 VID_BA_EXT_1 Registers
          225. 14.8.9.1.225 VID_BA_UV_EXT_0 Registers
          226. 14.8.9.1.226 VID_BA_UV_EXT_1 Registers
          227. 14.8.9.1.227 VID_CSC_COEF7 Registers
          228. 14.8.9.1.228 VID_ROW_INC_UV Registers
          229. 14.8.9.1.229 VID_CLUT_0 Registers
          230. 14.8.9.1.230 VID_CLUT_1 Registers
          231. 14.8.9.1.231 VID_CLUT_2 Registers
          232. 14.8.9.1.232 VID_CLUT_3 Registers
          233. 14.8.9.1.233 VID_CLUT_4 Registers
          234. 14.8.9.1.234 VID_CLUT_5 Registers
          235. 14.8.9.1.235 VID_CLUT_6 Registers
          236. 14.8.9.1.236 VID_CLUT_7 Registers
          237. 14.8.9.1.237 VID_CLUT_8 Registers
          238. 14.8.9.1.238 VID_CLUT_9 Registers
          239. 14.8.9.1.239 VID_CLUT_10 Registers
          240. 14.8.9.1.240 VID_CLUT_11 Registers
          241. 14.8.9.1.241 VID_CLUT_12 Registers
          242. 14.8.9.1.242 VID_CLUT_13 Registers
          243. 14.8.9.1.243 VID_CLUT_14 Registers
          244. 14.8.9.1.244 VID_CLUT_15 Registers
          245. 14.8.9.1.245 VID_SAFETY_ATTRIBUTES Registers
          246. 14.8.9.1.246 VID_SAFETY_CAPT_SIGNATURE Registers
          247. 14.8.9.1.247 VID_SAFETY_POSITION Registers
          248. 14.8.9.1.248 VID_SAFETY_REF_SIGNATURE Registers
          249. 14.8.9.1.249 VID_SAFETY_SIZE Registers
          250. 14.8.9.1.250 VID_SAFETY_LFSR_SEED Registers
          251. 14.8.9.1.251 VID_LUMAKEY Registers
          252. 14.8.9.1.252 OVR1_CONFIG Registers
          253. 14.8.9.1.253 OVR1_DEFAULT_COLOR Registers
          254. 14.8.9.1.254 OVR1_DEFAULT_COLOR2 Registers
          255. 14.8.9.1.255 OVR1_TRANS_COLOR_MAX Registers
          256. 14.8.9.1.256 OVR1_TRANS_COLOR_MAX2 Registers
          257. 14.8.9.1.257 OVR1_TRANS_COLOR_MIN Registers
          258. 14.8.9.1.258 OVR1_TRANS_COLOR_MIN2 Registers
          259. 14.8.9.1.259 OVR1_ATTRIBUTES_0 Registers
          260. 14.8.9.1.260 OVR1_ATTRIBUTES_1 Registers
          261. 14.8.9.1.261 OVR1_ATTRIBUTES_2 Registers
          262. 14.8.9.1.262 OVR1_ATTRIBUTES_3 Registers
          263. 14.8.9.1.263 OVR2_CONFIG Registers
          264. 14.8.9.1.264 OVR2_DEFAULT_COLOR Registers
          265. 14.8.9.1.265 OVR2_DEFAULT_COLOR2 Registers
          266. 14.8.9.1.266 OVR2_TRANS_COLOR_MAX Registers
          267. 14.8.9.1.267 OVR2_TRANS_COLOR_MAX2 Registers
          268. 14.8.9.1.268 OVR2_TRANS_COLOR_MIN Registers
          269. 14.8.9.1.269 OVR2_TRANS_COLOR_MIN2 Registers
          270. 14.8.9.1.270 OVR2_ATTRIBUTES_0 Registers
          271. 14.8.9.1.271 OVR2_ATTRIBUTES_1 Registers
          272. 14.8.9.1.272 OVR2_ATTRIBUTES_2 Registers
          273. 14.8.9.1.273 OVR2_ATTRIBUTES_3 Registers
          274. 14.8.9.1.274 VP1_CONFIG Registers
          275. 14.8.9.1.275 VP1_CONTROL Registers
          276. 14.8.9.1.276 VP1_CSC_COEF0 Registers
          277. 14.8.9.1.277 VP1_CSC_COEF1 Registers
          278. 14.8.9.1.278 VP1_CSC_COEF2 Registers
          279. 14.8.9.1.279 VP1_DATA_CYCLE_0 Registers
          280. 14.8.9.1.280 VP1_DATA_CYCLE_1 Registers
          281. 14.8.9.1.281 VP1_DATA_CYCLE_2 Registers
          282. 14.8.9.1.282 VP1_LINE_NUMBER Registers
          283. 14.8.9.1.283 VP1_POL_FREQ Registers
          284. 14.8.9.1.284 VP1_SIZE_SCREEN Registers
          285. 14.8.9.1.285 VP1_TIMING_H Registers
          286. 14.8.9.1.286 VP1_TIMING_V Registers
          287. 14.8.9.1.287 VP1_CSC_COEF3 Registers
          288. 14.8.9.1.288 VP1_CSC_COEF4 Registers
          289. 14.8.9.1.289 VP1_CSC_COEF5 Registers
          290. 14.8.9.1.290 VP1_CSC_COEF6 Registers
          291. 14.8.9.1.291 VP1_CSC_COEF7 Registers
          292. 14.8.9.1.292 VP1_SAFETY_ATTRIBUTES_0 Registers
          293. 14.8.9.1.293 VP1_SAFETY_ATTRIBUTES_1 Registers
          294. 14.8.9.1.294 VP1_SAFETY_ATTRIBUTES_2 Registers
          295. 14.8.9.1.295 VP1_SAFETY_ATTRIBUTES_3 Registers
          296. 14.8.9.1.296 VP1_SAFETY_CAPT_SIGNATURE_0 Registers
          297. 14.8.9.1.297 VP1_SAFETY_CAPT_SIGNATURE_1 Registers
          298. 14.8.9.1.298 VP1_SAFETY_CAPT_SIGNATURE_2 Registers
          299. 14.8.9.1.299 VP1_SAFETY_CAPT_SIGNATURE_3 Registers
          300. 14.8.9.1.300 VP1_SAFETY_POSITION_0 Registers
          301. 14.8.9.1.301 VP1_SAFETY_POSITION_1 Registers
          302. 14.8.9.1.302 VP1_SAFETY_POSITION_2 Registers
          303. 14.8.9.1.303 VP1_SAFETY_POSITION_3 Registers
          304. 14.8.9.1.304 VP1_SAFETY_REF_SIGNATURE_0 Registers
          305. 14.8.9.1.305 VP1_SAFETY_REF_SIGNATURE_1 Registers
          306. 14.8.9.1.306 VP1_SAFETY_REF_SIGNATURE_2 Registers
          307. 14.8.9.1.307 VP1_SAFETY_REF_SIGNATURE_3 Registers
          308. 14.8.9.1.308 VP1_SAFETY_SIZE_0 Registers
          309. 14.8.9.1.309 VP1_SAFETY_SIZE_1 Registers
          310. 14.8.9.1.310 VP1_SAFETY_SIZE_2 Registers
          311. 14.8.9.1.311 VP1_SAFETY_SIZE_3 Registers
          312. 14.8.9.1.312 VP1_SAFETY_LFSR_SEED Registers
          313. 14.8.9.1.313 VP1_GAMMA_TABLE_0 Registers
          314. 14.8.9.1.314 VP1_GAMMA_TABLE_1 Registers
          315. 14.8.9.1.315 VP1_GAMMA_TABLE_2 Registers
          316. 14.8.9.1.316 VP1_GAMMA_TABLE_3 Registers
          317. 14.8.9.1.317 VP1_GAMMA_TABLE_4 Registers
          318. 14.8.9.1.318 VP1_GAMMA_TABLE_5 Registers
          319. 14.8.9.1.319 VP1_GAMMA_TABLE_6 Registers
          320. 14.8.9.1.320 VP1_GAMMA_TABLE_7 Registers
          321. 14.8.9.1.321 VP1_GAMMA_TABLE_8 Registers
          322. 14.8.9.1.322 VP1_GAMMA_TABLE_9 Registers
          323. 14.8.9.1.323 VP1_GAMMA_TABLE_10 Registers
          324. 14.8.9.1.324 VP1_GAMMA_TABLE_11 Registers
          325. 14.8.9.1.325 VP1_GAMMA_TABLE_12 Registers
          326. 14.8.9.1.326 VP1_GAMMA_TABLE_13 Registers
          327. 14.8.9.1.327 VP1_GAMMA_TABLE_14 Registers
          328. 14.8.9.1.328 VP1_GAMMA_TABLE_15 Registers
          329. 14.8.9.1.329 VP1_DSS_OLDI_CFG Registers
          330. 14.8.9.1.330 VP1_DSS_OLDI_STATUS Registers
          331. 14.8.9.1.331 VP1_DSS_OLDI_LB Registers
          332. 14.8.9.1.332 VP2_CONFIG Registers
          333. 14.8.9.1.333 VP2_CONTROL Registers
          334. 14.8.9.1.334 VP2_CSC_COEF0 Registers
          335. 14.8.9.1.335 VP2_CSC_COEF1 Registers
          336. 14.8.9.1.336 VP2_CSC_COEF2 Registers
          337. 14.8.9.1.337 VP2_DATA_CYCLE_0 Registers
          338. 14.8.9.1.338 VP2_DATA_CYCLE_1 Registers
          339. 14.8.9.1.339 VP2_DATA_CYCLE_2 Registers
          340. 14.8.9.1.340 VP2_LINE_NUMBER Registers
          341. 14.8.9.1.341 VP2_POL_FREQ Registers
          342. 14.8.9.1.342 VP2_SIZE_SCREEN Registers
          343. 14.8.9.1.343 VP2_TIMING_H Registers
          344. 14.8.9.1.344 VP2_TIMING_V Registers
          345. 14.8.9.1.345 VP2_CSC_COEF3 Registers
          346. 14.8.9.1.346 VP2_CSC_COEF4 Registers
          347. 14.8.9.1.347 VP2_CSC_COEF5 Registers
          348. 14.8.9.1.348 VP2_CSC_COEF6 Registers
          349. 14.8.9.1.349 VP2_CSC_COEF7 Registers
          350. 14.8.9.1.350 VP2_SAFETY_ATTRIBUTES_0 Registers
          351. 14.8.9.1.351 VP2_SAFETY_ATTRIBUTES_1 Registers
          352. 14.8.9.1.352 VP2_SAFETY_ATTRIBUTES_2 Registers
          353. 14.8.9.1.353 VP2_SAFETY_ATTRIBUTES_3 Registers
          354. 14.8.9.1.354 VP2_SAFETY_CAPT_SIGNATURE_0 Registers
          355. 14.8.9.1.355 VP2_SAFETY_CAPT_SIGNATURE_1 Registers
          356. 14.8.9.1.356 VP2_SAFETY_CAPT_SIGNATURE_2 Registers
          357. 14.8.9.1.357 VP2_SAFETY_CAPT_SIGNATURE_3 Registers
          358. 14.8.9.1.358 VP2_SAFETY_POSITION_0 Registers
          359. 14.8.9.1.359 VP2_SAFETY_POSITION_1 Registers
          360. 14.8.9.1.360 VP2_SAFETY_POSITION_2 Registers
          361. 14.8.9.1.361 VP2_SAFETY_POSITION_3 Registers
          362. 14.8.9.1.362 VP2_SAFETY_REF_SIGNATURE_0 Registers
          363. 14.8.9.1.363 VP2_SAFETY_REF_SIGNATURE_1 Registers
          364. 14.8.9.1.364 VP2_SAFETY_REF_SIGNATURE_2 Registers
          365. 14.8.9.1.365 VP2_SAFETY_REF_SIGNATURE_3 Registers
          366. 14.8.9.1.366 VP2_SAFETY_SIZE_0 Registers
          367. 14.8.9.1.367 VP2_SAFETY_SIZE_1 Registers
          368. 14.8.9.1.368 VP2_SAFETY_SIZE_2 Registers
          369. 14.8.9.1.369 VP2_SAFETY_SIZE_3 Registers
          370. 14.8.9.1.370 VP2_SAFETY_LFSR_SEED Registers
          371. 14.8.9.1.371 VP2_GAMMA_TABLE_0 Registers
          372. 14.8.9.1.372 VP2_GAMMA_TABLE_1 Registers
          373. 14.8.9.1.373 VP2_GAMMA_TABLE_2 Registers
          374. 14.8.9.1.374 VP2_GAMMA_TABLE_3 Registers
          375. 14.8.9.1.375 VP2_GAMMA_TABLE_4 Registers
          376. 14.8.9.1.376 VP2_GAMMA_TABLE_5 Registers
          377. 14.8.9.1.377 VP2_GAMMA_TABLE_6 Registers
          378. 14.8.9.1.378 VP2_GAMMA_TABLE_7 Registers
          379. 14.8.9.1.379 VP2_GAMMA_TABLE_8 Registers
          380. 14.8.9.1.380 VP2_GAMMA_TABLE_9 Registers
          381. 14.8.9.1.381 VP2_GAMMA_TABLE_10 Registers
          382. 14.8.9.1.382 VP2_GAMMA_TABLE_11 Registers
          383. 14.8.9.1.383 VP2_GAMMA_TABLE_12 Registers
          384. 14.8.9.1.384 VP2_GAMMA_TABLE_13 Registers
          385. 14.8.9.1.385 VP2_GAMMA_TABLE_14 Registers
          386. 14.8.9.1.386 VP2_GAMMA_TABLE_15 Registers
          387. 14.8.9.1.387 Access Table
    9. 14.9 On-Chip Debug Registers
      1. 14.9.1 DEBUGSS Registers
        1. 14.9.1.1   SYS_TRACE Registers
        2. 14.9.1.2   ROM_ENTRY1 Registers
        3. 14.9.1.3   ROM_ENTRY2 Registers
        4. 14.9.1.4   ROM_ENTRY3 Registers
        5. 14.9.1.5   ROM_ENTRY4 Registers
        6. 14.9.1.6   ROM_ENTRY5 Registers
        7. 14.9.1.7   ROM_ENTRY6 Registers
        8. 14.9.1.8   ROM_ENTRY7 Registers
        9. 14.9.1.9   ROM_ENTRY8 Registers
        10. 14.9.1.10  ROM_ENTRY9 Registers
        11. 14.9.1.11  ROM_ENTRY10 Registers
        12. 14.9.1.12  ROM_ENTRY11 Registers
        13. 14.9.1.13  ROM_ENTRY12 Registers
        14. 14.9.1.14  ROM_ENTRY13 Registers
        15. 14.9.1.15  ROM_ENTRY14 Registers
        16. 14.9.1.16  ROM_PERIPHID4 Registers
        17. 14.9.1.17  ROM_PERIPHID5 Registers
        18. 14.9.1.18  ROM_PERIPHID6 Registers
        19. 14.9.1.19  ROM_PERIPHID7 Registers
        20. 14.9.1.20  ROM_PERIPHID0 Registers
        21. 14.9.1.21  ROM_PERIPHID1 Registers
        22. 14.9.1.22  ROM_PERIPHID2 Registers
        23. 14.9.1.23  ROM_PERIPHID3 Registers
        24. 14.9.1.24  ROM_COMPONENTID0 Registers
        25. 14.9.1.25  ROM_COMPONENTID1 Registers
        26. 14.9.1.26  ROM_COMPONENTID2 Registers
        27. 14.9.1.27  ROM_COMPONENTID3 Registers
        28. 14.9.1.28  CTSET2_WRAP_CFG_CTSET2_CFG_CTSETID Registers
        29. 14.9.1.29  CTSET2_WRAP_CFG_CTSET2_CFG_CTSETSYSCFG Registers
        30. 14.9.1.30  CTSET2_WRAP_CFG_CTSET2_CFG_SETSTR Registers
        31. 14.9.1.31  CTSET2_WRAP_CFG_CTSET2_CFG_DBGTIMELOW Registers
        32. 14.9.1.32  CTSET2_WRAP_CFG_CTSET2_CFG_DBGTIMEHI Registers
        33. 14.9.1.33  CTSET2_WRAP_CFG_CTSET2_CFG_CTSETCFG Registers
        34. 14.9.1.34  CTSET2_WRAP_CFG_CTSET2_CFG_SETSPLREG Registers
        35. 14.9.1.35  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL1 Registers
        36. 14.9.1.36  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL2 Registers
        37. 14.9.1.37  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL3 Registers
        38. 14.9.1.38  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL4 Registers
        39. 14.9.1.39  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL5 Registers
        40. 14.9.1.40  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL6 Registers
        41. 14.9.1.41  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL7 Registers
        42. 14.9.1.42  CTSET2_WRAP_CFG_CTSET2_CFG_SETEVTENBL8 Registers
        43. 14.9.1.43  CTSET2_WRAP_CFG_CTSET2_CFG_SETMSTID Registers
        44. 14.9.1.44  CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTL Registers
        45. 14.9.1.45  CTSET2_WRAP_CFG_CTSET2_CFG_CTNUMDBG Registers
        46. 14.9.1.46  CTSET2_WRAP_CFG_CTSET2_CFG_CTUSERACCCTL Registers
        47. 14.9.1.47  CTSET2_WRAP_CFG_CTSET2_CFG_CTSTMCNTL Registers
        48. 14.9.1.48  CTSET2_WRAP_CFG_CTSET2_CFG_CTSTMMSTID Registers
        49. 14.9.1.49  CTSET2_WRAP_CFG_CTSET2_CFG_CTSTMINTVL Registers
        50. 14.9.1.50  CTSET2_WRAP_CFG_CTSET2_CFG_CTSTMSEL0 Registers
        51. 14.9.1.51  CTSET2_WRAP_CFG_CTSET2_CFG_CTSTMSEL1 Registers
        52. 14.9.1.52  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR0 Registers
        53. 14.9.1.53  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR1 Registers
        54. 14.9.1.54  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR2 Registers
        55. 14.9.1.55  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR3 Registers
        56. 14.9.1.56  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR4 Registers
        57. 14.9.1.57  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR5 Registers
        58. 14.9.1.58  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR6 Registers
        59. 14.9.1.59  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR7 Registers
        60. 14.9.1.60  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR8 Registers
        61. 14.9.1.61  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR9 Registers
        62. 14.9.1.62  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR10 Registers
        63. 14.9.1.63  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR11 Registers
        64. 14.9.1.64  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR12 Registers
        65. 14.9.1.65  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR13 Registers
        66. 14.9.1.66  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR14 Registers
        67. 14.9.1.67  CTSET2_WRAP_CFG_CTSET2_CFG_CTINTVLR15 Registers
        68. 14.9.1.68  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL0 Registers
        69. 14.9.1.69  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL1 Registers
        70. 14.9.1.70  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL2 Registers
        71. 14.9.1.71  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL3 Registers
        72. 14.9.1.72  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL4 Registers
        73. 14.9.1.73  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL5 Registers
        74. 14.9.1.74  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL6 Registers
        75. 14.9.1.75  CTSET2_WRAP_CFG_CTSET2_CFG_CTDBGSGL7 Registers
        76. 14.9.1.76  CTSET2_WRAP_CFG_CTSET2_CFG_CTGNBL0 Registers
        77. 14.9.1.77  CTSET2_WRAP_CFG_CTSET2_CFG_CTGNBL1 Registers
        78. 14.9.1.78  CTSET2_WRAP_CFG_CTSET2_CFG_CTGRST0 Registers
        79. 14.9.1.79  CTSET2_WRAP_CFG_CTSET2_CFG_CTGRST1 Registers
        80. 14.9.1.80  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR0 Registers
        81. 14.9.1.81  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR1 Registers
        82. 14.9.1.82  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR2 Registers
        83. 14.9.1.83  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR3 Registers
        84. 14.9.1.84  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR4 Registers
        85. 14.9.1.85  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR5 Registers
        86. 14.9.1.86  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR6 Registers
        87. 14.9.1.87  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR7 Registers
        88. 14.9.1.88  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR8 Registers
        89. 14.9.1.89  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR9 Registers
        90. 14.9.1.90  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR10 Registers
        91. 14.9.1.91  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR11 Registers
        92. 14.9.1.92  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR12 Registers
        93. 14.9.1.93  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR13 Registers
        94. 14.9.1.94  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR14 Registers
        95. 14.9.1.95  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR15 Registers
        96. 14.9.1.96  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR16 Registers
        97. 14.9.1.97  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR17 Registers
        98. 14.9.1.98  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR18 Registers
        99. 14.9.1.99  CTSET2_WRAP_CFG_CTSET2_CFG_CTCR19 Registers
        100. 14.9.1.100 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR20 Registers
        101. 14.9.1.101 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR21 Registers
        102. 14.9.1.102 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR22 Registers
        103. 14.9.1.103 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR23 Registers
        104. 14.9.1.104 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR24 Registers
        105. 14.9.1.105 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR25 Registers
        106. 14.9.1.106 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR26 Registers
        107. 14.9.1.107 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR27 Registers
        108. 14.9.1.108 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR28 Registers
        109. 14.9.1.109 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR29 Registers
        110. 14.9.1.110 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR30 Registers
        111. 14.9.1.111 CTSET2_WRAP_CFG_CTSET2_CFG_CTCR31 Registers
        112. 14.9.1.112 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN0 Registers
        113. 14.9.1.113 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN1 Registers
        114. 14.9.1.114 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN2 Registers
        115. 14.9.1.115 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN3 Registers
        116. 14.9.1.116 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN4 Registers
        117. 14.9.1.117 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN5 Registers
        118. 14.9.1.118 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN6 Registers
        119. 14.9.1.119 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN7 Registers
        120. 14.9.1.120 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN8 Registers
        121. 14.9.1.121 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN9 Registers
        122. 14.9.1.122 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN10 Registers
        123. 14.9.1.123 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN11 Registers
        124. 14.9.1.124 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN12 Registers
        125. 14.9.1.125 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN13 Registers
        126. 14.9.1.126 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN14 Registers
        127. 14.9.1.127 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN15 Registers
        128. 14.9.1.128 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN16 Registers
        129. 14.9.1.129 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN17 Registers
        130. 14.9.1.130 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN18 Registers
        131. 14.9.1.131 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN19 Registers
        132. 14.9.1.132 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN20 Registers
        133. 14.9.1.133 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN21 Registers
        134. 14.9.1.134 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN22 Registers
        135. 14.9.1.135 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN23 Registers
        136. 14.9.1.136 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN24 Registers
        137. 14.9.1.137 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN25 Registers
        138. 14.9.1.138 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN26 Registers
        139. 14.9.1.139 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN27 Registers
        140. 14.9.1.140 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN28 Registers
        141. 14.9.1.141 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN29 Registers
        142. 14.9.1.142 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN30 Registers
        143. 14.9.1.143 CTSET2_WRAP_CFG_CTSET2_CFG_CTOWN31 Registers
        144. 14.9.1.144 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT0 Registers
        145. 14.9.1.145 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT1 Registers
        146. 14.9.1.146 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT2 Registers
        147. 14.9.1.147 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT3 Registers
        148. 14.9.1.148 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT4 Registers
        149. 14.9.1.149 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT5 Registers
        150. 14.9.1.150 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT6 Registers
        151. 14.9.1.151 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT7 Registers
        152. 14.9.1.152 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT8 Registers
        153. 14.9.1.153 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT9 Registers
        154. 14.9.1.154 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT10 Registers
        155. 14.9.1.155 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT11 Registers
        156. 14.9.1.156 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT12 Registers
        157. 14.9.1.157 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT13 Registers
        158. 14.9.1.158 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT14 Registers
        159. 14.9.1.159 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT15 Registers
        160. 14.9.1.160 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT16 Registers
        161. 14.9.1.161 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT17 Registers
        162. 14.9.1.162 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT18 Registers
        163. 14.9.1.163 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT19 Registers
        164. 14.9.1.164 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT20 Registers
        165. 14.9.1.165 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT21 Registers
        166. 14.9.1.166 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT22 Registers
        167. 14.9.1.167 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT23 Registers
        168. 14.9.1.168 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT24 Registers
        169. 14.9.1.169 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT25 Registers
        170. 14.9.1.170 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT26 Registers
        171. 14.9.1.171 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT27 Registers
        172. 14.9.1.172 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT28 Registers
        173. 14.9.1.173 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT29 Registers
        174. 14.9.1.174 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT30 Registers
        175. 14.9.1.175 CTSET2_WRAP_CFG_CTSET2_CFG_CTFILT31 Registers
        176. 14.9.1.176 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR0 Registers
        177. 14.9.1.177 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR1 Registers
        178. 14.9.1.178 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR2 Registers
        179. 14.9.1.179 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR3 Registers
        180. 14.9.1.180 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR4 Registers
        181. 14.9.1.181 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR5 Registers
        182. 14.9.1.182 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR6 Registers
        183. 14.9.1.183 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR7 Registers
        184. 14.9.1.184 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR8 Registers
        185. 14.9.1.185 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR9 Registers
        186. 14.9.1.186 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR10 Registers
        187. 14.9.1.187 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR11 Registers
        188. 14.9.1.188 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR12 Registers
        189. 14.9.1.189 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR13 Registers
        190. 14.9.1.190 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR14 Registers
        191. 14.9.1.191 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR15 Registers
        192. 14.9.1.192 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR16 Registers
        193. 14.9.1.193 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR17 Registers
        194. 14.9.1.194 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR18 Registers
        195. 14.9.1.195 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR19 Registers
        196. 14.9.1.196 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR20 Registers
        197. 14.9.1.197 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR21 Registers
        198. 14.9.1.198 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR22 Registers
        199. 14.9.1.199 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR23 Registers
        200. 14.9.1.200 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR24 Registers
        201. 14.9.1.201 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR25 Registers
        202. 14.9.1.202 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR26 Registers
        203. 14.9.1.203 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR27 Registers
        204. 14.9.1.204 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR28 Registers
        205. 14.9.1.205 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR29 Registers
        206. 14.9.1.206 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR30 Registers
        207. 14.9.1.207 CTSET2_WRAP_CFG_CTSET2_CFG_CTCNTR31 Registers
        208. 14.9.1.208 CTSET2_WRAP_CFG_CTSET2_CFG_CT_EOI Registers
        209. 14.9.1.209 CTSET2_WRAP_CFG_CTSET2_CFG_CTIRQSTAT_RAW Registers
        210. 14.9.1.210 CTSET2_WRAP_CFG_CTSET2_CFG_CTIRQSTAT Registers
        211. 14.9.1.211 CTSET2_WRAP_CFG_CTSET2_CFG_CTIRQENABLE_SET Registers
        212. 14.9.1.212 CTSET2_WRAP_CFG_CTSET2_CFG_CTIRQENABLE_CLR Registers
        213. 14.9.1.213 CTSET2_WRAP_CFG_CTSET2_CFG_STPTCR Registers
        214. 14.9.1.214 CTSET2_WRAP_CFG_CTSET2_CFG_STPTID Registers
        215. 14.9.1.215 CTSET2_WRAP_CFG_CTSET2_CFG_STPASYNC Registers
        216. 14.9.1.216 CTSET2_WRAP_CFG_CTSET2_CFG_STPFFCR Registers
        217. 14.9.1.217 CTSET2_WRAP_CFG_CTSET2_CFG_STPFEAT1 Registers
        218. 14.9.1.218 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_IDFILTER0 Registers
        219. 14.9.1.219 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_IDFILTER1 Registers
        220. 14.9.1.220 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_ITATBCTR1 Registers
        221. 14.9.1.221 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_ITATBCTR0 Registers
        222. 14.9.1.222 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_ITCTRL Registers
        223. 14.9.1.223 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_CLAIMSET Registers
        224. 14.9.1.224 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_CLAIMCLR Registers
        225. 14.9.1.225 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_LAR Registers
        226. 14.9.1.226 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_LSR Registers
        227. 14.9.1.227 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_AUTHSTATUS Registers
        228. 14.9.1.228 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_DEVID Registers
        229. 14.9.1.229 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_DEVTYPE Registers
        230. 14.9.1.230 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_PIDR4 Registers
        231. 14.9.1.231 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_PIDR0 Registers
        232. 14.9.1.232 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_PIDR1 Registers
        233. 14.9.1.233 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_PIDR2 Registers
        234. 14.9.1.234 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_PIDR3 Registers
        235. 14.9.1.235 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_CIDR0 Registers
        236. 14.9.1.236 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_CIDR1 Registers
        237. 14.9.1.237 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_CIDR2 Registers
        238. 14.9.1.238 ATB_REPLICATOR_CFG_CXATBREPLICATOR_CFG_CIDR3 Registers
        239. 14.9.1.239 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_CT_TBR_RAMSZ Registers
        240. 14.9.1.240 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_FIFOSZ Registers
        241. 14.9.1.241 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_STAT Registers
        242. 14.9.1.242 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_RAMRDAT Registers
        243. 14.9.1.243 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_RAMRPTR Registers
        244. 14.9.1.244 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_RAMWPTR Registers
        245. 14.9.1.245 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_TRGCNT Registers
        246. 14.9.1.246 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_TBR_CTRL Registers
        247. 14.9.1.247 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_RAMWDAT Registers
        248. 14.9.1.248 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_OUTLVL Registers
        249. 14.9.1.249 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_SICTRL Registers
        250. 14.9.1.250 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_IDPERIOD Registers
        251. 14.9.1.251 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_CT_TBR_SEQCNTL Registers
        252. 14.9.1.252 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_EOI Registers
        253. 14.9.1.253 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_IRQSTATUS_RAW Registers
        254. 14.9.1.254 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_IRQSTATUS Registers
        255. 14.9.1.255 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_IRQENABLE_SET Registers
        256. 14.9.1.256 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_IRQENABLE_CLR Registers
        257. 14.9.1.257 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_OPSTAT Registers
        258. 14.9.1.258 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_OPCTRL Registers
        259. 14.9.1.259 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_CLAIMSET Registers
        260. 14.9.1.260 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_CLAIMCLR Registers
        261. 14.9.1.261 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_LOCKACC Registers
        262. 14.9.1.262 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_LOCKSTAT Registers
        263. 14.9.1.263 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_AUTHSTAT Registers
        264. 14.9.1.264 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_DEVID Registers
        265. 14.9.1.265 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_DEVTYPE Registers
        266. 14.9.1.266 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID4 Registers
        267. 14.9.1.267 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID5 Registers
        268. 14.9.1.268 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID6 Registers
        269. 14.9.1.269 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID7 Registers
        270. 14.9.1.270 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID0 Registers
        271. 14.9.1.271 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID1 Registers
        272. 14.9.1.272 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID2 Registers
        273. 14.9.1.273 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_PERIPHID3 Registers
        274. 14.9.1.274 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_COMPID0 Registers
        275. 14.9.1.275 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_COMPID1 Registers
        276. 14.9.1.276 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_COMPID2 Registers
        277. 14.9.1.277 TBR_VBUSP_WRAP_TBR_CFG_TBR_CFG_COMPID3 Registers
        278. 14.9.1.278 ARM_CTI_0_CFG_CSCTI_CFG_CTICONTROL Registers
        279. 14.9.1.279 ARM_CTI_0_CFG_CSCTI_CFG_CTIINTACK Registers
        280. 14.9.1.280 ARM_CTI_0_CFG_CSCTI_CFG_CTIAPPSET Registers
        281. 14.9.1.281 ARM_CTI_0_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        282. 14.9.1.282 ARM_CTI_0_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        283. 14.9.1.283 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN0 Registers
        284. 14.9.1.284 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN1 Registers
        285. 14.9.1.285 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN2 Registers
        286. 14.9.1.286 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN3 Registers
        287. 14.9.1.287 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN4 Registers
        288. 14.9.1.288 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN5 Registers
        289. 14.9.1.289 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN6 Registers
        290. 14.9.1.290 ARM_CTI_0_CFG_CSCTI_CFG_CTIINEN7 Registers
        291. 14.9.1.291 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        292. 14.9.1.292 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        293. 14.9.1.293 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        294. 14.9.1.294 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        295. 14.9.1.295 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        296. 14.9.1.296 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        297. 14.9.1.297 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        298. 14.9.1.298 ARM_CTI_0_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        299. 14.9.1.299 ARM_CTI_0_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        300. 14.9.1.300 ARM_CTI_0_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        301. 14.9.1.301 ARM_CTI_0_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        302. 14.9.1.302 ARM_CTI_0_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        303. 14.9.1.303 ARM_CTI_0_CFG_CSCTI_CFG_CTIGATE Registers
        304. 14.9.1.304 ARM_CTI_0_CFG_CSCTI_CFG_ASICCTL Registers
        305. 14.9.1.305 ARM_CTI_0_CFG_CSCTI_CFG_ITCHINACK Registers
        306. 14.9.1.306 ARM_CTI_0_CFG_CSCTI_CFG_ITTRIGINACK Registers
        307. 14.9.1.307 ARM_CTI_0_CFG_CSCTI_CFG_ITCHOUT Registers
        308. 14.9.1.308 ARM_CTI_0_CFG_CSCTI_CFG_ITTRIGOUT Registers
        309. 14.9.1.309 ARM_CTI_0_CFG_CSCTI_CFG_ITCHOUTACK Registers
        310. 14.9.1.310 ARM_CTI_0_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        311. 14.9.1.311 ARM_CTI_0_CFG_CSCTI_CFG_ITCHIN Registers
        312. 14.9.1.312 ARM_CTI_0_CFG_CSCTI_CFG_ITTRIGIN Registers
        313. 14.9.1.313 ARM_CTI_0_CFG_CSCTI_CFG_ITCTRL Registers
        314. 14.9.1.314 ARM_CTI_0_CFG_CSCTI_CFG_CLAIMSET Registers
        315. 14.9.1.315 ARM_CTI_0_CFG_CSCTI_CFG_CLAIMCLR Registers
        316. 14.9.1.316 ARM_CTI_0_CFG_CSCTI_CFG_LAR Registers
        317. 14.9.1.317 ARM_CTI_0_CFG_CSCTI_CFG_LSR Registers
        318. 14.9.1.318 ARM_CTI_0_CFG_CSCTI_CFG_AUTHSTATUS Registers
        319. 14.9.1.319 ARM_CTI_0_CFG_CSCTI_CFG_DEVID Registers
        320. 14.9.1.320 ARM_CTI_0_CFG_CSCTI_CFG_DEVTYPE Registers
        321. 14.9.1.321 ARM_CTI_0_CFG_CSCTI_CFG_PERIPHID4 Registers
        322. 14.9.1.322 ARM_CTI_0_CFG_CSCTI_CFG_PERIPHID0 Registers
        323. 14.9.1.323 ARM_CTI_0_CFG_CSCTI_CFG_PERIPHID1 Registers
        324. 14.9.1.324 ARM_CTI_0_CFG_CSCTI_CFG_PERIPHID2 Registers
        325. 14.9.1.325 ARM_CTI_0_CFG_CSCTI_CFG_PERIPHID3 Registers
        326. 14.9.1.326 ARM_CTI_0_CFG_CSCTI_CFG_COMPID0 Registers
        327. 14.9.1.327 ARM_CTI_0_CFG_CSCTI_CFG_COMPID1 Registers
        328. 14.9.1.328 ARM_CTI_0_CFG_CSCTI_CFG_COMPID2 Registers
        329. 14.9.1.329 ARM_CTI_0_CFG_CSCTI_CFG_COMPID3 Registers
        330. 14.9.1.330 ARM_CTI_1_CFG_CSCTI_CFG_CTICONTROL Registers
        331. 14.9.1.331 ARM_CTI_1_CFG_CSCTI_CFG_CTIINTACK Registers
        332. 14.9.1.332 ARM_CTI_1_CFG_CSCTI_CFG_CTIAPPSET Registers
        333. 14.9.1.333 ARM_CTI_1_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        334. 14.9.1.334 ARM_CTI_1_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        335. 14.9.1.335 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN0 Registers
        336. 14.9.1.336 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN1 Registers
        337. 14.9.1.337 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN2 Registers
        338. 14.9.1.338 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN3 Registers
        339. 14.9.1.339 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN4 Registers
        340. 14.9.1.340 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN5 Registers
        341. 14.9.1.341 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN6 Registers
        342. 14.9.1.342 ARM_CTI_1_CFG_CSCTI_CFG_CTIINEN7 Registers
        343. 14.9.1.343 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        344. 14.9.1.344 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        345. 14.9.1.345 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        346. 14.9.1.346 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        347. 14.9.1.347 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        348. 14.9.1.348 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        349. 14.9.1.349 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        350. 14.9.1.350 ARM_CTI_1_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        351. 14.9.1.351 ARM_CTI_1_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        352. 14.9.1.352 ARM_CTI_1_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        353. 14.9.1.353 ARM_CTI_1_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        354. 14.9.1.354 ARM_CTI_1_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        355. 14.9.1.355 ARM_CTI_1_CFG_CSCTI_CFG_CTIGATE Registers
        356. 14.9.1.356 ARM_CTI_1_CFG_CSCTI_CFG_ASICCTL Registers
        357. 14.9.1.357 ARM_CTI_1_CFG_CSCTI_CFG_ITCHINACK Registers
        358. 14.9.1.358 ARM_CTI_1_CFG_CSCTI_CFG_ITTRIGINACK Registers
        359. 14.9.1.359 ARM_CTI_1_CFG_CSCTI_CFG_ITCHOUT Registers
        360. 14.9.1.360 ARM_CTI_1_CFG_CSCTI_CFG_ITTRIGOUT Registers
        361. 14.9.1.361 ARM_CTI_1_CFG_CSCTI_CFG_ITCHOUTACK Registers
        362. 14.9.1.362 ARM_CTI_1_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        363. 14.9.1.363 ARM_CTI_1_CFG_CSCTI_CFG_ITCHIN Registers
        364. 14.9.1.364 ARM_CTI_1_CFG_CSCTI_CFG_ITTRIGIN Registers
        365. 14.9.1.365 ARM_CTI_1_CFG_CSCTI_CFG_ITCTRL Registers
        366. 14.9.1.366 ARM_CTI_1_CFG_CSCTI_CFG_CLAIMSET Registers
        367. 14.9.1.367 ARM_CTI_1_CFG_CSCTI_CFG_CLAIMCLR Registers
        368. 14.9.1.368 ARM_CTI_1_CFG_CSCTI_CFG_LAR Registers
        369. 14.9.1.369 ARM_CTI_1_CFG_CSCTI_CFG_LSR Registers
        370. 14.9.1.370 ARM_CTI_1_CFG_CSCTI_CFG_AUTHSTATUS Registers
        371. 14.9.1.371 ARM_CTI_1_CFG_CSCTI_CFG_DEVID Registers
        372. 14.9.1.372 ARM_CTI_1_CFG_CSCTI_CFG_DEVTYPE Registers
        373. 14.9.1.373 ARM_CTI_1_CFG_CSCTI_CFG_PERIPHID4 Registers
        374. 14.9.1.374 ARM_CTI_1_CFG_CSCTI_CFG_PERIPHID0 Registers
        375. 14.9.1.375 ARM_CTI_1_CFG_CSCTI_CFG_PERIPHID1 Registers
        376. 14.9.1.376 ARM_CTI_1_CFG_CSCTI_CFG_PERIPHID2 Registers
        377. 14.9.1.377 ARM_CTI_1_CFG_CSCTI_CFG_PERIPHID3 Registers
        378. 14.9.1.378 ARM_CTI_1_CFG_CSCTI_CFG_COMPID0 Registers
        379. 14.9.1.379 ARM_CTI_1_CFG_CSCTI_CFG_COMPID1 Registers
        380. 14.9.1.380 ARM_CTI_1_CFG_CSCTI_CFG_COMPID2 Registers
        381. 14.9.1.381 ARM_CTI_1_CFG_CSCTI_CFG_COMPID3 Registers
        382. 14.9.1.382 ARM_CTI_2_CFG_CSCTI_CFG_CTICONTROL Registers
        383. 14.9.1.383 ARM_CTI_2_CFG_CSCTI_CFG_CTIINTACK Registers
        384. 14.9.1.384 ARM_CTI_2_CFG_CSCTI_CFG_CTIAPPSET Registers
        385. 14.9.1.385 ARM_CTI_2_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        386. 14.9.1.386 ARM_CTI_2_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        387. 14.9.1.387 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN0 Registers
        388. 14.9.1.388 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN1 Registers
        389. 14.9.1.389 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN2 Registers
        390. 14.9.1.390 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN3 Registers
        391. 14.9.1.391 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN4 Registers
        392. 14.9.1.392 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN5 Registers
        393. 14.9.1.393 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN6 Registers
        394. 14.9.1.394 ARM_CTI_2_CFG_CSCTI_CFG_CTIINEN7 Registers
        395. 14.9.1.395 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        396. 14.9.1.396 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        397. 14.9.1.397 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        398. 14.9.1.398 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        399. 14.9.1.399 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        400. 14.9.1.400 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        401. 14.9.1.401 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        402. 14.9.1.402 ARM_CTI_2_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        403. 14.9.1.403 ARM_CTI_2_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        404. 14.9.1.404 ARM_CTI_2_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        405. 14.9.1.405 ARM_CTI_2_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        406. 14.9.1.406 ARM_CTI_2_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        407. 14.9.1.407 ARM_CTI_2_CFG_CSCTI_CFG_CTIGATE Registers
        408. 14.9.1.408 ARM_CTI_2_CFG_CSCTI_CFG_ASICCTL Registers
        409. 14.9.1.409 ARM_CTI_2_CFG_CSCTI_CFG_ITCHINACK Registers
        410. 14.9.1.410 ARM_CTI_2_CFG_CSCTI_CFG_ITTRIGINACK Registers
        411. 14.9.1.411 ARM_CTI_2_CFG_CSCTI_CFG_ITCHOUT Registers
        412. 14.9.1.412 ARM_CTI_2_CFG_CSCTI_CFG_ITTRIGOUT Registers
        413. 14.9.1.413 ARM_CTI_2_CFG_CSCTI_CFG_ITCHOUTACK Registers
        414. 14.9.1.414 ARM_CTI_2_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        415. 14.9.1.415 ARM_CTI_2_CFG_CSCTI_CFG_ITCHIN Registers
        416. 14.9.1.416 ARM_CTI_2_CFG_CSCTI_CFG_ITTRIGIN Registers
        417. 14.9.1.417 ARM_CTI_2_CFG_CSCTI_CFG_ITCTRL Registers
        418. 14.9.1.418 ARM_CTI_2_CFG_CSCTI_CFG_CLAIMSET Registers
        419. 14.9.1.419 ARM_CTI_2_CFG_CSCTI_CFG_CLAIMCLR Registers
        420. 14.9.1.420 ARM_CTI_2_CFG_CSCTI_CFG_LAR Registers
        421. 14.9.1.421 ARM_CTI_2_CFG_CSCTI_CFG_LSR Registers
        422. 14.9.1.422 ARM_CTI_2_CFG_CSCTI_CFG_AUTHSTATUS Registers
        423. 14.9.1.423 ARM_CTI_2_CFG_CSCTI_CFG_DEVID Registers
        424. 14.9.1.424 ARM_CTI_2_CFG_CSCTI_CFG_DEVTYPE Registers
        425. 14.9.1.425 ARM_CTI_2_CFG_CSCTI_CFG_PERIPHID4 Registers
        426. 14.9.1.426 ARM_CTI_2_CFG_CSCTI_CFG_PERIPHID0 Registers
        427. 14.9.1.427 ARM_CTI_2_CFG_CSCTI_CFG_PERIPHID1 Registers
        428. 14.9.1.428 ARM_CTI_2_CFG_CSCTI_CFG_PERIPHID2 Registers
        429. 14.9.1.429 ARM_CTI_2_CFG_CSCTI_CFG_PERIPHID3 Registers
        430. 14.9.1.430 ARM_CTI_2_CFG_CSCTI_CFG_COMPID0 Registers
        431. 14.9.1.431 ARM_CTI_2_CFG_CSCTI_CFG_COMPID1 Registers
        432. 14.9.1.432 ARM_CTI_2_CFG_CSCTI_CFG_COMPID2 Registers
        433. 14.9.1.433 ARM_CTI_2_CFG_CSCTI_CFG_COMPID3 Registers
        434. 14.9.1.434 ARM_CTI_3_CFG_CSCTI_CFG_CTICONTROL Registers
        435. 14.9.1.435 ARM_CTI_3_CFG_CSCTI_CFG_CTIINTACK Registers
        436. 14.9.1.436 ARM_CTI_3_CFG_CSCTI_CFG_CTIAPPSET Registers
        437. 14.9.1.437 ARM_CTI_3_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        438. 14.9.1.438 ARM_CTI_3_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        439. 14.9.1.439 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN0 Registers
        440. 14.9.1.440 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN1 Registers
        441. 14.9.1.441 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN2 Registers
        442. 14.9.1.442 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN3 Registers
        443. 14.9.1.443 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN4 Registers
        444. 14.9.1.444 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN5 Registers
        445. 14.9.1.445 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN6 Registers
        446. 14.9.1.446 ARM_CTI_3_CFG_CSCTI_CFG_CTIINEN7 Registers
        447. 14.9.1.447 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        448. 14.9.1.448 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        449. 14.9.1.449 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        450. 14.9.1.450 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        451. 14.9.1.451 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        452. 14.9.1.452 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        453. 14.9.1.453 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        454. 14.9.1.454 ARM_CTI_3_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        455. 14.9.1.455 ARM_CTI_3_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        456. 14.9.1.456 ARM_CTI_3_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        457. 14.9.1.457 ARM_CTI_3_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        458. 14.9.1.458 ARM_CTI_3_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        459. 14.9.1.459 ARM_CTI_3_CFG_CSCTI_CFG_CTIGATE Registers
        460. 14.9.1.460 ARM_CTI_3_CFG_CSCTI_CFG_ASICCTL Registers
        461. 14.9.1.461 ARM_CTI_3_CFG_CSCTI_CFG_ITCHINACK Registers
        462. 14.9.1.462 ARM_CTI_3_CFG_CSCTI_CFG_ITTRIGINACK Registers
        463. 14.9.1.463 ARM_CTI_3_CFG_CSCTI_CFG_ITCHOUT Registers
        464. 14.9.1.464 ARM_CTI_3_CFG_CSCTI_CFG_ITTRIGOUT Registers
        465. 14.9.1.465 ARM_CTI_3_CFG_CSCTI_CFG_ITCHOUTACK Registers
        466. 14.9.1.466 ARM_CTI_3_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        467. 14.9.1.467 ARM_CTI_3_CFG_CSCTI_CFG_ITCHIN Registers
        468. 14.9.1.468 ARM_CTI_3_CFG_CSCTI_CFG_ITTRIGIN Registers
        469. 14.9.1.469 ARM_CTI_3_CFG_CSCTI_CFG_ITCTRL Registers
        470. 14.9.1.470 ARM_CTI_3_CFG_CSCTI_CFG_CLAIMSET Registers
        471. 14.9.1.471 ARM_CTI_3_CFG_CSCTI_CFG_CLAIMCLR Registers
        472. 14.9.1.472 ARM_CTI_3_CFG_CSCTI_CFG_LAR Registers
        473. 14.9.1.473 ARM_CTI_3_CFG_CSCTI_CFG_LSR Registers
        474. 14.9.1.474 ARM_CTI_3_CFG_CSCTI_CFG_AUTHSTATUS Registers
        475. 14.9.1.475 ARM_CTI_3_CFG_CSCTI_CFG_DEVID Registers
        476. 14.9.1.476 ARM_CTI_3_CFG_CSCTI_CFG_DEVTYPE Registers
        477. 14.9.1.477 ARM_CTI_3_CFG_CSCTI_CFG_PERIPHID4 Registers
        478. 14.9.1.478 ARM_CTI_3_CFG_CSCTI_CFG_PERIPHID0 Registers
        479. 14.9.1.479 ARM_CTI_3_CFG_CSCTI_CFG_PERIPHID1 Registers
        480. 14.9.1.480 ARM_CTI_3_CFG_CSCTI_CFG_PERIPHID2 Registers
        481. 14.9.1.481 ARM_CTI_3_CFG_CSCTI_CFG_PERIPHID3 Registers
        482. 14.9.1.482 ARM_CTI_3_CFG_CSCTI_CFG_COMPID0 Registers
        483. 14.9.1.483 ARM_CTI_3_CFG_CSCTI_CFG_COMPID1 Registers
        484. 14.9.1.484 ARM_CTI_3_CFG_CSCTI_CFG_COMPID2 Registers
        485. 14.9.1.485 ARM_CTI_3_CFG_CSCTI_CFG_COMPID3 Registers
        486. 14.9.1.486 ARM_CTI_4_CFG_CSCTI_CFG_CTICONTROL Registers
        487. 14.9.1.487 ARM_CTI_4_CFG_CSCTI_CFG_CTIINTACK Registers
        488. 14.9.1.488 ARM_CTI_4_CFG_CSCTI_CFG_CTIAPPSET Registers
        489. 14.9.1.489 ARM_CTI_4_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        490. 14.9.1.490 ARM_CTI_4_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        491. 14.9.1.491 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN0 Registers
        492. 14.9.1.492 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN1 Registers
        493. 14.9.1.493 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN2 Registers
        494. 14.9.1.494 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN3 Registers
        495. 14.9.1.495 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN4 Registers
        496. 14.9.1.496 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN5 Registers
        497. 14.9.1.497 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN6 Registers
        498. 14.9.1.498 ARM_CTI_4_CFG_CSCTI_CFG_CTIINEN7 Registers
        499. 14.9.1.499 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        500. 14.9.1.500 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        501. 14.9.1.501 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        502. 14.9.1.502 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        503. 14.9.1.503 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        504. 14.9.1.504 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        505. 14.9.1.505 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        506. 14.9.1.506 ARM_CTI_4_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        507. 14.9.1.507 ARM_CTI_4_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        508. 14.9.1.508 ARM_CTI_4_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        509. 14.9.1.509 ARM_CTI_4_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        510. 14.9.1.510 ARM_CTI_4_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        511. 14.9.1.511 ARM_CTI_4_CFG_CSCTI_CFG_CTIGATE Registers
        512. 14.9.1.512 ARM_CTI_4_CFG_CSCTI_CFG_ASICCTL Registers
        513. 14.9.1.513 ARM_CTI_4_CFG_CSCTI_CFG_ITCHINACK Registers
        514. 14.9.1.514 ARM_CTI_4_CFG_CSCTI_CFG_ITTRIGINACK Registers
        515. 14.9.1.515 ARM_CTI_4_CFG_CSCTI_CFG_ITCHOUT Registers
        516. 14.9.1.516 ARM_CTI_4_CFG_CSCTI_CFG_ITTRIGOUT Registers
        517. 14.9.1.517 ARM_CTI_4_CFG_CSCTI_CFG_ITCHOUTACK Registers
        518. 14.9.1.518 ARM_CTI_4_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        519. 14.9.1.519 ARM_CTI_4_CFG_CSCTI_CFG_ITCHIN Registers
        520. 14.9.1.520 ARM_CTI_4_CFG_CSCTI_CFG_ITTRIGIN Registers
        521. 14.9.1.521 ARM_CTI_4_CFG_CSCTI_CFG_ITCTRL Registers
        522. 14.9.1.522 ARM_CTI_4_CFG_CSCTI_CFG_CLAIMSET Registers
        523. 14.9.1.523 ARM_CTI_4_CFG_CSCTI_CFG_CLAIMCLR Registers
        524. 14.9.1.524 ARM_CTI_4_CFG_CSCTI_CFG_LAR Registers
        525. 14.9.1.525 ARM_CTI_4_CFG_CSCTI_CFG_LSR Registers
        526. 14.9.1.526 ARM_CTI_4_CFG_CSCTI_CFG_AUTHSTATUS Registers
        527. 14.9.1.527 ARM_CTI_4_CFG_CSCTI_CFG_DEVID Registers
        528. 14.9.1.528 ARM_CTI_4_CFG_CSCTI_CFG_DEVTYPE Registers
        529. 14.9.1.529 ARM_CTI_4_CFG_CSCTI_CFG_PERIPHID4 Registers
        530. 14.9.1.530 ARM_CTI_4_CFG_CSCTI_CFG_PERIPHID0 Registers
        531. 14.9.1.531 ARM_CTI_4_CFG_CSCTI_CFG_PERIPHID1 Registers
        532. 14.9.1.532 ARM_CTI_4_CFG_CSCTI_CFG_PERIPHID2 Registers
        533. 14.9.1.533 ARM_CTI_4_CFG_CSCTI_CFG_PERIPHID3 Registers
        534. 14.9.1.534 ARM_CTI_4_CFG_CSCTI_CFG_COMPID0 Registers
        535. 14.9.1.535 ARM_CTI_4_CFG_CSCTI_CFG_COMPID1 Registers
        536. 14.9.1.536 ARM_CTI_4_CFG_CSCTI_CFG_COMPID2 Registers
        537. 14.9.1.537 ARM_CTI_4_CFG_CSCTI_CFG_COMPID3 Registers
        538. 14.9.1.538 ARM_CTI_5_CFG_CSCTI_CFG_CTICONTROL Registers
        539. 14.9.1.539 ARM_CTI_5_CFG_CSCTI_CFG_CTIINTACK Registers
        540. 14.9.1.540 ARM_CTI_5_CFG_CSCTI_CFG_CTIAPPSET Registers
        541. 14.9.1.541 ARM_CTI_5_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        542. 14.9.1.542 ARM_CTI_5_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        543. 14.9.1.543 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN0 Registers
        544. 14.9.1.544 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN1 Registers
        545. 14.9.1.545 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN2 Registers
        546. 14.9.1.546 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN3 Registers
        547. 14.9.1.547 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN4 Registers
        548. 14.9.1.548 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN5 Registers
        549. 14.9.1.549 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN6 Registers
        550. 14.9.1.550 ARM_CTI_5_CFG_CSCTI_CFG_CTIINEN7 Registers
        551. 14.9.1.551 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        552. 14.9.1.552 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        553. 14.9.1.553 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        554. 14.9.1.554 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        555. 14.9.1.555 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        556. 14.9.1.556 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        557. 14.9.1.557 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        558. 14.9.1.558 ARM_CTI_5_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        559. 14.9.1.559 ARM_CTI_5_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        560. 14.9.1.560 ARM_CTI_5_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        561. 14.9.1.561 ARM_CTI_5_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        562. 14.9.1.562 ARM_CTI_5_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        563. 14.9.1.563 ARM_CTI_5_CFG_CSCTI_CFG_CTIGATE Registers
        564. 14.9.1.564 ARM_CTI_5_CFG_CSCTI_CFG_ASICCTL Registers
        565. 14.9.1.565 ARM_CTI_5_CFG_CSCTI_CFG_ITCHINACK Registers
        566. 14.9.1.566 ARM_CTI_5_CFG_CSCTI_CFG_ITTRIGINACK Registers
        567. 14.9.1.567 ARM_CTI_5_CFG_CSCTI_CFG_ITCHOUT Registers
        568. 14.9.1.568 ARM_CTI_5_CFG_CSCTI_CFG_ITTRIGOUT Registers
        569. 14.9.1.569 ARM_CTI_5_CFG_CSCTI_CFG_ITCHOUTACK Registers
        570. 14.9.1.570 ARM_CTI_5_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        571. 14.9.1.571 ARM_CTI_5_CFG_CSCTI_CFG_ITCHIN Registers
        572. 14.9.1.572 ARM_CTI_5_CFG_CSCTI_CFG_ITTRIGIN Registers
        573. 14.9.1.573 ARM_CTI_5_CFG_CSCTI_CFG_ITCTRL Registers
        574. 14.9.1.574 ARM_CTI_5_CFG_CSCTI_CFG_CLAIMSET Registers
        575. 14.9.1.575 ARM_CTI_5_CFG_CSCTI_CFG_CLAIMCLR Registers
        576. 14.9.1.576 ARM_CTI_5_CFG_CSCTI_CFG_LAR Registers
        577. 14.9.1.577 ARM_CTI_5_CFG_CSCTI_CFG_LSR Registers
        578. 14.9.1.578 ARM_CTI_5_CFG_CSCTI_CFG_AUTHSTATUS Registers
        579. 14.9.1.579 ARM_CTI_5_CFG_CSCTI_CFG_DEVID Registers
        580. 14.9.1.580 ARM_CTI_5_CFG_CSCTI_CFG_DEVTYPE Registers
        581. 14.9.1.581 ARM_CTI_5_CFG_CSCTI_CFG_PERIPHID4 Registers
        582. 14.9.1.582 ARM_CTI_5_CFG_CSCTI_CFG_PERIPHID0 Registers
        583. 14.9.1.583 ARM_CTI_5_CFG_CSCTI_CFG_PERIPHID1 Registers
        584. 14.9.1.584 ARM_CTI_5_CFG_CSCTI_CFG_PERIPHID2 Registers
        585. 14.9.1.585 ARM_CTI_5_CFG_CSCTI_CFG_PERIPHID3 Registers
        586. 14.9.1.586 ARM_CTI_5_CFG_CSCTI_CFG_COMPID0 Registers
        587. 14.9.1.587 ARM_CTI_5_CFG_CSCTI_CFG_COMPID1 Registers
        588. 14.9.1.588 ARM_CTI_5_CFG_CSCTI_CFG_COMPID2 Registers
        589. 14.9.1.589 ARM_CTI_5_CFG_CSCTI_CFG_COMPID3 Registers
        590. 14.9.1.590 ARM_CTI_6_CFG_CSCTI_CFG_CTICONTROL Registers
        591. 14.9.1.591 ARM_CTI_6_CFG_CSCTI_CFG_CTIINTACK Registers
        592. 14.9.1.592 ARM_CTI_6_CFG_CSCTI_CFG_CTIAPPSET Registers
        593. 14.9.1.593 ARM_CTI_6_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        594. 14.9.1.594 ARM_CTI_6_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        595. 14.9.1.595 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN0 Registers
        596. 14.9.1.596 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN1 Registers
        597. 14.9.1.597 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN2 Registers
        598. 14.9.1.598 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN3 Registers
        599. 14.9.1.599 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN4 Registers
        600. 14.9.1.600 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN5 Registers
        601. 14.9.1.601 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN6 Registers
        602. 14.9.1.602 ARM_CTI_6_CFG_CSCTI_CFG_CTIINEN7 Registers
        603. 14.9.1.603 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        604. 14.9.1.604 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        605. 14.9.1.605 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        606. 14.9.1.606 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        607. 14.9.1.607 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        608. 14.9.1.608 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        609. 14.9.1.609 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        610. 14.9.1.610 ARM_CTI_6_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        611. 14.9.1.611 ARM_CTI_6_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        612. 14.9.1.612 ARM_CTI_6_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        613. 14.9.1.613 ARM_CTI_6_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        614. 14.9.1.614 ARM_CTI_6_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        615. 14.9.1.615 ARM_CTI_6_CFG_CSCTI_CFG_CTIGATE Registers
        616. 14.9.1.616 ARM_CTI_6_CFG_CSCTI_CFG_ASICCTL Registers
        617. 14.9.1.617 ARM_CTI_6_CFG_CSCTI_CFG_ITCHINACK Registers
        618. 14.9.1.618 ARM_CTI_6_CFG_CSCTI_CFG_ITTRIGINACK Registers
        619. 14.9.1.619 ARM_CTI_6_CFG_CSCTI_CFG_ITCHOUT Registers
        620. 14.9.1.620 ARM_CTI_6_CFG_CSCTI_CFG_ITTRIGOUT Registers
        621. 14.9.1.621 ARM_CTI_6_CFG_CSCTI_CFG_ITCHOUTACK Registers
        622. 14.9.1.622 ARM_CTI_6_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        623. 14.9.1.623 ARM_CTI_6_CFG_CSCTI_CFG_ITCHIN Registers
        624. 14.9.1.624 ARM_CTI_6_CFG_CSCTI_CFG_ITTRIGIN Registers
        625. 14.9.1.625 ARM_CTI_6_CFG_CSCTI_CFG_ITCTRL Registers
        626. 14.9.1.626 ARM_CTI_6_CFG_CSCTI_CFG_CLAIMSET Registers
        627. 14.9.1.627 ARM_CTI_6_CFG_CSCTI_CFG_CLAIMCLR Registers
        628. 14.9.1.628 ARM_CTI_6_CFG_CSCTI_CFG_LAR Registers
        629. 14.9.1.629 ARM_CTI_6_CFG_CSCTI_CFG_LSR Registers
        630. 14.9.1.630 ARM_CTI_6_CFG_CSCTI_CFG_AUTHSTATUS Registers
        631. 14.9.1.631 ARM_CTI_6_CFG_CSCTI_CFG_DEVID Registers
        632. 14.9.1.632 ARM_CTI_6_CFG_CSCTI_CFG_DEVTYPE Registers
        633. 14.9.1.633 ARM_CTI_6_CFG_CSCTI_CFG_PERIPHID4 Registers
        634. 14.9.1.634 ARM_CTI_6_CFG_CSCTI_CFG_PERIPHID0 Registers
        635. 14.9.1.635 ARM_CTI_6_CFG_CSCTI_CFG_PERIPHID1 Registers
        636. 14.9.1.636 ARM_CTI_6_CFG_CSCTI_CFG_PERIPHID2 Registers
        637. 14.9.1.637 ARM_CTI_6_CFG_CSCTI_CFG_PERIPHID3 Registers
        638. 14.9.1.638 ARM_CTI_6_CFG_CSCTI_CFG_COMPID0 Registers
        639. 14.9.1.639 ARM_CTI_6_CFG_CSCTI_CFG_COMPID1 Registers
        640. 14.9.1.640 ARM_CTI_6_CFG_CSCTI_CFG_COMPID2 Registers
        641. 14.9.1.641 ARM_CTI_6_CFG_CSCTI_CFG_COMPID3 Registers
        642. 14.9.1.642 ARM_CTI_7_CFG_CSCTI_CFG_CTICONTROL Registers
        643. 14.9.1.643 ARM_CTI_7_CFG_CSCTI_CFG_CTIINTACK Registers
        644. 14.9.1.644 ARM_CTI_7_CFG_CSCTI_CFG_CTIAPPSET Registers
        645. 14.9.1.645 ARM_CTI_7_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        646. 14.9.1.646 ARM_CTI_7_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        647. 14.9.1.647 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN0 Registers
        648. 14.9.1.648 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN1 Registers
        649. 14.9.1.649 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN2 Registers
        650. 14.9.1.650 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN3 Registers
        651. 14.9.1.651 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN4 Registers
        652. 14.9.1.652 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN5 Registers
        653. 14.9.1.653 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN6 Registers
        654. 14.9.1.654 ARM_CTI_7_CFG_CSCTI_CFG_CTIINEN7 Registers
        655. 14.9.1.655 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        656. 14.9.1.656 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        657. 14.9.1.657 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        658. 14.9.1.658 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        659. 14.9.1.659 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        660. 14.9.1.660 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        661. 14.9.1.661 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        662. 14.9.1.662 ARM_CTI_7_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        663. 14.9.1.663 ARM_CTI_7_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        664. 14.9.1.664 ARM_CTI_7_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        665. 14.9.1.665 ARM_CTI_7_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        666. 14.9.1.666 ARM_CTI_7_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        667. 14.9.1.667 ARM_CTI_7_CFG_CSCTI_CFG_CTIGATE Registers
        668. 14.9.1.668 ARM_CTI_7_CFG_CSCTI_CFG_ASICCTL Registers
        669. 14.9.1.669 ARM_CTI_7_CFG_CSCTI_CFG_ITCHINACK Registers
        670. 14.9.1.670 ARM_CTI_7_CFG_CSCTI_CFG_ITTRIGINACK Registers
        671. 14.9.1.671 ARM_CTI_7_CFG_CSCTI_CFG_ITCHOUT Registers
        672. 14.9.1.672 ARM_CTI_7_CFG_CSCTI_CFG_ITTRIGOUT Registers
        673. 14.9.1.673 ARM_CTI_7_CFG_CSCTI_CFG_ITCHOUTACK Registers
        674. 14.9.1.674 ARM_CTI_7_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        675. 14.9.1.675 ARM_CTI_7_CFG_CSCTI_CFG_ITCHIN Registers
        676. 14.9.1.676 ARM_CTI_7_CFG_CSCTI_CFG_ITTRIGIN Registers
        677. 14.9.1.677 ARM_CTI_7_CFG_CSCTI_CFG_ITCTRL Registers
        678. 14.9.1.678 ARM_CTI_7_CFG_CSCTI_CFG_CLAIMSET Registers
        679. 14.9.1.679 ARM_CTI_7_CFG_CSCTI_CFG_CLAIMCLR Registers
        680. 14.9.1.680 ARM_CTI_7_CFG_CSCTI_CFG_LAR Registers
        681. 14.9.1.681 ARM_CTI_7_CFG_CSCTI_CFG_LSR Registers
        682. 14.9.1.682 ARM_CTI_7_CFG_CSCTI_CFG_AUTHSTATUS Registers
        683. 14.9.1.683 ARM_CTI_7_CFG_CSCTI_CFG_DEVID Registers
        684. 14.9.1.684 ARM_CTI_7_CFG_CSCTI_CFG_DEVTYPE Registers
        685. 14.9.1.685 ARM_CTI_7_CFG_CSCTI_CFG_PERIPHID4 Registers
        686. 14.9.1.686 ARM_CTI_7_CFG_CSCTI_CFG_PERIPHID0 Registers
        687. 14.9.1.687 ARM_CTI_7_CFG_CSCTI_CFG_PERIPHID1 Registers
        688. 14.9.1.688 ARM_CTI_7_CFG_CSCTI_CFG_PERIPHID2 Registers
        689. 14.9.1.689 ARM_CTI_7_CFG_CSCTI_CFG_PERIPHID3 Registers
        690. 14.9.1.690 ARM_CTI_7_CFG_CSCTI_CFG_COMPID0 Registers
        691. 14.9.1.691 ARM_CTI_7_CFG_CSCTI_CFG_COMPID1 Registers
        692. 14.9.1.692 ARM_CTI_7_CFG_CSCTI_CFG_COMPID2 Registers
        693. 14.9.1.693 ARM_CTI_7_CFG_CSCTI_CFG_COMPID3 Registers
        694. 14.9.1.694 ARM_CTI_8_CFG_CSCTI_CFG_CTICONTROL Registers
        695. 14.9.1.695 ARM_CTI_8_CFG_CSCTI_CFG_CTIINTACK Registers
        696. 14.9.1.696 ARM_CTI_8_CFG_CSCTI_CFG_CTIAPPSET Registers
        697. 14.9.1.697 ARM_CTI_8_CFG_CSCTI_CFG_CTIAPPCLEAR Registers
        698. 14.9.1.698 ARM_CTI_8_CFG_CSCTI_CFG_CTIAPPPULSE Registers
        699. 14.9.1.699 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN0 Registers
        700. 14.9.1.700 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN1 Registers
        701. 14.9.1.701 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN2 Registers
        702. 14.9.1.702 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN3 Registers
        703. 14.9.1.703 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN4 Registers
        704. 14.9.1.704 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN5 Registers
        705. 14.9.1.705 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN6 Registers
        706. 14.9.1.706 ARM_CTI_8_CFG_CSCTI_CFG_CTIINEN7 Registers
        707. 14.9.1.707 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN0 Registers
        708. 14.9.1.708 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN1 Registers
        709. 14.9.1.709 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN2 Registers
        710. 14.9.1.710 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN3 Registers
        711. 14.9.1.711 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN4 Registers
        712. 14.9.1.712 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN5 Registers
        713. 14.9.1.713 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN6 Registers
        714. 14.9.1.714 ARM_CTI_8_CFG_CSCTI_CFG_CTIOUTEN7 Registers
        715. 14.9.1.715 ARM_CTI_8_CFG_CSCTI_CFG_CTITRIGINSTATUS Registers
        716. 14.9.1.716 ARM_CTI_8_CFG_CSCTI_CFG_CTITRIGOUTSTATUS Registers
        717. 14.9.1.717 ARM_CTI_8_CFG_CSCTI_CFG_CTICHINSTATUS Registers
        718. 14.9.1.718 ARM_CTI_8_CFG_CSCTI_CFG_CTICHOUTSTATUS Registers
        719. 14.9.1.719 ARM_CTI_8_CFG_CSCTI_CFG_CTIGATE Registers
        720. 14.9.1.720 ARM_CTI_8_CFG_CSCTI_CFG_ASICCTL Registers
        721. 14.9.1.721 ARM_CTI_8_CFG_CSCTI_CFG_ITCHINACK Registers
        722. 14.9.1.722 ARM_CTI_8_CFG_CSCTI_CFG_ITTRIGINACK Registers
        723. 14.9.1.723 ARM_CTI_8_CFG_CSCTI_CFG_ITCHOUT Registers
        724. 14.9.1.724 ARM_CTI_8_CFG_CSCTI_CFG_ITTRIGOUT Registers
        725. 14.9.1.725 ARM_CTI_8_CFG_CSCTI_CFG_ITCHOUTACK Registers
        726. 14.9.1.726 ARM_CTI_8_CFG_CSCTI_CFG_ITTRIGOUTACK Registers
        727. 14.9.1.727 ARM_CTI_8_CFG_CSCTI_CFG_ITCHIN Registers
        728. 14.9.1.728 ARM_CTI_8_CFG_CSCTI_CFG_ITTRIGIN Registers
        729. 14.9.1.729 ARM_CTI_8_CFG_CSCTI_CFG_ITCTRL Registers
        730. 14.9.1.730 ARM_CTI_8_CFG_CSCTI_CFG_CLAIMSET Registers
        731. 14.9.1.731 ARM_CTI_8_CFG_CSCTI_CFG_CLAIMCLR Registers
        732. 14.9.1.732 ARM_CTI_8_CFG_CSCTI_CFG_LAR Registers
        733. 14.9.1.733 ARM_CTI_8_CFG_CSCTI_CFG_LSR Registers
        734. 14.9.1.734 ARM_CTI_8_CFG_CSCTI_CFG_AUTHSTATUS Registers
        735. 14.9.1.735 ARM_CTI_8_CFG_CSCTI_CFG_DEVID Registers
        736. 14.9.1.736 ARM_CTI_8_CFG_CSCTI_CFG_DEVTYPE Registers
        737. 14.9.1.737 ARM_CTI_8_CFG_CSCTI_CFG_PERIPHID4 Registers
        738. 14.9.1.738 ARM_CTI_8_CFG_CSCTI_CFG_PERIPHID0 Registers
        739. 14.9.1.739 ARM_CTI_8_CFG_CSCTI_CFG_PERIPHID1 Registers
        740. 14.9.1.740 ARM_CTI_8_CFG_CSCTI_CFG_PERIPHID2 Registers
        741. 14.9.1.741 ARM_CTI_8_CFG_CSCTI_CFG_PERIPHID3 Registers
        742. 14.9.1.742 ARM_CTI_8_CFG_CSCTI_CFG_COMPID0 Registers
        743. 14.9.1.743 ARM_CTI_8_CFG_CSCTI_CFG_COMPID1 Registers
        744. 14.9.1.744 ARM_CTI_8_CFG_CSCTI_CFG_COMPID2 Registers
        745. 14.9.1.745 ARM_CTI_8_CFG_CSCTI_CFG_COMPID3 Registers
        746. 14.9.1.746 Access Table
      2. 14.9.2 DEBUGSS_WRAP Registers
        1. 14.9.2.1   ROM_TABLE_0_0_ROM_ENTRY0 Registers
        2. 14.9.2.2   ROM_TABLE_0_0_ROM_ENTRY1 Registers
        3. 14.9.2.3   ROM_TABLE_0_0_ROM_ENTRY2 Registers
        4. 14.9.2.4   ROM_TABLE_0_0_ROM_MANUAL_ENTRY0 Registers
        5. 14.9.2.5   ROM_TABLE_0_0_ROM_MANUAL_ENTRY1 Registers
        6. 14.9.2.6   ROM_TABLE_0_0_ROM_MANUAL_ENTRY2 Registers
        7. 14.9.2.7   ROM_TABLE_0_0_ROM_MANUAL_ENTRY3 Registers
        8. 14.9.2.8   ROM_TABLE_0_0_ROM_MANUAL_ENTRY4 Registers
        9. 14.9.2.9   ROM_TABLE_0_0_ROM_MANUAL_ENTRY5 Registers
        10. 14.9.2.10  ROM_TABLE_0_0_ROM_MANUAL_ENTRY6 Registers
        11. 14.9.2.11  ROM_TABLE_0_0_ROM_MANUAL_ENTRY7 Registers
        12. 14.9.2.12  ROM_TABLE_0_0_ROM_MANUAL_ENTRY8 Registers
        13. 14.9.2.13  ROM_TABLE_0_0_ROM_MANUAL_ENTRY9 Registers
        14. 14.9.2.14  ROM_TABLE_0_0_ROM_MANUAL_ENTRY10 Registers
        15. 14.9.2.15  ROM_TABLE_0_0_ROM_MANUAL_ENTRY11 Registers
        16. 14.9.2.16  ROM_TABLE_0_0_ROM_MANUAL_ENTRY12 Registers
        17. 14.9.2.17  ROM_TABLE_0_0_ROM_MANUAL_ENTRY13 Registers
        18. 14.9.2.18  ROM_TABLE_0_0_ROM_MANUAL_ENTRY14 Registers
        19. 14.9.2.19  ROM_TABLE_0_0_ROM_MANUAL_ENTRY15 Registers
        20. 14.9.2.20  ROM_TABLE_0_0_ROM_MANUAL_ENTRY16 Registers
        21. 14.9.2.21  ROM_TABLE_0_0_ROM_MANUAL_ENTRY17 Registers
        22. 14.9.2.22  ROM_TABLE_0_0_ROM_MANUAL_ENTRY18 Registers
        23. 14.9.2.23  ROM_TABLE_0_0_ROM_MANUAL_ENTRY19 Registers
        24. 14.9.2.24  ROM_TABLE_0_0_ROM_MANUAL_ENTRY20 Registers
        25. 14.9.2.25  ROM_TABLE_0_0_ROM_MANUAL_ENTRY21 Registers
        26. 14.9.2.26  ROM_TABLE_0_0_ROM_MANUAL_ENTRY22 Registers
        27. 14.9.2.27  ROM_TABLE_0_0_ROM_MANUAL_ENTRY23 Registers
        28. 14.9.2.28  ROM_TABLE_0_0_ROM_MANUAL_ENTRY24 Registers
        29. 14.9.2.29  ROM_TABLE_0_0_ROM_MANUAL_ENTRY25 Registers
        30. 14.9.2.30  ROM_TABLE_0_0_ROM_MANUAL_ENTRY26 Registers
        31. 14.9.2.31  ROM_TABLE_0_0_ROM_MANUAL_ENTRY27 Registers
        32. 14.9.2.32  ROM_TABLE_0_0_ROM_MANUAL_ENTRY28 Registers
        33. 14.9.2.33  ROM_TABLE_0_0_ROM_MANUAL_ENTRY29 Registers
        34. 14.9.2.34  ROM_TABLE_0_0_ROM_MANUAL_ENTRY30 Registers
        35. 14.9.2.35  ROM_TABLE_0_0_ROM_MANUAL_ENTRY31 Registers
        36. 14.9.2.36  ROM_TABLE_0_0_ROM_MANUAL_ENTRY32 Registers
        37. 14.9.2.37  ROM_TABLE_0_0_ROM_MANUAL_ENTRY33 Registers
        38. 14.9.2.38  ROM_TABLE_0_0_ROM_MANUAL_ENTRY34 Registers
        39. 14.9.2.39  ROM_TABLE_0_0_ROM_MANUAL_ENTRY35 Registers
        40. 14.9.2.40  ROM_TABLE_0_0_ROM_MANUAL_ENTRY36 Registers
        41. 14.9.2.41  ROM_TABLE_0_0_ROM_MANUAL_ENTRY37 Registers
        42. 14.9.2.42  ROM_TABLE_0_0_ROM_MANUAL_ENTRY38 Registers
        43. 14.9.2.43  ROM_TABLE_0_0_ROM_MANUAL_ENTRY39 Registers
        44. 14.9.2.44  ROM_TABLE_0_0_ROM_MANUAL_ENTRY40 Registers
        45. 14.9.2.45  ROM_TABLE_0_0_ROM_MANUAL_ENTRY41 Registers
        46. 14.9.2.46  ROM_TABLE_0_0_ROM_MANUAL_ENTRY42 Registers
        47. 14.9.2.47  ROM_TABLE_0_0_ROM_MANUAL_ENTRY43 Registers
        48. 14.9.2.48  ROM_TABLE_0_0_ROM_MANUAL_ENTRY44 Registers
        49. 14.9.2.49  ROM_TABLE_0_0_ROM_MANUAL_ENTRY45 Registers
        50. 14.9.2.50  ROM_TABLE_0_0_ROM_MANUAL_ENTRY46 Registers
        51. 14.9.2.51  ROM_TABLE_0_0_ROM_MANUAL_ENTRY47 Registers
        52. 14.9.2.52  ROM_TABLE_0_0_ROM_MANUAL_ENTRY48 Registers
        53. 14.9.2.53  ROM_TABLE_0_0_ROM_MANUAL_ENTRY49 Registers
        54. 14.9.2.54  ROM_TABLE_0_0_ROM_MANUAL_ENTRY50 Registers
        55. 14.9.2.55  ROM_TABLE_0_0_ROM_MANUAL_ENTRY51 Registers
        56. 14.9.2.56  ROM_TABLE_0_0_ROM_MANUAL_ENTRY52 Registers
        57. 14.9.2.57  ROM_TABLE_0_0_ROM_MANUAL_ENTRY53 Registers
        58. 14.9.2.58  ROM_TABLE_0_0_ROM_MANUAL_ENTRY54 Registers
        59. 14.9.2.59  ROM_TABLE_0_0_ROM_MANUAL_ENTRY55 Registers
        60. 14.9.2.60  ROM_TABLE_0_0_ROM_MANUAL_ENTRY56 Registers
        61. 14.9.2.61  ROM_TABLE_0_0_ROM_MANUAL_ENTRY57 Registers
        62. 14.9.2.62  ROM_TABLE_0_0_ROM_MANUAL_ENTRY58 Registers
        63. 14.9.2.63  ROM_TABLE_0_0_ROM_MANUAL_ENTRY59 Registers
        64. 14.9.2.64  ROM_TABLE_0_0_ROM_MANUAL_ENTRY60 Registers
        65. 14.9.2.65  ROM_TABLE_0_0_ROM_MANUAL_ENTRY61 Registers
        66. 14.9.2.66  ROM_TABLE_0_0_ROM_MANUAL_ENTRY62 Registers
        67. 14.9.2.67  ROM_TABLE_0_0_ROM_MANUAL_ENTRY63 Registers
        68. 14.9.2.68  ROM_TABLE_0_0_PERIPHID0 Registers
        69. 14.9.2.69  ROM_TABLE_0_0_PERIPHID1 Registers
        70. 14.9.2.70  ROM_TABLE_0_0_PERIPHID2 Registers
        71. 14.9.2.71  ROM_TABLE_0_0_PERIPHID3 Registers
        72. 14.9.2.72  ROM_TABLE_0_0_PERIPHID4 Registers
        73. 14.9.2.73  ROM_TABLE_0_0_COMPID0 Registers
        74. 14.9.2.74  ROM_TABLE_0_0_COMPID1 Registers
        75. 14.9.2.75  ROM_TABLE_0_0_COMPID2 Registers
        76. 14.9.2.76  ROM_TABLE_0_0_COMPID3 Registers
        77. 14.9.2.77  CFGAP0_JTAGID_REG Registers
        78. 14.9.2.78  CFGAP0_USERID_REG Registers
        79. 14.9.2.79  CFGAP0_VERSION_REG Registers
        80. 14.9.2.80  CFGAP0_SYSTEMSTATUS Registers
        81. 14.9.2.81  CFGAP0_APID_REGISTER Registers
        82. 14.9.2.82  APBAP0_CSWREG Registers
        83. 14.9.2.83  APBAP0_TAREG Registers
        84. 14.9.2.84  APBAP0_DRWREG Registers
        85. 14.9.2.85  APBAP0_BD0REG Registers
        86. 14.9.2.86  APBAP0_BD1REG Registers
        87. 14.9.2.87  APBAP0_BD2REG Registers
        88. 14.9.2.88  APBAP0_BD3REG Registers
        89. 14.9.2.89  APBAP0_ROM_REGISTER Registers
        90. 14.9.2.90  APBAP0_ID_REGISTER Registers
        91. 14.9.2.91  AXIAP0_CSWREG Registers
        92. 14.9.2.92  AXIAP0_TAREGL Registers
        93. 14.9.2.93  AXIAP0_TAREGH Registers
        94. 14.9.2.94  AXIAP0_DRWREG Registers
        95. 14.9.2.95  AXIAP0_BD0REG Registers
        96. 14.9.2.96  AXIAP0_BD1REG Registers
        97. 14.9.2.97  AXIAP0_BD2REG Registers
        98. 14.9.2.98  AXIAP0_BD3REG Registers
        99. 14.9.2.99  AXIAP0_MBT_REGISTER Registers
        100. 14.9.2.100 AXIAP0_ROM_HI_REGISTER Registers
        101. 14.9.2.101 AXIAP0_CFG_REGISTER Registers
        102. 14.9.2.102 AXIAP0_ROM_LO_REGISTER Registers
        103. 14.9.2.103 AXIAP0_ID_REGISTER Registers
        104. 14.9.2.104 PWRAP0_CORE_PRECREG0 Registers
        105. 14.9.2.105 PWRAP0_CORE_PRECREG1 Registers
        106. 14.9.2.106 PWRAP0_CORE_PRECREG2 Registers
        107. 14.9.2.107 PWRAP0_CORE_PRECREG3 Registers
        108. 14.9.2.108 PWRAP0_CORE_PRECREG4 Registers
        109. 14.9.2.109 PWRAP0_CORE_PRECREG5 Registers
        110. 14.9.2.110 PWRAP0_CORE_PRECREG6 Registers
        111. 14.9.2.111 PWRAP0_CORE_PRECREG7 Registers
        112. 14.9.2.112 PWRAP0_CORE_PRECREG8 Registers
        113. 14.9.2.113 PWRAP0_CORE_PRECREG9 Registers
        114. 14.9.2.114 PWRAP0_CORE_PRECREG10 Registers
        115. 14.9.2.115 PWRAP0_CORE_PRECREG11 Registers
        116. 14.9.2.116 PWRAP0_CORE_PRECREG12 Registers
        117. 14.9.2.117 PWRAP0_CORE_PRECREG13 Registers
        118. 14.9.2.118 PWRAP0_CORE_PRECREG14 Registers
        119. 14.9.2.119 PWRAP0_CORE_PRECREG15 Registers
        120. 14.9.2.120 PWRAP0_CORE_PRECREG16 Registers
        121. 14.9.2.121 PWRAP0_CORE_PRECREG17 Registers
        122. 14.9.2.122 PWRAP0_CORE_PRECREG18 Registers
        123. 14.9.2.123 PWRAP0_CORE_PRECREG19 Registers
        124. 14.9.2.124 PWRAP0_CORE_PRECREG20 Registers
        125. 14.9.2.125 PWRAP0_CORE_PRECREG21 Registers
        126. 14.9.2.126 PWRAP0_CORE_PRECREG22 Registers
        127. 14.9.2.127 PWRAP0_CORE_PRECREG23 Registers
        128. 14.9.2.128 PWRAP0_CORE_PRECREG24 Registers
        129. 14.9.2.129 PWRAP0_CORE_PRECREG25 Registers
        130. 14.9.2.130 PWRAP0_CORE_PRECREG26 Registers
        131. 14.9.2.131 PWRAP0_CORE_PRECREG27 Registers
        132. 14.9.2.132 PWRAP0_CORE_PRECREG28 Registers
        133. 14.9.2.133 PWRAP0_CORE_PRECREG29 Registers
        134. 14.9.2.134 PWRAP0_CORE_PRECREG30 Registers
        135. 14.9.2.135 PWRAP0_CORE_PRECREG31 Registers
        136. 14.9.2.136 PWRAP0_SYS_PRECREG Registers
        137. 14.9.2.137 PWRAP0_ID_REGISTER Registers
        138. 14.9.2.138 PVIEW0_PVIEW_STATE0 Registers
        139. 14.9.2.139 PVIEW0_PVIEW_CAPABILITY Registers
        140. 14.9.2.140 PVIEW0_ID_REGISTER Registers
        141. 14.9.2.141 JTAGAP0_CSW Registers
        142. 14.9.2.142 JTAGAP0_PSEL_REG Registers
        143. 14.9.2.143 JTAGAP0_PSTA_REG Registers
        144. 14.9.2.144 JTAGAP0_BYTEFIFO1 Registers
        145. 14.9.2.145 JTAGAP0_BYTEFIFO2 Registers
        146. 14.9.2.146 JTAGAP0_BYTEFIFO3 Registers
        147. 14.9.2.147 JTAGAP0_BYTEFIFO4 Registers
        148. 14.9.2.148 JTAGAP0_ID_REGISTER Registers
        149. 14.9.2.149 SECAP0_TXDATA Registers
        150. 14.9.2.150 SECAP0_TXCTRL Registers
        151. 14.9.2.151 SECAP0_RXDATA Registers
        152. 14.9.2.152 SECAP0_RXCTRL Registers
        153. 14.9.2.153 CORTEX0_CFG0_CSWREG Registers
        154. 14.9.2.154 CORTEX0_CFG0_TAREG Registers
        155. 14.9.2.155 CORTEX0_CFG0_DRWREG Registers
        156. 14.9.2.156 CORTEX0_CFG0_BD0REG Registers
        157. 14.9.2.157 CORTEX0_CFG0_BD1REG Registers
        158. 14.9.2.158 CORTEX0_CFG0_BD2REG Registers
        159. 14.9.2.159 CORTEX0_CFG0_BD3REG Registers
        160. 14.9.2.160 CORTEX0_CFG0_ROM_REGISTER Registers
        161. 14.9.2.161 CORTEX0_CFG0_ID_REGISTER Registers
        162. 14.9.2.162 CORTEX1_CFG0_CSWREG Registers
        163. 14.9.2.163 CORTEX1_CFG0_TAREG Registers
        164. 14.9.2.164 CORTEX1_CFG0_DRWREG Registers
        165. 14.9.2.165 CORTEX1_CFG0_BD0REG Registers
        166. 14.9.2.166 CORTEX1_CFG0_BD1REG Registers
        167. 14.9.2.167 CORTEX1_CFG0_BD2REG Registers
        168. 14.9.2.168 CORTEX1_CFG0_BD3REG Registers
        169. 14.9.2.169 CORTEX1_CFG0_ROM_REGISTER Registers
        170. 14.9.2.170 CORTEX1_CFG0_ID_REGISTER Registers
        171. 14.9.2.171 CORTEX2_CFG0_CSWREG Registers
        172. 14.9.2.172 CORTEX2_CFG0_TAREG Registers
        173. 14.9.2.173 CORTEX2_CFG0_DRWREG Registers
        174. 14.9.2.174 CORTEX2_CFG0_BD0REG Registers
        175. 14.9.2.175 CORTEX2_CFG0_BD1REG Registers
        176. 14.9.2.176 CORTEX2_CFG0_BD2REG Registers
        177. 14.9.2.177 CORTEX2_CFG0_BD3REG Registers
        178. 14.9.2.178 CORTEX2_CFG0_ROM_REGISTER Registers
        179. 14.9.2.179 CORTEX2_CFG0_ID_REGISTER Registers
        180. 14.9.2.180 CORTEX3_CFG0_CSWREG Registers
        181. 14.9.2.181 CORTEX3_CFG0_TAREG Registers
        182. 14.9.2.182 CORTEX3_CFG0_DRWREG Registers
        183. 14.9.2.183 CORTEX3_CFG0_BD0REG Registers
        184. 14.9.2.184 CORTEX3_CFG0_BD1REG Registers
        185. 14.9.2.185 CORTEX3_CFG0_BD2REG Registers
        186. 14.9.2.186 CORTEX3_CFG0_BD3REG Registers
        187. 14.9.2.187 CORTEX3_CFG0_ROM_REGISTER Registers
        188. 14.9.2.188 CORTEX3_CFG0_ID_REGISTER Registers
        189. 14.9.2.189 CORTEX4_CFG0_CSWREG Registers
        190. 14.9.2.190 CORTEX4_CFG0_TAREG Registers
        191. 14.9.2.191 CORTEX4_CFG0_DRWREG Registers
        192. 14.9.2.192 CORTEX4_CFG0_BD0REG Registers
        193. 14.9.2.193 CORTEX4_CFG0_BD1REG Registers
        194. 14.9.2.194 CORTEX4_CFG0_BD2REG Registers
        195. 14.9.2.195 CORTEX4_CFG0_BD3REG Registers
        196. 14.9.2.196 CORTEX4_CFG0_ROM_REGISTER Registers
        197. 14.9.2.197 CORTEX4_CFG0_ID_REGISTER Registers
        198. 14.9.2.198 CORTEX5_CFG0_CSWREG Registers
        199. 14.9.2.199 CORTEX5_CFG0_TAREG Registers
        200. 14.9.2.200 CORTEX5_CFG0_DRWREG Registers
        201. 14.9.2.201 CORTEX5_CFG0_BD0REG Registers
        202. 14.9.2.202 CORTEX5_CFG0_BD1REG Registers
        203. 14.9.2.203 CORTEX5_CFG0_BD2REG Registers
        204. 14.9.2.204 CORTEX5_CFG0_BD3REG Registers
        205. 14.9.2.205 CORTEX5_CFG0_ROM_REGISTER Registers
        206. 14.9.2.206 CORTEX5_CFG0_ID_REGISTER Registers
        207. 14.9.2.207 CORTEX6_CFG0_CSWREG Registers
        208. 14.9.2.208 CORTEX6_CFG0_TAREG Registers
        209. 14.9.2.209 CORTEX6_CFG0_DRWREG Registers
        210. 14.9.2.210 CORTEX6_CFG0_BD0REG Registers
        211. 14.9.2.211 CORTEX6_CFG0_BD1REG Registers
        212. 14.9.2.212 CORTEX6_CFG0_BD2REG Registers
        213. 14.9.2.213 CORTEX6_CFG0_BD3REG Registers
        214. 14.9.2.214 CORTEX6_CFG0_ROM_REGISTER Registers
        215. 14.9.2.215 CORTEX6_CFG0_ID_REGISTER Registers
        216. 14.9.2.216 CORTEX7_CFG0_CSWREG Registers
        217. 14.9.2.217 CORTEX7_CFG0_TAREG Registers
        218. 14.9.2.218 CORTEX7_CFG0_DRWREG Registers
        219. 14.9.2.219 CORTEX7_CFG0_BD0REG Registers
        220. 14.9.2.220 CORTEX7_CFG0_BD1REG Registers
        221. 14.9.2.221 CORTEX7_CFG0_BD2REG Registers
        222. 14.9.2.222 CORTEX7_CFG0_BD3REG Registers
        223. 14.9.2.223 CORTEX7_CFG0_ROM_REGISTER Registers
        224. 14.9.2.224 CORTEX7_CFG0_ID_REGISTER Registers
        225. 14.9.2.225 CORTEX8_CFG0_CSWREG Registers
        226. 14.9.2.226 CORTEX8_CFG0_TAREG Registers
        227. 14.9.2.227 CORTEX8_CFG0_DRWREG Registers
        228. 14.9.2.228 CORTEX8_CFG0_BD0REG Registers
        229. 14.9.2.229 CORTEX8_CFG0_BD1REG Registers
        230. 14.9.2.230 CORTEX8_CFG0_BD2REG Registers
        231. 14.9.2.231 CORTEX8_CFG0_BD3REG Registers
        232. 14.9.2.232 CORTEX8_CFG0_ROM_REGISTER Registers
        233. 14.9.2.233 CORTEX8_CFG0_ID_REGISTER Registers
        234. 14.9.2.234 ROM_TABLE_1_0_ROM_ENTRY0 Registers
        235. 14.9.2.235 ROM_TABLE_1_0_ROM_ENTRY1 Registers
        236. 14.9.2.236 ROM_TABLE_1_0_ROM_ENTRY2 Registers
        237. 14.9.2.237 ROM_TABLE_1_0_ROM_ENTRY3 Registers
        238. 14.9.2.238 ROM_TABLE_1_0_ROM_ENTRY4 Registers
        239. 14.9.2.239 ROM_TABLE_1_0_ROM_ENTRY5 Registers
        240. 14.9.2.240 ROM_TABLE_1_0_COMPUTE_CLUSTER0 Registers
        241. 14.9.2.241 ROM_TABLE_1_0_COMPUTE_CLUSTER1 Registers
        242. 14.9.2.242 ROM_TABLE_1_0_COMPUTE_CLUSTER2 Registers
        243. 14.9.2.243 ROM_TABLE_1_0_DEBUG_CELL0 Registers
        244. 14.9.2.244 ROM_TABLE_1_0_DEBUG_CELL1 Registers
        245. 14.9.2.245 ROM_TABLE_1_0_DEBUG_CELL2 Registers
        246. 14.9.2.246 ROM_TABLE_1_0_DEBUG_CELL3 Registers
        247. 14.9.2.247 ROM_TABLE_1_0_DEBUG_CELL4 Registers
        248. 14.9.2.248 ROM_TABLE_1_0_DEBUG_CELL5 Registers
        249. 14.9.2.249 ROM_TABLE_1_0_DEBUG_CELL6 Registers
        250. 14.9.2.250 ROM_TABLE_1_0_DEBUG_CELL7 Registers
        251. 14.9.2.251 ROM_TABLE_1_0_DEBUG_CELL8 Registers
        252. 14.9.2.252 ROM_TABLE_1_0_DEBUG_CELL9 Registers
        253. 14.9.2.253 ROM_TABLE_1_0_DEBUG_CELL10 Registers
        254. 14.9.2.254 ROM_TABLE_1_0_DEBUG_CELL11 Registers
        255. 14.9.2.255 ROM_TABLE_1_0_EXTCSCOMP0 Registers
        256. 14.9.2.256 ROM_TABLE_1_0_EXTCSCOMP1 Registers
        257. 14.9.2.257 ROM_TABLE_1_0_EXTCSCOMP2 Registers
        258. 14.9.2.258 ROM_TABLE_1_0_EXTCSCOMP3 Registers
        259. 14.9.2.259 ROM_TABLE_1_0_EXTCSCOMP4 Registers
        260. 14.9.2.260 ROM_TABLE_1_0_EXTCSCOMP5 Registers
        261. 14.9.2.261 ROM_TABLE_1_0_EXTCSCOMP6 Registers
        262. 14.9.2.262 ROM_TABLE_1_0_EXTCSCOMP7 Registers
        263. 14.9.2.263 ROM_TABLE_1_0_EXTCSCOMP8 Registers
        264. 14.9.2.264 ROM_TABLE_1_0_EXTCSCOMP9 Registers
        265. 14.9.2.265 ROM_TABLE_1_0_EXTCSCOMP10 Registers
        266. 14.9.2.266 ROM_TABLE_1_0_EXTCSCOMP11 Registers
        267. 14.9.2.267 CSCTI0_CTICONTROL Registers
        268. 14.9.2.268 CSCTI0_CTIINTACK Registers
        269. 14.9.2.269 CSCTI0_CTIAPPSET Registers
        270. 14.9.2.270 CSCTI0_CTIAPPCLEAR Registers
        271. 14.9.2.271 CSCTI0_CTIAPPPULSE Registers
        272. 14.9.2.272 CSCTI0_CTIINEN0 Registers
        273. 14.9.2.273 CSCTI0_CTIINEN1 Registers
        274. 14.9.2.274 CSCTI0_CTIINEN2 Registers
        275. 14.9.2.275 CSCTI0_CTIINEN3 Registers
        276. 14.9.2.276 CSCTI0_CTIINEN4 Registers
        277. 14.9.2.277 CSCTI0_CTIINEN5 Registers
        278. 14.9.2.278 CSCTI0_CTIINEN6 Registers
        279. 14.9.2.279 CSCTI0_CTIINEN7 Registers
        280. 14.9.2.280 CSCTI0_CTIOUTEN0 Registers
        281. 14.9.2.281 CSCTI0_CTIOUTEN1 Registers
        282. 14.9.2.282 CSCTI0_CTIOUTEN2 Registers
        283. 14.9.2.283 CSCTI0_CTIOUTEN3 Registers
        284. 14.9.2.284 CSCTI0_CTIOUTEN4 Registers
        285. 14.9.2.285 CSCTI0_CTIOUTEN5 Registers
        286. 14.9.2.286 CSCTI0_CTIOUTEN6 Registers
        287. 14.9.2.287 CSCTI0_CTIOUTEN7 Registers
        288. 14.9.2.288 CSCTI0_CTITRIGINSTATUS Registers
        289. 14.9.2.289 CSCTI0_CTITRIGOUTSTATUS Registers
        290. 14.9.2.290 CSCTI0_CTICHINSTATUS Registers
        291. 14.9.2.291 CSCTI0_CTICHOUTSTATUS Registers
        292. 14.9.2.292 CSCTI0_CTIGATE Registers
        293. 14.9.2.293 CSCTI0_ASICCTL Registers
        294. 14.9.2.294 CSCTI0_ITCHINACK Registers
        295. 14.9.2.295 CSCTI0_ITTRIGINACK Registers
        296. 14.9.2.296 CSCTI0_ITCHOUT Registers
        297. 14.9.2.297 CSCTI0_ITTRIGOUT Registers
        298. 14.9.2.298 CSCTI0_ITCHOUTACK Registers
        299. 14.9.2.299 CSCTI0_ITTRIGOUTACK Registers
        300. 14.9.2.300 CSCTI0_ITCHIN Registers
        301. 14.9.2.301 CSCTI0_ITTRIGIN Registers
        302. 14.9.2.302 CSCTI0_ITCTRL Registers
        303. 14.9.2.303 CSCTI0_CTSET Registers
        304. 14.9.2.304 CSCTI0_CTCLR Registers
        305. 14.9.2.305 CSCTI0_LAREG Registers
        306. 14.9.2.306 CSCTI0_LSREG Registers
        307. 14.9.2.307 CSCTI0_AUTHST Registers
        308. 14.9.2.308 CSCTI0_DEVID Registers
        309. 14.9.2.309 CSCTI0_DEVTYPEID Registers
        310. 14.9.2.310 CSCTI0_PERID4 Registers
        311. 14.9.2.311 CSCTI0_PERID0 Registers
        312. 14.9.2.312 CSCTI0_PERID1 Registers
        313. 14.9.2.313 CSCTI0_PERID2 Registers
        314. 14.9.2.314 CSCTI0_PERID3 Registers
        315. 14.9.2.315 CSCTI0_COMPID0 Registers
        316. 14.9.2.316 CSCTI0_COMPID1 Registers
        317. 14.9.2.317 CSCTI0_COMPID2 Registers
        318. 14.9.2.318 CSCTI0_COMPID3 Registers
        319. 14.9.2.319 DRM0_PERIPH_ID Registers
        320. 14.9.2.320 DRM0_VERSION Registers
        321. 14.9.2.321 DRM0_CAPABILITY Registers
        322. 14.9.2.322 DRM0_TRACE_CTRL Registers
        323. 14.9.2.323 DRM0_VBUSM_CTRL Registers
        324. 14.9.2.324 DRM0_DAP_TIMEOUT Registers
        325. 14.9.2.325 DRM0_CONFIG Registers
        326. 14.9.2.326 DRM0_EMUTRIGEN Registers
        327. 14.9.2.327 DRM0_BINVALLO Registers
        328. 14.9.2.328 DRM0_BINVALHI Registers
        329. 14.9.2.329 DRM0_SUSPEND_REG0 Registers
        330. 14.9.2.330 DRM0_SUSPEND_REG1 Registers
        331. 14.9.2.331 DRM0_SUSPEND_REG2 Registers
        332. 14.9.2.332 DRM0_SUSPEND_REG3 Registers
        333. 14.9.2.333 DRM0_SUSPEND_REG4 Registers
        334. 14.9.2.334 DRM0_SUSPEND_REG5 Registers
        335. 14.9.2.335 DRM0_SUSPEND_REG6 Registers
        336. 14.9.2.336 DRM0_SUSPEND_REG7 Registers
        337. 14.9.2.337 DRM0_SUSPEND_REG8 Registers
        338. 14.9.2.338 DRM0_SUSPEND_REG9 Registers
        339. 14.9.2.339 DRM0_SUSPEND_REG10 Registers
        340. 14.9.2.340 DRM0_SUSPEND_REG11 Registers
        341. 14.9.2.341 DRM0_SUSPEND_REG12 Registers
        342. 14.9.2.342 DRM0_SUSPEND_REG13 Registers
        343. 14.9.2.343 DRM0_SUSPEND_REG14 Registers
        344. 14.9.2.344 DRM0_SUSPEND_REG15 Registers
        345. 14.9.2.345 DRM0_SUSPEND_REG16 Registers
        346. 14.9.2.346 DRM0_SUSPEND_REG17 Registers
        347. 14.9.2.347 DRM0_SUSPEND_REG18 Registers
        348. 14.9.2.348 DRM0_SUSPEND_REG19 Registers
        349. 14.9.2.349 DRM0_SUSPEND_REG20 Registers
        350. 14.9.2.350 DRM0_SUSPEND_REG21 Registers
        351. 14.9.2.351 DRM0_SUSPEND_REG22 Registers
        352. 14.9.2.352 DRM0_SUSPEND_REG23 Registers
        353. 14.9.2.353 DRM0_SUSPEND_REG24 Registers
        354. 14.9.2.354 DRM0_SUSPEND_REG25 Registers
        355. 14.9.2.355 DRM0_SUSPEND_REG26 Registers
        356. 14.9.2.356 DRM0_SUSPEND_REG27 Registers
        357. 14.9.2.357 DRM0_SUSPEND_REG28 Registers
        358. 14.9.2.358 DRM0_SUSPEND_REG29 Registers
        359. 14.9.2.359 DRM0_SUSPEND_REG30 Registers
        360. 14.9.2.360 DRM0_SUSPEND_REG31 Registers
        361. 14.9.2.361 CSTPIU0_SUPPORTSIZE Registers
        362. 14.9.2.362 CSTPIU0_CURPORTSIZE Registers
        363. 14.9.2.363 CSTPIU0_TRIGMODEREG Registers
        364. 14.9.2.364 CSTPIU0_TRIGCTRREG Registers
        365. 14.9.2.365 CSTPIU0_TRIGMPYREG Registers
        366. 14.9.2.366 CSTPIU0_SUPTESTPAT Registers
        367. 14.9.2.367 CSTPIU0_CURTESTPAT Registers
        368. 14.9.2.368 CSTPIU0_TESTPATCNT Registers
        369. 14.9.2.369 CSTPIU0_FORMFLUSHSTAT Registers
        370. 14.9.2.370 CSTPIU0_FORMFLUSHCTL Registers
        371. 14.9.2.371 CSTPIU0_FORMSYNCCTR Registers
        372. 14.9.2.372 CSTPIU0_EXTCTLIN Registers
        373. 14.9.2.373 CSTPIU0_EXTCTLOUT Registers
        374. 14.9.2.374 CSTPIU0_ITTRFLINACK Registers
        375. 14.9.2.375 CSTPIU0_ITTRFLIN Registers
        376. 14.9.2.376 CSTPIU0_ITATBDATA0 Registers
        377. 14.9.2.377 CSTPIU0_ITATBCTR2 Registers
        378. 14.9.2.378 CSTPIU0_ITATBCTR1 Registers
        379. 14.9.2.379 CSTPIU0_ITATBCTR0 Registers
        380. 14.9.2.380 CSTPIU0_INTCTRL Registers
        381. 14.9.2.381 CSTPIU0_CTSET Registers
        382. 14.9.2.382 CSTPIU0_CTCLR Registers
        383. 14.9.2.383 CSTPIU0_LAREG Registers
        384. 14.9.2.384 CSTPIU0_LSREG Registers
        385. 14.9.2.385 CSTPIU0_AUTHST Registers
        386. 14.9.2.386 CSTPIU0_DEVID Registers
        387. 14.9.2.387 CSTPIU0_DEVTYPEID Registers
        388. 14.9.2.388 CSTPIU0_PERID4 Registers
        389. 14.9.2.389 CSTPIU0_PERID0 Registers
        390. 14.9.2.390 CSTPIU0_PERID1 Registers
        391. 14.9.2.391 CSTPIU0_PERID2 Registers
        392. 14.9.2.392 CSTPIU0_PERID3 Registers
        393. 14.9.2.393 CSTPIU0_COMPID0 Registers
        394. 14.9.2.394 CSTPIU0_COMPID1 Registers
        395. 14.9.2.395 CSTPIU0_COMPID2 Registers
        396. 14.9.2.396 CSTPIU0_COMPID3 Registers
        397. 14.9.2.397 CTF0_CSTFCTLREG Registers
        398. 14.9.2.398 CTF0_PRIORCTLREG Registers
        399. 14.9.2.399 CTF0_ITATBDATA0 Registers
        400. 14.9.2.400 CTF0_ITATBCTR2 Registers
        401. 14.9.2.401 CTF0_ITATBCTR1 Registers
        402. 14.9.2.402 CTF0_ITATBCTR0 Registers
        403. 14.9.2.403 CTF0_INTCTRL Registers
        404. 14.9.2.404 CTF0_CTSET Registers
        405. 14.9.2.405 CTF0_CTCLR Registers
        406. 14.9.2.406 CTF0_LAREG Registers
        407. 14.9.2.407 CTF0_LSREG Registers
        408. 14.9.2.408 CTF0_AUTHST Registers
        409. 14.9.2.409 CTF0_DEVID Registers
        410. 14.9.2.410 CTF0_DEVTYPEID Registers
        411. 14.9.2.411 CTF0_PERID4 Registers
        412. 14.9.2.412 CTF0_PERID5 Registers
        413. 14.9.2.413 CTF0_PERID6 Registers
        414. 14.9.2.414 CTF0_PERID7 Registers
        415. 14.9.2.415 CTF0_PERID0 Registers
        416. 14.9.2.416 CTF0_PERID1 Registers
        417. 14.9.2.417 CTF0_PERID2 Registers
        418. 14.9.2.418 CTF0_PERID3 Registers
        419. 14.9.2.419 CTF0_COMPID0 Registers
        420. 14.9.2.420 CTF0_COMPID1 Registers
        421. 14.9.2.421 CTF0_COMPID2 Registers
        422. 14.9.2.422 CTF0_COMPID3 Registers
        423. 14.9.2.423 ROM_TABLE_0_1_ROM_ENTRY0 Registers
        424. 14.9.2.424 ROM_TABLE_0_1_ROM_ENTRY1 Registers
        425. 14.9.2.425 ROM_TABLE_0_1_ROM_ENTRY2 Registers
        426. 14.9.2.426 ROM_TABLE_0_1_ROM_MANUAL_ENTRY0 Registers
        427. 14.9.2.427 ROM_TABLE_0_1_ROM_MANUAL_ENTRY1 Registers
        428. 14.9.2.428 ROM_TABLE_0_1_ROM_MANUAL_ENTRY2 Registers
        429. 14.9.2.429 ROM_TABLE_0_1_ROM_MANUAL_ENTRY3 Registers
        430. 14.9.2.430 ROM_TABLE_0_1_ROM_MANUAL_ENTRY4 Registers
        431. 14.9.2.431 ROM_TABLE_0_1_ROM_MANUAL_ENTRY5 Registers
        432. 14.9.2.432 ROM_TABLE_0_1_ROM_MANUAL_ENTRY6 Registers
        433. 14.9.2.433 ROM_TABLE_0_1_ROM_MANUAL_ENTRY7 Registers
        434. 14.9.2.434 ROM_TABLE_0_1_ROM_MANUAL_ENTRY8 Registers
        435. 14.9.2.435 ROM_TABLE_0_1_ROM_MANUAL_ENTRY9 Registers
        436. 14.9.2.436 ROM_TABLE_0_1_ROM_MANUAL_ENTRY10 Registers
        437. 14.9.2.437 ROM_TABLE_0_1_ROM_MANUAL_ENTRY11 Registers
        438. 14.9.2.438 ROM_TABLE_0_1_ROM_MANUAL_ENTRY12 Registers
        439. 14.9.2.439 ROM_TABLE_0_1_ROM_MANUAL_ENTRY13 Registers
        440. 14.9.2.440 ROM_TABLE_0_1_ROM_MANUAL_ENTRY14 Registers
        441. 14.9.2.441 ROM_TABLE_0_1_ROM_MANUAL_ENTRY15 Registers
        442. 14.9.2.442 ROM_TABLE_0_1_ROM_MANUAL_ENTRY16 Registers
        443. 14.9.2.443 ROM_TABLE_0_1_ROM_MANUAL_ENTRY17 Registers
        444. 14.9.2.444 ROM_TABLE_0_1_ROM_MANUAL_ENTRY18 Registers
        445. 14.9.2.445 ROM_TABLE_0_1_ROM_MANUAL_ENTRY19 Registers
        446. 14.9.2.446 ROM_TABLE_0_1_ROM_MANUAL_ENTRY20 Registers
        447. 14.9.2.447 ROM_TABLE_0_1_ROM_MANUAL_ENTRY21 Registers
        448. 14.9.2.448 ROM_TABLE_0_1_ROM_MANUAL_ENTRY22 Registers
        449. 14.9.2.449 ROM_TABLE_0_1_ROM_MANUAL_ENTRY23 Registers
        450. 14.9.2.450 ROM_TABLE_0_1_ROM_MANUAL_ENTRY24 Registers
        451. 14.9.2.451 ROM_TABLE_0_1_ROM_MANUAL_ENTRY25 Registers
        452. 14.9.2.452 ROM_TABLE_0_1_ROM_MANUAL_ENTRY26 Registers
        453. 14.9.2.453 ROM_TABLE_0_1_ROM_MANUAL_ENTRY27 Registers
        454. 14.9.2.454 ROM_TABLE_0_1_ROM_MANUAL_ENTRY28 Registers
        455. 14.9.2.455 ROM_TABLE_0_1_ROM_MANUAL_ENTRY29 Registers
        456. 14.9.2.456 ROM_TABLE_0_1_ROM_MANUAL_ENTRY30 Registers
        457. 14.9.2.457 ROM_TABLE_0_1_ROM_MANUAL_ENTRY31 Registers
        458. 14.9.2.458 ROM_TABLE_0_1_ROM_MANUAL_ENTRY32 Registers
        459. 14.9.2.459 ROM_TABLE_0_1_ROM_MANUAL_ENTRY33 Registers
        460. 14.9.2.460 ROM_TABLE_0_1_ROM_MANUAL_ENTRY34 Registers
        461. 14.9.2.461 ROM_TABLE_0_1_ROM_MANUAL_ENTRY35 Registers
        462. 14.9.2.462 ROM_TABLE_0_1_ROM_MANUAL_ENTRY36 Registers
        463. 14.9.2.463 ROM_TABLE_0_1_ROM_MANUAL_ENTRY37 Registers
        464. 14.9.2.464 ROM_TABLE_0_1_ROM_MANUAL_ENTRY38 Registers
        465. 14.9.2.465 ROM_TABLE_0_1_ROM_MANUAL_ENTRY39 Registers
        466. 14.9.2.466 ROM_TABLE_0_1_ROM_MANUAL_ENTRY40 Registers
        467. 14.9.2.467 ROM_TABLE_0_1_ROM_MANUAL_ENTRY41 Registers
        468. 14.9.2.468 ROM_TABLE_0_1_ROM_MANUAL_ENTRY42 Registers
        469. 14.9.2.469 ROM_TABLE_0_1_ROM_MANUAL_ENTRY43 Registers
        470. 14.9.2.470 ROM_TABLE_0_1_ROM_MANUAL_ENTRY44 Registers
        471. 14.9.2.471 ROM_TABLE_0_1_ROM_MANUAL_ENTRY45 Registers
        472. 14.9.2.472 ROM_TABLE_0_1_ROM_MANUAL_ENTRY46 Registers
        473. 14.9.2.473 ROM_TABLE_0_1_ROM_MANUAL_ENTRY47 Registers
        474. 14.9.2.474 ROM_TABLE_0_1_ROM_MANUAL_ENTRY48 Registers
        475. 14.9.2.475 ROM_TABLE_0_1_ROM_MANUAL_ENTRY49 Registers
        476. 14.9.2.476 ROM_TABLE_0_1_ROM_MANUAL_ENTRY50 Registers
        477. 14.9.2.477 ROM_TABLE_0_1_ROM_MANUAL_ENTRY51 Registers
        478. 14.9.2.478 ROM_TABLE_0_1_ROM_MANUAL_ENTRY52 Registers
        479. 14.9.2.479 ROM_TABLE_0_1_ROM_MANUAL_ENTRY53 Registers
        480. 14.9.2.480 ROM_TABLE_0_1_ROM_MANUAL_ENTRY54 Registers
        481. 14.9.2.481 ROM_TABLE_0_1_ROM_MANUAL_ENTRY55 Registers
        482. 14.9.2.482 ROM_TABLE_0_1_ROM_MANUAL_ENTRY56 Registers
        483. 14.9.2.483 ROM_TABLE_0_1_ROM_MANUAL_ENTRY57 Registers
        484. 14.9.2.484 ROM_TABLE_0_1_ROM_MANUAL_ENTRY58 Registers
        485. 14.9.2.485 ROM_TABLE_0_1_ROM_MANUAL_ENTRY59 Registers
        486. 14.9.2.486 ROM_TABLE_0_1_ROM_MANUAL_ENTRY60 Registers
        487. 14.9.2.487 ROM_TABLE_0_1_ROM_MANUAL_ENTRY61 Registers
        488. 14.9.2.488 ROM_TABLE_0_1_ROM_MANUAL_ENTRY62 Registers
        489. 14.9.2.489 ROM_TABLE_0_1_ROM_MANUAL_ENTRY63 Registers
        490. 14.9.2.490 ROM_TABLE_0_1_PERIPHID0 Registers
        491. 14.9.2.491 ROM_TABLE_0_1_PERIPHID1 Registers
        492. 14.9.2.492 ROM_TABLE_0_1_PERIPHID2 Registers
        493. 14.9.2.493 ROM_TABLE_0_1_PERIPHID3 Registers
        494. 14.9.2.494 ROM_TABLE_0_1_PERIPHID4 Registers
        495. 14.9.2.495 ROM_TABLE_0_1_COMPID0 Registers
        496. 14.9.2.496 ROM_TABLE_0_1_COMPID1 Registers
        497. 14.9.2.497 ROM_TABLE_0_1_COMPID2 Registers
        498. 14.9.2.498 ROM_TABLE_0_1_COMPID3 Registers
        499. 14.9.2.499 CFGAP1_JTAGID_REG Registers
        500. 14.9.2.500 CFGAP1_USERID_REG Registers
        501. 14.9.2.501 CFGAP1_VERSION_REG Registers
        502. 14.9.2.502 CFGAP1_SYSTEMSTATUS Registers
        503. 14.9.2.503 CFGAP1_APID_REGISTER Registers
        504. 14.9.2.504 APBAP1_CSWREG Registers
        505. 14.9.2.505 APBAP1_TAREG Registers
        506. 14.9.2.506 APBAP1_DRWREG Registers
        507. 14.9.2.507 APBAP1_BD0REG Registers
        508. 14.9.2.508 APBAP1_BD1REG Registers
        509. 14.9.2.509 APBAP1_BD2REG Registers
        510. 14.9.2.510 APBAP1_BD3REG Registers
        511. 14.9.2.511 APBAP1_ROM_REGISTER Registers
        512. 14.9.2.512 APBAP1_ID_REGISTER Registers
        513. 14.9.2.513 AXIAP1_CSWREG Registers
        514. 14.9.2.514 AXIAP1_TAREGL Registers
        515. 14.9.2.515 AXIAP1_TAREGH Registers
        516. 14.9.2.516 AXIAP1_DRWREG Registers
        517. 14.9.2.517 AXIAP1_BD0REG Registers
        518. 14.9.2.518 AXIAP1_BD1REG Registers
        519. 14.9.2.519 AXIAP1_BD2REG Registers
        520. 14.9.2.520 AXIAP1_BD3REG Registers
        521. 14.9.2.521 AXIAP1_MBT_REGISTER Registers
        522. 14.9.2.522 AXIAP1_ROM_HI_REGISTER Registers
        523. 14.9.2.523 AXIAP1_CFG_REGISTER Registers
        524. 14.9.2.524 AXIAP1_ROM_LO_REGISTER Registers
        525. 14.9.2.525 AXIAP1_ID_REGISTER Registers
        526. 14.9.2.526 PWRAP1_CORE_PRECREG0 Registers
        527. 14.9.2.527 PWRAP1_CORE_PRECREG1 Registers
        528. 14.9.2.528 PWRAP1_CORE_PRECREG2 Registers
        529. 14.9.2.529 PWRAP1_CORE_PRECREG3 Registers
        530. 14.9.2.530 PWRAP1_CORE_PRECREG4 Registers
        531. 14.9.2.531 PWRAP1_CORE_PRECREG5 Registers
        532. 14.9.2.532 PWRAP1_CORE_PRECREG6 Registers
        533. 14.9.2.533 PWRAP1_CORE_PRECREG7 Registers
        534. 14.9.2.534 PWRAP1_CORE_PRECREG8 Registers
        535. 14.9.2.535 PWRAP1_CORE_PRECREG9 Registers
        536. 14.9.2.536 PWRAP1_CORE_PRECREG10 Registers
        537. 14.9.2.537 PWRAP1_CORE_PRECREG11 Registers
        538. 14.9.2.538 PWRAP1_CORE_PRECREG12 Registers
        539. 14.9.2.539 PWRAP1_CORE_PRECREG13 Registers
        540. 14.9.2.540 PWRAP1_CORE_PRECREG14 Registers
        541. 14.9.2.541 PWRAP1_CORE_PRECREG15 Registers
        542. 14.9.2.542 PWRAP1_CORE_PRECREG16 Registers
        543. 14.9.2.543 PWRAP1_CORE_PRECREG17 Registers
        544. 14.9.2.544 PWRAP1_CORE_PRECREG18 Registers
        545. 14.9.2.545 PWRAP1_CORE_PRECREG19 Registers
        546. 14.9.2.546 PWRAP1_CORE_PRECREG20 Registers
        547. 14.9.2.547 PWRAP1_CORE_PRECREG21 Registers
        548. 14.9.2.548 PWRAP1_CORE_PRECREG22 Registers
        549. 14.9.2.549 PWRAP1_CORE_PRECREG23 Registers
        550. 14.9.2.550 PWRAP1_CORE_PRECREG24 Registers
        551. 14.9.2.551 PWRAP1_CORE_PRECREG25 Registers
        552. 14.9.2.552 PWRAP1_CORE_PRECREG26 Registers
        553. 14.9.2.553 PWRAP1_CORE_PRECREG27 Registers
        554. 14.9.2.554 PWRAP1_CORE_PRECREG28 Registers
        555. 14.9.2.555 PWRAP1_CORE_PRECREG29 Registers
        556. 14.9.2.556 PWRAP1_CORE_PRECREG30 Registers
        557. 14.9.2.557 PWRAP1_CORE_PRECREG31 Registers
        558. 14.9.2.558 PWRAP1_SYS_PRECREG Registers
        559. 14.9.2.559 PWRAP1_ID_REGISTER Registers
        560. 14.9.2.560 PVIEW1_PVIEW_STATE0 Registers
        561. 14.9.2.561 PVIEW1_PVIEW_CAPABILITY Registers
        562. 14.9.2.562 PVIEW1_ID_REGISTER Registers
        563. 14.9.2.563 JTAGAP1_CSW Registers
        564. 14.9.2.564 JTAGAP1_PSEL_REG Registers
        565. 14.9.2.565 JTAGAP1_PSTA_REG Registers
        566. 14.9.2.566 JTAGAP1_BYTEFIFO1 Registers
        567. 14.9.2.567 JTAGAP1_BYTEFIFO2 Registers
        568. 14.9.2.568 JTAGAP1_BYTEFIFO3 Registers
        569. 14.9.2.569 JTAGAP1_BYTEFIFO4 Registers
        570. 14.9.2.570 JTAGAP1_ID_REGISTER Registers
        571. 14.9.2.571 SECAP1_TXDATA Registers
        572. 14.9.2.572 SECAP1_TXCTRL Registers
        573. 14.9.2.573 SECAP1_RXDATA Registers
        574. 14.9.2.574 SECAP1_RXCTRL Registers
        575. 14.9.2.575 CORTEX0_CFG1_CSWREG Registers
        576. 14.9.2.576 CORTEX0_CFG1_TAREG Registers
        577. 14.9.2.577 CORTEX0_CFG1_DRWREG Registers
        578. 14.9.2.578 CORTEX0_CFG1_BD0REG Registers
        579. 14.9.2.579 CORTEX0_CFG1_BD1REG Registers
        580. 14.9.2.580 CORTEX0_CFG1_BD2REG Registers
        581. 14.9.2.581 CORTEX0_CFG1_BD3REG Registers
        582. 14.9.2.582 CORTEX0_CFG1_ROM_REGISTER Registers
        583. 14.9.2.583 CORTEX0_CFG1_ID_REGISTER Registers
        584. 14.9.2.584 CORTEX1_CFG1_CSWREG Registers
        585. 14.9.2.585 CORTEX1_CFG1_TAREG Registers
        586. 14.9.2.586 CORTEX1_CFG1_DRWREG Registers
        587. 14.9.2.587 CORTEX1_CFG1_BD0REG Registers
        588. 14.9.2.588 CORTEX1_CFG1_BD1REG Registers
        589. 14.9.2.589 CORTEX1_CFG1_BD2REG Registers
        590. 14.9.2.590 CORTEX1_CFG1_BD3REG Registers
        591. 14.9.2.591 CORTEX1_CFG1_ROM_REGISTER Registers
        592. 14.9.2.592 CORTEX1_CFG1_ID_REGISTER Registers
        593. 14.9.2.593 CORTEX2_CFG1_CSWREG Registers
        594. 14.9.2.594 CORTEX2_CFG1_TAREG Registers
        595. 14.9.2.595 CORTEX2_CFG1_DRWREG Registers
        596. 14.9.2.596 CORTEX2_CFG1_BD0REG Registers
        597. 14.9.2.597 CORTEX2_CFG1_BD1REG Registers
        598. 14.9.2.598 CORTEX2_CFG1_BD2REG Registers
        599. 14.9.2.599 CORTEX2_CFG1_BD3REG Registers
        600. 14.9.2.600 CORTEX2_CFG1_ROM_REGISTER Registers
        601. 14.9.2.601 CORTEX2_CFG1_ID_REGISTER Registers
        602. 14.9.2.602 CORTEX3_CFG1_CSWREG Registers
        603. 14.9.2.603 CORTEX3_CFG1_TAREG Registers
        604. 14.9.2.604 CORTEX3_CFG1_DRWREG Registers
        605. 14.9.2.605 CORTEX3_CFG1_BD0REG Registers
        606. 14.9.2.606 CORTEX3_CFG1_BD1REG Registers
        607. 14.9.2.607 CORTEX3_CFG1_BD2REG Registers
        608. 14.9.2.608 CORTEX3_CFG1_BD3REG Registers
        609. 14.9.2.609 CORTEX3_CFG1_ROM_REGISTER Registers
        610. 14.9.2.610 CORTEX3_CFG1_ID_REGISTER Registers
        611. 14.9.2.611 CORTEX4_CFG1_CSWREG Registers
        612. 14.9.2.612 CORTEX4_CFG1_TAREG Registers
        613. 14.9.2.613 CORTEX4_CFG1_DRWREG Registers
        614. 14.9.2.614 CORTEX4_CFG1_BD0REG Registers
        615. 14.9.2.615 CORTEX4_CFG1_BD1REG Registers
        616. 14.9.2.616 CORTEX4_CFG1_BD2REG Registers
        617. 14.9.2.617 CORTEX4_CFG1_BD3REG Registers
        618. 14.9.2.618 CORTEX4_CFG1_ROM_REGISTER Registers
        619. 14.9.2.619 CORTEX4_CFG1_ID_REGISTER Registers
        620. 14.9.2.620 CORTEX5_CFG1_CSWREG Registers
        621. 14.9.2.621 CORTEX5_CFG1_TAREG Registers
        622. 14.9.2.622 CORTEX5_CFG1_DRWREG Registers
        623. 14.9.2.623 CORTEX5_CFG1_BD0REG Registers
        624. 14.9.2.624 CORTEX5_CFG1_BD1REG Registers
        625. 14.9.2.625 CORTEX5_CFG1_BD2REG Registers
        626. 14.9.2.626 CORTEX5_CFG1_BD3REG Registers
        627. 14.9.2.627 CORTEX5_CFG1_ROM_REGISTER Registers
        628. 14.9.2.628 CORTEX5_CFG1_ID_REGISTER Registers
        629. 14.9.2.629 CORTEX6_CFG1_CSWREG Registers
        630. 14.9.2.630 CORTEX6_CFG1_TAREG Registers
        631. 14.9.2.631 CORTEX6_CFG1_DRWREG Registers
        632. 14.9.2.632 CORTEX6_CFG1_BD0REG Registers
        633. 14.9.2.633 CORTEX6_CFG1_BD1REG Registers
        634. 14.9.2.634 CORTEX6_CFG1_BD2REG Registers
        635. 14.9.2.635 CORTEX6_CFG1_BD3REG Registers
        636. 14.9.2.636 CORTEX6_CFG1_ROM_REGISTER Registers
        637. 14.9.2.637 CORTEX6_CFG1_ID_REGISTER Registers
        638. 14.9.2.638 CORTEX7_CFG1_CSWREG Registers
        639. 14.9.2.639 CORTEX7_CFG1_TAREG Registers
        640. 14.9.2.640 CORTEX7_CFG1_DRWREG Registers
        641. 14.9.2.641 CORTEX7_CFG1_BD0REG Registers
        642. 14.9.2.642 CORTEX7_CFG1_BD1REG Registers
        643. 14.9.2.643 CORTEX7_CFG1_BD2REG Registers
        644. 14.9.2.644 CORTEX7_CFG1_BD3REG Registers
        645. 14.9.2.645 CORTEX7_CFG1_ROM_REGISTER Registers
        646. 14.9.2.646 CORTEX7_CFG1_ID_REGISTER Registers
        647. 14.9.2.647 CORTEX8_CFG1_CSWREG Registers
        648. 14.9.2.648 CORTEX8_CFG1_TAREG Registers
        649. 14.9.2.649 CORTEX8_CFG1_DRWREG Registers
        650. 14.9.2.650 CORTEX8_CFG1_BD0REG Registers
        651. 14.9.2.651 CORTEX8_CFG1_BD1REG Registers
        652. 14.9.2.652 CORTEX8_CFG1_BD2REG Registers
        653. 14.9.2.653 CORTEX8_CFG1_BD3REG Registers
        654. 14.9.2.654 CORTEX8_CFG1_ROM_REGISTER Registers
        655. 14.9.2.655 CORTEX8_CFG1_ID_REGISTER Registers
        656. 14.9.2.656 ROM_TABLE_1_1_ROM_ENTRY0 Registers
        657. 14.9.2.657 ROM_TABLE_1_1_ROM_ENTRY1 Registers
        658. 14.9.2.658 ROM_TABLE_1_1_ROM_ENTRY2 Registers
        659. 14.9.2.659 ROM_TABLE_1_1_ROM_ENTRY3 Registers
        660. 14.9.2.660 ROM_TABLE_1_1_ROM_ENTRY4 Registers
        661. 14.9.2.661 ROM_TABLE_1_1_ROM_ENTRY5 Registers
        662. 14.9.2.662 ROM_TABLE_1_1_COMPUTE_CLUSTER0 Registers
        663. 14.9.2.663 ROM_TABLE_1_1_COMPUTE_CLUSTER1 Registers
        664. 14.9.2.664 ROM_TABLE_1_1_COMPUTE_CLUSTER2 Registers
        665. 14.9.2.665 ROM_TABLE_1_1_DEBUG_CELL0 Registers
        666. 14.9.2.666 ROM_TABLE_1_1_DEBUG_CELL1 Registers
        667. 14.9.2.667 ROM_TABLE_1_1_DEBUG_CELL2 Registers
        668. 14.9.2.668 ROM_TABLE_1_1_DEBUG_CELL3 Registers
        669. 14.9.2.669 ROM_TABLE_1_1_DEBUG_CELL4 Registers
        670. 14.9.2.670 ROM_TABLE_1_1_DEBUG_CELL5 Registers
        671. 14.9.2.671 ROM_TABLE_1_1_DEBUG_CELL6 Registers
        672. 14.9.2.672 ROM_TABLE_1_1_DEBUG_CELL7 Registers
        673. 14.9.2.673 ROM_TABLE_1_1_DEBUG_CELL8 Registers
        674. 14.9.2.674 ROM_TABLE_1_1_DEBUG_CELL9 Registers
        675. 14.9.2.675 ROM_TABLE_1_1_DEBUG_CELL10 Registers
        676. 14.9.2.676 ROM_TABLE_1_1_DEBUG_CELL11 Registers
        677. 14.9.2.677 ROM_TABLE_1_1_EXTCSCOMP0 Registers
        678. 14.9.2.678 ROM_TABLE_1_1_EXTCSCOMP1 Registers
        679. 14.9.2.679 ROM_TABLE_1_1_EXTCSCOMP2 Registers
        680. 14.9.2.680 ROM_TABLE_1_1_EXTCSCOMP3 Registers
        681. 14.9.2.681 ROM_TABLE_1_1_EXTCSCOMP4 Registers
        682. 14.9.2.682 ROM_TABLE_1_1_EXTCSCOMP5 Registers
        683. 14.9.2.683 ROM_TABLE_1_1_EXTCSCOMP6 Registers
        684. 14.9.2.684 ROM_TABLE_1_1_EXTCSCOMP7 Registers
        685. 14.9.2.685 ROM_TABLE_1_1_EXTCSCOMP8 Registers
        686. 14.9.2.686 ROM_TABLE_1_1_EXTCSCOMP9 Registers
        687. 14.9.2.687 ROM_TABLE_1_1_EXTCSCOMP10 Registers
        688. 14.9.2.688 ROM_TABLE_1_1_EXTCSCOMP11 Registers
        689. 14.9.2.689 CSCTI1_CTICONTROL Registers
        690. 14.9.2.690 CSCTI1_CTIINTACK Registers
        691. 14.9.2.691 CSCTI1_CTIAPPSET Registers
        692. 14.9.2.692 CSCTI1_CTIAPPCLEAR Registers
        693. 14.9.2.693 CSCTI1_CTIAPPPULSE Registers
        694. 14.9.2.694 CSCTI1_CTIINEN0 Registers
        695. 14.9.2.695 CSCTI1_CTIINEN1 Registers
        696. 14.9.2.696 CSCTI1_CTIINEN2 Registers
        697. 14.9.2.697 CSCTI1_CTIINEN3 Registers
        698. 14.9.2.698 CSCTI1_CTIINEN4 Registers
        699. 14.9.2.699 CSCTI1_CTIINEN5 Registers
        700. 14.9.2.700 CSCTI1_CTIINEN6 Registers
        701. 14.9.2.701 CSCTI1_CTIINEN7 Registers
        702. 14.9.2.702 CSCTI1_CTIOUTEN0 Registers
        703. 14.9.2.703 CSCTI1_CTIOUTEN1 Registers
        704. 14.9.2.704 CSCTI1_CTIOUTEN2 Registers
        705. 14.9.2.705 CSCTI1_CTIOUTEN3 Registers
        706. 14.9.2.706 CSCTI1_CTIOUTEN4 Registers
        707. 14.9.2.707 CSCTI1_CTIOUTEN5 Registers
        708. 14.9.2.708 CSCTI1_CTIOUTEN6 Registers
        709. 14.9.2.709 CSCTI1_CTIOUTEN7 Registers
        710. 14.9.2.710 CSCTI1_CTITRIGINSTATUS Registers
        711. 14.9.2.711 CSCTI1_CTITRIGOUTSTATUS Registers
        712. 14.9.2.712 CSCTI1_CTICHINSTATUS Registers
        713. 14.9.2.713 CSCTI1_CTICHOUTSTATUS Registers
        714. 14.9.2.714 CSCTI1_CTIGATE Registers
        715. 14.9.2.715 CSCTI1_ASICCTL Registers
        716. 14.9.2.716 CSCTI1_ITCHINACK Registers
        717. 14.9.2.717 CSCTI1_ITTRIGINACK Registers
        718. 14.9.2.718 CSCTI1_ITCHOUT Registers
        719. 14.9.2.719 CSCTI1_ITTRIGOUT Registers
        720. 14.9.2.720 CSCTI1_ITCHOUTACK Registers
        721. 14.9.2.721 CSCTI1_ITTRIGOUTACK Registers
        722. 14.9.2.722 CSCTI1_ITCHIN Registers
        723. 14.9.2.723 CSCTI1_ITTRIGIN Registers
        724. 14.9.2.724 CSCTI1_ITCTRL Registers
        725. 14.9.2.725 CSCTI1_CTSET Registers
        726. 14.9.2.726 CSCTI1_CTCLR Registers
        727. 14.9.2.727 CSCTI1_LAREG Registers
        728. 14.9.2.728 CSCTI1_LSREG Registers
        729. 14.9.2.729 CSCTI1_AUTHST Registers
        730. 14.9.2.730 CSCTI1_DEVID Registers
        731. 14.9.2.731 CSCTI1_DEVTYPEID Registers
        732. 14.9.2.732 CSCTI1_PERID4 Registers
        733. 14.9.2.733 CSCTI1_PERID0 Registers
        734. 14.9.2.734 CSCTI1_PERID1 Registers
        735. 14.9.2.735 CSCTI1_PERID2 Registers
        736. 14.9.2.736 CSCTI1_PERID3 Registers
        737. 14.9.2.737 CSCTI1_COMPID0 Registers
        738. 14.9.2.738 CSCTI1_COMPID1 Registers
        739. 14.9.2.739 CSCTI1_COMPID2 Registers
        740. 14.9.2.740 CSCTI1_COMPID3 Registers
        741. 14.9.2.741 DRM1_PERIPH_ID Registers
        742. 14.9.2.742 DRM1_VERSION Registers
        743. 14.9.2.743 DRM1_CAPABILITY Registers
        744. 14.9.2.744 DRM1_TRACE_CTRL Registers
        745. 14.9.2.745 DRM1_VBUSM_CTRL Registers
        746. 14.9.2.746 DRM1_DAP_TIMEOUT Registers
        747. 14.9.2.747 DRM1_CONFIG Registers
        748. 14.9.2.748 DRM1_EMUTRIGEN Registers
        749. 14.9.2.749 DRM1_BINVALLO Registers
        750. 14.9.2.750 DRM1_BINVALHI Registers
        751. 14.9.2.751 DRM1_SUSPEND_REG0 Registers
        752. 14.9.2.752 DRM1_SUSPEND_REG1 Registers
        753. 14.9.2.753 DRM1_SUSPEND_REG2 Registers
        754. 14.9.2.754 DRM1_SUSPEND_REG3 Registers
        755. 14.9.2.755 DRM1_SUSPEND_REG4 Registers
        756. 14.9.2.756 DRM1_SUSPEND_REG5 Registers
        757. 14.9.2.757 DRM1_SUSPEND_REG6 Registers
        758. 14.9.2.758 DRM1_SUSPEND_REG7 Registers
        759. 14.9.2.759 DRM1_SUSPEND_REG8 Registers
        760. 14.9.2.760 DRM1_SUSPEND_REG9 Registers
        761. 14.9.2.761 DRM1_SUSPEND_REG10 Registers
        762. 14.9.2.762 DRM1_SUSPEND_REG11 Registers
        763. 14.9.2.763 DRM1_SUSPEND_REG12 Registers
        764. 14.9.2.764 DRM1_SUSPEND_REG13 Registers
        765. 14.9.2.765 DRM1_SUSPEND_REG14 Registers
        766. 14.9.2.766 DRM1_SUSPEND_REG15 Registers
        767. 14.9.2.767 DRM1_SUSPEND_REG16 Registers
        768. 14.9.2.768 DRM1_SUSPEND_REG17 Registers
        769. 14.9.2.769 DRM1_SUSPEND_REG18 Registers
        770. 14.9.2.770 DRM1_SUSPEND_REG19 Registers
        771. 14.9.2.771 DRM1_SUSPEND_REG20 Registers
        772. 14.9.2.772 DRM1_SUSPEND_REG21 Registers
        773. 14.9.2.773 DRM1_SUSPEND_REG22 Registers
        774. 14.9.2.774 DRM1_SUSPEND_REG23 Registers
        775. 14.9.2.775 DRM1_SUSPEND_REG24 Registers
        776. 14.9.2.776 DRM1_SUSPEND_REG25 Registers
        777. 14.9.2.777 DRM1_SUSPEND_REG26 Registers
        778. 14.9.2.778 DRM1_SUSPEND_REG27 Registers
        779. 14.9.2.779 DRM1_SUSPEND_REG28 Registers
        780. 14.9.2.780 DRM1_SUSPEND_REG29 Registers
        781. 14.9.2.781 DRM1_SUSPEND_REG30 Registers
        782. 14.9.2.782 DRM1_SUSPEND_REG31 Registers
        783. 14.9.2.783 CSTPIU1_SUPPORTSIZE Registers
        784. 14.9.2.784 CSTPIU1_CURPORTSIZE Registers
        785. 14.9.2.785 CSTPIU1_TRIGMODEREG Registers
        786. 14.9.2.786 CSTPIU1_TRIGCTRREG Registers
        787. 14.9.2.787 CSTPIU1_TRIGMPYREG Registers
        788. 14.9.2.788 CSTPIU1_SUPTESTPAT Registers
        789. 14.9.2.789 CSTPIU1_CURTESTPAT Registers
        790. 14.9.2.790 CSTPIU1_TESTPATCNT Registers
        791. 14.9.2.791 CSTPIU1_FORMFLUSHSTAT Registers
        792. 14.9.2.792 CSTPIU1_FORMFLUSHCTL Registers
        793. 14.9.2.793 CSTPIU1_FORMSYNCCTR Registers
        794. 14.9.2.794 CSTPIU1_EXTCTLIN Registers
        795. 14.9.2.795 CSTPIU1_EXTCTLOUT Registers
        796. 14.9.2.796 CSTPIU1_ITTRFLINACK Registers
        797. 14.9.2.797 CSTPIU1_ITTRFLIN Registers
        798. 14.9.2.798 CSTPIU1_ITATBDATA0 Registers
        799. 14.9.2.799 CSTPIU1_ITATBCTR2 Registers
        800. 14.9.2.800 CSTPIU1_ITATBCTR1 Registers
        801. 14.9.2.801 CSTPIU1_ITATBCTR0 Registers
        802. 14.9.2.802 CSTPIU1_INTCTRL Registers
        803. 14.9.2.803 CSTPIU1_CTSET Registers
        804. 14.9.2.804 CSTPIU1_CTCLR Registers
        805. 14.9.2.805 CSTPIU1_LAREG Registers
        806. 14.9.2.806 CSTPIU1_LSREG Registers
        807. 14.9.2.807 CSTPIU1_AUTHST Registers
        808. 14.9.2.808 CSTPIU1_DEVID Registers
        809. 14.9.2.809 CSTPIU1_DEVTYPEID Registers
        810. 14.9.2.810 CSTPIU1_PERID4 Registers
        811. 14.9.2.811 CSTPIU1_PERID0 Registers
        812. 14.9.2.812 CSTPIU1_PERID1 Registers
        813. 14.9.2.813 CSTPIU1_PERID2 Registers
        814. 14.9.2.814 CSTPIU1_PERID3 Registers
        815. 14.9.2.815 CSTPIU1_COMPID0 Registers
        816. 14.9.2.816 CSTPIU1_COMPID1 Registers
        817. 14.9.2.817 CSTPIU1_COMPID2 Registers
        818. 14.9.2.818 CSTPIU1_COMPID3 Registers
        819. 14.9.2.819 CTF1_CSTFCTLREG Registers
        820. 14.9.2.820 CTF1_PRIORCTLREG Registers
        821. 14.9.2.821 CTF1_ITATBDATA0 Registers
        822. 14.9.2.822 CTF1_ITATBCTR2 Registers
        823. 14.9.2.823 CTF1_ITATBCTR1 Registers
        824. 14.9.2.824 CTF1_ITATBCTR0 Registers
        825. 14.9.2.825 CTF1_INTCTRL Registers
        826. 14.9.2.826 CTF1_CTSET Registers
        827. 14.9.2.827 CTF1_CTCLR Registers
        828. 14.9.2.828 CTF1_LAREG Registers
        829. 14.9.2.829 CTF1_LSREG Registers
        830. 14.9.2.830 CTF1_AUTHST Registers
        831. 14.9.2.831 CTF1_DEVID Registers
        832. 14.9.2.832 CTF1_DEVTYPEID Registers
        833. 14.9.2.833 CTF1_PERID4 Registers
        834. 14.9.2.834 CTF1_PERID5 Registers
        835. 14.9.2.835 CTF1_PERID6 Registers
        836. 14.9.2.836 CTF1_PERID7 Registers
        837. 14.9.2.837 CTF1_PERID0 Registers
        838. 14.9.2.838 CTF1_PERID1 Registers
        839. 14.9.2.839 CTF1_PERID2 Registers
        840. 14.9.2.840 CTF1_PERID3 Registers
        841. 14.9.2.841 CTF1_COMPID0 Registers
        842. 14.9.2.842 CTF1_COMPID1 Registers
        843. 14.9.2.843 CTF1_COMPID2 Registers
        844. 14.9.2.844 CTF1_COMPID3 Registers
        845. 14.9.2.845 Access Table
      3. 14.9.3 DBGSUSPENDROUTER Registers
        1. 14.9.3.1 INTR_ROUTER_CFG_PID Registers
        2. 14.9.3.2 INTR_ROUTER_CFG_MUXCNTL_N Registers
        3. 14.9.3.3 Access Table
      4. 14.9.4 PBIST Registers
        1. 14.9.4.1  _PBIST_RF0L Registers
        2. 14.9.4.2  _PBIST_RF1L Registers
        3. 14.9.4.3  _PBIST_RF2L Registers
        4. 14.9.4.4  _PBIST_RF3L Registers
        5. 14.9.4.5  _PBIST_RF4L Registers
        6. 14.9.4.6  _PBIST_RF5L Registers
        7. 14.9.4.7  _PBIST_RF6L Registers
        8. 14.9.4.8  _PBIST_RF7L Registers
        9. 14.9.4.9  _PBIST_RF8L Registers
        10. 14.9.4.10 _PBIST_RF9L Registers
        11. 14.9.4.11 _PBIST_RF10L Registers
        12. 14.9.4.12 _PBIST_RF11L Registers
        13. 14.9.4.13 _PBIST_RF12L Registers
        14. 14.9.4.14 _PBIST_RF13L Registers
        15. 14.9.4.15 _PBIST_RF14L Registers
        16. 14.9.4.16 _PBIST_RF15L Registers
        17. 14.9.4.17 _PBIST_RF0U Registers
        18. 14.9.4.18 _PBIST_RF1U Registers
        19. 14.9.4.19 _PBIST_RF2U Registers
        20. 14.9.4.20 _PBIST_RF3U Registers
        21. 14.9.4.21 _PBIST_RF4U Registers
        22. 14.9.4.22 _PBIST_RF5U Registers
        23. 14.9.4.23 _PBIST_RF6U Registers
        24. 14.9.4.24 _PBIST_RF7U Registers
        25. 14.9.4.25 _PBIST_RF8U Registers
        26. 14.9.4.26 _PBIST_RF9U Registers
        27. 14.9.4.27 _PBIST_RF10U Registers
        28. 14.9.4.28 _PBIST_RF11U Registers
        29. 14.9.4.29 _PBIST_RF12U Registers
        30. 14.9.4.30 _PBIST_RF13U Registers
        31. 14.9.4.31 _PBIST_RF14U Registers
        32. 14.9.4.32 _PBIST_RF15U Registers
        33. 14.9.4.33 _PBIST_A0 Registers
        34. 14.9.4.34 _PBIST_A1 Registers
        35. 14.9.4.35 _PBIST_A2 Registers
        36. 14.9.4.36 _PBIST_A3 Registers
        37. 14.9.4.37 _PBIST_L0 Registers
        38. 14.9.4.38 _PBIST_L1 Registers
        39. 14.9.4.39 _PBIST_L2 Registers
        40. 14.9.4.40 _PBIST_L3 Registers
        41. 14.9.4.41 _PBIST_D Registers
        42. 14.9.4.42 _PBIST_E Registers
        43. 14.9.4.43 _PBIST_CA0 Registers
        44. 14.9.4.44 _PBIST_CA1 Registers
        45. 14.9.4.45 _PBIST_CA2 Registers
        46. 14.9.4.46 _PBIST_CA3 Registers
        47. 14.9.4.47 _PBIST_CL0 Registers
        48. 14.9.4.48 _PBIST_CL1 Registers
        49. 14.9.4.49 _PBIST_CL2 Registers
        50. 14.9.4.50 _PBIST_CL3 Registers
        51. 14.9.4.51 _PBIST_I0 Registers
        52. 14.9.4.52 _PBIST_I1 Registers
        53. 14.9.4.53 _PBIST_I2 Registers
        54. 14.9.4.54 _PBIST_I3 Registers
        55. 14.9.4.55 _PBIST_RAMT Registers
        56. 14.9.4.56 _PBIST_DLR Registers
        57. 14.9.4.57 _PBIST_CMS Registers
        58. 14.9.4.58 _PBIST_STR Registers
        59. 14.9.4.59 _PBIST_SCR Registers
        60. 14.9.4.60 _PBIST_CSR Registers
        61. 14.9.4.61 _PBIST_FDLY Registers
        62. 14.9.4.62 _PBIST_PACT Registers
        63. 14.9.4.63 _PBIST_PID Registers
        64. 14.9.4.64 _PBIST_OVER Registers
        65. 14.9.4.65 _PBIST_FSRF Registers
        66. 14.9.4.66 _PBIST_FSRC Registers
        67. 14.9.4.67 _PBIST_FSRA Registers
        68. 14.9.4.68 _PBIST_FSRDL0 Registers
        69. 14.9.4.69 _PBIST_FSRDL1 Registers
        70. 14.9.4.70 _PBIST_MARGIN_MODE Registers
        71. 14.9.4.71 _PBIST_WRENZ Registers
        72. 14.9.4.72 _PBIST_PAGE_PGS Registers
        73. 14.9.4.73 _PBIST_ROM Registers
        74. 14.9.4.74 _PBIST_ALGO Registers
        75. 14.9.4.75 _PBIST_RINFO Registers
        76. 14.9.4.76 Access Table
  17. 15Revision History

12.5.4.1 EQEP Overview

The Enhanced Quadrature Encoder Pulse (EQEP) peripheral is used for direct interface with a linear or rotary incremental encoder to get position, direction and speed information from a rotating machine for use in high performance motion and position control system. The disk of an incremental encoder is patterned with a single track of slots patterns, as shown in Figure 12-364. These slots create an alternating pattern of dark and light lines. The disk count is defined as the number of dark/light line pairs that occur per revolution (lines per revolution). As a rule, a second track is added to generate a signal that occurs once per revolution (index signal: QEPI), which can be used to indicate an absolute position. Encoder manufacturers identify the index pulse using different terms such as index, marker, home position and zero reference.

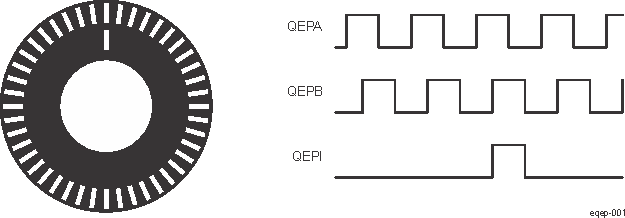GUID-30CD4539-6D1D-45B0-A185-D0940EC55B36-low.gifFigure 12-364 Optical Encoder Disk

To derive direction information, the lines on the disk are read out by two different photo-elements that "look" at the disk pattern with a mechanical shift of 1/4 the pitch of a line pair between them. This shift is realized with a reticle or mask that restricts the view of the photo-element to the desired part of the disk lines. As the disk rotates, the two photo-elements generate signals that are shifted 90 degrees out of phase from each other. These are commonly called the quadrature QEPA and QEPB signals. The clockwise direction for most encoders is defined as the QEPA channel going positive before the QEPB channel and vise versa as shown in Figure 12-365.

The encoder wheel typically makes one revolution for every revolution of the motor or the wheel may be at a geared rotation ratio with respect to the motor. Therefore, the frequency of the digital signal coming from the QEPA and QEPB outputs varies proportionally with the velocity of the motor. For example, a 2000-line encoder directly coupled to a motor running at 5000 revolutions per minute (rpm) results in a frequency of 166.6 kHz, so by measuring the frequency of either the QEPA or QEPB output, the processor can determine the velocity of the motor.

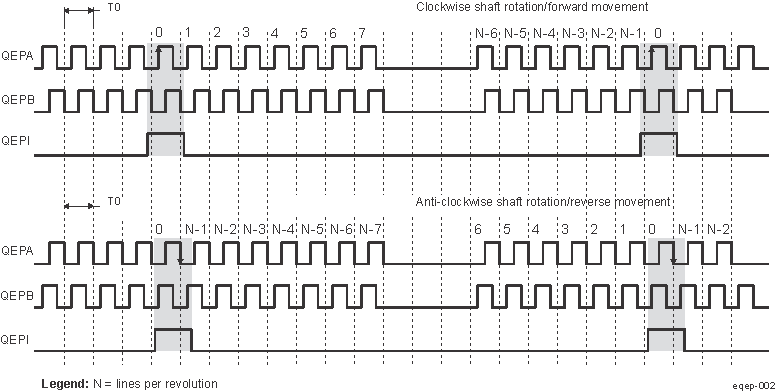GUID-1610398B-078E-4226-8B0A-139C24A1D33B-low.gifFigure 12-365 QEP Encoder Output Signal for Forward/Reverse Movement

Quadrature encoders from different manufacturers come with two forms of index pulse (gated index pulse or ungated index pulse) as shown in Figure 12-366. A nonstandard form of index pulse is ungated. In the ungated configuration, the index edges are not necessarily coincident with A and B signals. The gated index pulse is aligned to any of the four quadrature edges and width of the index pulse and can be equal to a quarter, half, or full period of the quadrature signal.

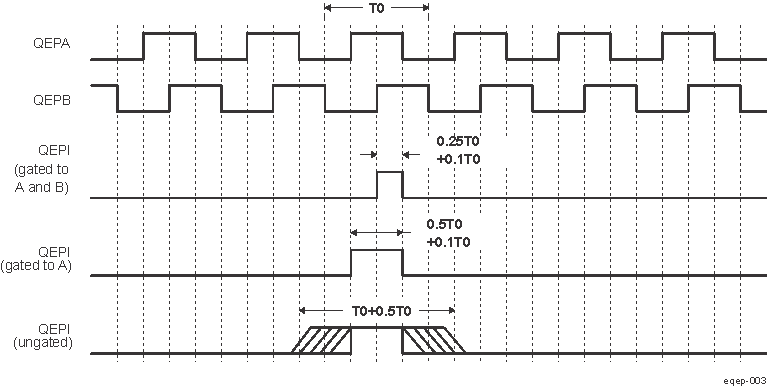GUID-2C2DDF83-D8F8-402C-9ED8-43DFE1E50C2C-low.gifFigure 12-366 Index Pulse Example

Some typical applications for rotary encoders range from fax machines to motor controllers, and even robot localization. Rotary sensors are fundamental to the robotics and motion control systems found today. The optical shaft encoder can be used to improve a robot in various ways. The encoder can measure rotational distance traveled and speed, which can be used to monitor, for example, the angular position of a robot gripper arm or the speed of a robot.

General Issues: Estimating velocity from a digital position sensor is a cost-effective strategy in motor control. Two different first order approximations for velocity may be written as:

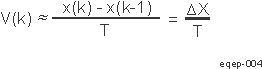
Equation 2. GUID-B5192DEA-C766-41DD-B503-D6098B0B6D73-low.gif
Equation 3. GUID-E06A7FE1-8C2A-4374-BCCD-014A2D33F5C3-low.gif

where

v(k): Velocity at time instant k

x(k): Position at time instant k

x(k-1): Position at time instant k - 1

T: Fixed unit time or inverse of velocity calculation rate

ΔX: Incremental position movement in unit time

t(k): Time instant "k"

t(k-1): Time instant "k - 1"

X: Fixed unit position

ΔT: Incremental time elapsed for unit position movement.

Equation 2 is the conventional approach to velocity estimation and it requires a time base to provide unit time event for velocity calculation. Unit time is the inverse of the velocity calculation rate.

The encoder count (position) is read once during each unit time event. The quantity [x(k) - x(k-1)] is formed by subtracting the previous reading from the current reading. Then the velocity estimate is computed by multiplying by the known constant 1/T (where T is the constant time between unit time events and is known in advance).

Estimation based on Equation 2 has an inherent accuracy limit directly related to the resolution of the position sensor and the unit time period T. For example, consider a 500-line per revolution quadrature encoder with a velocity calculation rate of 400 Hz. When used for position the quadrature encoder gives a four-fold increase in resolution, in this case, 2000 counts per revolution. The minimum rotation that can be detected is therefore 0.0005 revolutions, which gives a velocity resolution of 12 rpm when sampled at 400 Hz. While this resolution may be satisfactory at moderate or high speeds, for example, 1% error at 1200 rpm, it would clearly prove inadequate at low speeds. In fact, at speeds below 12 rpm, the speed estimate would erroneously be zero much of the time.

At low speed, Equation 3 provides a more accurate approach. It requires a position sensor that outputs a fixed interval pulse train, such as the aforementioned quadrature encoder. The width of each pulse is defined by motor speed for a given sensor resolution. Equation 3 can be used to calculate motor speed by measuring the elapsed time between successive quadrature pulse edges. However, this method suffers from the opposite limitation of Equation 2. A combination of relatively large motor speeds and high sensor resolution makes the time interval ΔT small, and thus more greatly influenced by the timer resolution. This can introduce considerable error into high-speed estimates.

For systems with a large speed range (that is, speed estimation is needed at both low and high speeds), one approach is to use Equation 3 at low speed and have the software switch over to Equation 2 when the motor speed rises above some specified threshold.

Figure 12-367 shows the EQEP module overview.

GUID-30D75659-EDD9-4C78-85EF-08FA8FEF2B6A-low.gif
A. i = 0 to number of instances - 1.
Figure 12-367 EQEP Overview