SSZTBI6 Technical article

SSZTBI6 March 2016

1
2
1. 3
2. Additional Resources

Manjing Xie

Ceramic capacitors are well-suited to manage ripple current because they can filter large currents generated by switched-mode power supplies. It is common to use ceramic capacitors of different sizes and values in parallel to achieve the optimum result. In such a case, each capacitor should meet its allowable ripple-current rating.

In this post, I’ll use a buck converter as an example to demonstrate how to select ceramic capacitors to meet ripple-current requirements. (Note that bulk capacitors such as aluminum electrolytic or tantalum capacitors have high equivalent-series-resistance (ESR). When put in parallel to ceramic capacitors, these bulk capacitors are not designed to take a large ripple current. Thus, I won’t discuss them here.)

Figure 1 shows a basic circuit of a buck converter. The converter input current, i_{IN_D}, consists of a large ripple current, Δi_{IN_D}.

Figure 1 The Basic Circuit of a Buck Converter

The buck converter parameters are:

Input voltage (V_IN) = 12V.
Allowable input ripple voltage (ΔV_IN) < 0.36V.
Output voltage (V_O) = 1.2V.
Output current (I_O) = 12A.
Inductor peak-to-peak ripple current (ΔIpp) = 3.625A.
Switching frequency (F_SW) = 600KHz.
Temperature-rise limit of the ceramic capacitors < 10°C.

Figure 2 shows the input ripple-current waveform.

Figure 2 Input Ripple-current Waveform

To meet the ripple-voltage requirement, the effective capacitance of the ceramic capacitor should be greater than that calculated with Equation 1:

Equation 1.

C_{c e_t o t a l} \geq \frac{I_{0} x D x (1 - D)}{F_{S W} x {∆ V}_{I N}}

With the converter parameters and requirements, C_{ce_total} should be greater than 5µF.

The selected ceramic capacitors must also meet the ripple-current limitation. Equation 2 calculates the root-mean-square (RMS) value of the ripple current:

Equation 2.

I_{Σ_R M S} = \sqrt{1_{0}^{2} x D x (1 - D) + \frac{{∆ i}_{p p}^{2}}{12} x D}

Given that I_O = 12A, ΔIpp = 3.625A and D = 10%, the RMS value of the input ripple is 3.615A_RMS.

Table 1 lists the characteristics of available ceramic capacitors with the proper voltage rating. These capacitors are of 10% tolerance.

Table 1 Capacitor Characteristics

While one piece of Capacitor A provides sufficient effective capacitance to meet the ripple-voltage requirement, its ripple-current rating of 3.24A_RMS is slightly less than that generated by the converter. While adding another piece of Capacitor A meets the requirement, it occupies more space and costs more than other smaller capacitors. The question is which capacitor or capacitors should be added. To answer that question, I conducted an analysis on ripple-current distribution. Figure 3 is a simplified schematic of two capacitors in parallel with an AC current source.

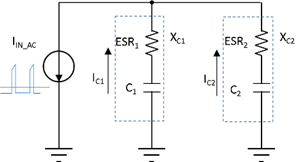Figure 3 Schematic of Ripple-current Distribution

According to Ohm’s law, current distribution should abide by Equation 3:

Equation 3.

I_{I N_A C} x \frac{X_{C 1} x X_{C 2}}{X_{C 1} + X_{C 2}} = I_{C 1} x X_{C 1} = I_{C 2} x X_{C 2}

Ceramic capacitors have small ESR. Figure 4 shows two examples.

Figure 4 Ceramic Capacitor Impedance |Z| and ESR R over Frequency

For frequencies lower than 1MHz, you can approximate the impedance of a ceramic capacitor, X_C, by X_C = 1/(jωC). Thus Equation 3 simplifies into Equation 4. According to Equation 4, ripple current is in proportion to the effective capacitance:

Equation 4.

\frac{I_{I N_A C}}{C_{1} + C_{2}} = \frac{I_{C 1}}{C 1} = \frac{I_{C 2}}{C 2}

When multiple capacitors are in parallel, the capacitor with the lowest allowable ripple current over effective-capacitance ratio, I_RMS-over-C, will hit the ripple-current rating first. Assuming that C1 has lower I_RMS-over-C than C2, Equation 5 estimates the total allowable ripple current, I_{∑_RMS_Allow}:

Equation 5.

I_{Σ_R M S_A l l o w} = I_{C 1_R M S_A l l o w} + \frac{I_{C 1_R M S_A l l o w}}{C_{1}} x C_{2}

When C1 hits its allowable ripple-current rating, the ripple current through C2 will not exceed its allowable ripple current, as Equation 6 shows:

Equation 6.

I_{C 2} = \frac{I_{C 1_R M S_A l l o w}}{C_{1}} x C_{2} \leq \frac{I_{C 2_R M S_A l l o w}}{C_{2}} x C_{2}

In order to have I_{∑_RMS_Allow} ≥ I_{IN_AC_RMS,} the additional capacitance should be greater than that calculated by Equation 7:

Equation 7.

C_{a d d i t i o n a l} \geq \frac{I_{{I N}_{{A C}_{R M S}}} - I_{{C 1}_{{R M S}_{A l l o w}}}}{\frac{I_{{C 1}_{{R M S}_{A l l o w}}}}{C_{1} x (1 + T o l .)}} \div (1 + T o l .)

Tol. is the capacitance tolerance of these ceramic capacitors. When tolerance is included in the calculation, the worst-case ripple current of the bottleneck capacitor would not exceed its rating.

I listed the I_RMS-to-C ratio as a parameter in Table 2.

Table 2 Capacitor Characteristics

Capacitor A has high effective capacitance at 12_VDC bias. To meet the ripple-current requirement, you should add an additional capacitor or capacitors to meet ripple current requirement. Since Capacitor A has the lowest I_RMS-to-C ratio, the added effective capacitance, C_additional, should be greater than that calculated with Equation 8:

C_{a d d i t i o n a l} \geq \frac{{3.615 A}_{R M S} - {3.24 A}_{R M S}}{\frac{{0.555}^{A_{R M S}}}{μ F} \div (1 + 10 %)} \div (1 + 10 %)

Equation 8.

C_{a d d i t i o n a l} \geq 0.818 μ F

There are two options. The first option is to add one piece of Capacitor B. The second option is to add one piece of Capacitor C and two pieces of Capacitor D. Both options provide sufficient additional effective capacitance and occupy similar printed circuit board (PCB) areas. Since the latter option is more cost-effective, I chose the second option.

To verify my hypothesis, I conducted a PSPICE simulation; Figure 5 shows the circuit I used. I also used the nominal values of the capacitors for a typical case.

Figure 5 Ripple-current Distribution Simulation Circuit

Figure 6 shows the simulation waveforms and the RMS values for the ripple currents of the capacitors, which are:

I_{CA_RMS_typ} = 3.13A_RMS.
I_{CC_RMS_typ} = 0.353A_RMS.
I_{CD_RMS_typ} = 0.081A_RMS.
V_IN ripple voltage = 0.299V.

Figure 6 Simulated Ripple-current Waveform of Each Ceramic Capacitor

I then used capacitor values that would render a worst case for the Capacitor A, the bottleneck capacitor.

The RMS values of the ripple currents of the capacitors are:

I_{CA_RMS_max} = 3.206A_RMS.
I_{CC_RMS_min} = 0.306A_RMS.
I_{CD_RMS_min} = 0.070A_RMS.

Each capacitor meets its allowable ripple-current rating.

Using ceramic capacitors of different sizes in parallel provides a compact and cost-effective way to filter large ripple current. But with different capacitances and ripple-current ratings, it is difficult to determine the total allowable ripple current. In this post, I proposed a parameter called allowable ripple current over effective-capacitance ratio, I_RMS/C. I_RMS/C helps you find the bottleneck capacitor for the allowable ripple current. Use the lowest I_RMS/C to estimate the total allowable ripple current and to select additional capacitors. Please be aware that PCB parasitics could greatly affect circuit performance. This method provides a good estimation; however, you must verify designs empirically.

Additional Resources

Explore more power-supply topics.
Watch Power Tips videos to help with your design challenges