TIDUEU6B September   2020  – December 2021 OPA810

 

  1.   Description
  2.   Resources
  3.   Features
  4.   Applications
  5.   5
  6. 1System Description
    1. 1.1 Key System Specifications
  7. 2System Overview
    1. 2.1 Block Diagram
    2. 2.2 Highlighted Products
      1. 2.2.1 OPA2810
      2. 2.2.2 BUF634A
    3. 2.3 Design Considerations
      1. 2.3.1 Existing architecture
        1. 2.3.1.1 Circuit Stability Issue
        2. 2.3.1.2 Solution in Existing Architecture (Compensation Cap)
      2. 2.3.2 Proposed Design
        1. 2.3.2.1 Stability Analysis of the Proposed Design
          1. 2.3.2.1.1 Without Measurement of Voltage at Inverting Node of A2
          2. 2.3.2.1.2 With Measuring Voltage at Inverting Node of A2
        2. 2.3.2.2 RG = RF Settings and Respective Impedance Ranges
        3. 2.3.2.3 Impedance Measurement Procedure
          1. 2.3.2.3.1 Short Cal
          2. 2.3.2.3.2 Impedance Cal
          3. 2.3.2.3.3 100k Setting Calibration
          4. 2.3.2.3.4 Open Cal
          5. 2.3.2.3.5 Calculations
          6. 2.3.2.3.6 Correction in ZX
          7. 2.3.2.3.7 Data Acquisition and Processing
          8. 2.3.2.3.8 Mathematical Explanation
  8. 3Hardware, Software, Testing Requirements, and Test Results
    1. 3.1 Required Hardware and Software
      1. 3.1.1 Hardware
    2. 3.2 Testing and Results
      1. 3.2.1 Test Setup
      2. 3.2.2 Test Results
  9. 4Design Files
    1. 4.1 Schematics
    2. 4.2 Bill of Materials
    3. 4.3 PCB Layout Recommendations
      1. 4.3.1 Layout Prints
    4. 4.4 Altium Project
    5. 4.5 Gerber Files
    6. 4.6 Assembly Drawings
  10. 5Software Files
  11. 6Related Documentation
    1. 6.1 Trademarks
    2. 6.2 Third-Party Products Disclaimer
  12. 7Revision History

2.3.1.1 Circuit Stability Issue

When the unknown impedance is capacitive as shown in Figure 2-3, the feedback transfer function can be calculated using Equation 2.

Equation 2. GUID-C1B155E0-E5E9-4CEC-B55C-CE437E5158FB-low.gif
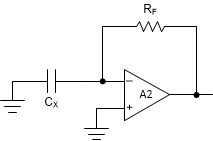GUID-86F3295F-B850-469C-8CBA-8B67669BE073-low.gifFigure 2-3 Capacitor Measurement Circuit

The transfer function implies that a zero is formed in 1/β. The frequency of this zero can be calculated using Equation 3.

Equation 3. GUID-861CFCD8-D945-44E7-A284-DEE59A696DA5-low.gif

It can be seen that the zero frequency depends on the unknown capacitance, CX. In Figure 2-4 it can be seen that Aolβ has a rate of closure of 40dB/dec. When the zero frequency is more than a decade below fCL, the phase margin will reduce to zero making the circuit unstable.

GUID-E01A0B9F-6D3D-498A-A80E-9BF9D03D6FBB-low.gifFigure 2-4 Bode Plot of Capacitor Measurement