SBAA530 September 2021 TMAG5170 , TMAG5170-Q1 , TMAG5173-Q1
3 Achieving Greater Flexibility
The single most important design consideration when designing with a Hall-effect sensor is the placement of the sensor in relation to the magnet. Sensor placement inflexibility can lead to an undesirable end-product form factor. Because various mechanical aspects of new designs are often not well-defined early on in the design process, linear 3D Hall-effect position sensors must have configurable features, such as selectable magnetic sensitivity ranges, gain and offset correction, variable update rates, and temperature compensation. The TMAG5170 offers this capability. The versatility of this device enables configuration during any phase of design and is suitable for many applications.
In general, the remanence of a magnet, which is an indication of the magnetic flux density, decreases as the temperature increases. To improve system performance with different types of magnets (such as neodymium iron boron or ferrite magnets), a linear 3D Hall-effect position sensor with temperature compensation offers further flexibility. The TMAG5170 has onboard configurable temperature compensation and can also turn off if only the magnet or only the sensor are exposed to temperature changes.
Gimbal motors are an example of an application that needs the flexibility of configurability to specific sensitivity ranges or other parameters. Gimbal motors are found in handheld camera stabilizers and drones to provide angle measurement information to the MCU. These motors stabilize footage by continuously adjusting the motor position as movement occurs. A sensor that can measure angles precisely and accurately while offering on- or off-axis placements (see Figure 3-1) enables mechanical flexibility in the magnet-to-sensor placement.
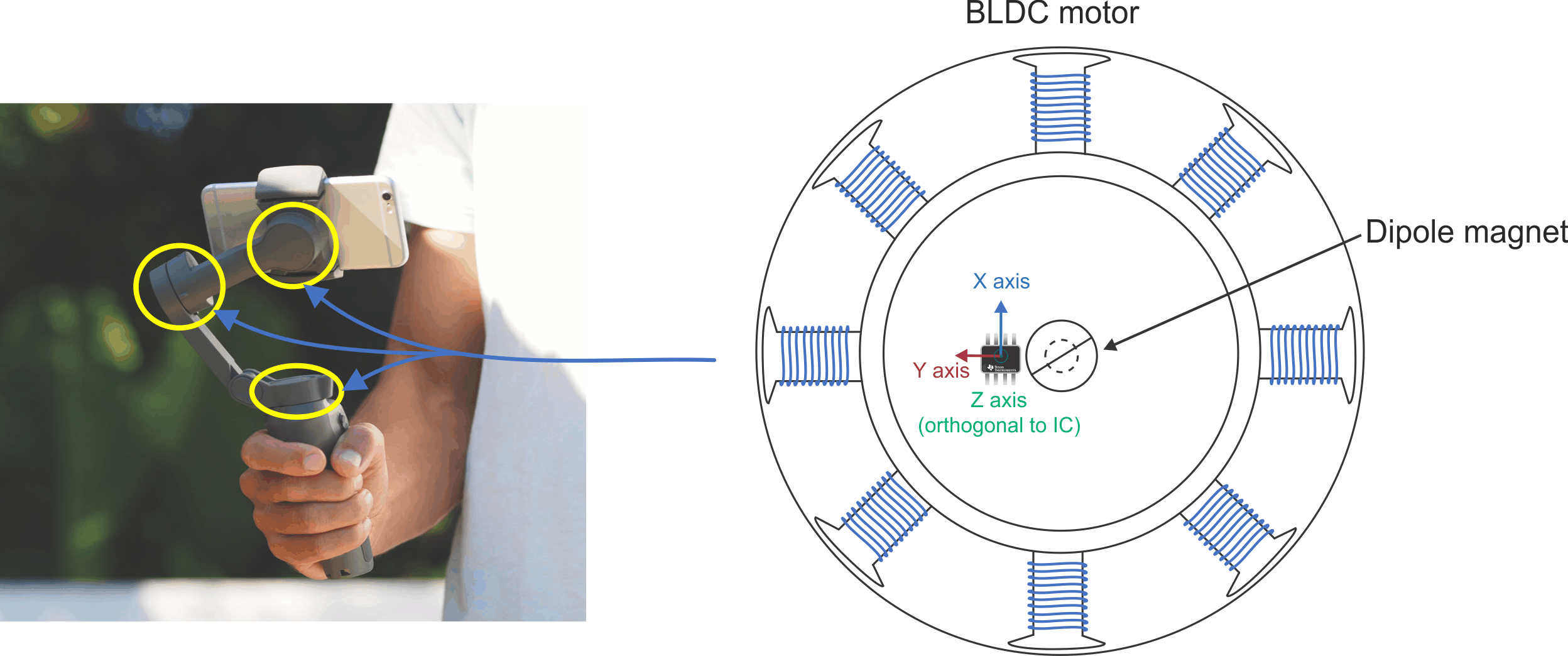
Figure 3-1 Off-Axis Angle Measurement Using 3D Linear in a Handheld Gimbal Motor
Human interface and controls in home appliances, test and measurement equipment, and personal electronics (see Figure 3-2) benefit from the capability of a linear 3D Hall-effect position sensor to precisely measure magnetic fields as the dial is turned. The magnetic field information is used to calculate the angle position between any two dimensions (XY, YZ, or ZX). As shown, the sensor out-of-plane configuration of the TMAG5170 implements the dial, but any of the three methods depicted in the figure can do so, enabling further flexibility. Aside from being able to implement a push feature by monitoring a large shift in the X and Y components, 3D sensitivity provides the ability to sense misalignment from the ideal configuration (by monitoring the third unused Z axis), providing alerts for predictive maintenance caused by wear and tear or damage to the dial.
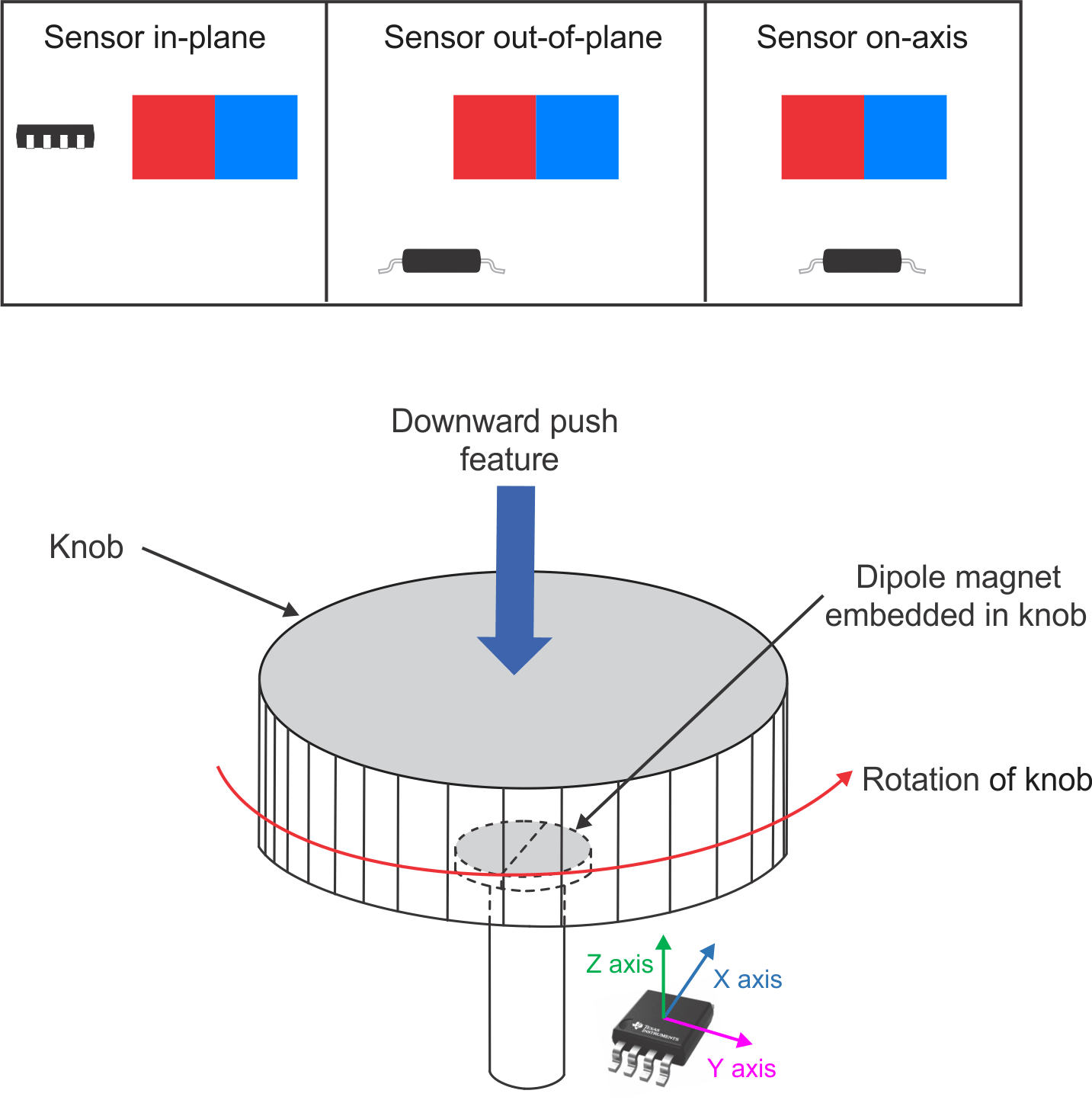
Figure 3-2 Example Out-of-Plane Angle Measurement Using a Linear 3D Hall-Effect Position Sensor in a Knob or Dial Application
When calculating the angle measurements of rotating shafts, on-axis measurements (where the sensor is directly beneath or above the rotating magnet) provide the most accurate magnetic field measurements given the equivalent magnitude field vectors. In the case of the human interface and control knob shown in Figure 3-2; however, an on-axis implementation is not feasible because the shaft is obstructing the placement of the sensor. By monitoring the X and Y components, the magnetic fields are represented by sine and cosine functions, making it possible to calculate the angle between them using the arctangent function.
Figure 3-3 shows magnetic fields produced by a constant-speed rotating magnet, as in a dial. BX represents the magnetic field in the X direction, while BY is in the Y direction. These sine and cosine waveforms, BX and BY, are representative of an on-axis measurement. Out-of-plane implementations (previously shown in Figure 3-2) add complexity to the angle calculation given disparate magnetic field strengths. In this case, one magnetic field vector may be smaller in magnitude than the other – this is shown in the figure as BX(OFF-AXIS) in comparison to BX. Instead of having two well-behaved waveforms, the BX(OFF-AXIS) field is distorted, which produces an angle calculation error.
Yet another aspect of magnetic field measurement to consider is offset. Reducing the entire set of measurements by offset (shown by the three down arrows in Figure 3-3) and effectively producing field vectors for BX(OFF-AXIS, OFFSET) that match that of BX(OFF-AXIS) will compensate for the small magnetic field offset and ensure accurate rotation-angle calculation. For simplicity, only one axis of measurement has this offset; in reality, all axes will have an inherent offset that needs compensating. With the offset removed, one of the field vectors must be normalized to match the other. In this example, normalizing BY (shown as BY(NORMALIZED)) to match BX(OFF-AXIS) reduces it to a magnitude equal to BX(OFF-AXIS) divided by BY. Configuring the TMAG5170 with this gain and offset correction ensures the most accurate angle calculations, while also providing the flexibility to be placed where it is most convenient for the design.
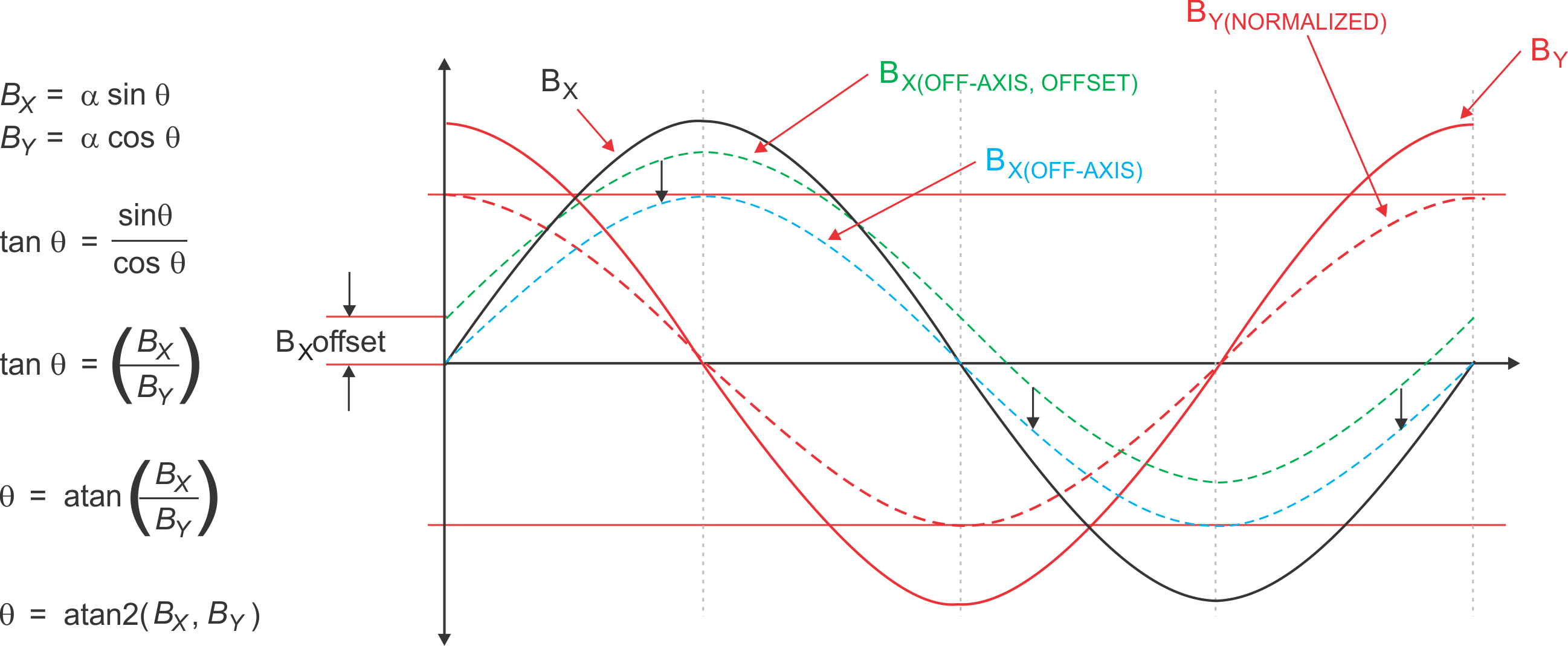
Figure 3-3 XY Example for Gain-and-Offset Correction