SLAA889A March 2019 – July 2021 MSP430FR6041 , MSP430FR6043 , MSP430FR60431 , MSP430FR6045 , MSP430FR6047 , MSP430FR60471
2.1 Correlation Based Technique for Differential TOF Estimation
The correlation based TOF estimation involves the following steps:
- A pulse is transmitted from transducer 1 in Figure 1-2.
- Immediately a clock counter is started with respect to the reference clock. The reference clock can be either 8 or 16 MHz.
- At a certain pre-determined time, the ADC is started to capture the data at the receive transducer. Let the received data be indicated as Equation 7.
Equation 7.
where
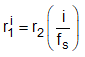
- fs = sampling rate of the ADC
- i = index of the sample
- Similarly, transmit the pulse from transducer 2 and receive the signal at the transducer. Let the sampled signal at transducer 1 be given by Equation 8.
Equation 8.
- Based on
r1 and
r2, a correlation value is calculated by Equation 9.
Equation 9.
where
- k = {–m, –(m–1), ..., (m–1), m}
 for i < 1 and i > N
for i < 1 and i > N
- The maximum of the correlation is calculated by Equation 10.
Equation 10.
- Let Z–1 = corr(k̂–1), Z0 = corr(k̂), and Z1 = corr(k̂+1) be the values of correlation at and around the maximum.
- The real maximum of the correlation is now given by the interpolation in Equation 11.
Equation 11.
- The net different time of flight is now given by Equation 12.
Equation 12.
- In USS Software Library implementations, m is typically chosen to be +1, implying that only 3 correlations must be computed most of the time.
This correlation-based TOF calculation has been reported in the literature previously as given in 2 and 3. The details of the equations for δ in Equation 12 can be found in 4 and provided in Section 2.2.1 for completeness. Figure 2-2 shows a block diagram of the receiver for the correlation. Figure 2-3 shows a block diagram of the signal processing algorithms.
 Figure 2-2 Block Diagram for Correlation-Based Differential TOF Estimator
Figure 2-2 Block Diagram for Correlation-Based Differential TOF Estimator Figure 2-3 Block Diagram of Signal Processing for Differential TOF Measurement Using the Correlation Method
Figure 2-3 Block Diagram of Signal Processing for Differential TOF Measurement Using the Correlation Method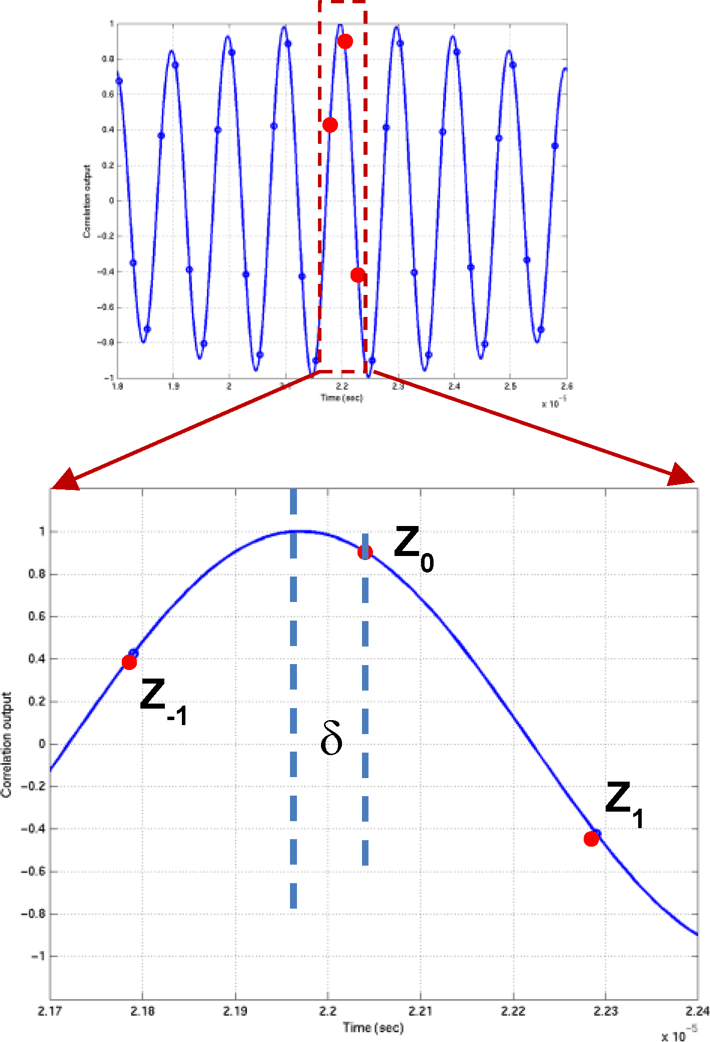 Figure 2-4 Interpolation Step in the ADC-Based Correlation Technique for Differential TOF Estimation
Figure 2-4 Interpolation Step in the ADC-Based Correlation Technique for Differential TOF EstimationEfficient interpolation techniques have been given in Reference [4]. As previously mentioned, for efficiency of implementation, the correlation is computed over few points leading to a low-power implementation.
To ensure that Z0 is the maximum point, the correlation peak runs through a search algorithm sequentially computing the three adjacent correlation terms (Z–1, Z0, and Z+1) until it finds the maximum Z0 that is larger than Z–1 and Z+1 and the earlier correlation terms. The search window for finding the correlation peak can be set using USS_ALG_NUM_CYCLES_SEARCH_CORR in USS_userConfig.h or ussAlgConfig.numCycleSearchCorrPeak. Typically, only an additional 1 or 2 adjacent correlation points are computed in addition to the 3 correlation points.