SPRUIN7C March   2020  – March 2024 TMS320F280021 , TMS320F280021-Q1 , TMS320F280023 , TMS320F280023-Q1 , TMS320F280023C , TMS320F280025 , TMS320F280025-Q1 , TMS320F280025C , TMS320F280025C-Q1

 

  1.   1
  2.   Read This First
    1.     About This Manual
    2.     Notational Conventions
    3.     Glossary
    4.     Related Documentation From Texas Instruments
    5.     Support Resources
    6.     Trademarks
  3. 1 C2000™ Microcontrollers Software Support
    1. 1.1 Introduction
    2. 1.2 C2000Ware Structure
    3. 1.3 Documentation
    4. 1.4 Devices
    5. 1.5 Libraries
    6. 1.6 Code Composer Studio™ Integrated Development Environment (IDE)
    7. 1.7 SysConfig and PinMUX Tool
  4. 2 C28x Processor
    1. 2.1 Introduction
    2. 2.2 C28X Related Collateral
    3. 2.3 Features
    4. 2.4 Floating-Point Unit
    5. 2.5 Trigonometric Math Unit (TMU)
    6. 2.6 VCRC Unit
  5. 3 System Control and Interrupts
    1. 3.1  Introduction
      1. 3.1.1 SYSCTL Related Collateral
      2. 3.1.2 LOCK Protection on System Configuration Registers
      3. 3.1.3 EALLOW Protection
    2. 3.2  Power Management
    3. 3.3  Device Identification and Configuration Registers
    4. 3.4  Resets
      1. 3.4.1  Reset Sources
      2. 3.4.2  External Reset (XRS)
      3. 3.4.3  Simulate External Reset
      4. 3.4.4  Power-On Reset (POR)
      5. 3.4.5  Brown-Out-Reset (BOR)
      6. 3.4.6  Debugger Reset (SYSRS)
      7. 3.4.7  Simulate CPU Reset
      8. 3.4.8  Watchdog Reset (WDRS)
      9. 3.4.9  Hardware BIST Reset (HWBISTRS)
      10. 3.4.10 NMI Watchdog Reset (NMIWDRS)
      11. 3.4.11 DCSM Safe Code Copy Reset (SCCRESET)
    5. 3.5  Peripheral Interrupts
      1. 3.5.1 Interrupt Concepts
      2. 3.5.2 Interrupt Architecture
        1. 3.5.2.1 Peripheral Stage
        2. 3.5.2.2 PIE Stage
        3. 3.5.2.3 CPU Stage
      3. 3.5.3 Interrupt Entry Sequence
      4. 3.5.4 Configuring and Using Interrupts
        1. 3.5.4.1 Enabling Interrupts
        2. 3.5.4.2 Handling Interrupts
        3. 3.5.4.3 Disabling Interrupts
        4. 3.5.4.4 Nesting Interrupts
        5. 3.5.4.5 Vector Address Validity Check
      5. 3.5.5 PIE Channel Mapping
        1. 3.5.5.1 PIE Interrupt Priority
          1. 3.5.5.1.1 Channel Priority
          2. 3.5.5.1.2 Group Priority
      6. 3.5.6 Vector Tables
    6. 3.6  Exceptions and Non-Maskable Interrupts
      1. 3.6.1 Configuring and Using NMIs
      2. 3.6.2 Emulation Considerations
      3. 3.6.3 NMI Sources
        1. 3.6.3.1 Missing Clock Detection
        2. 3.6.3.2 RAM Uncorrectable ECC Error
        3. 3.6.3.3 Flash Uncorrectable ECC Error
        4. 3.6.3.4 CPU HWBIST Error
        5. 3.6.3.5 Software-Forced Error
      4. 3.6.4 CRC Fail
      5. 3.6.5 ERAD NMI
      6. 3.6.6 Illegal Instruction Trap (ITRAP)
      7. 3.6.7 Error Pin
    7. 3.7  Clocking
      1. 3.7.1  Clock Sources
        1. 3.7.1.1 Primary Internal Oscillator (INTOSC2)
        2. 3.7.1.2 Backup Internal Oscillator (INTOSC1)
        3. 3.7.1.3 External Oscillator (XTAL)
      2. 3.7.2  Derived Clocks
        1. 3.7.2.1 Oscillator Clock (OSCCLK)
        2. 3.7.2.2 System PLL Output Clock (PLLRAWCLK)
      3. 3.7.3  Device Clock Domains
        1. 3.7.3.1 System Clock (PLLSYSCLK)
        2. 3.7.3.2 CPU Clock (CPUCLK)
        3. 3.7.3.3 CPU Subsystem Clock (SYSCLK and PERx.SYSCLK)
        4. 3.7.3.4 Low-Speed Peripheral Clock (LSPCLK and PERx.LSPCLK)
        5. 3.7.3.5 CAN Bit Clock
        6. 3.7.3.6 CPU Timer2 Clock (TIMER2CLK)
      4. 3.7.4  XCLKOUT
      5. 3.7.5  Clock Connectivity
      6. 3.7.6  Clock Source and PLL Setup
      7. 3.7.7  Using an External Crystal or Resonator
        1. 3.7.7.1 X1/X2 Precondition Circuit
      8. 3.7.8  Using an External Oscillator
      9. 3.7.9  Choosing PLL Settings
      10. 3.7.10 System Clock Setup
      11. 3.7.11 SYS PLL Bypass
      12. 3.7.12 Clock (OSCCLK) Failure Detection
        1. 3.7.12.1 Missing Clock Detection
    8. 3.8  32-Bit CPU Timers 0/1/2
    9. 3.9  Watchdog Timer
      1. 3.9.1 Servicing the Watchdog Timer
      2. 3.9.2 Minimum Window Check
      3. 3.9.3 Watchdog Reset or Watchdog Interrupt Mode
      4. 3.9.4 Watchdog Operation in Low-Power Modes
      5. 3.9.5 Emulation Considerations
    10. 3.10 Low-Power Modes
      1. 3.10.1 Clock-Gating Low-Power Modes
      2. 3.10.2 IDLE
      3. 3.10.3 STANDBY
      4. 3.10.4 HALT
      5. 3.10.5 Flash Power-down Considerations
    11. 3.11 Memory Controller Module
      1. 3.11.1 Functional Description
        1. 3.11.1.1 Dedicated RAM (Mx RAM)
        2. 3.11.1.2 Local Shared RAM (LSx RAM)
        3. 3.11.1.3 Global Shared RAM (GSx RAM)
        4. 3.11.1.4 Access Arbitration
        5. 3.11.1.5 Access Protection
          1. 3.11.1.5.1 CPU Fetch Protection
          2. 3.11.1.5.2 CPU Write Protection
          3. 3.11.1.5.3 CPU Read Protection
          4. 3.11.1.5.4 HIC Write Protection
          5. 3.11.1.5.5 DMA Write Protection
        6. 3.11.1.6 Memory Error Detection, Correction and Error Handling
          1. 3.11.1.6.1 Error Detection and Correction
          2. 3.11.1.6.2 Error Handling
        7. 3.11.1.7 Application Test Hooks for Error Detection and Correction
        8. 3.11.1.8 RAM Initialization
    12. 3.12 JTAG
      1. 3.12.1 JTAG Noise and TAP_STATUS
    13. 3.13 Dual Code Security Module (DCSM)
      1. 3.13.1 Functional Description
        1. 3.13.1.1 CSM Passwords
        2. 3.13.1.2 Emulation Code Security Logic (ECSL)
        3. 3.13.1.3 CPU Secure Logic
        4. 3.13.1.4 Execute-Only Protection
        5. 3.13.1.5 Password Lock
        6. 3.13.1.6 JTAG Lock
        7. 3.13.1.7 Link Pointer and Zone Select
      2. 3.13.2 C Code Example to Get Zone Select Block Addr for Zone1 in BANK0
      3. 3.13.3 Flash and OTP Erase/Program
      4. 3.13.4 Safe Copy Code
      5. 3.13.5 SafeCRC
      6. 3.13.6 CSM Impact on Other On-Chip Resources
      7. 3.13.7 Incorporating Code Security in User Applications
        1. 3.13.7.1 Environments That Require Security Unlocking
        2. 3.13.7.2 CSM Password Match Flow
        3. 3.13.7.3 C Code Example to Unsecure C28x Zone1
        4.       150
        5. 3.13.7.4 C Code Example to Resecure C28x Zone1
        6.       152
        7. 3.13.7.5 Environments That Require ECSL Unlocking
        8. 3.13.7.6 ECSL Password Match Flow
        9. 3.13.7.7 ECSL Disable Considerations for Any Zone
          1. 3.13.7.7.1 C Code Example to Disable ECSL for C28x-Zone1
        10.       157
        11. 3.13.7.8 Device Unique ID
    14. 3.14 System Control Register Configuration Restrictions
    15. 3.15 Software
      1. 3.15.1 SYSCTL Examples
        1. 3.15.1.1 Missing clock detection (MCD)
        2. 3.15.1.2 XCLKOUT (External Clock Output) Configuration
      2. 3.15.2 DCSM Examples
        1. 3.15.2.1 Empty DCSM Tool Example
      3. 3.15.3 MEMCFG Examples
        1. 3.15.3.1 Correctable & Uncorrectable Memory Error Handling
      4. 3.15.4 NMI Examples
      5. 3.15.5 TIMER Examples
        1. 3.15.5.1 CPU Timers
        2. 3.15.5.2 CPU Timers
      6. 3.15.6 WATCHDOG Examples
        1. 3.15.6.1 Watchdog
    16. 3.16 System Control Registers
      1. 3.16.1  SYSCTRL Base Address Table
      2. 3.16.2  CPUTIMER_REGS Registers
      3. 3.16.3  PIE_CTRL_REGS Registers
      4. 3.16.4  WD_REGS Registers
      5. 3.16.5  NMI_INTRUPT_REGS Registers
      6. 3.16.6  XINT_REGS Registers
      7. 3.16.7  SYNC_SOC_REGS Registers
      8. 3.16.8  DMA_CLA_SRC_SEL_REGS Registers
      9. 3.16.9  DEV_CFG_REGS Registers
      10. 3.16.10 CLK_CFG_REGS Registers
      11. 3.16.11 CPU_SYS_REGS Registers
      12. 3.16.12 PERIPH_AC_REGS Registers
      13. 3.16.13 DCSM_BANK0_Z1_REGS Registers
      14. 3.16.14 DCSM_BANK0_Z2_REGS Registers
      15. 3.16.15 DCSM_COMMON_REGS Registers
      16. 3.16.16 MEM_CFG_REGS Registers
      17. 3.16.17 ACCESS_PROTECTION_REGS Registers
      18. 3.16.18 MEMORY_ERROR_REGS Registers
      19. 3.16.19 TEST_ERROR_REGS Registers
      20. 3.16.20 UID_REGS Registers
      21. 3.16.21 DCSM_BANK0_Z1_OTP Registers
      22. 3.16.22 DCSM_BANK0_Z2_OTP Registers
      23. 3.16.23 Register to Driverlib Function Mapping
        1. 3.16.23.1 ASYSCTL Registers to Driverlib Functions
        2. 3.16.23.2 CPUTIMER Registers to Driverlib Functions
        3. 3.16.23.3 DCSM Registers to Driverlib Functions
        4. 3.16.23.4 MEMCFG Registers to Driverlib Functions
        5. 3.16.23.5 NMI Registers to Driverlib Functions
        6. 3.16.23.6 PIE Registers to Driverlib Functions
        7. 3.16.23.7 SYSCTL Registers to Driverlib Functions
        8. 3.16.23.8 XINT Registers to Driverlib Functions
  6. 4 ROM Code and Peripheral Booting
    1. 4.1 Introduction
      1. 4.1.1 ROM Related Collateral
    2. 4.2 Device Boot Sequence
    3. 4.3 Device Boot Modes
    4. 4.4 Device Boot Configurations
      1. 4.4.1 Configuring Boot Mode Pins
      2. 4.4.2 Configuring Boot Mode Table Options
      3. 4.4.3 Boot Mode Example Use Cases
        1. 4.4.3.1 Zero Boot Mode Select Pins
        2. 4.4.3.2 One Boot Mode Select Pin
        3. 4.4.3.3 Three Boot Mode Select Pins
    5. 4.5 Device Boot Flow Diagrams
      1. 4.5.1 Boot Flow
    6. 4.6 Device Reset and Exception Handling
      1. 4.6.1 Reset Causes and Handling
      2. 4.6.2 Exceptions and Interrupts Handling
    7. 4.7 Boot ROM Description
      1. 4.7.1  Boot ROM Configuration Registers
        1. 4.7.1.1 GPREG2 Usage and MPOST Configuration
      2. 4.7.2  Entry Points
      3. 4.7.3  Wait Points
      4. 4.7.4  Memory Maps
        1. 4.7.4.1 Boot ROM Memory Maps
        2. 4.7.4.2 Reserved RAM Memory Maps
      5. 4.7.5  ROM Tables
      6. 4.7.6  Boot Modes and Loaders
        1. 4.7.6.1 Boot Modes
          1. 4.7.6.1.1 Wait Boot
          2. 4.7.6.1.2 Flash Boot
          3. 4.7.6.1.3 RAM Boot
        2. 4.7.6.2 Bootloaders
          1. 4.7.6.2.1 SCI Boot Mode
          2. 4.7.6.2.2 SPI Boot Mode
          3. 4.7.6.2.3 I2C Boot Mode
          4. 4.7.6.2.4 Parallel Boot Mode
          5. 4.7.6.2.5 CAN Boot Mode
      7. 4.7.7  GPIO Assignments
      8. 4.7.8  Secure ROM Function APIs
      9. 4.7.9  Clock Initializations
      10. 4.7.10 Boot Status Information
        1. 4.7.10.1 Booting Status
        2. 4.7.10.2 Boot Mode and MPOST (Memory Power On Self-Test) Status
      11. 4.7.11 ROM Version
    8. 4.8 Application Notes for Using the Bootloaders
      1. 4.8.1 Boot Data Stream Structure
        1. 4.8.1.1 Bootloader Data Stream Structure
          1. 4.8.1.1.1 Data Stream Structure 8-bit
      2. 4.8.2 The C2000 Hex Utility
        1. 4.8.2.1 HEX2000.exe Command Syntax
    9. 4.9 Software
      1. 4.9.1 BOOT Examples
  7. 5 Flash Module
    1. 5.1  Introduction to Flash and OTP Memory
      1. 5.1.1 FLASH Related Collateral
      2. 5.1.2 Features
      3. 5.1.3 Flash Tools
      4. 5.1.4 Default Flash Configuration
    2. 5.2  Flash Bank, OTP, and Pump
    3. 5.3  Flash Module Controller (FMC)
    4. 5.4  Flash and OTP Memory Power-Down Modes and Wakeup
    5. 5.5  Active Grace Period
    6. 5.6  Flash and OTP Memory Performance
    7. 5.7  Flash Read Interface
      1. 5.7.1 C28x-FMC Flash Read Interface
        1. 5.7.1.1 Standard Read Mode
        2. 5.7.1.2 Prefetch Mode
          1. 5.7.1.2.1 Data Cache
    8. 5.8  Flash Erase and Program
      1. 5.8.1 Erase
      2. 5.8.2 Program
      3. 5.8.3 Verify
    9. 5.9  Error Correction Code (ECC) Protection
      1. 5.9.1 Single-Bit Data Error
      2. 5.9.2 Uncorrectable Error
      3. 5.9.3 SECDED Logic Correctness Check
    10. 5.10 Reserved Locations Within Flash and OTP Memory
    11. 5.11 Migrating an Application from RAM to Flash
    12. 5.12 Procedure to Change the Flash Control Registers
    13. 5.13 Software
      1. 5.13.1 FLASH Examples
        1. 5.13.1.1 Live Firmware Update Example
        2. 5.13.1.2 Flash Programming with AutoECC, DataAndECC, DataOnly and EccOnly
        3. 5.13.1.3 Flash ECC Test Mode
        4. 5.13.1.4 Boot Source Code
        5. 5.13.1.5 Erase Source Code
        6. 5.13.1.6 Live DFU Command Functionality
        7. 5.13.1.7 Verify Source Code
        8. 5.13.1.8 SCI Boot Mode Routines
        9. 5.13.1.9 Flash Programming Solution using SCI
    14. 5.14 Flash Registers
      1. 5.14.1 FLASH Base Address Table
      2. 5.14.2 FLASH_CTRL_REGS Registers
      3. 5.14.3 FLASH_ECC_REGS Registers
      4. 5.14.4 FLASH Registers to Driverlib Functions
  8. 6 Dual-Clock Comparator (DCC)
    1. 6.1 Introduction
      1. 6.1.1 Features
      2. 6.1.2 Block Diagram
    2. 6.2 Module Operation
      1. 6.2.1 Configuring DCC Counters
      2. 6.2.2 Single-Shot Measurement Mode
      3. 6.2.3 Continuous Monitoring Mode
      4. 6.2.4 Error Conditions
    3. 6.3 Interrupts
    4. 6.4 Software
      1. 6.4.1 DCC Examples
        1. 6.4.1.1 DCC Single shot Clock verification
        2. 6.4.1.2 DCC Single shot Clock measurement
        3. 6.4.1.3 DCC Continuous clock monitoring
        4. 6.4.1.4 DCC Continuous clock monitoring
        5. 6.4.1.5 DCC Detection of clock failure
    5. 6.5 DCC Registers
      1. 6.5.1 DCC Base Address Table
      2. 6.5.2 DCC_REGS Registers
      3. 6.5.3 DCC Registers to Driverlib Functions
  9. 7 Background CRC-32 (BGCRC)
    1. 7.1 Introduction
      1. 7.1.1 BGCRC Related Collateral
      2. 7.1.2 Features
      3. 7.1.3 Block Diagram
      4. 7.1.4 Memory Wait States and Memory Map
    2. 7.2 Functional Description
      1. 7.2.1 Data Read Unit
      2. 7.2.2 CRC-32 Compute Unit
      3. 7.2.3 CRC Notification Unit
        1. 7.2.3.1 CPU Interrupt and NMI
      4. 7.2.4 Operating Modes
        1. 7.2.4.1 CRC Mode
        2. 7.2.4.2 Scrub Mode
      5. 7.2.5 BGCRC Watchdog
      6. 7.2.6 Hardware and Software Faults Protection
    3. 7.3 Application of the BGCRC
      1. 7.3.1 Software Configuration
      2. 7.3.2 Decision on Error Response Severity
      3. 7.3.3 Execution of Time Critical Code from Wait-Stated Memories
      4. 7.3.4 BGCRC Execution
      5. 7.3.5 Debug/Error Response for BGCRC Errors
      6. 7.3.6 BGCRC Golden CRC-32 Value Computation
    4. 7.4 Software
      1. 7.4.1 BGCRC Examples
        1. 7.4.1.1 BGCRC CPU Interrupt Example
        2. 7.4.1.2 BGCRC Example with Watchdog and Lock
    5. 7.5 BGCRC Registers
      1. 7.5.1 BGCRC Base Address Table
      2. 7.5.2 BGCRC_REGS Registers
      3. 7.5.3 BGCRC Registers to Driverlib Functions
  10. 8 General-Purpose Input/Output (GPIO)
    1. 8.1 Introduction
      1. 8.1.1 GPIO Related Collateral
    2. 8.2 Configuration Overview
    3. 8.3 Digital Inputs on ADC Pins (AIOs)
    4. 8.4 Digital General-Purpose I/O Control
    5. 8.5 Input Qualification
      1. 8.5.1 No Synchronization (Asynchronous Input)
      2. 8.5.2 Synchronization to SYSCLKOUT Only
      3. 8.5.3 Qualification Using a Sampling Window
    6. 8.6 GPIO and Peripheral Muxing
      1. 8.6.1 GPIO Muxing
      2. 8.6.2 Peripheral Muxing
    7. 8.7 Internal Pullup Configuration Requirements
    8. 8.8 Software
      1. 8.8.1 GPIO Examples
        1. 8.8.1.1 Device GPIO Setup
        2. 8.8.1.2 Device GPIO Toggle
        3. 8.8.1.3 Device GPIO Interrupt
        4. 8.8.1.4 External Interrupt (XINT)
      2. 8.8.2 LED Examples
        1. 8.8.2.1 LED Blinky Example with DCSM
    9. 8.9 GPIO Registers
      1. 8.9.1 GPIO Base Address Table
      2. 8.9.2 GPIO_CTRL_REGS Registers
      3. 8.9.3 GPIO_DATA_REGS Registers
      4. 8.9.4 GPIO_DATA_READ_REGS Registers
      5. 8.9.5 GPIO Registers to Driverlib Functions
  11. 9 Crossbar (X-BAR)
    1. 9.1 Input X-BAR and CLB Input X-BAR
      1. 9.1.1 CLB Input X-BAR
    2. 9.2 ePWM, CLB, and GPIO Output X-BAR
      1. 9.2.1 ePWM X-BAR
        1. 9.2.1.1 ePWM X-BAR Architecture
      2. 9.2.2 CLB X-BAR
        1. 9.2.2.1 CLB X-BAR Architecture
      3. 9.2.3 GPIO Output X-BAR
        1. 9.2.3.1 GPIO Output X-BAR Architecture
      4. 9.2.4 CLB Output X-BAR
        1. 9.2.4.1 CLB Output X-BAR Architecture
      5. 9.2.5 X-BAR Flags
    3. 9.3 XBAR Registers
      1. 9.3.1 XBAR Base Address Table
      2. 9.3.2 INPUT_XBAR_REGS Registers
      3. 9.3.3 XBAR_REGS Registers
      4. 9.3.4 EPWM_XBAR_REGS Registers
      5. 9.3.5 CLB_XBAR_REGS Registers
      6. 9.3.6 OUTPUT_XBAR_REGS Registers
      7. 9.3.7 Register to Driverlib Function Mapping
        1. 9.3.7.1 INPUTXBAR Registers to Driverlib Functions
        2. 9.3.7.2 XBAR Registers to Driverlib Functions
        3. 9.3.7.3 EPWMXBAR Registers to Driverlib Functions
        4. 9.3.7.4 CLBXBAR Registers to Driverlib Functions
        5. 9.3.7.5 OUTPUTXBAR Registers to Driverlib Functions
        6. 9.3.7.6 TRIGXBAR Registers to Driverlib Functions
  12. 10Direct Memory Access (DMA)
    1. 10.1 Introduction
      1. 10.1.1 Features
      2. 10.1.2 Block Diagram
    2. 10.2 Architecture
      1. 10.2.1 Peripheral Interrupt Event Trigger Sources
      2. 10.2.2 DMA Bus
    3. 10.3 Address Pointer and Transfer Control
    4. 10.4 Pipeline Timing and Throughput
    5. 10.5 Channel Priority
      1. 10.5.1 Round-Robin Mode
      2. 10.5.2 Channel 1 High-Priority Mode
    6. 10.6 Overrun Detection Feature
    7. 10.7 Software
      1. 10.7.1 DMA Examples
        1. 10.7.1.1 DMA GSRAM Transfer (dma_ex1_gsram_transfer)
        2. 10.7.1.2 DMA GSRAM Transfer (dma_ex2_gsram_transfer)
    8. 10.8 DMA Registers
      1. 10.8.1 DMA Base Address Table
      2. 10.8.2 DMA_REGS Registers
      3. 10.8.3 DMA_CH_REGS Registers
      4. 10.8.4 DMA Registers to Driverlib Functions
  13. 11Embedded Real-time Analysis and Diagnostic (ERAD)
    1. 11.1 Introduction
      1. 11.1.1 ERAD Related Collateral
    2. 11.2 Enhanced Bus Comparator Unit
      1. 11.2.1 Enhanced Bus Comparator Unit Operations
      2. 11.2.2 Event Masking and Exporting
    3. 11.3 System Event Counter Unit
      1. 11.3.1 System Event Counter Modes
        1. 11.3.1.1 Counting Active Levels Versus Edges
        2. 11.3.1.2 Max Mode
        3. 11.3.1.3 Cumulative Mode
        4. 11.3.1.4 Input Signal Selection
      2. 11.3.2 Reset on Event
      3. 11.3.3 Operation Conditions
    4. 11.4 ERAD Ownership, Initialization and Reset
    5. 11.5 ERAD Programming Sequence
      1. 11.5.1 Hardware Breakpoint and Hardware Watch Point Programming Sequence
      2. 11.5.2 Timer and Counter Programming Sequence
    6. 11.6 Cyclic Redundancy Check Unit
      1. 11.6.1 CRC Unit Qualifier
      2. 11.6.2 CRC Unit Programming Sequence
    7. 11.7 Software
      1. 11.7.1 ERAD Examples
        1. 11.7.1.1  ERAD Profiling Interrupts
        2. 11.7.1.2  ERAD Profile Function
        3. 11.7.1.3  ERAD Profile Function
        4. 11.7.1.4  ERAD HWBP Monitor Program Counter
        5. 11.7.1.5  ERAD HWBP Monitor Program Counter
        6. 11.7.1.6  ERAD Profile Function
        7. 11.7.1.7  ERAD HWBP Stack Overflow Detection
        8. 11.7.1.8  ERAD HWBP Stack Overflow Detection
        9. 11.7.1.9  ERAD Stack Overflow
        10. 11.7.1.10 ERAD Profiling Interrupts
        11. 11.7.1.11 ERAD Profiling Interrupts
        12. 11.7.1.12 ERAD MEMORY ACCESS RESTRICT
        13. 11.7.1.13 ERAD INTERRUPT ORDER
        14. 11.7.1.14 ERAD AND CLB
        15. 11.7.1.15 ERAD PWM PROTECTION
    8. 11.8 ERAD Registers
      1. 11.8.1 ERAD Base Address Table
      2. 11.8.2 ERAD_GLOBAL_REGS Registers
      3. 11.8.3 ERAD_HWBP_REGS Registers
      4. 11.8.4 ERAD_COUNTER_REGS Registers
      5. 11.8.5 ERAD_CRC_GLOBAL_REGS Registers
      6. 11.8.6 ERAD_CRC_REGS Registers
      7. 11.8.7 ERAD Registers to Driverlib Functions
  14. 12Configurable Logic Block (CLB)
    1. 12.1 Introduction
      1. 12.1.1 CLB Related Collateral
    2. 12.2 Description
      1. 12.2.1 CLB Clock
    3. 12.3 CLB Input/Output Connection
      1. 12.3.1 Overview
      2. 12.3.2 CLB Input Selection
      3. 12.3.3 CLB Output Selection
      4. 12.3.4 CLB Output Signal Multiplexer
    4. 12.4 CLB Tile
      1. 12.4.1 Static Switch Block
      2. 12.4.2 Counter Block
        1. 12.4.2.1 Counter Description
        2. 12.4.2.2 Counter Operation
        3. 12.4.2.3 Serializer Mode
        4. 12.4.2.4 Linear Feedback Shift Register (LFSR) Mode
      3. 12.4.3 FSM Block
      4. 12.4.4 LUT4 Block
      5. 12.4.5 Output LUT Block
      6. 12.4.6 Asynchronous Output Conditioning (AOC) Block
      7. 12.4.7 High Level Controller (HLC)
        1. 12.4.7.1 High Level Controller Events
        2. 12.4.7.2 High Level Controller Instructions
        3. 12.4.7.3 <Src> and <Dest>
        4. 12.4.7.4 Operation of the PUSH and PULL Instructions (Overflow and Underflow Detection)
    5. 12.5 CPU Interface
      1. 12.5.1 Register Description
      2. 12.5.2 Non-Memory Mapped Registers
    6. 12.6 DMA Access
    7. 12.7 CLB Data Export Through SPI RX Buffer
    8. 12.8 Software
      1. 12.8.1 CLB Examples
        1. 12.8.1.1  CLB Empty Project
        2. 12.8.1.2  CLB Combinational Logic
        3. 12.8.1.3  CLB GPIO Input Filter
        4. 12.8.1.4  CLB Auxilary PWM
        5. 12.8.1.5  CLB PWM Protection
        6. 12.8.1.6  CLB Signal Generator
        7. 12.8.1.7  CLB State Machine
        8. 12.8.1.8  CLB External Signal AND Gate
        9. 12.8.1.9  CLB Timer
        10. 12.8.1.10 CLB Timer Two States
        11. 12.8.1.11 CLB Interrupt Tag
        12. 12.8.1.12 CLB Output Intersect
        13. 12.8.1.13 CLB PUSH PULL
        14. 12.8.1.14 CLB Multi Tile
        15. 12.8.1.15 CLB Glue Logic
        16. 12.8.1.16 CLB AOC Control
        17. 12.8.1.17 CLB AOC Release Control
        18. 12.8.1.18 CLB XBARs
        19. 12.8.1.19 CLB AOC Control
        20. 12.8.1.20 CLB Serializer
        21. 12.8.1.21 CLB LFSR
        22. 12.8.1.22 CLB Lock Output Mask
        23. 12.8.1.23 CLB INPUT Pipeline Mode
        24. 12.8.1.24 CLB Clocking and PIPELINE Mode
        25. 12.8.1.25 CLB SPI Data Export
        26. 12.8.1.26 CLB SPI Data Export DMA
        27. 12.8.1.27 CLB Trip Zone Timestamp
        28. 12.8.1.28 CLB CRC
        29. 12.8.1.29 CLB TDM Serial Port
        30. 12.8.1.30 CLB LED Driver
    9. 12.9 CLB Registers
      1. 12.9.1 CLB Base Address Table
      2. 12.9.2 CLB_LOGIC_CONFIG_REGS Registers
      3. 12.9.3 CLB_LOGIC_CONTROL_REGS Registers
      4. 12.9.4 CLB_DATA_EXCHANGE_REGS Registers
      5. 12.9.5 CLB Registers to Driverlib Functions
  15. 13Host Interface Controller (HIC)
    1. 13.1 Introduction
      1. 13.1.1 HIC Related Collateral
      2. 13.1.2 Features
      3. 13.1.3 Block Diagram
    2. 13.2 Functional Description
      1. 13.2.1 Memory Map
      2. 13.2.2 Connections
        1. 13.2.2.1 Functions of the Connections
      3. 13.2.3 Interrupts and Triggers
    3. 13.3 Operation
      1. 13.3.1 Mailbox Access Mode Overview
        1. 13.3.1.1 Mailbox Access Mode Operation
        2. 13.3.1.2 Configuring HIC Registers With External Host
        3. 13.3.1.3 Mailbox Access Mode Read/Write
      2. 13.3.2 Direct Access Mode Overview
        1. 13.3.2.1 Direct Access Mode Operation
        2. 13.3.2.2 Direct Access Mode Read/Write
      3. 13.3.3 Controlling Reads and Writes
        1. 13.3.3.1 Single-Pin Read/Write Mode (nOE/RnW Pin)
        2. 13.3.3.2 Dual-Pin Read/Write Mode (nOE and nWE Pins)
      4. 13.3.4 Data Lines, Data Width, Data Packing and Unpacking
      5. 13.3.5 Address Translation
      6. 13.3.6 Access Errors
      7. 13.3.7 Security
      8. 13.3.8 HIC Usage
    4. 13.4 Usage Scenarious for Reduced Number of Pins
    5. 13.5 Software
      1. 13.5.1 HIC Examples
        1. 13.5.1.1 HIC 16-bit Memory Access Example
        2. 13.5.1.2 HIC 8-bit Memory Access Example
        3. 13.5.1.3 HIC 16-bit Memory Access FSI Example
    6. 13.6 HIC Registers
      1. 13.6.1 HIC Base Address Table
      2. 13.6.2 HIC_CFG_REGS Registers
      3. 13.6.3 HIC Registers to Driverlib Functions
  16. 14Analog Subsystem
    1. 14.1 Introduction
      1. 14.1.1 Features
      2. 14.1.2 Block Diagram
    2. 14.2 Optimizing Power-Up Time
    3. 14.3 Digital Inputs on ADC Pins (AIOs)
    4. 14.4 Digital Inputs and Outputs on ADC Pins (AGPIOs)
    5. 14.5 Analog Pins and Internal Connections
    6. 14.6 Analog Subsystem Registers
      1. 14.6.1 ASBSYS Base Address Table
      2. 14.6.2 ANALOG_SUBSYS_REGS Registers
  17. 15Analog-to-Digital Converter (ADC)
    1. 15.1  Introduction
      1. 15.1.1 ADC Related Collateral
      2. 15.1.2 Features
      3. 15.1.3 Block Diagram
    2. 15.2  ADC Configurability
      1. 15.2.1 Clock Configuration
      2. 15.2.2 Resolution
      3. 15.2.3 Voltage Reference
        1. 15.2.3.1 External Reference Mode
        2. 15.2.3.2 Internal Reference Mode
        3. 15.2.3.3 Selecting Reference Mode
      4. 15.2.4 Signal Mode
      5. 15.2.5 Expected Conversion Results
      6. 15.2.6 Interpreting Conversion Results
    3. 15.3  SOC Principle of Operation
      1. 15.3.1 SOC Configuration
      2. 15.3.2 Trigger Operation
      3. 15.3.3 ADC Acquisition (Sample and Hold) Window
      4. 15.3.4 ADC Input Models
      5. 15.3.5 Channel Selection
    4. 15.4  SOC Configuration Examples
      1. 15.4.1 Single Conversion from ePWM Trigger
      2. 15.4.2 Oversampled Conversion from ePWM Trigger
      3. 15.4.3 Multiple Conversions from CPU Timer Trigger
      4. 15.4.4 Software Triggering of SOCs
    5. 15.5  ADC Conversion Priority
    6. 15.6  Burst Mode
      1. 15.6.1 Burst Mode Example
      2. 15.6.2 Burst Mode Priority Example
    7. 15.7  EOC and Interrupt Operation
      1. 15.7.1 Interrupt Overflow
      2. 15.7.2 Continue to Interrupt Mode
      3. 15.7.3 Early Interrupt Configuration Mode
    8. 15.8  Post-Processing Blocks
      1. 15.8.1 PPB Offset Correction
      2. 15.8.2 PPB Error Calculation
      3. 15.8.3 PPB Limit Detection and Zero-Crossing Detection
      4. 15.8.4 PPB Sample Delay Capture
    9. 15.9  Opens/Shorts Detection Circuit (OSDETECT)
      1. 15.9.1 Implementation
      2. 15.9.2 Detecting an Open Input Pin
      3. 15.9.3 Detecting a Shorted Input Pin
    10. 15.10 Power-Up Sequence
    11. 15.11 ADC Calibration
      1. 15.11.1 ADC Zero Offset Calibration
    12. 15.12 ADC Timings
      1. 15.12.1 ADC Timing Diagrams
    13. 15.13 Additional Information
      1. 15.13.1 Ensuring Synchronous Operation
        1. 15.13.1.1 Basic Synchronous Operation
        2. 15.13.1.2 Synchronous Operation with Multiple Trigger Sources
        3. 15.13.1.3 Synchronous Operation with Uneven SOC Numbers
        4. 15.13.1.4 Non-overlapping Conversions
      2. 15.13.2 Choosing an Acquisition Window Duration
      3. 15.13.3 Achieving Simultaneous Sampling
      4. 15.13.4 Result Register Mapping
      5. 15.13.5 Internal Temperature Sensor
      6. 15.13.6 Designing an External Reference Circuit
      7. 15.13.7 ADC-DAC Loopback Testing
      8. 15.13.8 Internal Test Mode
      9. 15.13.9 ADC Gain and Offset Calibration
    14. 15.14 Software
      1. 15.14.1 ADC Examples
        1. 15.14.1.1  ADC Software Triggering
        2. 15.14.1.2  ADC ePWM Triggering
        3. 15.14.1.3  ADC Temperature Sensor Conversion
        4. 15.14.1.4  ADC Synchronous SOC Software Force (adc_soc_software_sync)
        5. 15.14.1.5  ADC Continuous Triggering (adc_soc_continuous)
        6. 15.14.1.6  ADC Continuous Conversions Read by DMA (adc_soc_continuous_dma)
        7. 15.14.1.7  ADC PPB Offset (adc_ppb_offset)
        8. 15.14.1.8  ADC PPB Limits (adc_ppb_limits)
        9. 15.14.1.9  ADC PPB Delay Capture (adc_ppb_delay)
        10. 15.14.1.10 ADC ePWM Triggering Multiple SOC
        11. 15.14.1.11 ADC Burst Mode
        12. 15.14.1.12 ADC Burst Mode Oversampling
        13. 15.14.1.13 ADC SOC Oversampling
        14. 15.14.1.14 ADC PPB PWM trip (adc_ppb_pwm_trip)
        15. 15.14.1.15 ADC Open Shorts Detection (adc_open_shorts_detection)
    15. 15.15 ADC Registers
      1. 15.15.1 ADC Base Address Table
      2. 15.15.2 ADC_RESULT_REGS Registers
      3. 15.15.3 ADC_REGS Registers
      4. 15.15.4 ADC Registers to Driverlib Functions
  18. 16Comparator Subsystem (CMPSS)
    1. 16.1 Introduction
      1. 16.1.1 CMPSS Related Collateral
      2. 16.1.2 Features
      3. 16.1.3 Block Diagram
    2. 16.2 Comparator
    3. 16.3 Reference DAC
    4. 16.4 Ramp Generator
      1. 16.4.1 Ramp Generator Overview
      2. 16.4.2 Ramp Generator Behavior
      3. 16.4.3 Ramp Generator Behavior at Corner Cases
    5. 16.5 Digital Filter
      1. 16.5.1 Filter Initialization Sequence
    6. 16.6 Using the CMPSS
      1. 16.6.1 LATCHCLR, EPWMSYNCPER, and EPWMBLANK Signals
      2. 16.6.2 Synchronizer, Digital Filter, and Latch Delays
      3. 16.6.3 Calibrating the CMPSS
      4. 16.6.4 Enabling and Disabling the CMPSS Clock
    7. 16.7 Software
      1. 16.7.1 CMPSS Examples
        1. 16.7.1.1 CMPSS Asynchronous Trip
        2. 16.7.1.2 CMPSS Digital Filter Configuration
    8. 16.8 CMPSS Registers
      1. 16.8.1 CMPSS Base Address Table
      2. 16.8.2 CMPSS_REGS Registers
      3. 16.8.3 CMPSS Registers to Driverlib Functions
  19. 17Enhanced Pulse Width Modulator (ePWM)
    1. 17.1  Introduction
      1. 17.1.1 EPWM Related Collateral
      2. 17.1.2 Submodule Overview
    2. 17.2  Configuring Device Pins
    3. 17.3  ePWM Modules Overview
    4. 17.4  Time-Base (TB) Submodule
      1. 17.4.1 Purpose of the Time-Base Submodule
      2. 17.4.2 Controlling and Monitoring the Time-Base Submodule
      3. 17.4.3 Calculating PWM Period and Frequency
        1. 17.4.3.1 Time-Base Period Shadow Register
        2. 17.4.3.2 Time-Base Clock Synchronization
        3. 17.4.3.3 Time-Base Counter Synchronization
        4. 17.4.3.4 ePWM SYNC Selection
      4. 17.4.4 Phase Locking the Time-Base Clocks of Multiple ePWM Modules
      5. 17.4.5 Simultaneous Writes to TBPRD and CMPx Registers Between ePWM Modules
      6. 17.4.6 Time-Base Counter Modes and Timing Waveforms
      7. 17.4.7 Global Load
        1. 17.4.7.1 Global Load Pulse Pre-Scalar
        2. 17.4.7.2 One-Shot Load Mode
        3. 17.4.7.3 One-Shot Sync Mode
    5. 17.5  Counter-Compare (CC) Submodule
      1. 17.5.1 Purpose of the Counter-Compare Submodule
      2. 17.5.2 Controlling and Monitoring the Counter-Compare Submodule
      3. 17.5.3 Operational Highlights for the Counter-Compare Submodule
      4. 17.5.4 Count Mode Timing Waveforms
    6. 17.6  Action-Qualifier (AQ) Submodule
      1. 17.6.1 Purpose of the Action-Qualifier Submodule
      2. 17.6.2 Action-Qualifier Submodule Control and Status Register Definitions
      3. 17.6.3 Action-Qualifier Event Priority
      4. 17.6.4 AQCTLA and AQCTLB Shadow Mode Operations
      5. 17.6.5 Configuration Requirements for Common Waveforms
    7. 17.7  Dead-Band Generator (DB) Submodule
      1. 17.7.1 Purpose of the Dead-Band Submodule
      2. 17.7.2 Dead-band Submodule Additional Operating Modes
      3. 17.7.3 Operational Highlights for the Dead-Band Submodule
    8. 17.8  PWM Chopper (PC) Submodule
      1. 17.8.1 Purpose of the PWM Chopper Submodule
      2. 17.8.2 Operational Highlights for the PWM Chopper Submodule
      3. 17.8.3 Waveforms
        1. 17.8.3.1 One-Shot Pulse
        2. 17.8.3.2 Duty Cycle Control
    9. 17.9  Trip-Zone (TZ) Submodule
      1. 17.9.1 Purpose of the Trip-Zone Submodule
      2. 17.9.2 Operational Highlights for the Trip-Zone Submodule
        1. 17.9.2.1 Trip-Zone Configurations
      3. 17.9.3 Generating Trip Event Interrupts
    10. 17.10 Event-Trigger (ET) Submodule
      1. 17.10.1 Operational Overview of the ePWM Event-Trigger Submodule
    11. 17.11 Digital Compare (DC) Submodule
      1. 17.11.1 Purpose of the Digital Compare Submodule
      2. 17.11.2 Enhanced Trip Action Using CMPSS
      3. 17.11.3 Using CMPSS to Trip the ePWM on a Cycle-by-Cycle Basis
      4. 17.11.4 Operation Highlights of the Digital Compare Submodule
        1. 17.11.4.1 Digital Compare Events
        2. 17.11.4.2 Event Filtering
        3. 17.11.4.3 Valley Switching
    12. 17.12 ePWM Crossbar (X-BAR)
    13. 17.13 Applications to Power Topologies
      1. 17.13.1  Overview of Multiple Modules
      2. 17.13.2  Key Configuration Capabilities
      3. 17.13.3  Controlling Multiple Buck Converters With Independent Frequencies
      4. 17.13.4  Controlling Multiple Buck Converters With Same Frequencies
      5. 17.13.5  Controlling Multiple Half H-Bridge (HHB) Converters
      6. 17.13.6  Controlling Dual 3-Phase Inverters for Motors (ACI and PMSM)
      7. 17.13.7  Practical Applications Using Phase Control Between PWM Modules
      8. 17.13.8  Controlling a 3-Phase Interleaved DC/DC Converter
      9. 17.13.9  Controlling Zero Voltage Switched Full Bridge (ZVSFB) Converter
      10. 17.13.10 Controlling a Peak Current Mode Controlled Buck Module
      11. 17.13.11 Controlling H-Bridge LLC Resonant Converter
    14. 17.14 Register Lock Protection
    15. 17.15 High-Resolution Pulse Width Modulator (HRPWM)
      1. 17.15.1 Operational Description of HRPWM
        1. 17.15.1.1 Controlling the HRPWM Capabilities
        2. 17.15.1.2 HRPWM Source Clock
        3. 17.15.1.3 Configuring the HRPWM
        4. 17.15.1.4 Configuring High-Resolution in Deadband Rising-Edge and Falling-Edge Delay
        5. 17.15.1.5 Principle of Operation
          1. 17.15.1.5.1 Edge Positioning
          2. 17.15.1.5.2 Scaling Considerations
          3. 17.15.1.5.3 Duty Cycle Range Limitation
          4. 17.15.1.5.4 High-Resolution Period
            1. 17.15.1.5.4.1 High-Resolution Period Configuration
        6. 17.15.1.6 Deadband High-Resolution Operation
        7. 17.15.1.7 Scale Factor Optimizing Software (SFO)
        8. 17.15.1.8 HRPWM Examples Using Optimized Assembly Code
          1. 17.15.1.8.1 #Defines for HRPWM Header Files
          2. 17.15.1.8.2 Implementing a Simple Buck Converter
            1. 17.15.1.8.2.1 HRPWM Buck Converter Initialization Code
            2. 17.15.1.8.2.2 HRPWM Buck Converter Run-Time Code
          3. 17.15.1.8.3 Implementing a DAC Function Using an R+C Reconstruction Filter
            1. 17.15.1.8.3.1 PWM DAC Function Initialization Code
            2. 17.15.1.8.3.2 PWM DAC Function Run-Time Code
      2. 17.15.2 SFO Library Software - SFO_TI_Build_V8.lib
        1. 17.15.2.1 Scale Factor Optimizer Function - int SFO()
        2. 17.15.2.2 Software Usage
          1. 17.15.2.2.1 A Sample of How to Add "Include" Files
          2.        799
          3. 17.15.2.2.2 Declaring an Element
          4.        801
          5. 17.15.2.2.3 Initializing With a Scale Factor Value
          6.        803
          7. 17.15.2.2.4 SFO Function Calls
    16. 17.16 Software
      1. 17.16.1 EPWM Examples
        1. 17.16.1.1  ePWM Trip Zone
        2. 17.16.1.2  ePWM Up Down Count Action Qualifier
        3. 17.16.1.3  ePWM Synchronization
        4. 17.16.1.4  ePWM Digital Compare
        5. 17.16.1.5  ePWM Digital Compare Event Filter Blanking Window
        6. 17.16.1.6  ePWM Valley Switching
        7. 17.16.1.7  ePWM Digital Compare Edge Filter
        8. 17.16.1.8  ePWM Deadband
        9. 17.16.1.9  ePWM DMA
        10. 17.16.1.10 ePWM Chopper
        11. 17.16.1.11 EPWM Configure Signal
        12. 17.16.1.12 Realization of Monoshot mode
        13. 17.16.1.13 EPWM Action Qualifier (epwm_up_aq)
      2. 17.16.2 HRPWM Examples
        1. 17.16.2.1 HRPWM Duty Control with SFO
        2. 17.16.2.2 HRPWM Slider
        3. 17.16.2.3 HRPWM Period Control
        4. 17.16.2.4 HRPWM Duty Control with UPDOWN Mode
        5. 17.16.2.5 HRPWM Slider Test
        6. 17.16.2.6 HRPWM Duty Up Count
        7. 17.16.2.7 HRPWM Period Up-Down Count
    17. 17.17 ePWM Registers
      1. 17.17.1 EPWM Base Address Table
      2. 17.17.2 EPWM_REGS Registers
      3. 17.17.3 Register to Driverlib Function Mapping
        1. 17.17.3.1 EPWM Registers to Driverlib Functions
        2. 17.17.3.2 HRPWM Registers to Driverlib Functions
  20. 18Enhanced Capture (eCAP)
    1. 18.1 Introduction
      1. 18.1.1 Features
      2. 18.1.2 ECAP Related Collateral
    2. 18.2 Description
    3. 18.3 Configuring Device Pins for the eCAP
    4. 18.4 Capture and APWM Operating Mode
    5. 18.5 Capture Mode Description
      1. 18.5.1  Event Prescaler
      2. 18.5.2  Edge Polarity Select and Qualifier
      3. 18.5.3  Continuous/One-Shot Control
      4. 18.5.4  32-Bit Counter and Phase Control
      5. 18.5.5  CAP1-CAP4 Registers
      6. 18.5.6  eCAP Synchronization
        1. 18.5.6.1 Example 1 - Using SWSYNC with ECAP Module
      7. 18.5.7  Interrupt Control
      8. 18.5.8  DMA Interrupt
      9. 18.5.9  Shadow Load and Lockout Control
      10. 18.5.10 APWM Mode Operation
    6. 18.6 Application of the eCAP Module
      1. 18.6.1 Example 1 - Absolute Time-Stamp Operation Rising-Edge Trigger
      2. 18.6.2 Example 2 - Absolute Time-Stamp Operation Rising- and Falling-Edge Trigger
      3. 18.6.3 Example 3 - Time Difference (Delta) Operation Rising-Edge Trigger
      4. 18.6.4 Example 4 - Time Difference (Delta) Operation Rising- and Falling-Edge Trigger
    7. 18.7 Application of the APWM Mode
      1. 18.7.1 Example 1 - Simple PWM Generation (Independent Channels)
    8. 18.8 Software
      1. 18.8.1 ECAP Examples
        1. 18.8.1.1 eCAP APWM Example
        2. 18.8.1.2 eCAP Capture PWM Example
        3. 18.8.1.3 eCAP APWM Phase-shift Example
        4. 18.8.1.4 eCAP Software Sync Example
    9. 18.9 eCAP Registers
      1. 18.9.1 ECAP Base Address Table
      2. 18.9.2 ECAP_REGS Registers
      3. 18.9.3 ECAP Registers to Driverlib Functions
  21. 19High Resolution Capture (HRCAP)
    1. 19.1 Introduction
      1. 19.1.1 HRCAP Related Collateral
      2. 19.1.2 Features
      3. 19.1.3 Description
    2. 19.2 Operational Details
      1. 19.2.1 HRCAP Clocking
      2. 19.2.2 HRCAP Initialization Sequence
      3. 19.2.3 HRCAP Interrupts
      4. 19.2.4 HRCAP Calibration
        1. 19.2.4.1 Applying the Scale Factor
    3. 19.3 Known Exceptions
    4. 19.4 Software
      1. 19.4.1 HRCAP Examples
        1. 19.4.1.1 HRCAP Capture and Calibration Example
    5. 19.5 HRCAP Registers
      1. 19.5.1 HRCAP Base Address Table
      2. 19.5.2 HRCAP_REGS Registers
      3. 19.5.3 HRCAP Registers to Driverlib Functions
  22. 20Enhanced Quadrature Encoder Pulse (eQEP)
    1. 20.1  Introduction
      1. 20.1.1 EQEP Related Collateral
    2. 20.2  Configuring Device Pins
    3. 20.3  Description
      1. 20.3.1 EQEP Inputs
      2. 20.3.2 Functional Description
      3. 20.3.3 eQEP Memory Map
    4. 20.4  Quadrature Decoder Unit (QDU)
      1. 20.4.1 Position Counter Input Modes
        1. 20.4.1.1 Quadrature Count Mode
        2. 20.4.1.2 Direction-Count Mode
        3. 20.4.1.3 Up-Count Mode
        4. 20.4.1.4 Down-Count Mode
      2. 20.4.2 eQEP Input Polarity Selection
      3. 20.4.3 Position-Compare Sync Output
    5. 20.5  Position Counter and Control Unit (PCCU)
      1. 20.5.1 Position Counter Operating Modes
        1. 20.5.1.1 Position Counter Reset on Index Event (QEPCTL[PCRM]=00)
        2. 20.5.1.2 Position Counter Reset on Maximum Position (QEPCTL[PCRM]=01)
        3. 20.5.1.3 Position Counter Reset on the First Index Event (QEPCTL[PCRM] = 10)
        4. 20.5.1.4 Position Counter Reset on Unit Time-out Event (QEPCTL[PCRM] = 11)
      2. 20.5.2 Position Counter Latch
        1. 20.5.2.1 Index Event Latch
        2. 20.5.2.2 Strobe Event Latch
      3. 20.5.3 Position Counter Initialization
      4. 20.5.4 eQEP Position-compare Unit
    6. 20.6  eQEP Edge Capture Unit
    7. 20.7  eQEP Watchdog
    8. 20.8  eQEP Unit Timer Base
    9. 20.9  QMA Module
      1. 20.9.1 Modes of Operation
        1. 20.9.1.1 QMA Mode-1 (QMACTRL[MODE]=1)
        2. 20.9.1.2 QMA Mode-2 (QMACTRL[MODE]=2)
      2. 20.9.2 Interrupt and Error Generation
    10. 20.10 eQEP Interrupt Structure
    11. 20.11 Software
      1. 20.11.1 EQEP Examples
        1. 20.11.1.1 Frequency Measurement Using eQEP
        2. 20.11.1.2 Position and Speed Measurement Using eQEP
        3. 20.11.1.3 ePWM frequency Measurement Using eQEP via xbar connection
        4. 20.11.1.4 Frequency Measurement Using eQEP via unit timeout interrupt
        5. 20.11.1.5 Motor speed and direction measurement using eQEP via unit timeout interrupt
    12. 20.12 eQEP Registers
      1. 20.12.1 EQEP Base Address Table
      2. 20.12.2 EQEP_REGS Registers
      3. 20.12.3 EQEP Registers to Driverlib Functions
  23. 21Controller Area Network (CAN)
    1. 21.1  Introduction
      1. 21.1.1 DCAN Related Collateral
      2. 21.1.2 Features
      3. 21.1.3 Block Diagram
        1. 21.1.3.1 CAN Core
        2. 21.1.3.2 Message Handler
        3. 21.1.3.3 Message RAM
        4. 21.1.3.4 Registers and Message Object Access (IFx)
    2. 21.2  Functional Description
      1. 21.2.1 Configuring Device Pins
      2. 21.2.2 Address/Data Bus Bridge
    3. 21.3  Operating Modes
      1. 21.3.1 Initialization
      2. 21.3.2 CAN Message Transfer (Normal Operation)
        1. 21.3.2.1 Disabled Automatic Retransmission
        2. 21.3.2.2 Auto-Bus-On
      3. 21.3.3 Test Modes
        1. 21.3.3.1 Silent Mode
        2. 21.3.3.2 Loopback Mode
        3. 21.3.3.3 External Loopback Mode
        4. 21.3.3.4 Loopback Combined with Silent Mode
    4. 21.4  Multiple Clock Source
    5. 21.5  Interrupt Functionality
      1. 21.5.1 Message Object Interrupts
      2. 21.5.2 Status Change Interrupts
      3. 21.5.3 Error Interrupts
      4. 21.5.4 Peripheral Interrupt Expansion (PIE) Module Nomenclature for DCAN Interrupts
      5. 21.5.5 Interrupt Topologies
    6. 21.6  DMA Functionality
    7. 21.7  Parity Check Mechanism
      1. 21.7.1 Behavior on Parity Error
    8. 21.8  Debug Mode
    9. 21.9  Module Initialization
    10. 21.10 Configuration of Message Objects
      1. 21.10.1 Configuration of a Transmit Object for Data Frames
      2. 21.10.2 Configuration of a Transmit Object for Remote Frames
      3. 21.10.3 Configuration of a Single Receive Object for Data Frames
      4. 21.10.4 Configuration of a Single Receive Object for Remote Frames
      5. 21.10.5 Configuration of a FIFO Buffer
    11. 21.11 Message Handling
      1. 21.11.1  Message Handler Overview
      2. 21.11.2  Receive/Transmit Priority
      3. 21.11.3  Transmission of Messages in Event Driven CAN Communication
      4. 21.11.4  Updating a Transmit Object
      5. 21.11.5  Changing a Transmit Object
      6. 21.11.6  Acceptance Filtering of Received Messages
      7. 21.11.7  Reception of Data Frames
      8. 21.11.8  Reception of Remote Frames
      9. 21.11.9  Reading Received Messages
      10. 21.11.10 Requesting New Data for a Receive Object
      11. 21.11.11 Storing Received Messages in FIFO Buffers
      12. 21.11.12 Reading from a FIFO Buffer
    12. 21.12 CAN Bit Timing
      1. 21.12.1 Bit Time and Bit Rate
        1. 21.12.1.1 Synchronization Segment
        2. 21.12.1.2 Propagation Time Segment
        3. 21.12.1.3 Phase Buffer Segments and Synchronization
        4. 21.12.1.4 Oscillator Tolerance Range
      2. 21.12.2 Configuration of the CAN Bit Timing
        1. 21.12.2.1 Calculation of the Bit Timing Parameters
        2. 21.12.2.2 Example for Bit Timing at High Baudrate
        3. 21.12.2.3 Example for Bit Timing at Low Baudrate
    13. 21.13 Message Interface Register Sets
      1. 21.13.1 Message Interface Register Sets 1 and 2 (IF1 and IF2)
      2. 21.13.2 Message Interface Register Set 3 (IF3)
    14. 21.14 Message RAM
      1. 21.14.1 Structure of Message Objects
      2. 21.14.2 Addressing Message Objects in RAM
      3. 21.14.3 Message RAM Representation in Debug Mode
    15. 21.15 Software
      1. 21.15.1 CAN Examples
        1. 21.15.1.1 CAN External Loopback
        2. 21.15.1.2 CAN External Loopback with Interrupts
        3. 21.15.1.3 CAN External Loopback with DMA
        4. 21.15.1.4 CAN Transmit and Receive Configurations
        5. 21.15.1.5 CAN Error Generation Example
        6. 21.15.1.6 CAN Remote Request Loopback
        7. 21.15.1.7 CAN example that illustrates the usage of Mask registers
    16. 21.16 CAN Registers
      1. 21.16.1 CAN Base Address Table
      2. 21.16.2 CAN_REGS Registers
      3. 21.16.3 CAN Registers to Driverlib Functions
  24. 22Fast Serial Interface (FSI)
    1. 22.1 Introduction
      1. 22.1.1 FSI Related Collateral
      2. 22.1.2 FSI Features
    2. 22.2 System-level Integration
      1. 22.2.1 CPU Interface
      2. 22.2.2 Signal Description
        1. 22.2.2.1 Configuring Device Pins
      3. 22.2.3 FSI Interrupts
        1. 22.2.3.1 Transmitter Interrupts
        2. 22.2.3.2 Receiver Interrupts
        3. 22.2.3.3 Configuring Interrupts
        4. 22.2.3.4 Handling Interrupts
      4. 22.2.4 DMA Interface
      5. 22.2.5 External Frame Trigger Mux
    3. 22.3 FSI Functional Description
      1. 22.3.1  Introduction to Operation
      2. 22.3.2  FSI Transmitter Module
        1. 22.3.2.1 Initialization
        2. 22.3.2.2 FSI_TX Clocking
        3. 22.3.2.3 Transmitting Frames
          1. 22.3.2.3.1 Software Triggered Frames
          2. 22.3.2.3.2 Externally Triggered Frames
          3. 22.3.2.3.3 Ping Frame Generation
            1. 22.3.2.3.3.1 Automatic Ping Frames
            2. 22.3.2.3.3.2 Software Triggered Ping Frame
            3. 22.3.2.3.3.3 Externally Triggered Ping Frame
          4. 22.3.2.3.4 Transmitting Frames with DMA
        4. 22.3.2.4 Transmit Buffer Management
        5. 22.3.2.5 CRC Submodule
        6. 22.3.2.6 Conditions in Which the Transmitter Must Undergo a Soft Reset
        7. 22.3.2.7 Reset
      3. 22.3.3  FSI Receiver Module
        1. 22.3.3.1  Initialization
        2. 22.3.3.2  FSI_RX Clocking
        3. 22.3.3.3  Receiving Frames
          1. 22.3.3.3.1 Receiving Frames with DMA
        4. 22.3.3.4  Ping Frame Watchdog
        5. 22.3.3.5  Frame Watchdog
        6. 22.3.3.6  Delay Line Control
        7. 22.3.3.7  Buffer Management
        8. 22.3.3.8  CRC Submodule
        9. 22.3.3.9  Using the Zero Bits of the Receiver Tag Registers
        10. 22.3.3.10 Conditions in Which the Receiver Must Undergo a Soft Reset
        11. 22.3.3.11 FSI_RX Reset
      4. 22.3.4  Frame Format
        1. 22.3.4.1 FSI Frame Phases
        2. 22.3.4.2 Frame Types
          1. 22.3.4.2.1 Ping Frames
          2. 22.3.4.2.2 Error Frames
          3. 22.3.4.2.3 Data Frames
        3. 22.3.4.3 Multi-Lane Transmission
      5. 22.3.5  Flush Sequence
      6. 22.3.6  Internal Loopback
      7. 22.3.7  CRC Generation
      8. 22.3.8  ECC Module
      9. 22.3.9  Tag Matching
      10. 22.3.10 TDM Configurations
      11. 22.3.11 FSI Trigger Generation
      12. 22.3.12 FSI-SPI Compatibility Mode
        1. 22.3.12.1 Available SPI Modes
          1. 22.3.12.1.1 FSITX as SPI Master, Transmit Only
            1. 22.3.12.1.1.1 Initialization
            2. 22.3.12.1.1.2 Operation
          2. 22.3.12.1.2 FSIRX as SPI Slave, Receive Only
            1. 22.3.12.1.2.1 Initialization
            2. 22.3.12.1.2.2 Operation
          3. 22.3.12.1.3 FSITX and FSIRX Emulating a Full Duplex SPI Master
            1. 22.3.12.1.3.1 Initialization
            2. 22.3.12.1.3.2 Operation
    4. 22.4 FSI Programing Guide
      1. 22.4.1 Establishing the Communication Link
        1. 22.4.1.1 Establishing the Communication Link from the Master Device
        2. 22.4.1.2 Establishing the Communication Link from the Slave Device
      2. 22.4.2 Register Protection
      3. 22.4.3 Emulation Mode
    5. 22.5 Software
      1. 22.5.1 FSI Examples
        1. 22.5.1.1  FSI Loopback:CPU Control
        2. 22.5.1.2  FSI DMA frame transfers:DMA Control
        3. 22.5.1.3  FSI data transfer by external trigger
        4. 22.5.1.4  FSI data transfers upon CPU Timer event
        5. 22.5.1.5  FSI and SPI communication(fsi_ex6_spi_main_tx)
        6. 22.5.1.6  FSI and SPI communication(fsi_ex7_spi_remote_rx)
        7. 22.5.1.7  FSI P2Point Connection:Rx Side
        8. 22.5.1.8  FSI P2Point Connection:Tx Side
        9. 22.5.1.9  FSI daisy chain topology, lead device example
        10. 22.5.1.10 FSI daisy chain topology, node device example
    6. 22.6 FSI Registers
      1. 22.6.1 FSI Base Address Table
      2. 22.6.2 FSI_TX_REGS Registers
      3. 22.6.3 FSI_RX_REGS Registers
      4. 22.6.4 FSI Registers to Driverlib Functions
  25. 23Inter-Integrated Circuit Module (I2C)
    1. 23.1 Introduction
      1. 23.1.1 I2C Related Collateral
      2. 23.1.2 Features
      3. 23.1.3 Features Not Supported
      4. 23.1.4 Functional Overview
      5. 23.1.5 Clock Generation
      6. 23.1.6 I2C Clock Divider Registers (I2CCLKL and I2CCLKH)
        1. 23.1.6.1 Formula for the Master Clock Period
    2. 23.2 Configuring Device Pins
    3. 23.3 I2C Module Operational Details
      1. 23.3.1  Input and Output Voltage Levels
      2. 23.3.2  Selecting Pullup Resistors
      3. 23.3.3  Data Validity
      4. 23.3.4  Operating Modes
      5. 23.3.5  I2C Module START and STOP Conditions
      6. 23.3.6  Non-repeat Mode versus Repeat Mode
      7. 23.3.7  Serial Data Formats
        1. 23.3.7.1 7-Bit Addressing Format
        2. 23.3.7.2 10-Bit Addressing Format
        3. 23.3.7.3 Free Data Format
        4. 23.3.7.4 Using a Repeated START Condition
      8. 23.3.8  Clock Synchronization
      9. 23.3.9  Arbitration
      10. 23.3.10 Digital Loopback Mode
      11. 23.3.11 NACK Bit Generation
    4. 23.4 Interrupt Requests Generated by the I2C Module
      1. 23.4.1 Basic I2C Interrupt Requests
      2. 23.4.2 I2C FIFO Interrupts
    5. 23.5 Resetting or Disabling the I2C Module
    6. 23.6 Software
      1. 23.6.1 I2C Examples
        1. 23.6.1.1 C28x-I2C Library source file for FIFO interrupts
        2. 23.6.1.2 C28x-I2C Library source file for FIFO using polling
        3. 23.6.1.3 C28x-I2C Library source file for FIFO interrupts
        4. 23.6.1.4 I2C Digital Loopback with FIFO Interrupts
        5. 23.6.1.5 I2C EEPROM
        6. 23.6.1.6 I2C Digital External Loopback with FIFO Interrupts
        7. 23.6.1.7 I2C EEPROM
        8. 23.6.1.8 I2C controller target communication using FIFO interrupts
        9. 23.6.1.9 I2C EEPROM
    7. 23.7 I2C Registers
      1. 23.7.1 I2C Base Address Table
      2. 23.7.2 I2C_REGS Registers
      3. 23.7.3 I2C Registers to Driverlib Functions
  26. 24Local Interconnect Network (LIN)
    1. 24.1 Introduction
      1. 24.1.1 SCI Features
      2. 24.1.2 LIN Features
      3. 24.1.3 LIN Related Collateral
      4. 24.1.4 Block Diagram
    2. 24.2 Serial Communications Interface Module
      1. 24.2.1 SCI Communication Formats
        1. 24.2.1.1 SCI Frame Formats
        2. 24.2.1.2 SCI Asynchronous Timing Mode
        3. 24.2.1.3 SCI Baud Rate
          1. 24.2.1.3.1 Superfractional Divider, SCI Asynchronous Mode
        4. 24.2.1.4 SCI Multiprocessor Communication Modes
          1. 24.2.1.4.1 Idle-Line Multiprocessor Modes
          2. 24.2.1.4.2 Address-Bit Multiprocessor Mode
        5. 24.2.1.5 SCI Multibuffered Mode
      2. 24.2.2 SCI Interrupts
        1. 24.2.2.1 Transmit Interrupt
        2. 24.2.2.2 Receive Interrupt
        3. 24.2.2.3 WakeUp Interrupt
        4. 24.2.2.4 Error Interrupts
      3. 24.2.3 SCI DMA Interface
        1. 24.2.3.1 Receive DMA Requests
        2. 24.2.3.2 Transmit DMA Requests
      4. 24.2.4 SCI Configurations
        1. 24.2.4.1 Receiving Data
          1. 24.2.4.1.1 Receiving Data in Single-Buffer Mode
          2. 24.2.4.1.2 Receiving Data in Multibuffer Mode
        2. 24.2.4.2 Transmitting Data
          1. 24.2.4.2.1 Transmitting Data in Single-Buffer Mode
          2. 24.2.4.2.2 Transmitting Data in Multibuffer Mode
      5. 24.2.5 SCI Low-Power Mode
        1. 24.2.5.1 Sleep Mode for Multiprocessor Communication
    3. 24.3 Local Interconnect Network Module
      1. 24.3.1 LIN Communication Formats
        1. 24.3.1.1  LIN Standards
        2. 24.3.1.2  Message Frame
          1. 24.3.1.2.1 Message Header
          2. 24.3.1.2.2 Response
        3. 24.3.1.3  Synchronizer
        4. 24.3.1.4  Baud Rate
          1. 24.3.1.4.1 Fractional Divider
          2. 24.3.1.4.2 Superfractional Divider
            1. 24.3.1.4.2.1 Superfractional Divider In LIN Mode
        5. 24.3.1.5  Header Generation
          1. 24.3.1.5.1 Event Triggered Frame Handling
          2. 24.3.1.5.2 Header Reception and Adaptive Baud Rate
        6. 24.3.1.6  Extended Frames Handling
        7. 24.3.1.7  Timeout Control
          1. 24.3.1.7.1 No-Response Error (NRE)
          2. 24.3.1.7.2 Bus Idle Detection
          3. 24.3.1.7.3 Timeout After Wakeup Signal and Timeout After Three Wakeup Signals
        8. 24.3.1.8  TXRX Error Detector (TED)
          1. 24.3.1.8.1 Bit Errors
          2. 24.3.1.8.2 Physical Bus Errors
          3. 24.3.1.8.3 ID Parity Errors
          4. 24.3.1.8.4 Checksum Errors
        9. 24.3.1.9  Message Filtering and Validation
        10. 24.3.1.10 Receive Buffers
        11. 24.3.1.11 Transmit Buffers
      2. 24.3.2 LIN Interrupts
      3. 24.3.3 Servicing LIN Interrupts
      4. 24.3.4 LIN DMA Interface
        1. 24.3.4.1 LIN Receive DMA Requests
        2. 24.3.4.2 LIN Transmit DMA Requests
      5. 24.3.5 LIN Configurations
        1. 24.3.5.1 Receiving Data
          1. 24.3.5.1.1 Receiving Data in Single-Buffer Mode
          2. 24.3.5.1.2 Receiving Data in Multibuffer Mode
        2. 24.3.5.2 Transmitting Data
          1. 24.3.5.2.1 Transmitting Data in Single-Buffer Mode
          2. 24.3.5.2.2 Transmitting Data in Multibuffer Mode
    4. 24.4 Low-Power Mode
      1. 24.4.1 Entering Sleep Mode
      2. 24.4.2 Wakeup
      3. 24.4.3 Wakeup Timeouts
    5. 24.5 Emulation Mode
    6. 24.6 Software
      1. 24.6.1 LIN Examples
        1. 24.6.1.1 LIN Internal Loopback with Interrupts
        2. 24.6.1.2 LIN SCI Mode Internal Loopback with Interrupts
        3. 24.6.1.3 LIN SCI MODE Internal Loopback with DMA
        4. 24.6.1.4 LIN Internal Loopback without interrupts(polled mode)
        5. 24.6.1.5 LIN Internal Loopback with Interrupts using Sysconfig
        6. 24.6.1.6 LIN Incomplete Header Detection
        7. 24.6.1.7 LIN SCI MODE (Single Buffer) Internal Loopback with DMA
        8. 24.6.1.8 LIN External Loopback without interrupts(polled mode)
    7. 24.7 SCI/LIN Registers
      1. 24.7.1 LIN Base Address Table
      2. 24.7.2 LIN_REGS Registers
      3. 24.7.3 LIN Registers to Driverlib Functions
  27. 25Power Management Bus Module (PMBus)
    1. 25.1 Introduction
      1. 25.1.1 PMBUS Related Collateral
      2. 25.1.2 Features
      3. 25.1.3 Block Diagram
    2. 25.2 Configuring Device Pins
    3. 25.3 Slave Mode Operation
      1. 25.3.1 Configuration
      2. 25.3.2 Message Handling
        1. 25.3.2.1  Quick Command
        2. 25.3.2.2  Send Byte
        3. 25.3.2.3  Receive Byte
        4. 25.3.2.4  Write Byte and Write Word
        5. 25.3.2.5  Read Byte and Read Word
        6. 25.3.2.6  Process Call
        7. 25.3.2.7  Block Write
        8. 25.3.2.8  Block Read
        9. 25.3.2.9  Block Write-Block Read Process Call
        10. 25.3.2.10 Alert Response
        11. 25.3.2.11 Extended Command
        12. 25.3.2.12 Group Command
    4. 25.4 Master Mode Operation
      1. 25.4.1 Configuration
      2. 25.4.2 Message Handling
        1. 25.4.2.1  Quick Command
        2. 25.4.2.2  Send Byte
        3. 25.4.2.3  Receive Byte
        4. 25.4.2.4  Write Byte and Write Word
        5. 25.4.2.5  Read Byte and Read Word
        6. 25.4.2.6  Process Call
        7. 25.4.2.7  Block Write
        8. 25.4.2.8  Block Read
        9. 25.4.2.9  Block Write-Block Read Process Call
        10. 25.4.2.10 Alert Response
        11. 25.4.2.11 Extended Command
        12. 25.4.2.12 Group Command
    5. 25.5 PMBus Registers
      1. 25.5.1 PMBUS Base Address Table
      2. 25.5.2 PMBUS_REGS Registers
      3. 25.5.3 PMBUS Registers to Driverlib Functions
  28. 26Serial Communications Interface (SCI)
    1. 26.1  Introduction
      1. 26.1.1 Features
      2. 26.1.2 SCI Related Collateral
      3. 26.1.3 Block Diagram
    2. 26.2  Architecture
    3. 26.3  SCI Module Signal Summary
    4. 26.4  Configuring Device Pins
    5. 26.5  Multiprocessor and Asynchronous Communication Modes
    6. 26.6  SCI Programmable Data Format
    7. 26.7  SCI Multiprocessor Communication
      1. 26.7.1 Recognizing the Address Byte
      2. 26.7.2 Controlling the SCI TX and RX Features
      3. 26.7.3 Receipt Sequence
    8. 26.8  Idle-Line Multiprocessor Mode
      1. 26.8.1 Idle-Line Mode Steps
      2. 26.8.2 Block Start Signal
      3. 26.8.3 Wake-Up Temporary (WUT) Flag
        1. 26.8.3.1 Sending a Block Start Signal
      4. 26.8.4 Receiver Operation
    9. 26.9  Address-Bit Multiprocessor Mode
      1. 26.9.1 Sending an Address
    10. 26.10 SCI Communication Format
      1. 26.10.1 Receiver Signals in Communication Modes
      2. 26.10.2 Transmitter Signals in Communication Modes
    11. 26.11 SCI Port Interrupts
      1. 26.11.1 Break Detect
    12. 26.12 SCI Baud Rate Calculations
    13. 26.13 SCI Enhanced Features
      1. 26.13.1 SCI FIFO Description
      2. 26.13.2 SCI Auto-Baud
      3. 26.13.3 Autobaud-Detect Sequence
    14. 26.14 Software
      1. 26.14.1 SCI Examples
        1. 26.14.1.1 Tune Baud Rate via UART Example
        2. 26.14.1.2 SCI FIFO Digital Loop Back
        3. 26.14.1.3 SCI Digital Loop Back with Interrupts
        4. 26.14.1.4 SCI Echoback
        5. 26.14.1.5 stdout redirect example
    15. 26.15 SCI Registers
      1. 26.15.1 SCI Base Address Table
      2. 26.15.2 SCI_REGS Registers
      3. 26.15.3 SCI Registers to Driverlib Functions
  29. 27Serial Peripheral Interface (SPI)
    1. 27.1 Introduction
      1. 27.1.1 Features
      2. 27.1.2 SPI Related Collateral
      3. 27.1.3 Block Diagram
    2. 27.2 System-Level Integration
      1. 27.2.1 SPI Module Signals
      2. 27.2.2 Configuring Device Pins
        1. 27.2.2.1 GPIOs Required for High-Speed Mode
      3. 27.2.3 SPI Interrupts
      4. 27.2.4 DMA Support
    3. 27.3 SPI Operation
      1. 27.3.1  Introduction to Operation
      2. 27.3.2  Master Mode
      3. 27.3.3  Slave Mode
      4. 27.3.4  Data Format
        1. 27.3.4.1 Transmission of Bit from SPIRXBUF
      5. 27.3.5  Baud Rate Selection
        1. 27.3.5.1 Baud Rate Determination
        2. 27.3.5.2 Baud Rate Calculation in Non-High Speed Mode (HS_MODE = 0)
      6. 27.3.6  SPI Clocking Schemes
      7. 27.3.7  SPI FIFO Description
      8. 27.3.8  SPI DMA Transfers
        1. 27.3.8.1 Transmitting Data Using SPI with DMA
        2. 27.3.8.2 Receiving Data Using SPI with DMA
      9. 27.3.9  SPI High-Speed Mode
      10. 27.3.10 SPI 3-Wire Mode Description
    4. 27.4 Programming Procedure
      1. 27.4.1 Initialization Upon Reset
      2. 27.4.2 Configuring the SPI
      3. 27.4.3 Configuring the SPI for High-Speed Mode
      4. 27.4.4 Data Transfer Example
      5. 27.4.5 SPI 3-Wire Mode Code Examples
        1. 27.4.5.1 3-Wire Master Mode Transmit
        2.       1365
          1. 27.4.5.2.1 3-Wire Master Mode Receive
        3.       1367
          1. 27.4.5.2.1 3-Wire Slave Mode Transmit
        4.       1369
          1. 27.4.5.2.1 3-Wire Slave Mode Receive
      6. 27.4.6 SPI STEINV Bit in Digital Audio Transfers
    5. 27.5 Software
      1. 27.5.1 SPI Examples
        1. 27.5.1.1 SPI Digital Loopback
        2. 27.5.1.2 SPI Digital Loopback with FIFO Interrupts
        3. 27.5.1.3 SPI Digital External Loopback without FIFO Interrupts
        4. 27.5.1.4 SPI Digital External Loopback with FIFO Interrupts
        5. 27.5.1.5 SPI Digital Loopback with DMA
        6. 27.5.1.6 SPI EEPROM
        7. 27.5.1.7 SPI DMA EEPROM
    6. 27.6 SPI Registers
      1. 27.6.1 SPI Base Address Table
      2. 27.6.2 SPI_REGS Registers
      3. 27.6.3 SPI Registers to Driverlib Functions
  30. 28Revision History

20.1 Introduction

An incremental encoder disk is patterned with a track of slots along the periphery, as shown in Figure 20-1. These slots create an alternating pattern of dark and light lines. The disk count is defined as the number of dark and light line pairs that occur per revolution (lines per revolution). As a rule, a second track is added to generate a signal that occurs once per revolution (index signal: QEPI), which can be used to indicate an absolute position. Encoder manufacturers identify the index pulse using different terms such as index, marker, home position, and zero reference

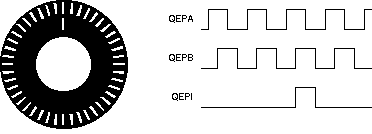GUID-542C9C0E-C63C-4776-85F3-4D142755AF0B-low.gif Figure 20-1 Optical Encoder Disk

 

To derive direction information, the lines on the disk are read out by two different photo-elements that "look" at the disk pattern with a mechanical shift of 1/4 the pitch of a line pair between them. This shift is detected with a reticle or mask that restricts the view of the photo-element to the desired part of the disk lines. As the disk rotates, the two photo-elements generate signals that are shifted 90° out of phase from each other. These are commonly called the quadrature QEPA and QEPB signals. The clockwise direction for most encoders is defined as the QEPA channel going positive before the QEPB channel and conversely, as shown in Figure 20-2.

GUID-97911150-4758-4246-AED5-3B12F1CCE382-low.gif Figure 20-2 QEP Encoder Output Signal for Forward/Reverse Movement

The encoder wheel typically makes one revolution for every revolution of the motor, or the wheel can be at a geared rotation ratio with respect to the motor. Therefore, the frequency of the digital signal coming from the QEPA and QEPB outputs varies proportionally with the velocity of the motor. For example, a 2000-line encoder directly coupled to a motor running at 5000 revolutions-per-minute (rpm) results in a frequency of 166.6kHz, so by measuring the frequency of either the QEPA or QEPB output, the processor can determine the velocity of the motor.

Quadrature encoders from different manufacturers come with two forms of index pulse (gated index pulse or ungated index pulse) as shown in Figure 20-3. A nonstandard form of index pulse is ungated. In the ungated configuration, the index edges are not necessarily coincident with A and B signals. The gated index pulse is aligned to any of the four quadrature edges and width of the index pulse and can be equal to a quarter, half, or full period of the quadrature signal.

GUID-EDD239AB-C2DA-47D8-ADA3-B5E0B136DEBA-low.gif Figure 20-3 Index Pulse Example

Some typical applications of shaft encoders include robotics and computer input in the form of a mouse. Inside your mouse you can see where the mouse ball spins a pair of axles (a left/right, and an up/down axle). These axles are connected to optical shaft encoders that effectively tell the computer how fast and in what direction the mouse is moving.

General Issues: Estimating velocity from a digital position sensor is a cost-effective strategy in motor control. Two different first order approximations for velocity can be written as:

Equation 13. GUID-BE2A10A4-A43D-4180-8631-F5FEAD251A59-low.gif
Equation 14. GUID-697B2724-7F3B-4FC8-BC3E-EB46C8985536-low.gif

where:

  • v(k) = Velocity at time instant k
  • x(k) = Position at time instant k
  • x(k-1) = Position at time instant k-1
  • T = Fixed unit time or inverse of velocity calculation rate
  • ΔX = Incremental position movement in unit time
  • t(k) = Time instant "k"
  • t(k-1) = Time instant "k-1"
  • X = Fixed unit position
  • ΔT = Incremental time elapsed for unit position movement

Equation 13 is the conventional approach to velocity estimation and requires a time base to provide a unit time event for velocity calculation. Unit time is basically the inverse of the velocity calculation rate.

The encoder count (position) is read once during each unit time event. The quantity [x(k) - x(k-1)] is formed by subtracting the previous reading from the current reading. Then the velocity estimate is computed by multiplying by the known constant 1/T (where T is the constant time between unit time events and is known in advance).

Estimation based on Equation 13 has an inherent accuracy limit directly related to the resolution of the position sensor and the unit time period T. For example, consider a 500 line-per-revolution quadrature encoder with a velocity calculation rate of 400Hz. When used for position, the quadrature encoder gives a four-fold increase in resolution; in this case, 2000 counts-per-revolution. The minimum rotation that can be detected is, therefore, 0.0005 revolutions, which gives a velocity resolution of 12rpm when sampled at 400Hz. While this resolution can be satisfactory at moderate or high speeds, for example 1% error at 1200rpm, this resolution clearly proves inadequate at low speeds. In fact, at speeds below 12rpm, the speed estimate is erroneously zero much of the time.

At low speed, Equation 14 provides a more accurate approach. It requires a position sensor that outputs a fixed interval pulse train, such as the aforementioned quadrature encoder. The width of each pulse is defined by motor speed for a given sensor resolution. Equation 14 can be used to calculate motor speed by measuring the elapsed time between successive quadrature pulse edges. However, this method suffers from the opposite limitation, as does Equation 13. A combination of relatively large motor speeds and high sensor resolution makes the time interval ΔT small, and thus more greatly influenced by the timer resolution. This can introduce considerable error into high-speed estimates.

For systems with a large speed range (that is, speed estimation is needed at both low and high speeds), one approach is to use Equation 14 at low speed and have the DSP software switch over to Equation 13 when the motor speed rises above some specified threshold.