Bryan Lizon

One of the fundamental challenges in any high-resolution signal-chain design is ensuring that the system noise floor is low enough for the analog-to-digital converter (ADC) to resolve your signals of interest. For example, if you chose the TI ADS1261 – a 24-bit low-noise delta-sigma ADC – you could resolve input signals as low as 6 nV_RMS at 2.5 SPS and a gain of 128 V/V.

From a system perspective, however, it’s not just the ADC’s noise that you need to worry about: all components, including amplifiers, voltage references, clocks and power supplies, contribute some noise. What’s the cumulative effect of these devices on your system’s noise? And more importantly, will your system be able to resolve your signals of interest?

To help you better understand system noise and apply this knowledge to your designs, I recently wrote a technical article series called “Resolving the Signal.” The series examines common noise sources in a typical signal chain and complements this understanding with methods to mitigate noise and maintain high-precision measurements.

Here are the 10 most critical questions and answers from the series to get you started designing with precision ADCs,

1. What Types of Noise Can You Expect to Find in ADCs?

Total ADC noise has two main components: quantization noise and thermal noise. Quantization noise comes from the process of mapping an infinite number of analog voltages to a finite number of digital codes (the left side of Figure 1). As a result, any single digital output can correspond to several analog input voltages that may differ by as much as one-half least significant bit (LSB).

Thermal noise is a phenomenon inherent in all electrical components as a result of the physical movement of charge inside electrical conductors (the right side of Figure 1). Unfortunately, ADC end users cannot affect the device’s thermal noise because it is a function of the ADC’s design.

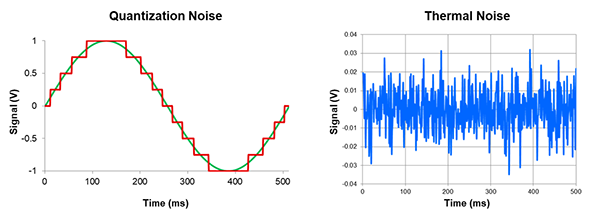Figure 1 Quantization Noise (Left) and Thermal Noise (Right)

Do thermal and quantization noise affect low- and high-resolution ADCs equally? Read part 1, “Introduction to Noise in Delta-Sigma ADCs,” to find out.

2. How Is ADC Noise Measured and Specified?

There are two methods ADC manufacturers use to measure ADC noise. The first method shorts the ADC’s inputs together to measure the slight variations in output code as a result of thermal noise. The second method involves inputting a sine wave with a specific amplitude and frequency (such as 1 V_PP at 1 kHz) and reporting how the ADC quantizes the sine wave. Figure 2 demonstrates these types of noise measurements.

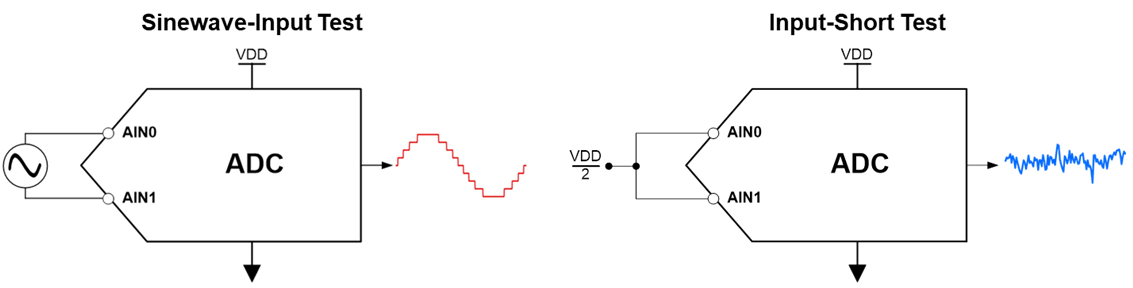Figure 2 Sine-wave-input Test Setup (Left) and Input-short Test Setup (Right)

Which ADCs use which type of measurement method? Read more about noise measurement methods and specifications in part 2.

3. What Is the Best Noise Parameter to Use for System Noise Analysis?

For ADC noise analysis, I recommend using input-referred noise. I’ve bolded this phrase because it’s not common practice to use input-referred noise to define ADC performance. In fact, a majority of engineers speak exclusively in terms of relative parameters such as effective and noise-free resolution and are deeply concerned when they cannot maximize those values. After all, if you need to use a 24-bit ADC to achieve a 16-bit effective resolution, it feels like you’re paying for ADC performance you won’t actually use.

However, an effective resolution of 16 bits doesn’t necessarily tell you anything about how much of the full-scale range (FSR) your ADC will use. You may only need 16 bits of effective resolution, but if the minimum input signal is 50 nV, you will never be able to resolve that with a 16-bit ADC. Therefore, the true benefit of a high-resolution delta-sigma ADC is the low levels of input-referred noise it offers. It does not mean that effective resolution is unimportant – just that it is not the best way to parameterize a system.

Part 3 takes these claims one step further with a design example that uses both noise-free resolution and input-referred noise to define a system noise parameter. Which one enables the quickest, most adaptable solution? Read the article to discover the answer.

4. What Is ENBW and Why Is It Important?

In general signal-processing terms, a filter’s effective noise bandwidth (ENBW) is the cutoff frequency, f_C, of an ideal brick-wall filter whose noise power is approximately equivalent to the noise power of the original filter, H(f).

As an analogy, consider your home on a cold night. To reduce energy costs and save money, you need to keep your doors and windows closed as much as possible in order to limit the amount of cold air coming in. In this case, your home is the system, your doors and windows are the filter, the cold air is noise, and the ENBW is a measurement of how open (or closed) your doors and windows are. The larger the gap (ENBW), the more cold air (noise) gets into your home (system) and vice versa, as shown in Figure 3.

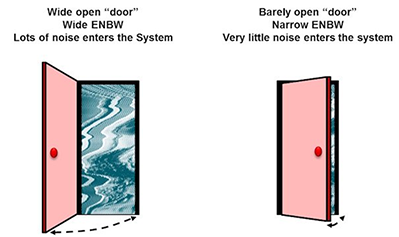Figure 3 Wide ENBW Leads to More Noise (Left); Narrow ENBW Leads to Less Noise (Right)

What system components contribute to ENBW? Read part 4 to learn more.

5. How do you calculate the noise bandwidth of your system?

If your signal chain has multiple filter components, you must calculate the ENBW for each component by combining all downstream filters in the signal chain. To combine filters, plot them as magnitude (in decibels) vs. frequency and add them point by point.

For example, to calculate the noise contribution of the amplifier in Figure 4, you would have to combine the amplifier’s bandwidth with the anti-aliasing filter, the ADC’s digital filter and any post-processing filters. You could ignore the electromagnetic interference (EMI) filter in this case since it is upstream relative to the amplifier.

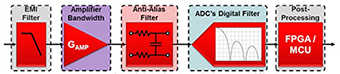Figure 4 Typical Signal Chain Showing Multiple Sources of Filtering

Since this can be complicated, read part 5 to learn ENBW approximation methods to simplify your analysis.

6. If You Add an External Amplifier to the Input of an ADC, How Does This Affect System Noise Performance?

You can make your noise analysis easier by separating both the ADC and amplifier from their respective noise sources. In this case, you can model your system as a noiseless amplifier and noiseless ADC preceded by a voltage source equal to the input-referred noise of both, as in Figure 5.

Figure 5 “Noiseless” ADC and Amplifier Preceded by Total Noise, Referred-to-input

Unfortunately, the measured output noise must refer back to the input, since input-referred noise is the specification used in most ADC data sheets. Assuming that the amplifier and ADC noise are uncorrelated, take the root-sum-square (RSS) of both values to determine the total output-referred noise. You also need to scale the amplifier noise by the amplifier’s gain, G_AMP. Equation 1 shows the resulting output-referred noise:

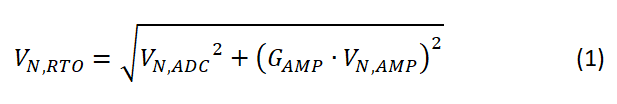
How do you translate this to input-referred noise? And what are the ramifications of the gain scaling factor, G_AMP? Read part 6 to find out.

7. Is There Such a Thing as Too Much Gain?

In the seventh series installment, I looked at an example that added multiple external amplifiers to the input of the ADS1261 and measured the resulting noise performance. I then compared these combinations to the ADS1261’s baseline noise performance using its integrated programmable gain amplifier. To make the comparison easier, I plotted the noise at different gain settings for each combination, which offers several insights about how adding external amplifiers to precision ADCs affects performance, as well as how performance changes with gain. Figure 6 depicts the plot.

Figure 6 Comparing Noise Performance of Different Amplifiers plus the ADS1261 as a Function of Gain

What are the key takeaways from this example and the plot in Figure 6? Read part 7, “The Effects of Amplifier Noise on Delta-Sigma ADCs,” to learn more.

8. How Do You Calculate the Amount of Reference Noise Passing into Your System?

One of the most interesting characteristics of reference noise is that it changes linearly with how much of the ADC’s FSR that you use. If you have a very small input signal, you won’t see much reference noise – and can potentially use a noisier reference as a result. Or if your input signals are greater than mid-scale, you can expect the reference noise to dominate. In this case, always make sure that the ADC noise and reference noise are comparable. Figure 7 qualitatively plots reference noise, ADC noise and total noise as a function of FSR utilization.

Figure 7 Reference Noise, ADC Noise and Total Noise as a Function of FSR Utilization

What do the key points – A, B and C – on this plot represent? And how does changing your input signal vs. changing your system gain affect reference noise? Find the answers to these questions in part 8.

9. How Can You Reduce the Amount of Reference Noise Passing into Your System?

One common way to reduce the amount of reference noise passed into the system is to limit the system’s overall ENBW. This can be achieved by slowing down the ADC’s output data rate. Figure 8 shows how reducing the ADC’s output data rate decreases both ADC noise and reference noise simultaneously. For example, between ENBW = 0.6 Hz (left) and ENBW = 96 Hz (right), the reference noise at 100% utilization decreases by a factor of 2.3, while the ADC noise decreases by a factor of 10, resulting in far less total noise.

Figure 8 Limiting ENBW Reduces Total Noise: 0.6 Hz (Left), 24 Hz (Middle), 96 Hz (Right)

Read part 9 to learn about how your reference configuration can also reduce the amount of reference noise passing into your system.

10. Can Clocks Affect Your ADC's Noise Performance?

Although you may expect an ADC’s sampling period to be perfectly constant, there is always some deviation from the ideal. “Clock jitter” refers to the variation in a clock waveform’s edges from one period to the next. Since all ADCs use a clock edge to control the sampling point, clock-edge variation creates deviations in the sampling instance. This deviation results in a non-constant sampling frequency that appears in the conversion result as another source of noise. Figure 9 shows the sampling-edge variation caused by clock jitter on a sinusoidal input signal.

Figure 9 Clock Signal Showing Sampling-edge Variation Caused by Jitter

To learn how clocks cause additional errors, as well as ways to reduce system noise due to clocking, read part 10.

While these are some of the most important questions answered in the “Resolving the Signal” series, I covered many more topics and examples to help you get the best noise performance out of your high-resolution, delta-sigma ADC signal chain. Read the series to learn more, and if you have any additional questions, feel free to post them in the comments below.