-
Power Tips: How to Select Ceramic Capacitors to Meet Ripple- Current Requirements
Power Tips: How to Select Ceramic Capacitors to Meet Ripple- Current Requirements
Manjing Xie
Ceramic capacitors are well-suited to manage ripple current because they can filter large currents generated by switched-mode power supplies. It is common to use ceramic capacitors of different sizes and values in parallel to achieve the optimum result. In such a case, each capacitor should meet its allowable ripple-current rating.
In this post, I’ll use a buck converter as an example to demonstrate how to select ceramic capacitors to meet ripple-current requirements. (Note that bulk capacitors such as aluminum electrolytic or tantalum capacitors have high equivalent-series-resistance (ESR). When put in parallel to ceramic capacitors, these bulk capacitors are not designed to take a large ripple current. Thus, I won’t discuss them here.)
Figure 1 shows a basic circuit of a buck converter. The converter input current, iIN_D, consists of a large ripple current, ΔiIN_D.
 Figure 1 The Basic Circuit of a Buck
Converter
Figure 1 The Basic Circuit of a Buck
ConverterThe buck converter parameters are:
- Input voltage (VIN) = 12V.
- Allowable input ripple voltage (ΔVIN) < 0.36V.
- Output voltage (VO) = 1.2V.
- Output current (IO) = 12A.
- Inductor peak-to-peak ripple current (ΔIpp) = 3.625A.
- Switching frequency (FSW) = 600KHz.
- Temperature-rise limit of the ceramic capacitors < 10°C.
Figure 2 shows the input ripple-current waveform.
 Figure 2 Input Ripple-current
Waveform
Figure 2 Input Ripple-current
WaveformTo meet the ripple-voltage requirement, the effective capacitance of the ceramic capacitor should be greater than that calculated with Equation 1:
With the converter parameters and requirements, Cce_total should be greater than 5µF.
The selected ceramic capacitors must also meet the ripple-current limitation. Equation 2 calculates the root-mean-square (RMS) value of the ripple current:
Given that IO = 12A, ΔIpp = 3.625A and D = 10%, the RMS value of the input ripple is 3.615ARMS.
Table 1 lists the characteristics of available ceramic capacitors with the proper voltage rating. These capacitors are of 10% tolerance.

|
While one piece of Capacitor A provides sufficient effective capacitance to meet the ripple-voltage requirement, its ripple-current rating of 3.24ARMS is slightly less than that generated by the converter. While adding another piece of Capacitor A meets the requirement, it occupies more space and costs more than other smaller capacitors. The question is which capacitor or capacitors should be added. To answer that question, I conducted an analysis on ripple-current distribution. Figure 3 is a simplified schematic of two capacitors in parallel with an AC current source.
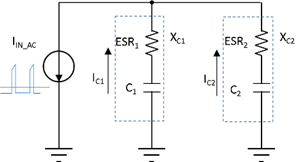 Figure 3 Schematic of Ripple-current
Distribution
Figure 3 Schematic of Ripple-current
DistributionAccording to Ohm’s law, current distribution should abide by Equation 3:
Ceramic capacitors have small ESR. Figure 4 shows two examples.
 Figure 4 Ceramic Capacitor Impedance |Z| and ESR R over Frequency
Figure 4 Ceramic Capacitor Impedance |Z| and ESR R over FrequencyFor frequencies lower than 1MHz, you can approximate the impedance of a ceramic capacitor, XC, by XC = 1/(jωC). Thus Equation 3 simplifies into Equation 4. According to Equation 4, ripple current is in proportion to the effective capacitance:
When multiple capacitors are in parallel, the capacitor with the lowest allowable ripple current over effective-capacitance ratio, IRMS-over-C, will hit the ripple-current rating first. Assuming that C1 has lower IRMS-over-C than C2, Equation 5 estimates the total allowable ripple current, I∑_RMS_Allow:
When C1 hits its allowable ripple-current rating, the ripple current through C2 will not exceed its allowable ripple current, as Equation 6 shows:
In order to have I∑_RMS_Allow ≥ IIN_AC_RMS, the additional capacitance should be greater than that calculated by Equation 7:
Tol. is the capacitance tolerance of these ceramic capacitors. When tolerance is included in the calculation, the worst-case ripple current of the bottleneck capacitor would not exceed its rating.
I listed the IRMS-to-C ratio as a parameter in Table 2.

|
Capacitor A has high effective capacitance at 12VDC bias. To meet the ripple-current requirement, you should add an additional capacitor or capacitors to meet ripple current requirement. Since Capacitor A has the lowest IRMS-to-C ratio, the added effective capacitance, Cadditional, should be greater than that calculated with Equation 8:
There are two options. The first option is to add one piece of Capacitor B. The second option is to add one piece of Capacitor C and two pieces of Capacitor D. Both options provide sufficient additional effective capacitance and occupy similar printed circuit board (PCB) areas. Since the latter option is more cost-effective, I chose the second option.
To verify my hypothesis, I conducted a PSPICE simulation; Figure 5 shows the circuit I used. I also used the nominal values of the capacitors for a typical case.
 Figure 5 Ripple-current Distribution Simulation Circuit
Figure 5 Ripple-current Distribution Simulation CircuitFigure 6 shows the simulation waveforms and the RMS values for the ripple currents of the capacitors, which are:
- ICA_RMS_typ = 3.13ARMS.
- ICC_RMS_typ = 0.353ARMS.
- ICD_RMS_typ = 0.081ARMS.
- VIN ripple voltage = 0.299V.
 Figure 6 Simulated Ripple-current Waveform of Each Ceramic Capacitor
Figure 6 Simulated Ripple-current Waveform of Each Ceramic CapacitorI then used capacitor values that would render a worst case for the Capacitor A, the bottleneck capacitor.
The RMS values of the ripple currents of the capacitors are:
- ICA_RMS_max = 3.206ARMS.
- ICC_RMS_min = 0.306ARMS.
- ICD_RMS_min = 0.070ARMS.
Each capacitor meets its allowable ripple-current rating.
Using ceramic capacitors of different sizes in parallel provides a compact and cost-effective way to filter large ripple current. But with different capacitances and ripple-current ratings, it is difficult to determine the total allowable ripple current. In this post, I proposed a parameter called allowable ripple current over effective-capacitance ratio, IRMS/C. IRMS/C helps you find the bottleneck capacitor for the allowable ripple current. Use the lowest IRMS/C to estimate the total allowable ripple current and to select additional capacitors. Please be aware that PCB parasitics could greatly affect circuit performance. This method provides a good estimation; however, you must verify designs empirically.
Additional Resources
- Explore more power-supply topics.
- Watch Power Tips videos to help with your design challenges
IMPORTANT NOTICE AND DISCLAIMER
TI PROVIDES TECHNICAL AND RELIABILITY DATA (INCLUDING DATASHEETS), DESIGN RESOURCES (INCLUDING REFERENCE DESIGNS), APPLICATION OR OTHER DESIGN ADVICE, WEB TOOLS, SAFETY INFORMATION, AND OTHER RESOURCES “AS IS” AND WITH ALL FAULTS, AND DISCLAIMS ALL WARRANTIES, EXPRESS AND IMPLIED, INCLUDING WITHOUT LIMITATION ANY IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE OR NON-INFRINGEMENT OF THIRD PARTY INTELLECTUAL PROPERTY RIGHTS.
These resources are intended for skilled developers designing with TI products. You are solely responsible for (1) selecting the appropriate TI products for your application, (2) designing, validating and testing your application, and (3) ensuring your application meets applicable standards, and any other safety, security, or other requirements. These resources are subject to change without notice. TI grants you permission to use these resources only for development of an application that uses the TI products described in the resource. Other reproduction and display of these resources is prohibited. No license is granted to any other TI intellectual property right or to any third party intellectual property right. TI disclaims responsibility for, and you will fully indemnify TI and its representatives against, any claims, damages, costs, losses, and liabilities arising out of your use of these resources.
TI’s products are provided subject to TI’s Terms of Sale (www.ti.com/legal/termsofsale.html) or other applicable terms available either on ti.com or provided in conjunction with such TI products. TI’s provision of these resources does not expand or otherwise alter TI’s applicable warranties or warranty disclaimers for TI products.
Mailing Address: Texas Instruments, Post Office Box 655303, Dallas, Texas 75265
Copyright © 2023, Texas Instruments Incorporated