TIDUES0E June 2019 – April 2024 TMS320F28P550SJ , TMS320F28P559SJ-Q1
- 1
- Description
- Resources
- Features
- Applications
- 6
- 1System Description
- 2System Overview
- 3Circuit Description
- 4Hardware, Software, Testing Requirements, and Test Results
- 5Design Files
- 6Related Documentation
- 7Terminology
- 8About the Author
- 9Revision History
2.3.4.5 Capacitor Selection
The output capacitor in the dual-active bridge must be designed to handle the ripple. Figure 2-19 illustrates that the capacitor current is the difference between the current IHB2 and the output current ILoad, also called Iout as shown in Equation 17. The waveforms are also shown in Figure 2-20. IHB2 is the rectified and scaled inductor current. The best output current Iout is obtained by Pout / V2. From the difference between Iout and IHB2 the charge ΔQ (marked in blue) can be obtained. Afterwards, the required capacitance can be calculated using Equation 18 for a maximum allowed ripple voltage.
Since the current waveforms depend on input-to-output voltage ratio and phase shift, this analysis needs to be done for all corner cases.
A MATLAB® script is used to obtain ΔQ for different input-to-output voltage ratios. The script first interpolates the ideal capacitor current waveform shown in Figure 2-20 and subtracts Iout. The resulting waveform is the capacitor current IC,out. Next, the integral of IC,out is calculated. Subtracting min(∫IC,out) of max(∫IC,out) provides ΔQ. This results in ΔQ of 12 µC for 10-kW output power and nominal input and output voltages. For lower output voltages, ΔQ increases to 50 µC. Using Equation 18 and a voltage ripple of 5 V leads to a required output capacitance of 10 µF. These are the best values assuming no parasitics in the capacitors. In the current design Aluminum Electrolytic Capacitors with relatively high ESR are used. Therefore 470 µF of output capacitance is necessary to reduce the ripple to 5%. In the next design revision, the design is changed to film-capacitors, with much lower ESR which allows a significant reduction in output capacitance.
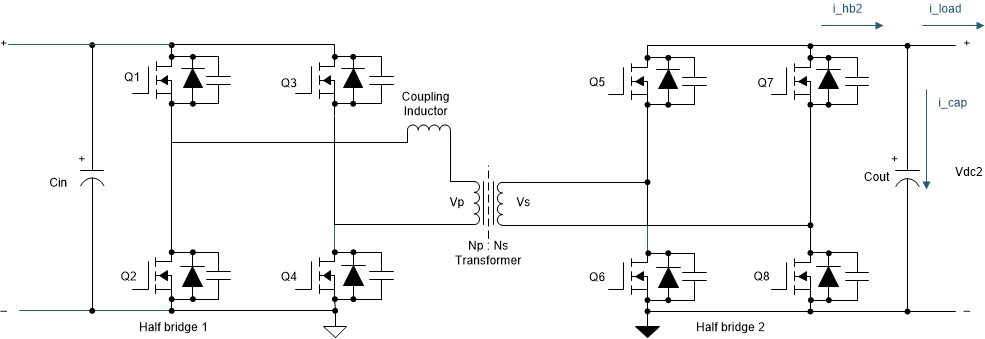 Figure 2-19 Output Current in Dual-Active
Bridge
Figure 2-19 Output Current in Dual-Active
Bridge Figure 2-20 Output Capacitor
Current
Figure 2-20 Output Capacitor
CurrentThe capacitor also needs to be able to handle the RMS current, which is calculated with Equation 19.
where