SLOS930C November   2015  – October 2024 THS4541-Q1

PRODUCTION DATA  

  1.   1
  2. 1 Features
  3. 2 Applications
  4. 3 Description
  5. 4 Device Comparison Table
  6. 5 Pin Configuration and Functions
  7. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Thermal Information
    5. 6.5 Electrical Characteristics: (Vs+) – Vs– = 5 V
    6. 6.6 Electrical Characteristics: (Vs+) – Vs– = 3 V
    7. 6.7 Typical Characteristics: 5-V Single Supply
    8. 6.8 Typical Characteristics: 3-V Single Supply
    9. 6.9 Typical Characteristics: 3-V to 5-V Supply Range
  8. 7 Parameter Measurement Information
    1. 7.1 Example Characterization Circuits
    2. 7.2 Frequency-Response Shape Factors
    3. 7.3 I/O Headroom Considerations
    4. 7.4 Output DC Error and Drift Calculations and the Effect of Resistor Imbalances
    5. 7.5 Noise Analysis
    6. 7.6 Factors Influencing Harmonic Distortion
    7. 7.7 Driving Capacitive Loads
    8. 7.8 Thermal Analysis
  9. 8 Detailed Description
    1. 8.1 Overview
      1. 8.1.1 Terminology and Application Assumptions
    2. 8.2 Functional Block Diagram
    3. 8.3 Feature Description
      1. 8.3.1 Differential I/O
      2. 8.3.2 Power-Down Control Pin ( PD)
        1. 8.3.2.1 Operating the Power Shutdown Feature
      3. 8.3.3 Input Overdrive Operation
    4. 8.4 Device Functional Modes
      1. 8.4.1 Operation from Single-Ended Sources to Differential Outputs
        1. 8.4.1.1 AC-Coupled Signal Path Considerations for Single-Ended Input to Differential Output Conversion
        2. 8.4.1.2 DC-Coupled Input Signal Path Considerations for Single-Ended to Differential Conversion
        3. 8.4.1.3 Resistor Design Equations for the Single-Ended to Differential Configuration of the FDA
        4. 8.4.1.4 Input Impedance for the Single-Ended to Differential FDA Configuration
      2. 8.4.2 Differential-Input to Differential-Output Operation
        1. 8.4.2.1 AC-Coupled, Differential-Input to Differential-Output Design Issues
        2. 8.4.2.2 DC-Coupled, Differential-Input to Differential-Output Design Issues
  10. 9 Application and Implementation
    1. 9.1 Application Information
    2. 9.2 Typical Applications
      1. 9.2.1 Designing Attenuators
        1. 9.2.1.1 Design Requirements
        2. 9.2.1.2 Detailed Design Procedure
        3. 9.2.1.3 Application Curve
      2. 9.2.2 Interfacing to High-Performance ADCs
        1. 9.2.2.1 Design Requirements
        2. 9.2.2.2 Detailed Design Procedure
        3. 9.2.2.3 Application Curve
    3. 9.3 Power Supply Recommendations
    4. 9.4 Layout
      1. 9.4.1 Layout Guidelines
      2. 9.4.2 Layout Example
  11. 10Device and Documentation Support
    1. 10.1 Device Support
      1. 10.1.1 Development Support
        1. 10.1.1.1 TINA Simulation Model Features
    2. 10.2 Documentation Support
      1. 10.2.1 Related Documentation
    3. 10.3 Receiving Notification of Documentation Updates
    4. 10.4 Support Resources
    5. 10.5 Trademarks
    6. 10.6 Electrostatic Discharge Caution
    7. 10.7 Glossary
  12. 11Revision History
  13. 12Mechanical, Packaging, and Orderable Information

Package Options

Refer to the PDF data sheet for device specific package drawings

Mechanical Data (Package|Pins)
  • RGT|16
Thermal pad, mechanical data (Package|Pins)
Orderable Information

8.4.1.3 Resistor Design Equations for the Single-Ended to Differential Configuration of the FDA

The design equations for setting the resistors around an FDA to convert from a single-ended input signal to differential output can be approached from several directions. Here, several critical assumptions are made to simplify the results:

  • The feedback resistors are selected first and set equal on the two sides.
  • The dc and ac impedances from the summing junctions back to the signal source and ground (or a bias voltage on the nonsignal input side) are set equal to retain feedback divider balance on each side of the FDA

Both of these assumptions are typical and aimed to delivering the best dynamic range through the FDA signal path.

After the feedback resistor values are chosen, the aim is to solve for the Rt (a termination resistor to ground on the signal input side), Rg1 (the input gain resistor for the signal path), and Rg2 (the matching gain resistor on the nonsignal input side); see Figure 7-1 and Figure 7-3. The same resistor solutions can be applied to either ac- or dc-coupled paths. Adding blocking capacitors in the input-signal chain is a simple option. Adding these blocking capacitors after the Rt element (as shown in Figure 7-1) has the advantage of removing any dc currents in the feedback path from the output Vocm to ground.

Earlier approaches to the solutions for Rt and Rg1 (when the input must be matched to a source impedance, Rs) follow an iterative approach. This complexity arises from the active input impedance at the Rg1 input. When the FDA is used to convert a single-ended signal to differential, the common-mode input voltage at the FDA inputs must move with the input signal to generate the inverted output signal as a current in the Rg2 element. A more recent solution is shown as Equation 7, where a quadratic in Rt can be solved for an exact required value. This quadratic emerges from the simultaneous solution for a matched input impedance and target gain. The only inputs required are:

  1. The selected Rf value.
  2. The target voltage gain (Av) from the input of Rt to the differential output voltage.
  3. The desired input impedance at the junction of Rt and Rg1 to match Rs.

Solving this quadratic for Rt starts the solution sequence, as shown in Equation 7.

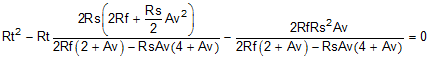
Equation 7. THS4541-Q1

Being a quadratic, there are limits to the range of solutions. Specifically, after Rf and Rs are chosen, there is physically a maximum gain beyond which Equation 7 starts to solve for negative Rt values (if input matching is a requirement). With Rf selected, use Equation 8 to verify that the maximum gain is greater than the desired gain.

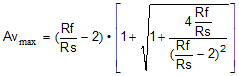
Equation 8. THS4541-Q1

If the achievable Avmax is less than desired, increase the Rf value. After Rt is derived from Equation 7, the Rg1 element is given by Equation 9:

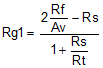
Equation 9. THS4541-Q1

Then, the simplest approach is to use a single Rg2 = Rt || Rs + Rg1 on the nonsignal input side. Often, this approach is shown as the separate Rg1 and Rs elements. Using these separate elements provides a better divider match on the two feedback paths, but a single Rg2 is often acceptable. A direct solution for Rg2 is given as Equation 10:

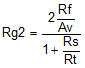
Equation 10. THS4541-Q1

This design proceeds from a target input impedance matched to Rs, signal gain Av from the matched input to the differential output voltage, and a selected Rf value. The nominal Rf value chosen for the THS4541-Q1 characterization is 402 Ω. As discussed previously, going lower improves noise and phase margin, but reduces the total output load impedance possibly degrading harmonic distortion. Going higher increases the output noise, and can reduce the loop-phase margin because of the feedback pole to the input capacitance, but reduces the total loading on the outputs. Using Equation 8 to Equation 10 to sweep the target gain from 1 to Avmax < 14.3 V/V gives Table 8-1, which shows exact values for Rt, Rg1, and Rg2, where a 50-Ω source must be matched while setting the two feedback resistors to 402 Ω. One possible solution for 1% standard values is shown, and the resulting actual input impedance and gain with % errors to the targets are also shown in Table 8-1.

Table 8-1 Required Resistors for a Single-Ended to Differential FDA Design Stepping Gain From
1 V/V to 14 V/V
Av(1) Rt, EXACT (Ω) Rt 1% Rg1, EXACT (Ω) Rg1 1% Rg2, EXACT (Ω) Rg2 1% ACTUAL ZIN %ERR TO Rs ACTUAL GAIN %ERR TO Av
1 55.2 54.9 395 392 421 422 49.731 –0.54% 1.006 0.62%
2 60.1 60.4 193 191 220 221 50.171 0.34% 2.014 0.72%
3 65.6 64.9 123 124 151 150 49.572 –0.86% 2.983 –0.57%
4 72.0 71.5 88.9 88.7 118 118 49.704 –0.59% 4.005 0.14%
5 79.7 80.6 68.4 68.1 99.2 100 50.451 0.90% 5.014 0.28%
6 89.1 88.7 53.7 53.6 85.7 86.6 49.909 –0.18% 6.008 0.14%
7 101 102 43.5 43.2 77.1 76.8 50.179 0.36% 7.029 0.42%
8 117 118 35.5 35.7 70.6 69.8 50.246 0.49% 7.974 –0.32%
9 138 137 28.8 28.7 65.4 64.9 49.605 –0.79% 9.016 0.18%
10 170 169 23.5 23.7 62.0 61.9 50.009 0.02% 9.961 –0.39%
11 220 221 18.8 18.7 59.6 59.0 49.815 –0.37% 11.024 0.22%
12 313 316 14.7 14.7 57.9 57.6 50.051 0.10% 11.995 –0.04%
13 545 549 10.9 11.0 56.7 56.2 49.926 –0.15% 12.967 –0.25%
14 2209 2210 7.26 7.32 56.2 56.2 50.079 0.16% 13.986 –0.10%
(1) Rf = 402 Ω, Rs = 50 Ω, and AvMAX = 14.32 V/V.

These equations and design flow apply to any FDA. Using the feedback resistor value as a starting point is particularly useful for current-feedback-based FDAs such as the LMH6554, where the value of these feedback resistors determines the frequency response flatness. Similar tables can be built using the equations provided here for other source impedances, Rf values, and gain ranges.

Note the extremely low Rg1 values at the higher gains. For instance, at a gain of 14 V/V, that 7.32-Ω standard value is transformed by the action of the common-mode loop moving the input common-mode voltage to appear like a 50-Ω input match. This active input impedance provides an improved input-referred noise at higher gains; see also Section 7.5. The TINA model correctly shows this actively-set input impedance in the single-ended to differential configuration, and is a good tool to validate the gains, input impedances, response shapes, and noise issues.