SLVS658C March   2006  – January 2016 TPS65811

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
  4. 4 Revision History
  5. 5 Description (continued)
  6. 6 Pin Configuration and Functions
  7. 7 Specifications
    1. 7.1  Absolute Maximum Ratings
    2. 7.2  ESD Ratings
    3. 7.3  Recommended Operating Conditions
    4. 7.4  Thermal Information
    5. 7.5  Electrical Characteristics - System Sequencing and Operating Modes
    6. 7.6  Electrical Characteristics - Power Path and Charge Management
    7. 7.7  Electrical Characteristics - Power Path and Charge Management (Continued)
    8. 7.8  Electrical Characteristics - Power Path and Charge Management (Continued)
    9. 7.9  Electrical Characteristics - Linear Regulators
    10. 7.10 Electrical Characteristics - Switched-Mode SM1 Step-Down Converter
    11. 7.11 Electrical Characteristics - Switched-Mode SM2 Step-Down Converter
    12. 7.12 Electrical Characteristics - GPIOs
    13. 7.13 Electrical Characteristics - ADC
    14. 7.14 Electrical Characteristics - LED and PWM Drivers
    15. 7.15 Electrical Characteristics - I2C Interface
    16. 7.16 Timing Requirements - I2C Interface
    17. 7.17 Trigger Timing Characteristics
    18. 7.18 Dissipation Ratings
    19. 7.19 Typical Characteristics
      1. 7.19.1 Power Path Management
      2. 7.19.2 Linear Regulators 0, 1, 2
      3. 7.19.3 Linear Regulators 3, 4, 5
      4. 7.19.4 SM1 and SM2 Buck Converters
  8. 8 Detailed Description
    1. 8.1 Overview
    2. 8.2 Functional Block Diagram
    3. 8.3 Feature Description
      1. 8.3.1 Interrupt Controller and System Sequencing
        1. 8.3.1.1 Overview
        2. 8.3.1.2 Interrupt Controller
        3. 8.3.1.3 System Sequencing and TPS65810 Operating Modes
          1. 8.3.1.3.1 Power Up
          2. 8.3.1.3.2 Enable
          3. 8.3.1.3.3 Sequencing
          4. 8.3.1.3.4 Reset
          5. 8.3.1.3.5 Power-Good Check
          6. 8.3.1.3.6 Sleep Mode
          7. 8.3.1.3.7 Normal Mode
          8. 8.3.1.3.8 Processor Standby State
        4. 8.3.1.4 TPS65810 Operating Mode Controls
        5. 8.3.1.5 Functionality Reference Guide - Host Interface and System Sequencing
      2. 8.3.2 Power Path and Charge Management
        1. 8.3.2.1 Overview
        2. 8.3.2.2 Power Path Management Function
          1. 8.3.2.2.1  Detecting the System Status
          2. 8.3.2.2.2  Power Path Logic: Priority Algorithm
          3. 8.3.2.2.3  Input Current Limit
          4. 8.3.2.2.4  System Voltage Regulation
          5. 8.3.2.2.5  Input Overvoltage Detection
          6. 8.3.2.2.6  Output Short-Circuit Detection
          7. 8.3.2.2.7  Battery Short-Circuit Detection
          8. 8.3.2.2.8  Initial Power Path Operation
          9. 8.3.2.2.9  No-Battery Detection Circuit
          10. 8.3.2.2.10 Using the Input Power to Run the System and Charge the Battery Pack
        3. 8.3.2.3 Battery Charge Management Function
          1. 8.3.2.3.1  Operating Modes
          2. 8.3.2.3.2  Battery Preconditioning
          3. 8.3.2.3.3  Constant Current Charging
          4. 8.3.2.3.4  Charge Termination and Recharge
          5. 8.3.2.3.5  Battery Voltage Regulation, Charge Voltage
          6. 8.3.2.3.6  Temperature Qualification
          7. 8.3.2.3.7  Dynamic Power Path Management
          8. 8.3.2.3.8  Charger Off Mode
          9. 8.3.2.3.9  Precharge Safety Timer
          10. 8.3.2.3.10 Charge Safety Timer
          11. 8.3.2.3.11 Timer Fault Recovery
          12. 8.3.2.3.12 Dynamic Timer Function
        4. 8.3.2.4 Functionality Guide — System Power and Charge Management
      3. 8.3.3 Linear Regulators
        1. 8.3.3.1 Simplified Block Diagram
        2. 8.3.3.2 Connecting the LDO Input Supply
        3. 8.3.3.3 ON/OFF Control
        4. 8.3.3.4 Output Discharge Switch
        5. 8.3.3.5 Special Functions
        6. 8.3.3.6 Output Voltage Monitoring
        7. 8.3.3.7 Functionality Guide — Linear Regulators
      4. 8.3.4 Step-Down Switched-Mode Converters: SM1 and SM2
        1. 8.3.4.1 Output Voltage Slew Rate
        2. 8.3.4.2 Soft-Start
        3. 8.3.4.3 Dropout Operation at 100% Duty Cycle
        4. 8.3.4.4 Output Voltage Monitoring
        5. 8.3.4.5 Stand-by Mode
        6. 8.3.4.6 PWM Operation
        7. 8.3.4.7 Phase Control in PWM Mode
        8. 8.3.4.8 PFM Mode Operation
        9. 8.3.4.9 Functionality Guide — Switched-Mode Step-Down Converters
      5. 8.3.5 Analog-to-Digital Converter
        1. 8.3.5.1 Overview
        2. 8.3.5.2 Input Channels
        3. 8.3.5.3 Functional Overview
          1. 8.3.5.3.1 ADC Conversion Cycle
          2. 8.3.5.3.2 External Trigger Operation
          3. 8.3.5.3.3 Detecting an External Trigger Event
          4. 8.3.5.3.4 Executing Multiple-Sample Cycles With an External Trigger
          5. 8.3.5.3.5 Continuous Conversion Operation (Repeat Mode)
          6. 8.3.5.3.6 ADC Input Signal Range Setting
          7. 8.3.5.3.7 ADC State Machine
        4. 8.3.5.4 Battery Detection Circuit
        5. 8.3.5.5 Functionality Guide - Analog to Digital Converter
      6. 8.3.6 LED and Peripheral Drivers
        1. 8.3.6.1 White LED Constant Current Driver
          1. 8.3.6.1.1 SM3 Control Logic Overview
          2. 8.3.6.1.2 Peak Current Control (Boost Converter)
          3. 8.3.6.1.3 Soft-Start
          4. 8.3.6.1.4 Enabling the SM3 Converter
          5. 8.3.6.1.5 Overvoltage Protection
          6. 8.3.6.1.6 Under Voltage Lockout Operation
          7. 8.3.6.1.7 Thermal Shutdown Operation
        2. 8.3.6.2 PWM Drivers
          1. 8.3.6.2.1 PWM Pin Driver
          2. 8.3.6.2.2 LED_PWM Pin Driver
          3. 8.3.6.2.3 RGB Driver
        3. 8.3.6.3 Functionality Guide — LED And Peripheral Drivers
      7. 8.3.7 General-Purpose I/Os — GPIO 1, 2, 3
        1. 8.3.7.1 GPIOs Input Level Configuration
        2. 8.3.7.2 Function Implementation: I2C Commands Versus GPIO Commands
          1. 8.3.7.2.1 GPIO Configuration Table
        3. 8.3.7.3 Functionality Guide - General-Purpose Inputs and Outputs
    4. 8.4 Device Functional Modes
      1. 8.4.1 Sleep Mode
      2. 8.4.2 Normal Mode
    5. 8.5 Programming
      1. 8.5.1 Serial Interface
        1. 8.5.1.1  Overview
        2. 8.5.1.2  Register Default Values
        3. 8.5.1.3  I2C Address
        4. 8.5.1.4  Incremental Read
        5. 8.5.1.5  I2C Bus Release
        6. 8.5.1.6  Sleep Mode Operation
        7. 8.5.1.7  I2C Communication Protocol
        8. 8.5.1.8  I2C Read and Write Operations
        9. 8.5.1.9  Valid Write Sequences
        10. 8.5.1.10 One-Byte Write
        11. 8.5.1.11 Valid Read Sequences
        12. 8.5.1.12 Non-Valid Sequences
    6. 8.6 Register Maps
      1. 8.6.1 Sequencing and Operating Modes - I2C Registers
      2. 8.6.2 System Status — I2C Registers
      3. 8.6.3 Interrupt Controller - I2C Registers
      4. 8.6.4 Charge and System Power Management — I2C Registers
      5. 8.6.5 Linear Regulators — I2C Registers
      6. 8.6.6 Switched-Mode Step-Down Converters — I2C Registers
      7. 8.6.7 ADC - I2C Registers
      8. 8.6.8 White LED, PWM Drivers — I2C Registers
      9. 8.6.9 GPIOs — I2C Registers
  9. 9 Application and Implementation
    1. 9.1 Application Information
    2. 9.2 Typical Applications
      1. 9.2.1 SM1, SM2 Converter Design Example
        1. 9.2.1.1 Design Requirements
        2. 9.2.1.2 Detailed Design Procedure
          1. 9.2.1.2.1 Inductor and Capacitor Selection — Converters SM1 and SM2
          2. 9.2.1.2.2 Output Capacitor Selection, SM1, SM2 Converters
          3. 9.2.1.2.3 Input Capacitor Selection, SM1, SM2 Converters
          4. 9.2.1.2.4 Output Voltage Selection, SM1, SM2 Converters
        3. 9.2.1.3 Application Curves
      2. 9.2.2 Charger Design Example
        1. 9.2.2.1 Design Requirements
        2. 9.2.2.2 Detailed Design Procedure
          1. 9.2.2.2.1 Program the Fast Charge Current Level:
          2. 9.2.2.2.2 Program the DPPM_OUT Voltage Level
          3. 9.2.2.2.3 Program the BAT Short Circuit Delay
          4. 9.2.2.2.4 Program the 5-Hour Safety Timer
  10. 10Power Supply Recommendations
  11. 11Layout
    1. 11.1 Layout Guidelines
    2. 11.2 Layout Example
  12. 12Device and Documentation Support
    1. 12.1 Device Support
      1. 12.1.1 Third-Party Products Disclaimer
    2. 12.2 Related Documentation
    3. 12.3 Related Links
    4. 12.4 Community Resources
    5. 12.5 Trademarks
    6. 12.6 Electrostatic Discharge Caution
    7. 12.7 Glossary
  13. 13Mechanical, Packaging, and Orderable Information

Package Options

Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information

9 Application and Implementation

NOTE

Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.

9.1 Application Information

The target application for this device is a smart phone operated from a single Lithium Ion battery that can be recharged from either a USB port or an AC adaptor.

9.2 Typical Applications

9.2.1 SM1, SM2 Converter Design Example

TPS65810 TPS65811 app_dia_lvs658.gif Figure 51. TPS65810 Application Diagram, Recommended External Components

9.2.1.1 Design Requirements

Use values listed in Table 45 as the design conditions and parameters for the SM1 or SM2 converter design example.

Table 45. Design Parameter

DESIGN PARAMETER EXAMPLE VALUE
VIN_SM1/2 4.6 V typical (may be less if input source is limited)
VOUT_SM1/2 1.24 V
IO(MAX) 0.6 A
fSW 1500 kHz
fC 25 kHz

Use Equation 13 to calculate the target inductance for this design application.

Equation 13. TPS65810 TPS65811 q17_ltarge_lvs606.gif

where

  • 3.3 µH is a good target value

Use Equation 14 to calculate the target capacitance for this design application.

Equation 14. TPS65810 TPS65811 q18_c_lvs606.gif

where

  • 10 µ is a good target value

9.2.1.2 Detailed Design Procedure

9.2.1.2.1 Inductor and Capacitor Selection — Converters SM1 and SM2

SM1 and SM2 are designed with internal voltage mode compensation and the stabilization is based on the selection of an LC filter that has a corner frequency around 27 kHz. TI does not recommend using LC values that would be outside the range of 13 kHz to 40 kHz.

Use Equation 15 to calculate the corner frequency of the output LC filter for L = 3.3 µH and C = 10 µF which are the standard recommended LC values.

Equation 15. TPS65810 TPS65811 q10_f_lvs606.gif

The inductor value, along with the input voltage VIN, output voltage VOUT and switching frequency f define the ripple current. Typically the ripple current target is 30% of the full load current. At light loads it is desirable for ripple current to be less then 150% of the light load current.

The inductor must be chosen with a rating to handle the peak ripple current, if a current of an inductor gets higher than its rated saturation level (DCR), the inductance starts to fall off, and the inductor’s ripple current increases exponentially. The DCR of the inductor plays an important role in efficiency and size of the inductor. Larger diameter wire has less DCR but may increase the size of the inductor

Use Equation 16 to calculate the target inductor value. If an inductor value was already selected, use Equation 17 to calculate the ripple current of the inductor under static operating conditions. The ripple amplitude can be calculated during the ON-time (positive ramp) or during the OFF-time (negative ramp). Calculating the ripple using the off time is the easiest method because the voltage of the inductor is the output voltage.

Equation 16. TPS65810 TPS65811 q11_ltar_lvs606.gif
Equation 17. TPS65810 TPS65811 q12_delta_lvs606.gif

Use Equation 18 to calculate the peak current because of the output load and ripple current.

Equation 18. TPS65810 TPS65811 q13_ilmax_lvs606.gif

For a faster transient response, a lower inductor and higher capacitance allows the output current to ramp faster, while the addition capacitance holds up the output longer (a 2.2-μH inductor in combination with a 22-μF output capacitor are recommended).

The highest inductor current occurs at the maximum input voltage. The peak inductor current during a transient may be higher than the steady state peak current and must be considered when selecting an inductor. Monitoring the inductor current for non-saturation operation during a transient of 1.2 × ILmax at VIN_MAX ensures adequate saturation margin. Table 46 lists recommended inductors for typical operating conditions.

Table 46. Inductors for Typical Operation Conditions

DEVICE INDUCTOR VALUE TYPE COMPONENT SUPPLIER
DCDC3 converter 3.3 μH CDRH2D14NP-3R3 Sumida
3.3 μH PDS3010-332 Coilcraft
3.3 μH VLF4012AT-3R3M1R3 TDK
2.2 μH VLF4012AT-2R2M1R5 TDK
2.2 μH NR3015T2R2 Taoup-Uidem
DCDC2 converter 3.3 μH CDRH2D18/HPNP-3R3 Sumida
3.3 μH VLF4012AT-3R3M1R3 TDK
2.2 μH VLCF4020-2R2 TDK
DCDC1 converter 3.3 μH CDRH3D14/HPNP-3R2 Sumida
3.3 μH CDRH4D28C-3R2 Sumida
3.3 μH MSS5131-332 Coilcraft
2.2 μH VLCF4020-2R2 TDK

9.2.1.2.2 Output Capacitor Selection, SM1, SM2 Converters

The advanced Fast Response voltage mode control scheme of the SM1, SM2 converters implemented in the TPS65020 allow the use of small ceramic capacitors with a typical value of 10 μF for a 3.3-μH inductor, without having large output voltage under and overshoots during heavy load transients.

Ceramic capacitors having low ESR values have low output voltage ripple, and recommended values and manufacturers are listed in Table 27. Often, because of the low ESR, the ripple current rating of the ceramic capacitor is adequate to meet the inductor’s currents requirements.

Use Equation 19 to calculate the RMS ripple current.

Equation 19. TPS65810 TPS65811 q14_irms_lvs606.gif

At nominal load current, the inductive converters operate in PWM mode. The overall output voltage ripple is the sum of the voltage spike caused by the output capacitor ESR plus the voltage ripple caused by charging and discharging the output capacitor: The output voltage ripple is maximum at the highest input voltage Vin. Use Equation 20 to calculate the voltage spike caused by the output capacitor ESR (VRMSCout).

Equation 20. TPS65810 TPS65811 q15_vrms_lvs606.gif

At light load currents, the converters operate in PFM and the output voltage ripple is dependent on the output capacitor value. The output voltage ripple is set by the internal PFM output voltage comparator delay and the external capacitor. The typical output voltage ripple is less than 1% of the nominal output voltage. Table 47 lists recommend I/O capacitors for typical operating conditions.

Table 47. Input and Output Capacitors for Typical Operation Conditions

CAPACITOR VALUE CASE SIZE COMPONENT SUPPLIER COMMENTS
22 μF 1260 TDK C3216X5R0J226M Ceramic
22 μF 1260 Taiyo Yuden JMK316BJ226ML Ceramic
10 μF 0805 Taiyo Yuden JMK212BJ106M Ceramic
10 μF 0805 TDK C2012X5R0J106M Ceramic
22 μF 0805 TDK C2012X5R0J226MT Ceramic
22 μF 0805 Taiyo Yuden JMK212BJ226MG Ceramic

9.2.1.2.3 Input Capacitor Selection, SM1, SM2 Converters

Buck converters have a pulsating input current that can generate high input voltage spikes at VIN. A low ESR input capacitor is required to filter the input voltage, minimizing the interference with other circuits connected to the same power supply rail. Each DC–DC converter requires a 10-μF ceramic input capacitor on its input pin.

9.2.1.2.4 Output Voltage Selection, SM1, SM2 Converters

Typically the output voltage is programmed by the I2C. An external divider can be added to raise the output voltage, if the available I2C values do not meet the application requirements. Take care with this special option, because this external divider (gain factor) would apply to any selected I2C output voltage value for this converter.

Use Table 46 to calculate the value of R1 with R2 = 20 kΩ.

Equation 21. TPS65810 TPS65811 q16_r1_lvs606.gif

where

  • VSMxOUT is the desired output voltage and R1/R2 is the feedback divider
  • VFB is the I2C selected voltage

9.2.1.3 Application Curves

The application curves were measured with the application circuit shown in Figure 51 (unless otherwise noted).

TPS65810 TPS65811 lin_trn_lvs606.gif Figure 52. Line Transient
TPS65810 TPS65811 trns_su_lvs606.gif Figure 54. Transient - SM1 Start-Up
TPS65810 TPS65811 soft_s_dvr_lvs606.gif Figure 56. SM3 White LED Driver Soft-Start
TPS65810 TPS65811 ld_trn_lvs606.gif Figure 53. Load Transient
TPS65810 TPS65811 trns2_su_lvs606.gif Figure 55. Transient - SM2 Start-Up
TPS65810 TPS65811 cur_dcyc_lvs606.gif Figure 57. SM3 Led Current vs PWM Duty Cycle

9.2.2 Charger Design Example

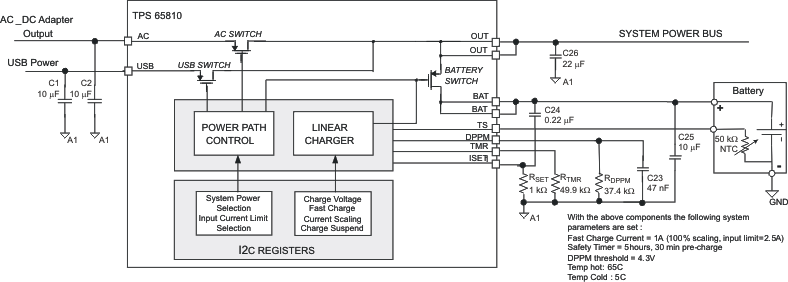TPS65810 TPS65811 ext_comp_lvs658.gif Figure 58. Required External Components, Recommended Values, External Connections

9.2.2.1 Design Requirements

Use values listed in Table 48 as the design conditions and parameters for the charger design example.

Table 48. Design Parameter

DESIGN PARAMETER EXAMPLE VALUE
V(OUT) 4.6 V; (OUT pin is input to charger)
Fast-charge current, IPGM 1 A
DPPM-OUT threshold 4.3 V; (charging current reduces when OUT falls to this level)
Safety timer 5 h
Battery short-circuit delay, tDELAY 47 μs; (delays BAT short circuit during hot plug of battery)
TS temperature range Disabled
K(SET) 400
V(SET) 2.5 V
KDPPM 1.15
IDPPM 100 μA
KTMR 0.36 s/Ω

9.2.2.2 Detailed Design Procedure

9.2.2.2.1 Program the Fast Charge Current Level:

Use Equation 22 to calculate the fast-charge current level.

Equation 22. TPS65810 TPS65811 q19_riset_lvs606.gif

9.2.2.2.2 Program the DPPM_OUT Voltage Level

Use Equation 23 to calculate the DPPM_OUT voltage level which is the level at which the charging current is reduced.

Equation 23. TPS65810 TPS65811 q20_rdppm_lvs606.gif

9.2.2.2.3 Program the BAT Short Circuit Delay

Use Equation 24 to calculate the BAT short-circuit delay which is used to insert the battery.

Equation 24. TPS65810 TPS65811 q21_cdppm_lvs606.gif

9.2.2.2.4 Program the 5-Hour Safety Timer

Use Equation 25 to calculate the value of the safety timer.

Equation 25. TPS65810 TPS65811 q22_rtmr_lvs606.gif