SNVS682D November 2010 – December 2015 LM3444
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Pin Configuration and Functions
- 6 Specifications
- 7 Detailed Description
-
8 Application and Implementation
- 8.1
Application Information
- 8.1.1 Determining Duty-Cycle (D)
- 8.1.2 Calculating Off-Time
- 8.1.3 Setting the Switching Frequency
- 8.1.4 Inductor Selection
- 8.1.5 Setting the LED Current
- 8.1.6 Valley Fill Capacitors
- 8.1.7 Determining the Capacitance Value of the Valley-Fill Capacitors
- 8.1.8 Determining Maximum Number of Series Connected LEDs Allowed
- 8.1.9 Output Capacitor
- 8.1.10 Switching MOSFET
- 8.1.11 Recirculating Diode
- 8.2 Typical Application
- 8.1
Application Information
- 9 Power Supply Recommendations
- 10Layout
- 11Device and Documentation Support
パッケージ・オプション
メカニカル・データ(パッケージ|ピン)
サーマルパッド・メカニカル・データ
発注情報
8 Application and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
8.1 Application Information
8.1.1 Determining Duty-Cycle (D)
Equation 4 shows the duty-cycle (D).
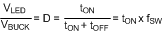
Equation 5 shows the duty-cycle with efficiency considered.
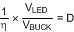
For simplicity, choose efficiency from 75% to 85%.
8.1.2 Calculating Off-Time
The off-time of the LM3444 is set by the user and remains fairly constant as long as the voltage of the LED stack remains constant. Calculating the off-time is the first step in determining the switching frequency of the converter, which is integral in determining some external component values.
PNP transistor Q3, resistor R4, and the LED string voltage define a charging current into capacitor C11. A constant current into a capacitor creates a linear charging characteristic.
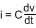
Resistor R4, capacitor C11 and the current through resistor R4 (iCOLL), which is approximately equal to VLED/R4, are all fixed. Therefore, dv is fixed and linear, and dt (tOFF) can now be calculated as shown in Equation 7.
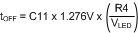
Common equations for determining duty-cycle and switching frequency in any buck converter are shown in Equation 8.
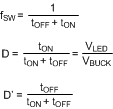
Therefore, Equation 9 shows:
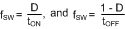
With efficiency of the buck converter in mind, Equation 10 shows:
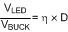
Substituting and rearranging the equations, Equation 11 shows:
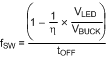
Off-time and switching frequency can now be calculated using the previous equations.
8.1.3 Setting the Switching Frequency
Selecting the switching frequency for nominal operating conditions is based on tradeoffs between efficiency (better at low frequency) and solution size and cost (smaller at high frequency).
The input voltage to the buck converter (VBUCK) changes with both line variations and over the course of each half-cycle of the input line voltage. The voltage across the LED string, however, remains constant, and therefore the off-time remains constant.
The on-time, and therefore the switching frequency, varies as the VBUCK voltage changes with line voltage. A good design practice is to choose a desired nominal switching frequency knowing that the switching frequency decreases as the line voltage drops, and increases as the line voltage increases (Figure 14).
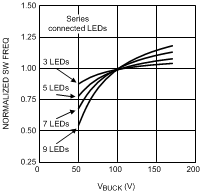 Figure 14. Graphical Illustration of Switching Frequency vs VBUCK
Figure 14. Graphical Illustration of Switching Frequency vs VBUCK
The off-time of the LM3444 can be programmed for switching frequencies ranging from 30 kHz to over 1 MHz. A trade-off between efficiency and solution size must be considered when designing the LM3444 application.
The maximum switching frequency attainable is limited only by the minimum on-time requirement (200 ns).
Worst case scenario for minimum on time is when VBUCK is at its maximum voltage (AC high line) and the LED string voltage (VLED) is at its minimum value, as shown in Equation 12.
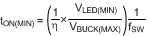
The maximum voltage seen by the Buck Converter is given by Equation 13.
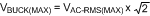
8.1.4 Inductor Selection
The controlled off-time architecture of the LM3444 regulates the average current through the inductor (L2), and therefore the LED string current. The input voltage to the buck converter (VBUCK) changes with line variations and over the course of each half-cycle of the input line voltage. The voltage across the LED string is relatively constant, and therefore the current through R4 is constant. This current sets the off-time of the converter and therefore the output volt-second product (VLED × off-time) remains constant. A constant volt-second product makes it possible to keep the ripple through the inductor constant as the voltage at VBUCK varies.
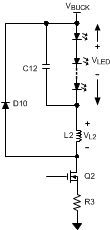 Figure 15. LM3444 External Components of the Buck Converter
Figure 15. LM3444 External Components of the Buck Converter
Use Equation 14 to calculate an ideal inductor.
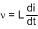
Given a fixed inductor value, L, Equation 14 states that the change in the inductor current over time is proportional to the voltage applied across the inductor.
During the on-time, the voltage applied across the inductor is given in Equation 15.
Because the voltage across the MOSFET switch (Q2) is relatively small, as is the voltage across sense resistor R3, we can approximately simplify this as shown in Equation 16,
During the off-time, the voltage seen by the inductor is given by Equation 17.
The value of VL(OFF-TIME) is relatively constant, because the LED stack voltage remains constant. If we rewrite the equation for an inductor inserting what we know about the circuit during the off-time, Equation 18 shows that we get:
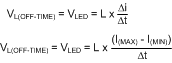
Rearranging this gives Equation 19.
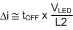
From this, we can see that the ripple current (Δi) is proportional to off-time (tOFF) multiplied by a voltage, which is dominated by VLED divided by a constant (L2).
These equations can be rearranged to calculate the desired value for inductor L2, as shown in Equation 20.
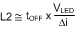
The off time can be calculated using Equation 21:
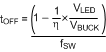
Substituting toff in Equation 21 results in Equation 22:
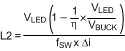
See Typical Application to better understand the design process.
8.1.5 Setting the LED Current
The LM3444 constant off-time control loop regulates the peak inductor current (IL2). The average inductor current equals the average LED current (IAVE). Therefore the average LED current is regulated by regulating the peak inductor current.
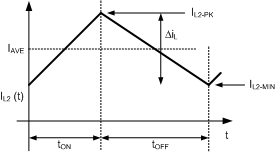 Figure 16. Inductor Current Waveform in CCM
Figure 16. Inductor Current Waveform in CCM
Knowing the desired average LED current, IAVE, and the nominal inductor current ripple, ΔiL, the peak current for an application running in continuous conduction mode (CCM) is defined in Equation 23.
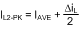
The LED current would then be calculated using Equation 24.
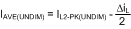
This is important to calculate because this peak current multiplied by the sense resistor R3 determines when the internal comparator is tripped. The internal comparator turns the control MOSFET off once the peak sensed voltage reaches 750 mV.
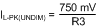
Current Limit: The trip voltage on the PWM comparator is 750 mV. However, if there is a short circuit or an excessive load on the output, higher than normal switch currents cause a voltage greater than 1.27 V on the ISNS pin which trip the I-LIM comparator. The I-LIM comparator resets the RS latch, turning off Q2. It also inhibits the Start Pulse Generator and the COFF comparator by holding the COFF pin low. A delay circuit prevents the start of another cycle for 180 µs.
8.1.6 Valley Fill Capacitors
Determining voltage rating and capacitance value of the valley-fill capacitors:
The maximum voltage seen by the valley-fill capacitors is calculated by Equation 26.
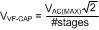
This is, of course, if the capacitors chosen have identical capacitance values and split the line voltage equally. Often a 20% difference in capacitance could be observed between like capacitors. Therefore a voltage rating margin of 25% to 50% should be considered.
8.1.7 Determining the Capacitance Value of the Valley-Fill Capacitors
The valley-fill capacitors must be sized to supply energy to the buck converter (VBUCK) when the input line is less than its peak divided by the number of stages used in the valley fill (tX). The capacitance value must be calculated for the maximum LED current.
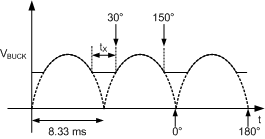 Figure 17. Two Stage Valley-Fill VBUCK Voltage
Figure 17. Two Stage Valley-Fill VBUCK Voltage
From Figure 17 and the equation for current in a capacitor, i = C × dV/dt, the amount of capacitance needed at VBUCK is calculated as follows.
At 60 Hz, and a valley-fill circuit of two stages, the hold-up time (tX) required at VBUCK is calculated as follows. The total angle of an AC half cycle is 180° and the total time of a half AC line cycle is 8.33 ms. When the angle of the AC waveform is at 30° and 150°, the voltage of the AC line is exactly ½ of its peak. With a two-stage valley-fill circuit, this is the point where the LED string switches from power being derived from AC line to power being derived from the hold up capacitors (C7 and C9). 60° out of 180° of the cycle or 1/3 of the cycle the power is derived from the hold up capacitors (1/3 × 8.33 ms = 2.78 ms). This is equal to the hold up time (dt) from the previous equation, and dv is the amount of voltage the circuit is allowed to droop. From Determining Maximum Number of Series Connected LEDs Allowed, we know the minimum VBUCK voltage is about 45 V for a
90-VAC to 135-VAC line. At 90-VAC low-line operating condition input, ½ of the peak voltage is 64 V. Thus, with some margin, the voltage at VBUCK can not droop more than about 15 V (dv). (i) is equal to (POUT/VBUCK), where POUT is equal to (VLED × ILED). Total capacitance (C7 in parallel with C9) can now be calculated. See Typical Application for further calculations of the valley-fill capacitors.
8.1.8 Determining Maximum Number of Series Connected LEDs Allowed
The LM3444 is an off-line buck topology LED driver. A buck converter topology requires that the input voltage (VBUCK) of the output circuit must be greater than the voltage of the LED stack (VLED) for proper regulation. One must determine what the minimum voltage observed by the buck converter is before the maximum number of LEDs allowed can be determined. The following two variables must be determined to accomplish this:
- AC line operating voltage. This is usually 90 VAC to 135 VAC for North America. Although the LM3444 can operate at much lower and higher input voltages, a range is needed to illustrate the design process.
- The number of stages implemented in the valley-fill circuit (1, 2, or 3).
In this example, the most common valley-fill circuit is used (two stages).
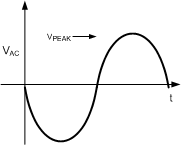 Figure 18. AC Line
Figure 18. AC Line
Figure 18 shows the AC waveform. One can easily see that the peak voltage (VPEAK) is always given by Equation 27.
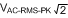
The voltage at VBUCK with a valley-fill stage of two looks similar to the waveforms in Figure 17.
The purpose of the valley-fill circuit is to allow the buck converter to pull power directly off of the AC line when the line voltage is greater than its peak voltage divided by two (two-stage valley-fill circuit). During this time, the capacitors within the valley fill circuit (C7 and C8) are charged up to the peak of the AC line voltage. Once the line drops below its peak divided by two, the two capacitors are placed in parallel and deliver power to the buck converter. One can now see that if the peak of the AC line voltage is lowered due to variations in the line voltage, the DC offset (VDC) lowers. VDC is the lowest value that voltage VBUCK encounters.
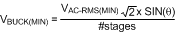
Example:
Line voltage = 90 VAC to 135 VAC
Valley-fill = two stage
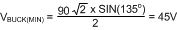
Depending on what type and value of capacitors are used, some derating should be used for voltage droop when the capacitors are delivering power to the buck converter. With this derating, the lowest voltage the buck converter sees is about 42.5 V in this example.
To determine how many LEDs can be driven, take the minimum voltage the buck converter sees (42.5 V) and divide it by the worst-case forward voltage drop of a single LED.
Example: 42.5 V / 3.7 V = 11.5 LEDs (11 LEDs with margin)
8.1.9 Output Capacitor
A capacitor placed in parallel with the LED or array of LEDs can be used to reduce the LED current ripple while keeping the same average current through both the inductor and the LED array. With a buck topology, the output inductance (L2) can now be lowered, making the magnetics smaller and less expensive. With a well designed converter, you can assume that all of the ripple is seen by the capacitor, and not the LEDs. One must ensure that the capacitor you choose can handle the RMS current of the inductor. See the manufacturer data sheets to ensure compliance. Usually an X5R or X7R capacitor from 1 µF and 10 µF of the proper voltage rating is sufficient.
8.1.10 Switching MOSFET
The main switching MOSFET should be chosen with efficiency and robustness in mind. As shown in Equation 30, the maximum voltage across the switching MOSFET equals:
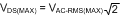
The average current rating should be greater than what is given in Equation 31.
8.1.11 Recirculating Diode
The LM3444 buck converter requires a recirculating diode D10 (see Figure 8) to carry the inductor current during the MOSFET Q2 off-time. The most efficient choice for D10 is a diode with a low forward drop and near-zero reverse recovery time that can withstand a reverse voltage of the maximum voltage seen at VBUCK. For a common 110 VAC ± 20% line, the reverse voltage could be as high as 190 V, as shown in Equation 32.
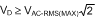
As shown in Equation 33, the current rating must be at least:
Or as shown in Equation 34:
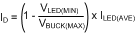
8.2 Typical Application
The following design example illustrates the process of calculating external component values.
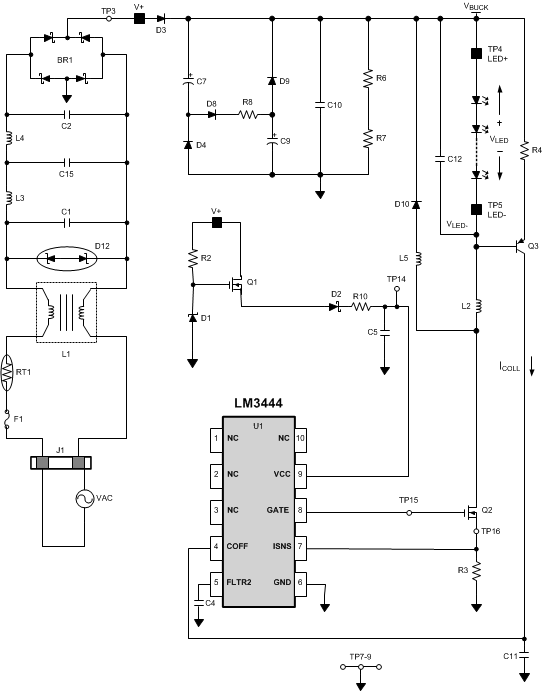 Figure 19. LM3444 Design Example 1 Input = 90 VAC to 135 VAC
Figure 19. LM3444 Design Example 1 Input = 90 VAC to 135 VAC
VLED = 7 × HB LED String Application at 400 mA
8.2.1 Design Requirements
Known:
- Input voltage range (90 VAC to 135 VAC)
- Number of LEDs in series = 7
- Forward voltage drop of a single LED = 3.6 V
- LED stack voltage = (7 × 3.6 V) = 25.2 V
Choose:
- Nominal switching frequency, fSW-TARGET = 350 kHz
- ILED(AVE) = 400 mA
- Δi (usually 15% to 30% of ILED(AVE)) = (0.30 × 400 mA) = 120 mA
- Valley-fill stages (1, 2, or 3) = 2
- Assumed minimum efficiency = 80%
8.2.2 Detailed Design Procedure
Calculate:
- Calculate minimum voltage VBUCK, as shown in Equation 35, which yields:
- Calculate maximum voltage VBUCK, as shown in Equation 36, which yields:
- Calculate tOFF at VBUCK nominal line voltage, as given by Equation 37.
- Calculate tON(MIN) at high line to ensure that tON(MIN) > 200 ns, as given by Equation 38.
- Calculate C11 and R4 in steps 6 through 9.
- Choose current through R4 (from 50 µA to 100 µA): 70 µA as given by Equation 39.
- Use a standard value of 365 kΩ.
- Calculate C11 as given by Equation 40.
- Use standard value of 120 pF.
- Calculate ripple current: 400 mA × 0.30 = 120 mA
- Calculate inductor value at tOFF = 3 µs as given by Equation 41.
- Choose C10: 1 µF, 200 V
- Calculate valley-fill capacitor values:
VAC low line = 90 VAC, VBUCK minimum equals 60 V. Set droop for 20-V maximum at full load and low line as shown in Equation 42. - i equals POUT/VBUCK (270 mA)
- dV equals 20 V
- dt equals 2.77 ms
- CTOTAL equals 37 µF
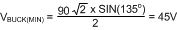
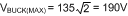
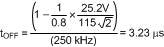
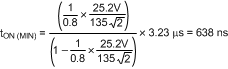
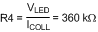
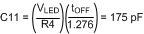
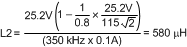
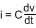
where
Therefore, C7 = C9 = 22 µF
8.2.3 Application Curve
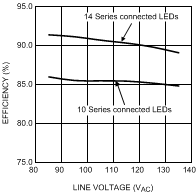 Figure 20. Efficiency vs Input Voltage
Figure 20. Efficiency vs Input Voltage