JAJS455B December   2009  – July 2017 TPS43331-Q1

PRODUCTION DATA.  

  1. 1 特長
  2. 2 アプリケーション
  3. 3 概要
  4. 4 改訂履歴
  5. 5 Pin Configuration and Functions
  6. 6 Specifications
    1. 6.1  Absolute Maximum Ratings
    2. 6.2  ESD Ratings
    3. 6.3  Recommended Operating Conditions
    4. 6.4  Thermal Information
    5. 6.5  DC Electrical Characteristics
    6. 6.6  I2C Interface Electrical Characteristics
    7. 6.7  Switching Regulators Electrical Characteristics
    8. 6.8  Standby Regulator (VSTBY) Electrical Characteristics
    9. 6.9  Linear Regulator (VLR) Electrical Characteristics
    10. 6.10 High-Side Driver (HSD) Electrical Characteristics
    11. 6.11 AC Switching Characteristics
    12. 6.12 I2C Interface Switching Characteristics
    13. 6.13 Switching Regulators Switching Characteristics
    14. 6.14 Linear Regulator Switching Characteristics
    15. 6.15 High-Side Driver (HSD) Switching Characteristics
    16. 6.16 Timing and Switching Diagrams
    17. 6.17 Typical Characteristics
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1  Unregulated Battery Input Voltage (VBAT)
      2. 7.3.2  Protected Unregulated Battery Input Voltage (VBATP)
      3. 7.3.3  Low-Voltage Warning Input (LVWIN)
      4. 7.3.4  Voltage Warning Output (VBATW)
      5. 7.3.5  Low-Voltage Reset (RST)
      6. 7.3.6  Power-Good Delay Timer Input (PGDLY)
      7. 7.3.7  Active Mode Enable Input (EN)
      8. 7.3.8  Slew Rate Control Capacitor Input (CSLEW)
      9. 7.3.9  Charge Pump Capacitor Input (VCP)
      10. 7.3.10 Power Ground (PGND)
      11. 7.3.11 Analog Ground Reference (AGND)
      12. 7.3.12 Inter-IC Communications Interface (I2CID)
      13. 7.3.13 Clock Input (SCL)
      14. 7.3.14 Data Line (SDA)
      15. 7.3.15 Interface Chip Identifier (I2CID)
      16. 7.3.16 Switch Mode Regulators
      17. 7.3.17 Upper FET Gate Drive Outputs (VGT1 and VGT2)
      18. 7.3.18 Lower FET Gate Driver Outputs (VGB1 and VGB2)
      19. 7.3.19 Bootstrap Capacitor Input (CBS1 and CBS2)
      20. 7.3.20 Phase Reference for High-Side Bootstrap Supply (PH1 and PH2)
      21. 7.3.21 Current Sense High-Side (ISHI1 and ISHI2)
      22. 7.3.22 Current Sense Low-Side (ISLO1 and ISLO2)
      23. 7.3.23 Regulated Output Sense Voltage Feedback (VFB1 and VFB2)
      24. 7.3.24 Feedback Compensation Input (VCMP1 and VCMP2)
      25. 7.3.25 Synchronization Input (SYNCH)
      26. 7.3.26 Standby Linear Regulator Input (VINSB)
      27. 7.3.27 Standby Regulator Output (VSTBY)
      28. 7.3.28 Standby Regulator Sense Voltage (VSTBYS)
      29. 7.3.29 Switched Linear Regulator Input (VINLR)
      30. 7.3.30 Switched Linear Regulator Output (VLR)
      31. 7.3.31 Switched Linear Regulator Sense Voltage (VLRS)
      32. 7.3.32 High-Side Driver Output (HSD)
    4. 7.4 Device Functional Modes
      1. 7.4.1 Operating Mode Definition
    5. 7.5 Programming
      1. 7.5.1 Register Definition for I2C
        1. 7.5.1.1 Chip Address Byte
    6. 7.6 Register Map
      1. 7.6.1 Data Register
  8. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 Typical Application
      1. 8.2.1 Design Requirements
      2. 8.2.2 Detailed Design Procedure
        1. 8.2.2.1 Type II Compensation
        2. 8.2.2.2 Type III Compensation
        3. 8.2.2.3 Component Calculations
          1. 8.2.2.3.1 Buck-Controllers (VBUCK1, VBUCK2)
        4. 8.2.2.4 Power Dissipation
        5. 8.2.2.5 Buck Regulators
          1. 8.2.2.5.1 Buck Regulator 1 (VBUCK 1)
            1. 8.2.2.5.1.1 Step 1. Calculate the Inductor Value
            2. 8.2.2.5.1.2 Step 2. Inductor Peak Current
            3. 8.2.2.5.1.3 Step 3. Calculating the Output Capacitance (CO)
            4. 8.2.2.5.1.4 Step 4. Calculating Loop Compensation Values
          2. 8.2.2.5.2 Buck Regulator 2 (VBUCK 2)
            1. 8.2.2.5.2.1 Step 5. Calculate the Inductor Value
            2. 8.2.2.5.2.2 Step 6. Inductor Peak Current
            3. 8.2.2.5.2.3 Step 7. Calculating the Output Capacitance (CO)
            4. 8.2.2.5.2.4 Step 8. Calculating Loop Compensation Values
      3. 8.2.3 Application Curves
    3. 8.3 System Example
      1. 8.3.1 Multiple Power Supply Configuration for Vehicle Audio Applications
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
      1. 10.1.1 Grounding and Circuit Layout Considerations
    2. 10.2 Layout Example
    3. 10.3 Power Dissipation Derating
  11. 11デバイスおよびドキュメントのサポート
    1. 11.1 ドキュメントのサポート
      1. 11.1.1 関連資料
    2. 11.2 ドキュメントの更新通知を受け取る方法
    3. 11.3 コミュニティ・リソース
    4. 11.4 商標
    5. 11.5 静電気放電に関する注意事項
    6. 11.6 Glossary
  12. 12メカニカル、パッケージ、および注文情報

パッケージ・オプション

メカニカル・データ（パッケージ｜ピン）
サーマルパッド・メカニカル・データ
発注情報

8 Application and Implementation

NOTE

Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.

8.1 Application Information

The TPS43331-Q1 is a combination of two switched-mode, synchronous step-down controllers and two linearly-regulated power supplies. These devices are configured to drive external NMOS power switches and control the energy in the inductor by limiting the current using a resistor current sense feedback. The output voltage is regulated using an external resistor feedback network. The regulated output voltage can be programmed to a specified range using different feedback thresholds at the VFB(x) terminal. To minimize ripple current on the input line, the two buck regulators are switched 180º out of phase.

The protected high-side output is controlled by a discrete input to switch auxiliary input power to other devices in the system. The standby regulator VSTBY is enabled when the input power from the protected terminal of the battery supply is available to the device. The standby regulator consumes less than 75 μA, with less than 100 μA of load current on the regulated output terminal (VSTBY).

8.2 Typical Application

The calculations from the Buck Regulators section result in the schematic shown in Figure 20.

The design requirements for the switching regulator design in Figure 20 are listed in Table 3.

Assume Type III Compensation network for each buck regulator.

TPS43331-Q1 cx_design_guide_lvsa38.gif Figure 20. Design Circuit Schematic

8.2.1 Design Requirements

For this design example, use the parameters listed in Table 3.

Table 3. Design Requirements

PARAMETER VALUE
Input voltage 8 V to 26 V (14 V typ)
Output voltage buck regulator 1– VBUCK 1 Min = 4.75 V, Max = 5.25 V
Output voltage buck regulator 2 – VBUCK 2 Min = 3.135 V, Max = 3.465 V
Converter switching frequency, fSW 250 kHz
Maximum output current on buck regulator 1– IO 2 A
Maximum output current on buck regulator 2 – IO 1.5 A
Maximum ripple current Iripple 0.2 × IO

8.2.2 Detailed Design Procedure

8.2.2.1 Type II Compensation

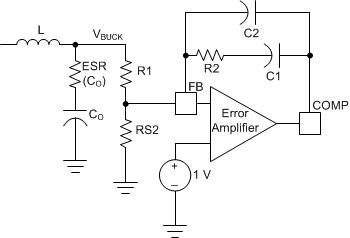
TPS43331-Q1 comp_type2_lvsa38.gif Figure 21. Type II Compensation

The LC output filter gives a Double Pole which has a –180° phase shift.

Equation 2. TPS43331-Q1 eq01_lvsa38.gif

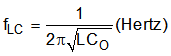
The ESR of the output capacitor, CO, gives a zero that has a 90° phase shift.

Equation 3. TPS43331-Q1 eq02_lvsa38.gif

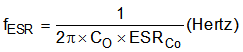
The values of R1 and RS2 are chosen based on the desired VBUCK.

Equation 4. TPS43331-Q1 eq03_lvsa38.gif

where

  • Vref = 1 V

Use the following equations to select the resistor vales:

Select RS2 = 10 kΩ

Equation 5. TPS43331-Q1 eq04_lvsa38.gif
Equation 6. TPS43331-Q1 eq05_lvsa38.gif
Equation 7. TPS43331-Q1 eq06_lvsa38.gif

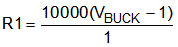
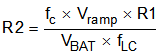
where

  • Vramp = 1.8 V, VBAT = typical input operating voltage
  • fc = fSW × 0.1 (the cutoff frequency, when the gain is 1 is called the unity gain frequency)

The fc is typically 1/5 to 1/10 of the switching frequency.

Use Equation 8 to calculate the PWM modulator gain (K).

Equation 8. TPS43331-Q1 eq07_lvsa38.gif

Use Equation 9 to calculate the amplifier gain (Av).

Equation 9. TPS43331-Q1 eq08_lvsa38.gif
Equation 10. TPS43331-Q1 eq09_lvsa38.gif
Equation 11. TPS43331-Q1 eq10_lvsa38.gif
Equation 12. TPS43331-Q1 eq11_lvsa38.gif
Equation 13. TPS43331-Q1 eq12_lvsa38.gif
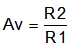
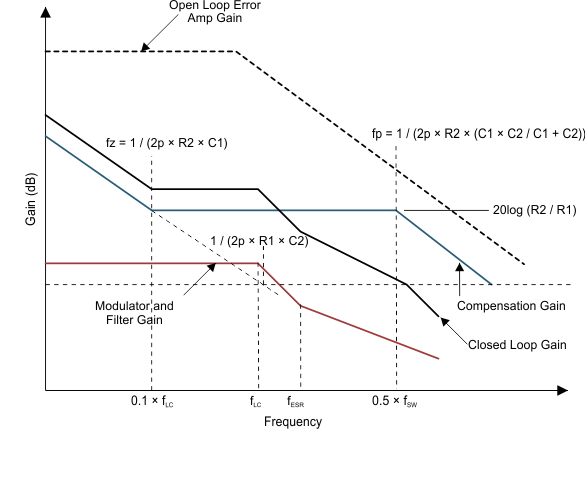TPS43331-Q1 type2_bode_plots_lvsa38.gif Figure 22. Type II Bode Plots

8.2.2.2 Type III Compensation

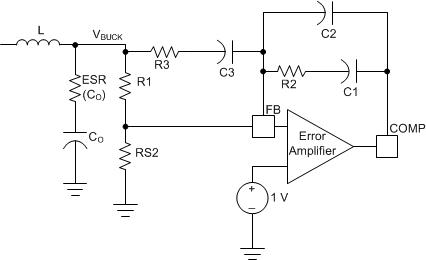TPS43331-Q1 comp_type3_lvsa38.gif Figure 23. Type III Compensation

fc = fSW × 0.1 (the cutoff frequency when the gain is 1 is called the unity gain frequency).

The fc is typically 1/5 to 1/10 of the switching frequency double pole frequency response due to the LC output filter.

The LC output filter gives a Double Pole which has a –180° phase shift.

Equation 14. TPS43331-Q1 eq13_lvsa38.gif

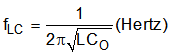
The ESR of the output capacitor, CO, gives a zero that has a 90° phase shift.

Equation 15. TPS43331-Q1 eq14_lvsa38.gif
Equation 16. TPS43331-Q1 eq15_lvsa38.gif

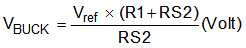
where

  • Vref = 1 V

Use Equation 17 to calculate the PWM modulator gain (K).

Equation 17. TPS43331-Q1 eq17_lvsa38.gif

where

  • Vramp = 1.8 V
  • VBAT = typical input operating voltage

Use Equation 18 to calculate the amplifier gain (Av).

Equation 18. TPS43331-Q1 eq18_lvsa38.gif
Equation 19. TPS43331-Q1 eq19_lvsa38.gif
Equation 20. TPS43331-Q1 eq20_lvsa38.gif
Equation 21. TPS43331-Q1 eq21_lvsa38.gif
Equation 22. TPS43331-Q1 eq22_lvsa38.gif

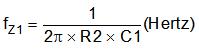
Use the following guidelines for compensation components:

Make the two zeroes close to the double pole (LC); for example, fZ1 ≈ fZ2 ≈ 1 / 2π × (LCO)1/2.

  1. Make the first zero below the filter double pole (approximately 50% to 75% of fLC).
  2. Make the second zero at filter double pole (fLC).

Make the two poles above the cross-over frequency fc.

  1. Make the first pole at the ESR frequency (fESR).
  2. Make the second pole at 0.5 the switching frequency (0.5 × fSW).

Use the following equations to select the resistor values:

Select RS2 = 10 kΩ

Equation 23. TPS43331-Q1 eq23_lvsa38.gif
Equation 24. TPS43331-Q1 eq24_lvsa38.gif
Equation 25. TPS43331-Q1 eq25_lvsa38.gif

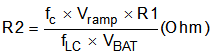
Calculate C1 based on placing a zero at 50% to 75% of the output filter double pole frequency.

Equation 26. TPS43331-Q1 eq26_lvsa38.gif

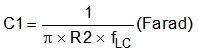
Calculate C2 by placing the first pole at the ESR zero frequency.

Equation 27. TPS43331-Q1 eq27_lvsa38.gif

Set the second pole at 0.5 the switching frequency and also set the second zero at the output filter double pole frequency.

Equation 28. TPS43331-Q1 eq28_lvsa38.gif
Equation 29. TPS43331-Q1 eq29_lvsa38.gif
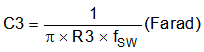
TPS43331-Q1 type3_bode_plots_lvsa38.gif Figure 24. Type III Bode Plots

8.2.2.3 Component Calculations

8.2.2.3.1 Buck-Controllers (VBUCK1, VBUCK2)

Use Equation 30 to calculate and select the desired inductor ripple current (ΔIL).

Equation 30. ΔIL= Iripple = 0.4×IO(max)

where

  • IO(max) = Maximum output current

The typical inductor ripple current is between 20% to 40% of the maximum output current.

Use Equation 31 to calculate the value of the inductor (L).

Equation 31. TPS43331-Q1 eq30_lvsa38.gif

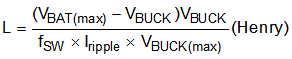
where

  • fSW is the switching frequency of the regulator
  • Iripple = Allowable ripple current in the inductor, 20% to 40% of maximum IO(max)

Use Equation 32 to calculate the value of the the rms and peak current flowing in the inductor is.

Equation 32. TPS43331-Q1 eq31_lvsa38.gif

Use Equation 33 to calculate the inductor peak current.

Equation 33. TPS43331-Q1 eq32_lvsa38.gif

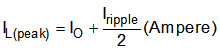
Use Equation 34 to calculate the value of the output voltage ripple.

Equation 34. TPS43331-Q1 eq33_lvsa38.gif

Usually the first term is dominant. The output ripple voltage is typically within the tolerance of the output specification.

Use Equation 35 to calculate the value of the output capacitor.

Equation 35. TPS43331-Q1 eq34_lvsa38.gif

where

  • IO(max) is the maximum output current
  • IO(min) is the minimum output current

The difference between the maximum to minimum output current is the worst case load step in the system where:

VBUCK(max) is the maximum tolerance of the regulated output voltage.

VBUCK(min) is the minimum tolerance of the regulated output voltage.

8.2.2.4 Power Dissipation

The power dissipation is largely dependent on the MOSFET driver current and input voltage. The drive current is proportional to the total gate charge of the external MOSFET.

Equation 36. PGate = Qg × VDR × fSW (Watt)

Assuming both high-side and low-side MOSFETs are identical in a synchronous configuration, use Equation 37 to calculate the total power dissipation.

Equation 37. Pcontroller1 = 2 × Qg × fSW × VBAT (Watt) per channel

The total power dissipation for the dual-channel controller is:

Equation 38. Pcontroller 1 and 2 = 4 × Qg × fSW × VBAT (Watt)

Use Equation 39 to calculate the device power consumption.

Equation 39. PIC = Iq × VBAT (Watt)

Use Equation 40 to calculate the power of the standby linear regulator.

Equation 40. PSTBY_REG = (VINSB – VSTBY ) × IVSTBY (Watt)

Use Equation 41 to calculate the power of the linear regulator.

Equation 41. PLIN_REG = (VINLR – VLR ) × IVLR (Watt)

Use Equation 39 to calculate the power of the high-side driver.

Equation 42. PHSD = IHSD × 0.6 (Watts ) for up to 300-mA output current

Therefore, use Equation 43 to calculate the total power dissipation (PTotal).

Equation 43. PTotal = Pcontroller 1 and 2 + PSTBY_REG + PLIN_REG + PIC + PHSD (Watt)

8.2.2.5 Buck Regulators

8.2.2.5.1 Buck Regulator 1 (VBUCK 1)

8.2.2.5.1.1 Step 1. Calculate the Inductor Value

Use Equation 31 to find the inductor value and assume an inductor ripple current of 0.8 A.

Equation 44. TPS43331-Q1 eq43_lvsa38.gif

L = 20.2 µH, use a value of 22 µH

8.2.2.5.1.2 Step 2. Inductor Peak Current

Use Equation 33 to calculate the peak inductor current (IL(peak)).

Equation 45. TPS43331-Q1 eq44_lvsa38.gif

IL(peak) = 2.4 A

8.2.2.5.1.3 Step 3. Calculating the Output Capacitance (CO)

Use Equation 35 to calculate the output capacitance.

Equation 46. TPS43331-Q1 eq45_lvsa38.gif

Assume a tolerance of ±3% to allow for some margin, the minimum IO current is 20 mA. Using Equation 34, the value of the minimum output capacitor, CO(min), is 29.3 µF. Considering temperature variations and manufacture tolerance, choose a value of 68 µF or greater for CO(min).

For this design, the value of CO is 100 µF.

8.2.2.5.1.4 Step 4. Calculating Loop Compensation Values

Use Equation 14 to determine the double pole:

Equation 47. TPS43331-Q1 eq46_lvsa38.gif

fLC = 3.39 kHz

Use Equation 15 to determine the zero due to the ESR of the output capacitor CO with ESR = 60 mΩ:

Equation 48. TPS43331-Q1 eq47_lvsa38.gif

fESR = 26.5 kHz

fC = 0.08 × fSW = 20 kHz

Us Equation 24 and assume R27 = 10 kΩ to find the value of R23:

Equation 49. TPS43331-Q1 eq48_lvsa38.gif

R23 = 40.2 kΩ

Use Equation 25 to find the value of R25:

Equation 50. TPS43331-Q1 eq49_lvsa38.gif

R25 = 30.5 kΩ, Choose R25 = 29.4 kΩ

Use Equation 26 to find the value of C20:

Equation 51. TPS43331-Q1 eq50_lvsa38.gif

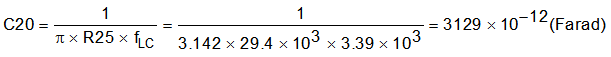
C20 = 3.13 nF, Choose C20 = 3.3 nF

Use Equation 27 to find the value of C23:

Equation 52. TPS43331-Q1 eq51_lvsa38.gif

C23 = 213 pF, Choose C23 = 220 pF

Us Equation 28 to find the value of R20:

Equation 53. TPS43331-Q1 eq52_lvsa38.gif

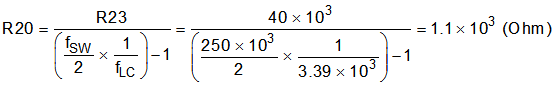
R20 = 1.12 kΩ, Choose R20 = 1.1 kΩ

Use Equation 29 to find the value of C18:

Equation 54. TPS43331-Q1 eq53_lvsa38.gif

C18 = 1142 pF, Choose C18 = 1200 pF

8.2.2.5.2 Buck Regulator 2 (VBUCK 2)

Using the same method for calculating the component values for Buck Regulator 2, with the set output conditions, the following values were selected.

8.2.2.5.2.1 Step 5. Calculate the Inductor Value

Use Equation 31 to find the inductor value and assume an inductor ripple current of 0.3 A:

L = 19.2 µH, use a value of 22 µH

8.2.2.5.2.2 Step 6. Inductor Peak Current

From Equation 33, the peak inductor current is:

IL(peak) = 1.65 A

8.2.2.5.2.3 Step 7. Calculating the Output Capacitance (CO)

Assume a tolerance of ±3% to allow for some margin and a minimum IO current of 20 mA. Use Equation 35 to calculate the value of the output capacitor:

CO(min) = 32.7 µF, with temperature variations and manufacture tolerance choose a value of 100 µF for this design.

CO = 100 µF

8.2.2.5.2.4 Step 8. Calculating Loop Compensation Values

Use Equation 14 to determine the double pole:

fLC = 3.39 kHz

Use Equation 15 to determine the zero from the ESR of the output capacitor, CO, with ESR = 60 mΩ:

fESR = 26.5 kHz

fc = 0.8 × fSW = 20 kHz

Use Equation 24 and the R32 value of 17.4 kΩ:

R34 = 40.2 kΩ

Use Equation 25:

R33 = 30.3 kΩ, Choose R33 = 29.4 kΩ

Use Equation 26:

C26 = 3.129 nF, Choose C26 = 3.3 nF

Use Equation 27:

C29 = 213 pF, Choose C29 = 220 pF

Use Equation 28:

R35 = 1.1 kΩ , Choose R35 = 1.1 kΩ

Use Equation 29:

C27 = 1142 pF, Choose C27 = 1200 pF

8.2.3 Application Curves

TPS43331-Q1 scope_hsd_power_off_delay_lvsa38.gif Figure 25. High-Side Driver (HSD) Output Power-Down Delay From I2C Bit Disable, ∆t = 43 µs
TPS43331-Q1 scope_hsd_turn_on_delay_lvsa38.gif Figure 27. High-Side Driver (HSD) Output Turnon Delay From I2C Bit Enable, ∆t = 7.6 µs
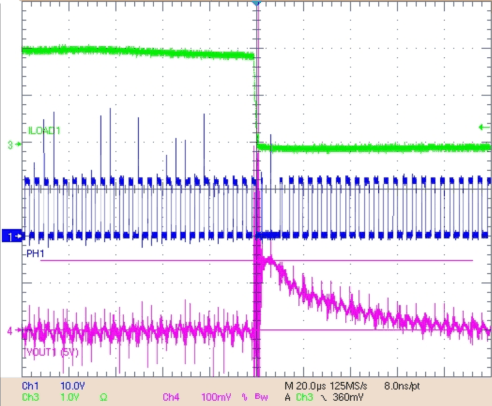TPS43331-Q1 scope_load_step_buck1_2a_0a_lvsa38.gif Figure 29. Load Step on VBUCK 1 From 2 A to 0 A, VOUT1 Overshoot = 148 mV
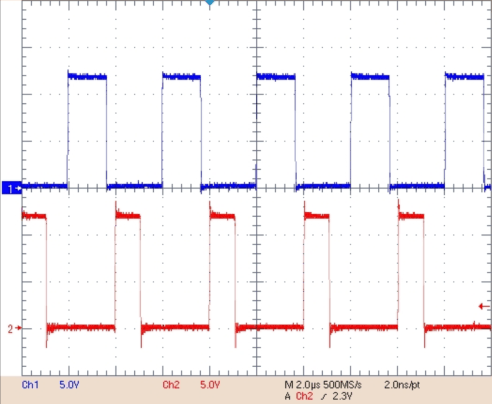TPS43331-Q1 scope_buck1_buck2_180deg_phase_lvsa38.gif Figure 31. VBUCK 1 and VBUCK 2 Switching 180° Out of Phase
TPS43331-Q1 scope_buck1_on_delay_enable_dt2p8ms_lvsa38.gif Figure 33. VBUCK 1 Power-On Delay From Enable Going High, ∆t = 2.8 ms (ILoad = 1.3 A)
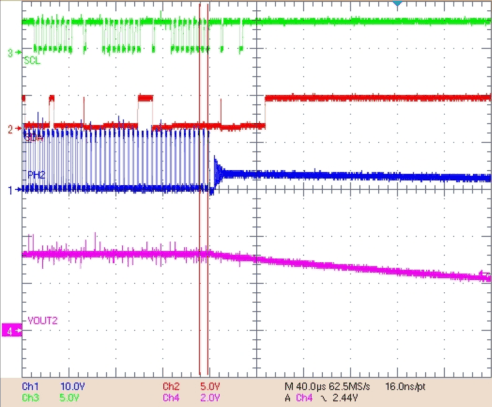TPS43331-Q1 scope_buck2_off_delay_i2c_dt7p2us_lvsa38.gif Figure 35. VBUCK 2 Turnoff Delay From I2C Enable Bit Going Low, ∆t = 7.2 µs
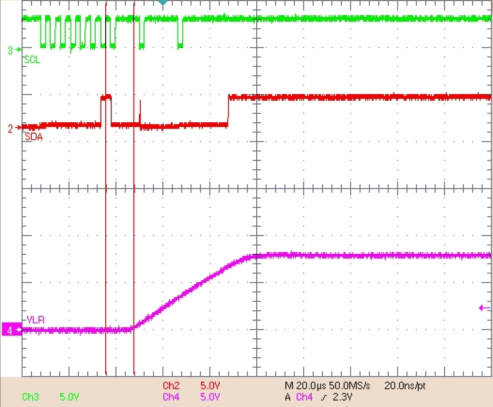TPS43331-Q1 scope_vlr_on_delay_i2c_dt12us_lvsa38.gif Figure 37. Linear Regulator (VLR) Turnon Delay From I2C Enable Bit Going High, ∆t = 12 µs
TPS43331-Q1 scope_vlr_off_delay_i2c_dt6p4us_lvsa38.gif Figure 39. Linear Regulator (VLR) Turnoff Delay From I2C Enable Bit Going Low, ∆t = 6.4 µs
TPS43331-Q1 scope_hsd_power_on_delay_lvsa38.gif Figure 26. High-Side Driver (HSD) Output Power-On Delay From I2C Bit Enable, ∆t = 47 µs
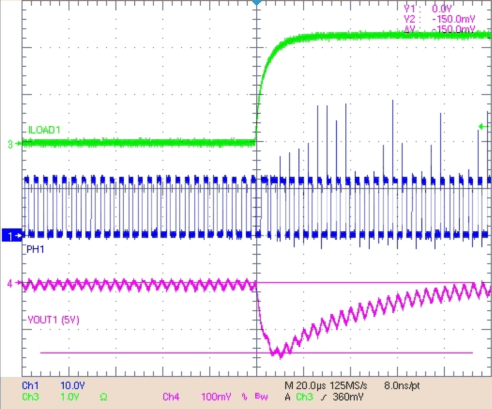TPS43331-Q1 scope_load_step_buck1_0a_2a_lvsa38.gif Figure 28. Load Step on VBUCK 1 From 0 A to 2 A, VOUT1 Droop = 150 mV
TPS43331-Q1 scope_load_step_buck2_0a_1p3a_lvsa38.gif Figure 30. Load Step on VBUCK 2 From 0 A to 1.3 A, VOUT1 Droop = 102 mV
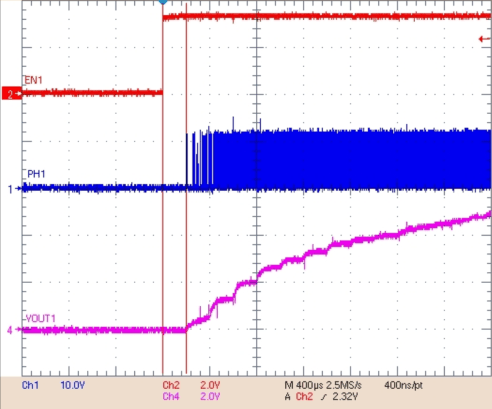TPS43331-Q1 scope_buck1_on_delay_enable_dt200us_lvsa38.gif Figure 32. VBUCK 1 Turnon Delay From Enable Going High, ∆t = 200 µs
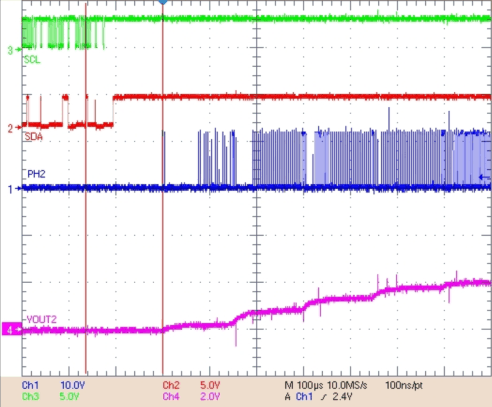TPS43331-Q1 scope_buck2_on_delay_i2c_dt164us_lvsa38.gif Figure 34. VBUCK 2 Turnon Delay From I2C Enable Bit Going High, ∆t = 164 µs
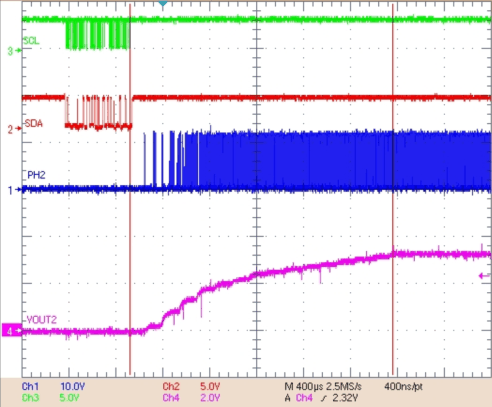TPS43331-Q1 scope_buck2_on_delay_i2c_dt2p24ms_lvsa38.gif Figure 36. VBUCK 2 Power-On Delay From I2C Enable Bit Going High, ∆t = 2.24 ms
TPS43331-Q1 scope_vlr_on_delay_i2c_dt61p2us_lvsa38.gif Figure 38. Linear Regulator (VLR) Power-On Delay From I2C Enable Bit Going High, ∆t = 61.2 µs

8.3 System Example

8.3.1 Multiple Power Supply Configuration for Vehicle Audio Applications

Figure 40 shows an example of configuration for car-audio power-supply application. Other combinations are possible depending on the system requirements.

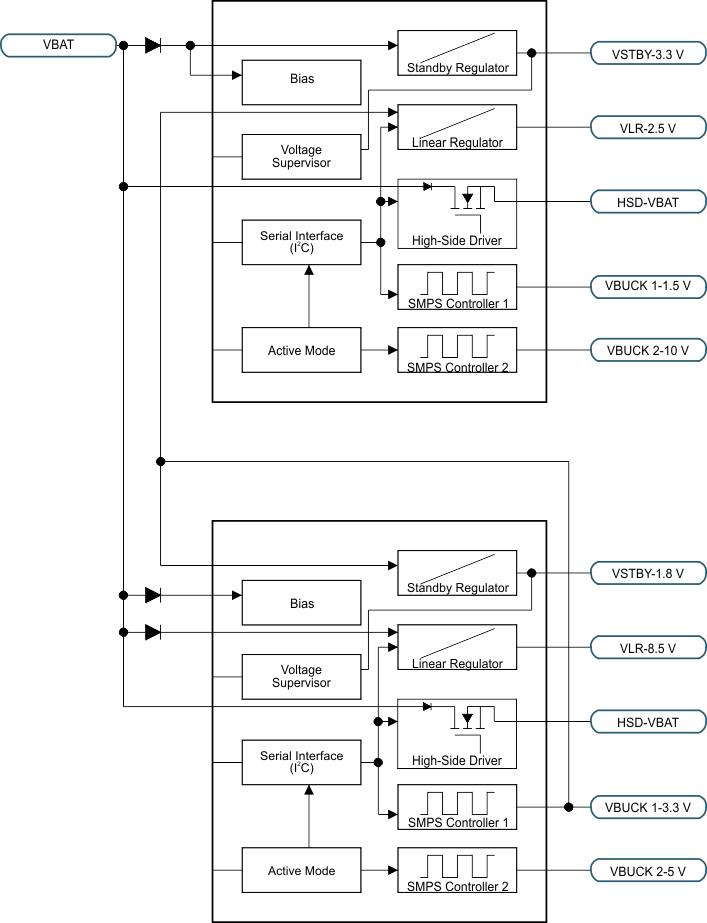TPS43331-Q1 multi_supply_vehic_audio_lvsa38.gif Figure 40. Multiple Power Supply for Vehicle Audio