JAJSCX3 January   2017 TPS568215OA

PRODUCTION DATA.  

  1. 1 特長
  2. 2 アプリケーション
  3. 3 概要
  4. 4 改訂履歴
  5. 5 Pin Configuration and Functions
  6. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Thermal Information
    5. 6.5 Electrical Characteristics
    6. 6.6 Timing Requirements
    7. 6.7 Typical Characteristics
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1  PWM Operation and D-CAP3 Control
      2. 7.3.2  Out-of-Audio Operation
      3. 7.3.3  4.7 V LDO and External Bias
      4. 7.3.4  MODE Selection
      5. 7.3.5  Soft Start and Pre-biased Soft Start
      6. 7.3.6  Enable and Adjustable UVLO
      7. 7.3.7  Power Good
      8. 7.3.8  Over Current Protection and Under Voltage Protection
      9. 7.3.9  Out-of-Bounds Operation
      10. 7.3.10 UVLO Protection
      11. 7.3.11 Thermal Shutdown
      12. 7.3.12 Output Voltage Discharge
    4. 7.4 Device Functional Modes
      1. 7.4.1 Light Load Operation
      2. 7.4.2 Standby Operation
  8. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 Typical Application
      1. 8.2.1 Design Requirements
      2. 8.2.2 Detailed Design Procedure
        1. 8.2.2.1 External Component Selection
          1. 8.2.2.1.1 Output Voltage Set Point
          2. 8.2.2.1.2 Switching Frequency and Mode Selection
          3. 8.2.2.1.3 Inductor Selection
          4. 8.2.2.1.4 Output Capacitor Selection
          5. 8.2.2.1.5 Input Capacitor Selection
      3. 8.2.3 Application Curves
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
    2. 10.2 Layout Example
  11. 11デバイスおよびドキュメントのサポート
    1. 11.1 デバイス・サポート
      1. 11.1.1 デベロッパー・ネットワークの製品に関する免責事項
      2. 11.1.2 開発サポート
    2. 11.2 ドキュメントの更新通知を受け取る方法
    3. 11.3 コミュニティ・リソース
    4. 11.4 商標
    5. 11.5 静電気放電に関する注意事項
    6. 11.6 Glossary
  12. 12メカニカル、パッケージ、および注文情報

パッケージ・オプション

メカニカル・データ（パッケージ｜ピン）
サーマルパッド・メカニカル・データ
発注情報

8 Application and Implementation

NOTE

Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.

8.1 Application Information

The schematic of Figure 22 shows a typical application for TPS568215OA. This design converts an input voltage range of 4.5 V to 17 V down to 1.2 V with a maximum output current of 10 A.

8.2 Typical Application

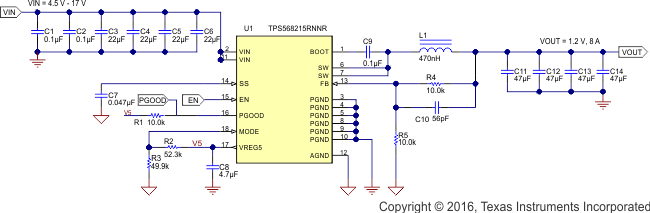TPS568215OA Schematic_app_SLVSDI8.gif Figure 22. Application Schematic

8.2.1 Design Requirements

Table 4. Design Parameters

PARAMETER CONDITIONS MIN TYP MAX UNIT
VOUT Output voltage 1.2 V
IOUT Output current 10 A
ΔVOUT Transient response 4-A load step ±30 mV
VIN Input voltage 4.5 12 17 V
VOUT(ripple) Output voltage ripple <10 mV(P-P)
Start input voltage Input voltage rising Internal UVLO V
Stop input voltage Input voltage falling Internal UVLO V
fSW Switching frequency 1.2 MHz
Operating Mode OOA
TA Ambient temperature 25 °C

8.2.2 Detailed Design Procedure

8.2.2.1 External Component Selection

8.2.2.1.1 Output Voltage Set Point

To change the output voltage of the application, it is necessary to change the value of the upper feedback resistor. By changing this resistor the user can change the output voltage above 0.6 V. See Equation 5

Equation 5. TPS568215OA EQ_Vout_SLVSD05.gif

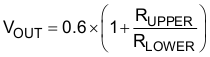
8.2.2.1.2 Switching Frequency and Mode Selection

Switching Frequency, current limit and switching mode (OOA or FCCM) are set by a voltage divider from VREG5 to GND connected to the MODE pin. See Table 3 for possible MODE pin configurations. Switching frequency selection is a tradeoff between higher efficiency and smaller system solution size. Lower switching frequency yields higher overall efficiency but relatively bigger external components. Higher switching frequencies cause additional switching losses which impact efficiency and thermal performance. For this design 1.2 MHz is chosen as the switching frequency, the switching mode is OOA and the output current is 8 A.

8.2.2.1.3 Inductor Selection

The inductor ripple current is filtered by the output capacitor. A higher inductor ripple current means the output capacitor should have a ripple current rating higher than the inductor ripple current. See Table 5 for recommended inductor values.

The RMS and peak currents through the inductor can be calculated using Equation 6 and Equation 7. It is important that the inductor is rated to handle these currents.

Equation 6. TPS568215OA EQ_ILrms_SLVSD05.gif
Equation 7. TPS568215OA EQ_ILpeak_SLVSD05.gif

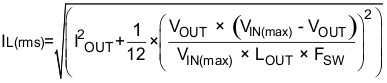
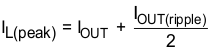
During transient/short circuit conditions the inductor current can increase up to the current limit of the device so it is safe to choose an inductor with a saturation current higher than the peak current under current limit condition.

8.2.2.1.4 Output Capacitor Selection

After selecting the inductor the output capacitor needs to be optimized. In DCAP3, the regulator reacts within one cycle to the change in the duty cycle so the good transient performance can be achieved without needing large amounts of output capacitance. The recommended output capacitance range is given in Table 5

Ceramic capacitors have very low ESR, otherwise the maximum ESR of the capacitor should be less than VOUT(ripple)/IOUT(ripple)

Table 5. Recommended Component Values

VOUT (V) RLOWER (kΩ) RUPPER (kΩ) FSW (kHz) LOUT (µH) COUT(min) (µF) COUT(max) (µF) CFF (pF)
0.6 10 0 400 0.68 300 500 –
800 0.47 100 500 –
1200 0.33 88 500 –
1.2 10 400 1.2 100 500 –
800 0.68 88 500 –
1200 0.47 88 500 –
3.3 45.3 400 2.4 88 500 100–220
800 1.5 88 500 100–220
1200 1.1 88 500 100–220
5.5 82.5 400 3.3 88 500 100–220
800 2.4 88 500 100–220
1200 1.2 88 700 100–220

8.2.2.1.5 Input Capacitor Selection

The minimum input capacitance required is given in Equation 8.

Equation 8. TPS568215OA EQ_CIN_min_SLVSD05.gif

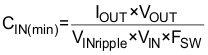
TI recommends using a high quality X5R or X7R input decoupling capacitors of 40 µF on the input voltage pin. The voltage rating on the input capacitor must be greater than the maximum input voltage. The capacitor must also have a ripple current rating greater than the maximum input current ripple of the application. The input ripple current is calculated by Equation 9 below:

Equation 9. TPS568215OA EQ_Icirms_SLVSD05.gif

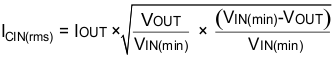
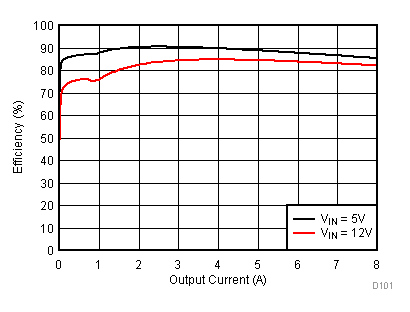
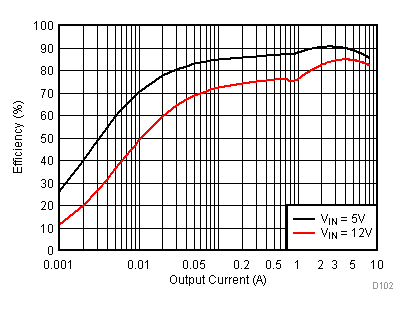
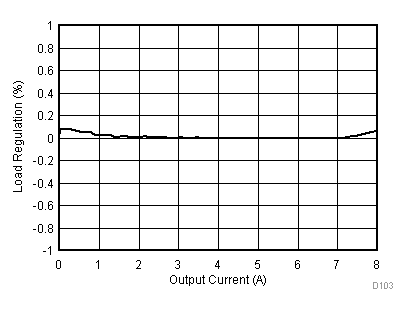
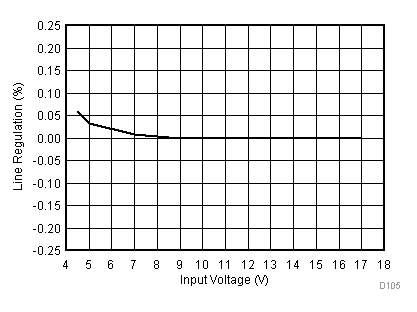
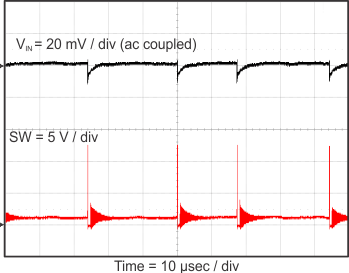
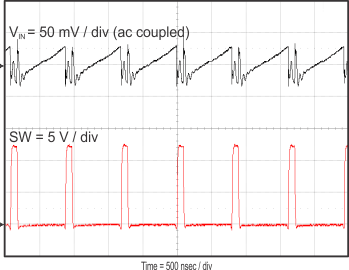
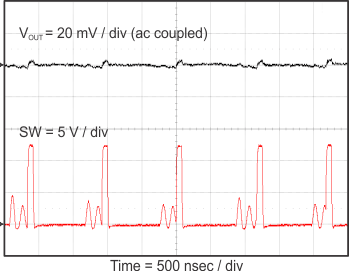
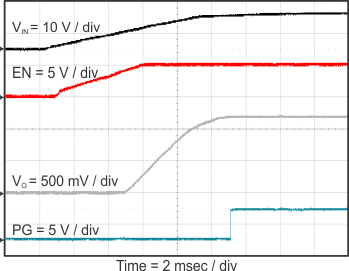
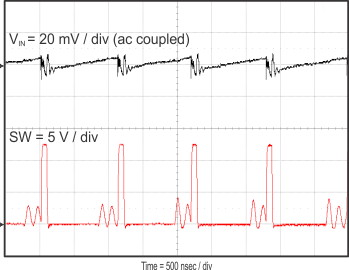
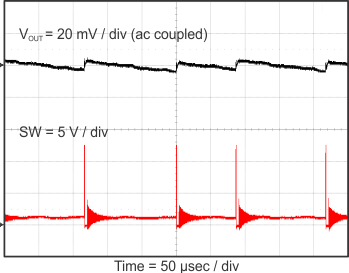
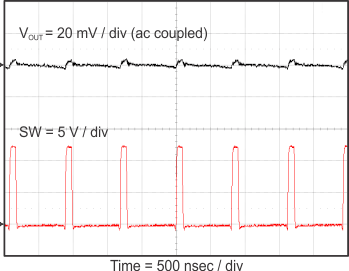
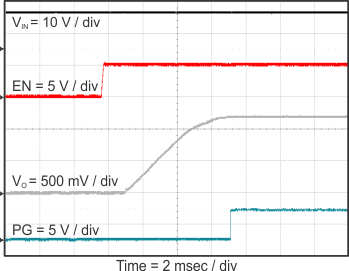
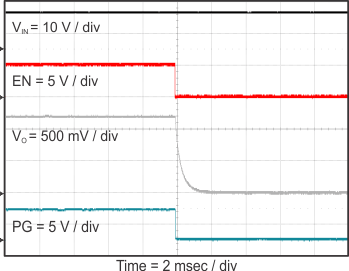
8.2.3 Application Curves

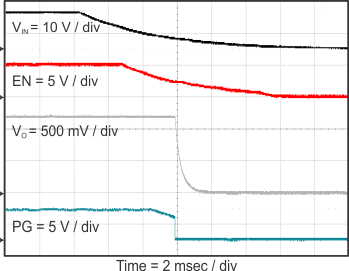
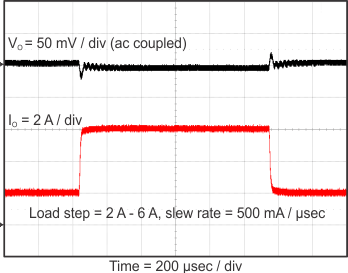
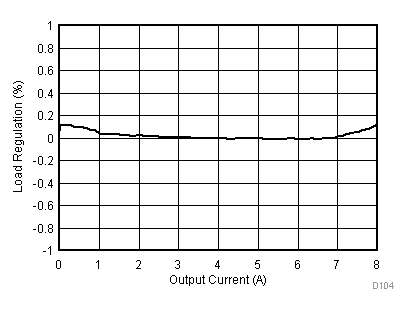
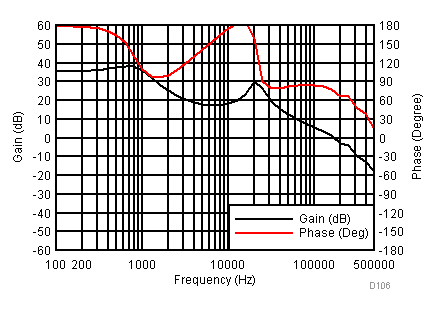
Figure 23 through Figure 39 apply to the circuit of Figure 22. VIN = 12 V. Ta = 25 °C unless otherwise specified.

TPS568215OA D101_SLVSDI8.gif
Figure 23. Efficiency
TPS568215OA D102_SLVSDI8.gif
Figure 24. Light Load Efficiency
TPS568215OA D103_SLVSDI8.gif
Figure 25. Load Regulation, VIN = 5 V
TPS568215OA D105_SLVSDI8.gif
Figure 27. Line Regulation, IOUT = 6 A
TPS568215OA Vin_ripple_10mA_slvsDI8.gif
Figure 29. Input Voltage Ripple, IOUT = 10 mA
TPS568215OA Vin_ripple_8A_slvsDI8.gif
Figure 31. Input Voltage Ripple, IOUT = 8 A
TPS568215OA Vout_ripple_700mA_slvsDI8.gif
Figure 33. Output Voltage Ripple, IOUT = 700 mA
TPS568215OA start_vin_slvsDI8.gif
Figure 35. Start Up Relative to VIN Rising
TPS568215OA stop_vin_slvsDI8.gif
Figure 37. Shut Down Relative to VIN Falling
TPS568215OA transient1_slvsDI8.gif
Figure 39. Transient Response
TPS568215OA D104_SLVSDI8.gif
Figure 26. Load Regulation, VIN = 12 V
TPS568215OA D106_SLVSDI8.gif
Figure 28. Loop Response, IOUT = 6 A
TPS568215OA Vin_ripple_700mA_slvsDI8.gif
Figure 30. Input Voltage Ripple, IOUT = 700 mA
TPS568215OA Vout_ripple_10mA_slvsDI8.gif
Figure 32. Output Voltage Ripple, IOUT = 10 mA
TPS568215OA Vout_ripple_8A_slvsDI8.gif
Figure 34. Output Voltage Ripple, IOUT = 8 A
TPS568215OA start_en_slvsDI8.gif
Figure 36. Start Up Relative to EN Rising
TPS568215OA stop_en_slvsDI8.gif
Figure 38. Shut Down Relative to EN Falling