JAJSDK2B September   2012  – January 2017 TPS65051-Q1

PRODUCTION DATA.  

  1. 1 特長
  2. 2 アプリケーション
  3. 3 概要
  4. 4 改訂履歴
  5. 5 Pin Configuration and Functions
  6. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Thermal Information
    5. 6.5 Electrical Characteristics
    6. 6.6 Switching Characteristics
    7. 6.7 Typical Characteristics
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1  Operation
      2. 7.3.2  DCDC1 Converter
      3. 7.3.3  DCDC2 Converter
      4. 7.3.4  Dynamic Voltage Positioning
      5. 7.3.5  Soft Start
      6. 7.3.6  100% Duty-Cycle Low-Dropout Operation
      7. 7.3.7  Undervoltage Lockout
      8. 7.3.8  Mode Selection
      9. 7.3.9  Enable
      10. 7.3.10 RESET
      11. 7.3.11 Short-Circuit Protection
      12. 7.3.12 Thermal Shutdown
      13. 7.3.13 Low Dropout Voltage Regulators
    4. 7.4 Device Functional Modes
      1. 7.4.1 Power-Save Mode
  8. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 Typical Application
      1. 8.2.1 Design Requirements
      2. 8.2.2 Detailed Design Procedure
        1. 8.2.2.1 Output-Voltage Setting
          1. 8.2.2.1.1 Converter 1 (DCDC1)
          2. 8.2.2.1.2 Converter 2 (DCDC2)
        2. 8.2.2.2 Output Filter Design (Inductor and Output Capacitor)
          1. 8.2.2.2.1 Inductor Selection
          2. 8.2.2.2.2 Output-Capacitor Selection
          3. 8.2.2.2.3 Input-Capacitor Selection
        3. 8.2.2.3 Low-Dropout Voltage Regulators (LDOs)
        4. 8.2.2.4 RESET
      3. 8.2.3 Application Curves
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
    2. 10.2 Layout Example
  11. 11デバイスおよびドキュメントのサポート
    1. 11.1 ドキュメントの更新通知を受け取る方法
    2. 11.2 コミュニティ・リソース
    3. 11.3 商標
    4. 11.4 静電気放電に関する注意事項
    5. 11.5 Glossary
  12. 12メカニカル、パッケージ、および注文情報

パッケージ・オプション

メカニカル・データ（パッケージ｜ピン）
サーマルパッド・メカニカル・データ
発注情報

8 Application and Implementation

NOTE

Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.

8.1 Application Information

This device integrates two step-down converters and four LDOs, which can be used to power the voltage rails needed by a processor or any other application. The power management IC (PMIC) can be controlled through the ENABLE and MODE pins or sequenced from the VIN using RC delay circuits. A logic output (RESET) provides the application processor or load a logic signal indicating power good or reset.

8.2 Typical Application

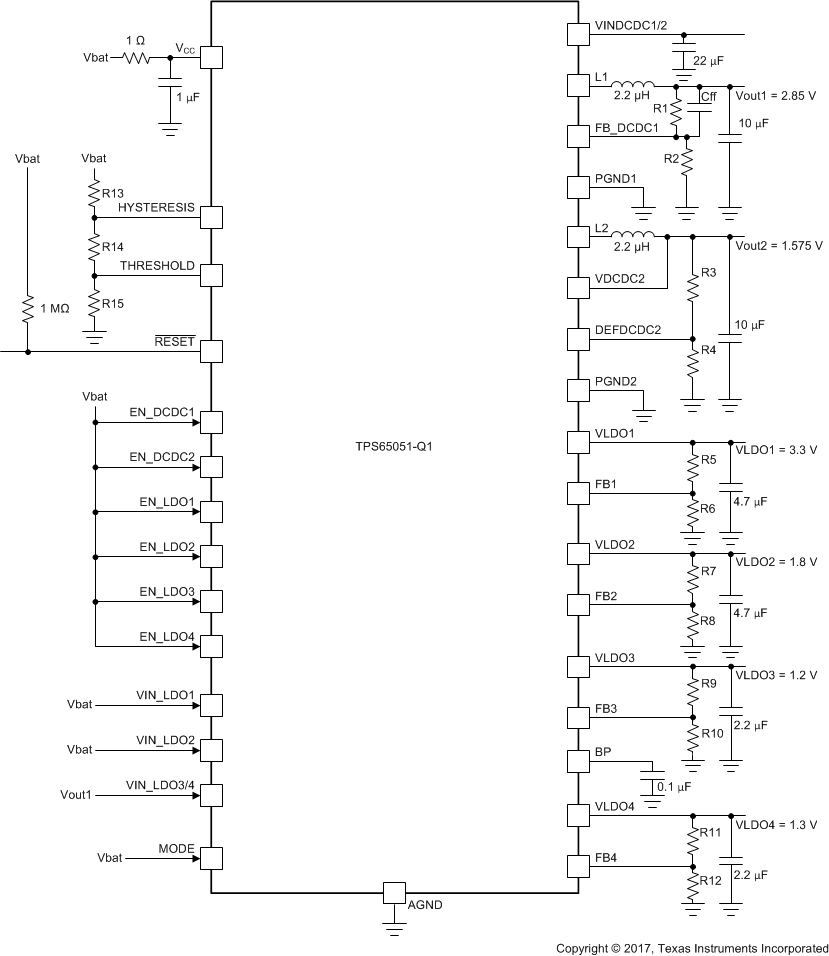TPS65051-Q1 tps65051-Q1-typical-application.gif Figure 9. Typical Application Schematic

8.2.1 Design Requirements

Table 1 lists the design requirements for this example.

Table 1. Design Parameters

PARAMETER VALUE
DCDC1 and DCDC2 input voltage 2.5 V to 6 V
DCDC1 output voltage 2.85 V
DCDC1 output current 1 A
DCDC2 output voltage 1.575 V
DCDC2 output current 600 mA
LDO1 output voltage 3.3 V
LDO1 output current 400 mA
LDO2 output voltage 1.8 V
LDO2 output current 400 mA
LDO3 output voltage 1.2 V
LDO3 output current 200 mA
LDO4 output voltage 1.3 V
LDO4 output current 200 mA

8.2.2 Detailed Design Procedure

8.2.2.1 Output-Voltage Setting

8.2.2.1.1 Converter 1 (DCDC1)

An external resistor network can set the output voltage of converter 1. Calculate the output voltage using Equation 4,

Equation 4. TPS65051-Q1 eq_vo_r1_lvs710.gif

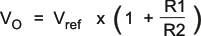
where

  • the internal reference voltage, Vref, is 0.6 V

TI recommends setting the total resistance of R1 + R2 to less than 1 MΩ. The resistor network connects to the input of the feedback amplifier, therefore requiring a small feed-forward capacitor in parallel with R1. A typical value of 47 pF is sufficient.

8.2.2.1.2 Converter 2 (DCDC2)

The adjustable output voltage is defined with external resistor network on the DEFDCDC2 pin.

Calculation of the adjustable output voltage is similar to that for the DCDC1 converter. TI recommends setting the total resistance of R3 + R4 to less than 1 MΩ. Route the DEFDCDC2 line separate from noise sources, such as the inductor or the L2 line. Connect the VDCDC2 line directly to the output capacitor. As VDCDC2 is the sense pin for the output of L2, there is no need for a feedforward capacitor in conjunction with R3.

Use an external resistor divider at DEFDCDC2 as shown in Figure 10.

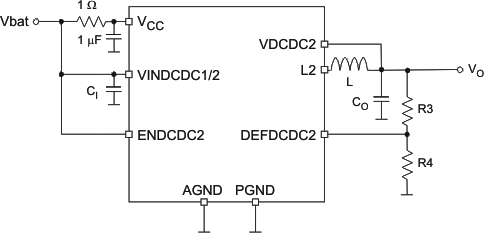TPS65051-Q1 ext_res_lvs710.gif Figure 10. External Resistor Divider

V(DEFDCDC2) = 0.6 V

Equation 5. TPS65051-Q1 eq_vo_r3r4_lvs710.gif

See Table 2 for typical resistor values:

Table 2. Typical Resistor Values

OUTPUT VOLTAGE R3 R4 NOMINAL VOLTAGE Typical CFF
3.3 V 680 kΩ 150 kΩ 3.32 V 47 pF
3 V 510 kΩ 130 kΩ 2.95 V 47 pF
2.85 V 560 kΩ 150 kΩ 2.84 V 47 pF
2.5 V 510 kΩ 160 kΩ 2.51 V 47 pF
1.8 V 300 kΩ 150 kΩ 1.8 V 47 pF
1.6 V 200 kΩ 120 kΩ 1.6 V 47 pF
1.5 V 300 kΩ 200 kΩ 1.5 V 47 pF
1.2 V 330 kΩ 330 kΩ 1.2 V 47 pF

8.2.2.2 Output Filter Design (Inductor and Output Capacitor)

8.2.2.2.1 Inductor Selection

The two converters operate with a 2.2-μH output inductor. A designer can use larger or smaller inductor values to optimize the performance of the device for specific operation conditions. The selected inductor must be rated for its dc resistance and saturation current. The dc resistance of the inductance directly influences the efficiency of the converters. Therefore, select an inductor with lowest dc resistance for highest efficiency. The minimum inductor value is 1.5 μH, but the circuit requires an output capacitor of 22 μF minimum in this case. For an output voltage above 2.8 V, TI recommends an inductor value of 3.3 μH minimum. Lower values result in an increased output-voltage ripple in PFM mode.

Equation 6 calculates the maximum inductor current under static load conditions. The saturation-current rating of the inductor should be higher than the maximum inductor current as calculated with Equation 6. This recommendation is because during heavy load transient the inductor current rises above the calculated value.

Equation 6. TPS65051-Q1 eq_delta_il_lvs710.gif

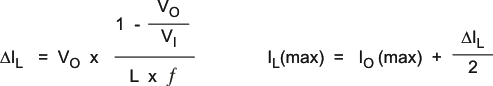
where

  • f = Switching frequency (2.25-MHz typical)
  • L = Inductor value
  • Δ IL= Peak-to-peak inductor ripple current
  • ILmax = Maximum inductor current

The highest inductor current occurs at maximum VI. Open-core inductors have a soft saturation characteristic, and they can normally handle higher inductor currents versus a comparable shielded inductor.

A more-conservative approach is to select the inductor current rating just for the maximum switch current of the corresponding converter. Give consideration to the difference in the core material from inductor to inductor, which has an impact on the efficiency, especially at high switching frequencies. See Table 3 and the typical applications for possible inductors.

Table 3. Tested Inductors

INDUCTOR TYPE INDUCTOR VALUE SUPPLIER
LPS3010 2.2 μH Coilcraft
LPS3015 3.3 μH Coilcraft
LPS4012 2.2 μH Coilcraft
VLF4012 2.2 μH TDK

8.2.2.2.2 Output-Capacitor Selection

The advanced fast-response voltage-mode control scheme of the two converters allows the use of small ceramic capacitors with a value of 22-μF (typical), without having large output-voltage undershoots and overshoots during heavy load transients. TI recommends ceramic capacitors having low ESR values, which result in the lowest output-voltage ripple.

If ceramic output capacitors are used, the capacitor RMS ripple current rating always meets the application requirements. For completeness, the RMS ripple current is calculated as:

Equation 7. TPS65051-Q1 eq_irsm_lvs710.gif

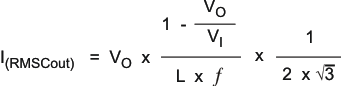
At nominal load current, the inductive converters operate in PWM mode, and the overall output voltage ripple is the sum of the voltage spike caused by the output-capacitor ESR plus the voltage ripple caused by charging and discharging the output capacitor:

Equation 8. TPS65051-Q1 eq_delta_vo_lvs710.gif

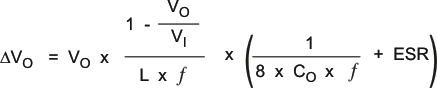
where the highest output voltage ripple occurs at the highest input voltage VI.

At light load currents, the converters operate in power-save mode and the output-voltage ripple depends on the output-capacitor value. The internal comparator delay and the external capacitor set the output-voltage ripple. The typical output-voltage ripple is less than 1% of the nominal output voltage.

8.2.2.2.3 Input-Capacitor Selection

The nature of the buck converters having a pulsating input current requires a low-ESR input capacitor for best input-voltage filtering and minimizing the interference with other circuits caused by high input-voltage spikes. The converters require a ceramic input capacitor of 10 μF. Increase the input capacitor as desired for better input-voltage filtering, without any limit.

Table 4. Possible Capacitors

CAPACITOR VALUE SIZE SUPPLIER TYPE
2.2 μF 0805 TDK C2012X5R0J226MT Ceramic
2.2 μF 0805 Taiyo Yuden JMK212BJ226MG Ceramic
10 μF 0805 Taiyo Yuden JMK212BJ106M Ceramic
10 μF 0805 TDK C2012X5R0J106M Ceramic
10 μF 0603 Taiyo Yuden JMK107BJ106MA Ceramic

8.2.2.3 Low-Dropout Voltage Regulators (LDOs)

An external resistor network sets the output voltage of all four LDOs. Calculate the output voltage using Equation 9:

Equation 9. TPS65051-Q1 eq_vo_r5r6_lvs710.gif

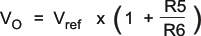
where

  • the internal reference voltage, Vref, is 1 V (typical).

TI recommends setting the total resistance of R5 + R6 to less than 1 MΩ. Typically, there is no feedforward capacitor needed at the voltage dividers for the LDOs.

Equation 10. TPS65051-Q1 eq_vo2_r5r6_lvs710.gif

Typical resistor values:

Table 5. Typical Resistor Values

OUTPUT VOLTAGE R5 R6 NOMINAL VOLTAGE
3.3 V 300 kΩ 130 kΩ 3.31 V
3 V 300 kΩ 150 kΩ 3 V
2.85 V 240 kΩ 130 kΩ 2.85 V
2.8 V 360 kΩ 200 kΩ 2.8 V
2.5 V 300 kΩ 200 kΩ 2.5 V
1.8 V 240 kΩ 300 kΩ 1.8 V
1.5 V 150 kΩ 300 kΩ 1.5 V
1.3 V 36 kΩ 120 kΩ 1.3 V
1.2 V 100 kΩ 510 kΩ 1.19 V
1.1 V 33 kΩ 330 kΩ 1.1 V

8.2.2.4 RESET

The device contains a comparator for supervising a voltage connected to an external voltage divider, and generating a reset signal if the voltage is lower than the threshold. The rising-edge delay is 100 ms at the open-drain RESET output. Calculate the values for the external resistors R13 to R15 as follows:

VL = lower voltage threshold

VH = higher voltage threshold

VREF = reference voltage (1 V)

Example:

  • VL = 3.3 V
  • VH = 3.4 V

    • Set R15 = 100 kΩ

    → R13 + R14 = 240 kΩ

    → R14 = 3.03 kΩ

    → R13 = 237 kΩ

    Equation 11. TPS65051-Q1 tps65051-q1-reset-equation.gif

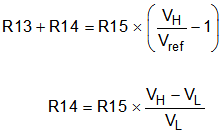
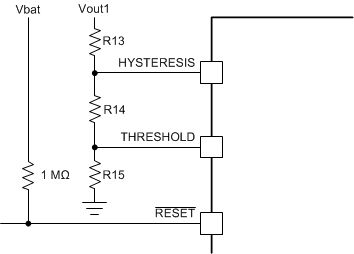TPS65051-Q1 reset_app_SLVSBJ1.gif Figure 11. RESET Circuit

8.2.3 Application Curves

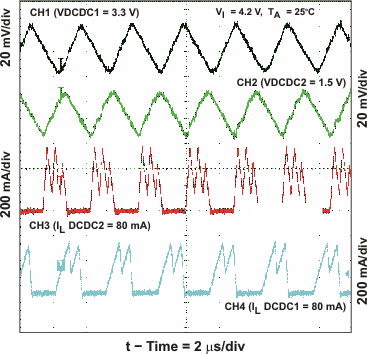TPS65051-Q1 vo_rip_low_lvs710.gif Figure 12. Output Voltage Ripple PWM or PFM MODE = LOW
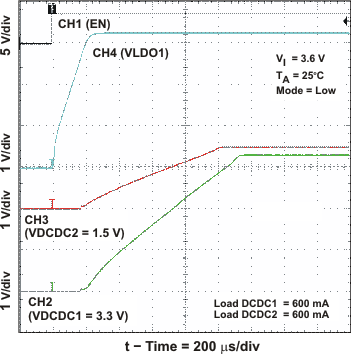TPS65051-Q1 dcdc1_startup_lvs710.gif Figure 14. DCDC1 Startup Timing
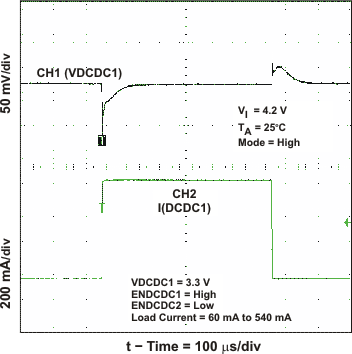TPS65051-Q1 dcdc1_load_hi_lvs710.gif Figure 16. DCDC1 Load Transient Response
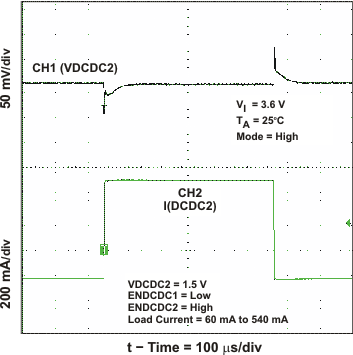TPS65051-Q1 dcdc2_load_hi_lvs710.gif Figure 18. DCDC2 Load Transient Response
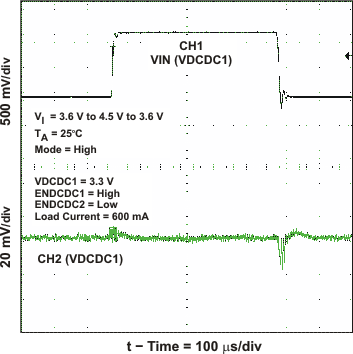TPS65051-Q1 dcdc1_line_hi_lvs710.gif Figure 20. DCDC1 Line Transient Response
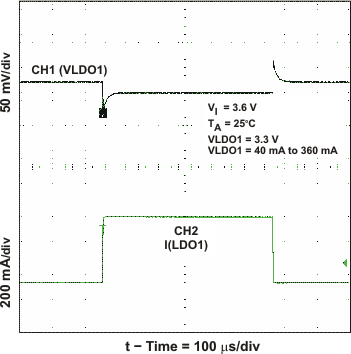TPS65051-Q1 ldo1_load_lvs710.gif Figure 22. LDO1 Load Transient Response
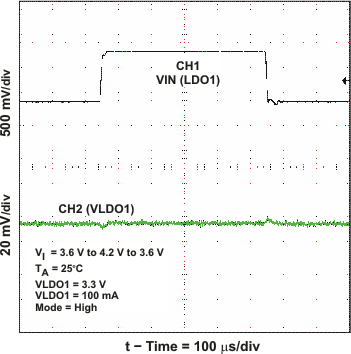TPS65051-Q1 ldo1_line_lvs710.gif Figure 24. LDO1 Line Transient Response
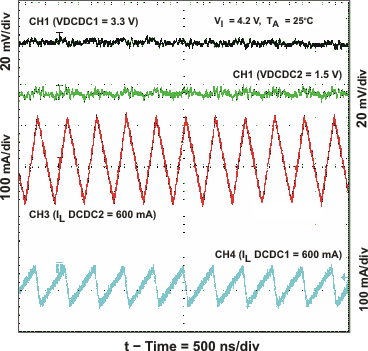TPS65051-Q1 vo_rip_high_lvs710.gif Figure 13. Output Voltage Ripple PWM MODE = HIGH
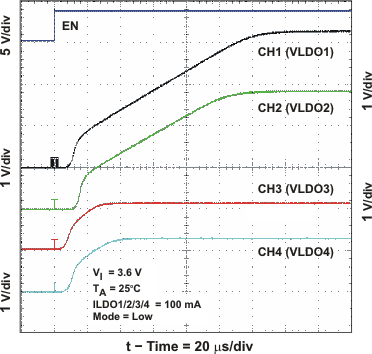TPS65051-Q1 ldo_startup_lvs710.gif Figure 15. LDO1 to LDO4 Startup Timing
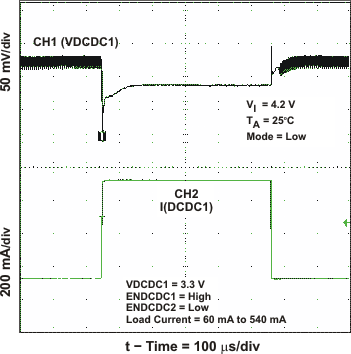TPS65051-Q1 dcdc1_load_low_lvs710.gif Figure 17. DCDC1 Load Transient Response
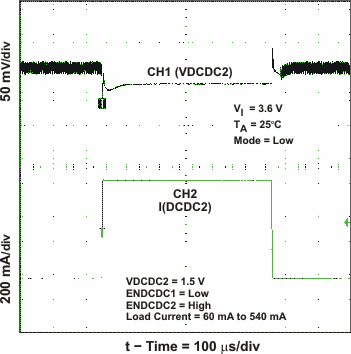TPS65051-Q1 dcdc2_load_low_lvs710.gif Figure 19. DCDC2 Load Transient Response
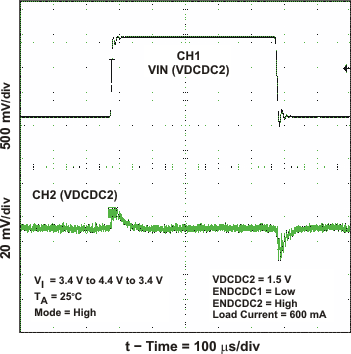TPS65051-Q1 dcdc2_line_hi_lvs710.gif Figure 21. DCDC2 Line Transient Response
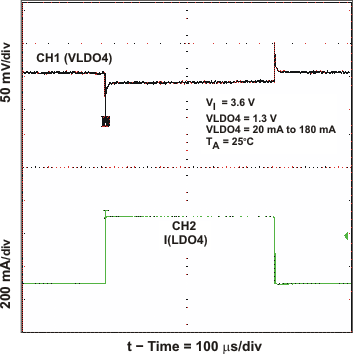TPS65051-Q1 ldo4_load_lvs710.gif Figure 23. LDO4 Load Transient Response