JAJSVA1F May 2012 – August 2024 TPS65131-Q1
PRODUCTION DATA
- 1
- 1 特長
- 2 アプリケーション
- 3 概要
- 4 Device Comparison
- 5 Pin Configuration and Functions
- 6 Specifications
- 7 Detailed Description
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Applications
- 8.2.1 TPS65131-Q1 With VPOS = 10.5V, VNEG = –10V
- 8.2.2 Design Requirements
- 8.2.3 Detailed Design Procedure
- 8.2.4 Analog Supply Input Filter
- 8.2.5 Thermal Information
- 8.2.6 Application Curves
- 8.3 Power Supply Recommendations
- 8.4 Layout
- 9 Device and Documentation Support
- 10Revision History
- 11Mechanical, Packaging, and Orderable Information
パッケージ・オプション
メカニカル・データ(パッケージ|ピン)
- RGE|24
サーマルパッド・メカニカル・データ
- RGE|24
発注情報
8.2.3.2.2 Output Capacitors
One of the major parameters necessary to define the capacitance value of the output capacitor is the maximum allowed output voltage ripple of the converter. Two parameters, which are the capacitance and the equivalent series resitance (ESR), affect this ripple. It is possible to calculate the minimum capacitance needed for the defined ripple, supposing that the ESR is zero. Use Equation 7 for the boost-converter output capacitor (C4min) and Equation 8 for the inverting-converter output capacitor (C5min).
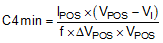
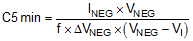
The parameter f is the switching frequency. ΔVPOS and ΔVNEG are the maximum allowed ripple voltages for each converter.
Choosing a ripple voltage in the range of 10mV requires a minimum capacitance of 12µF. The total ripple is larger due to the ESR of the output capacitor. Use Equation 9 for the boost converter and Equation 10 for the inverting converter to calculate this additional ripple component.
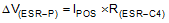
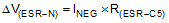
In this example, an additional ripple of 2mV is the result of using a typical ceramic capacitor with an ESR in the 10mΩ range. The total ripple is the sum of the ripple caused by the capacitance and the ripple caused by the ESR of the capacitor. In this example, the total ripple is 10mV.
Load transients can create additional ripple. When the load current increases rapidly, the output capacitor must provide the additional current until the inductor current increases by the control loop which sets a higher on-time (duty cycle) of the main switch. The higher duty cycle results in longer inductor charging periods. The inductance itself also limits the rate of increase of the inductor current. When the load current decreases rapidly, the output capacitor must store the excess energy (stored in the inductor) until the regulator has decreased the inductor current by reducing the duty cycle. The recommendation is to use higher capacitance values, as the foregoing calculations show.