JAJSHS0C March   2019  – March 2021 TPS92682-Q1

PRODUCTION DATA  

  1. 1 特長
  2. 2 アプリケーション
  3. 3 概要
  4. 4 Revision History
  5. 5 Pin Configuration and Functions
  6. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Thermal Information
    5. 6.5 Electrical Characteristics
    6. 6.6 Typical Characteristics
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1  Device Enable
      2. 7.3.2  Internal Regulator and Undervoltage Lockout (UVLO)
      3. 7.3.3  Oscillator
      4. 7.3.4  Spread Spectrum Function
      5. 7.3.5  Gate Driver
      6. 7.3.6  Rail-to-Rail Current Sense Amplifier
      7. 7.3.7  Transconductance Error Amplifier
      8. 7.3.8  Switch Current Sense
      9. 7.3.9  Slope Compensation
      10. 7.3.10 ILED Setting in CC Mode
      11. 7.3.11 Output Voltage Setting in CV Mode
      12. 7.3.12 PWM Dimming
      13. 7.3.13 P-Channel FET Gate Driver Output
      14. 7.3.14 Soft Start
      15. 7.3.15 Two-Phase Operation
        1. 7.3.15.1 Current Sharing In Two-Phase
      16. 7.3.16 Faults and Diagnostics
        1. 7.3.16.1  Main Fault Timer (MFT)
        2. 7.3.16.2  OV Fault
        3. 7.3.16.3  UV Fault
        4. 7.3.16.4  ILIM Fault
        5. 7.3.16.5  UVLO
        6. 7.3.16.6  ILED Over Current (OC)
        7. 7.3.16.7  ILED Undercurrent (UC)
        8. 7.3.16.8  ISNOPEN, FBOPEN, and RTOPEN Faults
        9. 7.3.16.9  TW and TSD
        10. 7.3.16.10 COMPx Pull-Down and Comp-Low signal
    4. 7.4 Device Functional Modes
      1. 7.4.1 POR Mode
      2. 7.4.2 Normal Operation
      3. 7.4.3 Limp Home
    5. 7.5 Programming
      1. 7.5.1 Serial Interface
      2. 7.5.2 Command Frame
      3. 7.5.3 Response Frame
        1. 7.5.3.1 Read Response Frame Format
        2. 7.5.3.2 Write Response Frame Format
        3. 7.5.3.3 Write Error/POR Frame Format
      4. 7.5.4 SPI Error
    6. 7.6 TPS92682 Registers
      1. 7.6.1  EN Register
      2. 7.6.2  CFG1 Register
      3. 7.6.3  CFG2 Register
      4. 7.6.4  SWDIV Register
      5. 7.6.5  ISLOPE Register
      6. 7.6.6  FM Register
      7. 7.6.7  SOFTSTART Register
      8. 7.6.8  CH1IADJ Register
      9. 7.6.9  CH2IADJ Register
      10. 7.6.10 PWMDIV Register
      11. 7.6.11 CH1PWML Register
      12. 7.6.12 CH1PWMH Register
      13. 7.6.13 CH2PWML Register
      14. 7.6.14 CH2PWMH Register
      15. 7.6.15 ILIM Register
      16. 7.6.16 IFT Register
      17. 7.6.17 MFT Register
      18. 7.6.18 FLT1 Register (read only)
      19. 7.6.19 FLT2 Register (read only)
      20. 7.6.20 FEN1 Register
      21. 7.6.21 FEN2 Register
      22. 7.6.22 FLATEN Register
      23. 7.6.23 OV Register
      24. 7.6.24 LHCFG Register
      25. 7.6.25 LHCH1IADJ Register
      26. 7.6.26 LHCH2IADJ Register
      27. 7.6.27 LHCH1PWML Register
      28. 7.6.28 LHCH1PWMH Register
      29. 7.6.29 LHCH2PWML Register
      30. 7.6.30 LHCH2PWMH Register
      31. 7.6.31 LHILIM Register
      32. 7.6.32 LHIFT Register
      33. 7.6.33 LHMFT Register
      34. 7.6.34 LHFEN1 Register
      35. 7.6.35 LHFEN2 Register
      36. 7.6.36 LHFLATEN Register
      37. 7.6.37 LHOV Register
      38. 7.6.38 CAL Register
      39. 7.6.39 RESET Register
  8. 8 Application and Implementation
    1. 8.1 Application Information General Design Considerations
      1. 8.1.1 Switching Frequency, fSW
      2. 8.1.2 Duty Cycle Considerations
      3. 8.1.3 Main Power MOSFET Selection
      4. 8.1.4 Rectifier Diode Selection
      5. 8.1.5 Switch Current Sense Resistor
      6. 8.1.6 Slope Compensation
      7. 8.1.7 Soft Start
    2. 8.2 Application Information CC Mode
      1. 8.2.1 Inductor Selection
      2. 8.2.2 Output Capacitor Selection
      3. 8.2.3 Input Capacitor Selection
      4. 8.2.4 Programming LED Current
      5. 8.2.5 Feedback Compensation
      6. 8.2.6 Overvoltage and Undervoltage Protection
      7. 8.2.7 Series P-Channel MOSFET Selection
      8. 8.2.8 Programming Example for Two-Channel CC Mode
    3. 8.3 Typical Application CV Mode
      1. 8.3.1 Inductor Selection
      2. 8.3.2 Output Capacitor Selection
      3. 8.3.3 Input Capacitor Selection
      4. 8.3.4 Programming Output Voltage VOUT
      5. 8.3.5 Feedback Compensation
      6. 8.3.6 Overvoltage and Undervoltage Protection
      7. 8.3.7 Programing Example for Two-Phase CV BOOST
    4. 8.4 Typical Application CC Mode
      1. 8.4.1 CC Boost Design Requirements
      2. 8.4.2 CC Boost Detailed Design Procedure
        1. 8.4.2.1  Calculating Duty Cycle
        2. 8.4.2.2  Setting Switching Frequency
        3. 8.4.2.3  Setting Dither Modulation Frequency
        4. 8.4.2.4  Inductor Selection
        5. 8.4.2.5  Output Capacitor Selection
        6. 8.4.2.6  Input Capacitor Selection
        7. 8.4.2.7  Main N-Channel MOSFET Selection
        8. 8.4.2.8  Rectifier Diode Selection
        9. 8.4.2.9  Setting ILED and Selecting RCS
        10. 8.4.2.10 Setting Switch Current Limit
        11. 8.4.2.11 Slope Compensation
        12. 8.4.2.12 Compensator Parameters
        13. 8.4.2.13 Overvoltage Protection
        14. 8.4.2.14 Series P-Channel MOSFET Selection
      3. 8.4.3 CC Buck-Boost Design Requirements
      4. 8.4.4 CC Buck-Boost Detailed Design Procedure
        1. 8.4.4.1  Calculating Duty Cycle
        2. 8.4.4.2  Setting Switching Frequency
        3. 8.4.4.3  Setting Dither Modulation Frequency
        4. 8.4.4.4  Inductor Selection
        5. 8.4.4.5  Output Capacitor Selection
        6. 8.4.4.6  Input Capacitor Selection
        7. 8.4.4.7  Main N-Channel MOSFET Selection
        8. 8.4.4.8  Rectifier Diode Selection
        9. 8.4.4.9  Setting ILED and Selecting RCS
        10. 8.4.4.10 Setting Switch Current Limit
        11. 8.4.4.11 Slope Compensation
        12. 8.4.4.12 Compensator Parameters
        13. 8.4.4.13 Overvoltage Protection
      5. 8.4.5 PWM Dimming Consideration
      6. 8.4.6 Application Curves
    5. 8.5 Typical Application CV Mode
      1. 8.5.1 CV Design Requirements
      2. 8.5.2 Detailed Design Procedure
        1. 8.5.2.1  Calculating Duty Cycle
        2. 8.5.2.2  Setting Switching Frequency
        3. 8.5.2.3  Setting Dither Modulation Frequency
        4. 8.5.2.4  Inductor Selection
        5. 8.5.2.5  Output Capacitor Selection
        6. 8.5.2.6  Input Capacitor Selection
        7. 8.5.2.7  Main N-Channel MOSFET Selection
        8. 8.5.2.8  Rectifier Diode Selection
        9. 8.5.2.9  Programming VOUT
        10. 8.5.2.10 Setting Switch Current Limit
        11. 8.5.2.11 Slope Compensation
        12. 8.5.2.12 Compensator Parameters
        13. 8.5.2.13 Overvoltage Protection
      3. 8.5.3 Application Curves
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
    2. 10.2 Layout Example
  11. 11Device and Documentation Support
    1. 11.1 ドキュメントの更新通知を受け取る方法
    2. 11.2 サポート・リソース
    3. 11.3 Trademarks
    4. 11.4 静電気放電に関する注意事項
    5. 11.5 用語集
  12. 12Mechanical, Packaging, and Orderable Information

パッケージ・オプション

メカニカル・データ（パッケージ｜ピン）
サーマルパッド・メカニカル・データ
発注情報

8.2.5 Feedback Compensation

The loop gain T(s) is the product of the converter transfer function Givc(s) (Equation 28) and the feedback transfer function Gc(s).

Using a first-order approximation, the converter transfer function can be modeled as a single pole created by the output capacitor and the LED string dynamic resistance, rD. In the boost and buck-boost topologies, the transfer function has a right half-plane zero created by the inductor, and the DC output current ILED. The ESR of the output capacitor is neglected in this analysis.

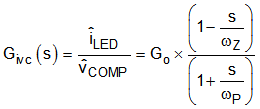
Equation 28. GUID-4F40BAEC-619E-4151-B0A7-1AD7AF9F389E-low.gif

Table 8-1 summarizes the expression for the small-signal model parameters.

Table 8-1 Small-Signal Model Parameters for CC Operation
DC GAIN (G0)POLE FREQUENCY (ωP)ZERO FREQUENCY (ωZ)
Boost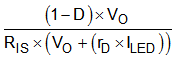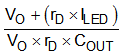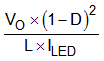GUID-439F54F3-8049-4557-8323-C38A01C3249E-low.gifGUID-1634B5FA-7412-43CE-8C64-3B00F43CC0B9-low.gifGUID-4F13DCA3-8F5E-43F9-B2A1-2BEE8E0103DE-low.gif
Buck-Boost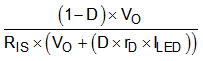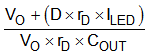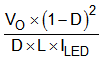GUID-CD094660-28B7-4438-AE0B-E381B7812D67-low.gifGUID-38554B9F-9EE1-4B3F-A896-5CF43B27557B-low.gifGUID-20CB1C11-840D-437A-BCE1-345C54459734-low.gif

The feedback transfer function includes the current sense resistor and the loop compensation of the transconductance amplifier. A compensation network at the output of the error amplifier is used to configure loop gain and phase characteristics. A simple capacitor, CCOMP, from COMPx to GND (as shown in Figure 8-4) provides integral compensation and creates a pole at the origin. Alternatively, a network of RCOMP, CCOMP, and CHF, shown in Figure 8-5, can be used to implement Proportional-Integral (PI) compensation to create a pole at the origin, a low-frequency zero, and a high-frequency pole.

The feedback transfer function is defined as follows.

Feedback transfer function with integral compensation:

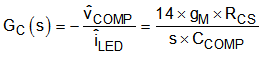
Equation 29. GUID-636EF228-AE35-4BEB-897A-73F64FCE0BE9-low.gif

Feedback transfer function with proportional integral compensation:

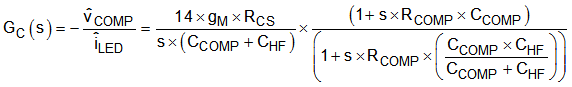
Equation 30. GUID-BAF979FD-7D64-4158-8186-A11161F2C3CC-low.gif
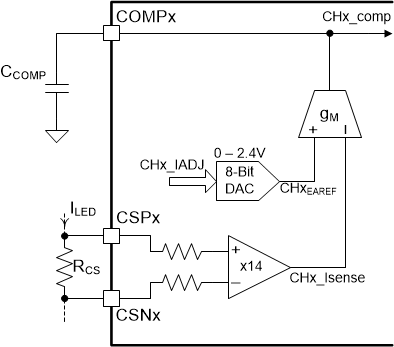GUID-D7C9F7D6-FD71-4357-A606-4D6C05305F72-low.gifFigure 8-4 Integral Compensator
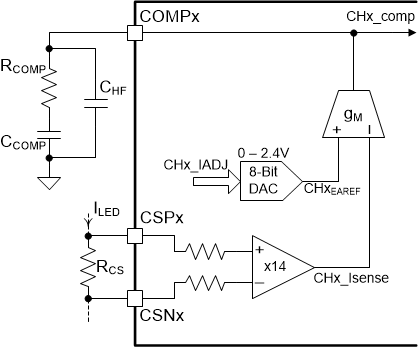GUID-32EC8780-B9AD-4189-983E-2B8C8F4040CB-low.gifFigure 8-5 Proportional Integral Compensator

The pole at the origin minimizes output steady-state error. High bandwidth is achieved with the PI compensator by introducing a phase lead using a low-frequency zero. Use the following expressions to calculate the compensation network.

  • BOOST and BUCK-BOOST with an Integral Compensator:
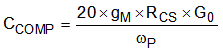
    Equation 31. GUID-79F8AAB7-86CB-4A1B-8116-48A0DC87AA28-low.gif
  • BOOST and BUCK-BOOST with a Proportional-Integral Compensator:
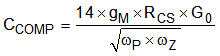    Equation 32. GUID-72D0133A-1399-48AF-87AE-0189F44351B3-low.gif
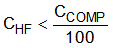    Equation 33. GUID-11AA42A3-A8E3-48AA-8300-5B0AE76E4ED1-low.gif
    Equation 34.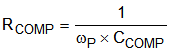 GUID-2A1D85E0-0E37-4B12-B37C-8318A0276190-low.gif

The above compensation values are calculated to provide reasonable phase margin (> 45°) and bandwidth. In practice, the above values can be modified for desired dynamic performance (for example: PWM dimming rise/fall-time or overshoot/undershoot).