JAJSV12A July 2024 – October 2024 TLC3555-Q1
PRODMIX
- 1
- 1 特長
- 2 アプリケーション
- 3 概要
- 4 Pin Configuration and Functions
- 5 Specifications
- 6 Detailed Description
- 7 Application and Implementation
- 8 Device and Documentation Support
- 9 Revision History
- 10Mechanical, Packaging, and Orderable Information
6.3.2 Astable Operation
Figure 6-4 shows that adding a second resistor (RB) to the circuit and connecting the trigger input to the threshold input causes the timer to self-trigger and run as a multivibrator. The CT capacitor charges through RA and RB and then only discharges through RB. As a result, the values of RA and RB control the duty cycle. DB is optional and typically used only when a duty cycle below 50% is required, as the diode bypasses RB to allow faster charging of CT.
This astable connection results in the CT capacitor charging and discharging between the threshold-voltage level (≅ 0.67 × VDD) and the trigger-voltage level (≅ 0.33 × VDD). Driving the CONT pin externally shifts the threshold-voltage and trigger-voltage levels to VCONT and 0.5 × VCONT, respectively. As in the monostable circuit, charge and discharge times (and as a result, the frequency and duty cycle) are independent of the supply voltage.
 Figure 6-4 Circuit
for Astable Operation
Figure 6-4 Circuit
for Astable Operation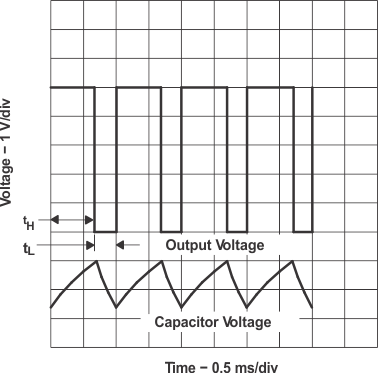
| RA = 5kΩ | RB = 3kΩ | CT = 0.15µF |
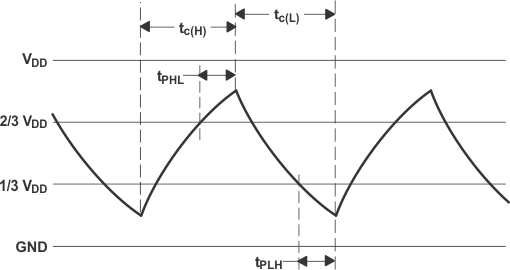
Figure 6-6 shows typical waveforms generated during astable operation. The output high-level duration (tH) and low-level duration tL can be calculated as follows:
Other useful relationships for period, frequency, and driver-referred and waveform-referred duty cycle are shown as follows:
These equations do not account for any propagation delay times from the TRIG and THRES inputs to DISCH output. These delay times add directly to the period and overcharge the capacitor, creating differences between calculated and actual values that increase with frequency. In addition, the discharge on-state resistance ron during the discharge event contributes another source of timing error in the calculation when RB is very low. The following equations provide better agreement with measured values. Equation 7 and Equation 8 represent the actual low and high times when used at higher frequencies (at 100kHz and beyond) because propagation delay and discharge on resistance is added to the formulas. The value of CT includes both the nominal or deliberate timing capacitance, as well as parasitic capacitance on the PCB. Decoupling capacitance on CONT also affects the duty cycle, with an error contribution that depends on the capacitor leakage resistance. For additional discussion, see the Design low-duty-cycle timer circuits article.
These equations and those given earlier are similar in that a time constant is multiplied by the logarithm of a number or function. The limit values of the logarithmic terms must be between ln(2) at low frequencies, and ln(3) at extremely high frequencies. For a duty cycle close to 50%, an appropriate constant for the logarithmic terms can be substituted with good results. Output waveform duty cycles less than 50% require that tc(H) / tc(L) < 1 and possibly that RA ≤ ron. These conditions can be difficult to obtain. DB can be used to reduce the effective RB during the capacitor charging event, but has a nonlinear response. If using DB, verify performance through simulation and bench evaluation before selecting final timing component values.
Figure 6-7 and Figure 6-8 show the nominal free-running frequency associated with various combinations of CT and RA + 2 × RB for a 66% duty cycle (such that RA = RB). The values of ron, tPD falling and tPD rising vary according to the device supply voltage and temperature. Tolerances of RA, RB, and CT also contribute variation. The difference of simulation results calculated using the simplified and detailed equations becomes apparent by 100kHz, with approximately 2.15% error at VDD = 15V and 2.6% error at VDD = 5V. This error manifests as nonlinearity in the following curves. For applications where sub-1% error is required, use Equation 7 and Equation 8 for frequencies greater than 10kHz at VDD = 5V, or greater than 30kHz at VDD = 15V.

| VDD = 5V |

| VDD = 15V |