SLAAEH6 September   2024 TAA5212 , TAA5412-Q1 , TAC5111 , TAC5111-Q1 , TAC5112 , TAC5211 , TAC5212 , TAC5212-Q1 , TAC5311-Q1 , TAC5312-Q1 , TAC5411-Q1 , TAC5412-Q1 , TAD5112 , TAD5112-Q1 , TAD5212 , TAD5212-Q1

 

  1.   1
  2.   Abstract
  3.   Trademarks
  4. 1Introduction
  5. 2Infinite Impulse Response Filters
    1. 2.1 Digital Biquad Filter
  6. 3TAC5x1x and TAC5x1x-Q1 Digital Biquad Filters
    1. 3.1 Filter Design using PurePath™ Console
      1. 3.1.1 Example of Programming Biquad Filters Using PurePath™ Console
    2. 3.2 Generating Coefficients N0, N1, N2, D1, D2 using a Digital Filter Design Package
    3. 3.3 Avoiding Overflow Conditions
    4. 3.4 Biquad Filter Allocation on Recording Channel
    5. 3.5 Biquad Filter Allocation on Playback Channel
    6. 3.6 Biquad Filter Programming Example on the TAC5x1x
  7. 4Typical Audio Applications of Biquad Filters
    1. 4.1 Parametric Equalizers
    2. 4.2 Crossover Networks
    3. 4.3 Voice Boost
    4. 4.4 Bass Boost
    5. 4.5 Removing 50Hz–60Hz Hum With Notch Filters
  8. 5Summary
  9. 6References

3.1 Filter Design using PurePath™ Console

To facilitate the use of the biquad filters, the PurePath™ Console includes a graphical filter design section that plots the magnitude, phase, and group delay versus frequency. This filter design also generates the coefficients through several different filter design techniques filters.

Table 3-1 lists the different types of filters supported in the PurePath™ Console. Through bi-linear transformation (BLT), the analog filter equations shown in the table can be converted from the S-domain to the digital Z-domain. In these filters, each pole of the filter provides a –6dB per octave or –10dB per decade slope in the frequency response. Each zero of the filter provides a +6dB per octave or +10dB per decade slope in the frequency response.

In the transfer functions shown in the Table 3-1, ωc corresponds to the center/corner frequency of the filter, and Q refers to the quality factor of the filter.

Table 3-1 PurePath™ Console Digital Biquad Filter Options
Filter TypeFilter Transfer FunctioN (S-domain)Filter Description
Band Pass
H s =   ω c Q s s 2 +   ω c Q s + ω c 2
Band-Pass filter at the specified center frequency and passband width (filter bandwidth)
Bass Shelf
H s =   ω c 2 s 2 +   ω c s + ω c 2
Specified gain applied at the low frequency up to the specified cutoff frequency
Equalizer (Bandwidth)
H s =   ω c Q s s 2 +   ω c Q s + ω c 2
Band-pass filters at the specified center frequency and passband width, with the specified gain
Equalizer (Q Factor) Band-pass filter at the specified center frequency and quality factor, with the specified gain. The quality factor is the center frequency divided by the passband width.
Gain
H s =   s 2 -   ω c Q s + ω c 2 s 2 +   ω c Q s + ω c 2
All pass filter at the specified gain
High-Pass Butterworth 1
H s =   s 2 s 2 +   2 ω c s + ω c 2
First-order high-pass filter with specified gain, specified cutoff frequency, maximally flat passband and stopband response. Stopband frequency response has a –10dB / decade slope.
High-Pass Butterworth 2 Second-order high-pass filter with specified gain, specified cutoff frequency, maximally flat passband and stopband response. Stopband frequency response has a –20dB / decade.
High-Pass Bessel 2
H s =   s 2 s 2 +   3 ω c s + ω c 2
Second-order high-pass filter with specified gain, specified cutoff frequency, maximally flat phase and constant group delay across passband.
High-Pass Linkwitz Riley 2
H s = ω c s 1 +   ω c s 2
Second-order high-pass filter composed of a Butterworth filter with –3dB at the cutoff frequency. When cascading a low-pass and high-pass Linkwitz Riley filters, the overall gain at the crossover frequency is 0dB.
High-Pass Variable Q 2
H s =   s 2 s 2 +   ω c Q s + ω c 2
Second-order high-pass filter at the specified center frequency, gain, and quality factor. The quality factor is the center frequency divided by the passband width.
High-Pass Chebyshev
H s =   s 2 2 s 2 +   0.911 ω c s + ω c 2
High-pass filter with equiripple in the passband with maximally flat response in stopband
Low-Pass Butterworth 1
H s =   ω c 2 s 2 +   2 ω c s + ω c 2
First-order low-pass filter with specified gain, specified cutoff frequency, maximally flat passband and stopband response. Stopband frequency response has a –10dB / decade slope.
Low-Pass Butterworth 2Second-order low-pass filter with specified gain, specified cutoff frequency, maximally flat passband and stopband response. Stopband frequency response has a –20dB / decade.
Low-Pass Bessel 2
H s =   ω c 2 s 2 +   3 ω c s + ω c 2
Second-order low-pass filter with specified gain, specified cutoff frequency, maximally flat group delay across passband
Low-Pass Linkwitz Riley 2
H s = 1 1 +   ω c s 2
Second-order low-pass filter composed of a Butterworth filter with –3dB at the cutoff frequency. When cascading a low-pass and high-pass Linkwitz Riley filters, the overall gain at the crossover frequency is 0dB.
Low-Pass Variable Q 2
H s =   ω c 2 s 2 +   ω c Q s + ω c 2
Second-order low-pass filter at the specified center frequency, gain and quality factor. The quality factor is the center frequency divided by the passband width.
Low-Pass Chebyshev
H s =   ω c 2 2 s 2 +   0.911 ω c s + ω c 2
Low-pass filter with equiripple in the passband with maximally flat response in stopband
Notch
H s =   s 2 + ω c 2 s 2 +   ω c Q s + ω c 2
Band stop filter at the specified center frequency and stopband width (filter bandwidth)
Phase Shift
H s =   1 -   s ω c 1 +   s ω c
All pass filter with 180 degree phase shift at the specified center frequency through the width given by the bandwidth
Treble Shelf
H s =   s 2 s 2 +   ω c s + ω c 2
Specified gain applied at the high frequencies past the specified cutoff frequency

In PurePath™ Console, the programmable biquad filter configuration is available in the "Advanced" tab of of user interface. Figure 3-2 shows the option to enable this feature.


Enabling Biquad Filter Programmability in PurePath™ Console

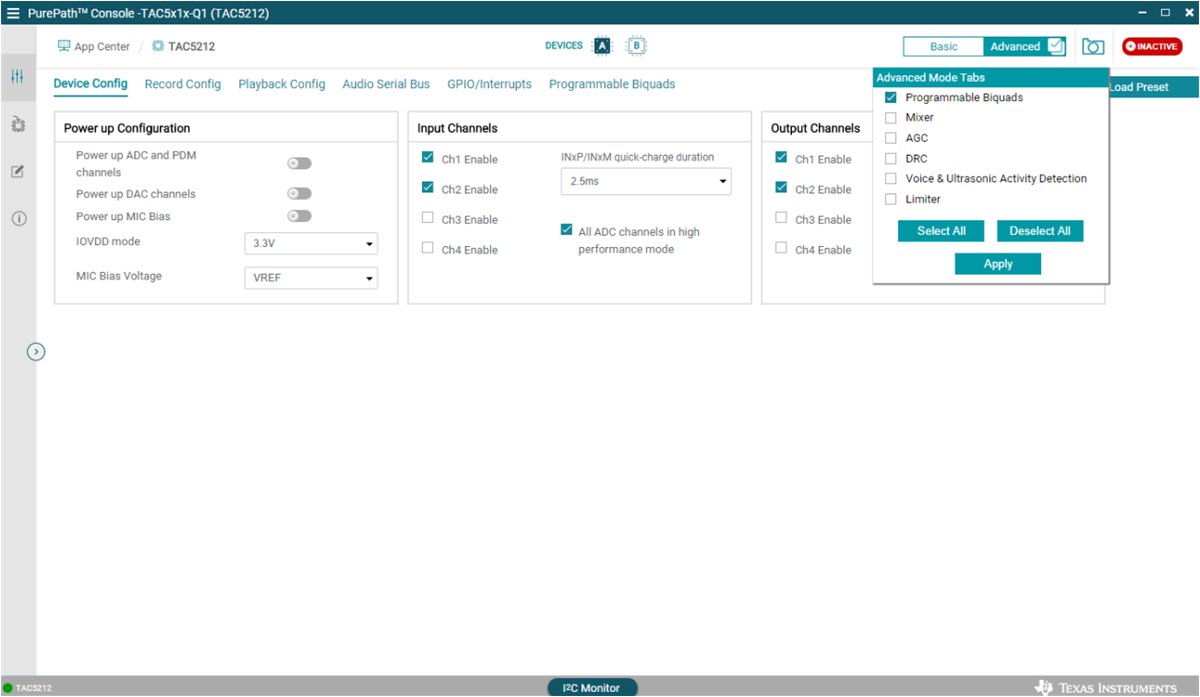
Figure 3-2 Enabling Biquad Filter Programmability in PurePath™ Console