SBAA625A March 2024 – March 2024 ADC32RF54 , ADC32RF55 , ADC34RF52 , AFE7950
Introduction
The analog-to-digital converter (ADC) is the last analog device in the receiver chain. The receiver generally discerns small signals in the presence of noise. Fittingly, a key ADC performance parameter is their own noise contribution to the system.
The traditional noise metric for the ADC is SNR (signal-to-noise ratio) or ENOB (Effective Number of Bits). Each of these parameters has a place, but there is a better metric for modern data converter parts: Noise Spectral Density (NSD). NSD better characterizes the ADC performance closer to a real-world scenario and is not impacted by different digital down-converting/decimation configurations.
SNR
The analog-to-digital converter (ADC) is the last analog device in the receiver chain. The receiver generally discerns small signals in the presence of noise. Fittingly, a key ADC performance parameter is their own noise contribution to the system.
The traditional noise metric for the ADC is SNR (Signal-to-Noise Ratio) or ENOB (Effective Number of Bits). Each of these parameters has a place, but there is a better metric for modern data converter parts: Noise Spectral Density (NSD). NSD better characterizes the ADC performance closer to a real-world scenario and is not impacted by different digital down-converting/decimation configurations.
Noise Elements
ADC noise comes from three core elements: quantization noise, thermal noise, and clock jitter. Each element contributes to the overall SNR performance per Equation 1.
High speed ADCs sampling over 1 GSPS are not generally limited by quantization noise. The other parameters of thermal noise and jitter dominate. Figure 1 provides a visual breakdown on the contributing factors of a hypothetical 12-bit converter operating at 10 GSPS.
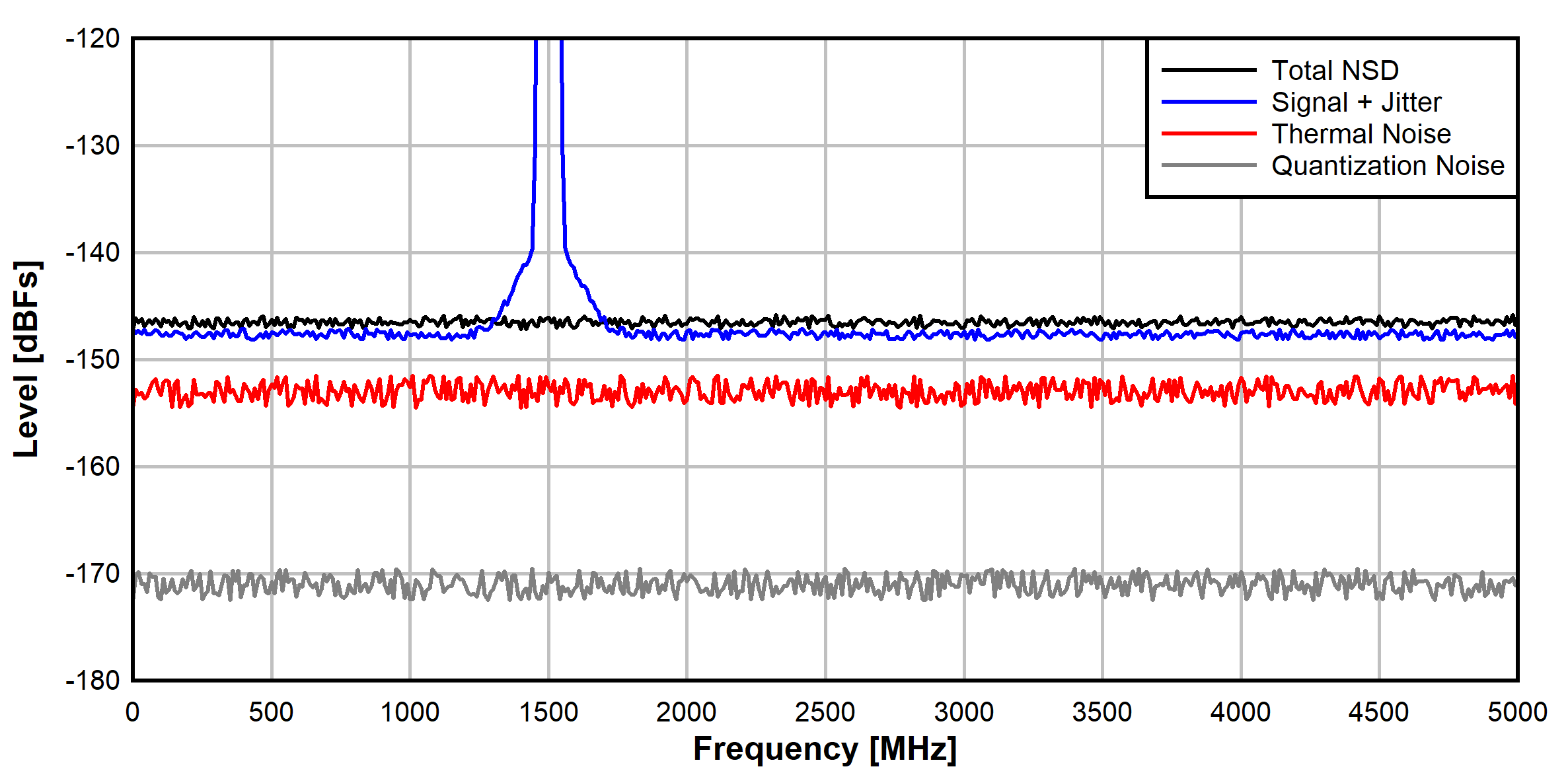 Figure 1 Noise Comparison
Breakdown
Figure 1 Noise Comparison
BreakdownENOB
ENOB is a different metric to portray the same information. ENOB converts the SNR value to an idealized case where the converter’s noise is solely limited by the quantization noise determined by the number of bits. ENOB is calculated from the SNR parameter by:
For example, if the 14-bit converter reports an SNR value of 62 dBFS, the ENOB is 10 bits. That is saying the converter’s noise performance behaves like a perfect 10-bit converter that is only limited by quantization noise.
The Nyquist Dilemma
The first Nyquist zone is defined from DC to the ADC sampling frequency divided by two (Fs/2). Per traditional sampling theory, all signals transform down to the first Nyquist zone. The quantization noise spreads across the entire first Nyquist zone. Broadband thermal noise aliases down into the first Nyquist zone. Calculations for SNR or ENOB integrate all of the noise that resides in the first Nyquist zone.
Modern RF sampling converters often employ digital down-converting and decimation to reduce the data rate needed for transferring the digital data to the FPGA or processor. Decimation removes data points from the stream which can reduce the data rate impacting the signal. Each decimate-by-2 effectively halves the Nyquist zone and correspondingly eliminates half of the noise (due to decimation filtering). Since the signal remains unchanged while the noise is reduced by half, the SNR improves by 3dB. SNR performance when using an arbitrary decimation value D follows Equation 3.
Comparing ADC performance between different devices gets tricky when the resolution, sampling rates, and decimation rates are not exactly the same. Parameters like SNR or ENOB potentially lead to false conclusions on which device has the lowest noise. There has to be a better way!
NSD: A Better Way
Noise Spectral Density (NSD) is a better metric for noise analysis and comparison. NSD normalizes the noise performance per unit bandwidth; typically, the units are dBFS/Hz (for example, relative to the full-scale voltage and normalized to a unit Hz bandwidth). NSD is usually measured with no signal or low signal which is a better gauge of the impact at low signal levels where sensitivity matters. At lower signal drive levels, the jitter component is negated and the thermal noise component is slightly improved. By using the NSD parameter, the noise performance dependence on the sampling rate and decimation are normalized to a unit bandwidth which is more easily compared to other devices.
To demonstrate the point, a couple of hypothetical examples are discussed here. In this case, assume the converters have equivalent full-scale voltage so that expressing the NSD in dBFS/Hz or dBm/Hz is equivalent. Table 1 shows performance comparison from two hypothetical ADCs. Device 1 operates at 10GSPS and Device 2 operates at 5GSPS. At first glance of the SNR or ENOB parameter that is reported in the data sheet, the Device 2 seems better. Device 2 has a higher SNR and correspondingly higher ENOB. The natural inclination is to assume that Device 2 is a lower noise converter, but that is not accurate because the sampling rate (and hence the Nyquist bands) are not equal. The NSD performance of Device 1 is actually 1dB lower. Device 1 is actually the lower noise converter. To see that manifest as an SNR parameter, decimate each device properly to get to an equivalent bandwidth. In the example, each device is decimated to get to a 2.5GHz bandwidth. Low and behold, the 1dB lower NSD parameter also translates to a 1dB better SNR parameter in an equivalent bandwidth. Another way to understand this phenomenon is to realize the benefit of over-sampling (for example, sampling at a much higher rate than required by Nyquist theorem) that translates to benefits in system noise performance.
| Device 1 | Device 2 | |
|---|---|---|
| Fs [GHz] | 10 | 5 |
| SNR [dBFS] | 58.0 | 60.0 |
| ENOB [bits] | 9.3 | 9.7 |
| NSD [dBFS/Hz] | -155 | -154 |
| Dec Factor | 4 | 2 |
| Nyq BW [GHz] | 2.5 | 2.5 |
| SNR [dBFS] | 64.0 | 63.0 |
Conclusion
When investigating high-speed data converters, do not just look at the resolution (number of bits) or the published signal-to-noise ratio. These parameter present challenges when comparing different converters operating at different sampling rates. For a proper comparison, the Nyquist bandwidth needs to be equivalent. This is easily streamlined by comparing the NSD performance as it mostly negates the external clock jitter impact to the measurement and normalizes to a 1Hz bandwidth.
References
- Texas Instruments, RF Sampling: How Over-sampling Is Cheating Physics, technical article.
- Texas Instruments, Blast past Interference Using Digital-down Converters in RF Sampling Receivers, technical article.