-
Power factor correction using peak current-mode control
Power factor correction using peak current-mode control
1 Introduction
An offline power supply requires power factor correction (PFC) when dealing with power levels greater than 75 W. The goal of PFC is to control the input current to follow the input voltage so that the load appears as if it is a pure resistor. With a sinusoidal AC input voltage, the input current also needs to be sinusoidal. In order to control the input current, it must be sensed.
Designers often use one of two current-sensing methods in a PFC application. The first method is to place a shunt resistor at the PFC ground return path (designated as R1 in Figure 1-1) to sense the input current, which is sent to an average current-mode controller [1] (shown in Figure 1-2) to force the input current to follow the input voltage. Because the shunt resistor senses the full boost inductor current, this current-sensing method provides a good power factor and low total harmonic distortion (THD). The shunt resistor does cause extra power losses, however, which could be a problem in applications that require high efficiency.
A second method is to place a current transformer in series with a boost switch to sense the switching current, designated as CT and R2 in Figure 1-1. This method is preferable when the use of a current shunt is not applicable, such as for interleaved PFC [2] and semi-bridgeless PFC [3]. Because the current transformer only senses the switching current (IQ) (not the full inductor current), to control the full inductor current, a simple solution is to sample at the middle of the current transformer output (the middle of the pulse-width modulation [PWM] on-time). Sampling works because the middle-point instantaneous current value equals the average inductor current value in continuous conduction mode (CCM), as shown in Figure 1-3. This method has fewer power losses than the first method, but it also has limitations: the duty cycle for PFC varies from 0% to 100%. When the duty cycle is small, the PWM on-time is small; therefore, it is difficult to sample exactly at the middle of the PWM on-time. Any sample position offset can cause feedback signal errors and deteriorate both THD and the power factor.
This document introduces a new method – a special peak current mode to control PFC and achieve a unity power factor. This method does not need a current shunt, so power losses are eliminated. And although it still uses the current transformer to sense the switching current, there is no need to sample at the middle of the PWM on-time, so the sample position offset issue goes away. There are additional benefits as well.
2 Peak current-mode control for CCM PFC
Peak current-mode control [4] is widely used in DC/DC converters, but it is not suitable for PFC because PFC needs to control the average current, not the peak current. Controlling the inductor peak current results in poor THD and a low-power factor.
Through the use of a special PWM generator, as shown in Figure 2-1, peak current-mode control becomes possible for PFC. In Figure 2-1, the sensed switching current IQ is compared with a saw wave. The saw wave peak voltage (VRAMP) starts at the beginning of each switching period, and its magnitude linearly drops to 0 V at the end of the switching period. The boost switch (Q) turns on at the beginning of the switching period. Q turns off when IQ exceeds the saw wave.
This kind of PWM generator already exists in almost all digital power controllers, such as TI’s C2000™ real-time microcontrollers and the UCD3138. These digital controllers have a peak current-mode control module with programmable slope compensation. Programming the compensation with a slope of VRAMP/T generates the intended saw wave.
To achieve a unity power factor, Equation 1 calculates the peak value of the saw wave VRAMP as:
where Gv is the voltage loop output, Vout is the PFC output voltage, L is the inductance of the boost inductor, R is the current-sense resistor at the current transformer output, and Ton is the PFC PWM on-time.
Since the PWM on-time is almost the same in two consecutive switching cycles, you can use the Ton information from the previous switching cycle to calculate the VRAMP value for this switching cycle.
Take a look at how to achieve a unity power factor with this control method. From Figure 3, during Ton time, the input voltage applies to the inductor, causing the inductor current to rise from I1 to I2. Employing Equation 2:
where Vin is the PFC input voltage. Equation 3 calculates the average inductor current in each switching cycle as:
Substituting Equation 2 into Equation 3 results in Equation 4:
From Figure 2-1, Equation 5 is:
Equation 6 applies to PFC operating at CCM in steady state:
Substituting Equation 6 into Equation 5 and solving for I2 results in Equation 7:
Substituting Equation 1 and Equation 7 into Equation 4 results in Equation 8:
In Equation 8, Gv is the PFC voltage loop output. It is constant in steady state; therefore, Iavg is proportional to Vin and follows the shape of Vin. If Vin is a sine wave, Iavg will also be a sine wave. Controlling the inductor peak current achieves a unity power factor.
Compared to traditional average current-mode control, this method eliminates the power losses caused by the current shunt resistor. And compared to the current transformer sensing method, which requires a precise sampling position, this method does not need to sample the current. Instead, an analog comparator determines the PWM off instant, eliminating the sample offset issue.
To save system costs, some designers prefer combo control, where a single controller controls both PFC and the DC/DC controller. You can place the combo controller on either the primary or secondary side of the AC/DC power supply; each has its advantages and disadvantages. If the combo controller is chosen to be put on the primary side, the DC/DC output voltage and current information need to be sent to primary side across the isolation boundary, and the communication between the controller and host also needs to across the isolation boundary. If the combo controller is chosen to be put on the secondary side, because the conventional average current-mode control method requires input AC voltage information, the input voltage must be sensed and used to modulate the current-loop reference. Sensing the input voltage across the isolation boundary is a challenge.
In the new control method, Equation 1 includes only Vout, not Vin. Because there is no need to sense Vin, you can eliminate the Vin sensing circuit. This control method needs only the current transformer output and Vout information. Because the current transformer provides isolation, a low-cost optocoupler can sense Vout and send it to the secondary side. You can then put the PFC controller on the secondary side of the AC/DC power supply and combine it with the DC/DC controller, which is also on the secondary side, to create a combo controller, which will significantly reduce system costs.
3 Peak current-mode control for DCM PFC
You can extend the same algorithm to discontinuous conduction mode (DCM) operation. Figure 3-1 shows the inductor current waveform in DCM. The inductor current drops to zero at the end of Toff and stays at zero for the rest of period Tdcm; therefore, T = Ton + Toff + Tdcm. The PWM waveform generator is the same as Figure 2-1, but the PWM off-time is Toff + Tdcm, not Toff, as shown in Figure 3-2.
Rewriting Equation 4 to Equation 9 calculates the average current in DCM for one switching cycle:
In steady state, inductor volt-second must be balanced in each switching cycle, resulting in Equation 10:
Solving for Toff and substituting Equation 9 results in Equation 11:
From Equation 6, Equation 12 is:
Equation 13 calculates the peak value of the saw wave VRAMP as:
Substituting Equation 13 into Equation 12 and solving for I2 results in Equation 14:
Substituting I2 into Equation 11 results in Equation 15:
In Equation 15, Gv is constant in steady state; therefore, Iavg is proportional to Vin and follows the shape of Vin. If Vin is a sine wave, Iavg will also be a sine wave, thus achieving a unity power factor.
Equation 9 through Equation 15 are valid for both CCM and DCM, so if the saw wave signal peak value is generated according to Equation 13, then it is possible to achieve a unity power factor for both CCM and DCM.
Equation 1 is a special case of Equation 13 where T = Ton + Toff. For applications in which light loads (PFC will be in DCM mode at light load), THD and the power factor are not important, use Equation 1 to simplify the implementation.
4 Test results
It was verified that this proposed control method on a 360-W PFC evaluation module (EVM). Figure 4-1 shows the input current waveform, where you can see a good sine current waveform.
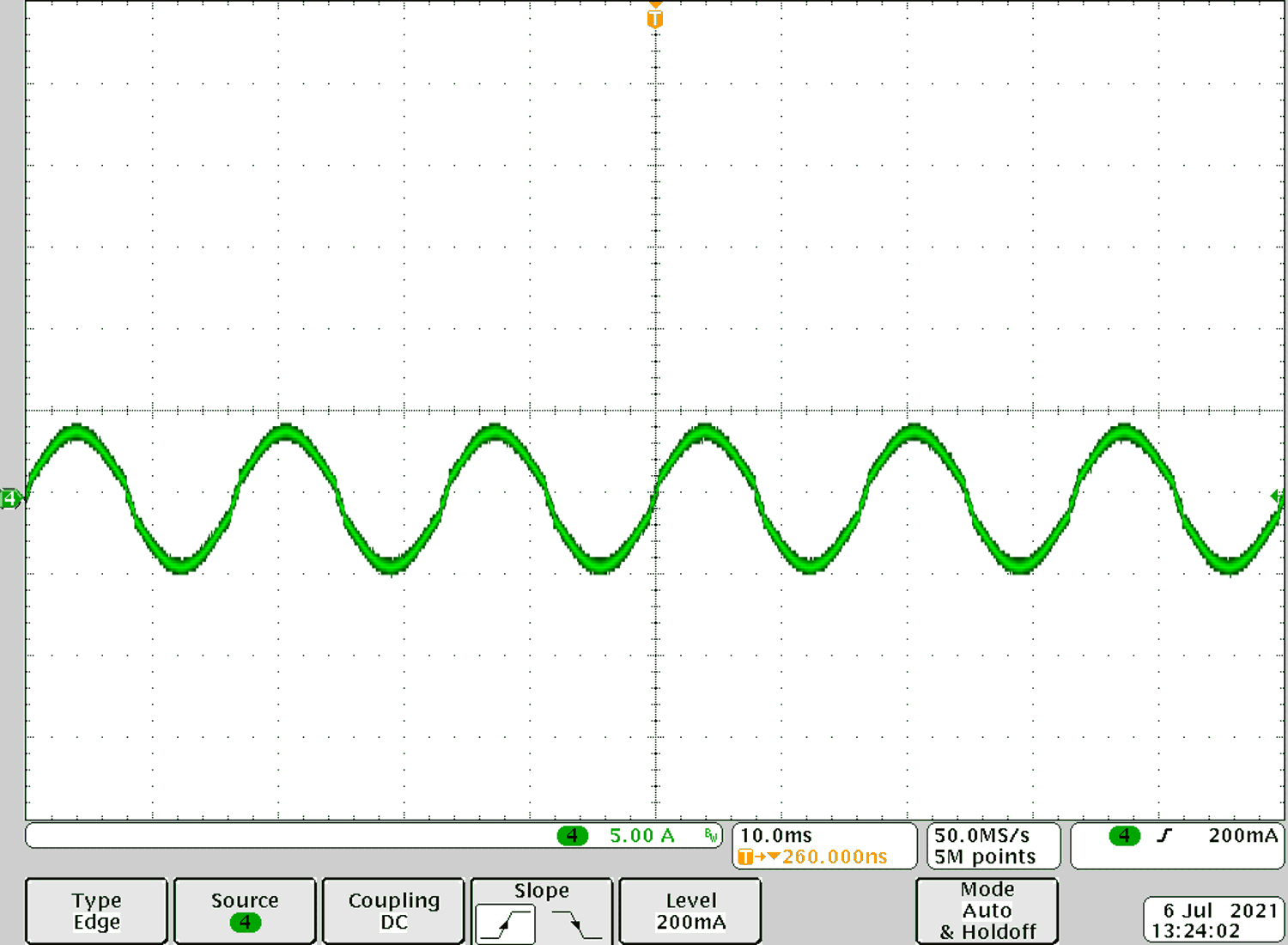 Figure 4-1 Test results on a 360-W PFC
EVM.
Figure 4-1 Test results on a 360-W PFC
EVM.5 Conclusion
This novel peak current mode control method for PFC has many advantages compare to traditional average current mode control method. Placing the PFC controller on the secondary side of the AC/DC power supply to create a combo controller with the DC/DC controller reduces costs. Eliminating the current shut resistor improves efficiency by eliminating power losses. Improving THD by eliminating the feedback signal error caused by small PWM duty when using current transformer. Finally, it is easy to implement this control method with existing digital power controllers such as C2000 MCUs and the UCD3138.
6 References
- Texas Instruments: High Power Factor Preregulator for Off-Line Power Supplies
- Texas Instruments: Designing a UCD3138 Controlled Interleaved PFC
- Texas Instruments: Designing a UCD3138 Controlled Bridgeless PFC
- Texas Instruments: Current-Mode Control of Switching Power Supplies
IMPORTANT NOTICE AND DISCLAIMER
TI PROVIDES TECHNICAL AND RELIABILITY DATA (INCLUDING DATASHEETS), DESIGN RESOURCES (INCLUDING REFERENCE DESIGNS), APPLICATION OR OTHER DESIGN ADVICE, WEB TOOLS, SAFETY INFORMATION, AND OTHER RESOURCES “AS IS” AND WITH ALL FAULTS, AND DISCLAIMS ALL WARRANTIES, EXPRESS AND IMPLIED, INCLUDING WITHOUT LIMITATION ANY IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE OR NON-INFRINGEMENT OF THIRD PARTY INTELLECTUAL PROPERTY RIGHTS.
These resources are intended for skilled developers designing with TI products. You are solely responsible for (1) selecting the appropriate TI products for your application, (2) designing, validating and testing your application, and (3) ensuring your application meets applicable standards, and any other safety, security, or other requirements. These resources are subject to change without notice. TI grants you permission to use these resources only for development of an application that uses the TI products described in the resource. Other reproduction and display of these resources is prohibited. No license is granted to any other TI intellectual property right or to any third party intellectual property right. TI disclaims responsibility for, and you will fully indemnify TI and its representatives against, any claims, damages, costs, losses, and liabilities arising out of your use of these resources.
TI’s products are provided subject to TI’s Terms of Sale (www.ti.com/legal/termsofsale.html) or other applicable terms available either on ti.com or provided in conjunction with such TI products. TI’s provision of these resources does not expand or otherwise alter TI’s applicable warranties or warranty disclaimers for TI products.
Mailing Address: Texas Instruments, Post Office Box 655303, Dallas, Texas 75265
Copyright © 2023, Texas Instruments Incorporated