SLYY211 E-book

SLYY211 October 2021 TMS320F2800132 , TMS320F2800133 , TMS320F2800135 , TMS320F2800137 , TMS320F2800152-Q1 , TMS320F2800153-Q1 , TMS320F2800154-Q1 , TMS320F2800155 , TMS320F2800155-Q1 , TMS320F2800156-Q1 , TMS320F2800157 , TMS320F2800157-Q1 , TMS320F280021 , TMS320F280021-Q1 , TMS320F280023 , TMS320F280023-Q1 , TMS320F280023C , TMS320F280025 , TMS320F280025-Q1 , TMS320F280025C , TMS320F280025C-Q1 , TMS320F280033 , TMS320F280034 , TMS320F280034-Q1 , TMS320F280036-Q1 , TMS320F280036C-Q1 , TMS320F280037 , TMS320F280037-Q1 , TMS320F280037C , TMS320F280037C-Q1 , TMS320F280038-Q1 , TMS320F280038C-Q1 , TMS320F280039 , TMS320F280039-Q1 , TMS320F280039C , TMS320F280039C-Q1 , TMS320F280040-Q1 , TMS320F280040C-Q1 , TMS320F280041 , TMS320F280041-Q1 , TMS320F280041C , TMS320F280041C-Q1 , TMS320F280045 , TMS320F280048-Q1 , TMS320F280048C-Q1 , TMS320F280049 , TMS320F280049-Q1 , TMS320F280049C , TMS320F280049C-Q1 , TMS320F28075 , TMS320F28075-Q1 , TMS320F28076 , TMS320F28374D , TMS320F28374S , TMS320F28375D , TMS320F28375S , TMS320F28375S-Q1 , TMS320F28376D , TMS320F28376S , TMS320F28377D , TMS320F28377D-EP , TMS320F28377D-Q1 , TMS320F28377S , TMS320F28377S-Q1 , TMS320F28378D , TMS320F28378S , TMS320F28379D , TMS320F28379D-Q1 , TMS320F28379S

10.4 Frequency response

If a steady state sine wave, $u (t) = u_{0} \sin (ω t + α)$ is applied to a linear system denoted by $G (s)$ , the linear system would respond at the same frequency with a certain phase and magnitude, giving output $y (t) = y_{0} \sin (ω t + β)$ . The amplitude is modified by $\frac{y_{0}}{u_{0}}$ and the phase is shifted by $\emptyset = β - α o r < G (j ω)$

Bode plot basics

The frequency response for the magnitude or gain plot is the change in voltage gain as frequency changes. The change is specified on a Bode plot, a plot of frequency versus voltage gain in dB (decibles). Bode plots are usually plotted as semi-log plots with frequency on the x-axis, log scale, and gain on the y-axis, linear scale. The other half of the frequency response is the phase shift versus frequency and is plotted as frequency versus degree phase shift. Phase plots are usually plotted as semi-log plots with frequency on the x-axis, log scale, and phase shift on the y-axis, linear scale.

Definitions

Voltage gain in decibels

Equation 100.

V o l t a g e g a i n (d B) = 20 l o g (\frac{V_{O U T}}{V_{I N}})

Power gain in decibels

Equation 101.

P o w e r g a i n (d B) = 10 l o g (\frac{P_{O U T}}{P_{I N}})

Used for input or output power

Equation 102.

P o w e r m e a s u r e d (d B m) = 10 l o g (\frac{P o w e r m e a s u r e d (W)}{1 m W})

Table 10-3 Examples of common gain values and dB equivalent.

A (V/V)	A (dB)
0.001	-60
0.01	-40
0.1	-20
1	0
10	20
100	40
1,000	60
10,000	80
100,000	100
1,000,000	120
10,000,000	140

Where

Roll-off rate is the decrease in gain with frequency

Decade is a tenfold increase or decrease in frequency (from 10 Hz to 100 Hz is one decade)

Octave is the doubling or halving of frequency (from 10 Hz to 20 Hz is one octave)

Bode plots: Poles

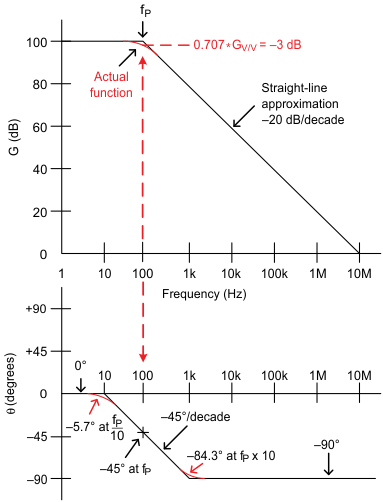Figure 10-1 Pole gain and phase.

Where

Pole location = $f_{p}$ (cutoff frequency)

Magnitude $(f < f_{p})$ = $G_{D C}$ (for example, 100 dB)

Magnitude $(f = f_{p})$ = -3 dB

Magnitude $(f > f_{p})$ = -20 dB/decade

Phase $(f = f_{p})$ = ${- 45}^{°}$

Phase $(0.1 f_{p} < f < 10 f_{p})$ = ${- 45}^{°}$ /decade

Phase $(f > 10 f_{p})$ = ${- 90}^{°}$

Phase $(f < 0.1 f_{p})$ = $0^{°}$

Pole (equations)

As a complex number

Equation 103.

G_{V} = \frac{V_{O U T}}{V_{I N}} = \frac{G_{D C}}{j (\frac{f}{f_{p}}) + 1}

Magnitude

Equation 104.

G_{V} = \frac{V_{O U T}}{V_{I N}} = \frac{G_{D C}}{\sqrt{{(\frac{f}{f_{p}})}^{2} + 1}}

Phase Shift

Equation 105.

θ = - \tan^{- 1} (\frac{f}{f_{p}})

Magnitude in dB

Equation 106.

G_{d B} = 20 L o g (G_{V})

Where

$G_{V}$ = voltage gain in V/V

$G_{D B}$ = voltage gain in decibels

$G_{D C}$ = the dc or low frequency voltage gain

f = frequency in Hz

$f_{p}$ = frequency at which the pole occurs

$θ$ = phase shift of the signal from input to output

j = indicates imaginary number or $\sqrt{- 1}$

Bode plot (zeros)

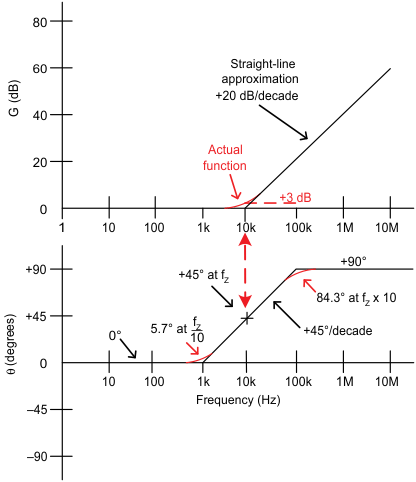Figure 10-2 Zero gain and phase.

Where

Zero location = $f_{z}$

Magnitude $(f < f_{z})$ = 0 dB

Magnitude $(f = f_{z})$ = +3 dB

Magnitude $(f > f_{z})$ = +20 dB/decade

Phase $(f = f_{z})$ = ${+ 45}^{°}$

Phase $(0.1 f_{z} < f < 10 f_{z})$ = ${+ 45}^{°}$ /decade

Phase $(f > 10 f_{z})$ = ${+ 90}^{°}$

Phase $(f < 0.1 f_{z})$ = $0^{°}$

Zero (equations)

As a complex number

Equation 107.

G_{V} = \frac{V_{O U T}}{V_{I N}} = G_{D C} (j (\frac{f}{f_{p}}) + 1)

Magnitude

Equation 108.

G_{V} = \frac{V_{O U T}}{V_{I N}} = G_{D C} \sqrt{{(\frac{f}{f_{z}})}^{2} + 1}

Phase Shift

Equation 109.

θ = \tan^{- 1} (\frac{f}{z})

Magnitude in dB

Equation 110.

G_{d B} = 20 L o g (G_{V})

Where

$G_{V}$ = voltage gain in V/V

$G_{D B}$ = voltage gain in decibels

$G_{D C}$ = the dc or low frequency voltage gain

f = frequency in Hz

$f_{z}$ = frequency at which the zero occurs

$θ$ = phase shift of the signal from input to output

j = indicates imaginary number or $\sqrt{- 1}$