SPRUHJ1I January   2013  – October 2021 TMS320F2802-Q1 , TMS320F28026-Q1 , TMS320F28026F , TMS320F28027-Q1 , TMS320F28027F , TMS320F28027F-Q1 , TMS320F28052-Q1 , TMS320F28052F , TMS320F28052F-Q1 , TMS320F28052M , TMS320F28052M-Q1 , TMS320F28054-Q1 , TMS320F28054F , TMS320F28054F-Q1 , TMS320F28054M , TMS320F28054M-Q1 , TMS320F2806-Q1 , TMS320F28062-Q1 , TMS320F28062F , TMS320F28062F-Q1 , TMS320F28068F , TMS320F28068M , TMS320F28069-Q1 , TMS320F28069F , TMS320F28069F-Q1 , TMS320F28069M , TMS320F28069M-Q1

 

  1. 1 Read This First
    1. 1.1 Glossary
    2. 1.1 Support Resources
    3. 1.1 Trademarks
  2. 1 Introduction
    1. 1.1 An Overview of InstaSPIN-FOC™ and FAST™
      1. 1.1.1 FAST™ Estimator Features
      2. 1.1.2 InstaSPIN-FOC™ Solution Features
      3. 1.1.3 InstaSPIN-FOC™ Block Diagrams
      4. 1.1.4 Comparing FAST™ Estimator to Typical Solutions
      5. 1.1.5 FAST™ Provides Sensorless FOC Performance
        1. 1.1.5.1 FAST Estimator Replaces Mechanical Sensor
        2. 1.1.5.2 Rotor Angle Accuracy Critical for Performance
    2. 1.2 An Overview of InstaSPIN-MOTION™ and SpinTAC™
      1. 1.2.1 InstaSPIN-MOTION™ Key Capabilities and Benefits
        1. 1.2.1.1 The FAST Unified Software Observer
        2. 1.2.1.2 The SpinTAC Motion Control Suite
          1. 1.2.1.2.1 IDENTIFY
          2. 1.2.1.2.2 CONTROL
          3. 1.2.1.2.3 MOVE
          4. 1.2.1.2.4 PLAN
        3. 1.2.1.3 Additional InstaSPIN-MOTION Features
      2. 1.2.2 InstaSPIN-MOTION™ Block Diagrams
      3. 1.2.3 Application Examples
        1. 1.2.3.1 Treadmill Conveyor: Smooth Motion Across Varying Speeds and Loads
        2. 1.2.3.2 Video Camera: Smooth Motion and Position Accuracy at Low Speeds
        3. 1.2.3.3 Washing Machine: Smooth Motion and Position Accuracy at Low Speeds
          1. 1.2.3.3.1 Agitation Cycle
          2. 1.2.3.3.2 Spin Cycles
          3. 1.2.3.3.3 InstaSPIN-MOTION Works Over the Entire Operating Range
  3. 2 Quick Start Kits - TI Provided Software and Hardware
    1. 2.1 Overview
    2. 2.2 Evaluating InstaSPIN-FOC™ and InstaSPIN-MOTION™
  4. 3 InstaSPIN™ and MotorWare™
    1. 3.1 Overview
    2. 3.2 MotorWare™ Directory Structure
      1. 3.2.1 MotorWare™ – drivers
      2. 3.2.2 MotorWare™ – ide
      3. 3.2.3 MotorWare™ – modules
      4. 3.2.4 MotorWare™ – solutions
    3. 3.3 MotorWare™ Object-Oriented Design
      1. 3.3.1 Objects
      2. 3.3.2 Methods
        1. 3.3.2.1 Init Method
        2. 3.3.2.2 Set Method
        3. 3.3.2.3 Get Method
        4. 3.3.2.4 Run Method
    4. 3.4 InstaSPIN-FOC™ API
      1. 3.4.1 Controller API Functions – ctrl.c, ctrl.h, CTRL_obj.h
        1. 3.4.1.1 CTRL Enumerations and Structures
          1.        CTRL_Obj
          2.        CTRL_State_e
          3.        CTRL_ErrorCode_e
          4.        CTRL_TargetProc_e
          5.        CTRL_Type_e
          6.        CTRL_Version
        2. 3.4.1.2 CTRL State Control and Error Handling
          1.        CTRL_initCtrl()
          2.        CTRL_updateState ()
          3.        CTRL_isError ()
          4.        CTRL_checkForErrors ()
        3. 3.4.1.3 CTRL Get Functions
          1.        CTRL_getCount_current ()
          2.        CTRL_getCount_isr ()
          3.        CTRL_getCount_speed ()
          4.        CTRL_getCount_state ()
          5.        CTRL_getCount_traj ()
          6.        CTRL_getCtrlFreq ()
          7.        CTRL_getCtrlPeriod_sec ()
          8.        CTRL_getErrorCode ()
          9.        CTRL_getEstHandle ()
          10.        CTRL_getFlag_enableCtrl ()
          11.        CTRL_getFlag_enableDcBusComp ()
          12.        CTRL_getFlag_enablePowerWarp ()
          13.        CTR CTRL_getFlag_enableOffset ()
          14.        CTRL_getFlag_enableSpeedCtrl ()
          15.        CTRL_getFlag_enableUserMotorParams ()
          16.        CTRL_getGains ()
          17.        CTRL_getIab_filt_pu ()
          18.        CTRL_getIab_filt_addr ()
          19.        CTRL_getIab_in_addr ()
          20.        CTRL_getIab_in_pu ()
          21.        CTRL_getId_in_pu ()
          22.        CTRL_getId_ref_pu ()
          23.        CTRL_getIdq_in_addr ()
          24.        CTRL_getIdq_in_pu ()
          25.        CTRL_getIdq_ref_pu ()
          26.        CTRL_getIdRated_pu ()
          27.        CTRL_getIq_in_pu ()
          28.        CTRL_getIq_ref_pu ()
          29.        CTRL_getKi ()
          30.        CTRL_getKd ()
          31.        CTRL_getKp ()
          32.        CTRL_getLhf ()
          33.        CTRL_getMagCurrent_pu ()
          34.        CTRL_getMaxVsMag_pu ()
          35.        CTRL_getMaximumSpeed_pu ()
          36.        CTRL_getMotorRatedFlux ()
          37.        CTRL_getMotorType ()
          38.        CTRL_getNumCtrlTicksPerCurrentTick ()
          39.        CTRL_getNumCtrlTicksPerSpeedTick ()
          40.        CTRL_getNumCtrlTicksPerTrajTick ()
          41.        CTRL_getNumIsrTicksPerCtrlTick ()
          42.        CTRL_getRefValue_pu ()
          43.        CTRL_getRhf ()
          44.        CTRL_getRoverL ()
          45.        CTRL_getSpd_max_pu ()
          46.        CTRL_getSpd_out_addr ()
          47.        CTRL_getSpd_out_pu ()
          48.        CTRL_getSpd_ref_pu ()
          49.        CTRL_getSpd_int_ref_pu ()
          50.        CTRL_getState ()
          51.        CTRL_getTrajFreq ()
          52.        CTRL_getTrajPeriod_sec ()
          53.        CTRL_getTrajStep ()
          54.        CTRL_getUi ()
          55.        CTRL_getVab_in_pu ()
          56.        CTRL_getVab_out_addr ()
          57.        CTRL_getVab_out_pu ()
          58.        CTRL_getVd_out_addr ()
          59.        CTRL_getVd_out_pu ()
          60.        CTRL_getVdq_out_addr ()
          61.        CTRL_getVdq_out_pu ()
          62.        CTRL_getVersion ()
          63.        CTRL_getVq_out_addr ()
          64.        CTRL_getVq_out_pu ()
          65.        CTRL_getWaitTime ()
        4. 3.4.1.4 CTRL Counter Functions
          1.        CTRL_incrCounter_current ()
          2.        CTRL_incrCounter_isr ()
          3.        CTRL_incrCounter_speed ()
          4.        CTRL_incrCounter_state ()
          5.        CTRL_incrCounter_traj ()
          6.        CTRL_resetCounter_current ()
          7.        CTRL_resetCounter_isr ()
          8.        CTRL_resetCounter_speed ()
          9.        CTRL_resetCounter_state ()
          10.        CTRL_resetCounter_traj ()
        5. 3.4.1.5 CTRL Set Functions
          1.        CTRL_setCtrlFreq_Hz ()
          2.        CTRL_setCtrlFreq_sec ()
          3.        CTRL_setErrorCode ()
          4.        CTRL_setEstParams ()
          5.        CTRL_setFlag_enableCtrl ()
          6.        CTRL_setFlag_enableDcBusComp ()
          7.        CTRL_setFlag_enablePowerWarp ()
          8.        CTRL_setFlag_enableOffset ()
          9.        calibrationCTRL_setFlag_enableSpeedCtrl ()
          10.        CTRL_setFlag_enableUserMotorParams ()
          11.        CTRL_setGains ()
          12.        CTRL_setIab_in_pu ()
          13.        CTRL_setIab_filt_pu ()
          14.        CTRL_setId_ref_pu ()
          15.        CTRL_setIdq_in_pu ()
          16.        CTRL_setIdq_ref_pu ()
          17.        CTRL_setIdRated_pu ()
          18.        CTRL_setIq_ref_pu ()
          19.        CTRL_setKd ()
          20.        CTRL_setKi ()
          21.        CTRL_setKp ()
          22.        CTRL_setLhf ()
          23.        CTRL_setMagCurrent_pu ()
          24.        CTRL_setMaxVsMag_pu ()
          25.        CTRL_setMaxAccel_pu ()
          26.        CTRL_setMaximumSpeed_pu ()
          27.        CTRL_setParams()
          28.        CTRL_setNumCtrlTicksPerCurrentTick ()
          29.        CTRL_setNumCtrlTicksPerSpeedTick ()
          30.        CTRL_setNumCtrlTicksPerTrajTick ()
          31.        CTRL_setNumIsrTicksPerCtrlTick ()
          32.        CTRL_setRhf ()
          33.        CTRL_setRoverL ()
          34.        CTRL_setSpdMax ()
          35.        CTRL_setSpd_max_pu ()
          36.        CTRL_setSpd_out_pu ()
          37.        CTRL_setSpd_ref_pu ()
          38.        CTRL_setSpd_ref_krpm ()
          39.        CTRL_setState ()
          40.        CTRL_setTrajFreq_Hz ()
          41.        CTRL_setTrajPeriod_sec ()
          42.        CTRL_setUi ()
          43.        CTRL_setupClarke_I ()
          44.        CTRL_setupClarke_V ()
          45.        CTRL_setupEstIdleState ()
          46.        CTRL_setupEstOnLineState ()
          47.        CTRL_setUserMotorParams ()
          48.        CTRL_setVab_in_pu ()
          49.        CTRL_setVab_out_pu ()
          50.        CTRL_setVdq_out_pu ()
          51.        CTRL_setWaitTimes ()
          52.        CTRL_setup ()
          53.        CTRL_setupCtrl ()
          54.        CTRL_setupEst ()
          55.        CTRL_setupTraj ()
        6. 3.4.1.6 CTRL Run and Compute Functions
          1.        CTRL_angleDelayComp ()
          2.        CTRL_computePhasor ()
          3.        CTRL_doCurrentCtrl ()
          4.        CTRL_doSpeedCtrl ()
          5.        CTRL_run()
          6.        CTRL_runTraj ()
          7.        CTRL_runOffLine ()
          8.        CTRL_runOnLine ()
          9.        CTRL_runOnLine_User ()
          10.        CTRL_useZeroIq_ref ()
      2. 3.4.2 Estimator API Functions – FAST™ Library – est.h, est_states.h
        1. 3.4.2.1 EST Enumerations and Structures
          1.        EST_RsOnLineFilterType_e
          2.        EST_ErrorCode_e
          3.        EST_State_e
        2. 3.4.2.2 EST Set Functions
          1.        EST_setRsOnLineId_pu ()
          2.        EST_setAngle_pu ()
          3.        EST_setDcBus_pu ()
          4.        EST_setDir_qFmt ()
          5.        EST_setFe_neg_max_pu ()
          6.        EST_setFe_pos_min_pu ()
          7.        EST_setFlag_enableFluxControl ()
          8.        EST_setFlag_enableForceAngle ()
          9.        EST_setFlag_enableRsOnLine ()
          10.        EST_setFlag_enableRsRecalc ()
          11.        EST_setFlag_estComplete ()
          12.        EST_setFlag_updateRs ()
          13.        EST_setForceAngleDelta_pu ()
          14.        EST_setFreqB0_lp_pu ()
          15.        EST_setFreqBeta_lp_pu ()
          16.        EST_setFullScaleCurrent ()
          17.        EST_setFullScaleFlux ()
          18.        EST_setFullScaleFreq ()
          19.        EST_setFullScaleInductance ()
          20.        EST_setFullScaleResistance ()
          21.        EST_setFullScaleVoltage ()
          22.        EST_setIdle ()
          23.        EST_setIdle_all ()
          24.        EST_setId_ref_pu ()
          25.        EST_setIdRated_pu ()
          26.        EST_setIq_ref_pu ()
          27.        EST_setLs_d_pu ()
          28.        EST_setLs_delta_pu ()
          29.        EST_setLs_dq_pu ()
          30.        EST_setLs_q_pu ()
          31.        EST_setLs_qFmt ()
          32.        EST_setMaxAccel_pu ()
          33.        EST_setMaxAccel_est_pu ()
          34.        EST_setMaxCurrentSlope_pu ()
          35.        EST_setMaxCurrentSlope_PowerWarp_pu ()
          36.        EST_setRr_pu ()
          37.        EST_setRr_qFmt ()
          38.        EST_setRs_delta_pu ()
          39.        EST_setRsOnLine_pu ()
          40.        EST_setRsOnLine_qFmt ()
          41.        EST_setRsOnLineFilterParams ()
          42.        EST_setRsOnLineId_mag_pu ()
          43.        EST_setRs_pu ()
          44.        EST_setRs_qFmt ()
          45.        EST_updateId_ref_pu ()
        3. 3.4.2.3 EST Get Functions
          1.        EST_get_krpm_to_pu_sf ()
          2.        EST_get_pu_to_krpm_sf ()
          3.        EST_getAngle_pu ()
          4.        EST_getDcBus_pu ()
          5.        EST_ErrorCode_e EST_getErrorCode ()
          6.        EST_getFe ()
          7.        EST_getFe_pu ()
          8.        EST_getFlag_enableForceAngle ()
          9.        EST_getFlag_enableRsOnLine ()
          10.        EST_getFlag_enableRsRecalc ()
          11.        EST_getFlag_estComplete ()
          12.        EST_getFlag_updateRs ()
          13.        EST_getFlux_VpHz ()
          14.        EST_getFlux_Wb ()
          15.        EST_getFlux_pu ()
          16.        EST_getFm ()
          17.        EST_getFm_pu ()
          18.        EST_getForceAngleDelta_pu ()
          19.        EST_getForceAngleStatus ()
          20.        EST_getFreqB0_lp_pu ()
          21.        EST_getFreqBeta_lp_pu ()
          22.        EST_getFslip ()
          23.        280
          24.        EST_getFslip_pu ()
          25.        EST_getFullScaleCurrent ()
          26.        EST_getFullScaleFlux ()
          27.        EST_getFullScaleFreq ()
          28.        EST_getFullScaleInductance ()
          29.        EST_getFullScaleResistance ()
          30.        EST_getFullScaleVoltage ()
          31.        EST_getIdRated ()
          32.        EST_getIdRated_pu ()
          33.        EST_getIdRated_indEst_pu ()
          34.        EST_getIdRated_ratedFlux_pu ()
          35.        EST_getLr_H ()
          36.        EST_getLr_pu ()
          37.        EST_getLr_qFmt ()
          38.        EST_getLs_d_H ()
          39.        EST_getLs_d_pu ()
          40.        EST_getLs_delta_pu ()
          41.        EST_getLs_dq_pu ()
          42.        EST_getLs_q_H ()
          43.        EST_getLs_q_pu ()
          44.        EST_getLs_qFmt ()
          45.        EST_getLs_max_pu ()
          46.        EST_getLs_min_pu ()
          47.        EST_getLs_coarse_max_pu ()
          48.        EST_getMaxAccel_pu ()
          49.        EST_getMaxAccel_est_pu ()
          50.        EST_getMaxCurrentSlope_pu ()
          51.        EST_getMaxCurrentSlope_PowerWarp_pu ()
          52.        EST_getOneOverDcBus_pu ()
          53.        EST_getRr_Ohm ()
          54.        EST_getRr_pu ()
          55.        EST_getRr_qFmt ()
          56.        EST_getRs_delta_pu ()
          57.        EST_getRs_Ohm ()
          58.        EST_getRs_pu ()
          59.        EST_getRs_qFmt ()
          60.        EST_getRs_qFmt ()
          61.        EST_getRsOnLine_Ohm ()
          62.        EST_getRsOnLine_pu ()
          63.        EST_getRsOnLineId_mag_pu ()
          64.        EST_getRsOnLineId_pu ()
          65.        EST_getSpeed_krpm ()
          66.        EST_getSignOfDirection ()
          67.        EST_getSpeed_krpm ()
          68.        EST_getState ()
          69.        EST_getTorque_lbin ()
          70.        EST_getTorque_Nm ()
          71.        EST_getDir_qFmt ()
        4. 3.4.2.4 EST Run and Compute Functions
          1.        EST_computeLr_H ()
          2.        EST_doCurrentCtrl ()
          3.        EST_genOutputLimits_Pid_Id ()
          4.        EST_genOutputLimits_Pid_Iq ()
          5.        EST_run ()
          6.        EST_computeDirection_qFmt ()
        5. 3.4.2.5 EST Counter Functions
          1.        EST_resetCounter_ctrl ()
          2.        EST_resetCounter_state ()
        6. 3.4.2.6 EST State Control and Error Handling Functions
          1.        EST_isError ()
          2.        EST_isIdle ()
          3.        EST_isLockRotor ()
          4.        EST_isMotorIdentified ()
          5.        EST_isOnLine ()
          6.        EST_updateState ()
          7.        EST_useZeroIq_ref ()
      3. 3.4.3 Hardware Abstraction Layer (HAL) API Functions – hal.c, hal.h, hal_obj.h
        1. 3.4.3.1 HAL Enumerations and Structures
          1.        HAL_AdcData_t
          2.        HAL_DacData_t
          3.        HAL_PwmData_t
          4.        HAL_LedNumber_e
          5.        GPIO_Number_e
          6.        HAL_SensorType_e
          7.        HAL_Obj
        2. 3.4.3.2 HAL – ADC and AFE
          1.        HAL_setupAdcs ()
          2.        HAL_setupAfe ()
          3.        HAL_acqAdcInt ()
          4.        HAL_readAdcData()
          5.        HAL_updateAdcBias ()
          6.        HAL_setBias ()
          7.        HAL_getBias ()
          8.        HAL_cal ()
          9.        HAL_AdcCalConversion ()
          10.        HAL_AdcOffsetSelfCal ()
          11.        HAL_getAdcSocSampleDelay ()
          12.        HAL_setAdcSocSampleDelay ()
          13.        HAL_getCurrentScaleFactor ()
          14.        HAL_setCurrentScaleFactor ()
          15.        HAL_getVoltageScaleFactor ()
          16.        HAL_setVoltageScaleFactor ()
          17.        HAL_getNumCurrentSensors ()
          18.        HAL_setNumCurrentSensors ()
          19.        HAL_getNumVoltageSensors ()
          20.        HAL_setNumVoltageSensors ()
          21.        377
          22.        HAL_getOffsetBeta_lp_pu ()
          23.        HAL_setOffsetBeta_lp_pu ()
          24.        HAL_setOffsetInitCond ()
          25.        HAL_getOffsetValue ()
          26.        HAL_setOffsetValue ()
          27.        HAL_runOffsetEst ()
        3. 3.4.3.3 HAL – PWM and PWM-DAC
          1.        HAL_setupPwms ()
          2.        HAL_setupPwmDacs ()
          3.        HAL_readTimerCnt ()
          4.        HAL_reloadTimer ()
          5.        HAL_readPwmPeriod ()
          6.        HAL_disablePwm ()
          7.        HAL_enablePwm ()
          8.        HAL_writeDacData ()
          9.        HAL_writePwmData()
          10.        HAL_readPwmCmpA ()
          11.        HAL_readPwmCmpB ()
          12.        HAL_setTrigger ()
          13.        HAL_acqPwmInt ()
          14.        HAL_enablePwmInt ()
          15.        HAL_hvProtection ()
        4. 3.4.3.4 HAL – CPU Timers
          1.        HAL_setupClks ()
          2.        HAL_setupTimers ()
          3.        HAL_startTimer ()
          4.        HAL_stopTimer ()
          5.        HAL_setTimerPeriod ()
          6.        HAL_getTimerPeriod ()
        5. 3.4.3.5 HAL – GPIO and LED
          1.        HAL_setupGpios ()
          2.        HAL_toggleGpio ()
          3.        HAL_setGpioHigh ()
          4.        HAL_setGpioLow ()
          5.        HAL_toggleLed
        6. 3.4.3.6 HAL – Miscellaneous
          1.        HAL_init()
          2.        HAL_initIntVectorTable ()
          3.        HAL_setParams ()
          4.        HAL_setupFlash ()
          5.        HAL_setupPie ()
          6.        HAL_setupPll ()
          7.        HAL_setupPeripheralClks ()
          8.        HAL_getOscTrimValue ()
          9.        HAL_OscTempComp ()
          10.        HAL_osc1Comp ()
          11.        HAL_osc2Comp ()
          12.        HAL_setupFaults ()
          13.        HAL_setParams()
          14.        HAL_enableDebugInt ()
          15.        HAL_enableGlobalInts ()
          16.        HAL_disableGlobalInts ()
          17.        HAL_disableWdog ()
      4. 3.4.4 User Settings – user.c, user.h, userParams.h
        1. 3.4.4.1 USER Enumerations and Structures
          1.        Struct_USER_Params_
          2.        USER_ErrorCode_e
        2. 3.4.4.2 USER Set and Compute Functions
          1.        USER_setParams()
          2.        USER_calcPIgains ()
          3.        USER_computeTorque_Ls_Id_Iq_pu_to_Nm_sf ()
          4.        USER_computeTorque_Flux_Iq_pu_to_Nm_sf ()
          5.        USER_computeFlux_pu_to_Wb_sf ()
          6.        USER_computeFlux_pu_to_VpHz_sf ()
          7.        USER_computeFlux ()
          8.        USER_computeTorque_Nm ()
          9.        USER_computeTorque_lbin ()
        3. 3.4.4.3 USER Error Handling Functions
          1.        USER_checkForErrors ()
          2.        USER_getErrorCode ()
          3.        USER_setErrorCode ()
      5. 3.4.5 Miscellaneous Functions
        1.       softwareUpdate1p6 ()
    5. 3.5 InstaSPIN-MOTION™ and the SpinTAC™ API
      1. 3.5.1 Header Files, Public Library, and ROM Library
      2. 3.5.2 Version Information
        1. 3.5.2.1 Code Example for Returning SpinTAC™ Version Information
          1. 3.5.2.1.1 Include the Header File
          2. 3.5.2.1.2 Declare the Global Structure
          3. 3.5.2.1.3 Initialize the Configuration Variables
          4. 3.5.2.1.4 Return the Version Information
      3. 3.5.3 SpinTAC™ Structure Names
      4. 3.5.4 SpinTAC™ Variables
    6. 3.6 SpinTAC™ API
      1. 3.6.1 SpinTAC™ Velocity Control
        1. 3.6.1.1 SpinTAC™ Velocity Control Interface
        2. 3.6.1.2 SpinTAC™ Velocity Control Run Function
      2. 3.6.2 SpinTAC™ Velocity Move
        1. 3.6.2.1 SpinTAC™ Velocity Move Interface
        2. 3.6.2.2 SpinTAC™ Velocity Move Run Function
      3. 3.6.3 SpinTAC™ Velocity Plan
        1. 3.6.3.1 SpinTAC™ Velocity Plan Interface
        2. 3.6.3.2 SpinTAC™ Velocity Plan Primary Functions
      4. 3.6.4 SpinTAC™ Velocity Identify
        1. 3.6.4.1 SpinTAC™ Velocity Identify Interface
        2. 3.6.4.2 SpinTAC™ Velocity Identify Run Function
      5. 3.6.5 SpinTAC™ Position Convert
        1. 3.6.5.1 SpinTAC™ Position Convert Interfaces
        2. 3.6.5.2 SpinTAC™ Position Convert Run Function
      6. 3.6.6 SpinTAC™ Position Control
        1. 3.6.6.1 SpinTAC™ Position Control Interface
        2. 3.6.6.2 SpinTAC™ Position Control Run Function
      7. 3.6.7 SpinTAC™ Position Move
        1. 3.6.7.1 SpinTAC™ Position Move Interface
        2. 3.6.7.2 SpinTAC™ Position Move Run Function
      8. 3.6.8 SpinTAC™ Position Plan
        1. 3.6.8.1 SpinTAC™ Position Plan Interface
        2. 3.6.8.2 SpinTAC™ Position Plan Primary Functions
      9. 3.6.9 SpinTAC™ Functions
  5. 4 User Parameters (user.h)
    1. 4.1 Currents and Voltages
      1. 4.1.1  USER_IQ_FULL_SCALE_FREQ_Hz
      2. 4.1.2  USER_IQ_FULL_SCALE_VOLTAGE_V
      3. 4.1.3  USER_ADC_FULL_SCALE_VOLTAGE_V
      4. 4.1.4  USER_VOLTAGE_SF
      5. 4.1.5  USER_IQ_FULL_SCALE_CURRENT_A
      6. 4.1.6  USER_ADC_FULL_SCALE_CURRENT_A
      7. 4.1.7  USER_CURRENT_SF
      8. 4.1.8  USER_NUM_CURRENT_SENSORS
      9. 4.1.9  USER_NUM_VOLTAGE_SENSORS
      10. 4.1.10 I_A_offset , I_B_offset , I_C_offset
      11. 4.1.11 V_A_offset , V_B_offset , V_C_offset
    2. 4.2 Clocks and Timers
      1. 4.2.1 USER_SYSTEM_FREQ_MHz
      2. 4.2.2 USER_PWM_FREQ_kHz
      3. 4.2.3 USER_MAX_VS_MAG_PU
      4. 4.2.4 USER_PWM_PERIOD_usec
      5. 4.2.5 USER_ISR_FREQ_Hz
      6. 4.2.6 USER_ISR_PERIOD_usec
    3. 4.3 Decimation
      1. 4.3.1  USER_NUM_PWM_TICKS_PER_ISR_TICK
      2. 4.3.2  USER_NUM_ISR_TICKS_PER_CTRL_TICK
      3. 4.3.3  USER_NUM_CTRL_TICKS_PER_CURRENT_TICK
      4. 4.3.4  USER_NUM_CTRL_TICKS_PER_EST_TICK
      5. 4.3.5  USER_NUM_CTRL_TICKS_PER_SPEED_TICK
      6. 4.3.6  USER_NUM_CTRL_TICKS_PER_TRAJ_TICK
      7. 4.3.7  USER_CTRL_FREQ_Hz
      8. 4.3.8  USER_EST_FREQ_Hz
      9. 4.3.9  USER_TRAJ_FREQ_Hz
      10. 4.3.10 USER_CTRL_PERIOD_usec
      11. 4.3.11 USER_CTRL_PERIOD_sec
    4. 4.4 Limits
      1. 4.4.1  USER_MAX_NEGATIVE_ID_REF_CURRENT_A
      2. 4.4.2  USER_ZEROSPEEDLIMIT
      3. 4.4.3  USER_FORCE_ANGLE_FREQ_Hz
      4. 4.4.4  USER_MAX_CURRENT_SLOPE_POWERWARP
      5. 4.4.5  USER_MAX_ACCEL_Hzps
      6. 4.4.6  USER_MAX_ACCEL_EST_Hzps
      7. 4.4.7  USER_MAX_CURRENT_SLOPE
      8. 4.4.8  USER_IDRATED_FRACTION_FOR_RATED_FLUX
      9. 4.4.9  USER_IDRATED_FRACTION_FOR_L_IDENT
      10. 4.4.10 USER_IDRATED_DELTA
      11. 4.4.11 USER_SPEEDMAX_FRACTION_FOR_L_IDENT
      12. 4.4.12 USER_FLUX_FRACTION
      13. 4.4.13 USER_POWERWARP_GAIN
      14. 4.4.14 USER_R_OVER_L_EST_FREQ_Hz
    5. 4.5 Poles
      1. 4.5.1 USER_VOLTAGE_FILTER_POLE_Hz
      2. 4.5.2 USER_VOLTAGE_FILTER_POLE_rps
      3. 4.5.3 USER_OFFSET_POLE_rps
      4. 4.5.4 USER_FLUX_POLE_rps
      5. 4.5.5 USER_DIRECTION_POLE_rps
      6. 4.5.6 USER_SPEED_POLE_rps
      7. 4.5.7 USER_DCBUS_POLE_rps
      8. 4.5.8 USER_EST_KAPPAQ
    6. 4.6 User Motor and ID Settings
      1. 4.6.1  USER_MOTOR_TYPE
      2. 4.6.2  USER_MOTOR_NUM_POLE_PAIRS
      3. 4.6.3  USER_MOTOR_Rr
      4. 4.6.4  USER_MOTOR_Rs
      5. 4.6.5  USER_MOTOR_Ls_d
      6. 4.6.6  USER_MOTOR_Ls_q
      7. 4.6.7  USER_MOTOR_RATED_FLUX
      8. 4.6.8  USER_MOTOR_MAGNETIZING_CURRENT
      9. 4.6.9  USER_MOTOR_RES_EST_CURRENT
      10. 4.6.10 USER_MOTOR_IND_EST_CURRENT
      11. 4.6.11 USER_MOTOR_MAX_CURRENT
      12. 4.6.12 USER_MOTOR_FLUX_EST_FREQ_Hz
      13. 4.6.13 USER_MOTOR_ENCODER_LINES (InstaSPIN-MOTION™ Only)
      14. 4.6.14 USER_MOTOR_MAX_SPEED_KRPM (InstaSPIN-MOTION™ Only)
      15. 4.6.15 USER_SYSTEM_INERTIA (InstaSPIN-MOTION™ Only)
      16. 4.6.16 USER_SYSTEM_FRICTION (InstaSPIN-MOTION™ Only)
      17. 4.6.17 USER_SYSTEM_BANDWIDTH_SCALE (InstaSPIN-MOTION™ Only)
    7. 4.7 SpinTAC™ Parameters (spintac_velocity.h and spintac_position.h)
      1. 4.7.1 Macro Definitions
        1. 4.7.1.1  ST_MREV_ROLLOVER (spintac_position.h only)
        2. 4.7.1.2  ST_EREV_MAXIMUM (spintac_position.h only)
        3. 4.7.1.3  ST_POS_ERROR_MAXIMUM_MREV (spintac_position.h only)
        4. 4.7.1.4  ST_ISR_TICKS_PER_SPINTAC_TICK
        5. 4.7.1.5  ST_SPEED_SAMPLE_TIME
        6. 4.7.1.6  ST_SPEED_PU_PER_KRPM
        7. 4.7.1.7  ST_SPEED_KRPM_PER_PU
        8. 4.7.1.8  ST_MOTOR_INERTIA_PU
        9. 4.7.1.9  ST_MOTOR_FRICTION_PU
        10. 4.7.1.10 ST_MIN_ID_SPEED_RPM
        11. 4.7.1.11 ST_MIN_ID_SPEED_PU
        12. 4.7.1.12 ST_ID_INCOMPLETE_ERROR
        13. 4.7.1.13 ST_VARS_DEFAULTS
      2. 4.7.2 Type Definitions
        1. 4.7.2.1 VEL_Params_t / POS_Params_t
        2. 4.7.2.2 ST_Obj
        3. 4.7.2.3 ST_Handle
        4. 4.7.2.4 ST_PlanButton_e
        5. 4.7.2.5 ST_Vars_t
      3. 4.7.3 Functions
        1. 4.7.3.1  ST_init
        2. 4.7.3.2  ST_setupPosConv
        3. 4.7.3.3  ST_setupVelCtl (Velocity Control Only)
        4. 4.7.3.4  ST_setupPosCtl (Position Control Only)
        5. 4.7.3.5  ST_setupVelMove (Velocity Control Only)
        6. 4.7.3.6  ST_setupPosMove (Position Control Only)
        7. 4.7.3.7  ST_setupVelPlan (Velocity Control Only)
        8. 4.7.3.8  ST_setupPosPlan (Position Control Only)
        9. 4.7.3.9  ST_setupVelId (Velocity Control Only)
        10. 4.7.3.10 ST_runPosConv
        11. 4.7.3.11 ST_runVelCtl (Velocity Control Only)
        12. 4.7.3.12 ST_runPosCtl (Position Control Only)
        13. 4.7.3.13 ST_runVelMove (Velocity Control Only)
        14. 4.7.3.14 ST_runPosMove (Position Control Only)
        15. 4.7.3.15 ST_runVelPlan (Velocity Control Only)
        16. 4.7.3.16 ST_runVelPlanTick (Velocity Control Only)
        17. 4.7.3.17 ST_runPosPlan (Position Control Only)
        18. 4.7.3.18 ST_runPosPlanTick (Position Control Only)
        19. 4.7.3.19 ST_runVelId (Velocity Control Only)
    8. 4.8 Setting ACIM Motor Parameters in user.h
      1. 4.8.1 Getting Parameters From an ACIM Datasheet
        1. 4.8.1.1 Number of Pole Pairs
        2. 4.8.1.2 Entering ACIM Motor Parameters from a Data Sheet to user.h
        3. 4.8.1.3 Getting the Rated Magnetizing Current of an ACIM
        4. 4.8.1.4 Getting the Rated Flux of an ACIM
  6. 5 Managing Motor Signals
    1. 5.1 Software Prerequisites
      1. 5.1.1 IQ Full-Scale Frequency
      2. 5.1.2 IQ Full-Scale Voltage
      3. 5.1.3 IQ Full-Scale Current
      4. 5.1.4 Max Current
      5. 5.1.5 Decimation Rates
      6. 5.1.6 System Frequency
      7. 5.1.7 PWM Frequency
      8. 5.1.8 Max Voltage Vector
    2. 5.2 Hardware Prerequisites
      1. 5.2.1 Current Feedback Gain
      2. 5.2.2 Current Feedback Polarity
        1. 5.2.2.1 Positive Feedback
        2. 5.2.2.2 Negative Feedback
      3. 5.2.3 Voltage Feedback
      4. 5.2.4 Voltage Filter Pole
      5. 5.2.5 Number of Shunt Resistors
      6. 5.2.6 Dead-Time Configuration
      7. 5.2.7 Analog Inputs Configuration
      8. 5.2.8 PWM Outputs Configuration
  7. 6 Motor Identification and State Diagrams
    1. 6.1  Overview
    2. 6.2  InstaSPIN™ Motor Identification
    3. 6.3  Motor Identification Process Overview
      1. 6.3.1 Controller (CTRL) State Machine
      2. 6.3.2 Estimator (EST) State Machine
      3. 6.3.3 Controller (CTRL) and Estimator (EST) State Machine Dependencies
    4. 6.4  Differences between PMSM and ACIM Identification Process
    5. 6.5  Prerequisites
      1. 6.5.1 Mechanical Prerequisites
        1. 6.5.1.1 Motor Connection
        2. 6.5.1.2 Order of the Phases
        3. 6.5.1.3 Minimum Mechanical Load
      2. 6.5.2 Hardware Prerequisites
      3. 6.5.3 Software Prerequisites
      4. 6.5.4 Software Configuration for PMSM Motor Identification
        1. 6.5.4.1 Motor Type
        2. 6.5.4.2 Number of Pole Pairs
        3. 6.5.4.3 Frequency for Rhf and Lhf
        4. 6.5.4.4 Current for Rs
        5. 6.5.4.5 Current for Ls
        6. 6.5.4.6 Frequency for Ls and Flux
      5. 6.5.5 Software Configuration for ACIM Motor Identification
        1. 6.5.5.1 Motor Type
        2. 6.5.5.2 Number of Pole Pairs
        3. 6.5.5.3 Frequency for Rhf and Lhf
        4. 6.5.5.4 Rated Flux
        5. 6.5.5.5 Current for Rs
        6. 6.5.5.6 Frequency for IdRated, Ls and Rr
    6. 6.6  Full Identification of PMSM Motors
      1. 6.6.1  CTRL_State_Idle and EST_State_Idle
      2. 6.6.2  CTRL_State_OffLine and EST_State_Idle (Hardware Offsets Calibrated)
      3. 6.6.3  CTRL_State_OnLine and EST_State_RoverL
        1. 6.6.3.1 Amplitude of Injected Current for RoverL
        2. 6.6.3.2 Frequency of Injected Current for RoverL
        3. 6.6.3.3 Measurement Time for RoverL
        4. 6.6.3.4 Troubleshooting Current Controller Stability During RoverL Identification
        5. 6.6.3.5 Adjusting Resulting Current Controller Gains for High-Speeds
      4. 6.6.4  CTRL_State_OnLine and EST_State_Rs
        1. 6.6.4.1 Troubleshooting Current Controller Stability During Rs Identification
      5. 6.6.5  CTRL_State_OnLine and EST_State_RampUp
        1. 6.6.5.1 Ramp-Up Current Amplitude
          1. 6.6.5.1.1 Troubleshooting Motor Shaft Stopping During Ramp-Up
        2. 6.6.5.2 Ramp-Up Time and Acceleration
          1. 6.6.5.2.1 Troubleshooting Motor Shaft for Smoother Ramp
        3. 6.6.5.3 Ramp-Up Final Speed for PMSM
      6. 6.6.6  CTRL_State_OnLine and EST_State_RatedFlux
        1. 6.6.6.1 Current Ramp-Down
        2. 6.6.6.2 Total Measurement Time
        3. 6.6.6.3 Troubleshooting Flux Measurement
      7. 6.6.7  CTRL_State_OnLine and EST_State_Ls
        1. 6.6.7.1 Ramp-Up Current
        2. 6.6.7.2 Troubleshooting Ls Identification
        3. 6.6.7.3 Ls_d and Ls_q, Direct and Quadrature Stator Inductance
      8. 6.6.8  CTRL_State_OnLine and EST_State_RampDown
      9. 6.6.9  CTRL_State_OnLine and EST_State_MotorIdentified
      10. 6.6.10 CTRL_State_Idle and EST_State_Idle
    7. 6.7  Full Identification of ACIM Motors
      1. 6.7.1  CTRL_State_Idle and EST_State_Idle
      2. 6.7.2  CTRL_State_OffLine and EST_State_Idle
      3. 6.7.3  CTRL_State_OnLine and EST_State_RoverL
      4. 6.7.4  CTRL_State_OnLine and EST_State_Rs
      5. 6.7.5  CTRL_State_OnLine and EST_State_RampUp
        1. 6.7.5.1 Ramp-Up Final Speed for ACIM
      6. 6.7.6  CTRL_State_OnLine and EST_State_IdRated
        1. 6.7.6.1 Reducing Oscillation to Improve Id Rated Measurement
        2. 6.7.6.2 Reading Id Rated Final Value
      7. 6.7.7  CTRL_State_OnLine and EST_State_RatedFlux
        1. 6.7.7.1 Troubleshooting Flux Measurement
      8. 6.7.8  CTRL_State_OnLine and EST_State_RampDown
      9. 6.7.9  CTRL_State_Idle and EST_State_LockRotor
        1. 6.7.9.1 Troubleshooting Locked Rotor Test
      10. 6.7.10 CTRL_State_OnLine and EST_State_Ls
      11. 6.7.11 CTRL_State_OnLine and EST_State_Rr
      12. 6.7.12 CTRL_State_OnLine and EST_State_RampDown
      13. 6.7.13 CTRL_State_OnLine and EST_State_MotorIdentified
      14. 6.7.14 CTRL_State_Idle and EST_State_Idle
    8. 6.8  Recalibration of PMSM and ACIM Motor Identification
      1. 6.8.1 Recalibration of PMSM and ACIM Motors After Full Identification
        1. 6.8.1.1 Start-Up Time Consideration
        2. 6.8.1.2 CTRL_State_Idle and EST_State_Idle
        3. 6.8.1.3 CTRL_State_OffLine and EST_State_Idle
        4. 6.8.1.4 CTRL_State_OnLine and EST_State_Rs
          1. 6.8.1.4.1 Managing Time Required for Rs Recalibration
          2. 6.8.1.4.2 Software configuration for Rs recalibration
        5. 6.8.1.5 CTRL_State_OnLine and EST_State_OnLine
          1. 6.8.1.5.1 Transitioning to Online State from CTRL Online and EST Rs
          2. 6.8.1.5.2 Transitioning to Online state from (CTRL Idle or CTRL Offline) and EST Idle
        6. 6.8.1.6 CTRL_State_Idle and EST_State_Idle
      2. 6.8.2 Recalibration of PMSM and ACIM Motors after Using Parameters from user.h
    9. 6.9  Setting PMSM Motor Parameters in user.h
      1. 6.9.1 Getting Parameters from a PMSM Datasheet
        1. 6.9.1.1 Number of Pole Pairs
        2. 6.9.1.2 Stator Resistance (Rs)
        3. 6.9.1.3 Stator Inductance (Ls_d and Ls_q)
        4. 6.9.1.4 Rated Flux (ψ)
    10. 6.10 Troubleshooting Motor Identification
      1. 6.10.1 Troubleshooting PMSM Motor Identification
        1. 6.10.1.1 Identifying PMSM Motors When Load Cannot be Detached
        2. 6.10.1.2 Can Motor Rotate with the Attached Load?
        3. 6.10.1.3 Run First Three Steps of Identification
        4. 6.10.1.4 Run Using Motor Parameters from user.h
        5. 6.10.1.5 Troubleshooting Motor Shaft Stopping During Ramp-Up
        6. 6.10.1.6 Troubleshooting Motor Shaft for Smoother Ramp
        7. 6.10.1.7 Troubleshooting Flux Measurement
        8. 6.10.1.8 Troubleshooting Ls Identification
          1. 6.10.1.8.1 Identifying Low Inductance PMSM Motors
            1. 6.10.1.8.1.1 Hardware Considerations
            2. 6.10.1.8.1.2 Software Considerations
          2. 6.10.1.8.2 Identifying Inductance of Salient PMSM Motors
            1. 6.10.1.8.2.1 Hardware Considerations
            2. 6.10.1.8.2.2 Software Considerations
        9. 6.10.1.9 Identifying High-Cogging Torque PMSM Motors
      2. 6.10.2 Troubleshooting ACIM Motor Identification
        1. 6.10.2.1 Troubleshooting Flux Measurement
        2. 6.10.2.2 Troubleshooting Locked Rotor Test
  8. 7 Inertia Identification
    1. 7.1 Overview
    2. 7.2 InstaSPIN-MOTION™ Inertia Identification
    3. 7.3 Inertia Identification Process Overview
    4. 7.4 Software Configuration for SpinTAC™ Velocity Identify
      1. 7.4.1 Include the Header File
      2. 7.4.2 Declare the Global Variables
      3. 7.4.3 Initialize the Configuration Variables
      4. 7.4.4 Call SpinTAC™ Velocity Identify
    5. 7.5 Troubleshooting Inertia Identification
      1. 7.5.1 ERR_ID
      2. 7.5.2 2003 Error
      3. 7.5.3 2004 Error
        1. 7.5.3.1 Motor Spins Continuously
        2. 7.5.3.2 Motor Does Not Spin Initially
      4. 7.5.4 2006 Error
    6. 7.6 Difficult Applications for Inertia Identification
      1. 7.6.1 Automotive Pumps (Large-Cogging Force / Large Friction)
      2. 7.6.2 Direct Drive Washing Machines (Low-Rated Speed and Large Back EMF)
      3. 7.6.3 Compressors (Large Start-Up Current)
  9. 8 MCU Considerations
    1. 8.1 Overview
    2. 8.2 InstaSPIN-Enabled Devices
      1. 8.2.1 softwareUpdate1p6() - Function is Required in User Code
    3. 8.3 ROM and User Memory Overview
      1. 8.3.1 InstaSPIN-FOC™ Full Implementation in ROM
        1. 8.3.1.1 Executing from ROM and RAM
        2. 8.3.1.2 Executing from ROM and FLASH
      2. 8.3.2 InstaSPIN-FOC™ Minimum Implementation in ROM
        1. 8.3.2.1 Executing from ROM and RAM
        2. 8.3.2.2 Executing from ROM and FLASH
      3. 8.3.3 InstaSPIN-MOTION™ in ROM
        1. 8.3.3.1 Executing InstaSPIN™-MOTION in the Main Interrupt
        2. 8.3.3.2 Executing Library from RAM
        3. 8.3.3.3 Executing Library from Flash
    4. 8.4 Details on CPU Load and Memory Footprint Measurements
      1. 8.4.1 CPU Utilization Measurement Details
      2. 8.4.2 Memory Allocation Measurement Details
      3. 8.4.3 IQ Math Built in ROM
      4. 8.4.4 Stack Utilization Measurement Details
      5. 8.4.5 InstaSPIN™ Main Interrupt
      6. 8.4.6 Clock Rate
    5. 8.5 Memory Footprint
      1. 8.5.1 Device Memory Map
        1. 8.5.1.1 F2806xF and F2806xM Devices
        2. 8.5.1.2 F2805xF and F2805xM Devices
        3. 8.5.1.3 F2802xF Devices
      2. 8.5.2 InstaSPIN™ Memory Footprint
        1. 8.5.2.1 F2806xF and F2805xF Devices
        2. 8.5.2.2 F2802xF Devices
        3. 8.5.2.3 F2806xM and F2805xM Devices
      3. 8.5.3 Memory Wait-States
        1. 8.5.3.1 F2806xF/M Devices
        2. 8.5.3.2 F2805xF/M Devices
        3. 8.5.3.3 F2802xF Devices
      4. 8.5.4 Flash Configuration Required Even for RAM-Only Execution
      5. 8.5.5 Debug (IDE) of EXE-Only Memory
    6. 8.6 CPU Load
      1. 8.6.1 F2806xF Devices
        1. 8.6.1.1 CPU Cycles
          1. 8.6.1.1.1 User Code in RAM
            1. 8.6.1.1.1.1 Full Implementation
            2. 8.6.1.1.1.2 Minimum Implementation
          2. 8.6.1.1.2 User Code in FLASH
            1. 8.6.1.1.2.1 Full Implementation
            2. 8.6.1.1.2.2 Minimum Implementation
        2. 8.6.1.2 CPU Load with PWM = 10 kHz
        3. 8.6.1.3 CPU Load with PWM = 20 kHz
        4. 8.6.1.4 CPU Load Examples
          1. 8.6.1.4.1 F2806xF Devices Example 1
          2. 8.6.1.4.2 F2806xF Devices Example 2
      2. 8.6.2 F2806xM Devices
        1. 8.6.2.1 CPU Cycles
          1. 8.6.2.1.1 RAM Execution - SpinTAC™ Library and User Code
          2. 8.6.2.1.2 FLASH Execution - SpinTAC™ Library and User Code
        2. 8.6.2.2 CPU Load Examples
          1. 8.6.2.2.1 F2806xM Devices Example 1
          2. 8.6.2.2.2 F2806xM Devices Example 2
          3. 8.6.2.2.3 F2806xM Devices Example 3
          4. 8.6.2.2.4 F2806xM Devices Example 4 (SpinTAC™ Position)
      3. 8.6.3 F805xF Devices
        1. 8.6.3.1 CPU Cycles
        2. 8.6.3.2 CPU Load with PWM = 10 kHz
        3. 8.6.3.3 CPU Load with PWM = 20 kHz
      4. 8.6.4 F2805xM Devices
        1. 8.6.4.1 CPU Cycles
          1. 8.6.4.1.1 FLASH Execution - SpinTAC™ Library and User Code
      5. 8.6.5 F2802xF Devices
        1. 8.6.5.1 CPU Cycles
        2. 8.6.5.2 CPU Load with PWM = 10 kHz
        3. 8.6.5.3 CPU Load with PWM = 20 kHz
    7. 8.7 Digital and Analog Pins
      1. 8.7.1 Pin Utilization
      2. 8.7.2 F2805x Analog Front-End (AFE)
        1. 8.7.2.1 Consideration of AFE Module
        2. 8.7.2.2 Routing Current Signals
        3. 8.7.2.3 Voltage Reference Connection
        4. 8.7.2.4 Routing Voltage Signals
  10. 9 Real-Time Structure
    1. 9.1 InstaSPIN™ Software Execution Clock Tree
    2. 9.2 Decimating in Software for Real-Time Scheduling
      1. 9.2.1 USER_NUM_ISR_TICKS_PER_CTRL_TICK
      2. 9.2.2 USER_NUM_CTRL_TICKS_PER_CURRENT_TICK
      3. 9.2.3 USER_NUM_CTRL_TICKS_PER_EST_TICK
      4. 9.2.4 Practical Example
      5. 9.2.5 USER_NUM_CTRL_TICKS_PER_SPEED_TICK
      6. 9.2.6 USER_NUM_CTRL_TICKS_PER_TRAJ_TICK
    3. 9.3 Decimating in Hardware
  11. 10Managing Startup Time
    1. 10.1 Startup with Offsets and Rs Recalibration
    2. 10.2 Startup with Only Offsets Recalibration
    3. 10.3 Startup with Rs Recalibration
    4. 10.4 Startup with No Recalibration
    5. 10.5 Bypassing Inertia Estimation
  12. 11Tuning Regulators
    1. 11.1 PI Controllers Introduction
    2. 11.2 PI Design for Current Controllers
    3. 11.3 PI Design for Speed Controllers
    4. 11.4 Calculating PI Gains Based On Stability and Bandwidth
    5. 11.5 Calculating Speed and Current PI Gains Based on Damping Factor
    6. 11.6 Considerations When Adding Poles to the Speed Loop
    7. 11.7 Speed PI Controller Considerations: Current Limits, Clamping and Inertia
    8. 11.8 Considerations When Designing PI Controllers for FOC Systems
      1. 11.8.1 FOC Differences Between Motor Types
      2. 11.8.2 Coupling Between Q-Axis and D-Axis
    9. 11.9 Sampling and Digital Systems Considerations
      1. 11.9.1 Sampling Period Considerations in the Integral Gain
      2. 11.9.2 Number Format Considerations
      3. 11.9.3 PI Coefficients Scaling Considerations
  13. 12InstaSPIN-MOTION™ Controllers
    1. 12.1 Overview
    2. 12.2 Stability
      1. 12.2.1 Quantifying Stability
        1. 12.2.1.1 SpinTAC™ Velocity Control Stability
        2. 12.2.1.2 SpinTAC™ Position Control Stability
      2. 12.2.2 Performance
        1. 12.2.2.1 Frequency Domain Analysis
        2. 12.2.2.2 Time Domain Analysis
      3. 12.2.3 Trade-Off Between Stability and Performance
      4. 12.2.4 Tuning the SpinTAC™ Controller
        1. 12.2.4.1 Considerations
        2. 12.2.4.2 Tuning the InstaSPIN™-MOTION Controller
    3. 12.3 Software Configuration for the SpinTAC™ Velocity Control
      1. 12.3.1 Include the Header File
      2. 12.3.2 Declare the Global Structure
      3. 12.3.3 Initialize the Configuration Variables
      4. 12.3.4 Call SpinTAC™ Velocity Control
      5. 12.3.5 Troubleshooting SpinTAC™ Velocity Control
        1. 12.3.5.1 ERR_ID
    4. 12.4 Optimal Performance in Speed Control
      1. 12.4.1 Introduction
      2. 12.4.2 Comparing Speed Controllers
      3. 12.4.3 Disturbance Rejection
      4. 12.4.4 Profile Tracking
      5. 12.4.5 InstaSPIN-MOTION™ Velocity Control Advantage
        1. 12.4.5.1 Single Parameter Tuning
        2. 12.4.5.2 Disturbance Rejection Test
        3. 12.4.5.3 Feedforward
        4. 12.4.5.4 No Integrator Windup
        5. 12.4.5.5 Minimum Startup Overshoot
        6. 12.4.5.6 Conclusions
    5. 12.5 Software Configuration for SpinTAC™ Position Control
      1. 12.5.1 Include the Header File
      2. 12.5.2 Declare the Global Structure
      3. 12.5.3 Initialize the Configuration Variables
      4. 12.5.4 Call SpinTAC™ Position Control
      5. 12.5.5 Troubleshooting SpinTAC™ Position Control
        1. 12.5.5.1 ERR_ID
    6. 12.6 Optimal Performance in Position Control
      1. 12.6.1 Introduction
      2. 12.6.2 Comparing Position Controllers
      3. 12.6.3 Disturbance Rejection
      4. 12.6.4 Profile Tracking
      5. 12.6.5 InstaSPIN-MOTION™ Position Control Advantage
        1. 12.6.5.1 Single Parameter Tuning
        2. 12.6.5.2 Disturbance Rejection
        3. 12.6.5.3 Feedforward
        4. 12.6.5.4 Low-Speed Operation and Smooth Startup
        5. 12.6.5.5 Minimum Step Response Settling Time
        6. 12.6.5.6 Conclusions
  14. 13Trajectory Planning
    1. 13.1 InstaSPIN-MOTION™ Profile Generation
      1. 13.1.1 Jerk Impact on System Performance
    2. 13.2 Software Configuration for SpinTAC™ Velocity Move
      1. 13.2.1 Include the Header File
      2. 13.2.2 Declare the Global Structure
      3. 13.2.3 Initialize the Configuration Variables
      4. 13.2.4 Call SpinTAC™ Velocity Move
      5. 13.2.5 Troubleshooting SpinTAC™ Velocity Move
        1. 13.2.5.1 ERR_ID
    3. 13.3 Software Configuration for SpinTAC™ Position Move
      1. 13.3.1 Include the Header File
      2. 13.3.2 Declare the Global Structure
      3. 13.3.3 Initialize the Configuration Variables
      4. 13.3.4 Call SpinTAC™ Position Move
      5. 13.3.5 Troubleshooting SpinTAC™ Position Move
        1. 13.3.5.1 Position Profile Limits
        2. 13.3.5.2 ERR_ID
    4. 13.4 InstaSPIN-MOTION™ Sequence Planning
      1. 13.4.1 SpinTAC™ Velocity Plan Elements
        1. 13.4.1.1 States
        2. 13.4.1.2 Transitions
        3. 13.4.1.3 Conditions
        4. 13.4.1.4 Variables
        5. 13.4.1.5 Actions
      2. 13.4.2 SpinTAC™ Velocity Plan Element Limits
        1. 13.4.2.1 Example of Sizing SpinTAC™ Velocity Plan Configuration Array
      3. 13.4.3 SpinTAC™ Velocity Plan Example: Washing Machine Agitation
      4. 13.4.4 SpinTAC™ Velocity Plan Example: Garage Door
      5. 13.4.5 SpinTAC™ Velocity Plan Example: Washing Machine
      6. 13.4.6 SpinTAC™ Position Plan Example: Vending Machine
    5. 13.5 Software Configuration for SpinTAC™ Velocity Plan
      1. 13.5.1 Include the Header File
      2. 13.5.2 Define the Size of the Configuration Array
      3. 13.5.3 Declare the Global Structure
      4. 13.5.4 Initialize the Configuration Variables
      5. 13.5.5 Call SpinTAC™ Velocity Plan
      6. 13.5.6 Call SpinTAC™ Velocity Plan Tick
      7. 13.5.7 Update SpinTAC™ Velocity Plan with SpinTAC™ Velocity Move Status
    6. 13.6 Troubleshooting SpinTAC™ Velocity Plan
      1. 13.6.1 ERR_ID
      2. 13.6.2 Configuration Errors
    7. 13.7 Software Configuration for SpinTAC™ Position Plan
      1. 13.7.1 Include the Header File
      2. 13.7.2 Define the Size of the Configuration Array
      3. 13.7.3 Declare the Global Structure
      4. 13.7.4 Initialize the Configuration Variables
      5. 13.7.5 Call SpinTAC™ Position Plan
      6. 13.7.6 Call SpinTAC™ Position Plan Tick
      7. 13.7.7 Update SpinTAC™ Position Plan with SpinTAC™ Position Move Status
    8. 13.8 Troubleshooting SpinTAC™ Position Plan
      1. 13.8.1 ERR_ID
      2. 13.8.2 Configuration Errors
    9. 13.9 Conclusion
  15. 14Managing Full Load at Startup, Low-Speed, and Speed Reversal
    1. 14.1 Overview
    2. 14.2 Low-Speed Operation with Full Load
      1. 14.2.1 Low Speed with Full Load Considerations
        1. 14.2.1.1 Enable Offsets Recalibration
        2. 14.2.1.2 Enable Stator Rs Recalibration
        3. 14.2.1.3 Disable Forced Angle
        4. 14.2.1.4 Tune Speed Controller to Avoid Motor Stall
        5. 14.2.1.5 Tune Voltage Feedback Circuit
      2. 14.2.2 Low Speed With Full Load Transient Examples
        1. 14.2.2.1 4-Hz, No-Load to Full-Load Transient
        2. 14.2.2.2 2-Hz, No-Load to Full-Load Transient
    3. 14.3 Speed Reversal with Full Load
      1. 14.3.1 Low Speed with Full Load Speed Reversal Considerations
      2. 14.3.2 Low Speed with Full Load Speed Reversal Examples
        1. 14.3.2.1 From -4 to +4 Hz with Full Load
        2. 14.3.2.2 From -2 to +2 Hz with Full Load
    4. 14.4 Motor Startup with Full Load
      1. 14.4.1 Motor Startup with Full Load Considerations
        1. 14.4.1.1 Enable Forced Angle
      2. 14.4.2 Motor Startup with Full Load Examples
        1. 14.4.2.1 From Standstill to 4 Hz with Full Load
        2. 14.4.2.2 From Standstill to 2 Hz with Full Load
    5. 14.5 Rapid Acceleration from Standstill With Full Load
      1. 14.5.1 Fastest Motor Startup with Full Load without Motor Alignment Considerations
        1. 14.5.1.1 Load Valid Offsets and Disable Offset Recalibration
        2. 14.5.1.2 Load Valid Rs and Disable Rs Recalibration
        3. 14.5.1.3 Fastest Motor Startup with Full Load without Motor Alignment Example
      2. 14.5.2 Fastest Motor Startup with Full Load with Motor Alignment Considerations
        1. 14.5.2.1 Maximize Current Slope
        2. 14.5.2.2 Fastest Motor Startup with Full Load with Motor Alignment Example
    6. 14.6 Overloading and Motor Overheating
      1. 14.6.1 Overloading and Motor Overheating Considerations
      2. 14.6.2 Overloading and Motor Overheating Example
    7. 14.7 InstaSPIN-MOTION™ and Low-Speed Considerations
  16. 15Rs Online Recalibration
    1. 15.1  Overview
    2. 15.2  Resistance vs. Temperature
    3. 15.3  Accurate Rs Knowledge Needed at Low Speeds Including Startup
    4. 15.4  Introduction to Rs Online Recalibration
    5. 15.5  Rs Online vs. Rs Offline
    6. 15.6  Enabling Rs Online Recalibration
    7. 15.7  Disabling Rs Online Recalibration
    8. 15.8  Modifying Rs Online Parameters
      1. 15.8.1 Adjusting Injected Current Magnitude
      2. 15.8.2 Adjusting Slow Rotating Angle
      3. 15.8.3 Adjusting Delta Increments and Decrements of the Rs Online Value
      4. 15.8.4 Adjusting Filter Parameters
    9. 15.9  Monitoring Rs Online Resistance Value
      1. 15.9.1 Rs Online Floating Point Value
      2. 15.9.2 Rs Online Fixed Point Value
    10. 15.10 Using the Rs Online Feature as a Temperature Sensor
    11. 15.11 Rs Online Related State Diagrams (CTRL and EST)
  17. 16PowerWarp™
    1. 16.1 Overview
    2. 16.2 Enabling PowerWarp™ Software
    3. 16.3 PowerWarp™ Current Slopes
    4. 16.4 Practical Example
    5. 16.5 Case Study
  18. 17Shunt Current Measurements
    1. 17.1 Introduction
    2. 17.2 Signals
    3. 17.3 1-Shunt
    4. 17.4 2-Shunt
    5. 17.5 3-Shunt
    6. 17.6 Development Kits
      1. 17.6.1 DRV8312 Kit
      2. 17.6.2 DRV8301 Kit
    7. 17.7 Conclusion
  19. 18Sensored Systems
    1. 18.1 Hardware Configuration for Quadrature Encoder
      1. 18.1.1 Pin Usage
    2. 18.2 Software Configuration for Quadrature Encoder
      1. 18.2.1 Configure Motor for EQEP Operation
      2. 18.2.2 Initialize EQEP Handle
      3. 18.2.3 Set Digital IO to Connect to QEP Peripheral
      4. 18.2.4 Enable Clock to eQEP
      5. 18.2.5 Initialize ENC Module
      6. 18.2.6 Set Up ENC Module
      7. 18.2.7 Call eQEP Function
      8. 18.2.8 Provide eQEP Angle to FOC
    3. 18.3 InstaSPIN-MOTION™ Position Convert
      1. 18.3.1 Software Configuration for SpinTAC™ Position Convert
        1. 18.3.1.1 Include the Header File
        2. 18.3.1.2 Declare the Global Structure
        3. 18.3.1.3 Initialize the Configuration Variables
        4. 18.3.1.4 Call SpinTAC™ Position Convert
      2. 18.3.2 Troubleshooting SpinTAC™ Position Convert
        1. 18.3.2.1 ERR_ID
          1.        A Definition of Terms and Acronyms
            1.         B Revision History

11.3 PI Design for Speed Controllers

In the last section we explained how to calculate the P and I coefficients (actually the GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif and GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif coefficients in a series structure) for a current loop controller for a motor. We saw that GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif could be used to eliminate the zero in the closed-loop system response, resulting in a system having only one real pole (that is, well behaved and stable). GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif sets the bandwidth of the closed-loop system response.

In this section let's back out and take a look at the speed control loop, which contains another PI controller. Can designing the speed loop be just as simple? Do the coefficient values perform the same system functions they did with the current controller?

It turns out that closing the speed loop is a little more complicated than closing the current loop. Also, to properly design the speed loop, we need to know more system parameters than we did for the current loop. This can be seen in Figure 12-6 which shows all of the components that comprise a cascaded speed control loop. By "cascaded," we mean a control system that consists of an outer loop with one or more inner loops. It bears mentioning again that we are only considering the case of a load with a single lumped sum inertia which is tightly coupled to the motor shaft and no viscous damping.

GUID-4FAB9FC8-875C-4565-8CBE-2D681A46195B-low.pngFigure 11-6 Cascaded Speed Control Loop

Let's start with the current control loop since this is where we left off in our last section. Assuming we design the current loop as discussed in my previous section, the closed-loop transfer function is:

Equation 41. GUID-406EBF42-0BEB-4741-BCD3-4CFEC3189FFC-low.gif

Where GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif is the error multiplier term in the current regulator's PI structure.

GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif is not visible to the outside world since it is set to cause pole/zero cancellation within the current controller's transfer function. To avoid confusing the coefficients of the speed controller with those of the current controller, we will call the speed controller's coefficients GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif and GUID-95B1FF69-058D-46E5-B16F-6D119A0F8EF8-low.gif as shown in Figure 12-6. In the series form of the PI controller, GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif is the error multiplier term (GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif), and GUID-95B1FF69-058D-46E5-B16F-6D119A0F8EF8-low.gif is the integrator multiplier term (GUID-95B1FF69-058D-46E5-B16F-6D119A0F8EF8-low.gif). We can use the same equation we did in the last section to define the transfer function of the speed PI controller:

Equation 42. GUID-65B4D9F3-7CDF-4DC5-BC18-2626E5D9D1F6-low.gif

The transfer function from motor current to motor torque will vary as a function of what type of motor you are using. For a Permanent Magnet Synchronous Motor under Field Oriented Control, the transfer function between q-axis current and motor torque is:

Equation 43. GUID-15814339-6216-4DCC-BC99-876F02E36CFD-low.gif

Where:

P = the number of rotor poles

λr = the rotor flux (which is also equal to the back-EMF constant (Ke) in SI units)

For an AC Induction machine, the transfer function between q-axis current and motor torque would be:

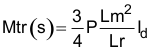
Equation 44. GUID-46782400-F1E5-48E3-AB28-254FCF3BA743-low.gif

Where:

P = the number of stator poles

Lm = the magnetizing inductance

Lr = the rotor inductance

Id = the component of current that is lined up with the rotor flux

For now, let's assume we are using a Permanent Magnet Synchronous Motor.

Finally, the load transfer function from motor torque to load speed is:

Equation 45. GUID-5F54A6E9-C5D3-4506-B3A0-BDB3F717CBC9-low.gif

Where:

J = the inertia of the motor plus the load

Multiplying all these terms together results in the composite open-loop transfer function:

Equation 46. GUID-E345047F-3C20-4E70-8903-0426571F97EB-low.gif

Let's combine all the motor and load parameters at the end of this equation into a single constant K:

Equation 47. GUID-334F099F-0188-47CF-A512-A2702DDDE7BF-low.gif

Simplifying, we get:

Equation 48. GUID-D369C9F4-1A2A-480F-81BB-11F3C0BC6B67-low.gif

From inspection of Equation 48, we can determine the following characteristics of the speed controller's open-loop transfer function:

  • Two poles at s = 0, resulting in an attenuation rate at low frequencies of 40 dB per decade of frequency.
  • An additional pole at GUID-228218A6-F505-4FEF-90E5-886A797B8AFB-low.gif (the current controller's pole)
  • A zero at GUID-6F9A799D-38C4-4936-AFC6-5B012A7FD88A-low.gif

In order for stable operation, the pole at GUID-228218A6-F505-4FEF-90E5-886A797B8AFB-low.gif must be higher in frequency than the zero at GUID-6F9A799D-38C4-4936-AFC6-5B012A7FD88A-low.gif. Other than that, there is an infinite number of combinations of GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif and GUID-95B1FF69-058D-46E5-B16F-6D119A0F8EF8-low.gif which could be used to yield different system responses, depending on whether you want higher bandwidth or better stability. There is a procedure to define a single parameter which is proportional to system stability and inversely proportional to bandwidth, which can be used to set both GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif and GUID-95B1FF69-058D-46E5-B16F-6D119A0F8EF8-low.gif automatically to yield the maximum phase margin for the selected bandwidth. We will cover the details of this procedure in the next section.