SPRUHJ1 User guide

SPRUHJ1I January 2013 – October 2021 TMS320F2802-Q1 , TMS320F28026-Q1 , TMS320F28026F , TMS320F28027-Q1 , TMS320F28027F , TMS320F28027F-Q1 , TMS320F28052-Q1 , TMS320F28052F , TMS320F28052F-Q1 , TMS320F28052M , TMS320F28052M-Q1 , TMS320F28054-Q1 , TMS320F28054F , TMS320F28054F-Q1 , TMS320F28054M , TMS320F28054M-Q1 , TMS320F2806-Q1 , TMS320F28062-Q1 , TMS320F28062F , TMS320F28062F-Q1 , TMS320F28068F , TMS320F28068M , TMS320F28069-Q1 , TMS320F28069F , TMS320F28069F-Q1 , TMS320F28069M , TMS320F28069M-Q1

11.1 PI Controllers Introduction

Looking back at some history, this is how the PI controller was invented in the 1920s. An engineer named Nicolas Minorsky was designing automatic steering systems for the US Navy in the early 1920s by observing how a helmsman steered a ship under different conditions. According to Wikipedia.org, he noticed that the actions of the helmsman could be approximated by a simple amplification of the error signal under calm conditions, but this simple model was inadequate to describe the helmsman's response during a steady disturbance like a stiff gale. This finally led to the addition of an integral term to correct for continuous steady-state errors. Later, the derivative term was added to improve controllability even further.

Continuing with the Wikipedia.org narrative, test trials of his automatic steering system based on a PI controller were carried out on the USS New Mexico. After some adjustments, he was able to control the angular error to less than two degrees. When the D term was added, the error improved to within one sixth of a degree, which was better than what most helmsmen could achieve manually. Minorsky published his findings (also in the early 1920s). We know today that his discovery launched a new era in the design of control systems.

Figure 11-1 USS New Mexico Around the Time it was Retrofitted with PID Control

A very common question we get in our seminars is, "How do you tune a PI controller?" We typically show Bode plots or show some simulation data to show that the process is somewhat empirical, and very subjective to the kind of response for which you are looking.

This section of InstaSPIN User's Guide is put together to help customers design and tune PI control loops (regardless of whether they are speed loops or current loops) in a much more deterministic way. Granted, there are still plenty of degrees of freedom depending on what kind of response users are looking for, as well as an endless litany of subtle variations on the basic PI structure itself. But by following some basic rules that will be explained later in this document, users should be able to tune a PI loop.

This analysis is limited to loads having only real poles. If the load under consideration has prominent complex poles resulting from excessive torsional resonance between the motor and load, then the controller will have to be more sophisticated than a simple PI structure anyway to cancel the resonance effects. But in most cases, a stiff shaft coupler should tame the torsional resonance to the point where the use of a standard PI control structure is acceptable. Also, it is assumed that the load has no viscous damping. In most designs these assumptions are valid. However, if the tuning process described in this section does not work for a given design, it is likely that complex poles or viscous damping exist somewhere in the load which is affecting the results.

Figure 12-2 shows a parallel path topology of a PI controller. The error signal is split into two separate paths: one which is directly amplified and the other is amplified and then integrated. The integrator is included to drive the steady-state error of the system to zero, since any non-zero steady-state error will result in a boundless integrator output. These two signal paths are then combined at the output once again via a simple addition operation.

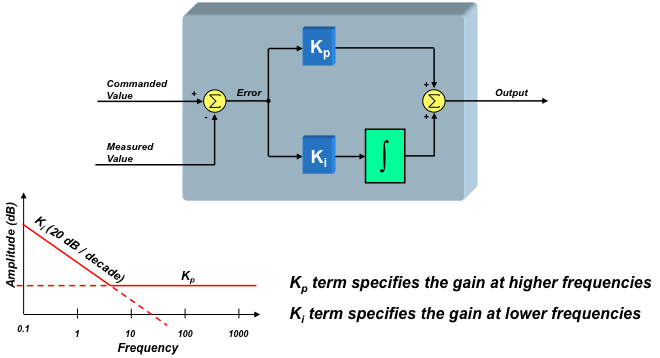Figure 11-2 Parallel Path Topology

But how do you set the values for Kp and Ki? This has been the subject for much debate, and it is rather difficult to intuitively understand the effect that each term has on your motor control system. The Kp term sets the high frequency gain of the control loop, as shown above. The Ki term sets the low frequency gain, and theoretically has infinite gain at DC. The frequency which delineates the high frequencies from the low frequencies is referred to as the "zero" of the controller and corresponds to the inflection point in the frequency plot.

While the integrator plays a crucial role in the operation of the PI controller, it also brings a set of challenges with it. For example, let's say that the error in your control loop is zero, which means the controlled signal is equal to the commanded signal. Now add a small offset to the controlled signal and watch what happens. Since the error signal is no longer zero, the integrator output will start growing, and growing in an attempt to null the error signal again.

Now remove the offset and watch what happens. The controlled signal will eventually return to the commanded value once again, but not right away. The integrator output is still very large, which causes the controlled signal to wildly overshoot the commanded value while the integrator output is cleared. During this time, the profile of the "controlled" signal is not controlled at all, and may even result in damage to your system if not constrained. It is like winding up a spring tightly and then suddenly releasing it. That is why this effect in PI controllers is called windup. There are many ways to mitigate the windup effect, but most techniques involve some sort of limiting of the integrator's output. We will discuss this in more detail later in this section.

Another popular form of the PI controller (and the one we will use for our analysis) is the "series" topology which is shown in Figure 12-3.

Figure 11-3 Series Topology

From this diagram, we can see that:

Equation 27.

But in this structure, sets the gain for ALL frequencies, and directly defines the inflection point (zero) of the controller in rad/sec. Both forms are pretty much equal in terms of software complexity. However, many engineers prefer the series form over the parallel form since and directly correlate to tangible system parameters. It's pretty easy to understand the effect that has on the controller's performance, since it is simply a gain term in your open-loop transfer function. But what is the system significance of the zero inflection point? This will be discussed next.