SPRUHJ1 User guide

SPRUHJ1I January 2013 – October 2021 TMS320F2802-Q1 , TMS320F28026-Q1 , TMS320F28026F , TMS320F28027-Q1 , TMS320F28027F , TMS320F28027F-Q1 , TMS320F28052-Q1 , TMS320F28052F , TMS320F28052F-Q1 , TMS320F28052M , TMS320F28052M-Q1 , TMS320F28054-Q1 , TMS320F28054F , TMS320F28054F-Q1 , TMS320F28054M , TMS320F28054M-Q1 , TMS320F2806-Q1 , TMS320F28062-Q1 , TMS320F28062F , TMS320F28062F-Q1 , TMS320F28068F , TMS320F28068M , TMS320F28069-Q1 , TMS320F28069F , TMS320F28069F-Q1 , TMS320F28069M , TMS320F28069M-Q1

11.6 Considerations When Adding Poles to the Speed Loop

At the end of last section, we presented a problem that could potentially derail this whole discussion. Throughout the PI tuning sections, we have been discussing a way to find the values for the PI coefficients in a theoretical system where the speed loop contains two poles at "s" equals zero, and a third pole from the current controller. Usually there are one or more additional poles in the transfer function. For example, a very common deviation from this utopian situation is when the speed feedback signal requires filtering, as shown in Figure 12-12.

Figure 11-12 Speed Controller with Filtered Speed Feedback

Creating a good quality high-bandwidth speed signal without spending too much design time and without adding too much system cost can be a real challenge. Techniques have been developed to glean information from the encoder edge transitions, and also using observer technology. But still, the speed signal is usually filtered. This alters the open-loop transfer function of the speed loop to the form shown in Equation 68.

Equation 68.

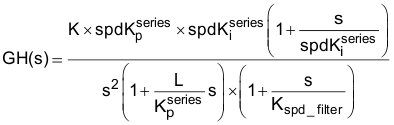
Where:

K is a coefficient that contains several terms related to the motor and load
and are the PI coefficients for the speed loop
L is the motor inductance
is one of the PI coefficients for the current loop
Kspd_filter is the pole of the speed feedback filter
s is the Laplace frequency variable.

So what does this do to the tuning procedure? There are several dimensions to this problem, as well as possible solutions. The selected damping factor and the relative location of the poles all contribute to these challenges. So let's target these challenges one at a time.

The procedure outlined in the last section assumes that a suitable speed bandwidth and damping factor are chosen based on application requirements, and then using the equation presented in step 3, we can calculate the required current controller bandwidth to satisfy these design requirements. But it turns out that the pole calculated in step 3 defines the minimum frequency of any pole which occurs above the unity gain frequency. Armed with this knowledge, we can define a more general expression for :

Equation 69.

Where:

p = the lowest value pole above the 0 dB frequency in the speed open-loop frequency response.

The value of p could be set by the current controller, the speed filter, or something else. Since is referenced to , then its value will also be potentially affected:

Equation 70.

If you can't meet the required frequency separation between the desired closed-loop speed bandwidth and p as dictated by your chosen value for δ, then something has got to give. It's like a water balloon—you can squeeze one part of the balloon, but it will pop out somewhere else. In this case, you can have your bandwidth at the expense of the damping factor, or vice versa.

The problem is exacerbated when the current controller pole and the speed filter pole are within a half decade of each other and δ is less than 3. With both poles so close to the 0 dB frequency and fighting together to bring down the phase margin, you will get a more underdamped response than you might otherwise expect. For example, Figure 12-13 shows the step response of a system where we used a damping factor of 2.5 to calculate the PI coefficients as described in the last section. The green curve assumes there is no filtering of the speed signal. The red curve shows the addition of a speed feedback filter where the value of the filter's pole equals the current controller's pole. The system is still stable, but the damping is much less than expected for a δ value of 2.5. At this point, we have two options, either increase the damping factor (and consequently lower the speed loop frequency response), or move one of the poles to a higher frequency. The cyan curve shows the first option where we increase the damping factor from 2.5 to 3.8 in order to bring the overshoot down to the original expected value. Unfortunately this reduces the bandwidth as indicated by the increased transient time. The yellow curve shows the latter option where we increase the value of one of the poles by a factor of 3 (about half a decade). In this case, the transient time is relatively unaffected, but the damping is still not as good as the green waveform. You can continue to increase the pole value, and at about one decade of separation you get a response that looks pretty close to the green waveform again. But in many cases, moving one of the poles this drastically has other negative effects on your system.

Figure 11-13 Step Response of a System with Variable Damping and Pole Placement

Up to now, we have only dealt with "small signal" conditions (that is, linear operation with no saturation effects). But in the real world, step transient responses almost always involve saturation of the system's voltage or current levels, which tends to lengthen the response times. When this happens, you can increase the PI gains all you want, but it won't speed up the response. In fact, it will usually just make the overshoot worse, since the integrator is acting on a gained-up error signal, which it will just have to dump eventually. So how do we deal with this problem? Are we doomed to simply using low integrator gains? It turns out that there is another solution which doesn't involve changing your integrator gains, which we will cover in the next section.