SNVS639G December 2009 – December 2015 LM21305
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Description (continued)
- 6 Pin Configuration and Functions
- 7 Specifications
-
8 Detailed Description
- 8.1 Overview
- 8.2 Functional Block Diagram
- 8.3
Feature Description
- 8.3.1 Synchronous DC-DC Switching Converter
- 8.3.2 Peak Current-Mode Control
- 8.3.3 Switching Frequency Setting and Synchronization
- 8.3.4 Light-Load Operation
- 8.3.5 Precision Enable
- 8.3.6 Device Enable, Soft-Start, and Pre-Bias Startup Capability
- 8.3.7 Peak Current Protection and Negative Current Limiting
- 8.3.8 PGOOD Indicator
- 8.3.9 Internal Bias Regulators
- 8.3.10 Minimum On-Time Considerations
- 8.4 Device Functional Modes
-
9 Application and Implementation
- 9.1 Application Information
- 9.2
Typical Application
- 9.2.1 Design Requirements
- 9.2.2
Detailed Design Procedure
- 9.2.2.1 Setting the Output Voltage
- 9.2.2.2 Calculating the Duty Cycle
- 9.2.2.3 Input Capacitors
- 9.2.2.4 AVIN Filter
- 9.2.2.5 Switching Frequency Selection
- 9.2.2.6 Filter Inductor
- 9.2.2.7 Output Capacitor
- 9.2.2.8 Efficiency Considerations
- 9.2.2.9 Load Current Derating When Duty Cycle Exceeds 50%
- 9.2.2.10 Control Loop Compensation
- 9.2.2.11 Compensation Components Selection
- 9.2.2.12 Plotting the Loop Gain
- 9.2.2.13 High Frequency Considerations
- 9.2.2.14 Bootstrap Capacitor
- 9.2.2.15 5V0 and 2V5 Capacitors
- 9.2.2.16 Maximum Ambient Temperature
- 9.2.3 Application Curves
- 10Power Supply Recommendations
- 11Layout
- 12Device and Documentation Support
- 13Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
- RSG|28
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9 Application and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
9.1 Application Information
The LM21305 is a step-down dc-dc converter, typically used to convert a higher dc voltage to a lower dc voltage with a maximum output current of 5 A. The following design procedure can be used to select components for the LM21305. Alternately, the WEBENCH® design tool can be used to generate a complete design. This tool uses an iterative design procedure and has access to a comprehensive database of components that allows the tool to create an optimized design and allows the user to experiment with various design options.
As well as numerous LM21305 reference designs populated in the TI Designs reference design library, the LM21305 QuickStart Calculator is also available as a free download.
9.2 Typical Application
This section walks the designer through the steps necessary to select the external components to build a fully-functional, efficient, step-down power supply. As with any dc-dc converter, numerous tradeoffs are possible to optimize the design for efficiency, size, and performance. These tradeoffs are taken into account and highlighted throughout this discussion. To facilitate component selection discussions, the typical application circuit shown in Figure 23 is used as a reference.
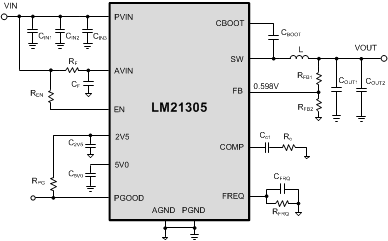 Figure 23. LM21305 Typical Application Circuit
Figure 23. LM21305 Typical Application Circuit
9.2.1 Design Requirements
Table 1 shows the Bill of Materials for an LM21305 converter.
Table 1. Bill of Materials (FSW = 500 kHz)
| VOUT | 1.2 V | 1.8 V | 2.5 V | 3.3 V | 5 V | PACKAGE |
|---|---|---|---|---|---|---|
| CIN1 | TANT, 47 µF, 25 V | TANT, 47 µF, 25 V | TANT, 47 µF, 25 V | TANT, 47 µF, 25 V | TANT, 47 µF, 25 V | CASE D |
| CIN2 | 10 µF, 25 V, X5R | 10 µF, 25 V, X5R | 10 µF, 25 V, X5R | 10 µF, 25 V, X5R | 22 µF, 25 V, X5R | 1210 |
| CIN3 | 0.1 µF, 25 V, X7R | 0.1 µF, 25 V, X7R | 0.1 µF, 25 V, X7R | 0.1 µF, 25 V, X7R | 0.1 µF, 25 V, X7R | 1206 |
| CF | 1.0 µF, 25 V, X7R | 1.0 µF, 25 V, X7R | 1.0 µF, 25 V, X7R | 1.0 µF, 25 V, X7R | 1.0 µF, 25 V, X7R | 0603 |
| C2V5, CBOOT | 0.1 µF, 16 V, X7R | 0.1 µF, 16 V, X7R | 0.1 µF, 16 V, X7R | 0.1 µF, 16 V, X7R | 0.1 µF, 16 V, X7R | 0603 |
| C5V0 | 1.0 µF, 16 V, X7R | 1.0 µF, 16 V, X7R | 1.0 µF, 16 V, X7R | 1.0 µF, 16 V, X7R | 1.0 µF, 16 V, X7R | 0603 |
| CFRQ | 100 pF, 25 V, X7R | 100 pF, 25 V, X7R | 100 pF, 25 V, X7R | 100 pF, 25 V, X7R | 100 pF, 25 V, X7R | 0603 |
| CC1 | 3.3 nF, 16 V, X7R | 3.3 nF, 16 V, X7R | 3.3 nF, 16 V, X7R | 3.3 nF, 16 V, X7R | 3.3 nF, 16 V, X7R | 0603 |
| COUT1, COUT2 | 47 µF, 6.3 V, X5R | 47 µF, 6.3 V, X5R | 47 µF, 6.3 V, X5R | 47 µF, 6.3 V, X5R | 47 µF, 10 V, X5R | 1206 |
| L | 1.5 µH, 10 A | 2.2 µH, 10 A | 2.2 µH, 10 A | 3.3 µH, 10 A | 3.3 µH, 10 A | SMD |
| RF | 1 Ω , 5% | 1 Ω , 5% | 1 Ω , 5% | 1 Ω , 5% | 1 Ω , 5% | 0603 |
| RFRQ, RPG | 100 kΩ, 1% | 100 kΩ, 1% | 100 kΩ, 1% | 100 kΩ, 1% | 100 kΩ, 1% | 0603 |
| RFB2, REN | 10 kΩ, 1% | 10 kΩ, 1% | 10 kΩ, 1% | 10 kΩ, 1% | 10 kΩ, 1% | 0603 |
| RC | 3.32 kΩ, 1% | 4.22 kΩ, 1% | 5.10 kΩ, 1% | 7.15 kΩ, 1% | 8.2 kΩ, 1% | 0603 |
| RFB1 | 10 kΩ, 1% | 20 kΩ, 1% | 31.6 kΩ, 1% | 45.3 kΩ, 1% | 73.2 kΩ, 1% | 0603 |
9.2.2 Detailed Design Procedure
9.2.2.1 Setting the Output Voltage
Connect the FB pin of the LM21305 directly to VOUT or through a feedback resistor divider network to scale up from the 0.598-V feedback voltage to the desired output voltage. Figure 24 shows the resistor divider connection and the FB pin.
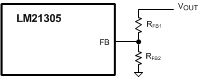 Figure 24. Setting the Output Voltage by Resistor Divider
Figure 24. Setting the Output Voltage by Resistor Divider
The output voltage is found by Equation 7:
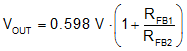
For example, if the desired output voltage is 1.8 V, RFB1 = 20 kΩ and RFB2 = 10 kΩ can be used.
9.2.2.2 Calculating the Duty Cycle
The first parameter to calculate for any buck converter is duty cycle. In an ideal (no-loss) buck converter, the duty cycle is found by Equation 8:
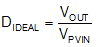
In applications with low output voltage (< 1.2 V) and high load current (> 3 A), the losses must not be ignored when calculating the duty cycle. Considering the effect of conduction losses associated with the MOSFETs and inductor, the duty cycle is approximated by Equation 9:
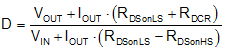
RDSonHS and RDSonLS are the on-state resistances of the high-side and low-side MOSFETs, respectively. RDCR is the equivalent dc resistance of the inductor used in the output filter. Other parasitics, such as printed circuit board (PCB) trace resistance, can be included if desired. IOUT is the load current and is also equal to the average inductor current. The duty cycle increases slightly when load current increases.
9.2.2.3 Input Capacitors
PVIN is the supply voltage for the switcher power stage and is the input source that delivers the output power to the load. The input capacitors on the PVIN rail supply the large ac switching current drawn by the switching action of the internal power MOSFETs. The input current of a buck converter is discontinuous and the ripple current supplied by the input capacitor can be quite large. The input capacitor must be rated to handle this current. To prevent large voltage transients, use a low ESR input capacitor sized for the maximum RMS current. The maximum RMS current is given by Equation 10:
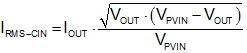
The power dissipation of the input capacitor is given by Equation 11:
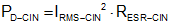
where
- RESR–CIN is the ESR of the input capacitor
Equation 10 has a maximum at PVIN = 2 VOUT, where IRMS-CIN ≅ IOUT / 2 and D ≅ 50%. This simple worst-case condition is commonly used for design purposes because even significant deviations from the worst-case duty cycle operating point do not offer much difference. Note that ripple current ratings from capacitor manufacturers are often based on only 2000 hours of life. Several capacitors can be paralleled to meet size or height requirements in the design. For low input voltage applications, sufficient bulk input capacitance is needed to minimize transient effects during load current changes. A 1-µF ceramic bypass capacitor is also recommended directly adjacent to the device between the PVIN and PGND pins. See Figure 38 and the Layout Guidelines section.
9.2.2.4 AVIN Filter
Add an RC filter to prevent any switching noise on PVIN from interfering with the internal analog circuits connected to AVIN, as shown in the schematic of Figure 23 and denoted by components RF and CF. There is a practical limit to the resistance of resistor RF because the AVIN pin draws a short 60-mA burst of current during startup. If RF is too large, the resulting voltage drop can trigger the UVLO comparator. A recommended 1-Ω resistor and 1-μF capacitor provides approximately 10 dB of attenuation at a 500-kHz switching frequency.
9.2.2.5 Switching Frequency Selection
The LM21305 supports a wide range of switching frequencies: 300 kHz to 1.5 MHz. The choice of switching frequency is usually a compromise between conversion efficiency and the size of the circuit. A lower switching frequency implies reduced switching losses (including gate drive and switch transition losses) and usually results in higher overall efficiency. However, a higher switching frequency allows use of smaller LC output filter components and thus a more compact design. Lower inductance also helps transient response (higher large-signal slew rate of the inductor current) and reduces the DCR losses. The optimal switching frequency is usually a tradeoff in a given application and thus must be determined on a case-by-case basis. In practice, the optimal switching frequency is related to input voltage, output voltage, most common load current level, external component choices, and circuit size requirements. The choice of switching frequency is also limited if an operating condition triggers TON-MIN or TOFF-MIN; see the Minimum On-Time Considerations section for more detail.
Use Equation 12 or Figure 25 to calculate the resistance to obtain a desired frequency of operation.
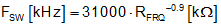
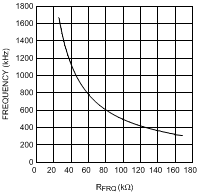 Figure 25. External Resistor Selection to Set
Figure 25. External Resistor Selection to Setthe Switching Frequency
9.2.2.6 Filter Inductor
A general recommendation for the filter inductor in an LM21305 application is to keep a peak-to-peak ripple current between 25% and 50% of the maximum load current of 5 A. The filter inductor must have a sufficiently high saturation current rating and a DCR as low as possible. Calculate the peak-to-peak inductor current ripple current from Equation 13:
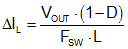
Select the inductance as shown by Equation 14:
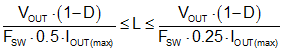
The peak inductor current at full load corresponds to the maximum output current plus the ripple current, as shown in Equation 15:
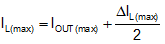
Choose an inductor with a saturation current rating at maximum operating temperature that is higher than the overcurrent protection limit. In general, having lower inductance is desirable in switching power supplies because lower inductance equates to faster transient response, lower DCR, and reduced size for more compact designs. However, too low of an inductance implies large inductor ripple current such that OCP is falsely triggered at the full load. Larger inductor ripple current also implies higher output voltage ripple.
When the inductance is determined, choose the type of inductor to meet the application requirements. Ferrite designs have very low core losses and are preferred at high switching frequencies, thus design goals can then concentrate on copper loss and preventing saturation. However, ferrite core material saturates hard, meaning that inductance collapses abruptly when the saturation current is exceeded. The hard saturation results in an large increase in inductor ripple current and output voltage ripple. Do not allow the core to saturate!
9.2.2.7 Output Capacitor
The LM21305 is designed to function with a wide variety of LC filters. Using as little output capacitance as possible is generally desirable to keep cost and size down. Choose the output capacitor, COUT, carefully because it directly affects the steady-state output voltage ripple, loop stability, and the voltage overshoot and undershoot during a load transient.
The output voltage ripple is essentially composed of two parts, resistive and capacitive. More specifically, the inductor ripple current flowing through the equivalent series resistance (ESR) of the output capacitors gives a resistive component as given by Equation 16:
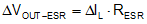
Also, consider the inductor ripple current charging and discharging the output capacitors, producing a capacitive ripple voltage component given by Equation 17:
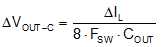
Figure 26 shows an illustration of the two ripple components. The actual peak-to-peak voltage ripple is smaller than the sum of the two peaks because the two ripple components are not in phase. The cumulative output ripple is given by Equation 18:
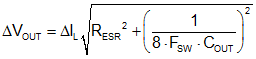
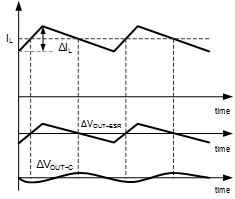 Figure 26. Inductor Current and Two Components of Output Voltage Ripple
Figure 26. Inductor Current and Two Components of Output Voltage Ripple
Output capacitance is usually limited by system transient performance specifications if the system requires tight voltage regulation with the presence of large current steps and fast slew rates. When a fast or large load transient occurs, output capacitors provide the required charge before the inductor current slews to the appropriate level. The initial output voltage deviation is equal to the load current step multiplied by ESR. VOUT continues to droop until the control loop response increases the inductor current to supply the load. To maintain a small overshoot or undershoot during a load transient, small ESR and large capacitance are desired. However, these factors also come with the penalty of higher cost and size. Thus, the motivation is to seek a fast control loop response to reduce the output voltage deviation.
One or more ceramic capacitors are generally recommended because these capacitors have very low ESR and remain capacitive up to high frequencies. Choose an X5R or X7R capacitor dielectric to maintain proper tolerance. Other types of capacitors (such as tantalum, POSCAP, and OSCON) are used if bulk energy storage is required. Such electrolytic capacitors have lower ESR zero frequency (relative to ceramic capacitors) that can influence the control loop, particularly if the zero frequency is close to the desired crossover target. If high switching frequency and high loop crossover frequency are warranted, an all-ceramic capacitor design is often more appealing.
9.2.2.8 Efficiency Considerations
The efficiency of a switching regulator is defined as the output power divided by the input power times 100%. Efficiency is also found by using Equation 19:
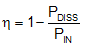
Analyzing individual losses is often useful to determine what is limiting the efficiency and what change can produce the most improvement. Although all dissipative elements in the circuit produce losses, three main sources usually account for most of the losses in LM21305-based converters: 1) conduction losses; 2) switching and gate drive losses; and 3) bias losses. Conduction losses are the I2R losses in parasitic resistances including MOSFET on-state resistances RDSon, equivalent inductor dc resistance RDCR, and PCB trace resistances RTRACE. Approximate the conduction loss using Equation 20:
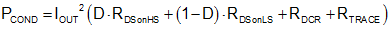
Lower the total conduction loss by reducing these parasitic resistances. For example, the LM21305 is designed to have low RDSon internal MOSFET switches. Keep the inductor DCR low, and ensure that the traces that conduct the current are wide, thick, and as short as possible. Obviously, conduction losses increasingly affect the efficiency at heavier loads. RMS currents through the input and output capacitor ESR also generate loss.
Switching losses include all the dissipation caused by the switching action of the two power MOSFETs. Each time the switch node swings from low to high or vice versa, charges are applied or removed from the parasitic capacitance from the SW node to GND. Each time a power MOSFET gate is switched from low to high to low again, a packet of charge moves from 5V0 to ground. Furthermore, each time a power MOSFET is turned on or off, a transition loss is generated related to the overlap of voltage and current. The low-side MOSFET body diode generates reverse recovery loss and dead-time conduction loss. All of these losses must be evaluated and carefully considered to design a high-efficiency switching power converter. Because these losses only occur during switching, reducing the switching frequency always helps reduce the switching loss and the resultant improvement in efficiency is more pronounced at lighter load.
The current drawn from AVIN is equivalent to IDRIVE and the associated power loss is VAVIN × IDRIVE because the 5V0 rail is an LDO output from AVIN. The other portion of AVIN power loss is the bias current through the 2V5 rail that equals VAVIN × IBIAS. Powering AVIN from a 5-V system rail provides an optimal tradeoff between bias power loss and switching loss.
9.2.2.9 Load Current Derating When Duty Cycle Exceeds 50%
The LM21305 is optimized for lower duty cycle operation (for example, high input-to-output voltage ratio). The high-side MOSFET is designed to be half the size of the low-side MOSFET, thus optimizing the relative levels of switching loss in the high-side switch and the conduction loss in the low-side switch. The continuous current rating of the low-side switch is the maximum load current of 5 A, whereas the high-side MOSFET is rated at 2.5 A. If the LM21305 is operating with duty cycles higher than 50%, the maximum output current must be derated, as shown in Equation 21.
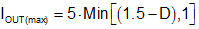
Derating of the maximum load current when D > 50% is also shown in Figure 27.
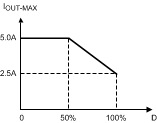 Figure 27. LM21305 Maximum Load Current Derating when D > 50%
Figure 27. LM21305 Maximum Load Current Derating when D > 50%
9.2.2.10 Control Loop Compensation
This section does not provide a rigorous analysis of current-mode control, but rather a simplified yet relatively accurate method to determine the control loop compensation network. The LM21305 employs a peak current-mode controller and, therefore, the control loop block diagram representation involves two feedback loops, as shown in Figure 28.
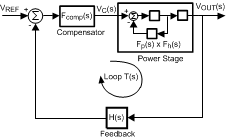 Figure 28. Control Block Diagram of a Peak Current-Mode Controlled Buck Converter
Figure 28. Control Block Diagram of a Peak Current-Mode Controlled Buck Converter
The inner feedback loop derives its feedback from the sensed inductor current and the outer loop monitors the output voltage. The LM21305 compensation components installed from COMP to AGND are shown in Figure 29. The purpose of the compensator block is to stabilize the control loop and achieve high performance in terms of load transient response, audio susceptibility, and output impedance. The LM21305 typically requires only a single resistor RC and capacitor CC1 for compensation. However, depending on the location of the power stage ESR zero, a second (small) capacitor, CC2, may be required to create a high-frequency pole.
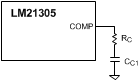 Figure 29. LM21305 Compensation Network
Figure 29. LM21305 Compensation Network
The overall loop transfer function is a product of the power stage transfer function, internal amplifier gains and the feedback network transfer function and is expressed by Equation 22:
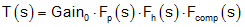
where
- Gain0 includes all the dc gains in the loop,
- Fp(s) represents the power stage pole and zero (including the inner current loop),
- Fh(s) represents the sampling effect in such a current-mode converter, and
- Fcomp(s) is the compensation network impedance
Figure 30 shows an asymptotic approximation plot of the loop gain.
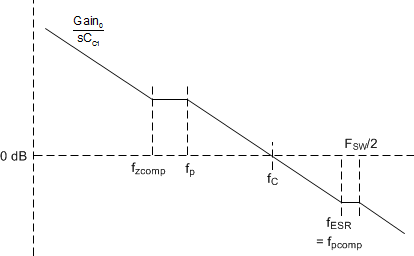 Figure 30. LM21305 Loop Gain Asymptotic Approximation
Figure 30. LM21305 Loop Gain Asymptotic Approximation
The loop gain determines both static and dynamic performance of the converter. The power stage response is fixed by the selection of the power components and the compensator is therefore designed around the power stage response to achieve the desired loop response. The goal is to design a control loop characteristic with high crossover frequency (or loop bandwidth) and adequate gain and phase margins under all operation conditions.
9.2.2.11 Compensation Components Selection
To select the compensation components, a desired crossover frequency must be selected. Select fC equal to or lower than 1/6 of the switching frequency. The effect of Fh(s) can be ignored to simplify the design. The capacitor ESR zero is also assumed to be at least three times higher than fC. Calculate the compensation resistor using Equation 23:
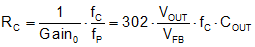
CC1 does not affect the crossover frequency fC, but sets the compensator zero fZcomp and affects the phase margin of the loop. For a fast design, CC1 = 4.7 nF gives adequate performance in most LM21305 applications. Higher CC1 capacitance gives higher phase margin but at the expense of longer transient response settling time. Set the compensation zero no higher than fC / 3 to ensure enough phase margin, as implied by Equation 24:
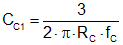
9.2.2.12 Plotting the Loop Gain
To include the effect of Fh(s) and the ESR zero, plot the complete loop gain using a software tool (such as MATLAB, Mathcad, or Excel). Determine the loop gain constituents as follows. First, calculate the dc gain of the power stage using Equation 25:
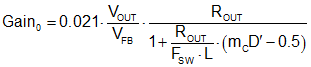
where mC for the LM21305 is given by Equation 26:
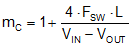
and D' = 1 − D. Use the minimum ROUT in the calculation of ROUT = VOUT / IOUT.
Fp(s) is expressed using Equation 27:
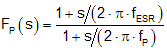
where the power stage pole (including slope compensation effect) and ESR zero frequencies are given respectively by Equation 28 and Equation 29:
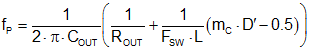
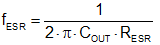
The high frequency behavior Fh(s) is expressed by Equation 30:
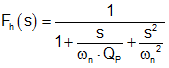
where the relevant frequency and quality factor are given by Equation 31
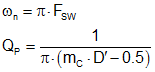
The compensation network impedance is given in Equation 32:
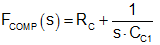
Using the above equations, it becomes an easy task to plot the loop gain T(s) and determine the loop performance metrics, such as crossover frequency and phase margin.
9.2.2.13 High Frequency Considerations
Fh(s) represents the additional magnitude and phase drop around FSW / 2 caused by the switching behavior of the current-mode converter. Fh(s) contains a pair of double poles with quality factor Qp at half of the switching frequency. Good practice is to check that Qp is between 0.15 and 2, ideally around 0.6. If Qp is too high, the resonant peaking at FSW / 2 can become severe and coincide with sub-harmonic oscillations in the duty cycle and inductor current. If Qp is too low, the two complex poles split, the converter begins to function as a voltage-mode controlled converter, and the compensation scheme used above must be adjusted.
In a typical converter design with ceramic output capacitors, the ESR zero frequency, fESR, is typically three times higher than the desired crossover frequency fC. If fESR is lower than FSW / 2, add a capacitor CC2 between COMP and AGND to give a high-frequency pole, as shown in Equation 33:
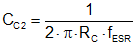
Select CC2 much smaller than CC1 to avoid affecting the compensation zero. The high-frequency pole also provides high-frequency noise attenuation at COMP.
9.2.2.14 Bootstrap Capacitor
Use a capacitor between CBOOT and SW to supply the gate drive charge when the high-side MOSFET is turning on. Ensure that the capacitor is large enough to supply the charge without significant voltage drop. A 0.1-µF ceramic bootstrap capacitor is recommended in LM21305 applications.
9.2.2.15 5V0 and 2V5 Capacitors
The 5V0 and 2V5 pins are internal bias rail LDO outputs. As previously mentioned, the two LDOs are used for internal circuits only and must not be substantially loaded. Output capacitors are needed to stabilize the LDOs. Ceramic capacitors within a specified range must be used to meet stability requirements. Choose an X5R or X7R dielectric rated for the required operating temperature range. Use Table 2 to choose a suitable LDO output capacitor.
Table 2. Bias Rail LDO Capacitance
| RAIL | NOMINAL VOLTAGE | CAPACITOR (Recommended Capacitance, Dielectric, Minimum Voltage Rating) |
|---|---|---|
| 5V0 | 4.88 V | 1 µF ± 20%, X7R, 16 V |
| 2V5 | 2.47 V | 0.1 µF ± 20%, X7R, 10 V |
9.2.2.16 Maximum Ambient Temperature
As with any power conversion device, the LM21305 dissipates internal power while operating. The effect of this power dissipation is to raise the internal temperature of the converter above ambient. The internal die temperature, TJ, is a function of the ambient temperature, TA, the power dissipation and the effective thermal resistance, RθJA , of the device and PCB combination. The maximum internal die temperature for the LM21305 is 125°C, thus establishing a limit on the maximum device power dissipation and therefore the load current at high ambient temperatures. Equation 34 shows the relationships between these parameters.
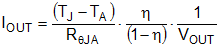
High ambient temperatures and large values of RθJA reduce the maximum available output current. If the junction temperature exceeds 160°C, the LM21305 cycles in and out of thermal shutdown. If thermal shutdown occurs, then this shutdown is a sign of inadequate heat-sinking or excessive power dissipation in the device. Improve PCB heat-sinking by using more thermal vias, a larger board, or more heat-spreading layers within that board.
As stated in application note Semiconductor and IC Package Thermal Metrics, SPRA953, the values given in the Thermal Information table are not valid for design purposes to estimate the thermal performance of the application. The values reported in the Thermal Information table are measured under a specific set of conditions that are seldom obtained in an actual application. The effective RθJA is a critical parameter and depends on many factors (such as power dissipation, air temperature, PCB area, copper heat-sink area, number of thermal vias under the package, air flow, and adjacent component placement). The LM21305 uses an advanced package with a heat-spreading pad (DAP) on the bottom. This pad must be soldered directly to the PCB copper ground plane to provide an effective heat-sink, as well as a proper electrical connection. Use the resources listed in Resources for Thermal PCB Design as a guide to optimal thermal PCB design and estimating RθJA for a given application environment.
9.2.3 Application Curves
For additional details on the wavefroms shown in this section, see AN-2175 LM21305 POL Demonstration Module and Reference Design, SNVA497.
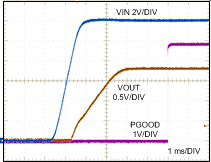
| VIN = 12 V, VOUT = 1.8 V | No Load |
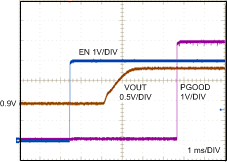
| VIN = 12 V, VOUT = 1.8 V | No Load |
| (Pre-Biased to 0.9 V) |
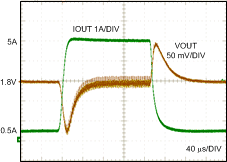
| VIN = 12 V, VOUT = 1.8 V | IOUT = 0.5-A to 5-A Load |
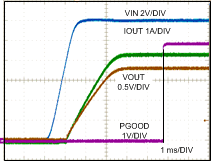
| VIN = 12 V, VOUT = 1.8 V | IOUT = 5-A Resistive Load |
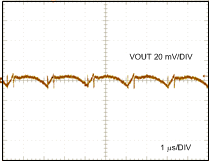
| VIN = 12 V, VOUT = 1.8 V | IOUT = 0.5-A to 5-A Load |
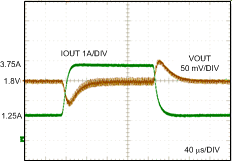
| VIN = 12 V, VOUT = 1.8 V | IOUT = 1.25-A to 3.75-A Load |