SLVS500D DECEMBER   2003  – June 2019 TPS54110

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
    1.     Device Images
  4. 4 Revision History
  5. 5 Device Information
  6. 6 Pin Configuration and Functions
    1.     Pin Functions
  7. 7 Specifications
    1. 7.1 Absolute Maximum Ratings
    2. 7.2 Recommended Operating Conditions
    3. 7.3 Thermal Information
    4. 7.4 Electrical Characteristics
    5. 7.5 Typical Characteristics
  8. 8 Detailed Description
    1. 8.1 Overview
    2. 8.2 Functional Block Diagram
    3. 8.3 Feature Description
      1. 8.3.1 VBIAS Regulator (VBIAS)
      2. 8.3.2 Voltage Reference
      3. 8.3.3 Oscillator and PWM Ramp
      4. 8.3.4 Error Amplifier
      5. 8.3.5 PWM Control
      6. 8.3.6 Dead-Time Control and MOSFET Drivers
      7. 8.3.7 Overcurrent Protection
      8. 8.3.8 Thermal Shutdown
      9. 8.3.9 Power Good (PWRDG)
    4. 8.4 Undervoltage Lockout (UVLO)
    5. 8.5 Slow-Start/Enable (SS/ENA)
  9. 9 Application and Implementation
    1. 9.1 Application Information
    2. 9.2 Typical Applications
      1. 9.2.1 Typical TPS54110 Application
        1. 9.2.1.1 Design Requirements
        2. 9.2.1.2 Detailed Design Procedure
          1. 9.2.1.2.1 Switching Frequency
          2. 9.2.1.2.2 Input Capacitors
          3. 9.2.1.2.3 Output Filter Components
            1. 9.2.1.2.3.1 Inductor Selection
            2. 9.2.1.2.3.2 Capacitor Selection
          4. 9.2.1.2.4 Compensation Components
          5. 9.2.1.2.5 Bias and Bootstrap Capacitors
        3. 9.2.1.3 Application Curves
      2. 9.2.2 Very-Small Form-Factor Application
        1. 9.2.2.1 Design Requirements
        2. 9.2.2.2 Detailed Design Procedure
        3. 9.2.2.3 Application Curves
      3. 9.2.3 Two-Output Sequenced-Startup Application
        1. 9.2.3.1 Design Requirements
        2. 9.2.3.2 Detailed Design Procedure
        3. 9.2.3.3 Application Curve
  10. 10Layout
    1. 10.1 Layout Guidelines
    2. 10.2 Layout Example
    3. 10.3 Layout Considerations For Thermal Performance
    4. 10.4 Grounding and Powerpad Layout
  11. 11Device and Documentation Support
    1. 11.1 Device Support
      1. 11.1.1 Third-Party Products Disclaimer
    2. 11.2 Receiving Notification of Documentation Updates
    3. 11.3 Community Resources
    4. 11.4 Trademarks
    5. 11.5 Electrostatic Discharge Caution
    6. 11.6 Glossary
  12. 12Mechanical, Packaging, and Orderable Information

Package Options

Refer to the PDF data sheet for device specific package drawings

Mechanical Data (Package|Pins)
  • PWP|20
Thermal pad, mechanical data (Package|Pins)
Orderable Information

9.2.1.2.4 Compensation Components

The external compensation used with the TPS54110 allows for a wide range of output-filter configurations. A large range of capacitor values and dielectric types are supported. The design example uses type 3 compensation consisting of R1, R3, R5, C6, C7 and C8. Additionally, R2 and R1 form a voltage-divider network that sets the output voltage. These component reference designators are the same as those used in the SWIFT Designer Software.

There are a number of different ways to design a compensation network. This procedure outlines a relatively simple procedure that produces good results with most output filter combinations. Use the SWIFT Designer Software for designs with unusually high closed-loop crossover frequencies; with low-value, low-ESR output capacitors such as ceramics; or if you are unsure about the design procedure.

A number of considerations apply when designing compensation networks for the TPS54110. The compensated error-amplifier gain must not be limited by the open-loop amplifier gain characteristics and must not produce excessive gain at the switching frequency. Also, the closed-loop crossover frequency must be set less than one fifth of the switching frequency, and the phase margin at crossover must be greater than 45 degrees. The general procedure outlined here meets these requirements without going into great detail about the theory of loop compensation.

First, calculate the output filter LC corner frequency using Equation 13:

Equation 13. TPS54110 equation10_lvs500.gif

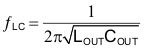
For the design example, ƒLC = 6103 Hz.

Choose a closed-loop crossover frequency greater than fLC and less than one fifth of the switching frequency. Also, keep the crossover frequency below 100 kHz, as the error amplifier may not provide the desired gain at higher frequencies. The 60-kHz crossover frequency chosen for this design provides comparatively wide loop bandwidth while still allowing adequate phase boost to ensure stability.

Next, the values for the compensation components that set the poles and zeros of the compensation network are calculated. Assuming an R1 value > than R5 and a C6 value > C7, the pole and zero locations are given by Equation 14 through Equation 17:

Equation 14. TPS54110 equation11_lvs500.gif
Equation 15. TPS54110 equation12_lvs500.gif
Equation 16. TPS54110 equation13_lvs500.gif
Equation 17. TPS54110 equation14_lvs500.gif

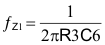
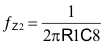
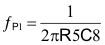
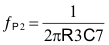
Additionally there is a pole at the origin, which has unity gain at a frequency:

Equation 18. TPS54110 equation15_lvs500.gif

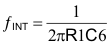
This pole is used to set the overall gain of the compensated error amplifier and determines the closed loop crossover frequency. Since R1 is given as 10 kΩ and the crossover frequency is selected as 60 kHz, the desired fINT is calculated from Equation 19:

Equation 19. TPS54110 equation16_lvs500.gif

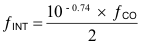
And the value for C6 is given by Equation 20:

Equation 20. TPS54110 equation17_lvs500.gif

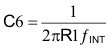
Since C6 is calculated to be 2900 pF, and the location of the integrator crossover frequency is important in setting the overall loop crossover, adjust the value of R1 so that C6 is a standard value of 2700 pF, using Equation 21:

Equation 21. TPS54110 equation18_lvs500.gif

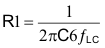
The value for R1 is 10.7 KΩ

The first zero, fZ1 is located at one half the output filter LC corner frequency, so R3 is calculated from:

Equation 22. TPS54110 equation19_lvs500.gif

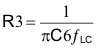
The second zero, fZ2 is located at the output filter LC corner frequency, so C8 is calculated from:

Equation 23. TPS54110 equation20_lvs500.gif

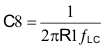
The first pole, fP1 is located to coincide with output filter ESR zero frequency. This frequency is given by:

Equation 24. TPS54110 equation21_lvs500.gif

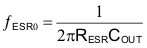
where

  • RESR is the equivalent series resistance of the output capacitor

In this case, the ESR zero frequency is 35.4 kHz, and R5 is calculated from:

Equation 25. TPS54110 equation22_lvs500.gif

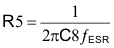
The final pole is placed at a frequency high enough above the closed-loop crossover frequency to avoid causing an excessive phase decrease at the crossover frequency while still providing enough attenuation so that there is little or no gain at the switching frequency. The fP2 pole location for this circuit is set to 4 times the closed-loop crossover frequency and the last compensation component value C7 is derived:

Equation 26. TPS54110 equation23_lvs500.gif

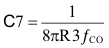
Finally, calculate the R2 resistor value for the output voltage of 3.3 V using Equation 27:

Equation 27. TPS54110 equation24_lvs500.gif

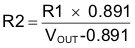
For this TPS54110 design, use R1 = 10.7 kΩ instead of 10.0 kΩ. R2 is then 3.92 kΩ.

Since capacitors are only available in a limited range of standard values, the nearest standard value was chosen for each capacitor. The measured closed-loop response for this design is shown in Figure 18.