SLVSFJ0B March   2021  – October 2021 TPS61379-Q1

PRODUCTION DATA  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
  4. 4 Revision History
  5. 5 Device Comparison Table
  6. 6 Pin Configuration and Functions
  7. 7 Specifications
    1. 7.1 Absolute Maximum Ratings
    2. 7.2 ESD Ratings
    3. 7.3 Recommended Operating Conditions
    4. 7.4 Thermal Information
    5. 7.5 Electrical Characteristics
    6. 7.6 Typical Characteristics
  8. 8 Detailed Description
    1. 8.1 Overview
    2. 8.2 Functional Block Diagrams
    3. 8.3 Feature Description
      1. 8.3.1  VCC Power Supply
      2. 8.3.2  Input Undervoltage Lockout (UVLO)
      3. 8.3.3  Enable and Soft Start
      4. 8.3.4  Shut Down
      5. 8.3.5  Switching Frequency Setting
      6. 8.3.6  Spread Spectrum Frequency Modulation
      7. 8.3.7  Bootstrap
      8. 8.3.8  Load Disconnect
      9. 8.3.9  MODE/SYNC Configuration
      10. 8.3.10 Overvoltage Protection (OVP)
      11. 8.3.11 Output Short Protection/Hiccup
      12. 8.3.12 Power-Good Indicator
      13. 8.3.13 Thermal Shutdown
    4. 8.4 Device Functional Modes
      1. 8.4.1 Forced PWM Mode
      2. 8.4.2 Auto PFM Mode
      3. 8.4.3 External Clock Synchronization
      4. 8.4.4 Down Mode
  9. 9 Application and Implementation
    1. 9.1 Application Information
    2. 9.2 Typical Application
      1. 9.2.1 Design Requirements
      2. 9.2.2 Detailed Design Procedure
        1. 9.2.2.1 Programming the Output Voltage
        2. 9.2.2.2 Setting the Switching Frequency
        3. 9.2.2.3 Selecting the Inductor
        4. 9.2.2.4 Selecting the Output Capacitors
        5. 9.2.2.5 Selecting the Input Capacitors
        6. 9.2.2.6 Loop Stability and Compensation
          1. 9.2.2.6.1 Small Signal Model
          2. 9.2.2.6.2 Loop Compensation Design Steps
          3. 9.2.2.6.3 Selecting the Bootstrap Capacitor
          4. 9.2.2.6.4 VCC Capacitor
      3. 9.2.3 Application Curves
  10. 10Power Supply Recommendations
  11. 11Layout
    1. 11.1 Layout Guidelines
    2. 11.2 Layout Example
  12. 12Device and Documentation Support
    1. 12.1 Device Support
      1. 12.1.1 Third-Party Products Disclaimer
    2. 12.2 Receiving Notification of Documentation Updates
    3. 12.3 Support Resources
    4. 12.4 Trademarks
    5. 12.5 Glossary
    6. 12.6 Electrostatic Discharge Caution
  13. 13Mechanical, Packaging, and Orderable Information

Package Options

Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9.2.2.6.2 Loop Compensation Design Steps

With the small signal models coming out, the next step is to calculate the compensation network parameters with the given inductor and output capacitance.

  1. Set the Cross Over Frequency, ƒC.

    The first step is to set the loop crossover frequency, ƒC. The higher crossover frequency, the faster the loop response is. It is generally accepted that the loop gain cross over no higher than the lower of either 1/10 of the switching frequency, ƒSW, or 1/5 of the RHPZ frequency, ƒRHPZ. Then calculate the loop compensation network values of RC, CC, and CP by the following equations.

  2. Set the Compensation Resistor, RC.

    By placing ƒZ below ƒC, for frequencies above ƒC, RC | | REA ~ = RC and so RC × GEA sets the compensation gain. Setting the compensation gain, KCOMP-dB, at ƒZ, results in the total loop gain, T(s) = KPS(s) × HEA(s) being zero at ƒC.

    Therefore, to approximate a single-pole roll-off up to fP2, rearrange Equation 17 to solve for RC so that the compensation gain, KEA, at fC is the negative of the gain, KPS, read at frequency fC for the power stage bode plot or more simply:

    Equation 21. GUID-E6C32B25-C615-4DC4-BB25-BBD662999974-low.gif

    where

    • KEA is gain of the error amplifier network
    • KPS is the gain of the power stage
    • GEA is the transconductance of the amplifier, the typical value of GEA = 70 µA / V
  3. Set the Compensation Zero capacitor, CC.

    Place the compensation zero at the power stage ROUT ,COUT pole’s position to get:

    Equation 22. GUID-32AC920D-A8C5-4C1F-80AB-B41865A5D7DA-low.gif

    Set ƒZ = ƒP, and get

    Equation 23. GUID-EF1E233C-77D9-4969-B7D9-8EBA5EC02026-low.gif

  4. Set the Compensation Pole Capacitor, CP.

    Place the compensation pole at the zero produced by the RESR and the COUT. It is useful for canceling unhelpful effects of the ESR zero.

    Equation 24.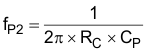 GUID-794743B5-26E7-4E7C-ADA1-26AA557CE64A-low.gif
    Equation 25. GUID-8F3DDFC3-66AB-4F98-9D0A-A16D5E2835D3-low.gif

    Set ƒP2 = ƒESR, and get

    Equation 26. GUID-BBDDE126-2F71-4EB2-BBF2-915D5BF4683A-low.gif