With large capacitive loads there are thermal considerations in the Smart High Side Switch during current limiting that must be considered. While the capacitor is charging, the Smart High Side Switch limits I_INRUSH by regulating the gate voltage of the MOSFET inside of the Smart High Side Switch.

Lets refer back to Equation 25 for charging a capacitor.

Equation 28.

For a regulated constant I_INRUSH, the capacitor needs to see a constant dV_CAP/dT . This means the voltage must linearly increase across the capacitor rather than the near instantaneous voltage increase that occurs with no current limiting. The voltage applied over the capacitor is V_CAP and is shown in Equation 20.

Equation 20.

With a constant V_SUPPLY, Equation 20 shows that if V_CAP increases linearly, V_DS must be the inverse of V_CAP and decrease linearly. Therefore, for a constant current capacitive charging the Smart High Side Switch V_DS will initially be equal to V_SUPPLY before dropping towards zero while V_CAP simultaneously increases to reach V_SUPPLY. Figure 3-11 shows this behavior with the TPS2H160-Q1 driving a large (470µF) capacitive load to 24V with a current limit of 500mA.

Figure 3-11 V_DS While Charging Capacitance

We see the Smart High Side Switch limiting the output current to 500mA as the OUT1 voltage over the capacitance linearly increases from 0V to 24V and the V_DS slowly decreases inversely from the supply voltage towards 0V.

During this charging period the power dissipation, P_DIS, in the Smart High Side Switch is calculated in Equation 21.

Equation 21.

The current is now limited and no longer unchecked inrush current so the equations will now consider I_LIM rather than I_INRUSH. Since I_LIM is constant and initially V_DS = V_SUPPLY, the peak power dissipation occurs at the beginning of the pulse and is given in Equation 22.

Equation 22.

When the capacitor is fully charged, V_DS ≈ 0 so P_DIS ≈ 0. For a first approximation this means that the average power dissipation during the charging period is given in Equation 23.

Equation 23.

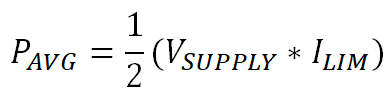
This average dissipation will occur for a period equal to the charging period which is calculated in Equation 24.

Equation 24.

In Figure 3-11 we see a peak power dissipation of 24V × 500mA = 12W, an average dissipation of 6W, and a charging time of 22.9ms. In order to have reliable operation the FET must be able to dissipate this heat over the charging time.

Lets look at what happens in Figure 3-12 when the current limit is increased to 1A.

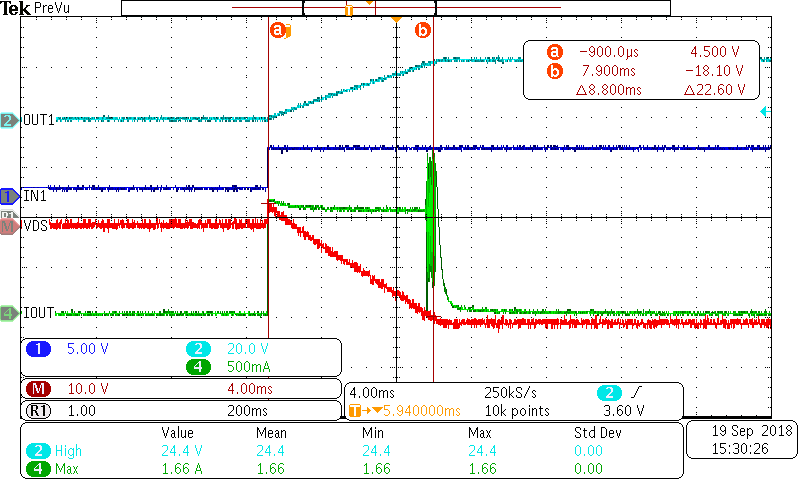Figure 3-12 TPS2H160-Q1 Charging at 1A

The peak power dissipation has increased to 24W and the average dissipation to 12W, however the charging time has decreased to 8.8 ms. A higher current limit equates to a higher peak power dissipation with a shorter pulse while a lower current limit equates to a low peak dissipation for a longer time.